Детерминанты матрицы: Онлайн калькулятор. Определитель матрицы. Детерминант матрицы

03. Определители (детерминанты)

Определение. Определителем Квадратной матрицы А= называется число, которое может быть вычислено по элементам матрицы по формуле:

det A = , где (1)

М1к – детерминант матрицы, полученной из исходной вычеркиванием первой строки и k – го столбца. Следует обратить внимание на то, что определители имеют только квадратные матрицы, т. е. матрицы, у которых число строк равно числу столбцов.

Формула (1) позволяет вычислить определитель матрицы по первой строке, также справедлива формула вычисления определителя по первому столбцу:

det A = (2)

Вообще говоря, определитель может вычисляться по любой строке или столбцу матрицы, т. е. справедлива формула:

detA = , i = 1,2,…,n. (3)

Очевидно, что различные матрицы могут иметь одинаковые определители.

Определитель единичной матрицы равен 1.

Для указанной матрицы А число М1к называется Дополнительным минором элемента матрицы a1k.

Таким образом, можно заключить, что каждый элемент матрицы имеет свой дополнительный минор. Дополнительные миноры существуют только в квадратных матрицах.

Определение. Дополнительный минор произвольного элемента квадратной матрицы aij равен определителю матрицы, полученной из исходной вычеркиванием i-ой строки и j-го столбца.

Свойство1. Важным свойством определителей является следующее соотношение:

det A = det AT;

Свойство 2. det ( A ± B) = det A ± det B.

Свойство 3. det (AB) = detA×detB

Свойство 4. Если в квадратной матрице поменять местами какие-либо две строки (или столбца), то определитель матрицы изменит знак, не изменившись по абсолютной величине.

Свойство 5. При умножении столбца (или строки) матрицы на число ее определитель умножается на это число.

Свойство 6. Если в матрице А строки или столбцы линейно зависимы, то ее определитель равен нулю.

Определение: Столбцы (строки) матрицы называются Линейно зависимыми, если существует их линейная комбинация, равная нулю, имеющая нетривиальные (не равные нулю) решения.

Свойство 7. Если матрица содержит нулевой столбец или нулевую строку, то ее определитель равен нулю. (Данное утверждение очевидно, т. к. считать определитель можно именно по нулевой строке или столбцу.)

Свойство 8. Определитель матрицы не изменится, если к элементам одной из его строк(столбца) прибавить(вычесть) элементы другой строки(столбца), умноженные на какое-либо число, не равное нулю.

Свойство 9. Если для элементов какой — либо строки или столбца матрицы верно соотношение: D = D1 ± D2

, E = E1 ± E2 , F = F1 ± F2 , То верно:

Пример. Вычислить определитель матрицы А =

= -5 + 18 + 6 = 19.

Пример:. Даны матрицы А = , В = . Найти det (AB).

1-й способ: det A = 4 – 6 = -2; det B = 15 – 2 = 13; det (AB) = det A ×det B = -26.

2- й способ: AB = , det (AB) = 7×18 — 8×19 = 126 –

– 152 = -26.

< Предыдущая		Следующая >

Детерминанты

Детерминанты

Главная » Аналитическая геометрия » Матрицы и системы линейных уравнений » Детерминанты

детерминант матрицыформула разложения детерминанта

Содержание

1. Определение детерминанта.

   Начать изучение

2. Единственность детерминанта.

   Начать изучение

3. Существование детерминанта. Разложение по столбцу.

   Начать изучение

4. Свойства детерминантов.

   Начать изучение

5. Формула полного разложения детерминанта.

   Начать изучение

 

Определение детерминанта.

Мы будем говорить, что на множестве квадратных матриц порядка n задана числовая функция, если каждой матрице из этого множества сопоставлено некоторое число. Примерами могут служить две часто употребляемые функции:

• след матрицы — функция, сопоставляющая каждой квадратной матрице сумму ее диагональных элементов a_{11}+…+a_{nn};
• евклидова норма матрицы — функция, сопоставляющая каждой матрице квадратный корень из суммы квадратов всех ее элементов.

Во многих вопросах необходимо уметь определить, вырождена данная матрица или нет. При этом полезна такая функция от матрицы, которая равна нулю для вырожденных матриц, отлична от нуля для невырожденных и при этом сравнительно просто вычисляется. Для матриц второго и третьего порядка такими функциями являются их детерминанты, уже известные нам.

Определение

Числовая функция f на множестве всех квадратных матриц порядка n называется детерминантом (или определителем) порядка n, а ее значение на матрице A — детерминантом A, если она обладает следующими тремя свойствами.

1. Какую бы строку матрицы мы ни взяли, функция является линейным однородным многочленом от элементов этой строки. Для i-й строки матрицы A это значит, что \tag{1} f(A)=h_{1}a_{i1}+h_{2}a_{i2}+…+h_{n}a_{in}, где h_{1},…, h_{n} — коэффициенты, не зависящие от элементов i-й строки a_{i1},…, a_{in}, но зависящие от остальных элементов матрицы.
2. Значение функции на любой вырожденной матрице равно нулю.
3. Значение функции на единичной матрице равно 1.

Детерминант матрицы A обозначается \mathbf{det}\,A или, если нужно выписать элементы матрицы, прямыми линиями по бокам матрицы.

Рекомендуем читателю проверить, что известные нам детерминанты второго и третьего порядков удовлетворяют приведенному определению.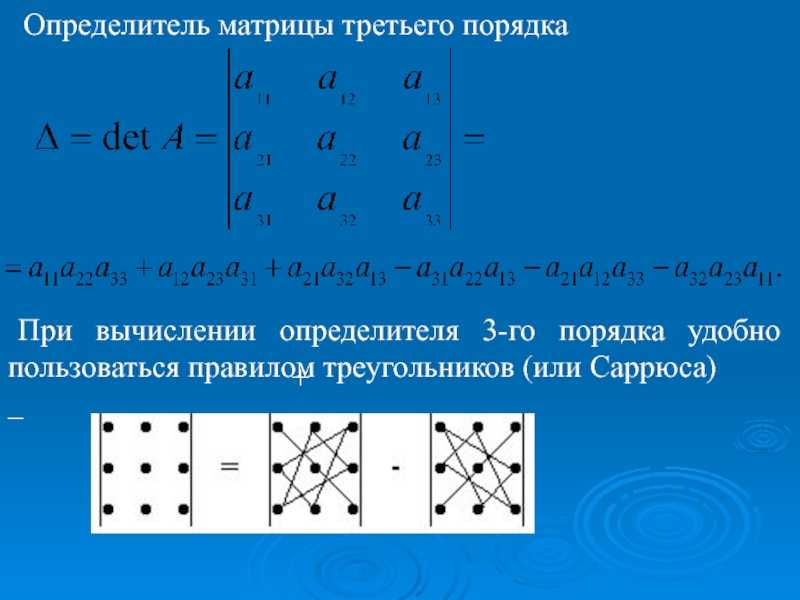 Для матрицы порядка 1, состоящей из одного элемента, детерминантом является этот элемент.

Когда определение состоит из условий, которым должен удовлетворять определяемый объект, заранее не ясно, выполнимы ли эти условия, то есть существует ли объект, им удовлетворяющий. Кроме того, если такой объект существует, то не ясно, однозначно ли он определен этими условиями. Ниже мы докажем существование и единственность детерминанта.

Мы докажем также, что для любой невырожденной матрицы детерминант отличен от нуля. Однако сначала необходимо изучить условия, определяющие детерминант.

Условие 1 выражает свойство линейности детерминанта по строке. Его равносильную формулировку дает следующее

Сформулированное в утверждении 1 свойство также называют свойством линейности по строке и часто формулируют в виде двух отдельных утверждений.

\bullet Множитель, общий для всех элементов строки, может быть вынесен за знак детерминанта.

\bullet Если какая-либо из строк матрицы A есть сумма двух строк, то \mathbf{det}\,A равен сумме детерминантов матриц, получаемых из A заменой этой строки на каждое из слагаемых.

Разумеется, если строка матрицы представлена как линейная комбинация \alpha_{1}\boldsymbol{p}_{1}+…+\alpha_{s}\boldsymbol{p}_{s} любого числа s строк, то
\tag{3}\mathbf{det}\,A=\alpha_{1} \mathbf{det}\,A_{1}+…+\alpha_{s} \mathbf{det}\,A_{s},
где A_{1},…, A_{s} — матрицы, получаемые из A заменой рассматриваемой строки соответственно на \boldsymbol{p}_{1},…, \boldsymbol{p}_{s}.

Свойство, выраженное утверждением 3, носит название антисимметрии детерминанта по строкам.

Единственность детерминанта.

Начнем с того, что с помощью известных нам свойств детерминанта вычислим детерминанты элементарных матриц.

Если матрица S_{1} получена из единичной умножением какой-либо строки на число \lambda \neq 0, то \mathbf{det}\,S_{1}=\lambda \mathbf{det}\,E=\lambda, согласно свойству линейности детерминанта по строке. Если матрица S_{2} получена из единичной матрицы прибавлением одной строки к другой, то из утверждения 2 видно, что \mathbf{det}\,S_{2}=\mathbf{det}\,E=1.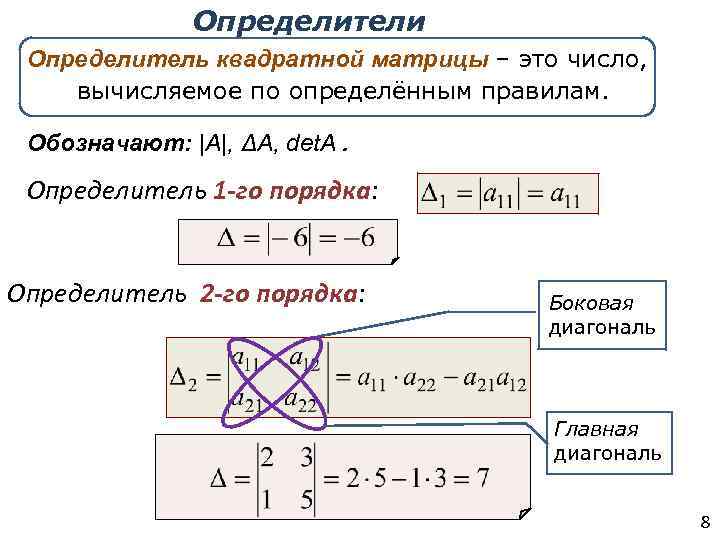 Таким образом, имеет место

Кроме того, легко проверить, что для любой матрицы A и любой элементарной матрицы S выполнено равенство \tag{4}\mathbf{det}\,(SA)=\mathbf{det}\,S \mathbf{det}\,A.
Действительно, достаточно вспомнить, что SA получается из A тем же элементарным преобразованием, что и S из E. Отсюда для матриц первого типа \mathbf{det}\,(S_{1}A)=\lambda \mathbf{det}\,A. Поскольку \mathbf{det}\,S_{1}=\lambda, равенство (4) справедливо. Точно так же, для матриц второго типа \mathbf{det}\,(S_{2}A)=\mathbf{det}\,A и \mathbf{det}\,S_{2}=1.

Теперь может быть доказана

Теорема 1.

На множестве квадратных матриц порядка n не может быть более одной функции, удовлетворяющей определению детерминанта.

Доказательство.

Пусть существуют две такие функции d_{1} и d_{2}. Докажем, что d_{1}(A)=d_{2}(A) для любой квадратной матрицы A. Если A — вырожденная матрица, то по определению d_{1}(A)=d_{2}(A)=0. Рассмотрим невырожденную матрицу A. По уже доказанному утверждению она может быть разложена в произведение элементарных матриц. Последовательно применяя формулу (4), мы получаем d_{1}(A)=d_{1}(S_{1}…S_{N})=d_{1}(S_{1})d_{1}(S_{2}…S_{N})=…=d_{1}(S_{1})…d_{1}(S_{N}). Аналогично, d_{2}(A)=d_{2}(S_{1})…d_{2}(S_{N}) Теперь из утверждения 5 следует d_{1}(A)=d_{2}(A), как и требовалось.

Вместе с доказательством теоремы, мы получили важную формулу: если невырожденная матрица A разложена в произведение элементарных матриц, то \tag{5} \mathbf{det}\,A=\mathbf{det}\,S_{1}…\mathbf{det}\,S_{N}.

Отметим, что детерминант элементарной матрицы либо равен числу \lambda \neq 0, либо равен единице, то есть в любом случае отличен от нуля. Из равенства (5) тогда следует

Следствие.

Для того чтобы матрица была вырожденной, необходимо и достаточно, чтобы ее детерминант был равен нулю.

Существование детерминанта. Разложение по столбцу.

Минором матрицы называется детерминант какой-либо ее квадратной подматрицы. В частности, вводится

Определение.

Пусть a_{ij} — элемент матрицы A порядка n, расположенный в i-й строке и j-м столбце. {k+j}d_{kj}.

Правая часть этой формулы — линейный многочлен от элементов j-ro столбца, следовательно, имеет место

Свойства детерминантов.

Используя формулу (8) разложения детерминанта по столбцу, мы можем найти коэффициенты в формуле (1).

Из утверждения 9 следует равноправность строк и столбцов. Именно, если справедливо какое-либо утверждение о детерминантах, касающееся строк матриц, то верно и аналогичное утверждение, касающееся столбцов, и обратно. Поэтому известные нам свойства детерминантов можно переформулировать для столбцов.

Если же матрица A порядка n вырождена, то \mathbf{Rg}\,A < n. Из доказанного нами ранее утверждения тогда следует \mathbf{Rg}\,AB < n. Значит, произведение AB также вырождено и \mathbf{det}\,AB равен нулю так же, как и \mathbf{det}\,A \mathbf{det}\,B.

Формула полного разложения детерминанта.

Здесь мы получим формулу полного разложения детерминанта порядка n, представляющую его как многочлен от элементов матрицы.

Введем предварительно некоторые определения. Мы будем называть

перестановкой чисел 1,…, n эти числа, написанные в каком-либо определенном порядке. Например, из чисел 1 и 2 образуются две перестановки: 1, 2 и 2, 1. Перестановку чисел 1,…, n обозначим i_{1},…, i_{n}.

Число i_{k} виновно в нарушении порядка в перестановке i_{1},…, i_{n}, если оно стоит левее меньшего числа: k < s, но i_{k} > i_{s} Например, при n-4 в перестановке 2, 4, 3, 1 числа 2 и 3 виновны каждое в одном нарушении порядка, а число 4 — в двух. Итак, общее число нарушений порядка в перестановке равно четырем. Число всех нарушений порядка в перестановке i_{1},…, i_{n} мы обозначим N(i_{1},…, i_{n}).

Перестановка называется четной, если N(i_{1},…, i_{n}) — четное число, и нечетной в противном случае.

Теорема.

Формула полного разложения детерминанта: \tag{10} \mathbf{det}\,\begin{Vmatrix}a_{11}&…& a_{1n}\\\cdots\\a_{n1}&…& a_{nn}\end{Vmatrix}=\sum_{(i_{1},.

{N(k,i_{1},…, i_{n-1})}a_{1k}a_{2i_{1}}a_{3i_{2}}…a_{ni_{n-1}}.

В правой части этого выражения собраны все те члены из суммы (10), которые соответствуют перестановкам, имеющим к на первом месте. В сумму (11) входят слагаемые для любого k, и потому сумма (11) содержит все члены суммы (10) и, конечно, не содержит никаких других членов. Этим формула полного разложения доказана.

Модуль 1: Детерминанты — исследование BCA

Введение и примеры

ОПРЕДЕЛЕНИЕ: Матрица определяется как упорядоченный прямоугольный массив чисел. Их можно использовать для представления систем линейных уравнений, как будет объяснено ниже.

Вот пример

Сложение и вычитание матриц

ОПРЕДЕЛЕНИЕ: Две матрицы A и B можно складывать или вычитать тогда и только тогда, когда их размеры одинаковы (т. е. обе матрицы имеют одинаковое количество строк и столбцов. Возьми:

Сложение

Если A и B выше матрицы одного типа, то сумма находится путем сложения соответствующих элементов a _ij  +  b _ij .

Вот пример сложения A и B вместе.

Вычитание

Если A и B матрицы одного типа, то вычитание находится путем вычитания соответствующих элементов a _ij  −  b _ij .

Вот пример вычитания матриц.

Умножение матриц

ОПРЕДЕЛЕНИЕ:  Если количество столбцов первой матрицы совпадает с количеством строк во второй матрице, можно выполнить умножение матриц.

Вот пример умножения двух матриц 2×2.

Вот пример умножения двух матриц 3×3.

Примечание. A×B не совпадает с B×A

Транспонирование матриц

ОПРЕДЕЛЕНИЕ: Транспонирование матрицы достигается заменой строк на столбцы, т. е. матрица A = (a _ij ), а транспонирование матрицы A равно:

A ^T  = (a _ji ), где j — номер столбца, а i — номер строки матрицы A.

Например, транспонирование матрицы будет:

В случае квадратной матрицы (m = n) транспонирование может использоваться для проверки симметричности матрицы. Для симметричной матрицы A = A ^T .

Определитель матрицы

ОПРЕДЕЛЕНИЕ:  Определители играют важную роль в нахождении обратной матрицы, а также в решении систем линейных уравнений. В дальнейшем мы предполагаем, что у нас есть квадратная матрица (m = n). Определитель матрицы A будем обозначать через det(A) или |A|. Сначала будет введен определитель матрицы 2 × 2 и 3 × 3, затем будет показан случай n × n.

Определитель матрицы 2×2

Предположим, что A является произвольной матрицей 2×2 A, где элементы заданы как:

тогда определитель этой матрицы будет следующим:

Определитель 3× 3 matrix

Определитель матрицы 3×3 немного сложнее и находится следующим образом (для этого случая предположим, что A — произвольная матрица 3×3 A, элементы которой приведены ниже).

, то определитель этой матрицы будет следующим:

Обратная матрица

ОПРЕДЕЛЕНИЕ:  Предполагая, что у нас есть квадратная матрица A, которая не является единственной (т. е. det(A) не равна нулю), тогда существует матрица n×n A ^-1 который называется обратным к A, так что выполняется это свойство:

AA ^-1  = A ^-1 A = I, где I — единичная матрица.

Обратная матрица 2×2

Возьмем, к примеру, произвольную матрицу 2×2 A, определитель которой (ad − bc) не равен нулю.

, где a,b,c,d – числа. Обратное значение:

Метод обратной матрицы

ОПРЕДЕЛЕНИЕ:  В методе обратной матрицы используется обратная матрица для решения системы уравнений, подобной приведенной выше. Ах = б. Предварительное умножение обеих частей этого уравнения на A ^-1 дает:

или, альтернативно,

Таким образом, вычислив обратную матрицу и умножив ее на вектор b, мы можем найти решение системы уравнений напрямую. А ранее мы обнаружили, что обратное значение равно 9.0007

Из вышеизложенного видно, что существование решения зависит от значения определителя A. Возможны три случая:

1. Если det(A) не равно нулю, то решения существуют с использованием 
2. Если det(A) равен нулю и b=0, то решение будет не единственным или не существует.
3. Если det(A) равно нулю и b=0, то решение может быть x = 0, но, как и в случае 2., оно не единственное или не существует.

Глядя на два уравнения, мы могли бы получить, что

Запись в матричной форме будет выглядеть как

, а путем перестановки мы получим, что решение будет выглядеть как

Ранг матрицы

Ранг матрицы с m строками и n столбцами есть число r  с следующие свойства:

• r меньше или равно наименьшему числу из m и n.
• r равно порядку наибольшего минора матрицы, отличного от 0.

Определение ранга матрицы

• Мы выбираем элемент матрицы, который не равен 0.
• Мы вычисляем миноры порядка 2, которые содержат этот элемент, пока не найдем минор, который не равен 0.
• Если каждый минор порядка 2 равен 0, то ранг матрицы равно 1.
• Если существует какой-либо минор порядка 2, который не равен 0, мы вычисляем минор порядка 3, который содержит предыдущий минор, пока не найдем минор, который не равен 0.
• Если каждый минор порядка 3 равен 0, тогда ранг матрицы равен 2.
• Если существует какой-либо минор порядка 3, отличный от 0, мы вычисляем минор порядка 4, пока не найдем минор порядка 4, не равный 0.
• Продолжаем так до тех пор, пока не получим миноры порядка, равного наименьшему числу из числа строк и числа столбцов.

Пример

Собственные значения и собственные векторы

Собственный вектор матрицы A — это вектор, представленный матрицей X такой, что при умножении X на матрицу A направление результирующей матрицы остается таким же, как у вектора X.

Математически приведенное выше утверждение может быть представлено как:

AX = λX

, где A — произвольная матрица, λ — собственные значения, а X — собственный вектор, соответствующий каждому собственному значению.

Здесь мы видим, что AX параллелен X. Итак, X — собственный вектор.

Метод нахождения собственных векторов и собственных значений любой квадратной матрицы A
Мы знаем, что

AX = λX

=> AX – λX = 0

             => (A – 0 λI. ) .(1)

Приведенное выше условие будет верным, только если (A – λI) сингулярно. значит

|А – λI| = 0 …..(2)

(2) называется характеристическим уравнением матрицы.
null

Корнями характеристического уравнения являются собственные значения матрицы A.

Теперь, чтобы найти собственные векторы, мы просто подставляем каждое собственное значение в (1) и решаем его методом исключения Гаусса, т. е. преобразуем расширенную матрицу (A – λI) = 0, чтобы сформировать эшелон строк и решить полученную линейную систему уравнений.

Некоторые важные свойства собственных значений

• Собственные значения вещественных симметричных и эрмитовых матриц вещественны
• Собственные значения вещественных кососимметричных и косоэрмитовых матриц либо чисто мнимы, либо равны нулю
• Собственные значения унитарных и ортогональных матриц имеют модуль единицы |λ| = 1
• Если λ _1, λ ₂ …….λ _n — собственные значения A, то kλ ₁ , kλ ₂ ……. kAeigen
• Если λ _1, λ ₂ …….λ _n — собственные значения A, тогда 1/λ ₁ , 1/λ ₂ …….1/λ _n — собственные значения A ^-1
• If λ _1, λ ₂ ……. 1. _N — это значения собственных значений A, затем λ ₁ ^K , λ ₂ ^K ……. Λ _N ^K …  – собственные значения A ^k
  null
• Собственные значения A = собственные значения A ^T  (транспонирование)
• Сумма собственных значений = след A (сумма диагональных элементов A)
• Произведение собственных значений = |A|
• Максимальное количество различных собственных значений A = размер A
• Если A и B две матрицы одного порядка, тогда собственные значения AB = собственные значения BA

Примечание – Собственные значения и собственные векторы квадратные матрицы.

Собственные векторы равны по определению ненулевым . Собственные значения могут быть равны нулю.

Нравится:

Нравится Загрузка…

3: Детерминанты — Математика LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

14516

• Кен Каттлер
• Университет Бригама Янга через Lyryx

• 3.1: Основные методы

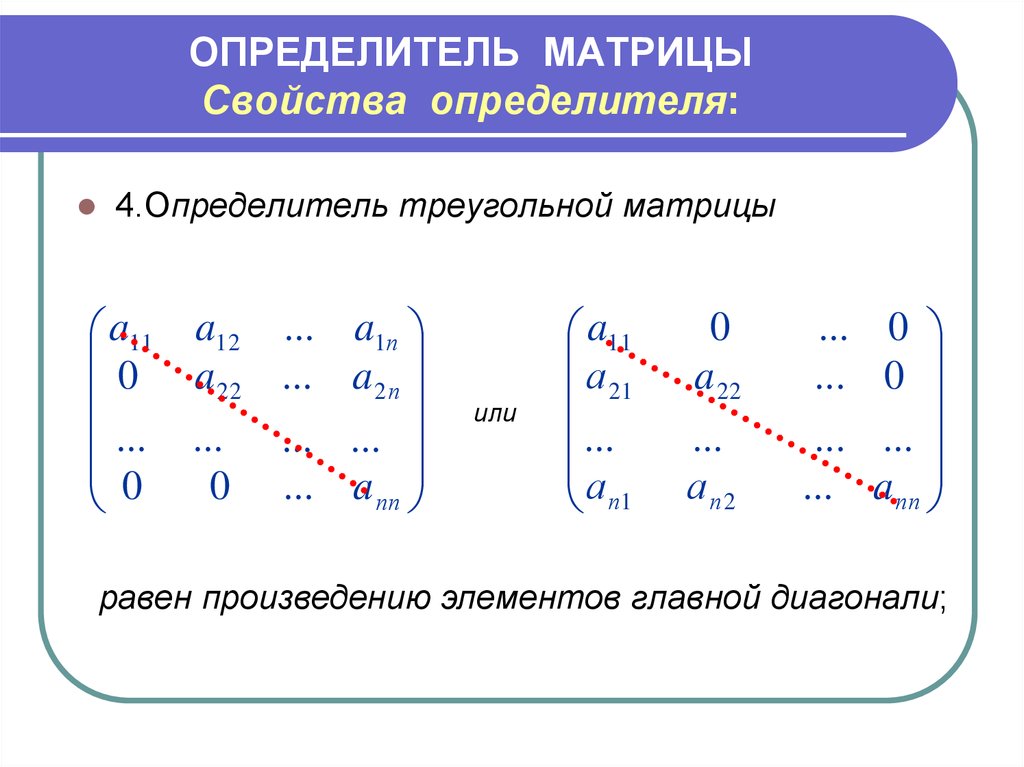
  Пусть A — матрица размера n × n. То есть пусть A — квадратная матрица. Определитель A, обозначаемый det(A), является очень важным числом, которое мы будем исследовать в этом разделе.

• 3. 2: Свойства определителей

  У определителей много важных свойств. Поскольку многие из этих свойств связаны с операциями со строками, которые обсуждались в главе 1, мы сейчас вспомним это определение. Теперь рассмотрим влияние операций над строками на определитель матрицы. В следующих разделах мы увидим, что использование следующих свойств может сильно помочь в поиске определителей. В этом разделе теоремы будут использоваться в качестве мотивации для предоставления различных примеров полезности свойств.

• 3.3: Поиск определителей с помощью операций со строками

  В этом разделе мы рассмотрим два примера, где операции со строками используются для нахождения определителя большой матрицы.

• 3.4: Применение определителя

  Определитель матрицы также позволяет найти обратную матрицу.

• 3.E: Упражнения

---

контент, отредактированный в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.