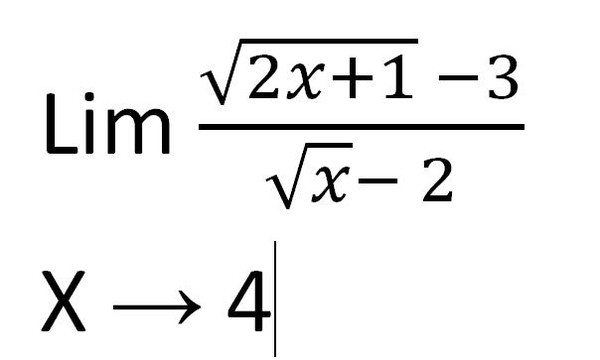Для этого примера вы получите подробное решение:
Возьмём предел
::
__________ _________
/ 2 / 2
lim \/ x + 2*x - \/ -3 + x
x->oo
Устраним неопределённость oo - oo
Домножим и разделим на
::
_________ __________
/ 2 / 2
\/ -3 + x + \/ x + 2*x
тогда
::
__________ _________
/ 2 / 2
lim \/ x + 2*x - \/ -3 + x =
x->oo
::
/ __________ _________\ / _________ __________\
| / 2 / 2 | | / 2 / 2 |
\\/ x + 2*x - \/ -3 + x /*\\/ -3 + x + \/ x + 2*x /
lim ------------------------------------------------------------- =
x->oo _________ __________
/ 2 / 2
\/ -3 + x + \/ x + 2*x
::
2 2
__________ _________
/ 2 / 2
\/ x + 2*x - \/ -3 + x
lim ------------------------------ =
x->oo _________ __________
/ 2 / 2
\/ -3 + x + \/ x + 2*x
::
2 2
x + 2*x + 3 - x
lim ----------------------------
x->oo _________ __________ =
/ 2 / 2
\/ -3 + x + \/ x + 2*x
::
3 + 2*x
lim ----------------------------
x->oo _________ __________
/ 2 / 2
\/ -3 + x + \/ x + 2*x
Разделим числитель и знаменатель на x:
::
3
2 + -
x
lim ----------------------------
x->oo _________ __________ =
/ 2 / 2
\/ -3 + x \/ x + 2*x
------------ + -------------
x x
::
3
2 + -
x
lim ----------------------------------
x->oo _________ __________
/ 2 / 2 =
/ -3 + x / x + 2*x
/ ------- + / --------
/ 2 / 2
\/ x \/ x
::
3
2 + -
x
lim ---------------------------
x->oo ________ _______
/ 3 / 2
/ 1 - -- + / 1 + -
/ 2 \/ x
\/ x
Сделаем замену
::
1
u = -
x
тогда
::
3
2 + -
x
lim ---------------------------
x->oo ________ _______ =
/ 3 / 2
/ 1 - -- + / 1 + -
/ 2 \/ x
\/ x
::
2 + 3*u
lim ---------------------------
u->0+ __________ =
/ 2 _________
\/ 1 - 3*u + \/ 1 + 2*u
::
2 + 3*0
--------------------------- = 1
= __________
/ 2 _________
\/ 1 - 3*0 + \/ 1 + 2*0
Получаем окончательный ответ:
::
__________ _________
/ 2 / 2
lim \/ x + 2*x - \/ -3 + x = 1
x->oo
Для случая, когда корень находится в числителе или знаменателе дроби, то, к примеру, введите так:
(sqrt(x + 1) — sqrt(2*x — 2))/(x — 3)
Не забудьте указать к чему стремится переменная x.
Для указанного примера Вы также получите подробное решение, но с применением правила Лопиталя.
Ещё раз приводим ссылку на калькулятор:
>> решение пределов функций <<
Как решать пределы с корнями с примерами решения
Содержание:
- Примеры с решением
- Раскрытие неопределенностей вида
При вычислении предела вначале проверяют принадлежит ли точка области определения. Если то предел равен значению функции в точке
(это объясняется непрерывностью элементарной функции на своей области определения)
По этой ссылке вы найдёте полный курс лекций по высшей математике:
| Высшая математика: лекции, формулы, теоремы, примеры задач с решением |
Примеры с решением
Пример 1:
Вычислить:
a)
б)
в)
Решение:
а)
б)
в)
Правило сохраняет силу, если Запись например, означает, что когда абсолютное значение
неограниченно возрастает, функция стремится к нулю (это ясно из графика функции).
Возможно вам будут полезны данные страницы:
Как решать пределы: пример решения |
Пределы для чайников |
Уравнение прямой в пространстве |
Метод вариации произвольных постоянных |
Пример 2:
Найти:
а)
б)
в)
Решение:
а)
б)
в)
Пример 3:
Найти
Решение:
При подстановке в значение функции вместосимвола бесконечности, результат может оказаться не конечным числом. Например:
Что считать ответом в этом случае?
При вычислении подобных пределов пользуются одним из следующих правил (в приводимых ниже формулах с означает число):
Приведенные формулы следуют из соображений здравого смысла.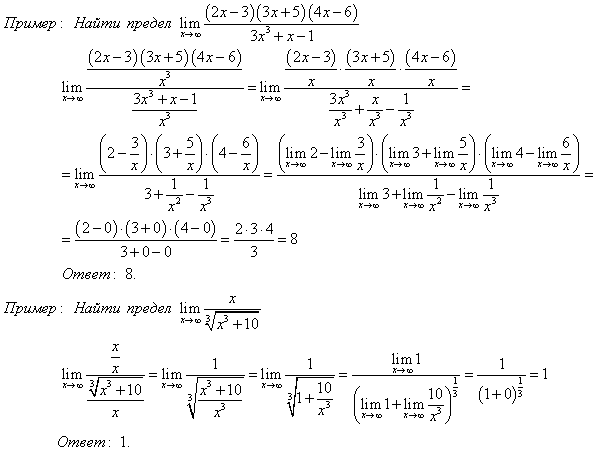
Например, первая из приведенных формул по существу утверждает, что если одна из функций становится очень большой и положительной, а другая ограничена, то сумма их становится очень большой и положительной.
Те же соображения приводят и к формальному доказательству: надо только вместо «очень больших» значений говорить о «больших любого заданного числа».
Применим эти правила для вычисления пределов, которые были оставлены без вычисления:
Соображениями здравого смысла руководствуются и при вычислении пределов от функций при Надо проследить ио графику функции куда стремится значение функции, если аргумент стремится к
Пример 4:
Вычислить:
а)
б)
в)
Решение:
а) При знаменатель неограниченно растет, т.е. является величиной бесконечно большой, а обратная величина бесконечно малой. Произведение бесконечно малой на ограниченную величину (постоянная — частный случай ограниченной еличины) есть величина бесконечно малая, и предел ее при равен нулю.
Следовательно,
Этот же ответ получается при применении последнего из приведенных выше правил
б)
в)
Приведенные рассуждения не являются строгими. Однако они вполне достаточны для приложений и интуитивно понятны . Как уже было отмечено ранее, выражение при можно считать равным
Выражение взято в скобки, чтобы подчеркнуть условность записи.
Пример 5:
Найти:
а)
б)
в)
Решение:
а)
б)
в)
Имеются случаи, не охватываемые правилами из предыдущего параграфа. Не существует «общей формулы» для выражения . В самом деле, пусть где —целое число. Частное этих функций. при является частным бесконечно малых. Оно может стремиться к нулю (при), или (при ), или (при ). Поэтому выражение и подобные ему называются неопределенностями.
К неопределенностям относятся следующие выражения:
Как для случая неопределенности вида встретившейся при сравнении бесконечно малых, здесь для раскрытия неопределенности уже недостаточно знать лишь пределы функций и а нужно учесть и закон их изменения. Примеры раскрытия неопределенностей приведены ниже.
Пример 6:
Найти
Решение:
Непосредственной подстановкой вместо аргумента его предельного значения вычислить предел нельзя, поскольку получается неопределенность вида
Разложим числитель и знаменатель на множители, чтобы сократить дробь на общий множитель, стремящийся к нулю. Нужно иметь в виду, что здесь не производится сокращение на нуль, что недопустимо. По определению предела функции аргумент стремится к своему предельному значению, никогда не принимая этого значения (вспомним, что в определении предела по Коши оэтому до перехода к пределу можно произвести сокращение на множитель, стремящийся к нулю. Имеем:
Пример 7:
Найти
Решение:
Пределы числителя и знаменателя при равны нулю
Разложим квадратный трехчлен в числителе на линейные множители по формуле где и — корни трехчлена.
Разложив на множители и знаменатель, сократим на получим
Пример 8:
Найти
Решение:
и
Пример 9:
Найти
Решение:
Пределы числителя и знаменателя при равны нулю. Умножим числитель и знаменатель на сопряженный знаменателю множитель и затем, сократив дробь на получим:
Пример 10:
Найти
Решение:
Когда числитель и знаменатель дроби стремятся к нулю, получается неопределенность вида Желая избавится от иррациональности в знаменателе, преобразуем данное выражение:
Перейдя к пределу, получим
В предыдущих примерах неопределенность вида раскрывалась путем выделения в числителе и знаменателе общего множителя. Однако этот прием «срабатывает» не во всех случаях. Например, в случае предела неясно, как выделить общий множитель. Этот предел можно вычислить с помощью принципа замены эквивалентных. Вычислим этот предел другим способом — сведением к пределу
называемому 300 лет назад первым замечательным пределом.
Доказательство равенства нетрудно и опирается оно не приводится.
Заметим, что выражение взято в скобки, поскольку писать нельзя! Скобки в записи подчеркивают ее условность. Равенство означает, что в данном конкретном случае неопределенность раскрыта и значение соответствующего предела равно единице.
Пример 11:
Найти
Решение:
Пример 12:
Найти
Решение:
Пример 13:
Найти
Решение:
При числитель и знаменатель — величины бесконечно большие. Поэтому при непосредственной подстановке символа вместо получаем выражение которое представляет собой неопределенность. Для вычисления предела этой функции нужно и числитель и знаменатель разделить на (наивысшую степень аргумента в знаменателе):
Пример 14:
Найти
Решение:
При непосредственной подстановке символа вместо получаем неопределенность вида Для вычисления предела этой функции нужно и числитель и знаменатель разделить на (наивысшую степень аргумента в знаменателе):
(при слагаемые — величины бесконечно малые и, следовательно, их пределы равны нулю).
Пример 14:
Наити
Решение:
Вообще, предел отношения полиномов при равен отношению коэффициентов при старших членах, если степени числителя и знаменателя одинаковы, и равен нулю или бесконечности, если степень числителя соответственно меньше или больше знаменателя.
Пример 15:
Найти
Решение:
Пример 16:
Найти
Решение:
В подобных примерах полезно иметь в виду, что функция где — многочлен степени стремится к бесконечности так же, как и функция Это позволяет выделить высшую степень входящую в данное выражение, и разделить числитель и знаменатель на эту степень В данном примере надо делить на
Неопределенности вида и путем преобразования можно привести к неопределенности вида или которая раскрывается уже известными способами.
Покажем на примерах, как находятся такие пределы.
Пример 17:
Найти
Решение:
Произведем вычитание дробей, получим
Пример 18:
Найти
Решение:
Пример 19:
Найти
Решение:
(сделали замену ).
Пример 20:
Найти
Ответ:
Раскрытие неопределенностей вида
Рассмотрим последовательность где
Может показаться, что неограниченное возрастание показателя степени должно повлечь неограниченное возрастание целочисленной функции Но рост показателя компенсируется тем, что основание стремится к В результате последовательность оказывается возрастающей и ограниченной. А всякая ограниченная и возрастающая последовательность имеет конечный предел. Предел, к торому стремится при обозначается
Обозначением числа и его широким применением во многих вопросах математики мы обязаны Эйлеру. Это число иррационально и с точностью до шестой значащей цифры равно
Функция имеет пределом число не только при целочисленных значениях но и тогда, когда стремится к бесконечности, пробегая числовую прямую непрерывно. Более того, аргументможет принимать как положительные, так и отрицательные значения, лишь бы неограниченно росло по абсолютному значению.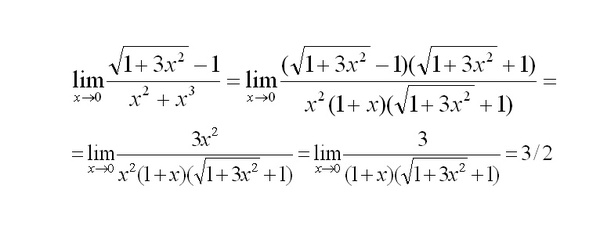
Чтобы отмстить это обстоятельство, заменим букву буквой и напишем:
или короче
Этот предел часто используется в математике для раскрытия неопределенности и именуется вторым замечательным пределом
Пример 21:
Найти пределы:
а)
б)
Решение:
а)
б)
Пример 22:
Найти пределы
а)
б)
Решение:
а) При основание степени стремится к единице, а показатель стремится к бесконечности. Следовательно, имеем неопределенность вида Представим основание в виде суммы единицы и некоторой бесконечно малой величины:
тогда
б)
Число во многих случаях выгодно брать за основание логарифмов. Логарифм от с основанием носит название натурального логарифма и обозначается Показательная функция широко используется в науке и называется экспоненциальной.
Другое обозначение этой функции —
Неопределенности вида и можно свести к неопределенности вида следующим образом:
Математическое исчисление — Решение пределов с квадратными корнями
Задавать вопрос
спросил
Изменено 7 лет, 9 месяцев назад
Просмотрено 49 тысяч раз
$\begingroup$ 92+11} — 6}{y} = \frac{\frac{5}{6}y+ o(y)}{y} = \frac{5}{6} + o(1) \xrightarrow[y\ до 0]{} \frac{5}{6}.$$
$\endgroup$
исчисление — Пределы функций с квадратными корнями в знаменателе
Задавать вопрос
спросил
Изменено 6 лет, 11 месяцев назад
Просмотрено 19 тысяч раз
$\begingroup$
Для приведенной ниже функции покажите, что $\displaystyle\lim_{x \to -2} f(x) = 4$, и обоснуйте свой ответ.
(без использования правила Лопиталя).
$$f(x)= \dfrac{x+2}{\sqrt{6+x}-2}$$
Моя попытка состоит в следующем:
Так как $f(x)$ определено, когда $6 +x>0$, т.е. пока $x>-6$, функция определена в окрестности $-2$ и предел действительно существует и можно продолжать…
(я не знаю, каким методом можно доказать этот предел, когда у нас есть квадратный корень). Какой подход вы бы использовали, чтобы показать это?
- исчисление
- реальный анализ
- пределы
$\endgroup$
1
$\begingroup$
Обычный способ работы с квадратным корнем — замена переменной: поскольку квадратный корень выглядит раздражающим, мы можем установить его как новую переменную $t$, тем самым исключая квадратный корень — этот принцип также может быть полезен при интегрировании проблемы. Для этой задачи, если положить $t = \sqrt{x + 6}$, то $x = t^2 — 6$, а поскольку $x \to -2$, $t \to 2$.
$\endgroup$
$\begingroup$
Подсказка Один из вариантов — распознать $\frac{1}{f(x)}$ как разностное частное для конкретной функции в конкретной точке и использовать определение производной.
Второй вариант — умножить и числитель, и знаменатель на , сопряженное знаменателя, а именно $\sqrt{6 + x} + 2$, а затем упростить.
$\endgroup$
$\begingroup$
Уверен, что умножение на сопряженное число знаменателя делает задачу простой, когда требуется только предел.
Ради вашего любопытства позвольте мне показать вам еще один метод, который позволит решить проблему довольно простым способом.
Сначала измените $x=y-2$ $$f= \dfrac{x+2}{\sqrt{6+x}-2}=\dfrac{y}{\sqrt{4+y}-2 }=\frac12\dfrac{y}{\sqrt{1+\frac y4}-1}$$ Теперь рассмотрим ряд Тейлора $$\sqrt{1+z}=1+\frac{z}{2} -\frac{z^2}{8}+O\left(z^3\right)$$ и замените $z$ на $\frac y4$.