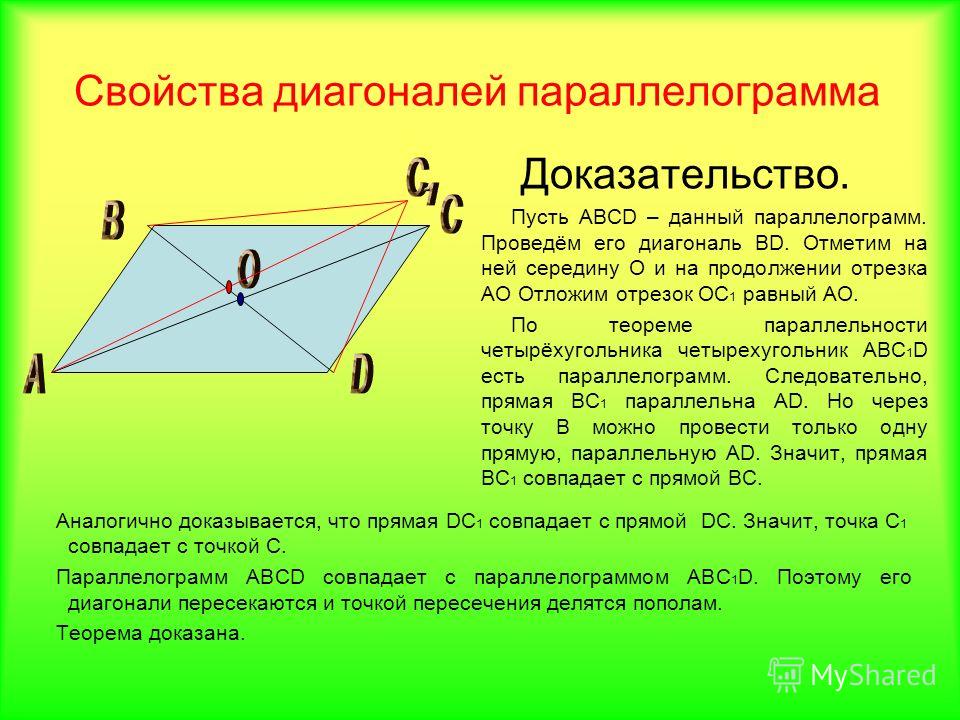
Параллелограмм и его свойства. Площадь параллелограмма. Биссектрисы углов параллелограмма
Параллелограмм — это четырехугольник, имеющий две пары параллельных сторон. Свойства параллелограмма:
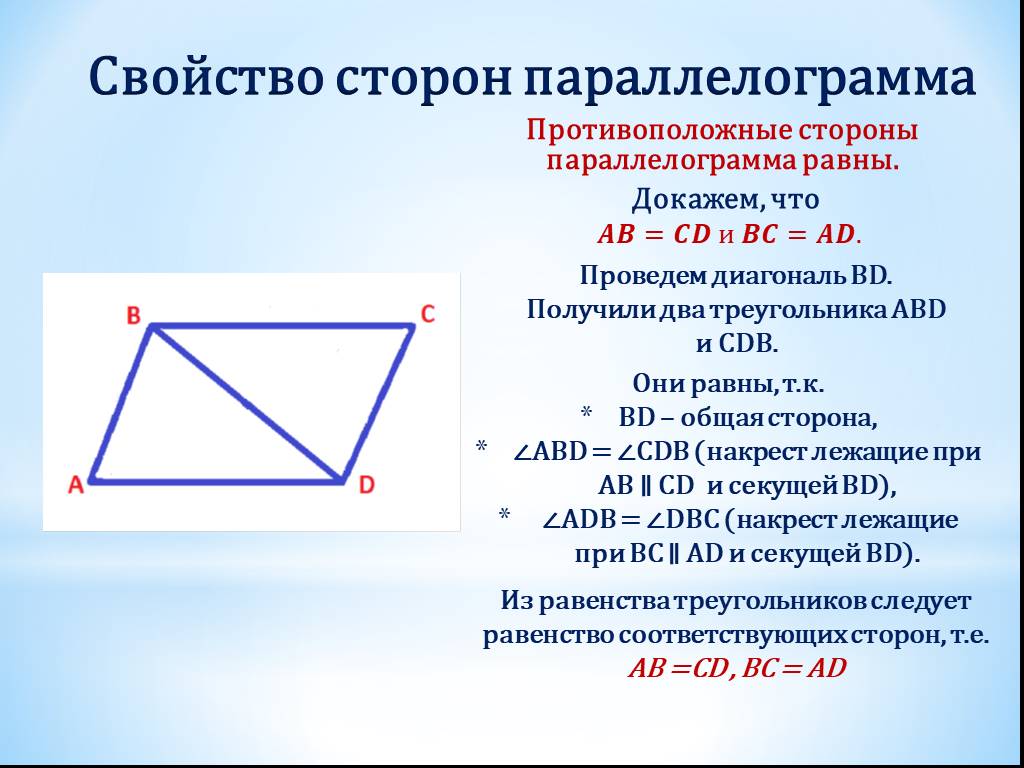
Противоположные стороны параллелограмма равны.
Противоположные углы параллелограмма равны.
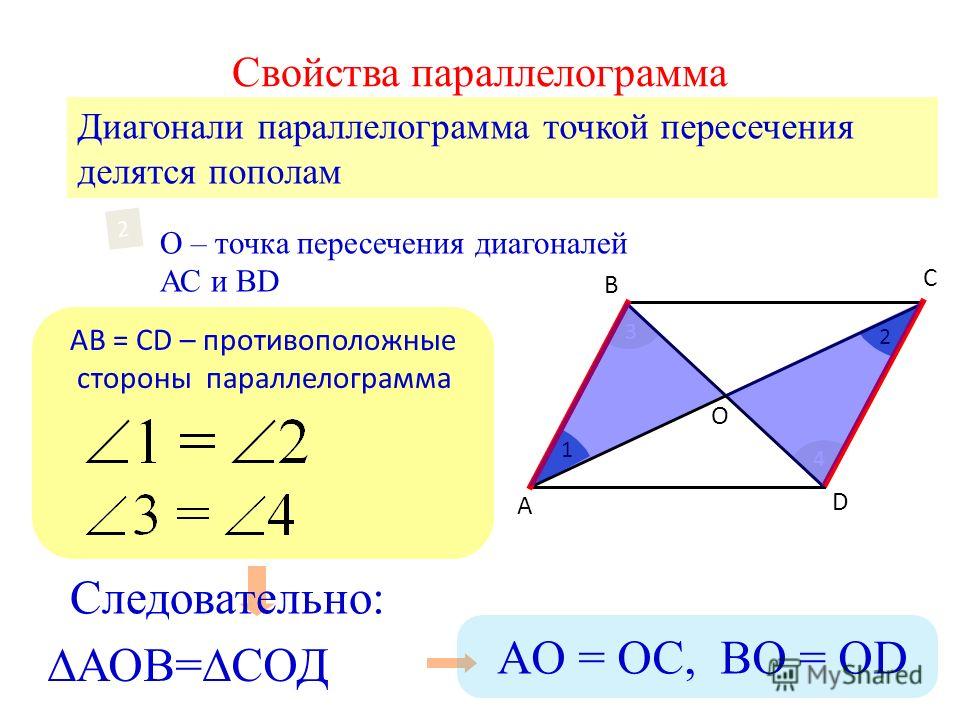
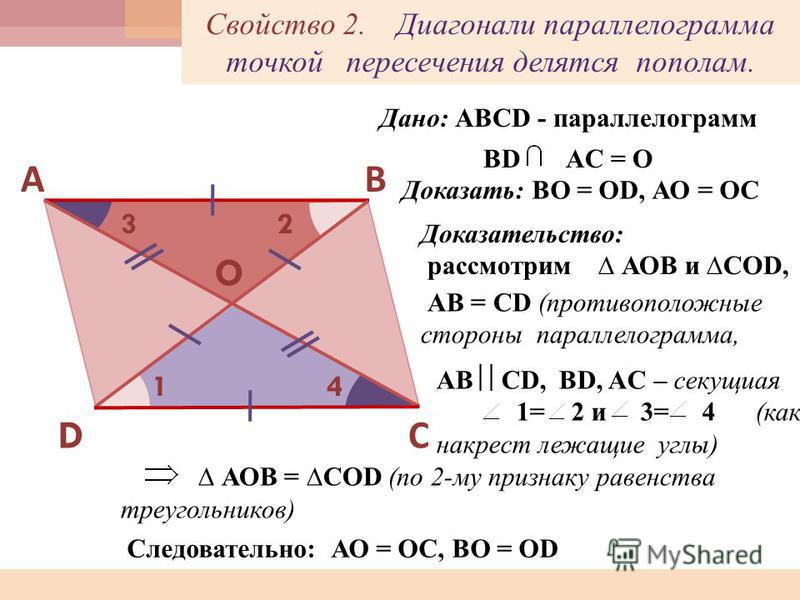
Диагонали параллелограмма в точке пересечения делятся пополам.
Давайте посмотрим, как свойства параллелограмма применяются в решении задач ЕГЭ.
1. Найдите угол между биссектрисами углов параллелограмма, прилежащих к одной стороне. Ответ дайте в градусах.
Пусть ВМ и СК — биссектрисы углов параллелограмма, прилежащих к стороне ВС. Сумма углов АВС и BCD равна 180°. Углы ОВС и ОСВ — половинки углов АВС и ВСD. Значит, сумма углов АВС и ВСD равна 90 градусов. Из треугольника ВОС находим, что угол ВОС — прямой. Ответ: 90.
Биссектрисы
углов параллелограмма, прилежащих
к одной стороне, — перпендикулярны.
Легко доказывается и другое свойство биссектрис параллелограмма:
Биссектрисы противоположных углов параллелограмма — параллельны.
2. Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна 5. Найдите его большую сторону.
Найдем на этом рисунке накрест лежащие углы. Мы уже рассказывали, что это такое.
Углы СВЕ и ВЕА, а также СЕD и ВСЕ — накрест лежащие. Накрест лежащие углы равны. Значит, угол СВЕ равен углу ВЕА, а угол СЕD — углу ВСЕ. Получаем, что треугольники АВС и CDE — равнобедренные, то есть АЕ = АВ, а DЕ = CD. Тогда AD = 5 + 5 = 10.
Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник.
Запишем формулы площади параллелограмма:
S = ah, где а — основание параллелограмма, h — его высота. S = ab sin φ, где а и b — стороны параллелограмма, φ — угол между ними.
И еще
одна формула.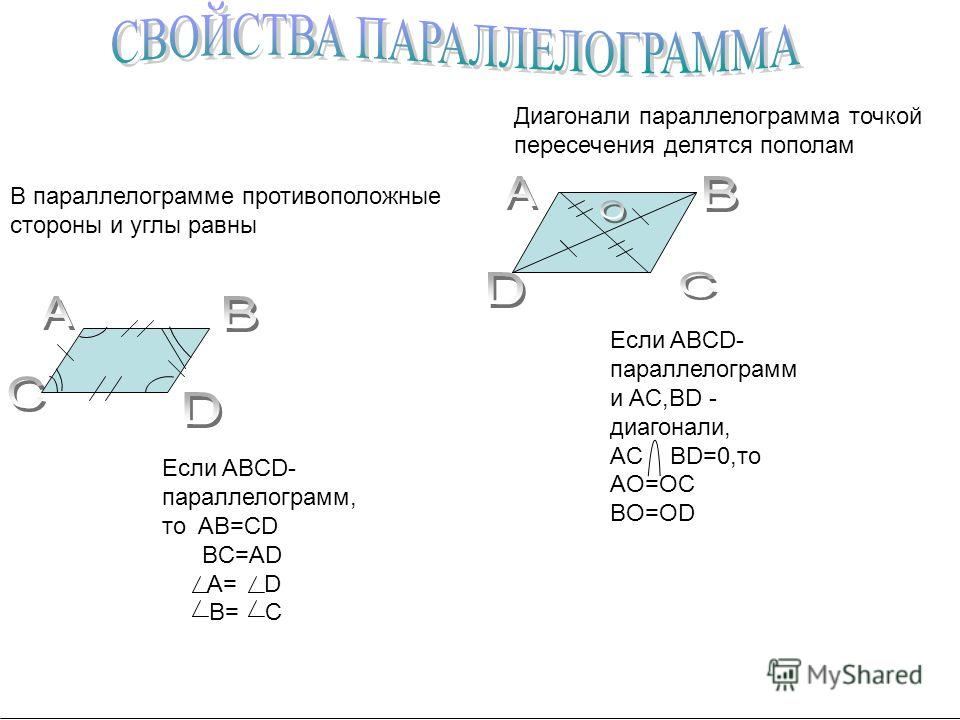
S = d1 d2 sin α, где d1 и d2 — диагонали параллелограмма, α — угол между ними.
Прямоугольник и его свойства
Прямоугольник — это параллелограмм, у которого все углы прямые.
Диагонали прямоугольника равны.
1. В прямоугольнике диагональ делит угол в отношении 1:2, меньшая его сторона равна 6. Найдите диагональ данного прямоугольника.
Всё просто. Рассмотрите прямоугольный треугольник АВС. Найдите, чему равен угол САВ и его синус, а затем найдите АС.
Ответ: 12.
А сейчас рассмотрим еще одну задачу, в которой применяются свойства диагоналей прямоугольника.
2. Острые углы прямоугольного треугольника равны 24° и 66°. Найдите угол между высотой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.
Казалось бы,
при чем здесь прямоугольник? Дан
прямоугольный треугольник, из вершины
прямого угла проведены высота и медиана.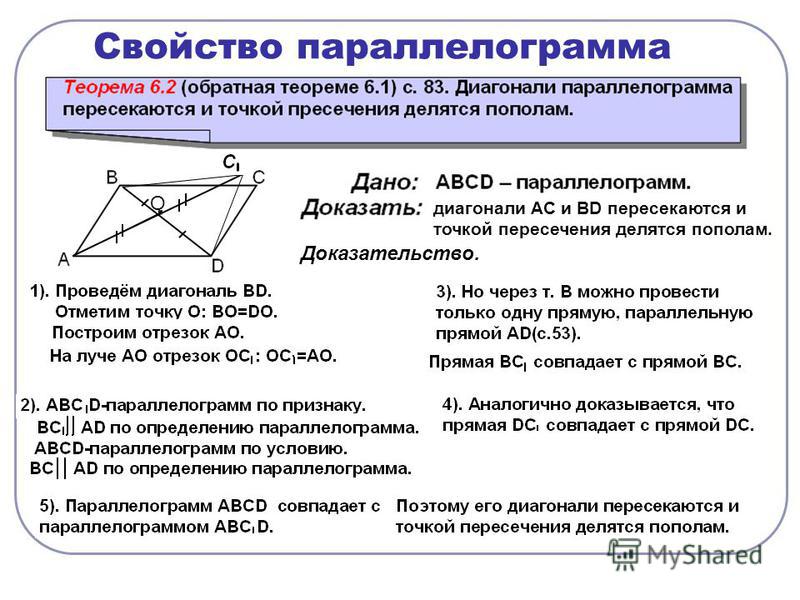 А что можно сказать о длине этой
медианы?
А что можно сказать о длине этой
медианы?
Давайте достроим чертеж до прямоугольника. Поскольку диагонали прямоугольника равны (это свойство прямоугольника) и делятся пополам в точке пересечения, отрезки СМ, ВМ и АМ тоже будут равны. Каждый из них равен половине диагонали прямоугольника. Мы доказали теорему:
В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.
Итак, ВМ = СМ, значит, треугольник ВМС равнобедренный, и угол ВСМ равен 24°.
По свойству высоты, проведенной из вершины прямого угла, ∠АСН = ∠АВС = 24°.
Тогда угол МСН (между медианой и высотой треугольника АВС) равен 90° — 24° — 24° = 42°. Ответ: 42.
Как вы думаете, где находится центр окружности, описанной вокруг прямоугольного треугольника? Ведь центр описанной окружности — точка, равноудаленная от всех вершин треугольника. Очевидно, эта точка — середина гипотенузы.
В прямоугольном
треугольнике центром описанной окружности
является середина гипотенузы.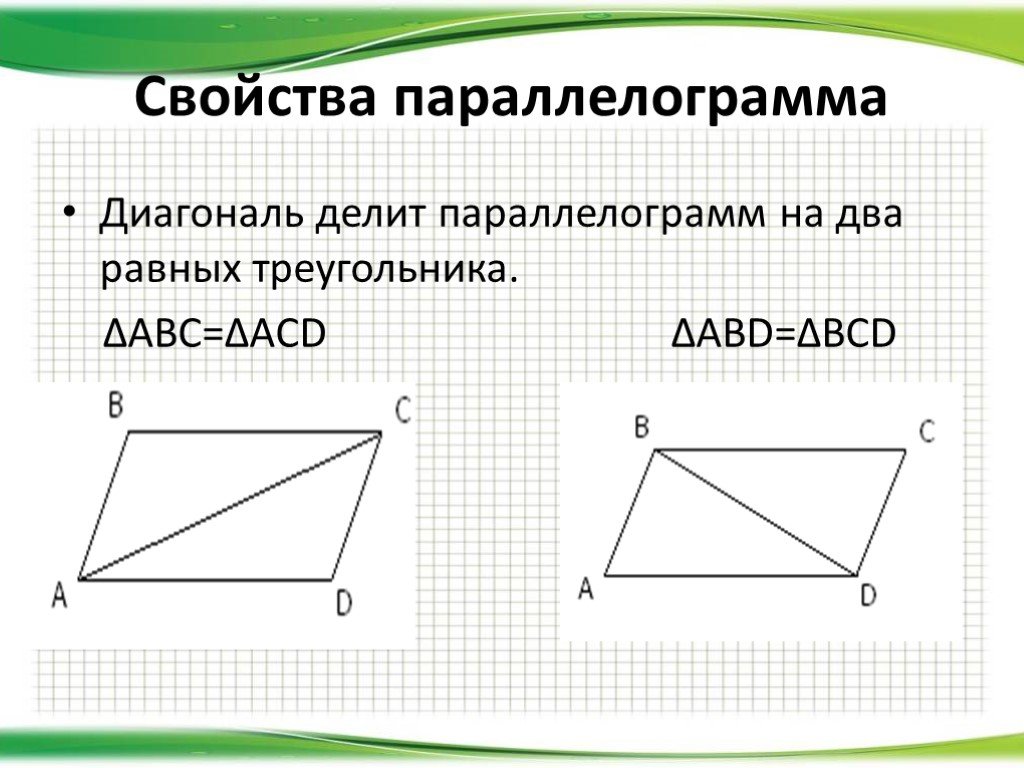
1. Найдите диагональ прямоугольника, вписанного в окружность, радиус которой равен 5.
Проведем диагональ АС. Получим, что АС равна 2R. Ответ: 10.
Ромб и его свойства
По определению, ромб — это параллелограмм, все стороны которого равны.
Свойства ромба:
Диагонали ромба перпендикулярны.
Диагонали ромба делят его углы пополам.
Воспользуемся свойствами ромба для решения задач.
1. Найдите меньшую диагональ ромба, стороны которого равны 2, а острый угол равен 60°.
Проведите меньшую диагональ ромба и рассмотрите треугольник ADB. Поскольку AD = DB, а угол DAB равен 60°, треугольник ADB — равносторонний. Следовательно, меньшая диагональ ромба равна 2.
1. Найдите высоту ромба, сторона которого равна v3, а острый угол равен 60?.
Один
из подходов к решению задач
по геометрии — метод площадей.
Он состоит в том, что площадь фигуры
выражается двумя разными способами,
а затем из полученного уравнения
находится неизвестная величина.
Пусть а — сторона ромба. Тогда
S = a2 sin 60° = ah,
Отсюда .
2. Диагонали ромба относятся как 3:4. Периметр ромба равен 200. Найдите высоту ромба.
Пусть диагонали ромба равны 6х и 8х. Диагонали ромба перпендикулярны, значит, треугольник АОВ — прямоугольный. По теореме Пифагора АВ2 = АО2 + ОВ 2 АВ2 = 9×2 + 16×2, АВ2 = 25×2, Отсюда АВ = 5х. Поскольку периметр равен 200, 5х · 4 = 200 х = 10, АВ = 50, а диагонали ромба равны 60 и 80.
Нам надо найти высоту ромба. Давайте запишем, чему равна площадь ромба. С одной стороны, S = ah. С другой стороны, площадь ромба складывается из площадей двух равных треугольников АВС и ADC, то есть равна 60 · 40 = 2400. Отсюда h = S : a = 2400 : 50 = 48.
Ответ: 48.
Квадрат — определение и свойства
Квадрат —
это прямоугольник, у которого все
стороны равны.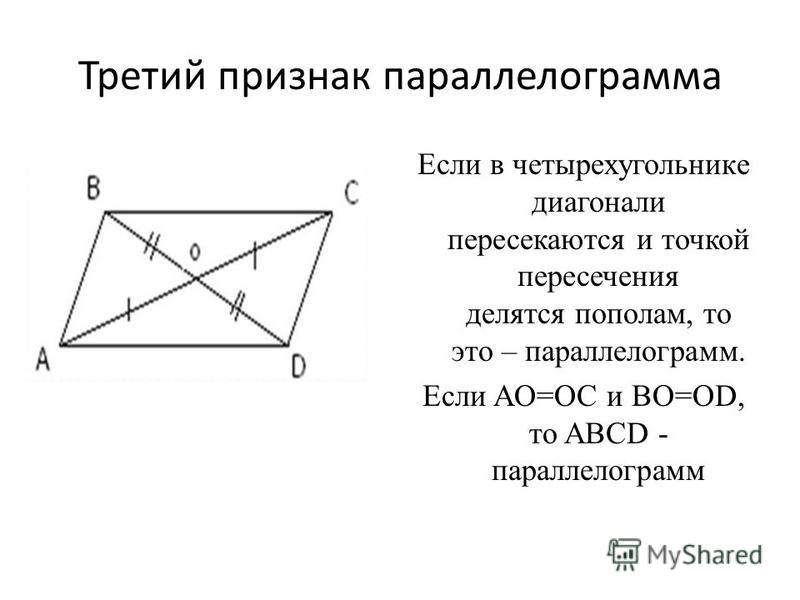 Можно дать и другое определение
квадрата: квадрат —
это ромб, у которого все углы прямые.
Можно дать и другое определение
квадрата: квадрат —
это ромб, у которого все углы прямые.
Получается, что квадрат обладает всеми свойствами параллелограмма, прямоугольника и ромба.
Перечислим свойства квадрата:
Все углы квадрата — прямые, все стороны квадрата — равны.
Диагонали квадрата равны и пересекаются под прямым углом.
Диагонали квадрата делят его углы пополам.
Площадь квадрата, очевидно, равна квадрату его стороны: S = a2. Диагональ квадрата равна произведению его стороны на , то есть ,
Разберем несколько простых задач на тему «Квадрат». Все они взяты из Банка заданий ФИПИ.
1. Найдите сторону квадрата, диагональ которого равна .
Мы знаем, что . Тогда .
2. Найдите радиус окружности, описанной около квадрата со стороной, равной .
Очевидно, радиус окружности равен диагонали квадрата.
Ответ: 4.
3. Найдите сторону квадрата, описанного
около окружности радиуса 4.
Найдите сторону квадрата, описанного
около окружности радиуса 4.
Диаметр окружности равен стороне квадрата.
Ответ: 8.
4. Найдите радиус окружности, вписанной в квадрат ABCD, считая стороны квадратных клеток равными .
Чуть более сложная задача. Нарисуйте окружность, вписанную в данный квадрат, то есть касающуюся всех его сторон. Вы увидите, что диаметр этой окружности равен стороне квадрата.
Ответ: 2.
5. Найдите радиус r окружности, вписанной в четырехугольник ABCD. В ответе укажите .
Считаем стороны клеток равными единице. Четырехугольник ABCD — квадрат. Все его стороны равны, все углы — прямые. Как и в предыдущей задаче, радиус окружности, вписанной в квадрат, равен половине его стороны.
Найдем на чертеже прямоугольный треугольник. По теореме Пифагора найдем сторону, например, АВ. Она равна . Тогда радиус вписанной окружности равен . В ответ запишем .
Ответ: 5.
Трапеция и ее свойства
Трапеция —
четырехугольник, у которого две
стороны параллельны, а две другие —
нет.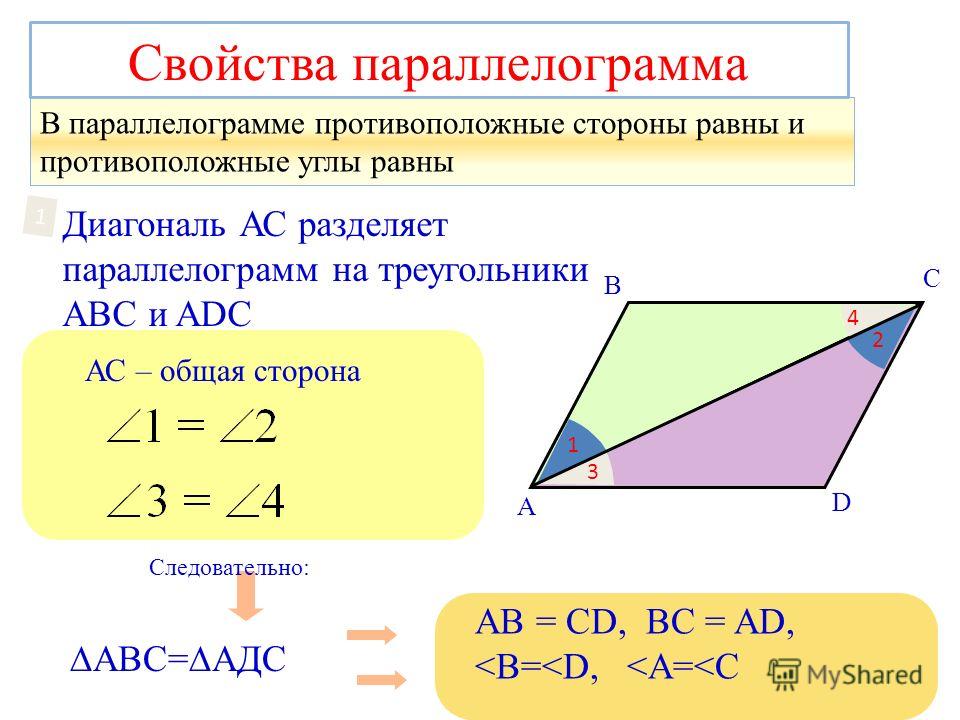
Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны. Если боковые стороны равны, трапеция называется равнобедренной.
Площадь трапеции равна произведению полусуммы оснований на высоту:
Отрезок, соединяющий середины оснований трапеции, называется средней линией трапеции. Средняя линия трапеции параллельна основаниям, а длина ее равна полусумме оснований:
Как видим, теория очень проста. А задачи, в которых применяются свойства трапеции, весьма разнообразны. В этой статье разобраны и стандартные задачи (номер 1 и 2), и более интересные.
1. Найдите высоту трапеции ABCD, опущенную из вершины B, если стороны квадратных клеток равны .
Высота трапеции — это отрезок, перпендикулярный ее основаниям. Проведем высоту из вершины В.
Ответ: 2.
2. Основания трапеции равны 18 и 6, боковая сторона, равная 7, образует с одним из оснований трапеции угол 150. Найдите площадь трапеции.
Это
стандартная задача. Углы АВН и ВАН —
односторонние, значит, их сумма равна
180°, и тогда угол ВАН равен 30°.
Из треугольника АВН найдем высоту
ВН. Катет, лежащий напротив угла в 30,
равен половине гипотенузы. Получаем,
что ВН = 3,5 и площадь трапеции
равна 42.
Углы АВН и ВАН —
односторонние, значит, их сумма равна
180°, и тогда угол ВАН равен 30°.
Из треугольника АВН найдем высоту
ВН. Катет, лежащий напротив угла в 30,
равен половине гипотенузы. Получаем,
что ВН = 3,5 и площадь трапеции
равна 42.
3. Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей.
Скажите, что вы видите на чертеже? Можно сказать, что изображена трапеция АВСD, и в ней проведена средняя линия. А можно увидеть и другое — два треугольника, АВС и АСD, в которых проведены средние линии.
Мы помним, что средняя линия треугольника — это отрезок, соединяющий середины двух его сторон. Средняя линия треугольника параллельна третьей его стороне и равна половине этой стороны.
Из треугольника АВD находим: х = 5.
В следующей задаче мы тоже воспользуемся свойством средней линии треугольника.
4.
Основания трапеции равны 3 и 2.
Найдите отрезок, соединяющий середины
диагоналей трапеции.
Проведем PQ — среднюю линию трапеции, PQ = 2,5. Легко доказать, что отрезок MN, соединяющий середины диагоналей трапеции, лежит на средней линии. Дальше все просто. Найдем отрезки РМ и NQ, являющиеся средними линиями треугольников ABC и BCD, а затем отрезок MN. Он равен 0,5.
5. Прямая, проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного 4, отсекает треугольник, периметр которого равен 15. Найдите периметр трапеции.
Периметр треугольника равен сумме его сторон, то есть a + b + c. Периметр трапеции равен а + b + 4 + c + 4. На сколько периметр трапеции больше периметра треугольника? Чему равен периметр трапеции?
Ответ: 23.
Окружность. Центральный и вписанный угол
Центральный угол — это угол, вершина которого находится в центре окружности. Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают ее.
На рисунке —
центральные и вписанные углы, а также
их важнейшие свойства.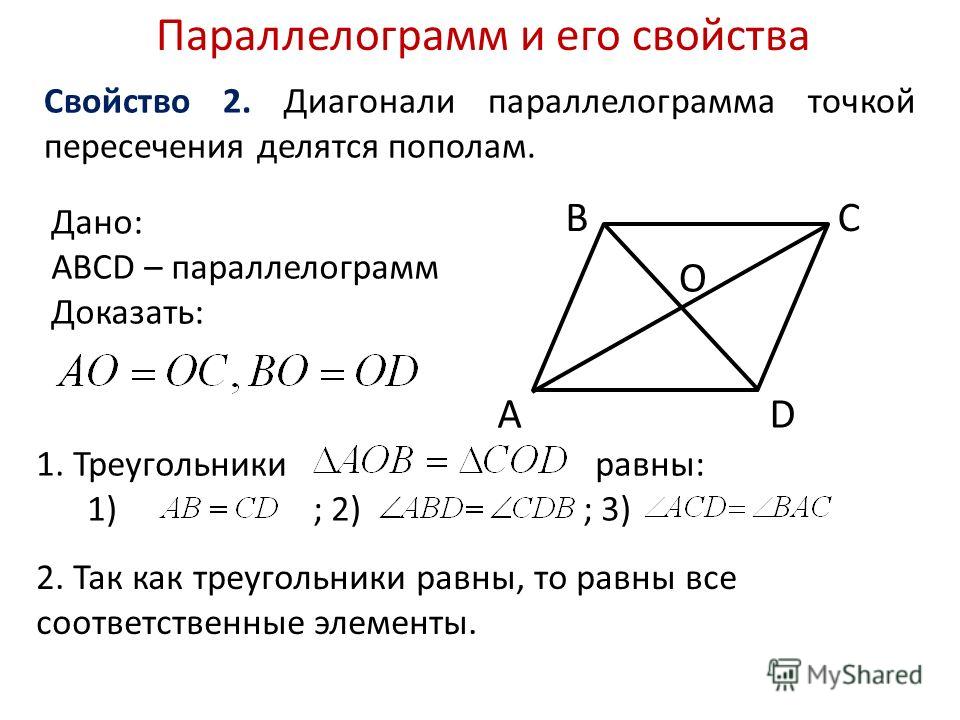
Итак, величина центрального угла равна угловой величине дуги, на которую он опирается. Значит, центральный угол величиной в 90 градусов будет опираться на дугу, равную 90°, то есть круга. Центральный угол, равный 60°, опирается на дугу в 60 градусов, то есть на шестую часть круга.
Величина вписанного угла в два раза меньше центрального, опирающегося на ту же дугу.
Также для решения задач нам понадобится понятие «хорда».
Равные центральные углы опираются на равные хорды.
1. Чему равен вписанный угол, опирающийся на диаметр окружности? Ответ дайте в градусах.
Вписанный угол, опирающийся на диаметр, — прямой.
Ответ: 90.
2. Центральный угол на 36° больше острого вписанного угла, опирающегося на ту же дугу окружности. Найдите вписанный угол. Ответ дайте в градусах.
Пусть центральный угол равен х, а вписанный угол, опирающийся на ту же дугу, равен у.
Мы знаем,
что х = 2у.
Отсюда 2у = 36 + у,
у = 36.
Ответ: 36.
3. Радиус окружности равен 1. Найдите величину тупого вписанного угла, опирающегося на хорду, равную . Ответ дайте в градусах.
Пусть хорда АВ равна . Тупой вписанный угол, опирающийся на эту хорду, обозначим ?. В треугольнике АОВ стороны АО и ОВ равны 1, сторона АВ равна . Нам уже встречались такие треугольники. Очевидно, что треугольник АОВ — прямоугольный и равнобедренный, то есть угол АОВ равен 90°. Тогда дуга АСВ равна 90°, а дуга АКВ равна 360° — 90° = 270°. Вписанный угол ? опирается на дугу АКВ и равен половине угловой величины этой дуги, то есть 135°.
Ответ: 135.
4. Хорда AB делит окружность на две части, градусные величины которых относятся как 5:7. Под каким углом видна эта хорда из точки C, принадлежащей меньшей дуге окружности? Ответ дайте в градусах.
Главное
в этой задаче — правильный чертеж
и понимание условия. Как вы понимаете
вопрос: «Под каким углом хорда видна
из точки С?»
Представьте, что
вы сидите в точке С и вам
необходимо видеть всё, что происходит
на хорде АВ.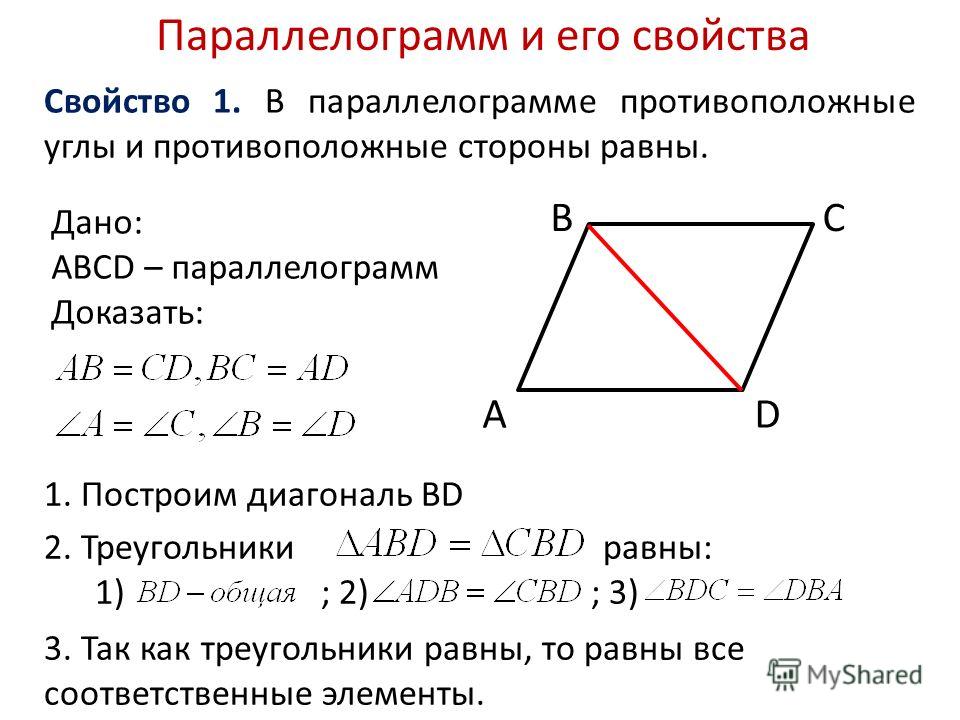 Так, как будто хорда АВ —
это экран в кинотеатре 🙂
Очевидно,
что найти нужно угол АСВ.
Сумма двух
дуг, на которые хорда АВ делит
окружность, равна 360°, то есть
5х +
7х = 360°
Отсюда х = 30°, и тогда вписанный
угол АСВ опирается на дугу, равную
210°.
Величина вписанного угла равна
половине угловой величины дуги, на которую
он опирается, значит, угол АСВ равен
105°.
Так, как будто хорда АВ —
это экран в кинотеатре 🙂
Очевидно,
что найти нужно угол АСВ.
Сумма двух
дуг, на которые хорда АВ делит
окружность, равна 360°, то есть
5х +
7х = 360°
Отсюда х = 30°, и тогда вписанный
угол АСВ опирается на дугу, равную
210°.
Величина вписанного угла равна
половине угловой величины дуги, на которую
он опирается, значит, угол АСВ равен
105°.
Ответ: 105.
Касательная к окружности
Касательная к окружности — прямая, имеющая с окружностью единственную общую точку.
Понятие касательной к окружности и основные свойства касательной проиллюстрированы ниже на рисунке.
1. Угол ACO равен 28°, где O — центр окружности. Его сторона CA касается окружности. Найдите величину меньшей дуги AB окружности, заключенной внутри этого угла. Ответ дайте в градусах.
Касательная
к окружности перпендикулярна радиусу,
проведенному в точку касания. Значит,
угол САО — прямой. Из треугольника
АСО получим, что угол АОС равен 62 градуса.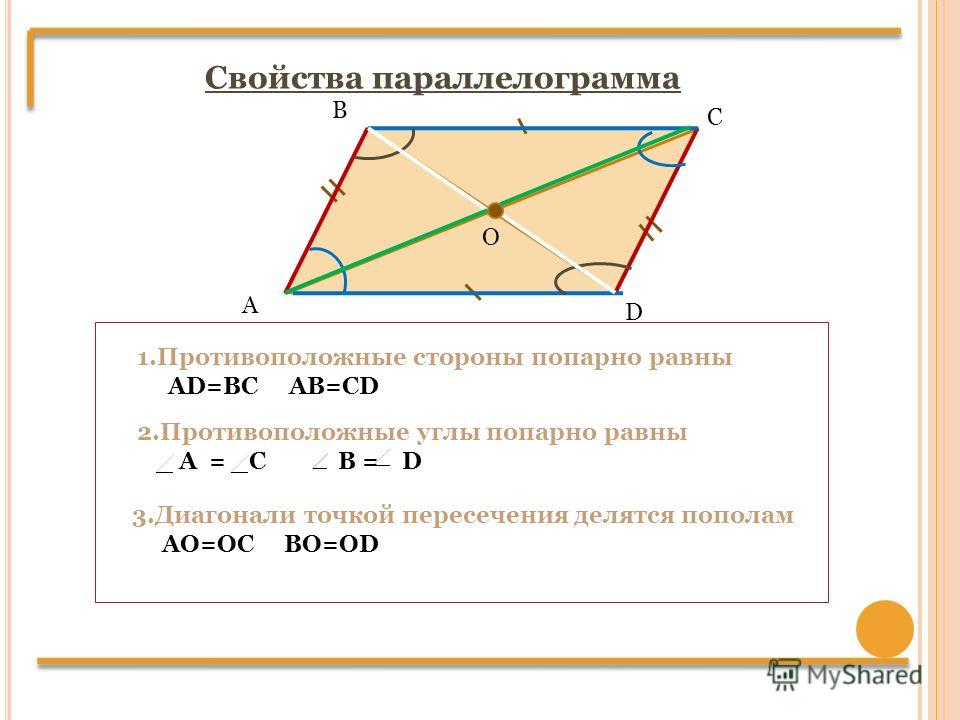 Величина центрального угла равна угловой
величине дуги, на которую он опирается,
значит, величина дуги АВ — тоже
62 градуса.
Величина центрального угла равна угловой
величине дуги, на которую он опирается,
значит, величина дуги АВ — тоже
62 градуса.
Ответ: 62.
2. Найдите угол ACO, если его сторона CA касается окружности, O — центр окружности, а большая дуга AD окружности, заключенная внутри этого угла, равна 116°. Ответ дайте в градусах.
Это чуть более сложная задача. Центральный угол АОD опирается на дугу AD, следовательно, он равен 116 градусов. Тогда угол АОС равен 180° — 116° = 64°. Касательная перпендикулярна радиусу, проведенному в точку касания, значит, угол ОАС — прямой. Тогда угол АСО равен 90° — 64° = 26°.
Ответ: 26.
3. Хорда AB стягивает дугу окружности в 92°. Найдите угол ABC между этой хордой и касательной к окружности, проведенной через точку B. Ответ дайте в градусах.
Проведем
радиус ОВ в точку касания, а также
радиус ОА. Угол ОВС равен 90°. Треугольник
ВОА — равнобедренный. Нетрудно найти,
что угол ОВА равен 44 градуса, и тогда
угол СВА равен 46 градусов, то есть половине угловой величины дуги АВ.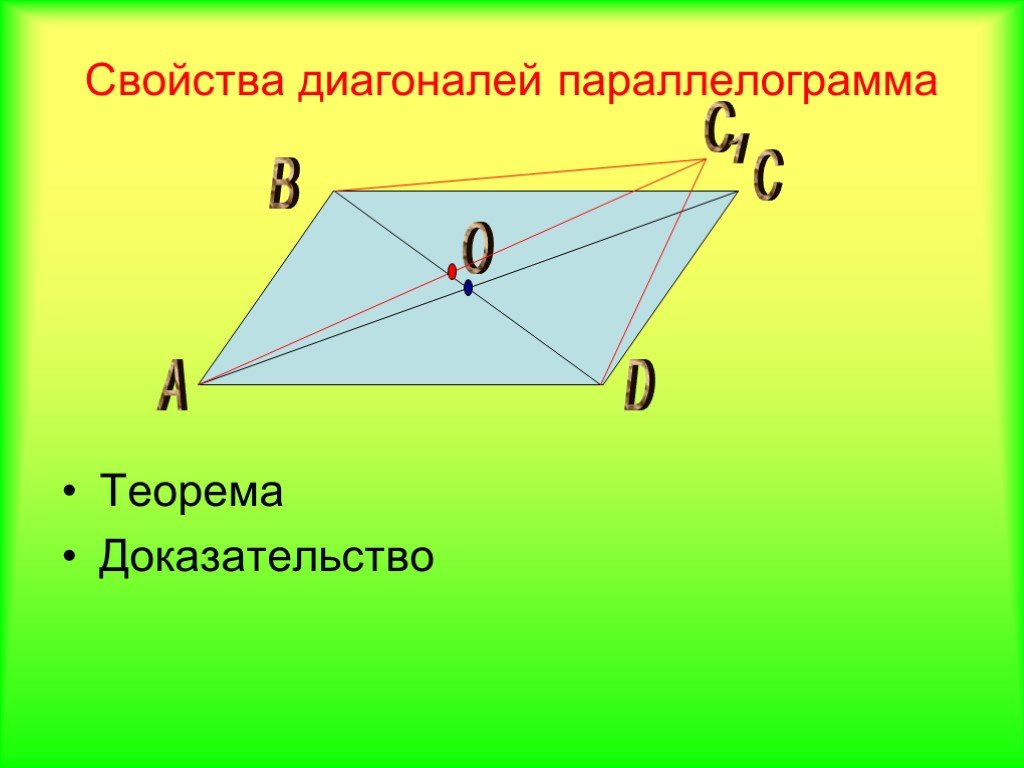
Получается, что угол между касательной и хордой, проведенной через точку касания, равен половине угловой величины дуги, заключенной между ними.
4. Через концы A, B дуги окружности в 62° проведены касательные AC и BC. Найдите угол ACB. Ответ дайте в градусах.
Рассмотрите четырехугольник ОВСА. Сумма углов любого выпуклого четырехугольника равна 360°. Углы ОВА и ОВС и ОАС — прямые, угол ВОА равен 62°, значит, угол АСВ равен 28 градусов.
Ответ: 28.
5. К окружности, вписанной в треугольник ABC, проведены три касательные. Периметры отсеченных треугольников равны 6, 8, 10. Найдите периметр данного треугольника.
Вспомним
еще одно важное свойство касательных
к окружности: Отрезки
касательных, проведенных из одной
точки, равны.
Периметр треугольника — это сумма
всех его сторон. Обратите внимание
на точки на нашем чертеже, являющиеся
вершинами шестиугольника. Из каждой
такой точки проведены два отрезка
касательных к окружности.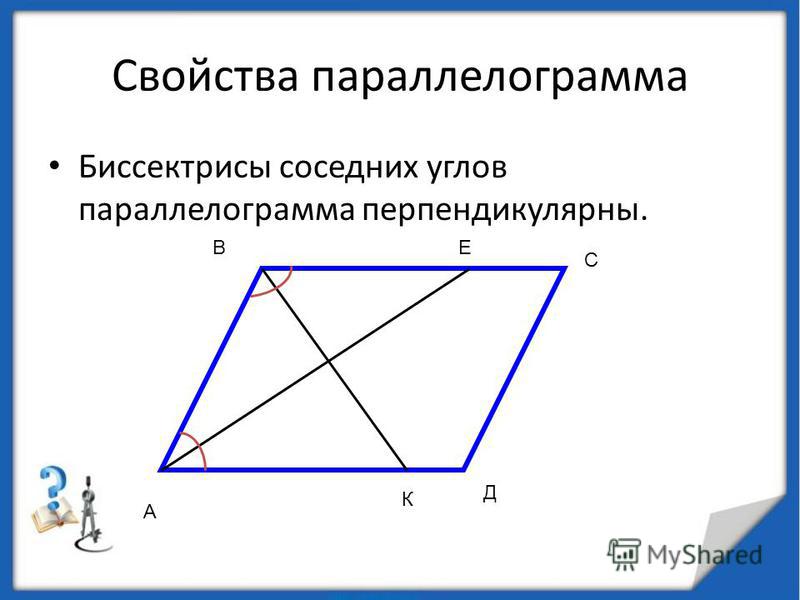 Отметьте
на чертеже такие равные отрезки. Еще
лучше, если одинаковые отрезки вы будете
отмечать одним цветом. Постарайтесь
увидеть, как периметр треугольника АВС
складывается из периметров отсеченных
треугольников.
Отметьте
на чертеже такие равные отрезки. Еще
лучше, если одинаковые отрезки вы будете
отмечать одним цветом. Постарайтесь
увидеть, как периметр треугольника АВС
складывается из периметров отсеченных
треугольников.
Ответ: 24.
Все эти задачи встречаются в Банке заданий ФИПИ под номером В6. А вот одна из сложных задач В3:
6. Около окружности описан многоугольник, площадь которого равна 5. Его периметр равен 10. Найдите радиус этой окружности.
Обратите внимание — в условии даже не сказано, сколько сторон у этого многоугольника. Видимо, это неважно. Пусть их будет пять, как на рисунке. Окружность касается всех сторон многоугольника. Отметьте центр окружности — точку О — и проведите перпендикулярные сторонам радиусы в точки касания.
Соедините
точку О с вершинами А, В, С, D, E.
Получились треугольники АОВ, ВОС, СОD,
DOE и ЕОА.
Очевидно, что площадь
многоугольника S = SАОВ + SВОС + SСОD + SDOE + SЕОА.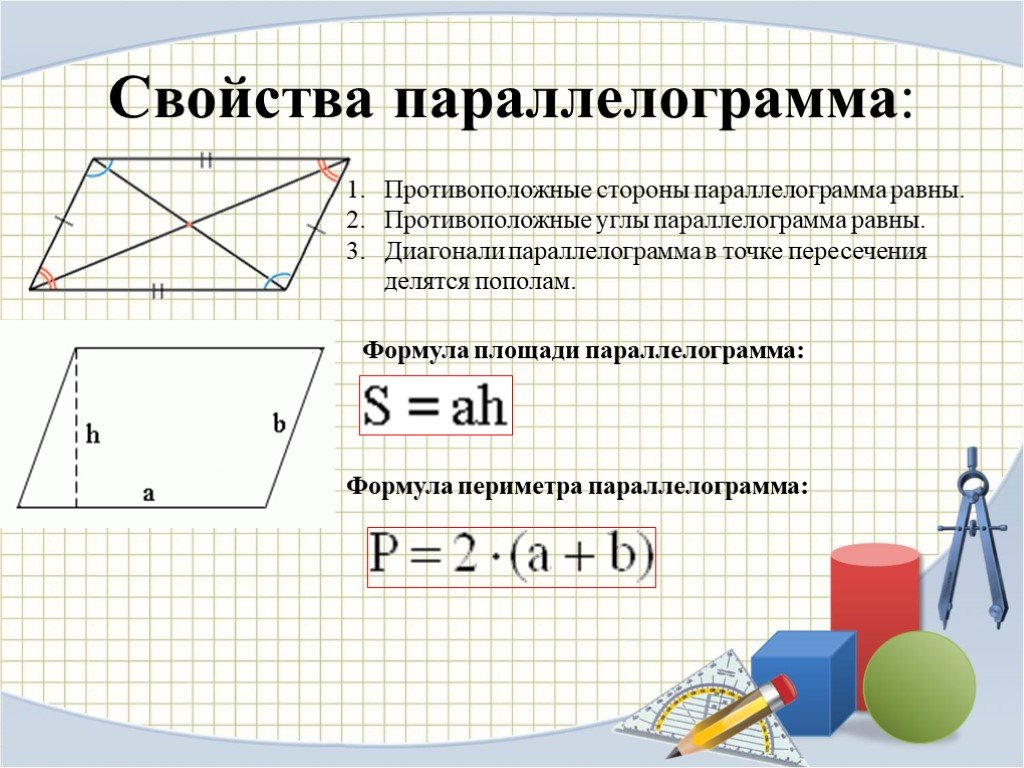 Как вы думаете, чему равны высоты
всех этих треугольников и как,
пользуясь этим, найти радиус окружности?
Как вы думаете, чему равны высоты
всех этих треугольников и как,
пользуясь этим, найти радиус окружности?
Ответ: 1.
Геометрия 7-9 класс. Свойства параллелограмма — math200.ru
Skip to contentГеометрия 7-9 класс. Свойства параллелограммаadmin2022-12-18T22:08:01+03:00
Скачать файл в формате pdf.
Геометрия 7-9 класс. Свойства параллелограмма
Параллелограмм. Параллелограммом называется четырёхугольник, противоположные стороны которого попарно параллельны.
Свойства и признаки параллелограмма
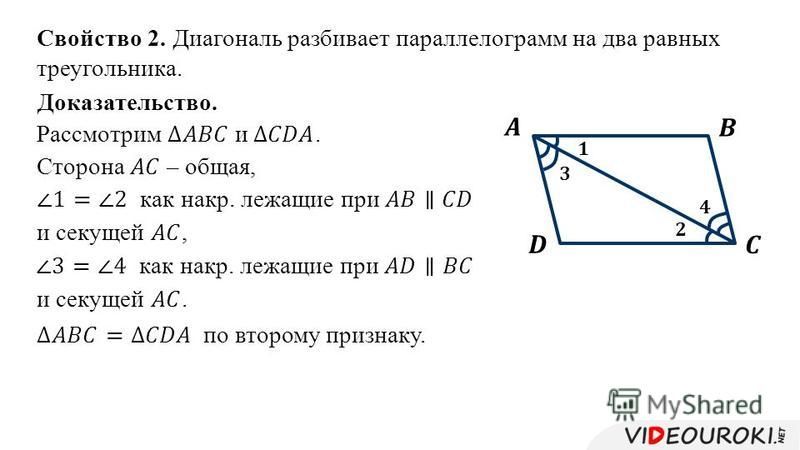
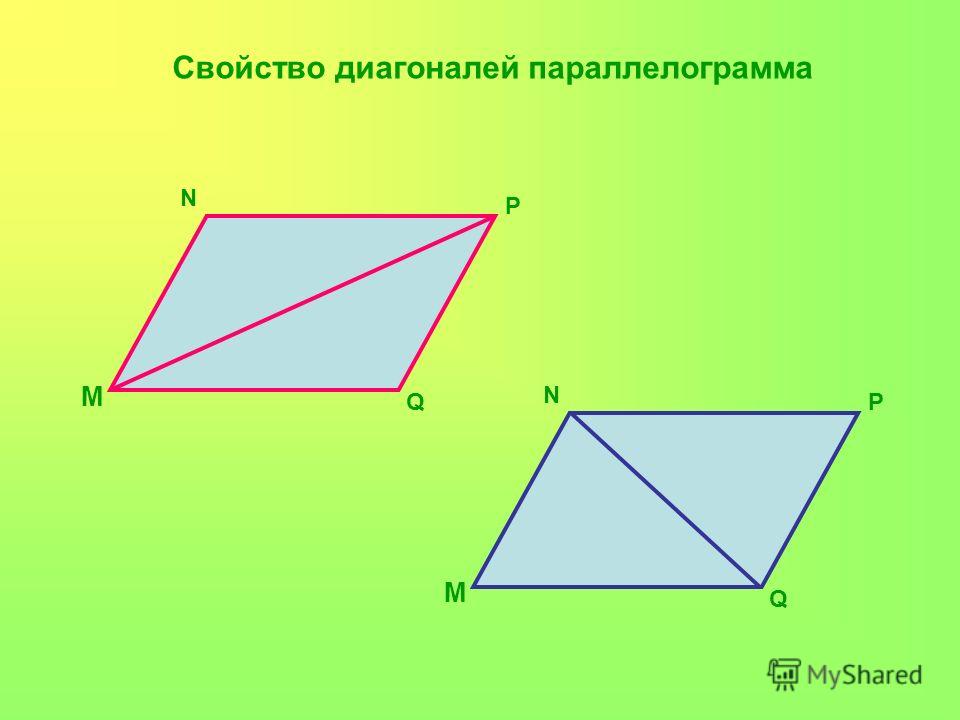
- Диагональ разбивает параллелограмм на два равных треугольника.
- Противоположные стороны параллелограмма попарно равны.
- Противоположные углы параллелограмма попарно равны.
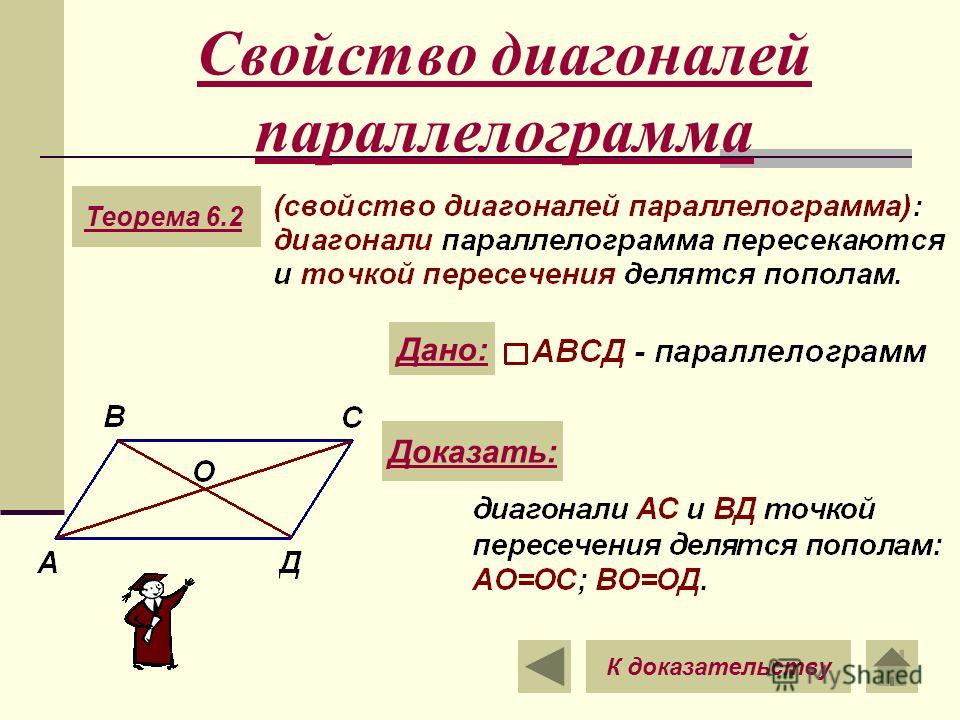
- Диагонали параллелограмма пересекаются и делятся точкой пересечения пополам.
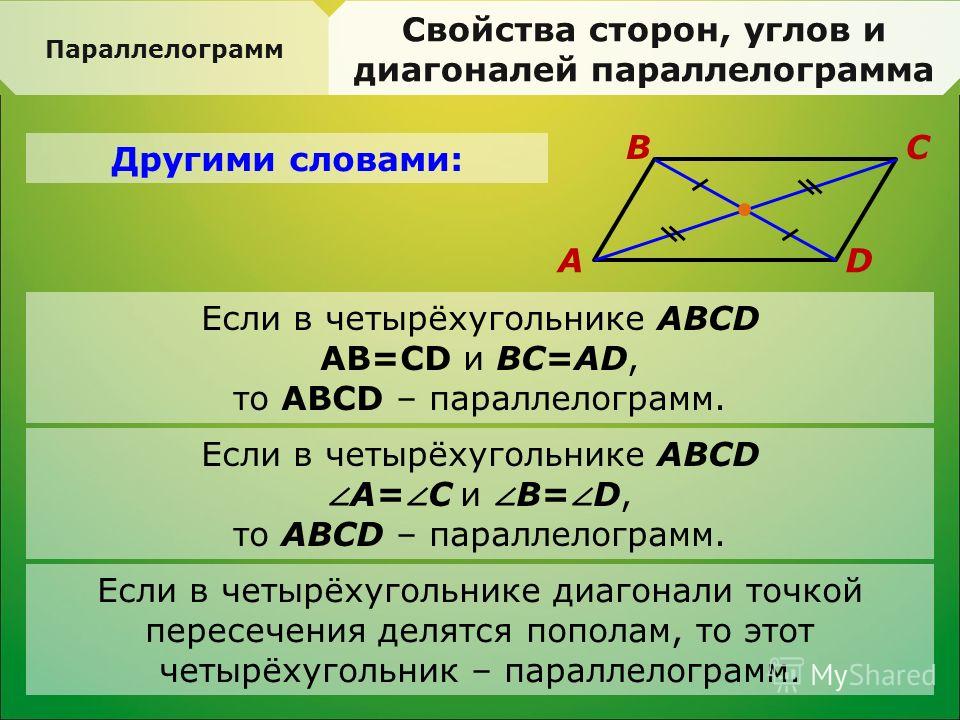
- Если противоположные стороны четырёхугольника попарно равны, то этот четырёхугольник ̶ параллелограмм.
 \circ }.\) Найдите \(\angle \,ACB.\) Ответ дайте в градусах.
\circ }.\) Найдите \(\angle \,ACB.\) Ответ дайте в градусах.Ответ
ОТВЕТ: 20.
Задача 15. Дан ромб ABCD в котором AB = BD. Найдите \(\angle \,BAC + \angle \,BDC.\) Ответ дайте в градусах. Ответ
ОТВЕТ: 90.
Задача 16. Дан квадрат ABCD и равносторонний треугольник ABO так, что точка O находится внутри квадрата. Найдите \(\angle \,BOC.\) Ответ дайте в градусах. Ответ
ОТВЕТ: 75.
Задача 17. Дан квадрат ABCD и равносторонний треугольник ABO так, что точка O находится вне квадрата. Найдите \(\angle \,BOC.\) Ответ дайте в градусах. Ответ
ОТВЕТ: 15.
Задача 18. Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите \(\angle \,AKB.\) Ответ
ОТВЕТ: 90.
Задача 19.  \circ },\) BC = 8, AK = 6. Найдите периметр параллелограмма.
\circ },\) BC = 8, AK = 6. Найдите периметр параллелограмма.Ответ
ОТВЕТ: 24.
Задача 27. В параллелограмме ABCD AK и DM биссектрисы (см. рис.), AD = 14, DC = 10. Найдите MK. Ответ
ОТВЕТ: 6.
Задача 28. В параллелограмме ABCD CK и BM биссектрисы (см. рис.), AD = 22, DC = 7. Найдите MK. Ответ
ОТВЕТ: 8.
Задача 29. Дан прямоугольник ABCD, \(BK \bot AC,\) AK : KC = 1 : 3, CD = 10. Найдите диагональ BD. Ответ
ОТВЕТ: 20.
Задача 30. Дан прямоугольник ABCD диагонали которого пересекаются в точке O, AK – биссектриса \(\angle \,BAO,\) BK : OD = 1 : 2, CO = 5.  \circ },\) \(KD\parallel AC,\) \(DM\parallel AB.\) Найдите периметр четырехугольника AKDM.
\circ },\) \(KD\parallel AC,\) \(DM\parallel AB.\) Найдите периметр четырехугольника AKDM.Ответ
ОТВЕТ: 28.
Задача 32. Точки M и K являются соответственно серединами сторон AB и BC треугольника ABC. Через вершину C проведена прямая, параллельная AB и пересекающая луч MK в точке E. Докажите, что KE равен половине AC. Реклама
Поддержать нас
Диагональ в геометрии — объяснение, определения, формулы, свойства
Диагональ в геометрии — это отрезок, соединяющий две вершины многоугольника или многогранника, если присутствующие вершины не находятся на одном ребре. Вообще любая наклонная линия называется диагональю.
Здесь вы можете прочитать об основных свойствах диагоналей, различных типах диагоналей и некоторых простых примерах.

Ключевые определения, которые следует помнить при изучении диагоналей
Существует два типа многоугольников: правильный многоугольник и неправильный многоугольник
Количество диагоналей в многоугольнике
Количество диагоналей в многоугольнике зависит от количества сторон этого конкретного многоугольника. Мы можем легко вычислить количество диагоналей в многоугольнике, используя простую формулу.
Количество диагоналей = (n(n-3))/2, где n — количество вершин в многоугольнике
Например: вычислите количество диагоналей в 12-стороннем правильном многоугольнике.
Согласно формуле количество диагоналей в многоугольнике = (n (n-3))/ 2,
Итак, 12-угольник будет содержать 12(12-3)/2 = 54 диагонали.
Диагональ многоугольника Формула
Если какая-либо вершина соединена сторонами с двумя другими вершинами, эти соединения не могут считаться диагоналями.
 Эта вершина также не может соединиться сама с собой.
Эта вершина также не может соединиться сама с собой.n: количество сторон
сумма диагоналей = [(5-3) *5] / 2 = 5
Диагональ квадрата
Квадрат имеет две диагонали. Отрезок, соединяющий два угла квадрата, называется его диагональю.
Свойства диагоналей квадрата
Диагонали квадрата делят друг друга пополам.
Каждая диагональ квадрата делит квадрат таким образом, что он становится равнобедренным треугольником. Образованные равнобедренные треугольники конгруэнтны друг другу.
Диагонали квадрата параллельны и перпендикулярны друг другу.
Если у вас есть длина стороны диагонали, то вы можете легко узнать длину диагонали квадрата. Вы должны использовать данную формулу, чтобы узнать длину диагонали квадрата.

Длина диагонали квадрата = a/sqrt(2), где a — длина любой из сторон квадрата.
Диагональ прямоугольника
Особый тип параллелограмма, углы которого составляют девяносто градусов, называется прямоугольником. Диагонали прямоугольника равны друг другу и делят друг друга пополам. Прямоугольник – это один из четырехугольников с равными диагоналями. Противоположные углы, образованные в точке пересечения диагоналей, также равны.
Вы можете легко вычислить длину диагонали прямоугольника, если вам известны размеры его сторон. Приведенная здесь формула позволяет вычислить длину диагонали прямоугольника.
Длина диагонали прямоугольника = sqrt (a² + b²), где «a» — длина прямоугольника, а «b» — ширина прямоугольника.
Прямоугольник и формулы
Площадь = длина * ширина
Периметр = 2Д + 2Ш
9{2}}\]Диагональ ромба
В ромбе углы, противолежащие друг другу, равны.
 Эти образованные углы делятся пополам диагоналями ромба. У ромба четыре стороны с двумя диагоналями. Когда все углы ромба повернутся на 90 градусов, он станет квадратом.
Эти образованные углы делятся пополам диагоналями ромба. У ромба четыре стороны с двумя диагоналями. Когда все углы ромба повернутся на 90 градусов, он станет квадратом.Вы также можете вычислить длину диагонали ромба, если вам дана площадь.
A= (PQ)/2, где p и q — длины диагоналей ромба. 9{2}}\]
Диагональ параллелограмма
Параллелограмм — это тип прямоугольника, угол которого не равен 90 градусам. Две диагонали параллелограмма делят друг друга пополам, а противоположные стороны и углы любого параллелограмма равны.
Вы также можете рассчитать длину одной диагонали параллелограмма, если Вам предоставлены размеры его сторон и длина другой диагонали.
Длина одной диагонали параллелограмма = p = sqrt (2a² + 2b² – (q)²), где p – длина диагонали, которую вы не знаете, q – предоставленная вам длина диагонали, a
и b — длина и ширина параллелограмма соответственно.
Диагональ параллелограмма
Отношение между сторонами и диагоналями параллелограмма
Введите уравнение здесь.

d12 + d22 = 2(a2+b2)
Свойства, химическая структура и применение
Четырехугольник с равными парами противоположных сторон и углов называется параллелограммом. У него есть пара противоположных сторон, которые параллельны друг другу. Диагональ Внутренние углы параллелограмма формулы являются дополнительными, то есть их сумма равна 180 градусам. Диагонали параллелограмма делятся пополам или на две равные части. Внутренние углы параллелограмма, к которым относится диагональ формулы параллелограмма , составляют в сумме 360 градусов.
Параллелограмм — это двумерная геометрическая фигура, стороны которой параллельны друг другу. Это многоугольник с четырьмя сторонами (иногда называемый четырехугольником), в котором каждая пара параллельных сторон имеет одинаковую длину. Параллелограмм, к которому относится Диагональ параллелограмма Формула относится, имеет смежные углы, которые в сумме составляют 180 градусов.
Учащиеся должны изучить различные 2D-фигуры, формулу диагонали параллелограмма, и несколько геометрических фигур, включая круги, квадраты, прямоугольники, ромбы и т.
 д. Каждая из этих форм имеет уникальный набор характеристик. Кроме того, формула диагонали параллелограмма представляет собой разницу между формулами площади и периметра этих фигур, которые применяются к различным вопросам.
д. Каждая из этих форм имеет уникальный набор характеристик. Кроме того, формула диагонали параллелограмма представляет собой разницу между формулами площади и периметра этих фигур, которые применяются к различным вопросам.Что такое диагональ параллелограмма?
A Диагональ параллелограмма Формула может быть построена путем соединения двух несмежных вершин. Следует заметить, что две диагонали параллелограмма пересекаются друг с другом, разделяя его на конгруэнтные треугольники.
На плоском двумерном параллелограмме четыре угла. Внутренние углы по обе стороны равны. Поперечные углы с одной и той же стороны являются дополнительными, а значит, их сумма равна 180 градусам. В результате внутренние углы параллелограмма в сумме составляют 360 градусов.
Качества параллелограмма присущи формам квадрата и прямоугольника. Оба имеют противоположные стороны, которые параллельны и равны друг другу. Диагонали обеих фигур делят друг друга пополам.
Формула диагонали параллелограмма Параллелограмм — это уникальный тип геометрической фигуры, у которого соседние стороны не имеют одинаковой длины, а противоположные стороны параллельны. Кроме того, диагональ параллелограмма формулы и углы равны 90 градусам. Это трапеция, если только одна пара ее сторон параллельна, а две другие нет.
Параллелограмм — это уникальный тип геометрической фигуры, у которого соседние стороны не имеют одинаковой длины, а противоположные стороны параллельны. Кроме того, диагональ параллелограмма формулы и углы равны 90 градусам. Это трапеция, если только одна пара ее сторон параллельна, а две другие нет.Длину диагоналей данного параллелограмма можно определить с помощью формулы для Формула диагонали параллелограмма . Различные типы параллелограмма имеют разные формулы. Четырехугольник, у которого противоположные стороны параллельны и равны, называется параллелограммом. Из-за выравнивания и равенства противоположных сторон они имеют равные углы на них. Диагональ параллелограмма Формула , связывающая противоположные углы параллелограмма, относится к его диагоналям.
Математические понятия, такие как многоугольники, существуют уже очень давно. Греческие архитекторы и математики создали математические модели (статуты), хранящиеся в музеях, чтобы доказать, что они знали о правильных многоугольниках.

Многоугольник — это основной строительный блок, используемый при моделировании и визуализации в компьютерной графике. Они более конкретно описаны в системе баз данных, которая содержит массивы вершин (координаты геометрических вершин и другие полигональные атрибуты).
Свойства диагоналей параллелограммаКогда противоположные стороны четырехугольника параллельны и равны, форма называется параллелограммом. Диагональ параллелограмма формулы имеет четыре угла при вершинах. Диагональ параллелограмма Формула легче связать углы и стороны параллелограмма, если знать его характеристики. Кроме того, качества помогают вычислить стороны и углы параллелограмма.
Теоремы о свойствах диагонали параллелограмма . Формула определяет основные принципы решения задач, связанных с параллелограммами. Диагональ параллелограмма Формула проста для понимания и использования свойств сторон и углов параллелограмма для решения различных задач.
 Кроме того, диагональ параллелограмма Формула помогает понять идеи других четырехугольников. Следующий список включает четыре важные теоремы, касающиеся характеристик параллелограмма:
Кроме того, диагональ параллелограмма Формула помогает понять идеи других четырехугольников. Следующий список включает четыре важные теоремы, касающиеся характеристик параллелограмма:- Противоположные стороны параллелограмма равны.
- В параллелограмме, к которому относится диагональ параллелограмма формулы , противоположные углы равны.
- Диагонали параллелограмма пересекаются пополам.
- Четырехугольник является параллелограммом, если один набор противоположных сторон равен и параллельен.
Пример 1: Найдите длину диагоналей ромба со стороной 4 дюйма, если внутренние углы равны 120° и 60°.
Решение:
Дано, внутренний угол A = 120°, а угол B = 60°.
x = 4, y = 4
Используя формулу диагонали параллелограмма,
p=√x2+y2−2xycosAp=x2+y2−2xycosA y2+2xycosA
Подставляя значения в формулу для p:
p=√42+42−(2×4×4×cos60)=√32−16p=4p=42+42−(2×4 ×4×cos60)=32−16p=4
Теперь, проделав то же самое для q,
q=√42+42+(2×4×4×cos60)=√32+16p=√48p= 6,92q=42+42+(2×4×4×cos60)=32+16p=48p=6,92
Ответ: Длина диагоналей 4 дюйма и 6,92 дюйма.

Пример 2. Вычислите длину диагонали параллелограмма со сторонами 4 единицы, 6 единиц и внутренним углом A, равным 60 градусам.
Решение:
Дано, a = 4 единицы, b = 6 единиц, угол A = 60°. A
Подставляя значения в формулу для p:
p=√42+62−24p=42+62−24= √2828 = 5,291
Ответ: Диагональ параллелограмма = 5,291 ед.
Практические вопросы по диагонали параллелограмма
Вопрос 1:
Найдите диагональ параллелограмма со сторонами 3 см, 5 см и углами 45 градусов.
Решение:
Дано a = 3 см
b = 5 см
угол A = 45°
Формула диагонали: 3×5cos45
q = 34–30×0,707
q = √12,79
=3,576 см
Диагональ параллелограмма = 3,576 см.
FAQ (Часто задаваемые вопросы)
1. Как определить диагонали параллелограмма без углов?
Даже не зная внутренних углов, можно вычислить длину диагонали формулы параллелограмма . Например, если параллелограмм представляет собой прямоугольник, учащиеся знают, что диагонали прямоугольника образуют прямоугольный треугольник.
 В этом случае диагональ становится гипотенузой, что позволяет теореме Пифагора определить длину диагонали, если известны длины сторон прямоугольника. Ту же процедуру можно использовать, если предоставленный параллелограмм является квадратом.
В этом случае диагональ становится гипотенузой, что позволяет теореме Пифагора определить длину диагонали, если известны длины сторон прямоугольника. Ту же процедуру можно использовать, если предоставленный параллелограмм является квадратом.2. Равны ли диагонали параллелограмма?
Квадрат, прямоугольник и ромб составляют параллелограмм. Диагонали ромба не всегда могут быть равны, хотя квадрат и прямоугольник равны.
3. Делят ли диагонали параллелограмма пополам?
Да, диагонали параллелограмма перпендикулярны друг другу. Отсюда следует, что диагонали параллелограмма делятся на две равные части.
4. Из чего состоит формула диагонали параллелограмма?
При использовании длин сторон и любых известных углов в формуле параллелограмма можно определить длину диагоналей. Таким образом, стороны параллелограмма и связанные с ними углы входят в состав его частей.
5. Что такое диагональ параллелограмма?
Отрезок, соединяющий две несмежные вершины параллелограмма, называется диагональю.


 \circ }.\) Найдите \(\angle \,ACB.\) Ответ дайте в градусах.
\circ }.\) Найдите \(\angle \,ACB.\) Ответ дайте в градусах.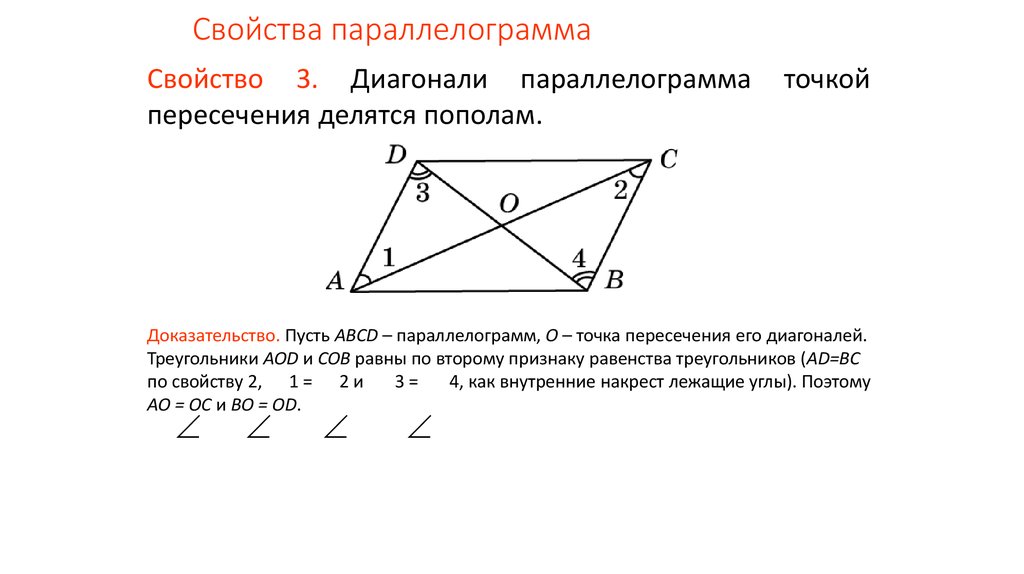 \circ },\) BC = 8, AK = 6. Найдите периметр параллелограмма.
\circ },\) BC = 8, AK = 6. Найдите периметр параллелограмма.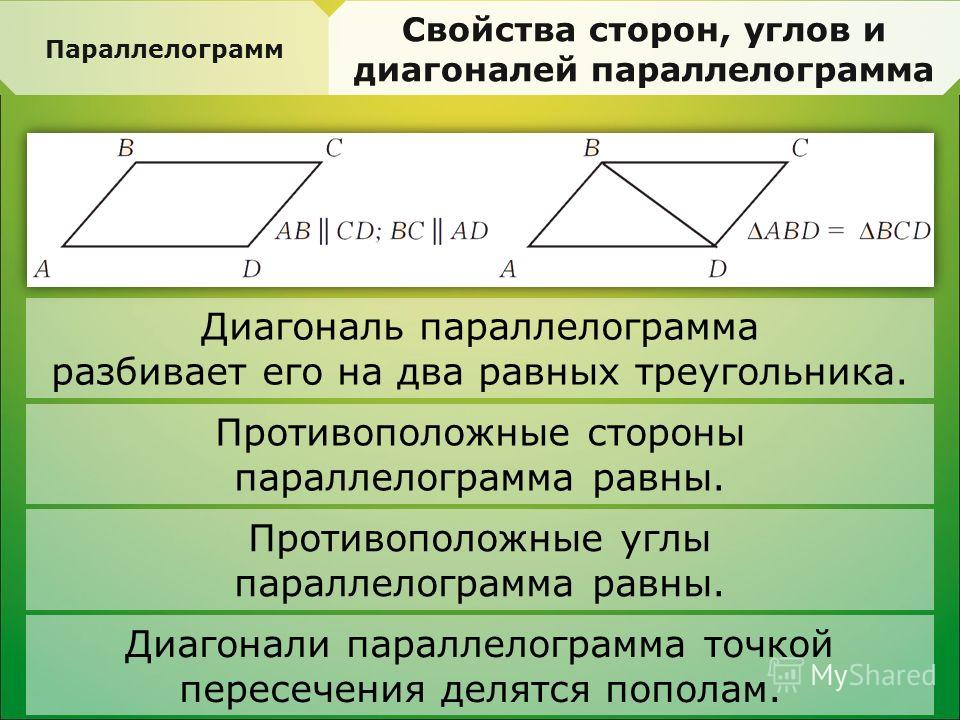 \circ },\) \(KD\parallel AC,\) \(DM\parallel AB.\) Найдите периметр четырехугольника AKDM.
\circ },\) \(KD\parallel AC,\) \(DM\parallel AB.\) Найдите периметр четырехугольника AKDM.
 Эта вершина также не может соединиться сама с собой.
Эта вершина также не может соединиться сама с собой.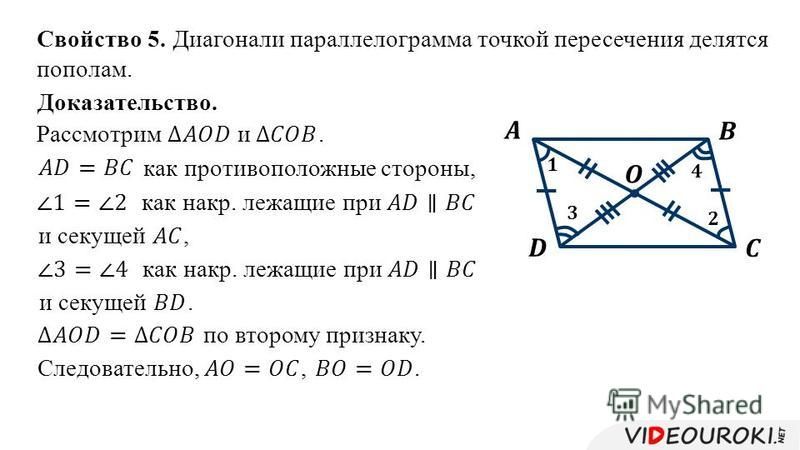
 Эти образованные углы делятся пополам диагоналями ромба. У ромба четыре стороны с двумя диагоналями. Когда все углы ромба повернутся на 90 градусов, он станет квадратом.
Эти образованные углы делятся пополам диагоналями ромба. У ромба четыре стороны с двумя диагоналями. Когда все углы ромба повернутся на 90 градусов, он станет квадратом.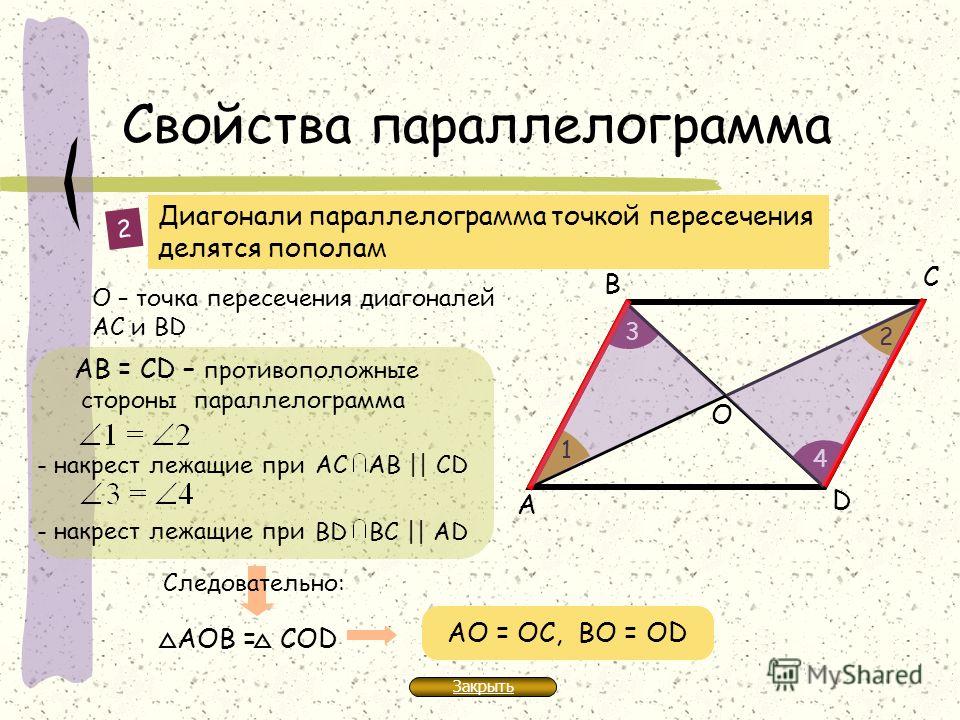
 д. Каждая из этих форм имеет уникальный набор характеристик. Кроме того, формула диагонали параллелограмма представляет собой разницу между формулами площади и периметра этих фигур, которые применяются к различным вопросам.
д. Каждая из этих форм имеет уникальный набор характеристик. Кроме того, формула диагонали параллелограмма представляет собой разницу между формулами площади и периметра этих фигур, которые применяются к различным вопросам.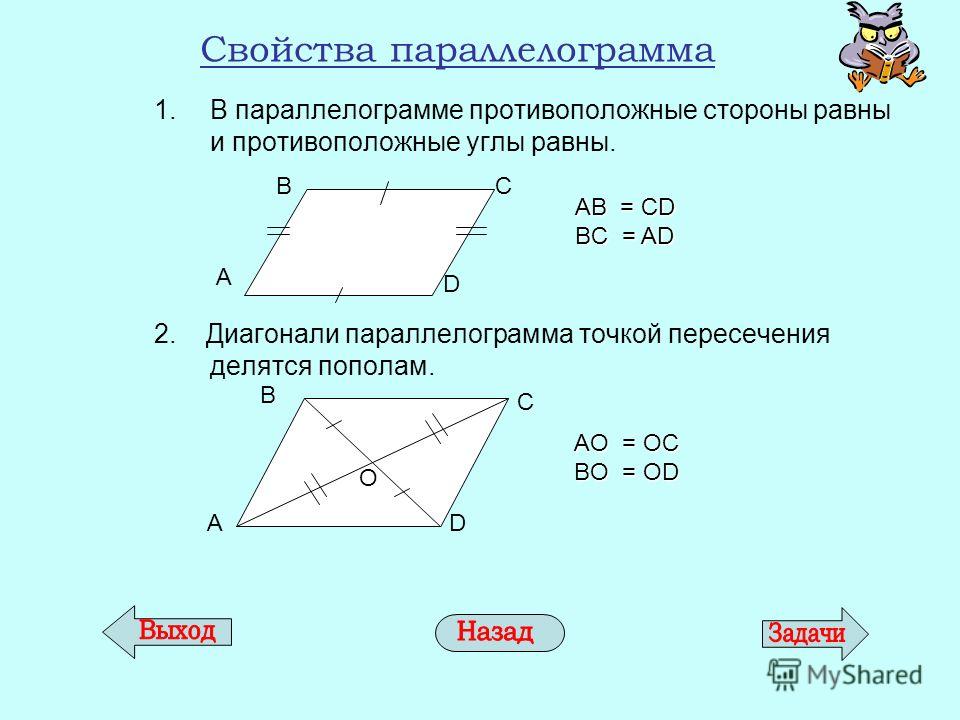 Параллелограмм — это уникальный тип геометрической фигуры, у которого соседние стороны не имеют одинаковой длины, а противоположные стороны параллельны. Кроме того, диагональ параллелограмма формулы и углы равны 90 градусам. Это трапеция, если только одна пара ее сторон параллельна, а две другие нет.
Параллелограмм — это уникальный тип геометрической фигуры, у которого соседние стороны не имеют одинаковой длины, а противоположные стороны параллельны. Кроме того, диагональ параллелограмма формулы и углы равны 90 градусам. Это трапеция, если только одна пара ее сторон параллельна, а две другие нет.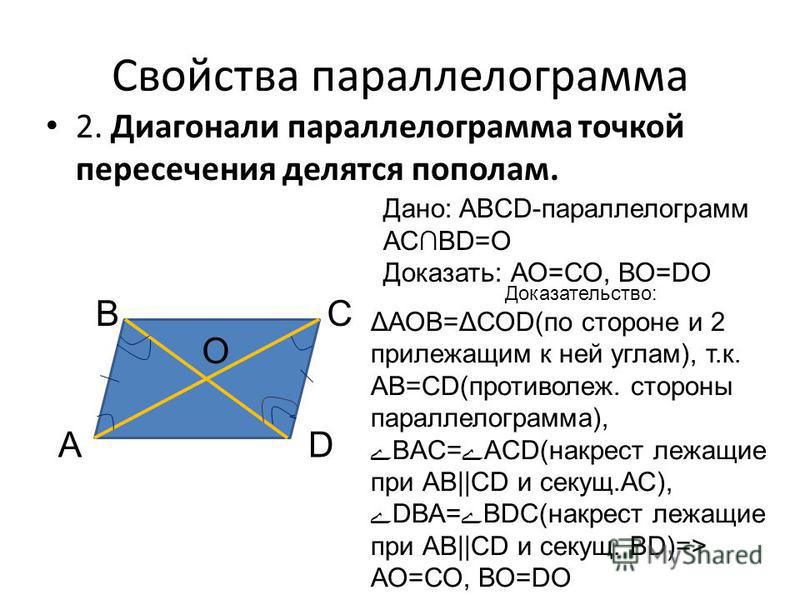
 Кроме того, диагональ параллелограмма Формула помогает понять идеи других четырехугольников. Следующий список включает четыре важные теоремы, касающиеся характеристик параллелограмма:
Кроме того, диагональ параллелограмма Формула помогает понять идеи других четырехугольников. Следующий список включает четыре важные теоремы, касающиеся характеристик параллелограмма: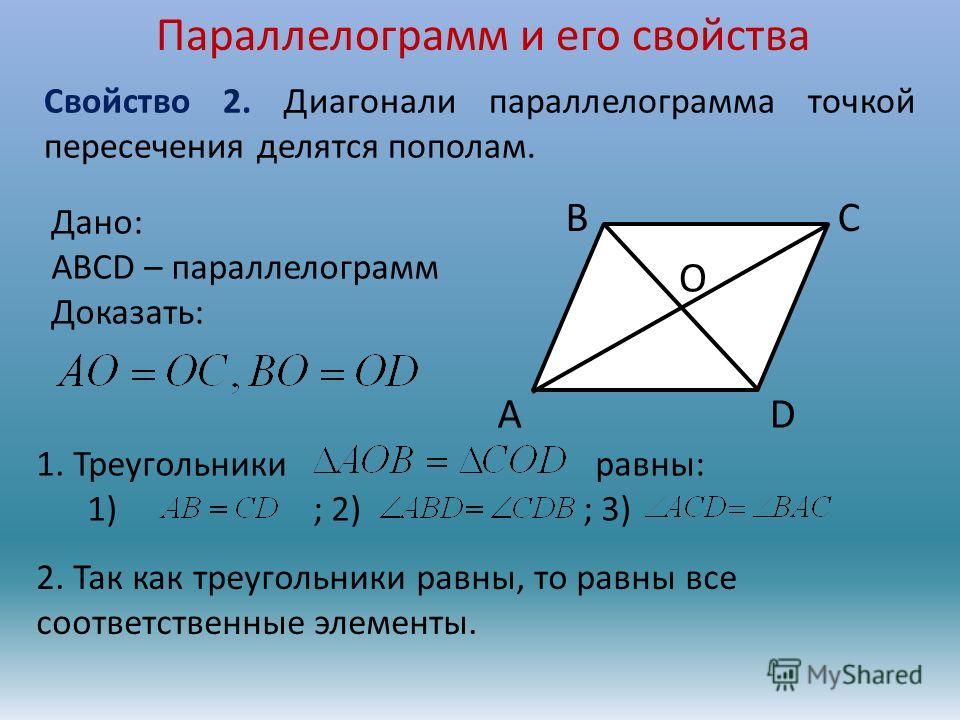
 В этом случае диагональ становится гипотенузой, что позволяет теореме Пифагора определить длину диагонали, если известны длины сторон прямоугольника. Ту же процедуру можно использовать, если предоставленный параллелограмм является квадратом.
В этом случае диагональ становится гипотенузой, что позволяет теореме Пифагора определить длину диагонали, если известны длины сторон прямоугольника. Ту же процедуру можно использовать, если предоставленный параллелограмм является квадратом.