Как найти периметр прямоугольного треугольника
Треугольники представляют собой основы геометрии. Они знакомят нас с понятиями, связанными с алгеброй, геометрией, площадью, периметром, теоремами и углами. Эта основа позволяет математикам понимать и исследовать более сложные концепции геометрии, такие как тригонометрия.
Треугольники также знакомят учащихся с совершенно новым миром терминологии, который иногда может быть ошеломляющим. В результате люди часто испытывают трудности при изучении геометрии в классе.
Эта статья призвана дать ясное и простое объяснение треугольников, теоремы Пифагора, площади и периметра.
Что такое прямоугольный треугольник?
Прямоугольный треугольник — это треугольник, содержащий угол 90°. Прямоугольные треугольники являются одними из самых важных треугольников в математике, поскольку они используются в теории Пифагора, а также в тригонометрии.
Типы треугольников
В математике есть три основных треугольника: равносторонний, равнобедренный и разносторонний .
Равносторонний треугольник имеет равные длины сторон, равнобедренный треугольник имеет две равные длины сторон, а разносторонний треугольник не имеет равных длин сторон.
Хотя основных треугольников три, только равнобедренные и разносторонние треугольники могут быть прямоугольными . Равнобедренный будет иметь угол 90 ° с двумя сопутствующими углами 45 °. Однако разносторонний треугольник является наиболее часто используемым треугольником в вопросах геометрии, его стороны не имеют одинаковой длины, а его углы не отличаются от угла, равного 9.0°.
Последняя часть терминологии, которую нужно понять, это то, как называются стороны треугольника. Единственное, что вы должны понимать и помнить, это то, что самая длинная сторона называется гипотенузой . В теореме Пифагора это обозначается как «с». Две другие стороны отмечены как «a» или «b», но они взаимозаменяемы.
Теорема Пифагора
Что такое Теорема Пифагора?
Теперь, когда вы понимаете основные свойства треугольников, важно понять теорему Пифагора.
Эта теорема, впервые установленная Пифагором 2000 лет назад в Древней Греции, открыла, что:0003
Когда угол треугольника равен 90°, если каждую сторону разделить на квадраты, площадь самого большого квадрата будет равна площади двух меньших квадратов вместе взятых .
Это может быть выражено как a2 + b2= c2
Тройка Пифагора
Как правило, в теореме Пифагора, когда вычисляется длина, она обычно содержит десятичную дробь. Однако есть примеры так называемых идеальных треугольников, ответом на которые является целое число. Если вы запомните их, это позволит вам быстро ответить на вопрос, если вы увидите следующие цифры.
Общие пифагорейские тройки:
- 3, 4, 5
- 6, 8, 10
- 9, 12, 15
Вы заметите, что тройка 3, 4, 5 является производной пифагорейской тройкой, от которой другие происходят от . Это означает, что если бы у вас был вопрос, где две длины равны 18 и 24, и вам нужно было бы определить длину третьей стороны, ответ был бы равен 30.
Это потому, что 3, 4, 5 могут быть получены из 18, 24, 30, умножив оригинал на 6.
Примеры и решения
До сих пор это было очень теоретическим, но математика — это практический предмет, поэтому важно рассмотреть некоторые примеры, чтобы убедиться, что вы полностью понимаете прямоугольные треугольники.
Как найти длину?
Чтобы найти периметр, нужно сначала найти длины .
По сути, это и есть пифагорейская теория. Если вы знаете только две стороны данного прямоугольного треугольника, теория позволяет вам вычислить третью длину. Ниже приведены два примера, если вы понимаете, как их рассчитать, то сможете рассчитать любой экзаменационный вопрос по Пифагору.
- Найдите гипотенузу
Чтобы найти гипотенузу, мы используем стандартную, заданную форму пифагорейской теории: a2 + b2= c2
Введем числа в уравнение . Помните — мы пытаемся найти гипотенузу, которая равна «с».
Если a = 13 см, а b = 9 см, то:
132 + 92= c2
Возведите числа в квадрат и сложите их вместе :
169 + 81 = c2
2950 = c20003
Наконец, извлеките из этого квадратный корень, чтобы получить «c» :
√250 = c
Это ответ и гипотенуза:
c = 15,81138830…
Помните, поскольку это сантиметры, ваш ответ должен быть равен сантиметрам. до правильного знака после запятой:
c = 15,81 см
Это так просто!
- Найти длину «b» .
В отличие от предыдущего вопроса, мы знаем гипотенузу, что означает, что мы должны применить теорему Пифагора, чтобы найти «b» .
Если a2 + b2= c2, то b2= c2 – a2
Если a = 6 см, а c = 18 см, то:
182 – 62 = b2
Возведите числа в квадрат и сложите их :
324 – 36 = b2
288 = b2
Наконец, извлеките из этого квадратный корень, чтобы получить «b» :
√288 = b
Это даст вам ответ и гипотенузу:
Как найти периметр треугольника?
Найти периметр треугольника очень просто .
Формула периметра состоит из сложения всех сторон треугольника. Возможно, вам придется использовать теорему Пифагора, чтобы найти длины, но как только вы узнаете все длины, вы просто сложите их вместе.
Например, если мы посмотрим на предыдущий вопрос, периметр равен 6 см + 18 см + 16,97 см, что равно 40,97 см.
Как найти площадь треугольника?
Найти площадь прямоугольного треугольника немного сложнее, чем его периметр. Для прямоугольного треугольника 9Площадь 0011 вычисляется путем умножения ширины и длины и деления на 2 .
Например, в предыдущем вопросе площадь вычисляется следующим образом:
Площадь = (6 x 16,97) ÷ 2
Площадь = 50,91 см2
Все еще достаточно просто, но помните, что поскольку это площадь, единица см2, а периметр всего см.
Все еще боретесь?
В этой статье содержится много информации. Мы изучили теорему Пифагора, поняли свойства треугольников и вычислили некоторые длины, периметры и площади.
Если вы все еще смущены, это совершенно нормально! Существует множество инструментов, которые могут вам помочь, включая веб-сайты, учебные пособия на YouTube, рабочие тетради и репетиторство.
h4: Репетиторство по математике
Вам сложно учиться самостоятельно, и вы предпочитаете работать с инструктором? В таком случае репетиторы — лучший выход. Вы лучше поймете предмет, работая с репетитором, потому что вы будете в небольшом классе или даже 1: 1.
Учащиеся начальной, средней, старшей школы и даже университета могут воспользоваться услугами репетиторства Tutorax на дому и онлайн. Доступны занятия с репетиторами по математике, английскому языку, естественным наукам, химии, физике, французскому языку и другим предметам.
Tutorax предлагает каждому учащемуся индивидуальную поддержку, чтобы помочь ему закрепить свое обучение и разработать стратегии обучения. Работа репетитора заключается в том, чтобы повысить уверенность и академическую мотивацию студента, а также помочь ему улучшить свои оценки.
Если у вас возникли проблемы с прямоугольными треугольниками в классе, Tutorax поможет вам с домашним заданием, планированием тестов, поддержкой класса и многим другим! Свяжитесь с нами сейчас, если вы хотите запросить репетитора, или нажмите здесь, если вы хотите подать заявку, чтобы стать репетитором!
Различные типы формул с примерами
Греческие слова пери, что означает вокруг, и метрон, что означает мера, являются корнями английского слова периметр. Периметр двумерной формы или периметр одномерной длины представляет собой замкнутый путь. Окружность круга или эллипса называется его периметром.
Периметр треугольника определяется сложением всех его сторон. Нахождение периметра треугольника имеет решающее значение для ряда целей. Это может быть что угодно: от расчета стоимости забора в саду на заднем дворе до измерения нити, необходимой для очертания периметра футбольного поля. Итак, давайте лучше поймем концепцию периметра треугольника с помощью формул для различных типов треугольников, шагов и решенных примеров.
Периметр треугольника
Периметр любой двумерной фигуры зависит от площади вокруг нее. Периметр любой замкнутой фигуры можно вычислить, сложив длины его сторон. Периметр многоугольника определяется суммой всех его сторон. Мы знаем, что длина каждой стороны правильного многоугольника одинакова.
Периметр правильного многоугольника = сумма всех его сторон = количество сторон ✕ длина одной стороны.
Треугольник — это многоугольник с тремя сторонами. Таким образом, периметр треугольника на самом деле равен сумме длин всех трех его сторон. Периметр треугольника — это общее расстояние, пройденное вдоль границы любого треугольника.
Периметр любой плоской фигуры можно представить как сумму ее границ. Поскольку периметр является мерой длины, он выражается в м, см, км и т. д. Треугольник — это многоугольник с тремя сторонами, и существует несколько способов вычисления его периметра.
Мы часто используем понятие периметра в реальной жизни. Например, когда мы расставляем вокруг дома фонари Дивали или когда мы хотим поставить забор вокруг заднего двора, мы находим его периметр, чтобы узнать длину провода, который нам понадобится.
Формула периметра треугольника
Периметр треугольника равен P= a + b + c, где a, b и c — стороны треугольников. Периметр любой двумерной фигуры определяется как расстояние вокруг нее. Комбинируя длины каждой из сторон, мы можем вычислить периметр любой замкнутой формы.
Периметр = сумма трех сторон в случае треугольника
Периметр треугольника можно рассчитать, сложив длины трех сторон треугольника. Но существуют и разные методы вычисления периметра треугольников разных типов.
Давайте рассмотрим это на примере:
Пример: Вычислите периметр заданного треугольника.
Мы знаем, что периметр треугольника равен
Периметр = A + B + C,
Где A, B, C = длина трех сторон.
Следовательно,
Для данного треугольника
Периметр = 5 см + 4 см + 3 см = 12 см
Узнать о периметре прямоугольного треугольника
Периметр равностороннего треугольника
В геометрии равносторонний треугольник — это треугольник, у которого все три стороны имеют одинаковую длину.
Поскольку все стороны равностороннего треугольника равны между собой, поэтому периметр равностороннего треугольника также можно рассчитать по формуле:
Периметр, P= 3L
Где L — длина сторон треугольника.
Эту формулу легко вывести из основной формулы периметра треугольника.
Как видно выше, периметр любого треугольника равен сумме всех сторон. Однако в случае равностороннего треугольника все стороны имеют одинаковую длину. Таким образом, A = B = C = L.
Следовательно, периметр = A + B + C = L + L + L = 3L
Периметр равнобедренного треугольника
Равнобедренный треугольник в геометрии — это треугольник, у которого по крайней мере две стороны имеют одинаковую длину. Поскольку две стороны равнобедренного треугольника равны, а одна сторона имеет другую длину, чем две другие, поэтому периметр равнобедренного треугольника также можно рассчитать по формуле:
Периметр, P = (2 × A) + B
Где A — длина двух равных сторон, а B — длина третьей стороны.
Это тоже можно вывести из основной формулы периметра треугольника.
Как видно выше, периметр любого треугольника равен сумме всех сторон. Однако в случае равнобедренного треугольника две стороны имеют одинаковую длину. Таким образом, A = C.
Следовательно, периметр = A + B + C = A + B + A = P= (2 × A) + B.
Периметр прямоугольного треугольника
Простейшая формула для нахождения площади прямоугольного треугольника — это сложение всех сторон вместе. Однако в некоторых случаях одна или две стороны могут быть неизвестны. Таким образом, мы должны применить некоторые теоремы или использовать некоторые формулы, чтобы найти периметр. Какую теорему мы применим, зависит от доступных нам данных. Если неизвестна только одна сторона, мы можем просто применить теорему Пифагора. Однако, если две стороны неизвестны, мы должны использовать закон синусов. 92\)
\(c = \sqrt{25}\)
\(c = 5\)
Закон синусов применим ко всем видам треугольников и кратко объясняется в следующих нескольких разделах.
Периметр равнобедренного прямоугольного треугольника
Треугольник, в котором один угол равен 90°, а два других угла по 45°, является равнобедренным прямоугольным треугольником. В равнобедренном прямоугольном треугольнике (рисунок ниже) ∠A и ∠C составляют по 45° каждая, а ∠B — по 90°. Стороны АВ и АС равны. Этот тип треугольника также известен как 45-9.0-45 треугольник
AC, сторона, противоположная ∠B, является гипотенузой. А АВ или АС можно принять за высоту или основание
Сумма всех сторон треугольника есть его периметр.
В прямоугольном равнобедренном треугольнике, поскольку две стороны (основание ВС и высота АВ) равны и каждая принимается за «В». А гипотенуза принимается за «Н».
Периметр = AB + BC + AC
= B+B+H
=2B+H
Периметр разностороннего треугольника
Разносторонний треугольник — это треугольник, в котором все три стороны имеют разную длину и все три угла имеют разную величину. Поскольку все стороны разностороннего треугольника имеют разную длину, его можно рассчитать только по обычной формуле:
Периметр разностороннего треугольника, P = A + B + C
, где A, B и C — длины сторон треугольника.
Периметр треугольника из вершин
Точка, в которой встречаются любые две стороны треугольника, называется вершиной треугольника. Мы можем найти периметр треугольника, зная координаты его вершин. Рассмотрим треугольник ABC, где \(A\equiv(x_1, y_1), B\equiv(x_2, y_2)\) и \(C\equiv(x_3, y_3)\) — вершины треугольника. Длины сторон равны длинам отрезков АВ, ВС и СА. Их можно найти, используя конечные точки сегментов по формуле расстояния: 92}\). Это доказывает, что этот закон согласуется с теоремой Пифагора.
Периметр треугольника, когда две стороны неизвестны (Закон синусов)
Этот закон можно использовать, когда известны как минимум два угла вместе с двумя сторонами. Этот закон также можно использовать в сочетании с другими законами и формулами для нахождения периметра любого треугольника. Этот закон также дает связь между синусом углов и сторонами треугольника.
\(\frac{sinx}{A} = \frac{siny}{B} = \frac{sinz}{C}\)
Здесь A, B и C стороны, противоположные углам x, y и z соответственно.
Полупериметр треугольника
В геометрии полупериметр многоугольника равен половине его периметра. Мы знаем, что периметр фигуры — это расстояние вокруг нее, но полупериметр — это половина расстояния вокруг нее. Полупериметр данного многоугольника можно вычислить, разделив его длину окружности на два для каждого заданного многоугольника. Несмотря на такое простое происхождение полупериметра от периметра, полупериметр достаточно часто встречается в формулах для треугольников и других фигур, поэтому ему дается отдельное название. Когда полупериметр встречается как часть формулы, он обычно обозначается буквой s.
Площадь треугольника по его периметру (формула Герона)
В большинстве формул для расчета площади используется высота треугольника. Когда высота треугольника неизвестна, мы используем формулу Герона для вычисления площади треугольника. Формула Герона дает площадь треугольника, не требуя произвольного выбора стороны в качестве основания или вершины в качестве начала координат, в отличие от других формул, вычисляющих площадь треугольника.
Площадь можно вычислить, используя все три стороны, где ни одна из сторон не равна.
\(\text {Площадь} =\sqrt{s(s-a)(s-b)(s-c)}\)
где \(a, b\) и \(c\) — длины сторон треугольника, а \(s\) – полупериметр треугольника, определяемый формулой \(s=\frac{a+b+c}{2}\).
Мы уже видели, что понимается под полупериметром треугольника. Таким образом, формула Герона может дать нам полупериметр треугольника, если известны площадь и стороны. По этому полупериметру можно легко вычислить периметр треугольника.
Шаги для нахождения периметра треугольника
Шаги для нахождения периметра треугольника зависят от доступных данных. Запомните следующие несколько моментов при нахождении периметра треугольника.
- Простой метод: Сложите все стороны
- Одна сторона неизвестна: Используйте теорему Пифагора для вычисления неизвестной стороны в случае прямоугольного треугольника. Используйте закон косинусов, чтобы найти неизвестную сторону в случае любого другого треугольника.
- Используйте закон синусов, если две стороны треугольника неизвестны.
- Используйте формулу площади, если известна площадь треугольника.
Ниже перечислены шаги:
Шаг 1: Вычислите/измерьте/отметьте все длины трех сторон.
Шаг 2: Сложите их вместе.
Шаг 3: Укажите в конце правильные единицы измерения.
Периметр против площади треугольника
Периметр — это сумма длин всех сторон фигуры. Площадь — это количество двухмерного пространства, которое занимает фигура. Чтобы лучше понять эти две концепции и их различия, давайте рассмотрим пример:
Рассмотрим треугольный участок земли со сторонами 10 м. Владелец хочет покрыть землю зеленой травой и поставить забор вокруг земли. Для этого он нанимает ландшафтного дизайнера. Ландшафтному дизайнеру необходимо заказать материалы. Как он рассчитает необходимое количество травяных циновок и деревянных заборов? Ответ прост: вычислив площадь и периметр треугольника.
В этом случае количество необходимых травяных матов будет определяться площадью треугольника, поскольку это дает нам количество пространства, покрытого землей. С другой стороны, периметр расскажет нам о длине забора.
Следует также помнить, что «Треугольник с фиксированным периметром может иметь множество различных площадей» .
Решенные примеры на периметре треугольника
Теперь, когда мы узнали о периметре треугольника, давайте посмотрим на некоторые решенные примеры.
Пример 1: Поскольку периметр равностороннего треугольника равен 24 см, найдите длины его трех сторон.
Решение: Периметр равностороннего треугольника равен трем длинам сторон, поскольку каждая из трех сторон треугольника имеет одинаковую длину.
Пусть длина любой стороны равна «a» единиц. Таким образом, периметр равен единицам «3а».
Итак, мы можем написать,
3a = 24
a = 8 см
Таким образом, длина каждой стороны равна 8 см.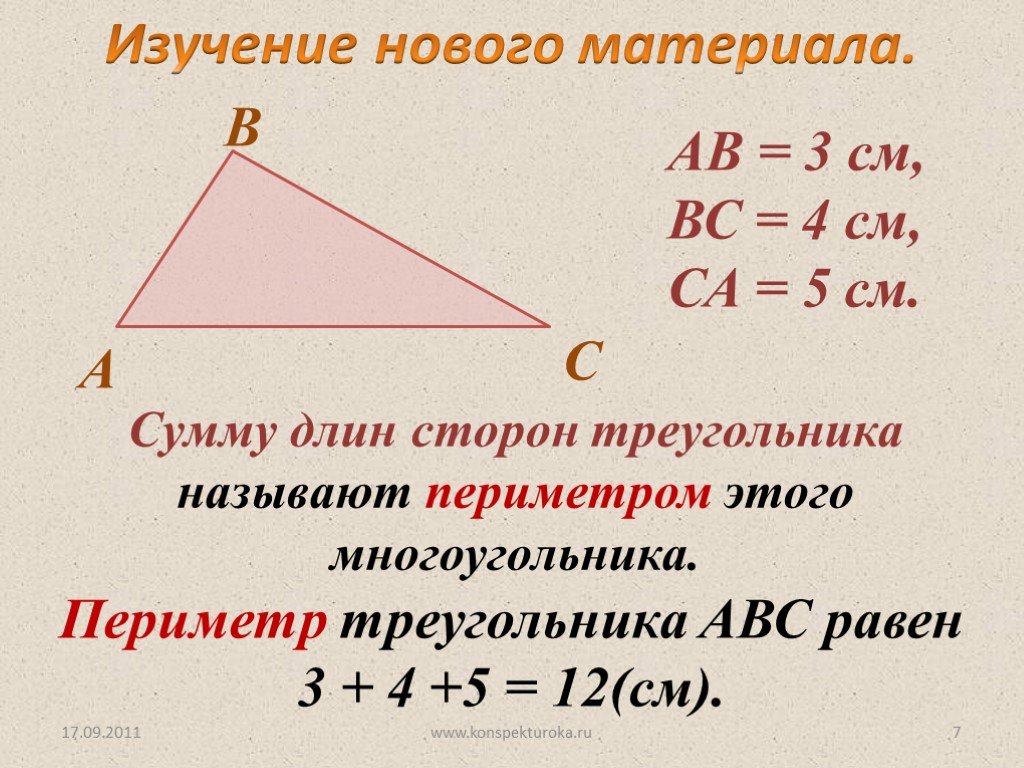
Пример 2: Если периметр треугольника равен 40 см, а длина двух его сторон по 8 см, какова будет длина третьей стороны треугольника?
Решение: Нам дано значение двух сторон треугольника, которые равны; следовательно, это равнобедренный треугольник.
Периметр равнобедренного треугольника = 2a + b
\(48 = (2\times 8) + b\)
\(b = \frac{48}{16}\)
b = 3 см
Пример 3: Рассмотрим прямоугольный треугольник ABC, в котором катетом AC является гипотенуза. Чему будет равен периметр треугольника, если стороны АВ и ВС равны 3 см и 4 см соответственно?
Решение: Нам нужны значения всех трех сторон, чтобы вычислить периметр прямоугольного треугольника. Поскольку это прямоугольный треугольник, мы можем вычислить длину стороны AC, используя теорему Пифагора. 9{2})}\)
\(AC = \sqrt{9+16}\)
\(AC = \sqrt{25}\)
AC = 5 см
Периметр = AB + BC + AC
Периметр = 3 + 4 + 5
Периметр = 12 см
Надеюсь, что эта статья о периметре треугольника была информативной.
Попрактикуйтесь в том же в нашем бесплатном приложении Testbook. Скачать сейчас!
Часто задаваемые вопросы о периметре треугольника
В.1 Как найти периметр треугольника?
Ответ 1 Периметр треугольника определяется сложением всех его сторон.
Q.2 Какова формула периметра треугольника?
Ответ 2 Периметр треугольника равен P= a + b + c, где a, b и c — стороны треугольников.
Q.3 Чему равен периметр равностороннего треугольника?
Ответ 3 Поскольку все стороны равностороннего треугольника равны друг другу, поэтому периметр равностороннего треугольника также можно рассчитать по формуле: Периметр, P = 3L.
Q.4 Чему равен периметр равнобедренного треугольника?
Ответ 4 Поскольку две стороны равнобедренного треугольника равны, а одна сторона имеет другую длину, чем две другие, поэтому периметр равнобедренного треугольника также можно рассчитать по формуле: Периметр, P = (2 × A) + B
Q.