Диаграмм эйлера венна: Диаграммы Эйлера-Венна

alexxlab / / Разное

Содержание

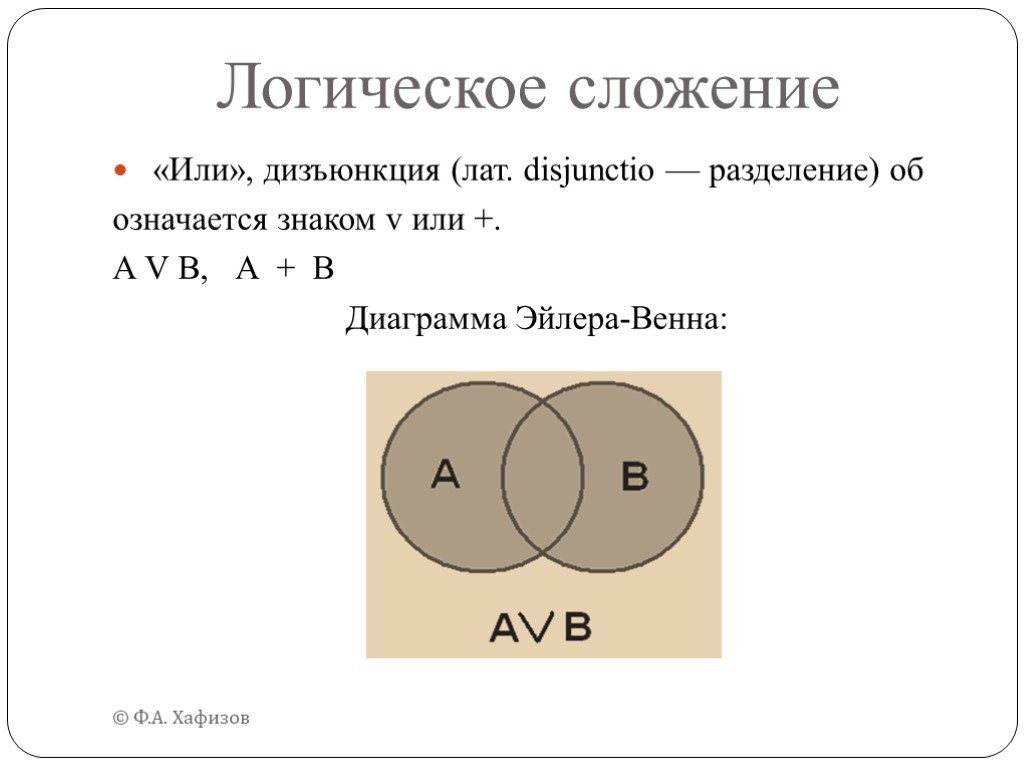
Диаграммы Эйлера-Венна

Диаграмма Эйлера-Венна — наглядное средство для работы со множествами. На этих диаграммах изображаются все возможные варианты пересечения множеств. Количество пересечений (областей) n определяется по формуле:

n=2N,

где N — количество множеств.

Таким образом, если в задаче используется два множества, то n=22=4, если три множества, то n=23=8, если четыре множества, то n=24=16. Поэтому диаграммы Эйлера-Венна используются в основном для двух или трех множеств.

Множества изображаются в виде кругов (если используется 2-3 множества) и эллипсов (если используется 4 множества), помещенных в прямоугольник (универсум).

Универсальное множество (универсум) U (в контексте задачи) — множество, содержащее все элементы рассматриваемой задачи: элементы всех множеств задачи и элементы, не входящие в них.

Пустое множество Ø (в контексте задачи) — множество, не содержащее ни одного элемента рассматриваемой задачи.


На диаграмме строят пересекающиеся множества, заключают их в универсум. Выделяют области, количество которых равно количеству пересечений.

Диаграммы Эйлера-Венна также используются для визуального представления логических операций.

Разберем примеры построения диаграмм Эйлера-Венна для двух и трех множеств.

Пример 1

Пусть есть следующие множества чисел:

А={1,2,3,4}

В={3,4,5,6}

Универсум U={0,1,2,3,4,5,6}

Диаграммы Эйлера-Венна для двух множеств А и В:

Определим области, и числа которые им принадлежат:

А
 B
 Обозначение
области
Числа
0
 0
 0)
0
0
 1
 1)
5,6
1
 0
 2)
1,2
1
 1
 3)
3,4

Пример 2

Пусть есть следующие множества чисел:

А={1,2,3,4}

В={3,4,5,6}

С={1,3,6,7}

Универсум U={0,1,2,3,4,5,6,7}

Диаграммы Эйлера-Венна для трех множеств А, В, С:

Определим области, и числа которые им принадлежат:

А
 B
 C
 Обозначение
области		Числа
0
 0
 0
 0)
0
0
 0
 1
 1)
7
0
 1
 0
 2)
5
0
 1
 1
 3)
6
1
 0
 0
 4)
2
1
 0
 1
 5)
1
1
 1
 0
 6)
 4
1
 1
 1
 7)
3

Пример 3

Пусть есть следующие множества чисел:

А={0,1,2,3,4,5,6,7}

В={3,4,5,7,8,9,10,13}

С={0,2,3,7,8,10,11,12}

D={0,3,4,6,9,10,11,14}

Универсум U={0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15}

Диаграммы Эйлера-Венна для четырех множеств А, В, С, D:

Определим области, и числа которые им принадлежат:

А
 B
 C
 D
Обозначение
области		Числа
0
 0
 0
 0
0)
15
0
 0
 0
 1
1)
14
0
 0
 1
 0
2)
12
0
 0
 1
 1
3)
11
0
 1
 0
 0
4)
13
0
 1
 0
 1
5)
9
0
1
 1
 0
6)
8
0
1
1
1
7)
10
1
 0
 0
 0
8)
1
1
0
0
1
9)
6
1
0
1
0
10)
2
1
0
1
1
11)
0
1
1
0
0
12)
5
1
1
0
1
13)
4
1
1
1
0
14)
7
1
1
1
1
15)
3

Если Вы хотите порешать типовые задач на множества, то перейдите к статье: «Как решать задачи с помощью диаграмм Эйлера-Венна». Там подробно разобрано 5 задач.

Перейти к разбору задач на множества из ЕГЭ по информатике:

  • В12-2012
  • В9-2011
  • В10-2010
  • В10-2009

как выглядит, как изобразить множества, примеры решения задач

Содержание:

  • Диаграмма Эйлера-Венна — что из себя представляет, где используется
  • Принципы построения, как изобразить множества
    • Дополнение множества
    • Объединение множеств
    • Пересечение множеств
    • Разность множеств
    • Симметричная разность множеств
  • Использование диаграмм Эйлера-Венна для доказательства логических равенств
  • Решение задачи поиска информации в Интернет с помощью диаграмм Эйлера-Венна
    • Как логические операции связаны с теорией множеств
  • Примеры задач с решением

Содержание

  • Диаграмма Эйлера-Венна — что из себя представляет, где используется
  • Принципы построения, как изобразить множества
    • Дополнение множества
    • Объединение множеств
    • Пересечение множеств
    • Разность множеств
    • Симметричная разность множеств
  • Использование диаграмм Эйлера-Венна для доказательства логических равенств
  • Решение задачи поиска информации в Интернет с помощью диаграмм Эйлера-Венна
    • Как логические операции связаны с теорией множеств
  • Примеры задач с решением

Диаграмма Эйлера-Венна — что из себя представляет, где используется

Определение

Диаграмма Эйлера-Венна представляет собой геометрическую схему, предназначенную для представления моделей множеств и схем их взаимосвязей.

Благодаря данной диаграмме, приводят наглядное объяснение разных фактов о множествах. При таком методе универсальное множество представляют в виде прямоугольника, а для изображения подмножества используют круги. Широкое применение диаграммы Эйлера-Венна нашли в таких дисциплинах, как математика, логика, менеджмент, финансы и другие прикладные направления.

Примечание

Способы отражения отношений между множествами ранее отличались. Джон Венн применял в качестве обозначения множеств замкнутые фигуры, а Эйлер – круги.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Диаграммы Эйлера-Венна представляют собой важный частный случай кругов, которые изображал Эйлер. На диаграммах представлены все 2n комбинаций n свойств, что является конечной булевой алгеброй. Если n = 3, на диаграмме, как правило, изображают три круга с центрами, которые расположены в углах равностороннего треугольника, и совпадающими радиусами, ориентировочно равными длине сторон этого многоугольника.

Принципы построения, как изобразить множества

Определение

Построить диаграмму Эйлера-Венна – значит, составить большой прямоугольник, представляющий универсальное множество U, и разместить внутри него замкнутые фигуры в качестве обозначения множеств.

В том случае, когда требуется строить на диаграмме не более трех множеств, целесообразно использовать круги. Для изображения свыше четырех множеств применяют эллипсы. Пересечение фигур соответствует максимально общему случаю, согласно условиям задачи, и изображается должным образом на диаграмме.

Если предположить, что диаграмма содержит круг, обозначающий множество А, его центральная часть будет отражать истинность выражения А, а область вне круга – обозначать ложь. Те области, которые соответствуют истинным значениям, заштриховывают, что является отражением логической операции на диаграмме.

Согласно алгебре логики, конъюнкция множеств А и В соответствует истине в том случае, когда истинны оба эти множества. При этом на диаграмме отмечают участок пересечения множеств.

Применяя диаграммы Эйлера-Венна, доказывают любые алгебраические законы с помощью их графического изображения. Алгоритм построения:

  • изображение диаграммы с заштрихованными множествами, которые представлены в левой части выражения;
  • чертеж другой диаграммы с заштрихованными множествами, расположенными в правой части уравнения;
  • сравнение заштрихованных областей на диаграммах: если это одна и та же область, то можно говорить об истинности тождества.

Данные диаграммы являются эффективным методом визуализации операций с множествами. Отдельные множества изображают в виде кругов, а универсальное множество представляют прямоугольником.

Дополнение множества

Источник: avatars.mds.yandex.net Источник: avatars.mds.yandex.net

Объединение множеств

Источник: avatars.mds.yandex.net Источник: avatars. mds.yandex.net

Пересечение множеств

Источник: avatars.mds.yandex.net Источник: avatars.mds.yandex.net

Разность множеств

Источник: avatars.mds.yandex.net Источник: avatars.mds.yandex.net

Симметричная разность множеств

Источник: avatars.mds.yandex.net Источник: avatars.mds.yandex.net

Использование диаграмм Эйлера-Венна для доказательства логических равенств

В качестве доказательства логического равенства подходит способ построения диаграмм Эйлера-Венна. Для примера можно представить доказательства следующего выражения: ¬(АvВ) = ¬А&¬В. Равенство демонстрирует запись закона де Моргана. В первую очередь следует наглядно изобразить левую часть уравнения. Для этого необходимо последовательно заштриховать серым цветом все круги, то есть применить дизъюнкцию. Отобразить инверсию можно с помощью закрашивания черным цветом области вне этих кругов.

Источник: urok.1sept.ru Источник: urok.1sept.ru

Далее следует визуально представить правую часть выражения. Последовательность действий в этом случае такова: необходимо заштриховать область, в которой отображается инверсия (¬А), с использованием серого цвета и аналогично закрасить область ¬В; отобразить конъюнкцию в виде пересечения этих серых областей. Результат такого наложения будет окрашен черным цветом.

Источник: urok.1sept.ru Источник: urok.1sept.ru Источник: urok.1sept.ru

На рисунке видно, что области, в которых отображены левая и правая части уравнения, равны друг другу. Таким образом, закономерность доказана.

Решение задачи поиска информации в Интернет с помощью диаграмм Эйлера-Венна

Изучая тему поиска информации в глобальной сети Интернет, нельзя обойтись без примеров поисковых запросов, в которых использованы логические связки. Как правило, их смысл аналогичен союзам «и», «или» из русского языка. Принцип действия можно понять, если изобразить логические связи с помощью графической схемы или диаграммы Эйлера-Венна.

Источник: urok.1sept.ru

Как логические операции связаны с теорией множеств

Используя диаграммы Эйлера-Венна, принято наглядно демонстрировать связь логических действий и теории множеств. Операции логики можно задать с помощью таблиц истинности. В этом случае следует руководствоваться общим принципом.

На диаграмме в виде области круга под названием А отображают истинность определения А, то есть теоретически круг А обозначает все элементы, которые включены в данное множество. Таким образом, область за пределами круга А будет обозначать ложь соответствующего утверждения.

Понимание, какая область диаграммы отражает логическую операцию, возникает после того, как будут заштрихованы только те области, в которых значения логической операции на наборах А и В соответствуют истине. К примеру, импликация истинна при (00, 01 и 11).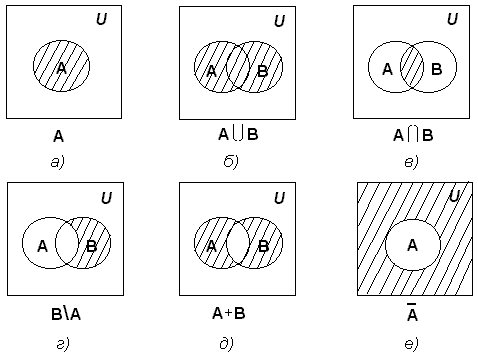

Необходимо заштриховать сначала область за пределами пары пересекающихся кругов в соответствии со значениями А=0, В=0. Затем закрасить область в круге В, которая относится к значениям А=0, В=1, и область, соответствующую и кругу А, и кругу В, то есть участок пересечения, отображающий значения А=1, В=1. Эти три области в комплексе являются графическим представлением логической импликации.

Примеры задач с решением

Диаграммы Эйлера-Венна могут содержать три и более круга. Преимуществом данного графического способа представления выражений является его высокая эффективность и наглядность. К примеру, можно изобразить диаграмму пересечений букв из русского, латинского и греческого алфавита:

Источник: avatars.mds.yandex.net

Понять суть методики удобно на практике. Можно решить несколько задач с применением диаграмм Эйлера-Венна.

Задача 1

По условию есть таблица поисковых запросов. В ней представлены страницы по некоторому сегменту. Требуется определить, сколько страниц в тысячах будет отображаться по запросу «Эсминец». Следует отметить, что запросы выполнялись практически в одно время, поэтому набор страниц с искомыми словами не менялся в процессе выполнения запросов.

Источник: urok.1sept.ru

Решение

Допустим, что:

Ф – является числом страниц (в тысячах) в соответствии с запросом «Фрегат»;

Э – является числом страниц (в тысячах) в соответствии с запросом «Эсминец»;

Х – представляет собой число страниц (в тысячах) по запросу, в котором присутствует «Фрегат» и отсутствует «Эсминец»;

У – определяет число страниц (в тысячах) по запросу, в котором указано слово «Эсминец» и отсутствует слово «Фрегат».

Диаграмма для каждого поискового запроса будет иметь следующий вид:

Источник: urok.1sept.ru

Исходя из информации по диаграммам, получим:

Х+900+У = Ф+У = 2100+У = 3400

Таким образом:

У = 3400-2100 = 1300

Э = 900+У = 900+1300= 2200

Ответ: по запросу «Эсминец» будет найдено 2200 страниц

Задача 2

Класс состоит из 36 учеников. Дети ходят на занятия в рамках математического, физического, химического кружка. Факультатив по математике посещают 18 учащихся, по физике – 14, по химии – 10. Также известно, что 2 ученика ходят на все три кружка, 8 – на математику и физику, 5 – на математику и химию, 3 – на физику и химию. Необходимо определить количество учеников, которые не посещают ни одного кружка.

Решение

Решить данную задачу можно с помощью удобного и наглядного метода в виде кругов Эйлера. Наибольшим кругом следует обозначить множество всех учащихся класса. Внутри этой окружности необходимо изобразить пересекающиеся множества в виде учащихся на факультативе по математике (М), физике (Ф), химии (Х).

Допустим, что:

МФХ – является множеством учеников, каждый из которых ходит на занятия во все три кружка;

МФ¬Х – определяет множество учащихся, которые посещают факультативы по математике и физике, но не ходят на занятия по химии.

¬М¬ФХ – представляет собой множество людей, каждый из которых посещает химический факультатив, но отказался от дополнительных занятий по физике и математике.

По аналогичному принципу можно ввести множества: ¬МФХ, М¬ФХ, М¬Ф¬Х, ¬МФ¬Х, ¬М¬Ф¬Х.

Согласно условиям задачи, пара учеников записаны во все три кружка. Поэтому в область МФХ требуется вписать число 2. Исходя из того, что 8 учащихся посещают факультативы по математике и физике, а из них двое школьников ходят во все кружки, то в области МФ¬Х следует отметить 6 человек (8-2). Аналогичным способом можно определить число учеников в остальных множествах:

Источник: urok.1sept.ru

Далее требуется определить сумму учеников по всем областям:

7+6+3+2+4+1+5=28

Таким образом, всего 28 учащихся посещают факультативные занятия.

Поэтому:

36 – 28 = 8

Ответ: 8 учеников из класса не посещают ни одного кружка.

Задача 3

Когда закончились зимние каникулы, преподаватель поинтересовался у учеников, кто из них посещал театр, кино или цирк. Всего в классе 36 человек. По полученной информации, два ребенка не были ни в кино, ни в театре, ни в цирке. Кино посетили 25 школьников, театр – 11, цирк – 17. И в кино, и в театр сходили 6 человек, и в кино, и в цирк – 10, и в театр, и в цирк – 4. Необходимо посчитать, какое количество учащихся из класса посетили и кино, и театр, и цирк.

Решение

Предположим, что х представляет собой число учеников, которые посетили и кино, и театр, и цирк. В таком случае, можно изобразить диаграмму и определить число школьников для каждой области:

Источник: urok.1sept.ru

Ответ: 1 ученик побывал и в кино, и в театре, и в цирке.

Насколько полезной была для вас статья?

Рейтинг: 2.75 (Голосов: 4)

Постройте диаграммы Эйлера и Венна — plot.euler • eulerr

  • Ссылка
  • Статьи
  • Список изменений

Источник: R/plot.euler.R

plot. euler.Rd

Диаграммы графика соответствуют euler() и venn() grid() 90:Grid() 190:Grid() с использованием 90:Grid() . Этот функция устанавливает все необходимые параметры графика и вычисляет геометрия схемы. plot.eulergram() , тем временем, делает фактическое построение диаграммы. См. раздел Подробная информация о . чтобы узнать об индивидуальных настройках для каждого аргумента.

 # S3 метод Эйлера
сюжет(
  Икс,
  заполняет = ИСТИНА,
  края = ИСТИНА,
  легенда = ЛОЖЬ,
  метки = идентичные (легенда, ЛОЖЬ),
  количества = ЛОЖЬ,
  полоски = NULL,
  основной = NULL,
  п = 200л,
  настроить_метки = ИСТИНА,
  ...
)
# Метод S3 для venn
сюжет(
  Икс,
  заполняет = ИСТИНА,
  края = ИСТИНА,
  легенда = ЛОЖЬ,
  метки = идентичные (легенда, ЛОЖЬ),
  количества = ИСТИНА,
  полоски = NULL,
  основной = NULL,
  п = 200л,
  настроить_метки = ИСТИНА,
  ...
)

Аргументы

x

объект класса 'euler' , сгенерированный из euler()

заполняет

логический, векторный или список графических параметров заливки на диаграмме. Предполагается, что векторы являются цветами для заливки. См. grid::grid.path() .

ребра

логический, векторный или список графических параметров для ребер на диаграмме. Предполагается, что векторы являются цветами ребер. См. grid::grid.polyline() .

легенда

логический скаляр или список. Если список, элемент со стороны можно использовать для установки расположения легенды. Видеть grid::grid.legend() .

этикетки

логический, векторный или список. Предполагается, что векторы текст для этикеток. См. grid::grid.text() .

количество

логический, векторный или список. Предполагается, что векторы текст для меток количеств, которые по умолчанию исходные значения на входе до эйлер() . Кроме того к аргументам, которые применяются к grid::grid.text() , аргумент типа может также использовать, что должно быть комбинацией "счетов" и "процент" . Первый элемент будет напечатан первым, а второй после этого будет напечатано внутри квадратных скобок. По умолчанию тип = "подсчитывает" .

полоски

список, игнорируемый, если не указан аргумент 'by' использовался в euler()

основной

титул на участок в виде символ, выражение, список или что-то, что может быть разумно преобразовано в метку через grDevices::as.graphicsAnnot() . А список длины один может быть предоставлен, и в этом случае его единственный элемент используется в качестве метки. Если предоставляется список большей длины, элемент named 'label' должен быть предоставлен (и будет использоваться для фактического текста).

п

количество вершин для края и заливки

настроить_метки

логический. Если TRUE , будет выполнена корректировка, чтобы избежать перекрытие или выход за пределы маркировки, количества и проценты.

...

параметры для обновления заполняет и края и тем самым ярлык чтобы установить эти параметры grid::grid.text() .

Значение

Предоставляет объект класса 'eulergram' , который является описание схемы, которую необходимо нарисовать. plot.eulergram() делает фактическое рисунок схемы.

Детали

Единственная разница между plot.euler() и plot.venn() заключается в том, что количество устанавливается на TRUE по умолчанию в последнем и FALSE в бывший.

Большинство аргументов этой функции принимают логические, векторные или список, где

  • логические значения включают или выключают атрибут,

    • Векторы

  • являются ярлыками для часто используемых опций (см. параметры) и

    • Списки

  • обеспечивают детальное управление, включая графическое параметры, как описано в grid::gpar() и управление аргументы, специфичные для каждого аргумента.

Различные значения grid::gpar() , доступные для каждого аргумента находятся:

0 9 0 x 09
заливки края этикетки количество полосы легенда основная цвет 909202
x x x x x заполнение x
альфа x x x x2 18
х х lty x
lwd x000 lex
x размер шрифта x
x x x x cex x x x 2 902 0202 х fontfamily x x x x x
lineheight0 9 x x x x шрифт

По умолчанию для этих значений, а также других параметров графиков можно быть установлен глобально с помощью eulerr_options() .

Если диаграмма подобрана с использованием матрицы data.frame или методы и используя аргумент на , область графика будет разделена на панели для каждое сочетание одного-двух факторов.

Для пользователей, которые хотят построить свою диаграмму с помощью другого пакета, все необходимые параметры можно собрать, если результат этого функция присваивается переменной (а не выводится на экран).

См. также

euler() , plot.eulergram() , grid::gpar() , сетка::grid.polyline() , сетка::grid.path() , grid::grid.legend() , grid::grid.text()

Примеры 

 fit <- euler(c("A" = 10, "B" = 5, "A&B" = 3 ))
# Настройка цветов, удаление границ, повышение альфа-канала, белые цветные метки
сюжет (подходит,
     fills = list(fill = c("красный", "steelblue4"), альфа = 0,5),
     метки = список (столбец = "белый", шрифт = 4))

# Добавляем количество на график
график (подгонка, количества = ИСТИНА)

# Добавьте пользовательскую легенду и сохраните количество
график (подгонка, количества = ИСТИНА, легенда = список (метки = c («foo», «bar»)))

# Нарисуйте без заливки и вместо этого различайте наборы с типами границ
график (подходит, заливки = "прозрачный", lty = 1: 2)

# Сохраняем параметры графика для построения другим методом
диаграмма_описание <- сюжет (подходит)
# Графики с использованием аргумента 'by'
сюжет (эйлер (фрукты [ 1: 4], по = список (пол)), легенда = ИСТИНА)

VennDiagram: пакет для создания диаграмм Венна и Эйлера с широкими возможностями настройки в R | BMC Биоинформатика

  • Программное обеспечение
  • Открытый доступ
  • Опубликовано:
  • Ханбо Чен 1 и
  • Пол Бутрос 1  

Биоинформатика BMC том 12 , номер статьи: 35 (2011) Процитировать эту статью

  • 109 тыс. обращений

  • 1346 цитирований

  • 16 Альтметрический

  • Сведения о показателях

Abstract

Background

Визуализация ортогональных (непересекающихся) или перекрывающихся наборов данных является обычной задачей в биоинформатике. Существует несколько инструментов для автоматизации создания широко настраиваемых диаграмм Венна и Эйлера с высоким разрешением в статистической среде R. Чтобы заполнить этот пробел, мы представляем VennDiagram , пакет R, который позволяет автоматически генерировать настраиваемые диаграммы Венна с высоким разрешением, содержащие до четырех наборов, и диаграммы Эйлера, содержащие до трех наборов.

Результаты

Пакет VennDiagram предлагает пользователю возможность настраивать практически все аспекты сгенерированных диаграмм, включая размеры шрифта, стили и расположение меток, а также общий поворот диаграммы. Мы внедрили масштабированные диаграммы Венна и Эйлера, которые повышают графическую точность и визуальную привлекательность. Диаграммы создаются в виде файлов TIFF высокого разрешения, что упрощает процесс создания показателей качества публикации и облегчает интеграцию с установленными конвейерами анализа.

Выводы

Пакет VennDiagram позволяет создавать высококачественные диаграммы Венна и Эйлера в статистической среде R.

История вопроса

Визуализация сложных наборов данных становится все более важной частью биологии. Многие эксперименты включают интеграцию нескольких наборов данных для понимания взаимодополняющих аспектов биологии. Эти перекрывающиеся результаты можно визуализировать несколькими способами, включая текстовые таблицы (например, двусторонние таблицы), сетевые диаграммы [1, 2] и, в некоторых случаях, тепловые карты [3, 4]. Диаграммы Венна находят все более широкое применение из-за их привычности, простоты интерпретации и графической простоты. Для целей данной публикации диаграммы Венна можно определить как диаграммы, использующие простые геометрические формы, такие как круги и эллипсы, для отображения всех 2 n -1 возможные области, созданные взаимодействием n множеств. Использование простых геометрических фигур снижает сложность и размер фигур по сравнению с занимающими много места таблицами или сетевыми макетами.

Однако, несмотря на эту популярность, в настоящее время существует несколько пакетов для создания диаграмм Венна в широко используемой статистической среде R. Эти пакеты ограничены в своих возможностях генерировать диаграммы Венна с высоким разрешением и качеством публикации, поскольку они допускают небольшую настройку цветов, типов линий, размещения меток и шрифта меток. Многочисленные особые случаи обрабатываются неправильно, и выходные данные обычно не имеют формат файлов TIFF с высоким разрешением и качеством публикации. Существуют другие локальные или веб-программы, не основанные на R, способные генерировать диаграммы Венна, такие как Venny [5], BioVenn [6], ConSet [7] и VennMaster [8]. Все они страдают некоторыми из недостатков, перечисленных выше. Кроме того, интеграция в стандартные статистические/вычислительные конвейеры на основе R, такие как широко используемые библиотеки BioConductor статистической среды R [9].] является жизнеспособным, но технически не тривиальным.

Кроме того, если некоторые пересекающиеся или непересекающиеся области на диаграмме Венна не существуют, более желательным может быть другой класс диаграмм, называемый диаграммами Эйлера. Диаграммы Эйлера эквивалентны диаграммам Венна, когда существуют все пересекающиеся и непересекающиеся области. Однако области, содержащие нулевые элементы, показаны на диаграммах Венна (по определению), тогда как диаграммы Эйлера показывают только ненулевые области. Во многих случаях диаграммы Эйлера дополнительно уменьшают сложность фигур, повышают графическую точность и улучшают общую читаемость по сравнению с диаграммами Венна. К сожалению, почти все существующие пакеты не могут генерировать диаграммы Эйлера с качеством публикации в R, хотя VennEuler создает диаграммы Эйлера.

Для решения этих проблем мы представляем VennDiagram , пакет R для создания настраиваемых диаграмм Венна с высоким разрешением, содержащих до четырех наборов, и диаграмм Эйлера, состоящих из двух или трех наборов, в статистической среде R.

Реализация

Пакет VennDiagram был разработан и предназначен для статистической среды R. Среда R имеет открытый исходный код и доступна в Интернете по Стандартной общественной лицензии GNU (GPLv2). R был выбран из-за его природы с открытым исходным кодом, универсальных функций и общих предпочтений в сообществе биоинформатики. Использование R должно облегчить интеграцию с существующими конвейерами анализа данных. Весь код был разработан и протестирован с использованием версии 2.12.1 (32-разрядная и 64-разрядная версии) R. Пакет VennDiagram доступен в виде дополнительных файлов 1 (файл .tar.gz для Linux) и 2 (файл .zip для Windows).

VennDiagram использует пакет сетки для графики. Пакет сетки является базовым (стандартным) пакетом, доступным во всех установках, и предлагает большую маневренность, чем графика R по умолчанию, с точки зрения графических параметров и наличия изменяемых объектов сетки. VennDiagram использует эти функции для динамического растягивания/сжатия диаграмм в соответствии с размерами выходного файла и предлагает большое количество графических опций.

Результаты

Почти все графические опции в 9Пакет 0450 VennDiagram был параметризован и стал настраиваемым. Значения по умолчанию были выбраны для создания разумных диаграмм, поэтому в простых случаях не требуется высокий уровень настройки. На рис. 1 показано разнообразие доступных параметризаций. Существуют четыре основные группы графических параметров: форма-заливка, форма-линия, метки и заголовки. Форма-заливка относится к цветам внутри каждого круга или эллипса. Можно использовать все цвета, доступные в среде R, а альфа-смешивание можно настроить для каждой фигуры. Линии фигуры — это линии, окружающие каждый круг или эллипс. Они могут полностью отсутствовать (рис. 1C), быть сплошными (рис. 1A и 1B) или иметь любой другой доступный тип R-линий (рис. 1D). Их цвет можно менять, и каждая фигура может иметь отдельный набор параметров. Метки относятся как к заголовкам, описывающим каждый круг или эллипс, так и к числам внутри них. Опять же, их можно настроить с точки зрения цвета, типа шрифта и размера шрифта с любым доступным параметром R. Положения меток заголовков также можно настроить. Заголовки, которые включают основной заголовок и подзаголовок, как показано на рисунке 1D, также можно настраивать так же, как и метки.

Рисунок 1

Четыре типа диаграмм Венна, нарисованные пакетом VennDiagram . A) Диаграмма Венна с одним набором, показывающая элементарные настраиваемые функции, такие как размер шрифта метки, шрифт метки и заливка формы. B) Диаграмма Венна с двумя наборами, показывающая более продвинутые функции, такие как масштабирование, индивидуальные характеристики заполнения формы и размещение отдельных подписей. C) Диаграмма Венна с тремя наборами, показывающая другой тип контурной линии («прозрачный») и «текстовый» вариант размещения метки заголовка, где метки заголовков прикреплены к меткам областей. D) Диаграмма Венна с четырьмя наборами, показывающая комбинацию всех предыдущих функций плюс возможность настройки заголовков. Код для создания всех показанных здесь диаграмм включен в дополнительный файл 3.

Полноразмерное изображение

Помимо этих конкретных графических элементов, VennDiagram также предлагает множество общих параметров, таких как масштабирование, поворот или инверсия диаграмм. Масштабирование диаграмм реализовано с целью отображения диаграмм Венна, где графические размеры частичных областей (областей, ограниченных со всех сторон кривыми и не поддающихся дальнейшему подразделению) фактически соответствуют числовым значениям количества элементов внутри каждой области. Масштабирование диаграмм Венна с двумя наборами и выбранного количества диаграмм Венна с тремя наборами возможно - ниже мы обсудим проблемы, связанные с тем, чтобы сделать это возможным для всех случаев с тремя наборами. Использование масштабирования иногда может привести к тому, что перекрывающиеся области будут слишком малы для числовых меток. На рис. 2, строка 1, столбец 1 показана программно сгенерированная соединительная линия, которая позволяет специально обрабатывать этот случай. Реализовано автоматическое распознавание большого количества диаграмм Эйлера, но этот режим можно отключить с помощью параметра вызова функции, чтобы вместо этого строить стандартные диаграммы Венна. На рис. 2, строка 1, столбцы 2 и 3 показаны два примера двухмножественных диаграмм Эйлера.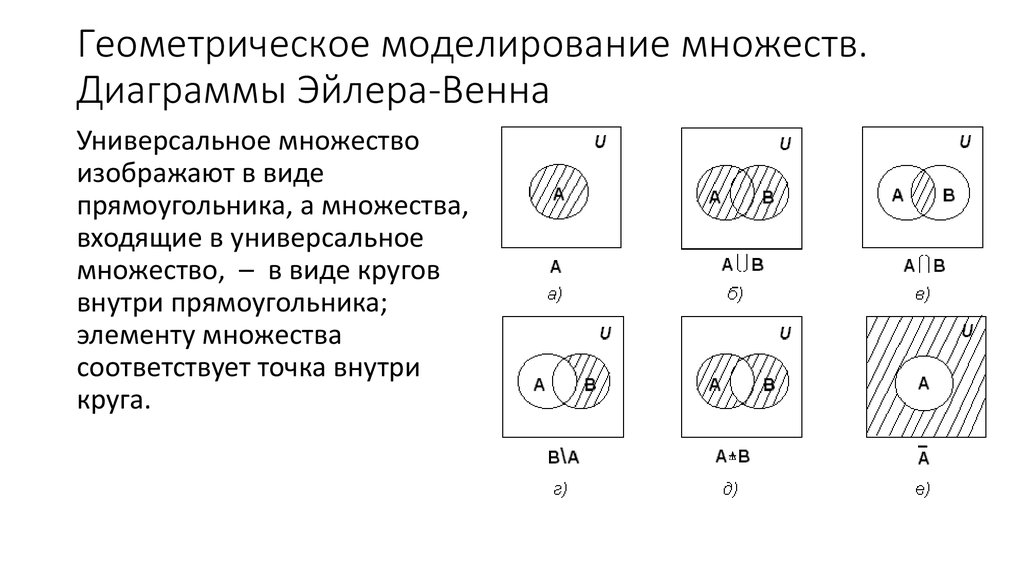 В строках 2 и 3 показано подмножество реализованных диаграмм Эйлера с тремя наборами, а в строке 3 показаны диаграммы масштабируемого разнообразия. Отметим, что рисунок 2 представлен в черно-белом цвете, чтобы подчеркнуть композиционные различия между диаграммами, но графические параметры и настройки, использованные на рисунке 1, полностью доступны. В то время как VennDiagram по умолчанию записывает графику в файлы TIFF с высоким разрешением, если для параметра имени файла установлено значение NULL, необработанный объект сетки может быть возвращен и использован в любом графическом режиме, доступном в R. Код для создания всех рисунков приведен в дополнительном файле 3. а пример всех доступных параметризаций показан в дополнительном файле 4.

Рисунок 2

Избранные частные случаи диаграммы Венна и диаграммы Эйлера, нарисованные пакетом VennDiagram . Строка 1, столбец 1: автоматически рисуемые настраиваемые линии, которые оптимизируют отображение частичных областей, когда отдельные частичные области становятся слишком маленькими на диаграммах Венна, состоящих из двух наборов. Строка 1, столбец 2: диаграмма Эйлера с двумя наборами, показывающая полное включение одного из наборов. Строка 1, столбец 3: диаграмма Эйлера с двумя множествами, показывающая два различных множества. Строка 2, столбец 1: диаграмма Эйлера с тремя множествами, где одно множество не имеет дискретных элементов. Строка 2, столбец 2: диаграмма Эйлера с тремя множествами, в которой одно множество не имеет дискретных элементов, полностью включено в одно из двух других множеств. Строка 2, столбец 3: диаграмма Эйлера с тремя множествами, где два множества не имеют дискретных элементов и включены в большее третье множество. Строка 3, столбец 1: диаграмма Эйлера с тремя наборами, показывающая полное включение двух наборов, отличных от третьего набора. Строка 3, столбец 2: диаграмма Эйлера с тремя наборами, где один набор полностью включен в другой набор, который сам полностью включен в третий набор. Строка 3, столбец 2: диаграмма Эйлера с тремя множествами, показывающая три различных множества. Код для создания всех показанных здесь диаграмм включен в дополнительный файл 3.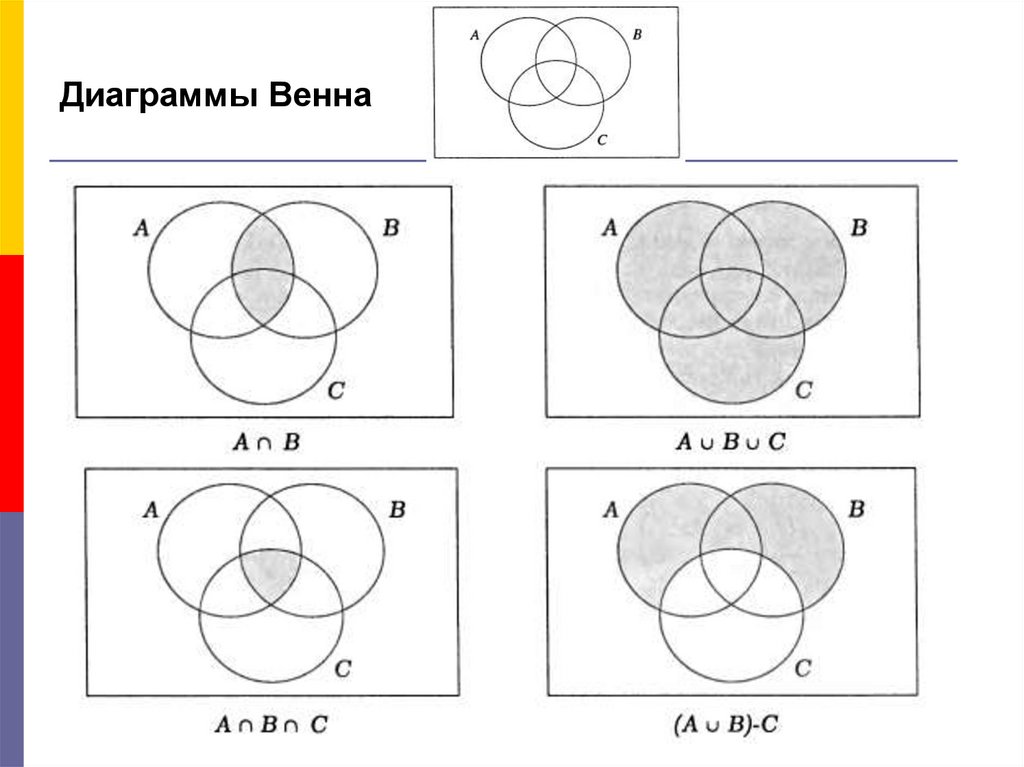

Изображение полного размера

Обсуждение

В ходе разработки пакета VennDiagram было обнаружено, что невозможно нарисовать точные, масштабированные диаграммы Венна с тремя наборами, используя круги. Эта загадка иллюстрируется следующим сценарием. В системе двух окружностей A и B расстояния между центрами окружностей d AB можно определить, если площади (A A и A B соответственно) и площадь пересечения (A A ∩ A B ) известны. Это возможно, потому что в системе с двумя кругами единственному A A ∩ A B соответствует уникальное значение для d AB . Следовательно, система из трех окружностей A, B и C, d AB , d BC , d AC может быть вычислена до тех пор, пока A A , A B , A C , A A ∩ A B , A A ∩ A C , A B ∩ A C все известны.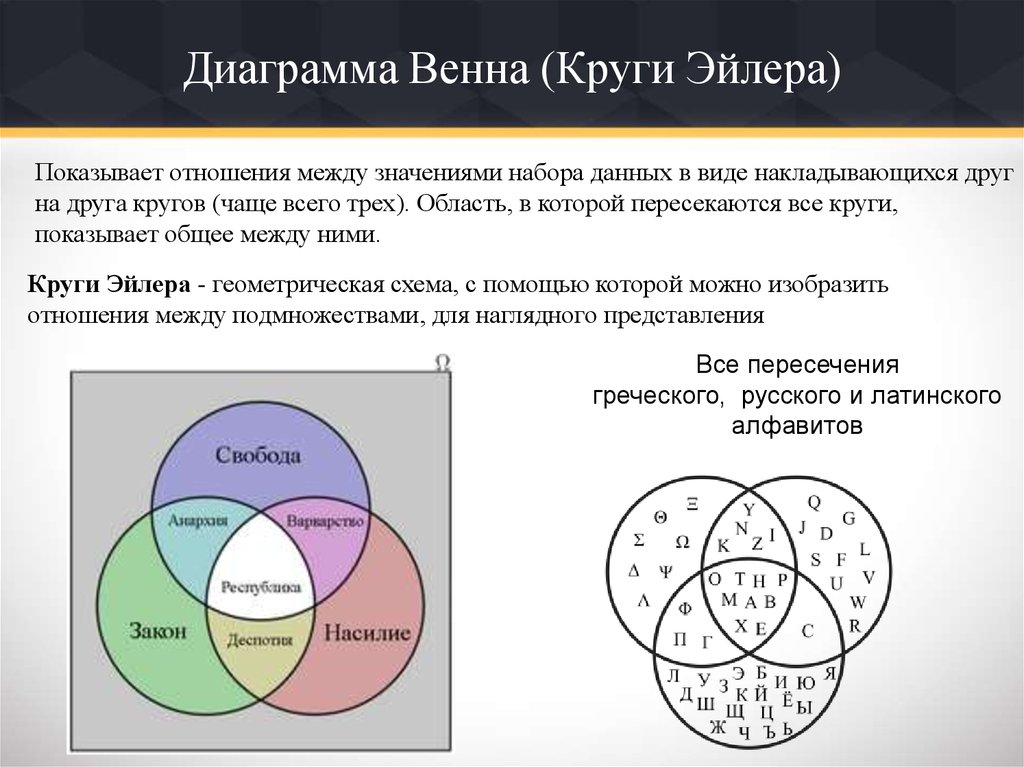 Однако д AB , d BC , d AC составляют уникальный треугольник, подразумевая, что диаграмму Венна можно нарисовать, даже не зная общего пересечения A A ∩ A B ∩ A C . Другими словами, размер перекрытия между всеми тремя кругами не меняет представление масштабированных диаграмм Венна — площадь не меняется, даже если одна система имеет нулевое полное пересечение (т.е. A A ∩ A B ∩ A С = 0)! Эта головоломка возникает из-за (произвольного) выбора кругов для представления размера набора, что уменьшает степень свободы на одну. Уникальные решения можно определить, используя эллипсы или многоугольники для рисования диаграмм Венна, но полученные диаграммы потеряют мгновенную узнаваемость и привычность, связанные с круговыми диаграммами Венна, что лишает возможности удобного отображения информации. Некруговые диаграммы также потребуют итерационных алгоритмов для вычисления положения и размеров фигур, что значительно увеличивает вычислительную нагрузку, как обсуждалось другими [10]. Следовательно, масштабирование трехмножественных диаграмм Венна отключено в Пакет VennDiagram . Точно так же диаграммы Венна, содержащие более четырех наборов [11, 12], не были реализованы в пакете VennDiagram , поскольку они стали слишком сложными для интуитивной визуализации.

Общее предостережение при использовании диаграмм Эйлера состоит в том, что, хотя они уменьшают графическую сложность некоторых диаграмм Венна, их нетрадиционные формы в некоторых случаях также могут быть менее узнаваемыми. Когда присутствуют пустые области, пользователю необходимо выбирать между знакомыми диаграммами Венна и повышенной точностью диаграмм Эйлера. На рис. 3 показана ситуация, когда в зависимости от предпочтений пользователя может подойти либо диаграмма Венна, либо диаграмма Эйлера.

Рисунок 3

Наглядное сравнение диаграммы Эйлера и диаграммы Венна для одних и тех же гипотетических наборов . А) Диаграмма Эйлера показывает только ненулевые площади и поэтому может быть более точной графически. Б) На диаграмме Венна несуществующая область показана как область с нулевым содержимым. Хотя это не является графически точным, оно сохраняет узнаваемость диаграммы Венна.

Изображение полного размера

Пакет VennDiagram обрабатывает все двухмножественные диаграммы Эйлера и большинство всех мыслимых трехмножественных диаграмм Эйлера. Диаграммы Эйлера с тремя наборами, которые нельзя нарисовать с помощью кругов или эллипсов, не поддерживаются. Например, диаграмму Эйлера для случая, когда два непересекающихся набора составляют третий набор, нельзя нарисовать с помощью кругов и эллипсов, хотя ее можно нарисовать с помощью многоугольников. Этот тип рисунка не имеет готового аналитического макета и требует итеративной подгонки; диаграммы Эйлера, требующие многоугольников, недоступны, но для этих нескольких неподдерживаемых случаев доступны стандартные диаграммы Венна.

По сравнению с другими программами, способными создавать диаграммы Венна (таблица 1), преимущества пакета VennDiagram включают:

  • Рисование диаграмм Эйлера с использованием кругов и/или эллипсов с двумя или тремя наборами

  • Расширенные возможности настройки для создания более элегантных диаграмм

  • Доступность в широко используемой статистической среде R

  • Создание файлов TIFF с высоким разрешением, которые являются стандартными в публикациях

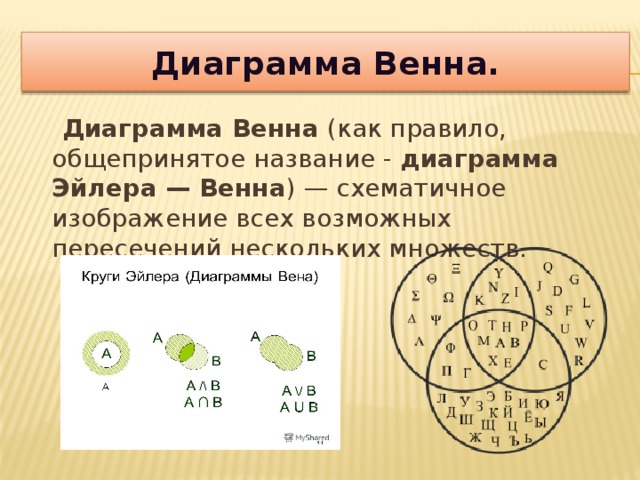
Таблица 1 Сравнение возможностей различных программ, способных генерировать диаграммы Венна.

Полноразмерная таблица

Выводы

Пакет VennDiagram повышает простоту использования и степень настраиваемости при создании диаграмм Венна в контексте биоинформатики. В то время как другие инструменты предлагают большую часть функций, представленных здесь, реализация всех функций вместе в широко используемой статистической среде R будет способствовать использованию автоматически сгенерированных диаграмм Венна в вычислительных конвейерах.

Наличие и требования

Сам пакет VennDiagram доступен как дополнительные файлы 1 и 2 и будет отправлен в CRAN — глобальный репозиторий пакетов R. VennDiagram требует R (>2.12.1) и пакет сетки для R. : Сетевой анализ, визуализация и построение графиков Торонто. Биоинформатика 2009, 25(24):3327–3329. 10.1093/биоинформатика/btp595

Статья ПабМед Центральный КАС пабмед Google Scholar

  • Мерико Д. , Гфеллер Д., Бадер Г.Д.: Как визуально интерпретировать биологические данные с помощью сетей. Nat Biotechnol 2009, 27(10):921–924. 10.1038/нбт.1567

    Артикул ПабМед Центральный КАС пабмед Google Scholar

  • Boutros PC, Okey AB: Неконтролируемое распознавание образов: введение в причины и причины кластеризации данных микрочипов. Бриф Биоинформ 2005, 6(4):331–343. 10.1093/bib/6.4.331

    Артикул КАС пабмед Google Scholar

  • Verhaak RG, Sanders MA, Bijl MA, Delwel R, Horsman S, Moorhouse MJ, van der Spek PJ, Lowenberg B, Valk PJ: HeatMapper: мощная комбинированная визуализация корреляций профиля экспрессии генов, генотипов, фенотипов и характеристик образцов . BMC Bioinfo 2006, 7: 337. 10.1186/1471-2105-7-337

    Статья Google Scholar

  • ">

    Оливерос Дж.: Венни. Интерактивный инструмент для сравнения списков с диаграммами Венна. для сравнения и визуализации биологических списков с использованием диаграмм Венна, пропорциональных площади. BMC Genomics 2008, 9: 488. 10.1186/1471-2164-9-488

    Статья ПабМед Центральный пабмед Google Scholar

  • Ким Б., Ли Б., Сео Дж.: Визуализация соответствия множества с помощью матриц перестановок и веерных диаграмм. Interact Comput 2007, 19(5):630–643. 10.1016/j.intcom.2007.05.004

    Статья ПабМед Центральный пабмед Google Scholar

  • Кестлер Х.А., Мюллер А., Краус Дж.М., Буххольц М., Гресс Т.М., Лю Х., Кейн Д.В., Зееберг Б.Р., Вайнштейн Дж.Н.: VennMaster: диаграммы Эйлера, пропорциональные площади, для функционального анализа GO микрочипов. БМС Биоинфо 2008, 9: 67. 10.1186/1471-2105-9-67

    Артикул Google Scholar

  • ">

    Джентльмен Р.С., Кэри В.Дж., Бейтс Д.М., Болстад Б., Деттлинг М., Дудойт С., Эллис Б., Готье Л., Гэ Ю., Джентри Дж. и др.: Биокондуктор: открытая разработка программного обеспечения для вычислительной биологии и биоинформатики. Геном Биол 2004, 5(10):R80. 10.1186/gb-2004-5-10-r80

    Артикул ПабМед Центральный пабмед Google Scholar

  • Чоу С., Роджерс П. Построение диаграмм Венна и Эйлера, пропорциональных площади, с тремя окружностями. В диаграммах Эйлера 2005: 2005. Париж, Франция; 2005.

    Google Scholar

  • Эдвардс А. Диаграммы Венна из семи наборов с вращательной и полярной симметрией. Комбинаторика, вероятность и вычисления 1998, 7 (2): 149–152. 10.1017/S0963548397003143

    Артикул Google Scholar

  • Schwenk A: Диаграмма Венна для пяти комплектов. Математический журнал 1984, 57 (5): 297–298. 10.2307/2689606

    Артикул Google Scholar

    • Ссылки на скачивание

    Благодарности

    Авторы благодарят всех сотрудников лаборатории Boutros за поддержку, и особенно доктора Кеннета Чу и Дэрила Ваггота за помощь в создании Windows-совместимой версии этого пакета. Это исследование было проведено при поддержке Института исследования рака Онтарио к ПХД за счет финансирования, предоставленного правительством Онтарио. Работа выполнена при финансовой поддержке гранта номер MOP579.03 от Канадских институтов исследований в области здравоохранения (ПХБ и доктору Аллану Б. Оки).

    Информация об авторе

    Авторы и организации

    1. Платформа информатики и биокомпьютеров, Институт исследований рака Онтарио, Центр MaRS, Южная башня, 101 College Street, Suite 800, Toronto, Ontario, M5G 0A3, Canada

      Hanbo Chen Paul C Boutros

    Авторы

    1. Hanbo Chen

      Посмотреть публикации автора

      Вы также можете искать этого автора в PubMed Google Академия

    2. Paul C Boutros

      Посмотреть публикации автора

      Вы также можете искать этого автора в PubMed Google Scholar

    Автор, ответственный за корреспонденцию

    Пол Си Бутрос.

    Дополнительная информация

    Вклад авторов

    HC и PCB задумали проект. HC написал программное обеспечение, которое HC и PCB протестировали и отладили. ХК написал первый черновик рукописи, которую все авторы отредактировали и одобрили.

    Дополнительный электронный материал

    Дополнительный файл 1: Пакет

    VennDiagram R в виде linux-совместимого файла .tar.gz (GZ 20 КБ)

    Дополнительный файл 2: Пакет

    VennDiagram R в формате a 9042 -совместимый файл .zip (ZIP 64 КБ)

    12859_2010_5075_MOESM3_ESM.R

    Дополнительный файл 3: Код для создания всех диаграмм Венна на рисунках 1 и 2. (R 4 КБ)

    Дополнительный файл 4: Иллюстрация параметров доступно в

    Диаграмма Венна . (PPT 2 МБ)

    Оригинальные файлы изображений, представленные авторами

    Ниже приведены ссылки на оригинальные файлы изображений, представленные авторами.

    Оригинальный файл авторов для рисунка 1

    Оригинальный файл авторов для рисунка 2

    Оригинальный файл авторов для рисунка 3

    Права и разрешения

    , Это статья в открытом доступе, распространяемая в соответствии с лицензией Creative Commons Attribution License (http://creativecommons.

    No related posts.

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *