Диаметр окружности через диаметр онлайн калькулятор: Онлайн калькулятор диаметра круга. Как узнать диаметр круга, окружности.

Калькулятор Перевода Окружности В Диаметр

Инструкции: Используйте этот калькулятор для вычисления диаметра круга из его окружности, показывая все шаги. Пожалуйста, введите значение окружности в форму ниже.

Об этом калькуляторе соотношения окружности и диаметра

Переход от окружности к диаметру — это то, что часто необходимо, и данный калькулятор позволит вам это сделать. Все, что вам нужно, это ввести правильное числовое выражение, такое как ‘1/3’ или ‘4’ и т.д. Единственное ограничение — выражение должно быть положительным.

Как только вы укажете действительный диаметр (он должен быть положительным числовым выражением), вам нужно нажать на кнопку «Рассчитать», и вам будут предоставлены расчеты и все шаги.

Этот калькулятор тесно связан с калькулятором, который принимает диаметр к окружности только это обратный процесс.

Как перейти от окружности к диаметру?

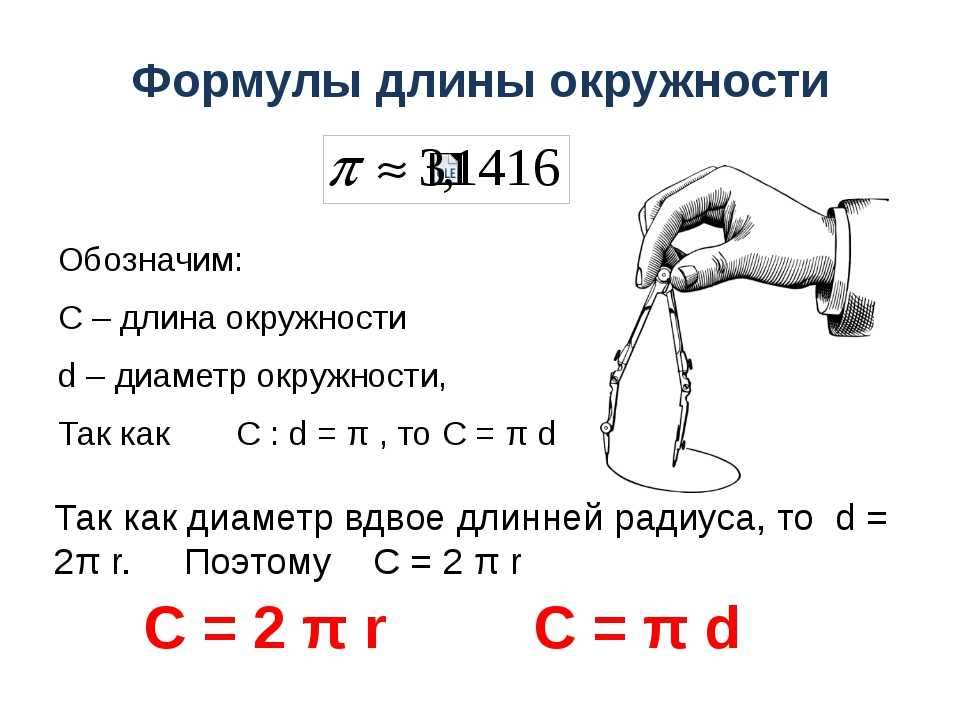
Главное в этом процессе — использовать основную формулу, связывающую окружность и диаметр. У нас есть следующая формула:

\[C = \pi d \]

То есть, окружность соответствует умножению π на d. Теперь, решая для d, мы непосредственно находим, что:

\[d = \displaystyle \frac{C}{\pi} \]

Затем, чтобы перейти от окружности к диаметру, нужно просто разделить окружность на π.

Каковы этапы перехода от окружности к диаметру?

• Шаг 1: Определите окружность и ее потенциальную единицу длины. Она должна быть положительной, иначе вы не сможете продолжить
• Шаг 2: Как только вы получили действительную окружность C, разделите ее на π, чтобы получить диаметр
• Шаг 3: Диаметр сохраняет ту же единицу длины, что и окружность, если таковая предусмотрена.
• Шаг 4: Диаметр может быть выражен в терминах π. Вы можете оставить его как есть, или получить его приблизительное числовое значение, используя калькулятор выражений .

Обычно принято оставлять результаты в терминах π, упрощая их настолько, насколько это возможно. Иногда вы захотите иметь представление о численном значении, в этом случае вполне можно воспользоваться калькулятором.

Сколько диаметров составляет окружность?

Окружность равна ровно π диаметра. В этом и заключается магия константы π, которая обеспечивает связь между окружностью и диаметром.

В определенном смысле π отражает то, как не существует рационального соотношения между длинами прямых и окружностей.

Зачем вычислять диаметр из окружности?

В качестве варианта может быть предоставлен либо площадь или окружность круга в этом случае было бы полезно иметь возможность получить из него диаметр или, для той же цели, узнать радиус.

Пример: вычисление диаметра из окружности

Вычислите диаметр, если известно, что окружность равна \\(3\\pi\\)

Отвечать: Нам нужно найти диаметр \(d\) круга, а из предоставленной информации мы знаем, что окружность круга равна \(C = 3\pi\).

Теперь формула для окружности \(C = 2\pi r\), но так как диаметр равен удвоенному периметру, то получается \(d = 2r\), и, следовательно, формула окружности становится:

\[C = d \pi \]

Приведенная выше формула, показывает, как выразить окружность в терминах диаметра, и мы также можем решить формулу для \(d\):

\[d = \displaystyle\frac{C}{\pi}\]

Поэтому все, что нам нужно сделать, это подставить в приведенную выше формулу известное значение окружности \(C = 3\pi\). Получается следующее:

\[ \begin{array}{ccl}\displaystyle d & = & \displaystyle\frac{C}{\pi} \\\\ \\\\ & = & \displaystyle\frac{3\pi}{\pi} \\\\ \\\\ & = & \displaystyle 3 \end{array} \]

На этом расчеты завершены. Мы выяснили, что диаметр окружности равен \(\displaystyle d = 3\).

Пример: отношение окружности к диаметру

Если известно, что окружность круга равна \(4\pi\), то каков его диаметр?

Отвечать: Нам нужно найти диаметр \(d\) круга, и в этом случае мы знаем, что окружность круга равна \(C = 4\pi\).

Мы должны использовать формулу:

\[d = \displaystyle\frac{C}{\pi} = \displaystyle\frac{4\pi}{\pi} = 4\]

Следовательно, диаметр равен \(\displaystyle d = 4\).

Пример: отношение окружности к диаметру

Предположим, что половина окружности равна \(\frac{3\pi}{2}\). Найдите диаметр окружности.

Отвечать: В этом случае нам дается не окружность, а половина окружности, то есть \(\frac{3\pi}{2}\).

Следовательно, окружность равна \(C = 2 \cdot \frac{3\pi}{2} = 3\pi \). Таким образом, теперь мы можем использовать формулу:

\[d = \displaystyle\frac{C}{\pi} = \displaystyle\frac{3\pi}{\pi} = 3\]

Следовательно, диаметр равен \(\displaystyle d = 3\).

Другие калькуляторы окружностей

Вы найдете круги везде, куда бы вы ни пошли в математике. Вам нужно будет вычислить площадь круга , Окружность круга .

Кроме того, при работе с кругами вы захотите сделать следующее Угловые преобразования , такие как радианы в градусы или же градусы в радианы .

Расчёт диаметра линз

Главная \ Сервис \ Расчет диаметра линз

 

Чтобы правильно произвести расчёт диаметр линзы, вы можете воспользоваться калькулятором для быстрого пересчета либо использовать определённые методы. На данный момент их существует всего два: расчётный и практический.

 

Быстрый расчёт диаметра линз

Введите данные:

Укажите максимальный диаметр окуляра оправы в мм (например 54):

Укажите ширину мостика (перегородки) в мм (например 16)

Укажите межцентровое расстояние в мм (например 64):

 

 

 

Информация необходимая для того чтобы рассчитать диаметр :

1. Горизонтальная ширина окуляра оправы (обычно изображается на заушнике оправы, это первая цифра  например 53.

2. Ширина переносицы оправы, она так же указывается на заушнике, это вторая цифра например 17.

3. Межзрачковое расстояние  в вашем рецепте PD, например 63.

  

 

 

 

При определении диаметра очковой линзы, необходимо учитывать тот факт, что центральная часть линзы должна совпадать со зрачками.

Если диаметр окажется слишком маленьким, линза будет смещаться к центральной части поэтому не получится выдержать межзрачковое расстояние в очках верно. Когда же линза выбрана с большим диаметром,  это сказывается на излишней толщине по краям, а также хроматическим аберрациям.

Именно поэтому необходимо заранее узнавать минимальный диаметр линзы для очков ещё до её обточки под определённую оправу. Как же подобрать диаметр линз?

 

Расчётный метод

Для начала необходимо узнать РЦ (PD) оправы. Определить такой показатель можно при суммировании максимального диаметра отдельного окуляра и ширины моста оправы. Такая информация чаще всего указывается на заушниках оправы. Как правило, там пишется информация подобного рода: «55 ¤ 17». Первая цифра обозначает максимальный диаметр отдельного окуляра, вторая ширину мостика. Измерить эти показатели можно при помощи простой линейки.

Далее необходимо определить показатель «D max». Для этого нужно знать первую цифру и добавить к ней 2 мм, которые отводятся на обработку. Необходимо также знать межцентровое расстояние (РЦ), которое указывается в рецепте.

Представляем показатели диаметра линзы в виде формулы:

(PD оправы — PD клиента)+D max=D min.

Теперь мы точно сможем определить диаметр линзы, которая подойдёт для той или иной оправы. Стандартный диаметр линзы 65 мм.

 

Практический метод

Этот метод получил большее распространение, его используют гораздо чаще, чем расчётный метод. Такой метод применяется в салонах оптики, так как позволяет быстро определить нужный размер. Суть заключается в следующем: оправа прислоняется к специальному изображению линз, обладающих различным диаметром со смещением на различное расстояние. В данном случае необходимо учитывать, что изображение должно соотноситься с реальным размером линзы.

Итак, сначала подбирается картинка, на которой нарисовано необходимое межцентровое расстояние. Затем прикладываем оправу к данному изображению и подбираем цвет окружности, перекрывающей окуляры. А после этого просто определяем диаметр данной окружности, он написан возле изображения. Вот и всё, быстрый перерасчёт диаметра линзы произведён.

 

Шаблон карта для определения диаметра очковой линзы:

(нажмите на изображение для увеличения масштаба)

  

 

У Вас остались вопросы?

Наши специалисты с удовольствием помогут Вам,
тел.: 8(3852)404-890
Или напишите:  [email protected]

Прозрение оптика Барнаул

Калькулятор диаметра окружности болта

— LittleMachineShop.com

Меню калькулятора Введите значения ниже, чтобы рассчитать диаметр окружности болта. Для измерения межосевого расстояния между двумя отверстиями одинаковой диаметр электронным штангенциркулем. 1. С помощью внутренних губок измерьте диаметр одного из отверстий. До тебя извлеките штангенциркуль из отверстия, нажмите кнопку, чтобы обнулить штангенциркуль, пока устанавливается по диаметру отверстия. 2. Продолжая использовать внутренние губки, измерьте расстояние между дальними поверхностями две дырки. Показание штангенциркуля – это расстояние между центрами два отверстия. ПРЕДЛОЖЕНИЕ НЕДЕЛИ 22,95 $ Дополнительная информация Сверлильный патрон, 1/2 дюйма, профессиональный класс Набор цанг, R8, метрическая, набор из 10 шт. Набор из десяти круглых цанг R8 метрических размеров Закалены и отшлифованы с жесткими допусками Изготовлены из высококачественной инструментальной стали Резьба тяги 7/16″ -20 Максимальное биение 0,0007″ (0,018 мм) 64,95 $ Больше таких продуктов Большой настольный фрезерный станок HiTorque Бесщеточный привод постоянного тока с регулируемой скоростью мощностью 1000 Вт (1-1/3 л.с.) Большой стол 29,1″ x 7,1″ (740 мм x 180 мм) Диапазон скорости вращения шпинделя 80-5000 об/мин Цифровой индикатор положения на пиноли, цифровая индикация скорости шпинделя Режим реверсивного метчика 3 199,00 $ Регулярно $3899,00 Больше таких продуктов Защита от стружки, магнитная для тисков 3–4 дюйма, прозрачная Защитный кожух фрезерного станка использует мощные неодимовые магниты для крепления к передней или задней части станка Удобное снятие без возни с помощью инструментов или винтов Регулируемые фрикционные петли позволяют устанавливать боковые панели под любым углом до 150 градусов Совместимы с любыми фрезерными тисками 3–4 дюйма с плоской поверхностью на обоих концах Приблизительные размеры: 11 1/4 дюйма x 3 3/4 дюйма x 1/4 дюйма 34,95 $ Больше таких продуктов

Площадь в Диаметр — MathCracker.

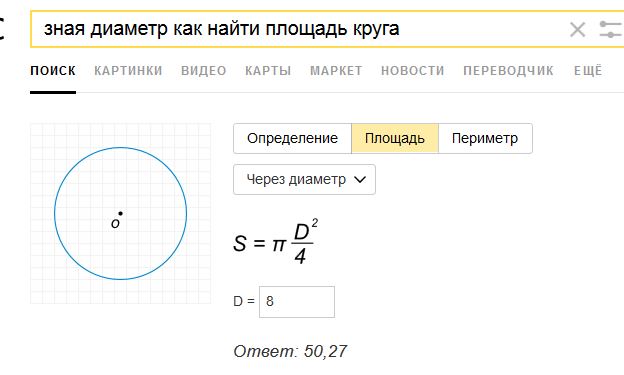com

Инструкции: Используйте этот пошаговый калькулятор, чтобы вычислить диаметр круга по его площади, показывая все шаги. Пожалуйста, введите площадь круга в форму ниже.

Подробнее об этом калькулятор площади в диаметр

Этот калькулятор покажет вам все расчеты, необходимые для перехода от площади круга к его диаметру, показывая вам все этапы процесса

Все, что вам нужно сделать, это указать действительное положительное числовое выражение. Например, вы можете указать 3/4, или 3, или sqrt(3) или составное выражение, если оно правильное и положительное.

После того, как вы укажете действительную область, вам просто нужно нажать «Рассчитать», и отобразится решение с его шагами.

Процесс перехода от площади к диаметру прост и основан на использовании одной формулы площади, но очень важно, чтобы указанная площадь была положительной. 92 = \displaystyle \frac{A}{\pi} \] \[\Rightarrow r = \displaystyle \sqrt{ \frac{A}{\pi}} \]

Но нужно помнить, что r = d/2, поэтому получаем

\[\displaystyle \frac{d}{2} = \displaystyle \sqrt{ \frac{A}{\pi}} \]

, что в конечном итоге приводит к формуле площади к диаметру:

\[d = \displaystyle 2 \sqrt{ \frac{A}{\pi}} \]

Как определить диаметр?

• Шаг 1: Определите заданную область. Если вместо этого указана длина окружности, вам нужно использовать формула длины окружности к диаметру, отличающаяся от
• Шаг 2: Получив действительную область A, вам нужно подставить ее в формулу: \(d = \displaystyle 2 \sqrt{ \frac{A}{\pi}}\)
• Шаг 3: Убедитесь, что если область A передается единицами длины, вы передаете их и диаметру

Например, если площадь А равна 3 см ² , то диаметр будет измеряться в см.

Обычно в геометрии и алгебре длина используется реже, и, возможно, более чем редко, предполагается, что она ясна и недвусмысленна, что обычно имеет место, за исключением случаев, когда требуется преобразование единиц.

Зачем заботиться о площадях и диаметрах?

Понятия площадей и диаметров имеют решающее значение в математике, и вполне естественно интересоваться взаимосвязью. Это правда, что есть четкая связь между площадью и радиусом, и этого, возможно, должно быть достаточно, но диаметр сам по себе представляет большой интерес.

Площади, окружности, радиус и диаметр являются центральными компонентами математики, и они важны для решения уравнений что связывает их.

Пример: Вычисление диаметра

Предположим, что площадь круга равна \(A = 4\pi\), найдите его диаметр d.

Решение: Из постановки задачи известно, что площадь равна \(A = 4\pi\).

Теперь нам нужно просто подставить это значение A в формулу:

\[d = \displaystyle 2 \sqrt{ \frac{A}{\pi}} = \displaystyle 2 \sqrt{ \frac{4\pi}{\pi}} = 4 \]

, что завершает расчет.

Пример: Больше площадей и диаметров

Сектор круга с углом 60 ^o имеет площадь \(\frac{3}{2}\pi\), найдите диаметр.

Решение: Мы знаем, что 60 ^o представляет собой 1/6 полного круга. Так как площадь сектора пропорциональна к его углу, поэтому площадь полного круга равна \(A = 6\cdot \frac{3}{2}\pi = 9\Пи\).

Все, что нам нужно сделать сейчас, это подставить это значение A в формулу:

\[d = \displaystyle 2 \sqrt{ \frac{A}{\pi}} = \displaystyle 2 \sqrt{ \frac{9\pi}{\pi}} = 6 \]

, что завершает расчет.

Пример: отрицательные области?

Учитывая площадь A = -3, можете ли вы вычислить диаметр?

Решение: Нет, нельзя. Чтобы вычислить диаметр по площади, вам нужна положительная площадь A. Или, если площадь A = 0, то и диаметр d = 0. Но нельзя делать расчет с отрицательной площадью.

Больше круговых калькуляторов

Вычисление окружностей и площадей является базовым навыком геометрии, и важно знать, как они взаимосвязаны.