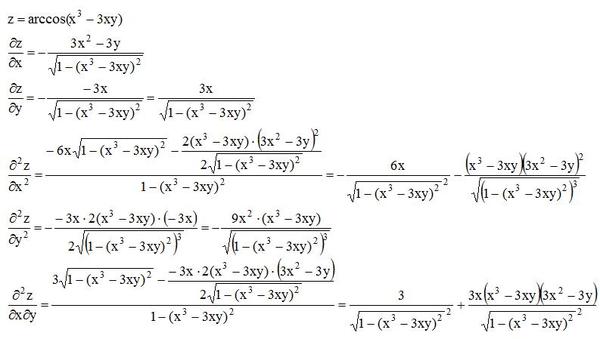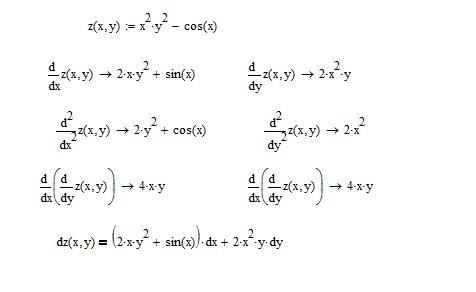Дифференциал функции y sin 2 2x равен: Mathway | Популярные задачи

Содержание

Дифференциал функции. Дифференциалы первого порядка.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

Определение. Функция $y=f(x)$ называется дифференцируемой в точке $x_0,$ если ее приращение $\Delta y(x_0, \Delta x)$ может быть представлено в виде $$\Delta y(x_0, \Delta x)=A\Delta x+o(\Delta x).$$

Главная линейная часть $A\Delta x$ приращения $\Delta y$ называется дифференциалом этой функции в точке $x_0,$ соответствующим приращению $\Delta x,$ и обозначается символом $dy(x_0, \Delta x).$

Для того, чтобы функция $y=f(x)$ была дифференцируема в точке $x_0,$ необходимо и достаточно, чтобы существовала производная $f'(x_0),$ при этом справедливо равенство $A=f'(x_0).$

Выражение для дифференциала имеет вид $$dy(x_0, dx)=f'(x_0)dx,$$ где $dx=\Delta x.$

Свойства дифференциала:

1. $d(C)=0,$ где $C -$ постоянная;

2. 2}.$

Ответ: $\frac{x+y}{x-y}dx.$

3.5: Производные тригонометрических функций

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 2494

Гилберт Странг и Эдвин «Джед» Герман
OpenStax

Цели обучения

Найти производные функции синуса и косинуса.
Найдите производные стандартных тригонометрических функций.
Вычислить высшие производные синуса и косинуса.

Одним из важнейших видов движения в физике является простое гармоническое движение, которое связано с такими системами, как объект с массой, колеблющейся на пружине.

Простое гармоническое движение может быть описано с помощью функции синуса или косинуса. В этом разделе мы расширим наши знания о формулах производных, включив в них производные этих и других тригонометрических функций. Мы начнем с производных функций синуса и косинуса, а затем используем их для получения формул для производных оставшихся четырех тригонометрических функций. Способность вычислять производные функций синуса и косинуса позволит нам найти скорость и ускорение простого гармонического движения.
Производные функции синуса и косинуса
Мы начнем исследование производной функции синуса, используя формулу, чтобы сделать обоснованное предположение о ее производной. Напомним, что для функции $f(x),$
\[f′(x)=\lim_{h→0}\dfrac{f(x+h)−f(x)}{h}. \nonumber \]
Следовательно, для значений $h$, очень близких к $0$,
\[f′(x)≈\dfrac{f(x+h)−f(x)} {час}. \nonumber \]
Мы видим, что, используя $h=0,01$,
\[\dfrac{d}{dx}(\sin x)≈\dfrac{\sin (x+0,01)−\sin х}{0,01} \номер \]
Установив
\[D(x)=\dfrac{\sin (x+0,01)−\sin x}{0,01} \nonumber \]
и используя графическую утилиту, мы можем получить график приближение к производной $\sin x$ (рисунок $\PageIndex{1}$).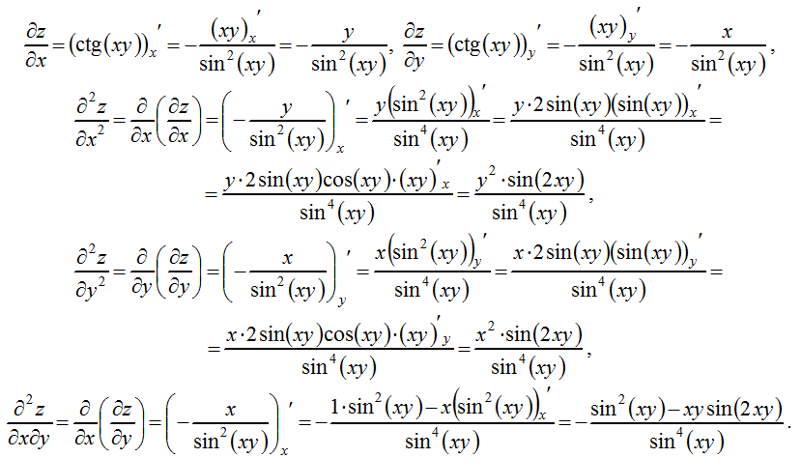
Рисунок $\PageIndex{1}$: График функции $D(x)$ очень похож на косинусоидальную кривую.
При осмотре график $D(x)$ оказался очень близким к графику функции косинуса. Действительно, мы покажем, что
\[\dfrac{d}{dx}(\sin x)=\cos x. \номер\]
Если бы мы проделали те же шаги для аппроксимации производной функции косинуса, мы бы обнаружили, что
\[\dfrac{d}{dx}(\cos x)=−\sin x. \nonumber \]
Производные от $\sin x$ и $\cos x$
Производной функции синуса является косинус, а производной функции косинуса является отрицательный синус.
\[\dfrac{d}{dx}(\sin x)=\cos x \nonumber \]
\[\dfrac{d}{dx}(\cos x)=-\sin x \nonumber \ ]
Доказательство
Поскольку доказательства для $\dfrac{d}{dx}(\sin x)=\cos x$ и $\dfrac{d}{dx}(\cos x)=-\sin x$ используют аналогичные методы, мы приводим только доказательство для $\dfrac{d}{dx}(\sin x)=\cos x$. Прежде чем начать, вспомните два важных тригонометрических предела:
$\displaystyle \lim_{h→0}\dfrac{\sin h}{h}=1$ и $\displaystyle \lim_{h→0}\dfrac {\ cos ч-1} {ч} = 0 $.

Графики $y=\dfrac{\sin h}{h}$ и $y=\dfrac{\cos h−1}{h}$ показаны на рисунке $\PageIndex{2 }$.
Рисунок $\PageIndex{2}$: На этих графиках показаны два важных предела, необходимых для установления формул производных для функций синуса и косинуса.
Напомним также следующее тригонометрическое тождество для синуса суммы двух углов:
\[\sin (x+h)=\sin x\cos h+\cos x\sin h. \nonumber \]
Теперь, когда мы собрали все необходимые уравнения и тождества, приступим к доказательству.
\[\begin{align*} \dfrac{d}{dx}(\sin x) &=\lim_{h→0}\dfrac{\sin(x+h)−\sin x}{h} & & \text{Применить определение производной.}\\[4pt]
&=\lim_{h→0}\dfrac{\sin x\cos h+\cos x\sin h−\sin x}{h } & & \text{Используйте тождество триггера для синуса суммы двух углов.}\\[4pt]
&=\lim_{h→0}\left(\dfrac{\sin x\cos h−\sin x}{h}+\dfrac{\cos x\sin h}{h}\right) & & \ text{Перегруппировать.}\\[4pt]
&=\lim_{h→0}\left(\sin x\left(\dfrac{\cos h−1}{h}\right)+(\cos x) \left(\dfrac{\sin h}{h}\right)\right) & & \text{Умножить}\sin x\text{и}\cos x \\[4pt]
&=(\sin x )\lim_{h→0}\left(\dfrac{\cos h−1}{h}\right)+(\cos x)\lim_{h→0}\left(\dfrac{\sinh}{ h}\right) & & \text{Коэффициент }\sin x\text{ и }\cos x \text{ вне пределов. } \\[4pt]
&=(\sin x)(0)+(\ cos x)(1) & & \text{Применить формулы ограничения триггеров.}\\[4pt]
&=\cos x & & \text{Упрощение.} \end{align*} \nonumber \]
□
На рисунке $\PageIndex{3}$ показано соотношение между графиком $f( x)=\sin x$ и его производная $f′(x)=\cos x$. Обратите внимание, что в точках, где $f(x)=\sin x$ имеет горизонтальную касательную, ее производная $f′(x)=\cos x$ принимает нулевое значение. Мы также видим, что где f$(x)=\sin x$ возрастает, $f′(x)=\cos x>0$ и где $f(x)=\sin x$ уменьшается, $f′(x)=\cos x<0.$
Рисунок $\PageIndex{3}$: где $f(x)$ имеет максимум или минимум, $f’ (x)=0$, то есть $f'(x)=0$, где $f(x)$ имеет горизонтальную касательную. Эти точки отмечены точками на графиках 92x}\)
Пример $\PageIndex{3}$: приложение к скорости
Частица движется вдоль координатной оси таким образом, что ее положение в момент времени $t$ определяется выражением $s(t)= 2\sin t−t$ при $0≤t≤2π. $ В какие моменты времени частица покоится?
Решение
Чтобы определить, когда частица находится в состоянии покоя, установите $s′(t)=v(t)=0.$ Начните с нахождения $s′(t).$ Мы получим
\[s′(t)=2 \cos t−1, \nonumber \]
поэтому мы должны решить
\[2 \cos t−1=0\text{ для }0≤t≤2π. \nonumber \]
Решениями этого уравнения являются $t=\dfrac{π}{3}$ и $t=\dfrac{5π}{3}$. Таким образом, частица покоится в моменты времени $t=\dfrac{π}{3}$ и $t=\dfrac{5π}{3}$.
Упражнение $\PageIndex{3}$
Частица движется вдоль координатной оси. Его положение в момент времени $t$ определяется как $s(t)=\sqrt{3}t+2\cos t$ для $0≤t≤2π.$ В какие моменты времени частица находится в отдых?
Подсказка
Используйте предыдущий пример в качестве руководства.
Ответить
$t=\dfrac{π}{3},\quad t=\dfrac{2π}{3}$
Производные других тригонометрических функций
Поскольку оставшиеся четыре тригонометрические функции могут быть выражены в виде частных, содержащих синус, косинус или и то, и другое, мы можем использовать правило частных, чтобы найти формулы для их производных.
Пример $\PageIndex{4}$: производная касательной функции 92x\\[4pt]

\dfrac{d}{dx}(\sec x)&=\sec x \tan x\\[4pt]
\dfrac{d}{dx}(\csc x)&=- \csc х \кот х. \end{align} \nonumber \]
Пример $\PageIndex{5}$: Нахождение уравнения касательной
Нахождение уравнения касательной к графику $f(x)=\ кроватка x $ в точке $x=\frac{π}{4}$.
Решение
Чтобы найти уравнение касательной, нам нужна точка и наклон в этой точке. Чтобы найти точку, вычислите
$f\left(\frac{π}{4}\right)=\cot\frac{π}{4}=1$. 92 \ влево (\ гидроразрыва {π} {4} \ вправо) = −2 \).
Используя уравнение точки-наклона линии, мы получаем
$y−1=−2\left(x−\frac{π}{4}\right)$
или эквивалентно,
\ (y=−2x+1+\frac{π}{2}\).
Пример $\PageIndex{6}$: нахождение производной тригонометрических функций
Найдите производную $f(x)=\csc x+x\tan x .$
Решение
Чтобы найти эту производную, мы должны использовать как правило сумм, так и правило произведения.
По правилу сумм находим 92 х\)
Упражнение $\PageIndex{6}$
Найдите наклон линии, касательной к графику $f(x)=\tan x $ в точке $x=\dfrac{π}{6} $.
Подсказка
Вычислите производную в точке $x=\dfrac{π}{6}$.
Ответить
$\dfrac{4}{3}$
Производные высшего порядка
Производные высшего порядка от $\sin x$ и $\cos x$ повторяются. Следуя шаблону, мы можем найти любую производную более высокого порядка от $\sin x$ и $\cos x.$ 9{4⋅14+3}}(\sin x)\)
Ответить
$-\cos х$
Пример $\PageIndex{9}$: Приложение к ускорению
Частица движется вдоль координатной оси таким образом, что ее положение в момент времени $t$ определяется выражением $s(t)= 2−\sint$. Найдите $v(π/4)$ и $a(π/4)$. Сравните эти значения и решите, ускоряется или замедляется частица.
Раствор
Сначала найдите $v(t)=s′(t)$
\[v(t)=s′(t)=−\cos t . \nonumber \]
Таким образом,
$v\left(\frac{π}{4}\right)=-\dfrac{1}{\sqrt{2}}=-\dfrac{\sqrt{2 }}{2}$.
Затем найдите $a(t)=v′(t)$. Таким образом, $a(t)=v′(t)=\sin t$, и мы имеем
$a\left(\frac{π}{4}\right)=\dfrac{1}{\ sqrt{2}}=\dfrac{\sqrt{2}}{2}$.
Так как $v\left(\frac{π}{4}\right)=-\dfrac{\sqrt{2}}{2}<0$ и $a\left(\frac{π} {4}\right)=\dfrac{\sqrt{2}}{2}>0$, мы видим, что скорость и ускорение действуют в противоположных направлениях; то есть объект ускоряется в направлении, противоположном направлению, в котором он движется. Следовательно, частица замедляется.
Упражнение $\PageIndex{9}$
Блок, прикрепленный к пружине, движется вертикально. Его положение в момент времени t определяется выражением $s(t)=2\sin t$. Найдите $v\left(\frac{5π}{6}\right)$ и $a\left(\frac{5π}{6}\right)$.
Сравните эти значения и решите, ускоряется блок или замедляется.
Подсказка
Используйте пример $\PageIndex{9}$ в качестве руководства.
Ответить
$v\left(\frac{5π}{6}\right)=-\sqrt{3}<0$ и $a\left(\frac{5π}{6}\right)=-1 <0$. Блок ускоряется.
Ключевые понятия
Мы можем найти производные от $\sin x$ и $\cos x$, используя определение производной и предельные формулы, найденные ранее. Результат
$\dfrac{d}{dx}\big(\sin x\big)=\cos x\quad\text{and}\quad\dfrac{d}{dx}\big(\cos x\big )=−\sin x$.

С помощью этих двух формул мы можем определить производные всех шести основных тригонометрических функций. 92x\)
Производная секущей функции
$\dfrac{d}{dx}(\sec x)=\sec x\tan x $

Производная функции косеканса
$\dfrac{d}{dx}(\csc x)=-\csc x\cot x $
Эта страница под названием 3. 5: Производные тригонометрических функций распространяется в соответствии с лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Гилбертом Странгом и Эдвином «Джедом» Германом (OpenStax) через исходный контент, который был отредактировано в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
Наверх
Была ли эта статья полезной?
Тип изделия

Раздел или Страница
Автор
ОпенСтакс
Лицензия
CC BY-NC-SA
Версия лицензии
4,0
Программа OER или Publisher
ОпенСтакс
Показать страницу TOC
нет
Теги
автор @ Эдвин «Джед» Герман
автор@Гилберт Странг
Производная функции косеканса
Производная функции косинуса
Производная функции котангенса
Производная секущей функции
Производная синусоидальной функции
Производная функции тангенса
https://math. libretexts.org/TextMaps/Calculus_TextMaps/Map%3A_Calculus_(OpenStax)/03%3A_Derivatives/3.6%3A_The_Chain_Rule
источник@https://openstax.org/details/books/calculus-volume-1
Неявное дифференцирование
Нахождение производной, когда вы не можете найти у

Вы можете сначала прочитать Введение в производные и производные правила.
Неявное против явного
Функция может быть явной или неявной:
Явный : «y = некоторая функция x».
Когда мы знаем x, мы можем вычислить y напрямую.
Неявный : «некоторая функция y и x равна чему-то другому». Знание x не ведет непосредственно к y.
Пример: Круг
Явная форма Неявная форма
y = ± √ (r ² − x ² ) х ² + у ² = г ²
В этой форме y выражается
как функция x. В этой форме функция
выражается через y и x.

График x ² + y ² = 3 ²
Как выполнить неявное дифференцирование
Дифференцировать по х
Собери все dy dx с одной стороны
Решить для dy dx
Пример: x
² + y ² = r ²
Продифференцировать по x:

d + 2 6 dx (x ) 901 6 (x ) д дх (у ² ) = d dx (r ² )

Решим каждый член:

Используем степенное правило: d dx (x ² ) = 2x

Используйте цепное правило (поясняется ниже): d dx (y ² ) = 107 10d 1

р ² есть константа, поэтому ее производная равна 0: d dx (r ² ) = 0

Что дает нам:

2x + 2y dy dx 4 = 2 0758 dy dx с одной стороны

y dy dx = −x

Решить для dy dx :

dy dx 7 −x 111

Цепное правило с использованием

dy dx
Давайте более подробно рассмотрим, как d dx (y ² ) превращается в 2y 1 dy 9x 42
Цепное правило гласит:
du дх = дю dy dy dx
Заменить в u = y ² :
d 7 dx 90 6 (5 6 907) 58 d dy (y ² ) dy dx
И затем:
d dx (y ² ) = 2y dy dx dx
В принципе, мы сделали все, чтобы дифференцировать
у и умножить на dy дх
Другим распространенным обозначением является использование ’ для обозначения d dx
Цепное правило с использованием ‘
Цепное правило также можно записать с использованием обозначения ‘:
f(g(x))’ = f'(g(x))g'(x)
g(x) is наша функция «y», поэтому:
f(y)’ = f'(y)y’
f(y) = y ² , поэтому f'(y) = 2y:
f(y) ‘= 2yy’
или альтернативно: f(y)’ = 2y dy dx
Опять же, все, что мы сделали, это продифференцировали по y и умножили на
дх дх
Явный
Давайте также найдем производную, используя явную форму уравнения.
Чтобы решить это явно, мы можем решить уравнение для y
Затем дифференцировать
Затем снова подставьте уравнение для y
Пример: x
² + y ² = r ²
Вычесть x ² с обеих сторон: y ² = r ² − x ²
Квадратный корень: y = ±√(r ² − x ² )
Сделаем только положительное −7 2 6 x 09 : 1 x 5 907(r 907(r ² − x ²) ² )
В виде степени: y = (r ² − x ² ) ^½
Производная (цепное правило) :y’ = ½ 7 2 9017 2 ) ^−½ (−2x)
Упростить:y’ = −x(r ² − x ² ) ^−½
Упростить больше:y’ = −x (r ² − x ² ) ^½
Теперь, потому что y = (r ² − 90 7 9 1 90 715 1 2 9) 716 : y’ = −x/ y
Таким образом мы получаем тот же результат!
Вы можете сами попробовать взять производную от отрицательного члена.
Снова цепное правило!
Да, мы снова использовали цепное правило. Вот так (обратите внимание на другие буквы, но то же правило):
dy dx = dy df df dx
Подставить в f = (r ² − x ² ):
5 9
9075 х (f ^½ ) = d df (f ^½ ) d dx (r ² − x ² )
Производные:
110910 9d 9d 11 (f ^½ ) = ½(f ^{− ½} ) (−2x)
И подставить обратно f = (r ² − х ² ):
d dx (r ² − х ² ) ^½ = 5 1 7 х 29((r ) ^−½ ) ( −2x)
Отсюда мы упростили.
Использование производной
Итак, зачем находить производную y’ = −x/y ?
Ну, например, мы можем найти наклон касательной.
Пример: каков наклон окружности с центром в начале координат и радиусом 5 в точке (3, 4)?
Нет проблем, просто подставьте это в наше уравнение:
dy dx = −x/y
dy dx = −4/4 для бонуса уравнения в касательная:
y = −3/4 x + 25/4
Другой пример
Иногда неявный способ работает там, где явный способ затруднен или невозможен.
Пример: 10x
⁴ − 18xy ² + 10y ³ = 48
Как найти у? Мы не должны!
Сначала продифференцируем по x (используйте правило произведения для термина xy ²).
Затем переместите все элементы dy/dx в левую часть.
Решите для dy/dx
Вот так:
Начните с: 10x ⁴ − 18xy ² + 10y ³ = 48
Производная : 10 7 8 90 (4x 3 90) (х(2г дн dx ) + y ² ) + 10(3y ² dy dx ) = 0
0715 3 − 36xy dy dx − 18y ² + 30y ² dy dx = 0
10901 9d 9d 11 слева: −36xy dy dx + 30y ² dy dx = −40x ³ + 18y ²
Упростить :(30y ² −36xy) dy dx = 18y ² − 40x 9042 9 042 ^{3 Упростить: 3(5y ² −6xy) dy dx = 9y ² − 20x ³}
И мы получаем:
dy dx = 5×9 1 2 3 3(5y ² − 6xy)

Продукт Правило
Для среднего члена мы использовали правило произведения: (fg)’ = f g’ + f’ g
(xy ² )’ = x(y ² )’ + (x)’y ²
= x(2y dy dx ) + y ²
Потому что (y ² )’ = 2y dy 917101 90 в предыдущем примере)
О , и dx dx = 1, другими словами, x’ = 1
Обратные функции
Неявное дифференцирование может помочь нам решить обратные функции.
No related posts.

Цепное правило с использованием

Цепное правило с использованием ‘

Опять же, все, что мы сделали, это продифференцировали по y и умножили на

Явный

Пример: x

Снова цепное правило!

Использование производной

Пример: каков наклон окружности с центром в начале координат и радиусом 5 в точке (3, 4)?

Другой пример

Пример: 10x

Продукт Правило

Обратные функции

Дифференциал функции y sin 2 2x равен: Mathway | Популярные задачи

Дифференциал функции. Дифференциалы первого порядка.

3.5: Производные тригонометрических функций

Цели обучения

Производные функции синуса и косинуса

Производные от \(\sin x\) и \(\cos x\)

Доказательство

Пример \(\PageIndex{3}\): приложение к скорости

Упражнение \(\PageIndex{3}\)

Производные других тригонометрических функций

Пример \(\PageIndex{4}\): производная касательной функции 92x\\[4pt]

Пример \(\PageIndex{5}\): Нахождение уравнения касательной

Пример \(\PageIndex{6}\): нахождение производной тригонометрических функций

Упражнение \(\PageIndex{6}\)

Производные высшего порядка

Пример \(\PageIndex{9}\): Приложение к ускорению

Упражнение \(\PageIndex{9}\)

Ключевые понятия

Неявное дифференцирование

Неявное против явного

Пример: Круг

Как выполнить неявное дифференцирование

Пример: x

Добавить комментарий Отменить ответ