Дискретная математика и математика: Основы дискретной математики / Хабр

Содержание

Основы дискретной математики / Хабр

Привет, хабр. В преддверии старта базового курса «Математика для Data Science» делимся с вами переводом еще одного полезного материала.

Об этой статье

Эта статья содержит лишь малую часть информации по заявленной теме. Рассматривайте ее как вводный курс перед началом всестороннего изучения предмета. Надеюсь, вы найдете в ней полезную информацию. Знание дискретной математики помогает описывать объекты и задачи в информатике, особенно когда дело касается алгоритмов, языков программирования, баз данных и криптографии. В дальнейшем я планирую подробнее раскрыть темы, затронутые в этой статье. Приятного чтения!

ЧТО ТАКОЕ ДИСКРЕТНАЯ МАТЕМАТИКА?

Это область математики, изучающая объекты, которые могут принимать только уникальные отдельные значения.

Мы рассмотрим пять основных разделов в следующем порядке.

Логика
Теория множеств
Отношения
Функции
Комбинаторика
Графы

ЛОГИКА

Что такое логика?

Это наука о корректных рассуждениях. Мы будем использовать приемы идеализации и формализации. Неформальная логика изучает использование аргументов в естественном языке.

Формальная логика анализирует выводы с чисто формальным содержанием. Примерами формальной логики являются символическая логика и силлогистическая логика (о которой писал Аристотель).

Начнем с азов. Рассмотрим следующее высказывание на естественном языке:

«Если я голоден, я ем».

Пусть «голоден» будет посылкой A, а «ем» — следствием B. Попробуем формализовать:

A => B (то есть из A следует B)

NB. Посылка и следствие являются суждениями.

Логические выражения

Для нас важна форма, а НЕ содержание. Значение будет истинным, если оно соответствует форме.

Например, 10 < 4 — ЛОЖЬ, а 10 > 4 — ИСТИНА.

Логические операции

Суждение P — это утверждение, которое может быть как истинным, так и ложным.

Обозначим истинное значение P единицей (1), а ложное значение P нулем (0).

Существует другое суждение; обозначим истинное значение Q единицей (1), а ложное значение Q нулем (0).

Рассмотрим логические операции с суждениями, значение которых истинно. Они могут сами образовывать истинные значения путем выполнения соответствующих операций над истинными значениями.

Отрицание

ИЛИ

Эквивалентность

Импликация

Исключающее ИЛИ

Три закона

Теперь введем суждение R — утверждение, которое может быть как истинным, так и ложным.

Обозначим истинное значение R единицей (1), а ложное значение R нулем (0).

Закон ассоциативности

Закон дистрибутивности

Законы де Моргана

Логическая формула

Включает суждения, выражения в скобках и следующие символы:

Квантификаторы

Что такое квантификатор? Квантификатор в естественном языке — это слово, которое используется для обозначения количественных отношений (сколько). Например: все, несколько, много, мало, большинство и нисколько.

ТЕОРИЯ МНОЖЕСТВ

Что такое множество?

Это набор данных. Эти данные называются элементами (множества). Элементы во множестве не дублируются. Важным свойством множества является его неупорядоченность, то есть при изменении порядка следования элементов суть множества не меняется.

Например, если A = {1, 2, 3, 4} и B = {2, 4, 1, 3} и порядок неважен, то A = B

Разобравшись в этом, мы можем дать более точное определение множества — это коллекция различных, строго определенных объектов.

Иногда нам нужно определить бесконечное множество. Проблема очевидна: мы не сможем записать все его элементы. Значит, мы можем определить множество с помощью характерных признаков всех его элементов.

Операции над множествами

Подмножество

Количество элементов

Объединение

Пересечение

Дополнение

ОТНОШЕНИЯ

Логика отношений изучает отношения между математическими объектами. Мы можем установить связь с N элементами (где N — положительное натуральное число).

Бинарное отношение — это отношение между двумя элементами (объектами). Формально мы можем записать любое отношение между x и y так: x ~ y

Например, 4 < 8 или «Я студент по отношению к моему преподавателю».

Свойства бинарных отношений

Числовые множества

ФУНКЦИИ

Функция — это отношение, которое присваивает переменным новые значения. То есть это отношение между множеством А и множеством В.

Свойства

Функциональная композиция

Это точечное использование функции, результатом которого является другая функция.

КОМБИНАТОРИКА

Простыми словами, это наука о счете.

Перестановки

Это упорядочение уникальных объектов, при котором важен порядок следования.

Комбинации

Это упорядочение уникальных объектов, при котором не важен порядок следования.

Блок-схема алгоритма

ГРАФЫ

Что такое граф?

Это коллекция точек, которые называются узлами или вершинами, и линий между этими точками, которые называются ребрами. Ребро соединяет только два узла. Ребро может быть ориентированным, если ему присвоено направление, или неориентированным.

Если вам понравилась эта статья, приглашаю почитать также мой блог:

www.quantq8.com

Успеть на курс по специальной цене

Читать ещё:

Роль математики в машинном обучении

ДИСКРЕТНАЯ МАТЕМАТИКА • Большая российская энциклопедия

ДИСКРЕ́ТНАЯ МАТЕМА́ТИКА, раздел математики, изучающий свойства дискретных структур, которые возникают как в самой математике, так и в её приложениях. При этом дискретными структурами называются объекты, для которых важнейшие характеристики принимают конечное или счётное число значений. К числу таких структур относятся, напр., конечные группы, конечные графы, некоторые математич. модели преобразователей информации, конечные автоматы, Тьюринга машины. Это примеры структур финитного (конечного) характера. Часть Д. м., изучающая их, иногда называется конечной математикой. Помимо финитных структур, Д. м. изучает также дискретные бесконечные структуры (напр., бесконечные алгебраич. системы, бесконечные графы, бесконечные автоматы).

Предмет и методы дискретной математики

Значит. часть классич. математики занимается изучением свойств объектов непрерывного характера. Использование дискретной или непрерывной модели изучаемого объекта связано как с самим объектом, так и с тем, какие задачи ставит перед собой исследователь. Само деление математики на Д. м. и математику, занимающуюся непрерывными моделями, в значит. мере условно, поскольку, с одной стороны, происходит обмен идеями и методами между ними, а с другой – часто возникает необходимость исследования моделей, обладающих как дискретными, так и непрерывными свойствами одновременно. В математике существуют разделы, использующие средства Д. м. для изучения непрерывных моделей (напр., алгебраическая геометрия), и наоборот, часто методы, развитые для анализа непрерывных моделей, используются при изучении дискретных структур (напр., асимптотические методы в теории чисел, в перечислительных задачах комбинаторики). Однако специфика мн. разделов Д. м. связана с необходимостью отказа от таких фундам. понятий классич. математики, как предел и непрерывность, в связи с чем для мн. задач Д. м. некоторые методы классич. математики оказываются неприменимыми.

Наряду с выделением Д. м. путём указания её предмета можно также описать Д. м. перечислением составляющих её частей. К ним относятся комбинаторный анализ, графов теория, теория кодирования, теория функциональных систем, теория управляющих систем, автоматов теория, алгоритмов теория. При более широком толковании к Д. м. могут быть отнесены как целые разделы математики, напр. математич. логика, так и части таких разделов, как теория чисел, алгебра, вычислительная математика, теория вероятностей, в которых изучаемые объекты имеют дискретный характер.

Исторический очерк

Элементы Д. м. возникли в глубокой древности; развиваясь параллельно с др. разделами математики, они являлись их составной частью. Типичными были задачи, связанные со свойствами целых чисел, позднее эти задачи привели к созданию теории чисел. Примеры таких задач: отыскание алгоритмов сложения и умножения натуральных чисел у древних египтян, вопросы делимости натуральных чисел и задачи суммирования в пифагорейской школе, а в более позднее время – вопросы, связанные с разрешимостью уравнений в целых числах. Этот этап развития Д. м. связан с именами Диофанта, Евлида, Пифагора и Эратосфена. В 17–18 вв., в осн. в связи с игровыми задачами, появились элементы комбинаторного анализа и дискретной теории вероятностей, а в связи с общими проблемами теории чисел, алгебры и геометрии в 18–19 вв. возникли такие важнейшие понятия алгебры, как группа, поле, кольцо, определившие дальнейшее развитие и содержание алгебры и имевшие, по существу, дискретную природу. На протяжении 17–19 вв. развитие Д. м. связано с именами Н. Абеля, Э. Варинга, У. Гамильтона, Э. Галуа, А. Кэли, Ж. Лагранжа, А. Лежандра, П. Ферма, Л. Эйлера. В 19–20 вв. стремление к строгости математич. рассуждений и анализ методов математики привели к выделению ещё одного раздела – математич. логики. В это время проблемами Д. м. занимались Л. Брауэр, Дж. Буль, Н. Винер, К. Гёдель, Д. Гильберт, А. Чёрч, К. Шеннон. В создании рос. школы Д. м. участвовали И. М. Виноградов, А. Н. Колмогоров, О. Б. Лупанов и С. В. Яблонский.

Современные задачи дискретной математики

В 20 в. развитие Д. м. определялось гл. обр. запросами практики. Возникла новая наука – кибернетика и её теоретич. часть – математич. кибернетика, изучающая математич. методами разнообразные проблемы, которые ставит перед кибернетикой практич. деятельность человека. Математич. кибернетика является поставщиком идей и задач Д. м. Так, прикладные вопросы, требующие больших вычислений, стимулировали появление и развитие численных методов решения задач, что привело к созданию вычислительной математики. Анализ понятий «вычислимость» и «алгоритм» привёл к созданию теории алгоритмов. Задачи хранения, обработки и передачи информации способствовали возникновению информации теории, теории кодирования и теоретич. криптографии. Экономич. задачи, задачи электротехники, равно как и внутренние проблемы математики, потребовали развития теории графов. Задачи описания работы и конструирования сложных управляющих систем составили предмет теории управляющих систем и теории автоматов.

Одна из особенностей Д. м. состоит в том, что вместе с задачами типа задач существования, имеющими общематематич. характер, важное место в Д. м. занимают задачи, связанные с алгоритмич. разрешимостью и построением конкретных решающих алгоритмов. Др. особенностью Д. м. является то, что в ней впервые начались исследования т. н. дискретных многоэкстремальных задач. Соответствующие методы поиска экстремумов, использующие гладкость функций, в этих случаях оказываются неприменимыми. Типичными задачами такого рода в Д. м. являются, напр., задачи отыскания в некотором смысле оптимальных стратегий в шахматах, а также задачи построения минимальных дизъюнктивных нормальных форм для булевых функций (см. также Алгебра логики).

Особенностью Д. м., связанной с задачами для конечных структур, является то, что для многих из них существуют алгоритмы решения, в то время как для задач с элементами непрерывности, как правило, полное решение возможно лишь при весьма жёстких ограничениях. Примером такого алгоритма может служить алгоритм просмотра всех возможных вариантов, т. е. алгоритм полного перебора. К задачам, в которых может быть применён алгоритм полного перебора, относятся упомянутые задачи о стратегиях в шахматной партии с ограниченным числом ходов и о минимизации дизъюнктивных нормальных форм для булевых функций. Алгоритмы полного перебора трудоёмки и часто не могут быть реализованы на практике, в связи с чем возникает ряд задач, связанных с нахождением условий, ограничивающих перебор.

Дискретная математика | Brilliant Math & Science Wiki

Энди Хейс, Мухаммад Расель Парвеж, Хуа Чжи Ви, а также

способствовал

Содержимое

Комбинаторика
Теория множеств
Теория графов
Вероятность
Статистика
Биекции
Логика

Основная статья: Комбинаторика

Комбинаторика — это математика счета и упорядочивания. Конечно, большинство людей умеет считать, но комбинаторика применяет математические операции для подсчета вещей, которые слишком велики, чтобы их можно было считать обычным способом.

Комбинаторика особенно полезна в информатике. Комбинаторные методы можно использовать для оценки того, сколько операций потребуется для компьютерного алгоритма. Комбинаторика также важна для изучения дискретной вероятности. Методы комбинаторики можно использовать для подсчета возможных исходов в однородном вероятностном эксперименте.

Комбинаторика часто изучает, как устроены вещи. В этом контексте расположение — это способ группировки объектов. Самыми основными правилами, касающимися договоренностей, являются правило произведения и правило суммы. Эти правила определяют, как подсчитывать аранжировки с использованием операций умножения и сложения соответственно.

В местном гастрономе предлагаются следующие варианты бутербродов:

Типы хлеба: Белый, Ржаной, Пшеничный
Типы сыра: Швейцарский, Чеддер, Хаварти, Проволоне
Типы мяса: ростбиф, индейка, ветчина, солонина, рваная свинина

Если покупатель выберет ровно по одному продукту каждого типа, то сколько возможных бутербродов можно приготовить?

Более специфичным типом расположения является перестановка. \text{rd}.3rd . Порядок ABC\text{ABC}ABC будет отличаться от ACB.\text{ACB}.ACB.

Сколько существует возможных полей для размещения лошадей?

Комбинация (не путать с комбинацией или ) — это еще один тип расположения, связанный с перестановками. Комбинация — это расположение объектов без учета порядка.

12 разных игроков собираются сыграть в футбол. Двумя капитанами команд являются Брэндон и Мередит (входят в число 12). Каждый из них будет по очереди выбирать игрока в свою команду, пока не будут выбраны все игроки.

Сколькими способами можно разделить игроков на команды?

Как область математики, комбинаторика почти так же широка, как дискретная математика. Другие темы комбинаторики включают

расстройства: перестановку, при которой ни один объект не находится на своем первоначальном месте в порядке;
обходов по прямоугольной решетке: определение количества способов обхода прямоугольной решетки;
распределение объектов по ячейкам: определение того, как объекты могут быть сгруппированы по ячейкам.

Основная статья: Теория множеств
См. также:

Мощность
Объединение и пересечение
Комплектация
Принцип включения и исключения
Законы Де Моргана

Теория множеств — это раздел математики, изучающий наборы объектов. Наборы могут быть дискретными или непрерывными; дискретная математика в первую очередь занимается первым. На базовом уровне теория множеств занимается тем, как можно упорядочивать, комбинировать и подсчитывать множества.

Мощность конечного множества — это количество элементов в этом множестве. Для данного множества A,A,A его мощность обозначается через ∣A∣.|A|.∣A∣.

Какова мощность множества простых чисел меньше 25?
Набор простых чисел меньше 25 равен
{2,3,5,7,11,13,17,19,23}.\{2,3,5,7,11,13,17,19,23\}.
{2,3,5, 7,11,13,17,19,23}.
В этом наборе 9 элементов, поэтому мощность равна 9. □_\square□

Кардинальность также может быть распространена на бесконечные множества. Хотя этот вид кардинальности нельзя сосчитать, каждую кардинальность можно сравнить с другой кардинальностью.

Пусть AAA и BBB — множества. Их мощности сравниваются следующим образом:
Если существует биекция между AAA и B,B,B, то ∣A∣=∣B∣.|A|=|B|.∣A∣=∣B∣.
Если существует инъективная функция из AAA в B,B,B, но нет биективной функции, то ∣A∣<∣B∣.|A|<|B|.∣A∣<∣B∣.

Покажите, что множество целых чисел и множество четных целых чисел имеют одинаковую мощность.
Может показаться странным, что эти множества имеют одинаковую мощность. В конце концов, четные числа более «редки». Однако оба этих набора бесконечны . Следовательно, «здравый смысл», предполагающий конечных множеств, должен быть отброшен.
Вместо этого цель состоит в том, чтобы получить биективную функцию из набора целых чисел в набор четных целых чисел:
f(n)=2n, n∈Z.f(n)=2n, \ n \in \mathbb{Z}.f(n)=2n, n∈Z.
Приведенная выше функция устанавливает однозначное соответствие между каждым целым числом nnn и каждым четным целым числом 2n.2n.2n. Поскольку биекция установлена, множество целых чисел и множество четных целых чисел имеют одинаковую мощность. □_\квадрат□

Дополнение набора AAA — это набор элементов, не входящих в A.A.A. Изучение дополнений множества дает ряд эффективных методов для вычисления мощностей конечных множеств. Например, можно эффективно получить мощность набора, который содержит «по крайней мере один» элемент другого набора.

Дэвид — лидер Комитета Дэвида. Он хочет назначить 3 человек в состав Главного совета. Ему предстоит выбрать из 9 претендентов, трое из которых Томми, Джек и Майкл. Сколькими способами он может выбрать людей в Совет так, чтобы хотя бы один из Томми, Джека и Майкла был выбран?

Объединение и пересечение позволяют описать, как можно комбинировать наборы.

Целое положительное число меньше 1000 является не только идеальным квадратом, но и идеальным кубом.

Сколько таких чисел?

6% 36% 42% 54% 60%

Человек «А» говорит правду в 60% случаев, а человек «Б» говорит правду в 90% случаев.

В каком проценте случаев они могут противоречить друг другу, констатируя один и тот же факт?

Законы Де Моргана

дают тождества для дополнений объединений и пересечений.

300 400 600 900

Сколько целых чисел от 1 до 1000 (включительно) не являются ни кратными 2, ни кратными 5?

Принцип включения и исключения , или ПИС, дает метод нахождения объединения или пересечения более чем двух наборов. 96106 (включительно) не являются ни совершенными квадратами, ни совершенными кубами, ни совершенными четвертыми степенями?

Основная статья: Теория графов

Теория графов — это изучение графов , которые представляют собой совокупность связанных узлов.

Базовый график 3-Cycle

Графики полезны для представления всех видов реальных проблем.

от 4 до 5 до 8 с 4 по 7 по 3 с 4 по 5 с 4 по 9От 4 до 7 от 2 до 10

Если существует жадный алгоритм, который будет проходить по графу, выбирая наибольшее значение узла в каждой точке, пока не достигнет листа графа, по какому пути пойдет жадный алгоритм на приведенном ниже графе?

Джон живет на Деревах Десяти Домов, и это самое идеальное и идиллическое место для него и других обитателей сени. Они потратили огромное количество времени на проектирование этих домов, и, чтобы ни один дом не чувствовал себя изолированным от других, они построили новый, искусно сделанный мост между каждым домом!

К сожалению, Деревья Десяти Домов не были застрахованы от гроз, а мосты не были хорошо спроектированы. Ночь была коварной, завывающей от ветра и замерзающей от дождя, так что шансы на мосты были невелики — казалось, что каждый мост скорее уцелеет, чем рухнет!
К счастью, поскольку на Деревах Десяти Домов было очень много мостов, когда Джон проснулся на следующее утро, он обнаружил, что может добраться до каждого дома, используя только существующие мосты, хотя и окольными путями. маршруты, возможно, были необходимы. Когда они начали восстанавливать, Джону стало любопытно… каковы были шансы, что им всем так повезет? 9{10} П \большой\rэтаж?⌊1010P⌋?
Детали и предположения:
Деревья десяти домов на самом деле содержат ровно 10 домов.
До бури существует единственный мост между каждой уникальной парой домов.
Буря разрушит каждый мост с независимой вероятностью 12\frac{1}{2}21.
Джону разрешено проходить через чужие дома, чтобы попытаться добраться до них всех, но он должен использовать только уцелевшие мосты, чтобы добраться туда. Не допускается раскачивание виноградной лозы.
Отмечен #ComputerScience, так как без него решить эту задачу довольно утомительно, хотя и не невозможно.
Изображение предоставлено: http://hdscreen.me/wallpaper/2645876-bridges-fantasy-art-landscapes-mountains
Основная статья: Вероятность
Вероятность — это число от 0 до 1 включительно, представляющее вероятность события. Дискретная вероятность — это вероятность, основанная на дискретных наборах результатов. Самым основным типом вероятности является равномерная вероятность. Если каждый исход в наборе равновероятен, то вероятность события равна отношению кардинальностей.
Пусть SSS будет выборочным пространством результатов. Если каждый исход в этом множестве равновероятен, то вероятность события ААА в SSS равна
.
P(A)=∣A∣∣S∣.P(A)=\frac{|A|}{|S|}.P(A)=∣S∣∣A∣.
Какова вероятность того, что в високосном году будет 53 воскресенья?
Многие правила вероятности аналогичны правилам комбинаторики. Вероятностные правила произведения, суммы и дополнения работают аналогично тем же правилам комбинаторики. Кроме того, структура вероятностного принципа включения и исключения такая же, как у ПИС для множеств.
121243\dfrac{121}{243}243121 122243\dfrac{122}{243}243122 124243\dfrac{124}{243}243124 125243\dfrac{125}{243}243125
Многократно подбрасывается смещенная монета. Предположим, что исходы различных бросков независимы и вероятность выпадения орла равна 23\frac{2}{3}32 при каждом броске.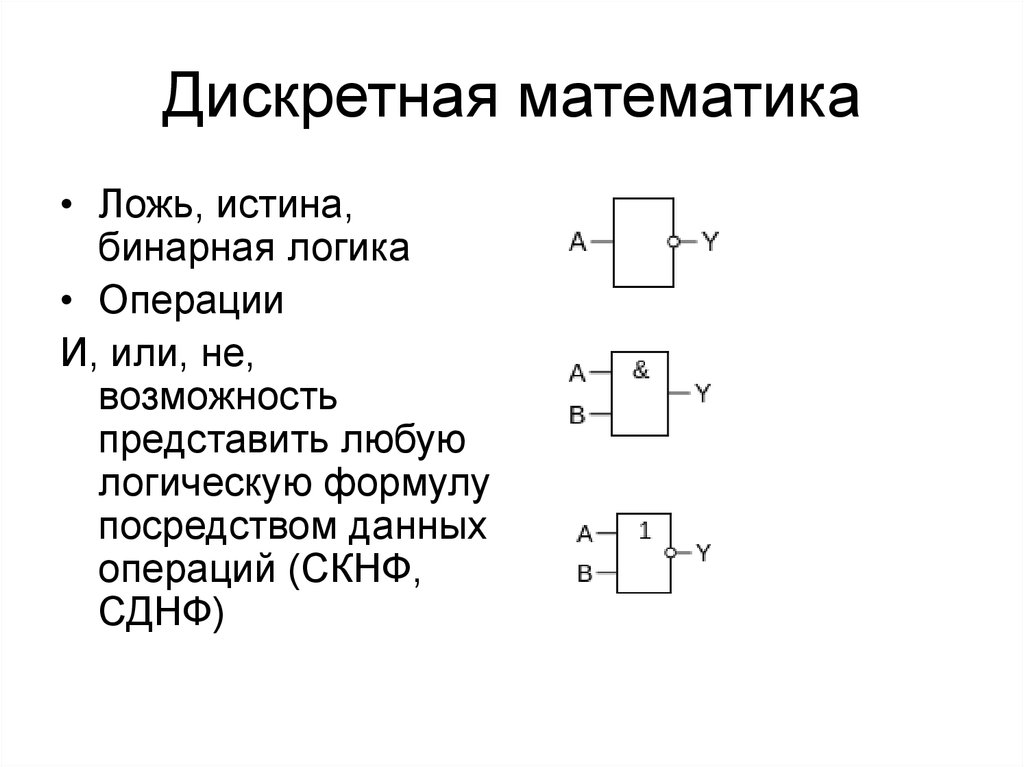 Какова вероятность выпадения четного числа голов за 5 бросков?
Дискретное распределение вероятностей — это функция, которая принимает числовой результат в качестве аргумента и дает в результате вероятность. Дискретные распределения вероятностей могут быть созданы с использованием правил и указаний, описанных выше. Есть также несколько дискретных распределений вероятностей, которые проявляются во многих задачах:
Геометрическое распределение: Учитывая повторяющиеся испытания, в которых вероятность успеха каждый раз одинакова, это дает вероятность того, что первый успех будет достигнут в определенном испытании. Пример : Вы бросаете кости, пока не выпадете 6. Какова вероятность того, что первые 6 выпадут при третьем броске?
Биномиальное распределение: Учитывая определенное количество испытаний, в которых вероятность успеха каждый раз одинакова, это дает вероятность определенного количества успехов. Пример : Вы подбрасываете монету 10 раз. Какова вероятность того, что выпадет ровно 5 орлов?
Распределение Пуассона: Учитывая период времени, в течение которого событие происходит определенное среднее количество раз, это дает вероятность того, что событие произойдет определенное количество раз. Пример : Ресторан быстрого питания принимает 3 клиентов в минуту. Какова вероятность того, что они получат 4 клиентов в следующую минуту?
Хотя базовые вероятности основаны на дискретных множествах, понятие вероятности можно распространить на непрерывные множества, используя концепции исчисления.
На единичном отрезке случайным образом отмечается точка.
Найдите математическое ожидание суммы квадратов длин двух частей.
Основная статья: биекция, инъекция и сюръекция
Биекция — это отношение между двумя наборами, такое, что каждый элемент в наборе связан ровно с одним элементом в другом наборе, и наоборот. Биекции можно применять для решения проблем, устанавливая взаимное соответствие между набором, который трудно перечислить, и хорошо понятной дискретной структурой. Устанавливая биекцию, можно воспользоваться известными формулами и теоремами, которые дает дискретная структура.
Трое братьев и сестер Моллой, Эйприл, Брэдли и Кларк, имеют целый возраст, который в сумме равен 15. Сколько существует возможных распределений возрастов?
Примечание : Возможно, что возраст может быть равен 0, что означает, что ребенок только что родился.
Можно установить биекцию между набором распределений возрастов и набором комбинаций. Рассмотрим расположение звездочек и полосок ниже:
⋆⋆∣⋆⋆⋆⋆∣⋆⋆⋆⋆⋆⋆⋆⋆⋆\звезда \звезда \мид \звезда \звезда \звезда \звезда \мид \звезда \звезда \звезда \звезда \звезда \звезда \звезда \звезда \star⋆⋆∣⋆⋆⋆⋆∣⋆⋆⋆⋆⋆⋆⋆⋆⋆
Это расположение соответствует следующему распределению возрастов: апрель — 2 года, Брэдли — 4 года, Кларк — 9 лет.. Обратите внимание, что в расположении выше 15 звезд и 2 полосы. Это дает в общей сложности 17 объектов, 2 из которых являются барами. Размещение полосок в разных местах среди 17 мест даст новое распределение возрастов. Таким образом, можно установить биекцию между множеством распределений возрастов и множеством комбинаций 2 объектов из 17.
Количество раздач возрастов
(172)=136. □\бином{17}{2}=136.\ _\квадрат(217)=136. □
На парковке 10 свободных мест подряд.
Прибывают 6 автомобилей, каждый из которых занимает ровно 1 парковочное место, выбранное случайным образом из числа доступных мест. Затем прибывает Робби на своем пикапе, для парковки которого требуется 2 пустых соседних места.
Если вероятность того, что Робби сможет припарковаться, равна ab,\frac{a}{b},ba, где aaa и bbb — взаимно простые положительные целые числа, то чему равно a+b?a+b?a+b ?
Основные статьи:
Логические головоломки
Логика высказываний
Булева алгебра
Предложение — это утверждение, которое может быть либо истинным, либо ложным. Логика высказываний направлена на то, чтобы наметить правила того, как эти утверждения могут быть изменены и объединены.
Какие из следующих утверждений верны, а какие ложны, зная, что весь набор непротиворечив?
С1. Утверждения 2 и 3 либо оба верны, либо оба ложны.
С2. Ровно одно из утверждений 4 и 5 верно.
С3. Ровно одно из утверждений 4 и 6 верно.
С4. Ровно одно из утверждений 1 и 6 верно.
С5. Утверждения 1 и 3 относятся к одному типу (оба истинны или оба ложны).
С6. Ровно одно утверждение из утверждений 2 и 5 верно.
Запишите ответ в виде конкатенации цифр 1 и 0 для значений истинности утверждений (истина и ложь), начиная с S1 до S6, где значению истинно соответствует 1, а значению ложь соответствует 0. Например, если бы первые 2 утверждения были истинными, а остальные ложными, ответ был бы 110000.
Если правильный ответ начинается с некоторого количества начальных нулей, удалите его из записи ответа. Например, если ответ 001100, все равно напишите 1100.
Аналогично, Булева алгебра описывает операции, определенные над переменными, которые могут принимать значения true (1) или false (0). Булева алгебра используется для проектирования компьютерных схем через логических элементов , которые принимают сигнал(ы) в качестве входных данных и возвращают сигнал в качестве выходного сигнала.
Элементы И на диаграмме выводят 1, если оба входа также равны 1.
Если A = 1, B = 1 и C = 0, каким будет конечный результат?
Процитировать как: Дискретная математика. Brilliant.org . Извлекаются из https://brilliant.org/wiki/discrete-mathematics/
Введение в дискретную математику
Введение в дискретную математику
Введение в дискретные структуры — Что и почему
Что такое дискретная математика?
Дискретная математика — это математика, имеющая дело с дискретными объектами. Дискретные объекты — это те, которые отделены от (не связаны с/отдельные из) друг друга. Целые числа (они же целые числа), рациональные числа (те, которые могут быть выражается как частное два целых числа), автомобили, дома, люди и т. д. — все это дискретные объекты. С другой стороны, действительные числа, которые включают в себя как иррациональные, так и рациональные числа. не являются дискретными. Как известно, между любыми двумя различными действительными числами существует другое действительное число, отличное от любого из них. Поэтому они упакованы без каких-либо пробелы и не могут быть отделены от своих непосредственных соседей. В этом смысле они не дискретны. В этом курсе нас будут интересовать такие объекты, как целые числа, высказывания, множества, отношения и функции, которые все дискретны. Мы изучаем понятия связанные с ними, их свойства и отношения между ними среди других.
Почему дискретная математика?
Давайте сначала посмотрим, почему нас интересуют формальные/теоретические подходы. в информатике.
Некоторые из основных причин, по которым мы применяем формальные подходы: 1) с ними мы можем обращаться с бесконечностью или большим количеством и неопределенностью, и 2) результаты формальных подходов можно использовать повторно.
В качестве примера рассмотрим простую задачу инвестирования. Предположим, что мы инвестируем 1000 долларов каждый год с ожидаемой доходностью 10% в год. Сколько мы будем иметь через 3 года, 5 лет или 10 лет? Самым наивным способом выяснить это было бы вычисление грубой силы.
Давайте посмотрим, что произойдет с 1000 долларов, вложенными в начале каждого года в течение трех лет.
Сначала рассмотрим 1000 долларов, вложенных в начале первого года. Через год это производит возврат 100 долларов. Таким образом, в начале второго года 1100 долл., т. е. равно 1000 долларов США * ( 1 + 0,1 ), составляет вложил. Эти 1100 долларов дают 110 долларов в конце второго года. Таким образом в начале третьего года у нас есть 1210 долларов, что равно 1000 долларов * ( 1 + 0,1 )( 1 + 0,1 ), или 1000 долларов * ( 1 + 0,1 ) ² . После третьего года это дает нам 1000 долларов * (1 + 0,1) ³.
Точно так же мы можем видеть, что 1000 долларов, вложенных в начале второго года производит 1000 долларов * ( 1 + 0,1 ) ² в конце третьего года, и 1000 долларов, вложенных в начале третьего года, становятся 1000 долларов * (1 + 0,1).
Таким образом, общая сумма основного долга и дохода через три года равна 1000 долл. США * (1 + 0,1) + 1000 долл. США * (1 + 0,1) ² + 1000 долл. США * (1 + 0,1) ³ , что равно 3641 доллару.
Аналогично можно рассчитать основную сумму и доход за 5 лет и на 10 лет. Однако это долгий утомительный расчет даже при калькуляторы. Далее, что, если вы хотите узнать принципала и вернуться за некоторые другие доходы, чем 10%, или другие периоды времени, такие как 15 лет ? Вам пришлось бы делать все эти расчеты снова и снова.
Мы можем значительно избежать этих утомительных вычислений, отметив сходство в этих задачах и решать их в более общем виде.
Поскольку все эти проблемы требуют в результате вложения определенной суммы каждый год в течение определенного количества лет с определенным ожидаемым годовым доходом, мы используем переменные, скажем, A, R и n , представлять основной капитал вновь вложенных каждый год, коэффициент доходности и количество лет инвестирования соответственно. Этими символами основной и возврат через n лет, обозначенный S , можно выразить как
S = A (1 + R ) + A (1 + R ) ² + … + A (1 + R ) ⁿ .
Как известно, этот S можно представить в более компактном виде путем первого вычисления S — (1 + R ) S как
S = A ( (1 + R ) ^{n + 1} — (1 + Р ) ) / Р .
Когда мы получим его в такой компактной форме, довольно легко вычислить S для разных значений A, R и n , хотя нужно еще вычислить (1 + R ) ^{n + 1} . Эта простая формула представляет бесконечно много случаев, связанных с все разные значения A, R и n . Однако вывод этой формулы связан с другой проблемой. При вычислении компактной формы для С , С — (1 + Р ) С был рассчитан с использованием S = A (1 + R ) + A (1 + R ) ² + … + А (1 + R ) ⁿ . Хотя этот аргумент кажется достаточно строгим, на практике он достаточно хорош. аргумент, когда хочется быть очень строгим, многоточие … в сумме для S не считается точным. Ожидается, что вы будете интерпретировать его определенным специфическим образом. Но это можно интерпретировать различными способами. На самом деле это может означать что угодно. Таким образом, если кто-то хочет быть строгим и абсолютно уверенным в правильности формулы, нужен какой-то другой способ проверки, кроме как с помощью многоточия. Поскольку его нужно проверять для бесконечно многих случаев (бесконечно многих значения A, R и n ), какой-то требуется формальный подход, абстрагированный от реальных цифр.
Теперь предположим, что мы каким-то образом формально успешно проверили формулу и мы абсолютно уверены, что это правильно. Это хорошая идея написать компьютерная программа для вычисления этого S , особенно с (1 + R ) ^{n + 1} подсчитывается. Предположим снова, что мы написали программу для вычисления S . Как мы можем знать, что программа правильная? Как мы знаем, существуют бесконечно много возможных входных значений (то есть значений A, R и и ). Очевидно, мы не можем проверить его для бесконечного множества случаев. Таким образом, мы должны принять какой-то формальный подход.
В связи с проблемой корректности компьютерных программ существует известная «проблема остановки». Эта проблема, если рассматривать ее в контексте корректность программы, спрашивает останавливается ли данная компьютерная программа на заданном входе через конечное время. Известно, что эта проблема неразрешима компьютерами. То есть никто может написать компьютерную программу, чтобы ответить на этот вопрос. Известно, что оно неразрешимо. Но как мы можем сказать, что это неразрешимо? Как мы можем сказать что такую программу нельзя написать? Вы не можете попробовать все возможные методы решения и увидеть, что все они терпят неудачу. Вы не можете думать о все (кандидат) методы решения проблемы Проблема с остановкой. Таким образом, вам нужны какие-то формальные подходы, чтобы избежать имеет дело с чрезвычайно большим количеством (если не бесконечным) возможностей.
Дискретная математика является основой формальных подходов. В нем обсуждаются языки, используемые в математических рассуждениях, основные понятия, их свойства и отношения между ними. Хотя нет времени рассматривать их в этом курсе, дискретная математика также касается методов решения определенных типов проблем например, как считать или перечислять количества. К задачам подсчета относятся: сколько существует маршрутов из точки А в точку Б; в компьютерной сети? Сколько времени выполнения требуется для сортировки список целых чисел в порядке возрастания? Какова вероятность выиграть в лотерею? Какой кратчайший путь из пункта А в пункт Б в компьютерной сети? и т. п.
Предметы, изучаемые в этом курсе, включают логику высказываний, логику предикатов, множества, отношения и функции, в частности рост функции.
Первый предмет — логика. Этому посвящена глава 1 учебника. это язык который отражает суть наши рассуждения и правильные рассуждения должны следовать правилам этого языка. Начнем с логики предложений называется пропозициональной логикой и изучает элементы логики, (логические) отношения между предложениями и рассуждения. Затем мы изучаем немного более мощную логику, называемую логикой предикатов. Это позволяет нам рассуждать операторы, включающие переменные среди прочего. В главе 1 мы также изучаем множества, отношения между множествами и операции над множествами. Почти все есть описывается на основе наборов, когда требуется строгость. Это основа любой теории в информатике и математика. В главе 3 мы изучаем математические рассуждения, в частности, рекурсивные определения. и математическая индукция. Есть множества, операции и функции которые могут быть точно определены рекурсивными определениями. Свойства тех рекурсивно определенные объекты могут быть устанавливается строго с помощью доказательства по индукции. Затем в главе 6 мы изучаем отношения. Они являются абстракцией отношений, которые мы знакомы в повседневной жизни, такие как отношения между мужем и женой, отношения между родителями и детьми и отношения собственности. Они также являются одним из ключевых понятий в обсуждение многих предметов на компьютер и вычисления. Например, база данных рассматривается как набор отношений. и языки запросов к базам данных строятся на основе операций над отношениями и множествами. Графики также покрыты кратко здесь. Они пример дискретных структур, и они являются одной из самых полезных моделей для ученых-компьютерщиков и инженеры в решении проблем. Более подробное описание графа можно найти в главе 7. Наконец, в главе 1 мы изучаем функции и их асимптотическое поведение. Функции – это особый вид отношение и в основном тот же вид концепции, что и те, которые мы видим в исчислении. Однако функция является одним из наиболее важные концепции при обсуждении многих тем, связанных с компьютером и вычислениями, таких как данные структуры, базы данных, формальные языки и автоматы, анализ алгоритмов который кратко описан в Глава 2.
No related posts.