3. Линейные и монотонные функции. Функции, сохраняющие константу. Самодвойственные функции. Замкнутые классы и полные системы в.
Опр 1. Функция называется самодвойственной, если . Класс само-
двойственных функций обозначается S.
Опр 2. Функция называется линейной, если она представима в виде
, где , . Множество всех линейных
функций обозначается L.
Опр 3. Говорят, что функция сохраняет константу 0 (константу 1), если
(). Множество функций, сохраняющих константу 0
или 1, обозначается соответственно и .
Опр 4. Булева функция называется монотонной, если для любых двух наборов и
 В противном
В противном случае функция называется немонотонной. Класс монотонных функций обозна-
чается M.
Опр 5. Наборы и называются соседними, если они имеют вид:
Опр 6. Пусть M — некоторое множество функций алгебры логики. Замыкание [M] мно-
жества M называется совокупностью всех функций из , являющихся суперпо-
зициями функций из множества M.
Опр 7. Множество M называется функционально замкнутым классом, если [
M]=M. Опр
8. Пусть M — замкнутый класс в .
Подмножество R из M называется функци-
Пусть M — замкнутый класс в .
Подмножество R из M называется функци-
онально полной системой в M, если [R]=M.
Опр 9. Множество , содержащееся в замкнутом классе M (в т.ч. M=) называется
полным классом в M, если оно не является полной системой в M, но для каждой
функции
Опр 10. Система G называется независимой, если никакая функция не представ-
лена суперпозициями функций из .
Опр 11. Независимая система G называется базисом функционально замкнутого класса
K,
если всякая функция из K есть суперпозиция функций из G.
Теорема 1. Система полна в , тогда и только тогда, когда она целиком не содержится
ни в одном классе ,, S, L, M.
Теорема 2. Булева функция немонотонная, тогда и только тогда, когда существует, хотя
бы два соседних набора , таких что
Лемма о немонотонной функции. Из немонотонной функции путём подстановок 0,1 и x можно получить функцию отрицания .Лемма о несамодвойственной функции. Из несамодвойственной функции, путём подстановки функций , можно получить несамодвойственную функцию одной переменной, т.е. const 1 или 0.
Лемма
о нелинейной функции. Из всякой нелинейной функции, путём
подстановок 0, 1 и функций x,
,
а также, быть может, навешиванием
отрицания над самой функцией, можно
получить конъюнкцию.
3.1. Разлагая функцию в полином Жегалкина, выяснить является ли она линейной.
1) 2)
3) 4)
3.2. Выяснить, является ли линейной функция .
1) 2)
3) 4)
3.3. Самодвойственна ли функция .
1)
Решение: Алгоритм определения самодвойственности функции:
a) строится истинностная таблица
b) сравниваем симметричные наборы переменных. Если значения функции
на этих наборах не равны, то данная функция самодвойственна.
0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
0 | 1 | 1 | 0 | 0 | 1 | 1 | |
1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 |
1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 |
1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Ответ: функция
самодвойственна.
2) 3)
4) 5)
3.4. Из несамодвойственной функции с помощью подстановки на места переменных функций и получить константу.
1) 2)
3) 4)
3.5. Какие из перечисленных ниже функций являются монотонными.
1)
Решение:
a) строим истинностную таблицу для данной функции
x | y | ||
0 | 0 | 1 | 1 |
0 | 1 | 1 | 1 |
1 | 0 | 0 | 0 |
1 | 1 | 1 | 1 |
b) согласно теореме 2, сравним значения функции для соседних наборов
Ответ: функция
—
монотонная.
2) 3)
4) 5)
6) 7)
8)
3.6. Перечислить все функции , удовлетворяющие следующим условиям:
1)
2)
3.7. Показать, что если , то .
3.8. Показать, что всякая монотонная функция содержится не менее чем в двух классах из
.
3.9. Из немонотонной функции с помощью подстановки на места переменных констант
0,1 и функции получите функцию .
1) 2)
3) 4)
5) 6)
3.10. Какие из следующих булевых функций сохраняют константу 0 (константу 1).
1) 2) 3) 4)
3.11. Используя критерий полноты, выяснить, полна ли в система R.
1)
Решение:
Составляем истинностную таблицу для
функций заданных в системе R.
Таблица 1 | Таблица 2 | ||||||
0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 |
1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 |
1 | 0 | 0 | 0 | 0 | |||
1 | 0 | 1 | 1 | 1 | |||
1 | 1 | 0 | 0 | 0 | |||
1 | 1 | 1 | 0 | 0 | |||
Определяем,
к какому из замкнутых классов принадлежит
данная функция, т. е.
е.
составляем таблицу Поста.
L | M | S | |||
— | + | — | — | — | |
— | — | — | — | — |
Ответ: система R — полна.
2) 3)
4) 5)
3. 12.
Какие из перечисленных систем зависимы.
Укажите независимые системы.
12.
Какие из перечисленных систем зависимы.
Укажите независимые системы.
1)
Решение:
Ответ: система независимая.
2) 3)
3.13. Из системы ,полной для замкнутого класса выделите базис.
1)
Решение:
f | M | S | L | ||
0 | + | — | + | — | + |
1 | — | + | + | — | + |
+ | + | + | + | + | |
— | — | — | + | + |
Ответ: -базис для замкнутого класса M
2) 3)
3. 14. Пример
№1. Пусть
функция задана формулой
14. Пример
№1. Пусть
функция задана формулой
x | y | z | f(x) |
0 | 0 | 0 | 1 |
0 | 0 | 1 | 1 |
0 | 1 | 0 | 1 |
0 | 1 | 1 | 1 |
1 | 0 | 0 | 1 |
1 | 0 | 1 | 1 |
1 | 1 | 0 | 0 |
1 | 1 | 1 | 1 |
Проверяем функцию на
монотонность. Выписываем наборы
переменных, где нарушается монотонность
функции.
Выписываем наборы
переменных, где нарушается монотонность
функции.
Составляем функцию , заменяя на x переменную, относительно которой нарушена монотонность. Остальные переменные оставляем как есть.
Подставляем функцию , в заданную формулу и выполняем указанные действия.
3.15. Пример №2. Проверить лемму о несамодвойственной функции, заданной таблично.
x1 | x2 | x3 | f(x) |
0 | 0 | 0 | 0 |
0 | 0 | 1 | 0 |
0 | 1 | 0 | 1 |
0 | 1 | 1 | 0 |
1 | 0 | 0 | 0 |
1 | 0 | 1 | 0 |
1 | 1 | 0 | 0 |
1 | 1 | 1 | 1 |
Выбираем наборы переменных,
на которых нарушена самодвойственность.
Составляем функцию f, заменяя 0 на –x, а 1 на x.
Подставляем функцию 1 или 2 в СДНФ, СКНФ или полином Жегалкина данной функции, и выполняем указанные действия.
–полином Жегалкина функции, заданной таблично.
3.16. Пример №3. Для функции заданной формулой, проверить лемму о нелинейной функции.
Представим функцию в виде четырех слагаемых.
Составим функцию .
Составим функцию .
Подставим функцию пси в полином Жегалкина, учитывая, что x3=0.
3.17. Выяснить какие системы образуют базис в L.
1) 2)
3) 4)
5)
3. 18.
Выяснить являются ли базисами в
следующие
системы.
18.
Выяснить являются ли базисами в
следующие
системы.
1) 2)
3) 4)
3.19. Выяснить являются ли базисами в следующие системы.
1) 2)
3) 4)
3.20. Показать, что множество образует базис в M.
3.21. Из множества выделить подмножества, являю-
щиеся базисами в M.
Дискретная математика, комбинаторика, теория чисел
Сообщения без ответов | Активные темы | Избранное
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения и указать конкретные затруднения.
Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.
| ozhigin |
| ||
25/12/08 |
| ||
| |||
| Xaositect |
| |||
06/10/08 |
| |||
| ||||
| ozhigin |
| ||
25/12/08 |
| ||
| |||
| Xaositect |
| |||
06/10/08 |
| |||
| ||||
| ozhigin |
| ||
25/12/08 |
| ||
| |||
| Xaositect |
| |||
06/10/08 |
| |||
| ||||
| ozhigin |
| ||
25/12/08 |
| ||
| |||
| Xaositect |
| |||
06/10/08 |
| |||
| ||||
| ozhigin |
| ||
25/12/08 |
| ||
| |||
| Xaositect |
| |||
06/10/08 |
| |||
| ||||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 10 ] |
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
| Найти: |
Линейная функция в дискретной математике
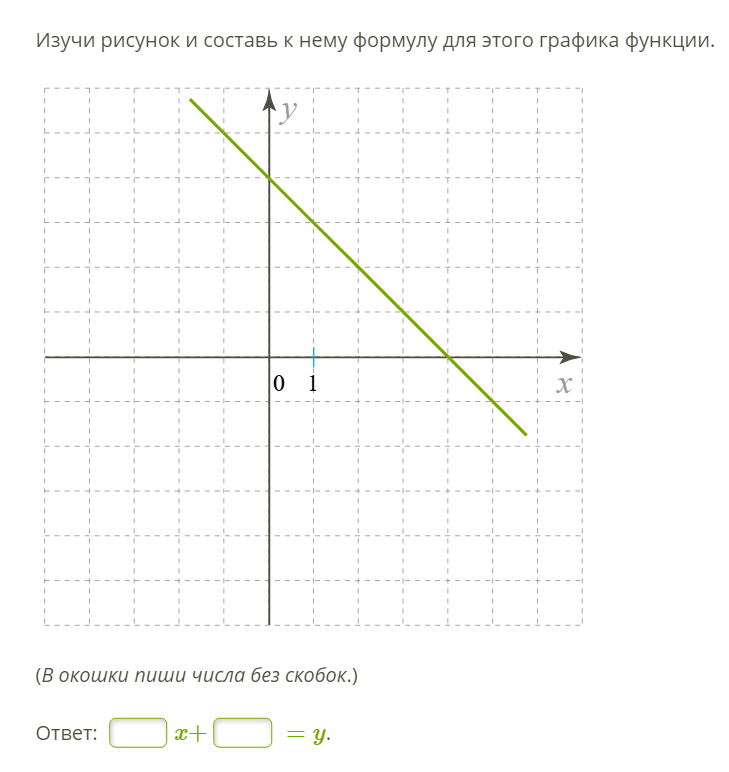
следующий → ← предыдущая Линейная функция может быть описана как функция, которая показывает прямую линию на координатной плоскости. Определение линейной функцииЛинейная функция может быть описана как функция, которая должна быть представлена в виде f(x) = mx+b. В этом уравнении m и b используются для обозначения действительных чисел. Это уравнение выглядит так же, как уравнение пересечения наклона с линией, которое равно y = mx+b. Они выглядят одинаково, потому что для представления линии используется линейная функция. Это означает, что график этой функции представляет собой линию. Здесь ‘м’ используется для обозначения наклона линии ‘b’ используется для обозначения точки пересечения y строки ‘x’ используется для обозначения независимой переменной. f(x) или ‘y’ используется для обозначения зависимой переменной. Линейная функция может быть описана как алгебраическая функция. Пример и уравнение линейной функцииРодительская линейная функция обозначается как f(x) = x, что на самом деле является линией, проходящей через начало координат. В общем случае уравнение линейной функции обозначается как f(x) = mx + b. Некоторые примеры линейной функции описываются следующим образом: f(x) = 6x-5. f(x) = -7x — 0,7 f(x) = 4 Реальный пример линейной функцииМы также можем объяснить линейную функцию с помощью некоторых реальных приложений, которые описываются следующим образом:
Нахождение линейной функцииМы можем найти линейную функцию с помощью либо формы точка-наклон, либо формы наклон-пересечение. Процесс определения линейной функции и определения уравнения прямой аналогичен, и мы объясним это с помощью следующего примера. Пример: В этом примере мы должны определить линейную функцию, которая содержит две функции (-1, 15) и (2, 27). Решение: Из вопроса у нас есть две точки, т. е. (x 1 , у 1 ) = (-1, 15) и (х 2 , у 2 ) = (2, 27). Шаг 1: На этом шаге мы будем использовать формулу наклона для определения наклона функции следующим образом: М = (у 2 -у 1 ) / (х 2 -х 1 ) = (27-15) / (2-(-1)) = 12/3 = 4. Шаг 2: На этом шаге мы будем использовать форму наклона точки, чтобы мы могли найти уравнение линейной функции следующим образом: у — у 1 = м(х — х1) у-15 = 4(х-(-1)) у-15 = 4(х+1) у-15 = 4x+4 у = 4х+19 Следовательно, уравнение линейной функции имеет вид f(x) = 4x + 19. Идентификация линейной функции Если мы получим информацию о функции в виде графика, и этот график является линией, то эта функция будет линейной функцией. Если мы получим информацию о функции в виде алгебраической формы, которая имеет вид f(x) = mx+b, то эта функция также будет линейной функцией.
Пример: В этом примере у нас есть некоторые данные в таблице, и мы должны показать, представляют ли эти данные линейную функцию.
Решение: Для этого мы будем вычислять разность значений x, значений y и отношение (разность y) / (разница x) каждый раз, и из этих вычислений мы увидим, является ли отношение является константой. График линейной функцииКак мы знаем, мы можем построить линию с помощью любых двух точек на ней. Когда мы сможем найти эти две точки, нам нужно просто соединить их в линию, а затем продолжить их с обеих сторон. Следующие вещи содержит график линейной функции f(x) = mx+b При m>0 в этом случае график будет представлять собой возрастающую линию. Когда м Когда м
График линейной функции путем нахождения двух точек Мы будем использовать функцию f(x) = mx+b, чтобы определить две точки на ней. Для этого возьмем несколько случайных значений x и найдем соответствующее значение y с помощью подстановки этих значений в функцию f(x). Теперь мы объясним процесс построения графика функции с помощью примера, в котором мы построим график функции f(x) = 3x + 5 следующим образом: Шаг 1: На этом шаге мы будем использовать некоторые случайные значения для определения двух точек на линии. Шаг 2: Теперь мы найдем соответствующие значения y с помощью подстановки указанных выше значений x в функцию. В следующей таблице мы видим линейную функцию y = 3x+5 следующим образом:
Следовательно, (-1, 2) и (0, 5) — это две точки на прямой. Шаг 3: Теперь мы нанесем эти точки на график и соединим их линией. Мы также продолжим линию слева и справа следующим образом: График линейной функции с использованием точки пересечения оси Y и наклона С помощью точки пересечения оси y ‘b’ и наклона ‘m’ линейной функции f(x) = mx+b мы можем построить график любой функции. Теперь мы объясним, как это сделать, снова используя ту же линейную функцию f(x) = 3x+5. (0, b) = (0, 5) используется, чтобы показать точку пересечения этой функции с осью y, а m = 3 используется, чтобы показать ее наклон. Шаг 1: На этом этапе мы построим точку пересечения по оси y (0, b), которая равна (0, 5). Итак, мы нанесем точки (0, 5). Шаг 2: Теперь нам нужно записать наклон в виде дроби подъем/набег, а затем узнать «нарастание» и «набег». Здесь наклон = 3 = 3/1 = подъем/спуск Итак, подъем = 3, а бег = 1. Шаг 3: На этом шаге мы получим новые точки, подняв точки пересечения по вертикали с помощью «подъема», а затем пробежавшись по горизонтали с помощью «пробега». Примечание. График будет повышаться, если «рост» положительный, и график будет снижаться, если «рост» отрицательный. Точно так же мы пойдем направо, если «пробег» положительный, и мы пойдем налево, если «прогон» отрицательный.На этом графике мы поднимемся на 3 единицы вверх от точки пересечения с осью y и, таким образом, сдвинемся вправо на 1 единицу. Шаг 4: Теперь мы воспользуемся линией, чтобы соединить точки с шага 1 по шаг 2, и продолжим эти линии с обеих сторон. Домен и диапазон линейной функцииНабор всех действительных чисел содержится в диапазоне и области определения линейной функции. На изображении ниже мы видим, что f(x) = 2x+3 и g(x) = 4-x обе функции нанесены на одни и те же оси следующим образом: Здесь R используется для отображения области определения линейной функции, а R также используется для отображения диапазона линейной функции. Примечание:
Инверсия линейной функции Функция f -1 (x) используется для обозначения обратной линейной функции f(x) = ax+b таким образом, что f(f -1 (x)) = f -1 (f(x)) = x. Теперь мы будем использовать пример, чтобы показать процесс определения обратной линейной функции. Шаг 1: На первом шаге мы заменим f(x) на y. Заменив, мы получим следующее уравнение: у = 3х+5 Шаг 2: Теперь мы поменяем переменные x и y местами и получим следующее уравнение: х = 3у+5 Шаг 3: Теперь мы решим приведенное выше уравнение для y следующим образом: х-5 = 3 года г = (х-5)/3 Шаг 4: Теперь заменим y обратной функцией f -1 (x), и получаем следующее: ф -1 (х) = (х-5) /3 Обратите внимание, что функция f(x) и обратная функция f -1 (x) всегда симметричны относительно прямой y = x. Теперь построим линейную функцию f(x) и обратную ей функцию f -1 (x). Здесь f(x) = 3x+5 и f -1 (x) = (x-5)/3. Здесь мы проверим, симметричны ли эти функции относительно y = x, а также увидим, когда (x, y) лежит на f(x), то (y, x) лежит на f -1 (х). Кусочно-линейная функцияВ некоторых случаях линейная функция определяется единообразно во всей области определения. Это связано с тем, что его область определения может быть разделена на две или более частей, поэтому в некоторых случаях линейная функция может быть определена двумя или более чем двумя способами. Этот тип линейной функции известен как кусочно-линейная функция. Пример кусочно-линейной функции описывается следующим образом: Пример: В этом примере у нас есть линейная функция, и мы должны построить график этой функции. Функция f(x) описывается следующим образом: Решение: Описанная выше кусочная функция является линейной в обеих описанных выше частях своей области определения. Теперь мы определим конечную точку линии, взяв оба случая. В случае x ∈ [-2, 1):
Когда x ∈ [1, 2):
Соответствующий граф описывается следующим образом: Важные примечания
Следующая темаДополнение графа в дискретной математике ← предыдущая следующий → |
последовательности и серии — Всегда ли линейные функции непрерывны?
==== Ответ 1: В котором я на самом деле не объясняю, что что-либо означает, но я объясняю, почему это не проблема =====
Определение линейного в 8-м классе как «по прямой линии» Это хорошо. Но определение непрерывности в 8-м классе как «можно рисовать, не отрывая карандаша» не соответствует действительности.
Линейная функция $x\mapsto 2x+3; x\in \mathbb Z$ — это множество отдельных точек, расположенных на одной линии. Эти точки: $(0,3), (1, 5), (2,7) и т. д.$ лежат на прямой.
Эти точки: $(0,3), (1, 5), (2,7) и т. д.$ лежат на прямой.
Интуитивно OP, вероятно, предполагает, что это не является непрерывным. он переходит из точки $(0,3)$ в $(1,5)$ и не проходит через промежуточные точки. НО , по математическому определению, это ЕСТЬ сплошное. В каждой точке, где существует функция, вы можете нарисовать 90 404 эту часть функции, не отрывая карандаша. То, что находится между ними, не считается, потому что… оно находится между ними.
Функция имеет домен. И когда мы анализируем, является ли функция непрерывной (или если функция что угодно ) нас интересуют только входные значения внутри домена. Если значение в домене равно , а не , это не имеет значения, поскольку оно не является входным, поэтому оно просто не учитывается. Его может и не быть.
Если $f: \mathbb Z \to \mathbb R$ равно $f(x) = 2x + 3$, то оно определено только для $x\in \mathbb Z$. Что такое $f(1.5)$, нас волнует не больше, чем $f(\text{бабар, слон})$. $1.5$ не является целым числом, поэтому $f(1.5)$ не существует. Его так же не существует, как $f(синий)$ или $f(голодный)$.
$1.5$ не является целым числом, поэтому $f(1.5)$ не существует. Его так же не существует, как $f(синий)$ или $f(голодный)$.
Таким образом, не имеет значения, нужно ли нам «поднять карандаш», чтобы перейти от $(0, 3)$ к $(1,5)$, потому что все $x$ между $0$ и $1$ делают не существует , насколько нам известно. Просто не существует.
Итак… если бы мы использовали определение «непрерывного» для 8-го класса, это было бы «мы можем нарисовать функцию, не отрывая карандаша в любой точке нашей вселенной «. Однако, если в нашей вселенной есть гиперпространственные порталы, в которых $1$ идет сразу после $0$, то прыжок с $0$ на $1$ не считается «поднятием карандаша».
===== Ответ 2: где я объясняю, что означают некоторые вещи ====
Две проблемы с определением линейной функции, означающей, что «график представляет собой прямую линию»: 1) кто на самом деле не иметь определение того, что такое «прямая линия», и 2) это предполагает, что мы измеряем все на геометрической плоскости, а не на каком-либо другом типе «вселенной».
Я думаю, что лучшим определением «линейной функции» было бы: функция, в которой разница выходов всегда пропорциональна разнице соответствующих входов. То есть, если ваши входные данные представляют собой разницу в $a$, а ваши выходные данные представляют собой разницу в $b$, то i) это будет истинным независимо от того, какие точки вы берете в качестве входных данных, и ii) если ваши входные данные представляют собой разницу в $k*a$ тогда ваши результаты будут отличаться на $k*b$. 92$ не является линейным, потому что $f(0)=0$ и $f(1)=0$ имеют разницу в $1$, но $f(99) = 9801$ и $f(100) = 10000$ имеют разницу $199$. И $f(1)=1$ и $f(2)=4$ имеют разницу в $3$, но $f(1)$ и $f(3)$ (где входы находятся в два раза дальше друг от друга) не имеют разницу $2*3$ (разница выходов не в два раза больше).
Это определение означает, что $\frac {f(b) — f(a)}{b-a}$ всегда будет некоторым постоянным пропорциональным коэффициентом, который мы можем назвать $m$ и …..
…. tl;dr… ..
..
Линейная функция имеет форму $f(x) = mx + b$, и это всегда делает график, где $m$ — постоянный наклон (все линии имеют постоянный наклон; это то, что делает их линиями — и функции, которые не являются линиями, будут иметь точки, где иногда график более крутой или менее крутой, чем другие). $b$ не так важно для того, что я пытаюсь донести. Это $y$-перехват вертикального смещения.
[Было бы упущением не упомянуть, что «линейная функция» имеет другое значение в линейной алгебре. В линейной алгебре любая линейная функция — это функция, где $f(x+y) = f(x) + f(y)$. По сути, алгебраически это означает, что $f(x) =mx $, где $m = f(1)$… Я позволю вам поиграть с этим. Это та же идея, но нам не разрешено иметь какие-либо смещения по вертикали.]
Вот и все, что я хочу сказать о линейных функциях.
График будет зависеть от домена. Если домен состоит из $\mathbb R$, график будет выглядеть как сплошная прямая линия. Если домен $\mathbb Z$, то график будет выглядеть как пунктирная прямая. А если домен $\mathbb Q$, то график будет выглядеть как расплывчатая прямая линия. (В каждой его части будут отверстия и точки, расположенные бесконечно близко друг к другу.)
А если домен $\mathbb Q$, то график будет выглядеть как расплывчатая прямая линия. (В каждой его части будут отверстия и точки, расположенные бесконечно близко друг к другу.)
Хорошо, а как насчет «непрерывного»?
Если вы уберете карандаш с бумаги, определение не поможет, потому что ваша бумага является доменом. Если в вашем домене есть разрывы, то и на вашей бумаге есть разрывы, и совершенно справедливо поднять карандаш над бумагой, чтобы перейти от одной части вашего домена к другой, чтобы преодолеть разрывы. Просто на вашей бумаге у вас не может быть никаких разрывов. Разрывы там, где разрывается бумага , допустимы.
Таким образом, непрерывный означает: что ж, если вы тщательно оттачиваете входные данные, вы также будете оттачивать и выходные данные.
Итак, линейная функция $f(x)= 2x + 3$ непрерывна. Если вы действительно тщательно оттачиваете $x$, то есть оттачиваете $x=1$, рассматривая $x=0,99$ и $x=1,01$, и смотрите на результаты $4,98$ и $5,02$, мы видим которую мы приблизили к $f(x) = 5$.

 ф-ии, — самодвойственные, -функции,сохраняющие константу 0
ф-ии, — самодвойственные, -функции,сохраняющие константу 0
 05.2009, 20:39
05.2009, 20:39 
 05.2009, 20:51
05.2009, 20:51  05.2009, 21:01
05.2009, 21:01  05.2009, 21:19
05.2009, 21:19  05.2009, 08:42
05.2009, 08:42  05.2009, 09:25
05.2009, 09:25