Дискретная случайная величина примеры: Математическое Бюро. Страница 404

Содержание

Дискретная случайная величина и ее числовые характеристики. Примеры решения задач

Дискретная случайная величина и ее числовые характеристики

Дискретными случайными величинами называются случайные величины, принимающие только отдаленные друг от друга значения, которые можно заранее перечислить.
Закон распределения
Законом распределения случайной величины называется соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.
Рядом распределения дискретной случайной величины называют перечень ее возможных значений и соответствующих им вероятностей.
Функцией распределения дискретной случайной величины называют функцию:
,
определяющую для каждого значения аргумента x вероятность того, что случайная величина X примет значение, меньшее этого x.

Математическое ожидание дискретной случайной величины
,
где — значение дискретной случайной величины; — вероятности принятия случайной величиной X значений .

Если случайная величина принимает счетное множество возможных значений, то:
.
Математическое ожидание числа наступлений события в n независимых испытаниях:
,
где p — вероятность наступления события.
Дисперсия и среднеквадратическое отклонение дискретной случайной величины
Дисперсия дискретной случайной величины:
или .
Дисперсия числа наступлений события в n независимых испытаниях
,
где p — вероятность наступления события.
Среднеквадратическое отклонение дискретной случайной величины:
.

Пример 1
Составьте закон распределения вероятностей дискретной  случайной величины (д.с.в.) X – числа k выпадений  хотя бы одной «шестерки» в n = 8  бросаниях пары игральных кубиков. Постройте многоугольник распределения. Найдите  числовые характеристики распределения (моду распределения, математическое  ожидание M(X), дисперсию D(X), среднее квадратическое отклонение s(X)).

Решение: Введем обозначение: событие A – «при бросании пары игральных кубиков шестерка появилась хотя бы один раз».

Для нахождения вероятности P(A) = p события A удобнее вначале найти вероятность P(Ā) = q противоположного события Ā – «при бросании пары игральных кубиков шестерка не появилась ни разу».
Поскольку вероятность непоявления «шестерки» при бросании одного кубика равна 5/6, то по теореме умножения вероятностей
P(Ā) = q = = .
Соответственно,
P(A) = p = 1 – P(Ā) = .
Испытания в задаче проходят по схеме Бернулли, поэтому д.с.в. величина X – число k выпадений хотя одной шестерки при бросании двух кубиков подчиняется биномиальному закону распределения вероятностей:

где = – число сочетаний из n по k.

Проведенные для данной задачи расчеты удобно оформить в виде таблицы:
Распределение вероятностей д.с.в. X º k (n = 8; p = ; q = )

k	0	1	2	3	4	5	6	7	8	Сумма
	1	8	28	56	70	56	28	8	1
Pn(k)	0,0541	0,1904	0,2932	0,258	0,1419	0,05	0,011	0,0013	0,0001	1

Полигон (многоугольник) распределения вероятностей дискретной случайной величины X представлен на рис. :

Рис. Полигон распределения вероятностей д.с.в. X=k.

Вертикальной линией показано математическое ожидание распределения M(X).

Найдем числовые характеристики распределения вероятностей д.с.в. X. Мода распределения равна 2 (здесь P8(2) = 0,2932 максимально). Математическое ожидание по определению равно:
M(X) = = 2,4444,
где xk = k – значение, принимаемое д.с.в. X. Дисперсию D(X) распределения найдем по формуле:
D(X) = = 4,8097.
Среднее квадратическое отклонение (СКО):
s(X) = = 2,1931.

Пример2
Дискретная случайная величинаX задана законом  распределения  
 Найти функцию распределения F(x) и построить ее график.

Решение. Если , то (третье свойство).
Если , то . Действительно, X может принять значение 1 с вероятностью 0,3.

Если , то . Действительно, если удовлетворяет неравенству
, то равно вероятности события , которое может быть осуществлено, когда X примет значение 1 (вероятность этого события равна 0,3) или значение 4 (вероятность этого события равна 0,1). Поскольку эти два события несовместны, то по теореме сложения вероятность события равна сумме вероятностей 0,3 + 0,1=0,4. Если , то . Действительно, событие достоверно, следовательно, его вероятность равна единице. Итак, функция распределения аналитически может быть записана так:

График этой функции:

Пример3
В магазине куплено 3 электроприбора: чайник, утюг и  пылесос. Вероятность выхода из строя в течение гарантийного срока для каждого  из них соответственно равны   . Составить закон распределения случайной величины X – числа приборов, вышедших из строя в течение гарантийного  срока.

Решение. X – число приборов, вышедших из строя, имеет следующие возможные значения:
— все три прибора не выйдут из строя в течении гарантийного срока;
— один прибор выйдет из строя;
— два прибора выйдут из строя;
— три прибора выйдут из строя.
Найдем соответствующие этим значениям вероятности. По условию, вероятности выхода из строя приборов равны: тогда вероятности того, что приборы будут рабочими в течение гарантийного срока равны:

Закон распределения имеет вид:

	0	1	2	3
	0,684	0,283	0,032	0,001

Проверка: 1.

Функция распределения вероятностей дискретной величины

Рассмотрим пространство элементарных событий, в котором каждому элементарному событию в соответствие ставится число или вектор , т.е. на множестве есть определенная функция , которая для каждого элементарного события находит элемент одномерного пространства или — мерного пространства .

Эту функцию называют случайной величиной. В случае, когда отражает множество на одномерное пространство случайную величину называют одномерной. Если отображение осуществляется на , то случайную величину называют n- мерной (системой n случайных величин или n — мерным случайным вектором).

Величина называется случайной, если в результате проведения опыта под влиянием случайных факторов она приобретает то или другое возможное числовое значение с определенной вероятностью.

Если множество возможных значений случайной величины является счетно, то ее называют дискретной. В противном случае ее называют непрерывной.

Случайные величины для удобства обозначают прописными буквами латинского алфавита , а их возможные значения — строчными .

Для установления случайной величины необходимо знать не только множество возможных ее значений, но и указать, с какими вероятностями она приобретает то или иное возможное значение.

С этой целью вводят понятие закона распределения вероятностей – зависимость, которая устанавливает связь между возможными значениями случайной величины и соответствующими им вероятностями.

Закон распределения дискретной случайной величины часто задают в табличной форме, функцией, или графически с помощью вероятностного многоугольника.

При табличной формы записи закона указывается множество возможных значений случайной величины находится в порядке их возрастания в первой строке, и соответствующих им вероятностей в следующей:

Случайные события должны быть попарно несовместимы и образовывать полную группу, то есть удовлетворять условие:

Приведенную зависимость называют условием нормировки для дискретной случайной величины , а таблицу распределения – рядом распределения.

Функция распределения вероятностей и ее свойства

Закон распределения вероятностей можно представить в виде функции распределения вероятностей случайной величины , которая может использоваться как для дискретных, так и для непрерывных случайных величин.

Функцию аргумента , устанавливающую вероятность случайного события называют функцией распределения вероятностей:

Ее следует понимать как функцию, которая устанавливает вероятность случайной величины, которая может принимать значения, меньше .

Функция распределения обладает следующими свойствами:

1. Она всегда положительная со значениями в пределах от нуля до единицы

2. Функция является монотонно возрастающей, а именно , если .

С этого свойства получают приведенные выводы:

a) Вероятность вступления случайной величиной возможных значений из промежутка равна прироста ее интегральной функции на этом промежутке:

б) Вероятность, что непрерывная случайная величина примет конкретное возможное значение, всегда равна нулю

Для непрерывной случайной величины выполняются такие равенства:

3. На крайних точках непрерывная случайная величина принимает значение 0 и 1.

Из этих границ следует, что для дискретной случайной величины с возможными значениями из ограниченного промежутка имеем

для

—————————-

Приведем решения задач на отыскание функции распределения.

Пример 1. Закон распределения дискретной случайной величины задан таблицей:

Построить функцию распределения и ее график.

Решение. Согласно свойствами функции получим приведенные дальше значение.
1)
2)
3)
4)
5)
6)

Компактно функция распределения иметь запись

График функции распределения изображен на рисунке ниже

—————————-

Пример 2. Есть три коробки с шарами. В первой содержится 6 желтых и 4 синие шарики, во втором — 7 желтых и 3 синие, а в третьем — 2 желтых и 8 синих. Из каждой коробки наугад берут по одному шарику. Построить закон распределения вероятностей дискретной случайной величины – появления числа синих шариков среди трех наугад взятых, определить закон распределения и построить график этой функции.

Решение. Среди трех наугад взятых шариков число синих может быть 0, 1, 2, 3.
В табличной форме закон распределения дискретной случайной величины имеет вид:

Вычислим вероятности . С этой целью обозначим — случайное событие, заключающееся соответственно в появлении желтого шарики и – появление синего с первой коробки. Подобным образом для остальных коробок . Вероятности этих событий такие:

Поскольку случайные события независимы, то вероятности находим по формулам:

Вычисление достаточно просты и сделаны обозначения полностью все объясняют. Проверим выполнение условия нормировки

Всегда выполняйте проверку данного условия: это достаточно просто сделать и позволяет быстро проверить правильность вычислений вероятности. В случаях, когда условие нормировки не выполняется нужно отыскать ошибку и исправить ее.

У нас же все вычисления правильны, потому записываем закон распределения вероятностей в табличной форме:

Вычисляем значение интегральной функции
1)
2)
3)
4)
5)

В случае ошибок при нахождении вероятностей последнее соотношение дает отличный от единицы результат, поэтому можете проверять и по этому значению.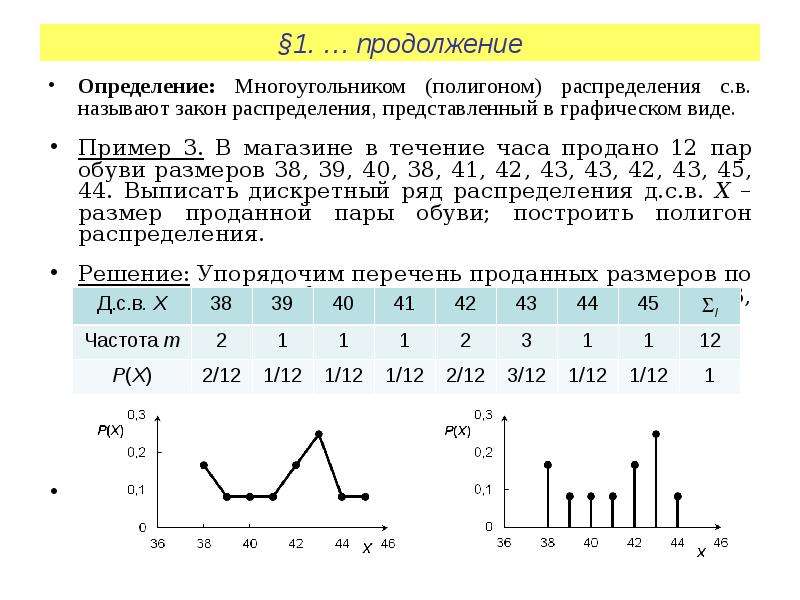 Упрощенно функция распределения будет иметь вид

а ее график следующий

—————————-

Пример 3. Закон распределения случайной величины задан функцией распределения вероятностей

Построить график функции распределения и вычислить вероятность, что случайная величина принадлежит промежутку .

Решение. Функция распределения будет иметь вид.

Используя определение, вычислим

Таким образом вероятность, что случайная величина принадлежит промежутку [1,4] равна 0,36.

—————————-

Внимательно разберитесь с приведенными примерами нахождения функции распределения, это Вам пригодится на практических занятиях. Старайтесь проверять условие нормирования, чтобы избежать дальнейших ошибок и правильно определяйте вероятности.

———————————————-

ДИСКРЕТНЫЕ И НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ ЗАКОНЫ РАСПРЕДЕЛЕНИЯ

Непрерывная случайная величина

Непрерывная случайная величина Непрерывная случайная величина принимает бесконечное количество значений из определенного интервала числовой прямой.

0 6 месяцев Срок службы лампочки 2 Пример. Рост человека

Подробнее )? (Вероятность попадания непрерывной СВ
Случайные величины. Определение СВ ( Случайной называется величина, которая в результате испытания может принимать то или иное значение, заранее не известное).. Какие бывают СВ? ( Дискретные и непрерывные.
Подробнее Медицинская информатика
Лукьянова Е. А. Медицинская информатика Теория вероятностей Специальность «Фармация» Заочное отделение 2010 Консультация 2 Темы контрольной работы 2 Случайные величины Числовые характеристики случайных
Подробнее ТЕМА 7. НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
ТЕМА 7. НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ Понятие непрерывной случайной величины.
Функция распределения, плотность распределения, их взаимосвязь и свойства. Математическое ожидание непрерывной случайной величины
Подробнее Основные понятия и определения
1 Основные понятия и определения Вспомним основные понятия и определения, которые употреблялись в курсе теории вероятностей. Вероятностный эксперимент (испытание) эксперимент, результат которого не предсказуем
Подробнее СЛУЧАЙНЫЕ ВЕЛИЧИНЫ. Лекция 5
ЧАСТЬ 4 СЛУЧАЙНЫЕ ВЕЛИЧИНЫ Лекция 5 СЛУЧАЙНЫЕ ВЕЛИЧИНЫ ЗАКОНЫ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН ЦЕЛЬ ЛЕКЦИИ: ввести понятие случайной величины и закона распределения; для дискретной случайной величины определить
Подробнее 6. Элементы математической статистики.
Минестерство образования Республики Беларусь УО «итебский государственный технологический университет» 6. Элементы математической статистики. Кафедра теоретической и прикладной математики. 90 80 70 60
Подробнее ЧАСТЬ І ОСНОВЫ ТЕОРИИ
.. Скалярные гиперслучайные величины 4 ЧАСТЬ І ОСНОВЫ ТЕОРИИ ГЛАВА ГИПЕРСЛУЧАЙНЫЕ СОБЫТИЯ И ВЕЛИЧИНЫ Введены понятия гиперслучайного события и гиперслучайной величины. Предложен ряд характеристик и параметров
Подробнее Дисциплина «Математика»
Дисциплина «Математика» Основные разделы: теория вероятностей; математическая статистика; дифференциальное исчисление. Рекомендуемая литература: Кремер Н.Ш. Теория вероятностей и математическая статистика:
Подробнее М.П. Харламов Конспект
М.П. Харламов http://vlgr.ranepa.ru/pp/hmp Конспект Теория вероятностей и математическая статистика Краткий конспект первого раздела (вопросы и ответы) Доктор физ. -мат. наук профессор Михаил Павлович Харламов
Подробнее Непрерывные случайные величины.
Непрерывные случайные величины. Случайная величина, значения которой заполняют некоторый промежуток, называется непрерывной. В частных случаях это может быть не один промежуток, а объединение нескольких
Подробнее Непрерывные случайные величины.
Тема Непрерывные случайные величины. Случайная величина, значения которой заполняют некоторый промежуток, называется непрерывной. В частных случаях это может быть не один промежуток, а объединение нескольких
Подробнее 6.4. Системы случайных величин
Лекция 4.9. Системы случайных величин. Функция распределения системы двух случайных величин (СДСВ). Свойства функции 6.4. Системы случайных величин В практике часто встречаются задачи которые описываются
Подробнее Математическое ожидание.
Лекция. Основные числовые характеристики дискретных и непрерывных случайных величин: математическое ожидание, дисперсия и среднее квадратическое отклонение. Их свойства и примеры. Закон распределения (функция
Подробнее Глава 3. Непрерывные случайные величины
Глава 3. Непрерывные случайные величины. Функция распределения. Если множество значений случайной величины X не конечно и не счетно, то такая случайная величина не может характеризоваться вероятностью
Подробнее 1.2. Элементы теории вероятностей.
.. Элементы теории вероятностей…. Случайные события. Случайные события обычное явление в жизни. Примеры случайных событий: выпадение «орла» или «решки» при бросании монеты, выпадение числа при бросании
Подробнее ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ.
ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ Математическая статистика (МС) раздел прикладной математики, который, основываясь на положении теории вероятностей, разрабатывает методы сбора, анализа и обработки результатов
Подробнее ФУНКЦИИ СЛУЧАЙНЫХ ВЕЛИЧИН. Лекция 11
ЧАСТЬ 6 ФУНКЦИИ СЛУЧАЙНЫХ ВЕЛИЧИН Лекция ЗАКОН РАСПРЕДЕЛЕНИЯ И ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ФУНКЦИЙ СЛУЧАЙНЫХ ВЕЛИЧИН ЦЕЛЬ ЛЕКЦИИ: ввести понятие функции случайной величины и провести классификацию возникающих
Подробнее 1. Биномиальный закон распределения
Лекция 4 Тема: Законы распределения СВ 1. Биномиальный закон распределения Опр. Дискретная СВ Х имеет биномиальный закон распределения, если выполнены следующие условия: 1) эксперимент заключается в последовательном
Подробнее Элементы математической статистики
Федеральное государственное бюджетное образовательное учреждение высшего образования «Российский национальный исследовательский медицинский университет имени Н. И. Пирогова» Министерства здравоохранения
Подробнее МАТЕМАТИЧЕСКАЯ СТАТИСТИКА. Лекция 14
ЧАСТЬ 8 МАТЕМАТИЧЕСКАЯ СТАТИСТИКА Лекция 4 ОСНОВНЫЕ ПОНЯТИЯ И ЗАДАЧИ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ ЦЕЛЬ ЛЕКЦИИ: определить понятие генеральной и выборочной совокупности и сформулировать три типичные задачи
Подробнее Функции многих переменных
Функции многих переменных Задача 7 Найти все производные второго порядка функции f ( x, y) : f ( x, y) y x Искомые производные: Задача 9 Найти полный дифференциал и градиент функции А: 3 4 f ( x, y) ln
Подробнее Retinskaya.jimdo.com
ЛЕКЦИЯ 1 Классификация экспериментальных исследований Определение и свойства функции распределения. Вероятность попадания случайной величины на заданный интервал Квантиль распределения Выборочная функция
Подробнее Формулы по теории вероятностей
Формулы по теории вероятностей I. Случайные события. Основные формулы комбинаторики а) перестановки P =! = 3…( ). б) размещения A m = ( )…( m + ). A! в) сочетания C = =. P ( )!!. Классическое определение
Подробнее Лекция 1. Выборочное пространство
Лекция 1. Выборочное пространство Буре В.М., Грауэр Л.В. ШАД Санкт-Петербург, 2013 Буре В.М., Грауэр Л.В. (ШАД) Лекция 1. Выборочное пространство Санкт-Петербург, 2013 1 / 35 Cодержание Содержание 1 Выборка.
Подробнее 2.5.3 Закон Пуассона (закон редких явлений)
Лекция 8 План лекции 53 Закон Пуассона 54 Показательный закон распределения 55 Нормальный (гауссов) закон распределения вероятностей 53 Закон Пуассона (закон редких явлений) Дискретная случайная величина
Подробнее Одномерные случайные величины
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Государственное образовательное учреждение высшего профессионального образования «Нижегородский государственный университет им Н. И. Лобачевского» Факультет
Подробнее 2.6. Эксцесс и асимметрия
Лекция 9 План лекции.5.6. Распределение Симпсона (треугольное распределение)..6 Эксцесс и асимметрия.7 Теорема Ляпунова и её следствия 3. Системы случайных величин (случайные векторы) 3.1 Закон распределения
Подробнее Закон распределения дискретной случайной величины.
Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.
Простейшей формой закона распределения дискретной случайной величины является ряд распределения.
Величина, которая может принимать только конечное или счетное множество значений, называется дискретной. Значение дискретной случайной величины можно записать в виде конечной или бесконечной последовательности Если для каждого из этих значений определить соответствующую вероятность

то мы получим ряд распределения данной случайной величины:
Чтобы последняя таблица была таблицей распределения случайной величины, должны выполняться два требования:
1) (вероятности не могут быть отрицательными величинами)
2)

Если принимает конечное число значений, то такая дискретная случайная величина называется конечной.

Функцией распределения случайной величины называется функция , определенная для любого действительного и выражающая вероятность того, что случайная величина примет значения, меньшее :

Функция распределения обладает следующими свойствами:
1) Для любого справедливо неравенство
2) Функция распределения является неубывающей функцией, т.е. если , то
3) Вероятность того, что случайная величина примет значения из полуинтервала равна разности значений функции распределения на концах, то есть:

4) Справедливо равенство:
5) Справедливы следующие предельные соотношения:

6) Функция распределения непрерывна слева, то есть

Математическим ожиданием, или средним значениям, дискретной случайной величины называется сумма произведений всех ее значений на соответствующие им вероятности:

Дисперсией случайной величины называется математическое ожидание квадрата ее отклонения от математического ожидания:

Средним квадратическим отклонением (стандартным отклонением, стандартом) случайной величины называется арифметическое значением корня квадратного из ее дисперсии:

Основные законы распределения дискретных случайных величин:
Задача на закон распределения двумерной дискретной случайной величины рассмотрена по ссылке
Задача
Записи страховой компании показали, что 30% держателей страховых полисов старше 50 лет потребовали возмещения страховых сумм. Для проверки в случайном порядке было отобрано 5 человек старше 50 лет, имеющих полисы. Случайная величина – количество требующих возмещения среди отобранных. Чему равна вероятность того, что потребуют возмещения более трех человек?
Запишите таблицу для данного закона распределения случайной величины .

Постройте многоугольник распределения.

Найдите числовые характеристики распределения – математическое ожидание, дисперсию, среднее квадратическое отклонение.

Запишите функцию распределения и постройте ее график.

Ответьте на вопрос о вероятности описанного события.

Если вам сейчас не требуется платная помощь с решением задач, контрольных работ и типовых расчетов, но может потребоваться в дальнейшем, то, чтобы не потерять контакт
вступайте в группу ВК
сохраните контакт WhatsApp (+79688494598)
сохраните контакт Телеграм (@helptask) .
Решение
Случайная величина может принимать значения 0, 1,2,3, 4,5.
Найдем вероятности этих значений по формуле Бернулли:

Проверка:
0 1 2 3 4 5
0.1681 0.3602 0.3087 0.1323 0. 0284 0.0023
Построим многоугольник распределения:

Математическое ожидание дискретной случайной величины:

Дисперсию дискретной случайной величины найдем по формуле:

Среднее квадратическое отклонение:

Запишем функцию распределения:

Вероятность того, что потребуют возмещения более трех человек:

Случайные величины и их характеристики /qualihelpy
Понятие случайной величины
Случайная величина – это величина, значения которой зависят от случая. Например, вес пойманной рыбы, температура воздуха в течение суток, сумма выигрыша лотерейного билета и т. п.
Случайная величина обозначается буквами  ,  ,  и т. д.
Виды случайных величин:
1) дискретная  – принимает конечное или счетное множество значений;2) непрерывная  – принимает все значения из заданного промежутка. Говорят, что задан закон распределения случайной величины  , если каждому значению  поставлена в соответствие вероятность его появления и сумма всех вероятностей равна числу . Закон распределения  может быть задан аналитически (формулой) или таблицей.Приведем табличный закон распределения дискретной  :Заметим, что  .
Функция распределения
Теоретическая функция распределения случайной величины  задается формулой:  , (10.17)где   – вероятность того, что  принимает значение, меньшее  .
Свойства функции распределения
1.  .
2. Функция распределения неубывающая.
3. Функция распределения непрерывна слева.
4.  ,  .
Например, на рисунках 10.1 и 10.2 изображены графики функций распределения некоторых непрерывных случайных величин.
Функция распределения дискретной  имеет вид: , (10.18)где   означает, что суммируются вероятности тех значений, которые меньше , или иначе  , (10.18.1)
Например, на рисунке 10.3 изображен график функции распределения некоторой дискретной случайной величины.
Плотностью распределения непрерывной случайной величины  в точке  называют функцию  . (10.19)Случайная величина  называется непрерывной, если существует неотрицательная функция такая, что  . (10.20)
Свойства плотности распределения
1.  .2.  . (10.21)3.  . (10.22)Вероятность того, что  примет значение из промежутка   можно найти по формуле:  , (10.23)
или по формуле
. (10.24)Вероятность того, что дискретная  примет значение из промежутка   равна сумме вероятностей всех ее значений, принадлежащих данному промежутку.
Числовые характеристики случайной величины
Математическое ожидание  – это среднее значение величины  или центр ее распределения.Математическое ожидание дискретной , находят по формуле:  , где  . (10.25)Математическое ожидание непрерывной  с плотностью распределения  , все значения которой принадлежат отрезку  , находят по формуле:  . (10.26)а ели все значения  принадлежат промежутку  , то по формуле , (10. 26.1)
при условии, что интеграл сходится.
Свойства математического ожидания
1. Математическое ожидание  заключено между ее наибольшим и наименьшим значениями.2.  , где  – константа.3.  , где  – постоянный множитель.4.  .5.  , если случайные величины  и  независимые.Дисперсия или рассеивание  – это математическое ожидание квадрата отклонения величины  от ее математического ожидания:  , (10.27)Дисперсию дискретной  можно найти по формуле: , (10.28)
где
, где  . (10.29)Дисперсию непрерывной  с плотностью распределения  , все значения которой принадлежат отрезку  , находят по формуле , (10.30)а ели все значения  принадлежат промежутку  , то по формуле , (10.30.1)
при условии, что интеграл сходится.
Свойства дисперсии
1.  , где  – константа.2.  , где  – постоянный множитель.3.  , если случайные величины  и  независимые.4.  , если случайные величины  и  независимые.Среднее квадратическое отклонение  – корень квадратный из ее дисперсии: . (10.31)
Двумерная случайная величина
Упорядоченная пара   случайных величин  и  называется двумерной случайной величиной (или системой случайных величин).Говорят, что задан закон распределения двумерной случайной величины  , если каждой паре значений  и  поставлена в соответствие вероятность и сумма всех вероятностей равна  .
Если случайная величина дискретная, то закон ее распределения может быть записан таблично:
Функцией распределения двумерной случайной величины  называют функцию вида . (10.32)Геометрически это означает, что мы находим вероятность того, что случайная точка  попадет в бесконечный квадрат с вершиной в точке  , так что точка  будет расположена ниже и левее точки   (рис. 10.4).
Математические ожидания дискретных случайных величин, входящих в систему, находят по формулам:
, (10.33) . (10.33.1)
Дисперсии дискретных случайных величин, входящих в систему, находят по формулам:
, (10.34) . (10.34.1)Ковариацией двух случайных величин  и  называют математическое ожидание произведения их отклонений от своих математических ожиданий:  . (10.35)Ковариацию  и  можно найти по формуле: . (10.36)Случайные величины  и  независимые, если  . (10.37)
Если случайные величины X и Y независимые, то
. (10.38)Коэффициентом корреляции двух случайных величин  и  называют число, которое характеризует степень зависимости  и  и находят по формуле: . (10.39)
Свойства коэффициента корреляции
1.  .2. В случае нормального распределения, если случайные величины  и  независимые, то  .
дискретных и непрерывных случайных величин
дискретных и непрерывных случайных величин
Дискретный и непрерывный Случайные переменные:
Переменная — это количество, значение которого изменяется.
A дискретная переменная — переменная, значение которой получается путем подсчета.
Примеры : количество присутствующих студентов
количество красных шариков в банке
количество голов при подбрасывании трех монет
учащиеся класса
A непрерывная переменная — это переменная, значение которой получается путем измерения.
Примеры : рост учеников в классе
вес учеников в классе
время, необходимое, чтобы добраться до школы
расстояние между классами
A случайная величина переменная, значение которой является числовым результатом случайного явления.
▪ Случайная величина обозначается заглавная буква
▪ Распределение вероятностей случайная величина X сообщает, каковы возможные значения X и как вероятности присваиваются этим значениям
▪ Случайная величина может быть дискретной или непрерывный
A дискретный случайный переменная X имеет счетное количество возможных значений.
Пример : Пусть X представляет собой сумму двух игральных костей.
Тогда вероятность распределение X выглядит следующим образом:
х
2
3
4
5
6
7
8
9
10
11
12
П ( X )
Построение графика вероятности распределения дискретной случайной величины, построить гистограмму вероятностей .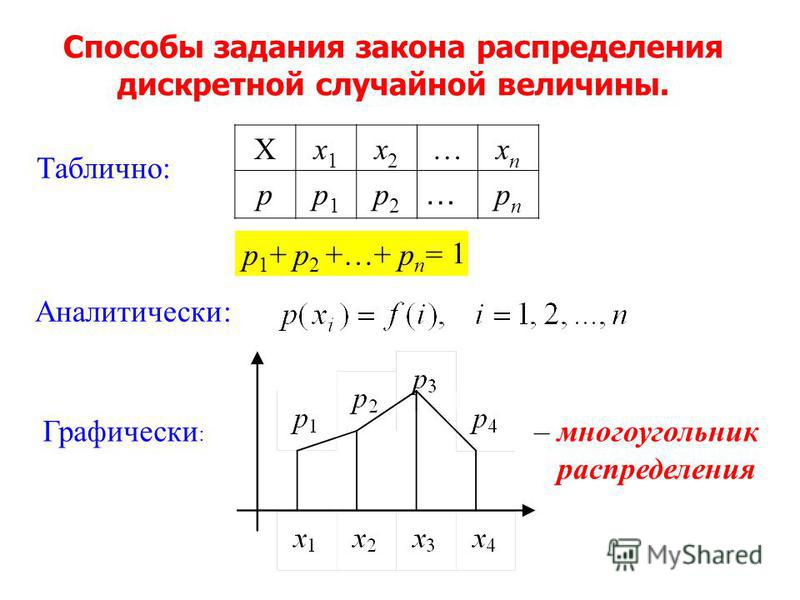
A непрерывный случайный переменная X принимает все значения в заданном интервале чисел.
▪ Распределение вероятностей непрерывная случайная величина показана кривой плотности .
▪ Вероятность того, что X находится между интервал чисел — это площадь под кривой плотности между интервалом конечные точки
▪ Вероятность того, что непрерывная случайная величина X точно равна числу ноль

Средства и варианты Случайные переменные:
Среднее значение дискретной случайная величина X — ее средневзвешенная величина.Каждое значение X взвешивается по его вероятность.
Чтобы найти среднее значение X, умножьте каждое значение X на его вероятность, затем сложите все продукты.
Среднее значение случайного переменная X называется ожидаемым значением X.

Закон больших чисел:

Как количество наблюдения увеличивается, среднее из наблюдаемых значений, , приближается к среднему значению по совокупности, .
Чем больше вариаций в результатов, тем больше испытаний необходимо, чтобы убедиться, что близко к.
Правила для средств:

Если X — случайная величина и a и b — фиксированные числа, тогда
Если X и Y случайны переменные, то
Пример:
Предположим, что уравнение Y = 20 + 100X преобразует оценку X по математике PSAT в SAT оценка по математике, Y.Предположим, средний балл по математике в PSAT равен 48. Каков средний балл? Результаты SAT по математике?

Пример :
Пусть представляют средний SAT оценка по математике.
Пусть представляют средний SAT словесная оценка.
представляет собой средний комбинированный балл SAT.потом средний совокупный общий балл за SAT.
Разница Дискретная случайная переменная:

Если X — дискретный случайный переменная со средним значением, тогда дисперсия X равна
Стандартное отклонение — квадратный корень из дисперсии.
Правила отклонений:
Если X — случайная величина и a и b — фиксированные числа, тогда
Если X и Y независимы случайные величины, то

Пример :
Предположим, что уравнение Y = 20 + 100X преобразует оценку X по математике PSAT в SAT оценка по математике, Y. Предположим, стандартное отклонение для математической оценки PSAT составляет 1,5. точки. Какое стандартное отклонение для СИДЕЛ оценка по математике?
Допустим, стандартный отклонение для оценки SAT по математике составляет 150 баллов, а стандартное отклонение для устная оценка по SAT — 165 баллов. Какое стандартное отклонение для комбинированный результат SAT?
*** Потому что SAT оценка по математике и вербальная оценка SAT не являются независимо, правило добавления отклонений не применяется!
7.1 — Дискретные случайные переменные
Выберите случайным образом трех болельщиков в футбольном матче, в котором Пенн Стейт играет в Нотр-Дам. Определите, является ли поклонник поклонником Пенсильванского университета (\ (P \)) или поклонником Нотр-Дама (\ (N \)). Этот эксперимент дает следующее пространство образцов:
\ (\ mathbf {S} = \ {PPP, PPN, PNP, NPP, NNP, NPN, PNN, NNN \} \)
Пусть \ (X \) = количество выбранных фанатов Penn State. Возможные значения \ (X \), таким образом, равны 0, 1, 2 или 3. Теперь мы можем найти вероятности отдельных событий, \ (P (PPP) \) или \ (P (PPN) \) , Например.В качестве альтернативы мы могли бы найти \ (P (X = x) \), вероятность того, что \ (X \) примет конкретное значение \ (x \). Давайте сделаем это!
Поскольку игра является домашней, предположим, что 80% фанатов, пришедших на игру, являются фанатами Пенсильванского университета, а 20% — поклонниками Нотр-Дама. То есть \ (P (P) = 0,8 \) и \ (P (N) = 0,2 \). Тогда по независимости:
\ (P (X = 0) = P (NNN) = 0,2 \ times0,2 \ times0,2 = 0,008 \)
И, в силу независимости и взаимной исключительности \ (NNP, NPN \) и \ (PNN \):
\ (P (X = 1) = P (NNP) + P (NPN) + P (PNN) = 3 \ times0.2 \ раз0,2 \ раз0,8 = 0,096 \)
Аналогичным образом, в силу независимости и взаимной исключительности \ (PPN, PNP \) и \ (NPP \):
\ (P (X = 2) = P (PPN) + P (PNP) + P (NPP) = 3 \ times0.8 \ times0. 8 \ times0.2 = 0.384 \)
Наконец, по независимости:
\ (P (X = 3) = P (PPP) = 0,8 \ times0,8 \ times0,8 = 0,512 \)
Здесь следует отметить несколько моментов:
Результаты имеют смысл! Учитывая, что 80% болельщиков на трибунах — это болельщики из Пенсильвании, неудивительно, что мы, скорее всего, выберем 2 или 3 болельщика из Пенсильвании.
Вероятности хорошо себя ведут в том смысле, что (1) все вероятности больше 0, то есть \ (P (X = x)> 0 \) и (2) вероятность пространства выборки равна 1, то есть \ (P (\ mathbf {S}) = P (X = 0) + P (X = 1) + P (X = 2) + P (X = 3) = 1 \).
Поскольку значения, которые она принимает, случайны, переменная \ (X \) имеет особое имя. Она называется случайной величиной ! Та-даааа!
Дадим формальное определение случайной величины.

Случайная переменная \ (X \)
Учитывая случайный эксперимент с пространством выборок \ (\ mathbf {S} \), случайная величина \ (X \) является функцией множества, которая присваивает одно и только одно действительное число каждому элементу \ (s \), который принадлежит в пространстве образцов \ (\ mathbf {S} \).
Набор всех возможных значений случайной величины \ (X \), обозначенный \ (x \), называется опорой , или пробелом , \ (X \).
Обратите внимание, что заглавные буквы в конце алфавита, такие как \ (W, X, Y \) и \ (Z \), обычно представляют собой определение случайной величины. Соответствующие строчные буквы, такие как \ (w, x, y \) и \ (z \), представляют возможные значения случайной переменной.
3.2.1 — Ожидаемое значение и дисперсия дискретной случайной величины
Пусть X = количество предыдущих судимостей для заключенных в государственной тюрьме, в которой есть 500 заключенных.(\ (х = 0,1,2,3,4 \))
\ (Х = х \) 0 1 2 3 4
\ (Количество \ заключенных \) 80 265 100 40 15
\ (f (x) = P (X = x) \) 80/500 265/500 100/500 40/500 15/500
\ (f (x) = P (X = x) \) 0. 16 0,53 0,2 0,08 0,03
Каково ожидаемое количество судимостей?
\ (Х = х \) 0 1 2 3 4
\ (Количество \ заключенных \) 80 265 100 40 15
\ (f (x) = P (X = x) \) 80/500 265/500 100/500 40/500 15/500
\ (f (x) = P (X = x) \) 0.16 0,53 0,2 0,08 0,03
Ответ
Для этого нам нужно средневзвешенное значение, поскольку не все результаты имеют равные шансы на исполнение (т.е. они не имеют равного веса). Итак, нам нужно найти ожидаемое значение \ (X \), или среднее значение \ (X \), или \ (E (X) = \ Sigma f (x_i) (x_i) \). Когда мы это записываем, получаем:
\ (= (0,16) (0) + (0,53) (1) + (0,2) (2) + (0,08) (3) + (0,03) (4) = 1,29 \)
Остановись и подумай! Имеет ли ожидаемое значение 1.29 имеют смысл?
Рассчитайте дисперсию и стандартное отклонение для примера «Предыдущие судимости»:
\ (Х = х \) 0 1 2 3 4
\ (Количество \ заключенных \) 80 265 100 40 15
\ (f (x) = P (X = x) \) 80/500 265/500 100/500 40/500 15/500
\ (f (x) = P (X = x) \) 0.2 \\ & = 2,53–1,66 \\ & = 0,87 \\ \ text {SD} (X) & = \ sqrt (0,87) \\ & = 0,93 \ end {align}
Примечание! Если дисперсия находится между 0 и 1, SD будет больше, чем дисперсия.
Какое ожидаемое количество судимостей? Ниже представлена таблица распределения вероятностей для данных о судимости. Используйте эту таблицу, чтобы ответить на следующие вопросы.
\ (Х = х \) 0 1 2 3 4
\ (f (x) = P (X = x) \) 0.16 0,53 0,2 0,08 0,03
а. Какова вероятность того, что случайно выбранный заключенный имеет ровно 2 априори?
Отвечать
\ (P (X = 2) = 100/500 = 0,2 \)
г. Какова вероятность того, что случайно выбранный заключенный имеет <2 априори?
Отвечать
\ (P (X <2) = P (X = 0 \ или \ 1) = P (X = 0) + P (X = 1) = 0,16 + 0,53 = 0,69 \)
г. Какова вероятность того, что случайно выбранный заключенный имеет 2 или меньше априориев?
Отвечать
\ (P (X≤2) = (X = 0) + P (X = 1) + P (X = 2) = 0. 16 + 0,53 + 0,2 = 0,89 \)
г. Какова вероятность того, что у случайно выбранного заключенного будет более двух априори?
Отвечать
\ (P (X> 2) = P (X = 3 \ или \ 4) = P (X = 3) + P (X = 4) \ или \ 1 − P (X≤2) = 0.11 \)
e. Наконец, какие из перечисленных выше элементов a, b, c и d являются дополнениями?
Отвечать
г. и d. являются дополнениями
Случайная переменная — определение, типы и роль в финансах
Что такое случайная переменная?
Случайная величина (стохастическая переменная) — это тип переменной в статистике Основные понятия статистики для финансов Твердое понимание статистики имеет решающее значение для того, чтобы помочь нам лучше понять финансы.Более того, концепции статистики могут помочь инвесторам отслеживать, чьи возможные значения зависят от результатов определенного случайного явления. Поскольку случайная величина может принимать разные значения, она обычно обозначается буквой (например, переменная «X»). Каждая переменная обладает определенной функцией распределения вероятностей (математической функцией, которая представляет вероятности наступления всех возможных результатов).
Типы случайных переменных
Случайные переменные подразделяются на дискретные и непрерывные.Основное различие между двумя категориями — это тип возможных значений, которые может принимать каждая переменная. Кроме того, тип (случайной) переменной подразумевает конкретный метод нахождения функции распределения вероятностей.
1. Дискретная
Дискретная случайная величина — это (случайная) величина, значения которой принимают только конечное число значений. Лучший пример дискретной переменной — игральные кости. Бросок кубика — это чисто случайное событие. В то же время игральные кости могут принимать только конечное число исходов {1, 2, 3, 4, 5 и 6}.
Каждый результат дискретной случайной величины содержит определенную вероятность. Например, вероятность выпадения каждого кубика равна 1/6, потому что результаты равновероятны. Обратите внимание, что общий вероятностный результат дискретной переменной равен 1.
2. Непрерывный
В отличие от дискретных переменных, непрерывные случайные величины могут принимать бесконечное количество возможных значений. Одним из примеров непрерывной переменной является доходность акций. Норма доходности. Норма доходности (ROR) — это прибыль или убыток от инвестиции за период времени, сопоставленная с первоначальной стоимостью инвестиций, выраженной в процентах.В этом руководстве представлены наиболее распространенные формулы. Доходность может принимать бесконечное количество возможных значений (в процентах).
По вышеуказанной причине вероятность определенного исхода для непрерывной случайной величины равна нулю. Однако всегда существует неотрицательная вероятность того, что определенный результат будет находиться в интервале между двумя значениями.
Случайные переменные в финансах
В финансах случайные переменные широко используются в финансовом моделировании Что такое финансовое моделирование Финансовое моделирование выполняется в Excel для прогнозирования финансовых показателей компании. Обзор того, что такое финансовое моделирование, как и зачем строить модель, анализ сценариев и управление рисками Управление рисками Управление рисками включает в себя идентификацию, анализ и реагирование на факторы риска, которые составляют часть жизни бизнеса. Обычно это делается с помощью. В финансовых моделях и симуляциях вероятности переменных представляют собой вероятности случайных явлений, которые влияют на цену ценной бумаги или определяют уровень риска инвестиций. Например, переменная может применяться, чтобы указать цену актива в какой-то момент в будущем или сигнализировать о наступлении неблагоприятного события.
Дополнительные ресурсы
CFI — официальный поставщик услуг глобального финансового моделирования и оценки (FMVA) ™. Стать сертифицированным аналитиком финансового моделирования и оценки (FMVA) ® Сертификация CFI по финансовому моделированию и оценке (FMVA) ® поможет вы обретете необходимую уверенность в своей финансовой карьере. Запишитесь сегодня! программа сертификации, призванная помочь любому стать финансовым аналитиком мирового уровня. Чтобы продолжать учиться и продвигаться по карьерной лестнице, вам будут полезны следующие дополнительные ресурсы CFI:
CorrelationCorrelationA correlation — это статистическая мера взаимосвязи между двумя переменными.Эту меру лучше всего использовать в переменных, которые демонстрируют линейную зависимость друг от друга. Соответствие данных можно визуально представить на диаграмме рассеяния.
Независимая переменная Независимая переменная Независимая переменная — это входные данные, предположения или драйверы, которые изменяются, чтобы оценить их влияние на зависимую переменную (результат).
Инвестирование: руководство для начинающихИнвестирование: руководство для новичков Руководство CFI «Инвестирование для начинающих» научит вас основам инвестирования и научит их начинать.Узнайте о различных стратегиях и методах торговли, а также о различных финансовых рынках, в которые вы можете инвестировать.
Количественный анализ Количественный анализ Количественный анализ — это процесс сбора и оценки поддающихся измерению и проверке данных, таких как доходы, доля рынка и заработная плата, с целью понимать поведение и эффективность бизнеса. В эпоху информационных технологий количественный анализ считается предпочтительным подходом к принятию обоснованных решений.
Учебные пособия и примечания по дискретным случайным переменным | Машинное обучение
В предыдущем уроке вы познакомились с различными концепциями вероятности. Теперь давайте посмотрим, как построить функции над результатами случайного эксперимента.
Дискретные случайные переменные
По умолчанию:
Дискретная случайная величина определяется как функция, которая отображает пространство выборки на набор дискретных реальных значений.\ begin {уравнение} X: S \ rightarrow {\ rm R} \ end {уравнение} где X — случайная величина, S — пространство выборки, а $$ {\ rm R} $$ — набор действительных чисел. Как и любая другая функция, X принимает значение и вычисляет результат в соответствии с определенным для него правилом.
Более подробно: если X — случайная величина, определенная для определенного случайного эксперимента с пространством выборки S, то $$ X = c $$ означает событие E, содержащее все возможные результаты $$ e_ {i} \ in S $$ такой, что $$ X (e_ {i}) = c $$.
Примечание:
Случайная переменная может принимать значения, которых также нет в выборке. Все значения, которых нет в пространстве выборки, отображаются в пустой набор.
Пример 1:
Из группы, состоящей из 5 мальчиков и 5 девочек, трое детей были отобраны для конкурса рисунков, но их пол неизвестен. Пусть X — случайная величина, обозначающая количество выбранных девушек. Что такое набор событий «c», такой что X (c) = 3.
Решение:
X (c) = 3 подразумевает все результаты, в которых все 3 выбранных ребенка — девочки.с = {(GGG)}.
Функция массы вероятности
Вероятностная функция масс (pmf) — это вероятность, определенная для данной случайной величины. Для случайной величины X p (X = c) обозначается как p (c), а отображение каждого значения в пространстве выборки на их соответствующие вероятности имеет вид известный как pmf. Для всех значений c, которые не находятся в пространстве выборки, p (c) указывает на вероятность пустого набора, и значение равно 0.
Примечание:
Pmf — это просто еще одна функция, которая имеет значения вероятности в качестве результатов .Следовательно, $$ 0 \ leq p (c) \ leq 1 $$ для любого значения c.
Пример 2:
В продолжение примера 1, каково значение p (3), а также запишите функцию pmf для случайной величины X.
Решение:
Единственный случай в пространстве выборки, в котором все трое детей равны девочкам (GGG). Вероятность этого составляет $$ 1/12 $$. Общая PMF составляет,
$$ a $$ $$ p (a) $$
$$ 0 $$ $$ 1/12 $$
$$ 1 $$ $$ 5/12 $$
$$ 2 $$ $$ 5/12 $$
$$ 3 $$ $$ 1/12 $$
$$ p (4) = 0 $$, поскольку случайная величина X никогда не может принимать значение 4 или, если на то пошло, любое значение больше 3.
Кумулятивная функция распределения
Выше мы видели, что равенство случайной величины приводит к pmf. Что, если мы будем иметь дело с неравенством? Согласно определению, $$ X \ leq c $$ приводит к набору событий, содержащему все результаты, удовлетворяющие условию равенства от $$ — \ infty $$ до $$ c $$. Когда функция вероятности применяется к такому неравенству, это приводит к кумулятивному значению вероятности, дающему оценку значения, меньшего или равного $$ c $$.
По умолчанию:
Кумулятивная функция распределения (cdf), обозначенная CD (c) = $$ \ sum_ {b} p (b) $$ для всех $$ — \ infty \ leq b \ leq c $$.
Пример:
Продолжая пример 2, каково значение CD (2)? Также рассчитайте весь CDF для X.
Решение:
$$ CD (2) = p (0) + p (1) + p (2) = 11/12 $$. Полный CDF выглядит следующим образом:
$$ a $$ $$ p (a) $$ $$ CD (a) $$
$$ 0 $$ $$ 1/12 $$ $$ 1/12 $$
$$ 1 $$ $$ 5/12 $$ $$ 6/12 $$
$$ 2 $$ $$ 5/12 $$ $$ 11/12 $$
$$ 3 $$ $$ 1/12 $$ $$ 1 $$
Некоторые специфические дистрибутивы
Равномерное распределение
Начиная с простейшего из всех распределений, X = Uniform (N) используется для моделирования сценариев, в которых все результаты одинаково возможны.Например, вероятность выпадения орла или решки одинакова в случае честной монеты. Итак, Uniform (N) означает, что существует N результатов, и каждый имеет вероятность $$ 1 / N $$.
Распределение Бернулли
Распределение Бернулли используется для моделирования сценариев, в которых каждый след случайного эксперимента имеет ровно два возможных результата. Один из возможных результатов называется успехом , а другой — неудачей . Главный параметр p — это вероятность успеха любого испытания случайного эксперимента.X = Бернулли (p) влечет следующие точки:
Обозначая случайную переменную в двоичных значениях, она может принимать значение 0 (неудача) или 1 (успех) для каждого трейла.
X = 1 достигается с вероятностью p и X = 0 с вероятностью 1-p .
Биномиальное распределение
Биномиальное распределение используется для моделирования n независимых следов распределений Бернулли. Если X следует за Binomial (n, p), то X = k влечет наличие k успешных попыток в серии из n независимых испытаний Бернулли.{k} * p \ end {уравнение} X = k — событие, в котором первый успех наблюдался после k неудач.
Арифметические правила применимы и к случайным величинам. Их можно складывать, вычитать или умножать вместе. Если X и Y подчиняются геометрическому распределению с одинаковой вероятностью p, то X + Y также является геометрическим распределением.
Примечание: Попробуйте написать таблицы PMF для каждого из этих дистрибутивов!
Ожидаемое значение Ожидаемое значение для случайной переменной дает среднее или среднее значение, рассчитанное для всех возможных результатов переменной.
По умолчанию:
Если X — случайная величина, которая принимает значение $$ v_ {i} $$ с вероятностью $$ p (v_ {i}) $$ и имеет пространство выборки размером n, тогда ожидаемое значение, \ begin {уравнение} E (X) = \ sum_ {n} v_ {i} * p (v_ {i}) \ end {уравнение} Ожидаемое значение часто обозначается $$ \ mu $$.
Из приведенного выше уравнения ясно видно, что ожидаемое значение не обязательно должно входить в набор случайных величин в пространстве выборки, а просто дает информацию о центральной тенденции случайной величины в целом.Ожидаемое значение будет таким же, когда случайная величина умножается на скаляр или добавляется к другой случайной величине. Это также относится к смещению переменной.
$$ E (X + Y) = E (X) + E (Y) $$
$$ E (cX + d) = c * E (X) + d $$
Дисперсия и стандартное отклонение
Ожидаемое значение — хорошая мера для представления случайного значения в виде одного значения. Но при этом не учитывается некоторая важная информация, необходимая для лучшего понимания. Дисперсия используется для понимания дисперсии вероятностной массы вокруг среднего значения случайной величины.2) $$$ $$$ \ sigma = \ sqrt (Var (X)) $$$ Где $$ \ sigma $$ — это так называемое стандартное отклонение. При детальном рассмотрении Var (X) становится очевидным, что расстояние каждого значения от среднего возводится в квадрат и вычисляется среднее значение. 2 $$
$$ Var (X + Y) = Var (X) + Var (Y) $$ тогда и только тогда, когда X и Y независимы.2} $$
Предоставил: Шубхакар Редди Типиредди
StatTrek
Все распределения вероятностей можно классифицировать как дискретные распределения вероятностей или как непрерывные распределения вероятностей, в зависимости от определяют ли они вероятности, связанные с дискретными переменные или непрерывные переменные.
Дискретные и непрерывные переменные
Если переменная может принимать любое значение между двумя указанными значениями, оно называется непрерывной переменной ; в противном случае она называется дискретной переменной .
Некоторые примеры поясняют разницу между дискретным и непрерывным переменные.
Предположим, пожарная служба требует, чтобы все пожарные взвешивались между 150 и 250 фунтов. Вес пожарного был бы примером непрерывная переменная; поскольку вес пожарного может принимать любые значения от 150 до 250 фунтов.
Предположим, мы подбрасываем монету и подсчитываем количество орлов. Количество голов могло быть любым целым числом от 0 до плюс бесконечность.Однако это не могло быть число от 0 до плюс бесконечность. У нас не получилось, например, получить 2,5 головы. Следовательно, количество головок должно быть дискретной переменной.
Как и переменные, распределения вероятностей можно разделить на дискретные и непрерывные.
Дискретные распределения вероятностей
Если случайная величина дискретная переменная, ее распределение вероятностей называется дискретной вероятностью . Распределение .
Пример прояснит это.Предположим, вы подбрасываете монету два раза. Этот простой статистический эксперимент может иметь четыре возможных результата: HH, HT, TH и TT. Теперь пусть случайная величина X представляет количество голов, которые приводят к из этого эксперимента. Случайная величина X может принимать только значения 0, 1, или 2, так что это дискретная случайная величина.
Распределение вероятностей для этого статистического эксперимента показано ниже.
Количество голов Вероятность
0 0.25
1 0,50
2 0,25
В приведенной выше таблице представлено дискретное распределение вероятностей , поскольку оно связывает каждое значение дискретной случайной величины с ее вероятностью вхождение. На этом веб-сайте мы рассмотрим следующие отдельные распределения вероятностей.
Примечание: При дискретном распределении вероятностей каждое возможное значение дискретная случайная величина может быть связана с ненулевой вероятностью.Таким образом, дискретное распределение вероятностей всегда можно представить в виде таблицы.
Непрерывное распределение вероятностей
Если случайная величина является непрерывной переменной, ее распределение вероятностей называется непрерывной вероятностью . Распределение .
Непрерывное распределение вероятностей отличается от дискретного распределения вероятностей. распространение несколькими способами.
Вместо этого используется уравнение или формула для описания непрерывной вероятности. распределение.
Чаще всего уравнение используется для описания непрерывного распределения вероятностей называется функцией плотности вероятности . Иногда бывает называется функцией плотности , PDF или pdf . Для непрерывного распределения вероятностей плотность функция имеет следующие свойства:
Вероятность того, что случайная величина принимает значение от a до b равна площади под функцией плотности, ограниченной значениями a и b .
Например, рассмотрим функцию плотности вероятности, показанную на графике ниже. Предположим, мы хотели узнать вероятность того, что случайная величина X была меньше или равно a . Вероятность того, что X меньше или равно , а равно площади под кривой, ограниченной , и минус бесконечность — на что указывает заштрихованная область.
Примечание: Заштрихованная область на графике представляет вероятность того, что случайный переменная X меньше или равна a .Это совокупная вероятность. Однако вероятность того, что X точно равно , а будет нулем. Непрерывная случайная величина может принимают бесконечное количество значений. Вероятность того, что она будет равна конкретное значение (например, a ) всегда равно нулю.
На этом веб-сайте мы рассматриваем следующие непрерывные распределения вероятностей.
Случайные переменные
Случайная переменная — это набор из возможных значений из случайного эксперимента.
Пример: Подбрасывание монеты: мы можем получить орел или решку.
Дадим им значения Голов = 0 и Хвостов = 1 , и у нас есть случайная переменная «X»:
Вкратце:
X = {0, 1}
Примечание: мы можем выбрать Heads = 100 и Tails = 150 или другие значения, если захотим! Это наш выбор.
Итак:
У нас есть эксперимент (например, подбрасывание монеты)
Каждому событию даем значений
Набор значений — это случайная переменная
Не как алгебра переменная
В алгебре переменная, например x, — это неизвестное значение:
Пример: x + 2 = 6
В этом случае мы можем найти, что x = 4
Но случайная переменная — другое дело…
Случайная переменная имеет полный набор
значений …
… и он может случайным образом принимать
любых из этих значений.
Пример: X = {0, 1, 2, 3}
X может быть 0, 1, 2 или 3 случайным образом .
И у каждого из них может быть разная вероятность.
Заглавные буквы
Мы используем заглавную букву, например X или Y , чтобы избежать путаницы с типом переменной «Алгебра».
Пробел
Набор значений случайной переменной — это пространство выборки.
Пример: бросить кубик один раз
Случайная переменная X = «Счет, отображаемый на верхней грани».
X может быть 1, 2, 3, 4, 5 или 6
Таким образом, пространство выборки равно {1, 2, 3, 4, 5, 6}
Вероятность
Мы можем показать вероятность любого одного значения, используя этот стиль:
P (X = значение) = вероятность этого значения
Пример (продолжение): бросить кубик один раз
X = {1, 2, 3, 4, 5, 6}
В этом случае они равновероятны, поэтому вероятность любого из них равна 1/6
P (X = 1) = 1/6
P (X = 2) = 1/6
P (X = 3) = 1/6
P (X = 4) = 1/6
P (X = 5) = 1/6
P (X = 6) = 1/6
Обратите внимание, что сумма вероятностей = 1 , как и должно быть.
Пример: Сколько орлов, когда мы подбрасываем 3 монеты?
X = «Количество голов» — это случайная переменная.
В этом случае может быть 0 голов (если все монеты приземлиться решкой вверх), 1 голова, 2 головы или 3 головы.
Итак, пробел = {0, 1, 2, 3}
Но на этот раз результаты НЕ все одинаковы вероятный.
Три монеты могут приземлиться восемью способами:
Глядя на таблицу, мы видим только 1 случай трех голов, но 3 случая двух голов, 3 случая одной головы и 1 случай нулевых голов.Итак:
P (X = 3) = 1/8
P (X = 2) = 3/8
P (X = 1) = 3/8
P (X = 0) = 1/8
Пример: брошены два кубика.
Случайная переменная: X = «Сумма очков на двух кубиках ».
Составим таблицу всех возможных значений:

1-й штамп
1 2 3 4 5 6
2-я
Штамп
1 2 3 4 5 6 7
2 3 4 5 6 7 8
3 4 5 6 7 8 9
4 5 6 7 8 9 10
5 6 7 8 9 10 11
6 7 8 9 10 11 12
Имеется 6 × 6 = 36 возможных исходов, а пространство выборки (которое является суммой количество очков на двух кубиках) равно {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}
Давайте посчитаем, как часто встречается каждое значение, и определим вероятности:
2 встречается только один раз, поэтому P (X = 2) = 1/36
3 встречается дважды, поэтому P (X = 3) = 2/36 = 1/18
4 встречается трижды, поэтому P (X = 4) = 3/36 = 1/12
5 встречается четыре раза, поэтому P (X = 5) = 4/36 = 1/9
6 встречается пять раз, поэтому P (X = 6) = 5/36
7 встречается шесть раз, поэтому P (X = 7) = 6/36 = 1/6
8 встречается пять раз, поэтому P (X = 8) = 5/36
9 встречается четыре раза, поэтому P (X = 9) = 4/36 = 1/9
10 встречается трижды, поэтому P (X = 10) = 3/36 = 1/12
11 встречается дважды, поэтому P (X = 11) = 2/36 = 1/18
12 встречается только один раз, поэтому P (X = 12) = 1/36
Диапазон значений
Мы также можем вычислить вероятность того, что случайное Переменная принимает ряд значений.
Пример (продолжение) Какова вероятность того, что сумма баллов 5, 6, 7 или 8?
Другими словами: что такое P (5 ≤ X ≤ 8) ?
P (5 ≤ X ≤ 8) = P (X = 5) + P (X = 6) + P (X = 7) + P (X = 8)
= (4 + 5 + 6 + 5) / 36
= 20/36
= 5/9
Решение
Мы также можем решить уравнение со случайной переменной.
Пример (продолжение) Если P (X = x) = 1/12, каково значение x?
Просматривая список выше, находим:
P (X = 4) = 1/12 и
P (X = 10) = 1/12
Итак, есть два решения: x = 4 или x = 10
Обратите внимание на различное использование X и x :
X это Случайная переменная «Сумма очков на двух кубиках».
x — это значение, которое может принимать X .
Непрерывный
Случайные переменные могут быть дискретными. или непрерывный:
Дискретные данные могут принимать только определенные значения (например, 1,2,3,4,5)
Непрерывные данные могут принимать любое значение в диапазоне (например, рост человека)
Все наши примеры были дискретными.
Дополнительные сведения см. В разделе «Непрерывные случайные переменные».
Среднее, дисперсия, стандартное отклонение
Вы также можете узнать, как найти среднее значение, дисперсию и стандартное отклонение случайных величин.
Сводка
Случайная переменная — это набор из возможных значений из случайного эксперимента.
Набор возможных значений называется Sample Space .
А Случайной переменной дается заглавная буква, например X или Z.
Случайный Переменные могут быть дискретными или непрерывными.
.
No related posts.