Дискриминант формула через k: Частный случай нахождения корней квадратного уравнения — урок. Алгебра, 8 класс.

О квадратных уравнениях в правильном порядке / Хабр

Как вам преподавали квадратные уравнения в школе? Это был 7-8 класс, примерно. Вероятнее всего, вам рассказали что есть формулы корней через дискриминант, что направление ветвей зависит от старшего коэффициента. Через пару занятий дали теорему Виета. Счастливчикам еще рассказали про метод переброски. И на этом решили отпустить.

Вы довольны такой базой? Вам не рассказали ни геометрический смысл, ни как это получить.

Спустя некоторое время обдумывания сей несправедливости, я решил написать эту статью и тем самым закрыть гештальт о фрагментарности знаний.

Вы не найдете здесь ничего нового по факту, но, возможно, это даст посмотреть на такое простое понятие с другой стороны.

Начнем с конца

Когда я перечислял темы, касающиеся квадратных уравнений, я делал это примерно в том же порядке, в котором изучают их в школе. Но такой порядок не оправдан с точки зрения обучения, и вот почему:

• Дискриминант дается просто как данность (за редким исключением, когда показывают вывод этих формул через приведение к полному квадрату)

• Мощнейшая по своей сути теорема Виета дается в конце и только как эвристический способ решения

Гораздо проще начать с теоремы Виета.

Рассмотрим квадратный трехчлен

В силу основной теоремы алгебры (примем её как данность, так как её действительно тяжело доказать), мы знаем, что у этого уравнения должно быть два корня. Допустим, что это некоторые числа . Тогда можно переписать изначальное уравнение как выражение его корней:

Оба эти уравнения эквиваленты, так как они оба зануляются в (первое по определению , второе по построению).

Раскрывая скобки, мы получим следующее:

Откуда приравняв соответствующие коэффициенты с имеющимися, получим знаменитую систему:

Мы только что доказали теорему Виета на случай квадратного трехчлена. Это потрясающий результат: мы начинаем получать некоторую информацию о корнях, которые, как мы предположили, существуют. И этот результат мы будем использовать далее.

Геометрия параболы

Вершина

Здесь можно было бы рассказать весь первый курс алгебры университета: о фокусах, директрисах, о конических сечениях, первой и второй производной…

Но раз мы ограничились школьной программой (7-8 класс, если быть точным), то и рассуждения у нас будут простые.

Самая, на мой субъективный взгляд, интересная точка параболы – это её вершина. Она уникальным образом задает положение параболе и дает понимание о том, как устроены корни.

Но формулу для нее мы не знаем, до первых понятий о производной нам еще 3 года в среднем. Будем выкручиваться.

Парабола – симметричная фигура. До того момента, как мы сдвинули ее относительно оси , ось служит для нее осью симметрии. Когда же мы начинаем ее сдвигать, становится видно, что она продолжает быть симметричной, но уже относительно оси, проходящей через вершину.

Парабола, вершина и ось симметрии

Тогда от вершины в обе стороны до корней равные расстояния, а это значит, что вершина параболы лежит ровно между корнями. Тогда координата вершины это среднее между ее корнями

Пока что мы не знаем наши корни. Но благодаря теореме Виета мы знаем, чему равна сумма корней!

Потрясающий результат, который нам пригодится далее.

Ещё немного про корни

Мы знаем, что корни, графически, это те точки, в которых кривая пересекает ось . Очень полезное знание, учитывая, что смотря на параболу, исключительно визуально, мы понимаем что у нас может быть 3 случая:

1. Корней нет, при этом
   

   1. Либо значение в вершине больше нуля и старший коэффициент больше нуля

   2. Либо значение в вершине меньше нуля и старший коэффициент меньше нуля

2. Корень один, но кратности 2 (не забываем основную теорему алгебры), и значение в вершине равно нулю

3. Корня два

Второй случай тривиален, до третьего мы еще дойдем. Интересно математически взглянуть на первый. Найдем значение квадратного трехчлена в вершине:

И теперь все же рассмотрим первый случай: парабола висит над осью ветвями вверх.

Первый случай

Домножим первое неравенство на . Учитывая, что , знак неравенства сменится на противоположный:

Это условие, при котором корней нет.

Рассмотрим вкратце противоположный случай: парабола висит под осью ветвями вниз.

Второй случай

Какая-то магия. Получается, что это условие инвариантно относительно положения параболы. Но тем оно лучше.

На данном этапе прошу заметить, что это только условие отсутствия действительных корней. Да, это похоже на дискриминант, но давайте представим, что вы этого не знаете.

Понятие дискриминанта

Мы уже многое поняли о корнях: в какой они связи с коэффициентами, когда они не существуют, каким образом они лежат относительно вершины. Все это безумно полезно, но это все до сих пор не способ найти значения алгебраически.

Давайте будем отталкиваться от того, что мы уже знаем: от вершины. Если бы мы каким-то образом знали расстояние между корнями, то могли бы однозначно найти и сами корни.

Таки что мешает нам это сделать? Но как настоящие математики, давайте находить квадрат расстояния между корнями. Не теряя общности, будем считать, что – больший корень. Тогда

Пока что выглядит не очень, но на что-то это очень сильно похоже. Не видите? Давайте выделим полный квадрат, но по сумме, а не по разности: добавим , но чтобы все осталось в точности так же, это же и вычтем.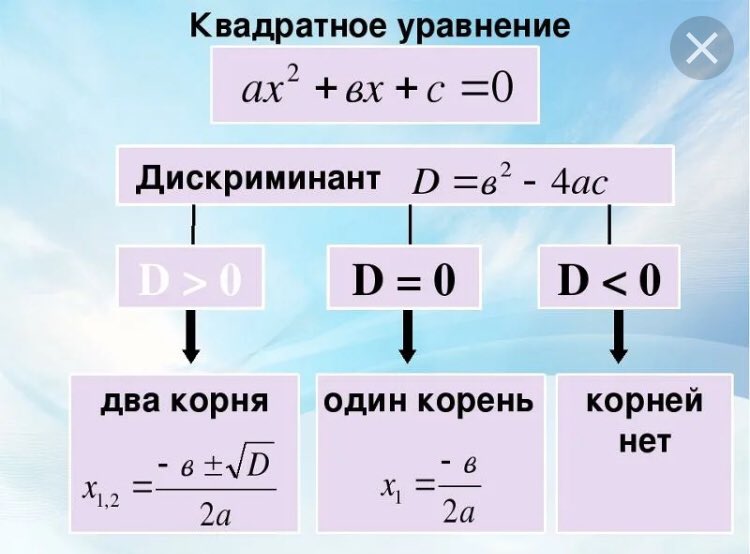

Все еще не видите? Воспользуемся снова теоремой Виета:

Мы получили квадрат расстояния между корнями с учетом растяжения коэффициентом .

Так мы теперь можем найти корни! Вершина параболы да половину расстояния между корнями в обе стороны:

Или, немного преобразовав

Квадрат расстояния между корнями квадратного трехчлена и есть дискриминант.

В общем случае, дискриминант — более сложное понятие, связанное с кратными корнями. Но для квадратного уравнения в 7 классе этого достаточно.

Теперь, если рассуждать о дискриминанте как о расстоянии, становится логично и понятно, почему если он равен нулю, то корень всего один; а если отрицательный, то действительных корней вообще нет.

Заключение

Заметьте, что единственное, что мы предположили, что корня два и они существуют. Единственное, что приняли на веру, это основную теорему алгебры. До всего остального мы дошли исключительно умозрительными заключениями и простейшей алгеброй.

Как по мне, это именно то, как должны преподавать эту тему в школе.

1 корень дискриминант

1 корень дискриминант

Вы искали 1 корень дискриминант? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и 2 формула дискриминанта, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «1 корень дискриминант».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает.

Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как 1 корень дискриминант,2 формула дискриминанта,2 формулы дискриминанта,b корень из дискриминанта,d 0 формула,d1 дискриминант,d1 дискриминант формула,d1 как найти,d1 формула,d1 формула дискриминанта,x1 x2 дискриминант,x1 дискриминант,алгебра дискриминант,все о дискриминанте,все формулы дискриминанта,вторая формула дискриминанта,вычисление дискриминанта,вычислить дискриминант,д1 дискриминант,две формулы дискриминанта,дескрименант формула,дескриминант,дискременант,дискреминант,дискрименант,дискриминант,дискриминант 0,дискриминант 0 формула,дискриминант 1,дискриминант 1 как найти,дискриминант 1 корень,дискриминант 1 корень формула,дискриминант 1 формула,дискриминант 1 формула д1,дискриминант 2,дискриминант 2 формула,дискриминант d1,дискриминант d1 формула,дискриминант k,дискриминант k2 ac,дискриминант x1,дискриминант x1 x2,дискриминант x1 x2 формула,дискриминант алгебра,дискриминант без с,дискриминант больше нуля,дискриминант в каком классе проходят,дискриминант все формулы,дискриминант вычислить,дискриминант д1,дискриминант д1 формула,дискриминант деленный на 4 формула,дискриминант для четного b,дискриминант и как найти корни,дискриминант и корни,дискриминант и корни формулы,дискриминант из 1,дискриминант икс 1 и икс 2,дискриминант к,дискриминант как найти,дискриминант как найти х,дискриминант как решать,дискриминант как считается,дискриминант квадратного уравнения,дискриминант квадратного уравнения формула,дискриминант квадратное уравнение,дискриминант квадратные уравнения,дискриминант когда равен 1,дискриминант корень,дискриминант корень 1,дискриминант корни,дискриминант корни формула,дискриминант математика,дискриминант матрицы как найти,дискриминант меньше нуля,дискриминант меньше нуля формула,дискриминант меньше нуля что значит,дискриминант неполный,дискриминант ноль,дискриминант один,дискриминант половинный,дискриминант при 0,дискриминант при четном b,дискриминант пример,дискриминант примеры,дискриминант примеры для решения,дискриминант примеры с решением,дискриминант равен,дискриминант равен 0,дискриминант равен 0 как найти,дискриминант равен 0 как найти корень,дискриминант равен 0 квадратное уравнение,дискриминант равен 0 сколько корней,дискриминант равен 0 формула,дискриминант равен 0 формула корня,дискриминант равен 1,дискриминант равен 1 формула,дискриминант равен нулю,дискриминант равен нулю формула,дискриминант решение,дискриминант решение квадратных уравнений,дискриминант решение уравнений,дискриминант решить,дискриминант с минусом,дискриминант сокращенный,дискриминант таблица,дискриминант тема,дискриминант теорема,дискриминант уравнение,дискриминант уравнения,дискриминант формула,дискриминант формула 0,дискриминант формула 1 корень,дискриминант формула 2,дискриминант формула д1,дискриминант формула если 0,дискриминант формула корней,дискриминант формула примеры,дискриминант формула примеры и решение с объяснением,дискриминант формула х1,дискриминант формула х1 х2,дискриминант формула через k,дискриминант формулы,дискриминант формулы и корни,дискриминант формулы х1 х2,дискриминант х1 формула,дискриминант х1 х2 формула,дискриминант через k формула,дискриминант через к,дискриминант четный,дискриминант что такое,дискриминант что это,дискриминант что это такое,дискриминант это,дискриминант это что,дискриминанта,дискриминанта уравнения,дискриминанта формула д1,дискриминантное уравнение,дискриминанты,дискриминация формула,дискримінант,дискримінант формула,если д равен 0,если дискриминант,если дискриминант 0 формула,если дискриминант 1,если дискриминант больше нуля,если дискриминант меньше 0,если дискриминант равен,если дискриминант равен 0 как найти корень,если дискриминант равен 0 какая формула,если дискриминант равен 1,если дискриминант равен 1 какая формула,если дискриминант равен нулю какая формула,если дискриминант равен нулю то как найти корень,задачи дискриминант,задачи с дискриминантом,как вычислить дискриминант,как вычисляется дискриминант,как дискриминант считается,как искать дискриминант,как найти 1 дискриминант,как найти d1,как найти x если дискриминант равен 0,как найти x через дискриминант,как найти x1 и x2 в дискриминанте,как найти дискриминант,как найти дискриминант 1,как найти дискриминант и х1 и х2,как найти дискриминант квадратного уравнения,как найти дискриминант равен 0,как найти дискриминант формула,как найти дискриминант х,как найти дискриминант х1 и х2,как найти дискриминант через k,как найти дискриминант через х,как найти корень дискриминанта,как найти корень если дискриминант равен 0,как найти корень квадратного уравнения если дискриминант равен 0,как найти корни дискриминанта,как найти корни квадратного уравнения через дискриминант,как найти корни уравнения через дискриминант,как найти х дискриминант,как найти х если дискриминант равен 0,как найти х через дискриминант,как найти х через дискриминант формула,как найти х1 и х2 дискриминант,как найти через k дискриминант,как найти через дискриминант x,как находится дискриминант,как находится дискриминант формула,как находить дискриминант,как находить дискриминант формула,как посчитать дискриминант,как решается дискриминант,как решать дискриминант,как решать дискриминант примеры,как решать дискриминантные уравнения,как решать квадратное уравнение через дискриминант,как решать квадратные уравнения через дискриминант,как решать по дискриминанту,как решать уравнение через дискриминант,как решать уравнения с дискриминантом,как решать уравнения через дискриминант,как решать через дискриминант,как решать через дискриминант 1,как решать через дискриминант формула,как решаются квадратные уравнения через дискриминант,как решить дискриминант,как решить дискриминантное уравнение,как решить уравнение с дискриминантом,как решить уравнение через дискриминант,как решить через дискриминант,как считается дискриминант,как считать дискриминант,как через дискриминант найти корни,какая формула если дискриминант равен 0,какая формула если дискриминант равен 1,какая формула если дискриминант равен нулю,какая формула когда дискриминант равен 0,какая формула при дискриминанте 0,квадратное уравнение дискриминант,квадратное уравнение дискриминант равен 0,квадратное уравнение примеры с решением через дискриминант,квадратное уравнение решение через дискриминант,квадратное уравнение с дискриминантом,квадратное уравнение через дискриминант,квадратное уравнение через дискриминант решение,квадратные уравнения дискриминант,квадратные уравнения дискриминант равен нулю,квадратные уравнения примеры с дискриминантом,квадратные уравнения через дискриминант,когда дискриминант равен 0 какая формула,когда дискриминант равен 1,когда дискриминант равен нулю формула,корень дискриминант,корень дискриминанта,корень дискриминанта формула,корень из дискриминанта,корень из дискриминанта формула,корень квадратного уравнения через дискриминант формула,корень при дискриминанте равном 0,корни дискриминант,корни дискриминанта,корни дискриминанта формула,корни из дискриминанта,корни уравнения через дискриминант,корни через дискриминант,математика дискриминант,может ли квадратное уравнение с целыми коэффициентами иметь дискриминант 23,найдите дискриминант уравнения,найти дискриминант,найти дискриминант квадратного уравнения,нахождение дискриминанта,нахождение дискриминанта формула,нахождение корней через дискриминант,нахождение корней через дискриминант формула,неполный дискриминант,нулевой дискриминант,определение дискриминанта,поиск дискриминанта,половинный дискриминант,половинный дискриминант формула,правила дискриминанта,правило дискриминанта,при дискриминанте равном 0,при дискриминанте равном 0 формула,пример дискриминант,пример дискриминанта,пример решения формула дискриминанта,пример с дискриминантом,пример формула дискриминанта,примеры дискриминант,примеры дискриминанта,примеры на дискриминант,примеры на дискриминант 9 класс,примеры по алгебре с дискриминантом,примеры решение квадратных уравнений через дискриминант,примеры решение уравнений через дискриминант,примеры с дискриминантом,примеры с дискриминантом по алгебре,примеры уравнения с дискриминантом примеры,примеры формула дискриминанта,примеры через дискриминант,равен х если дискриминант равен 0,решение дискриминант,решение дискриминанта,решение дискриминанта примеры,решение квадратного уравнения через дискриминант,решение квадратного уравнения через дискриминант формулы,решение квадратных уравнений дискриминант,решение квадратных уравнений через дискриминант,решение по дискриминанту,решение с дискриминантом,решение уравнений дискриминант,решение уравнений с дискриминантом,решение уравнений через дискриминант,решение уравнения через дискриминант,решение через дискриминант,решение через дискриминант формула,решить дискриминант,решить уравнение через дискриминант,свойства дискриминанта,сокращенная дискриминанта формула,сокращенная формула дискриминанта,сокращенный дискриминант,сокращенный дискриминант формула,таблица дискриминант,таблица дискриминанта,таблица дискриминантов,таблица дискриминантов по алгебре,тема дискриминант,теорема дискриминант,теорема дискриминант формула,теорема дискриминанта,уравнение дискриминант,уравнение дискриминанта,уравнение дискриминанта примеры решения,уравнение дискриминанта формула,уравнение с дискриминантом,уравнение с дискриминантом пример,уравнение с дискриминантом формула,уравнение через дискриминант,уравнение через дискриминант примеры,уравнение через дискриминант решить,уравнения дискриминант,уравнения дискриминанта,уравнения на дискриминант,уравнения с дискриминантом,уравнения с дискриминантом как решать,уравнения с дискриминантом примеры,уравнения через дискриминант,уравнения через дискриминант примеры,формула 0 дискриминанта,формула d 0,формула d1,формула d1 дискриминант,формула x1 x2 дискриминант,формула вычисления дискриминанта,формула д1 дискриминант,формула д1 дискриминант к,формула д1 дискриминанта,формула дескрименант,формула дискрименанта,формула дискриминант 0,формула дискриминант деленный на 4,формула дискриминант равен 1,формула дискриминант равен нулю,формула дискриминанта,формула дискриминанта 0,формула дискриминанта 1,формула дискриминанта 1 через k,формула дискриминанта 2,формула дискриминанта d1,формула дискриминанта вторая,формула дискриминанта д1,формула дискриминанта деленного на 4,формула дискриминанта для 0,формула дискриминанта для четных чисел,формула дискриминанта если он равен 0,формула дискриминанта и его,формула дискриминанта и его корней,формула дискриминанта и его корней при 0,формула дискриминанта и его корней через k,формула дискриминанта и корней,формула дискриминанта и нахождения корней,формула дискриминанта и х1,формула дискриминанта и х1 х2,формула дискриминанта квадратного уравнения,формула дискриминанта корня,формула дискриминанта нахождения корней,формула дискриминанта при 0,формула дискриминанта при b четном,формула дискриминанта при четном b,формула дискриминанта пример,формула дискриминанта пример решения,формула дискриминанта примеры,формула дискриминанта равного 0,формула дискриминанта сокращенная,формула дискриминанта сокращенного,формула дискриминанта х1 х2,формула дискриминанта через k,формула дискриминанта через к,формула дискриминанта четверти,формула дискриминанта четная,формула дискриминанта четного,формула дискриминация,формула дискримінант,формула дискримінанта,формула дискримінанту,формула для дискриминанта,формула для дискриминанта 0,формула для нахождения дискриминанта,формула если дискриминант 0,формула если дискриминант равен 0,формула как найти дискриминант,формула квадратного уравнения дискриминант,формула корень дискриминанта,формула корень из дискриминанта,формула корней дискриминанта,формула корня дискриминанта,формула корня если дискриминант равен 0,формула нахождения x1 и x2 через дискриминант,формула нахождения дискриминанта,формула нахождения дискриминанта и корней,формула нахождения корней дискриминанта,формула неполного дискриминанта,формула нулевого дискриминанта,формула отрицательного дискриминанта,формула половинного дискриминанта,формула при дискриминанте 0,формула при дискриминанте равном 0,формула решения квадратного уравнения через дискриминант,формула сокращенного дискриминанта,формула х в дискриминанте,формула х1 дискриминант,формула х1 и х2 дискриминант,формула х1 и х2 при дискриминанте,формула четверти дискриминанта,формула четного дискриминанта,формулы 2 дискриминанта,формулы дискриминанта,формулы дискриминанта 1,формулы дискриминанта 1 через k,формулы дискриминанта 2,формулы дискриминанта все,формулы дискриминанта и корней,формулы дискриминанта корней,формулы дискриминанта при 0,формулы дискриминанта через к,формулы дискриминантов,формулы для дискриминанта,формулы корней дискриминанта,формулы корней квадратного уравнения дискриминант,формулы нахождения дискриминанта,формулы с дискриминантом,формулы х1 х2 дискриминант,функция дискриминанта,чему равен дискриминант,чему равен дискриминант 1,чему равен дискриминант квадратного уравнения,через дискриминант,четверть дискриминанта,четверть дискриминанта формула,четная формула дискриминанта,четный дискриминант,четный дискриминант формула,что делать если дискриминант равен 1,что если дискриминант меньше нуля,что если дискриминант равен 1,что такое в алгебре дискриминант,что такое в математике дискриминант,что такое дискриминант,что такое дискриминант в алгебре,что такое дискриминант в математике. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и 1 корень дискриминант. Просто введите задачу в окошко и нажмите «решить» здесь (например, 2 формулы дискриминанта).

Решить задачу 1 корень дискриминант вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Видео-вопрос: Нахождение всех возможных значений константы, которые делают корни заданного квадратного уравнения недействительными найти интервал, который содержит 𝑘.

Итак, нам сказали, что корни этого квадратного уравнения, в котором 𝑘 — постоянный член, ненастоящие. Нам нужно вспомнить связь, которая существует между коэффициентами квадратного уравнения и типом его корней.

Предположим, у нас есть общее квадратное уравнение 𝑎𝑥 в квадрате плюс 𝑏𝑥 плюс 𝑐 равно нулю. Дискриминант квадратного уравнения равен величине 𝑏 в квадрате минус четыре 𝑎𝑐. Значение или, точнее, знак дискриминанта определяет тип корней, которые будут иметь квадратное уравнение.

Если дискриминант строго положителен, то квадратное уравнение будет иметь два действительных и различных корня. Если значение дискриминанта равно нулю, то квадратное уравнение имеет только один повторяющийся действительный корень. Если значение дискриминанта меньше нуля, то квадратное уравнение не имеет действительных корней, что и происходит в этом вопросе.

Итак, мы знаем, что дискриминант этого квадратичного числа должен быть меньше нуля. Давайте выясним, чему равен дискриминант с точки зрения 𝑘. Сравнивая коэффициенты в нашем квадрате с общей формой, мы видим, что 𝑎 равно 24, 𝑏 равно шести, а 𝑐 равно 𝑘.

Следовательно, дискриминант 𝑏 в квадрате минус четыре 𝑎𝑐 равен шести в квадрате минус четыре, умноженное на 24, умноженное на 𝑘. Это упрощается до 36 минус 96 𝑘. Помните, что корни этого квадратного уравнения не действительны. Значит, значение дискриминанта меньше нуля. Следовательно, имеем неравенство 36 минус 96 𝑘 меньше нуля.

Чтобы найти интервал, содержащий 𝑘, нужно решить это неравенство для 𝑘. Первый шаг — вычесть 36 с каждой стороны. Это дает отрицательное 96 𝑘 меньше отрицательного 36. Далее нам нужно разделить обе части неравенства на отрицательное 96.

Здесь нужно быть очень осторожным. Помните, что когда мы делим неравенство на отрицательное число, нам нужно изменить направление неравенства на противоположное. Таким образом, знак меньше становится знаком больше. И теперь у нас есть, что 𝑘 больше, чем минус 36 больше, чем минус 9.6. Отрицательное значение в числителе и отрицательное значение в знаменателе сокращаются. И дробь упрощается до трех на восемь путем деления числителя и знаменателя на 12.

Тогда мы имеем, что 𝑘 больше, чем три на восемь. Вопрос не требует от нас дать ответ в виде неравенства. Он просит нас указать интервал, который содержит 𝑘. Если 𝑘 должно быть больше трех на восемь, то множество возможных значений 𝑘 — это все от трех на восемь до бесконечности.

Поскольку нижняя граница интервала представляет собой строгое неравенство, а верхняя граница — бесконечность, мы можем выразить это как открытый интервал, на что указывают обращенные наружу квадратные скобки. 𝑘 принадлежит открытому интервалу с конечными точками три больше восьми и бесконечностью.

Объяснение урока: Дискриминанты квадратного уравнения

В этом объяснении мы узнаем, как найти дискриминант квадратного уравнения и использовать его для определения числа и типа его корней (решения), не решая его.

Напомним, что общее квадратное уравнение имеет вид

𝑎𝑥+𝑏𝑥+𝑐=0,

()1

где 𝑎, 𝑏 и 𝑐 — действительные числа, а 𝑥 — искомая переменная. Чтобы это уравнение было квадратным, мы требуем, чтобы 𝑎≠0, но мы не накладываем такое же ограничение на 𝑏 или 𝑐. Это уравнение «решается», когда найдено значение 𝑥 такое, что равенство (1) верно. Для квадратного уравнения может быть максимум два реальный решений уравнения (1), в отличие от единственного действительного решения линейного уравнения. Чтобы быть более конкретным, для любого квадратного уравнения с действительными коэффициентами будет либо 0, либо 1, либо 2 действительных решения.

Хорошо известно, что решение квадратного уравнения дается формулой квадратного корня,

𝑥=−𝑏±√𝑏−4𝑎𝑐2𝑎,

()2

с двумя возможными решениями, обозначенными знаком ±. Справедливость любого из этих двух решений может можно проверить алгебраически, подставив любое выражение в уравнении (2) в уравнение (1).

Формула квадратного корня намекает на то, что может быть 0, 1 или 2 действительных решения общего квадратичного уравнения уравнение, потому что символ ± предполагает, что есть два возможных вычисления, чтобы найти 𝑥. Если выражение внутри квадратного корня положительное, то проблем с поиском решения нет. Однако, если выражение внутри квадратного корня отрицательно, то мы будем пытаться извлечь квадратный корень из отрицательного числа, для которые не имеют решений в действительных числах. Наконец, если выражение внутри корневого символа равно нулю, то оба вычисления будут равны, поэтому у нас будет только один корень. Следовательно, число действительных решений определяется знаком выражение 𝑏−4𝑎𝑐, известное как дискриминант.

Определение: Дискриминант квадратного числа

Рассмотрим квадратное уравнение 𝑎𝑥+𝑏𝑥+𝑐=0, где 𝑎, 𝑏 и 𝑐 — действительные числа, а 𝑎≠0. Затем «дискриминант» квадратичного обозначается Δ=𝑏−4𝑎𝑐.

Если Δ положительно, то у квадратного уравнения есть два действительных решения. Если Δ=0, то существует одно (повторяющееся) действительное решение. А если Δ отрицательно, то реальных решений нет.

Сделав это определение, мы можем увидеть, как можно записать формулу квадратного корня через дискриминант в виде 𝑥=−𝑏±√Δ2𝑎, что дополнительно проясняет связь с числом решений квадратичного уравнения. Мы продемонстрируем эту идею на примере, рассматривая квадратное уравнение 4𝑥−1+4𝑥=0. Было бы полезно думать вместо этого с точки зрения функция 𝑓(𝑥)=4𝑥+4𝑥−1, а затем спросите значения 𝑥, которые дают 𝑓(𝑥)=0. Другими словами, мы тогда пытаясь найти корни функции 𝑓(𝑥). Начнем с построения графика функции, как показано ниже, это показывает, что есть два корня, один из которых отрицательный, а другой положительный.

Теперь мы подтвердим это, обратившись к нашему определению дискриминанта. Чтобы решить уравнение 4𝑥−1+4𝑥=0, сначала следует отметить, что это квадратное уравнение относительно 𝑥 с коэффициентами 𝑎=4, 𝑏=4 и 𝑐=−1. Тогда дискриминант вычисляется как ∆=𝑏−4𝑎𝑐=4−4×4×(−1)=32.

Следовательно, имеем ∆>0, что, согласно приведенному выше определению, означает наличие двух действительных решения.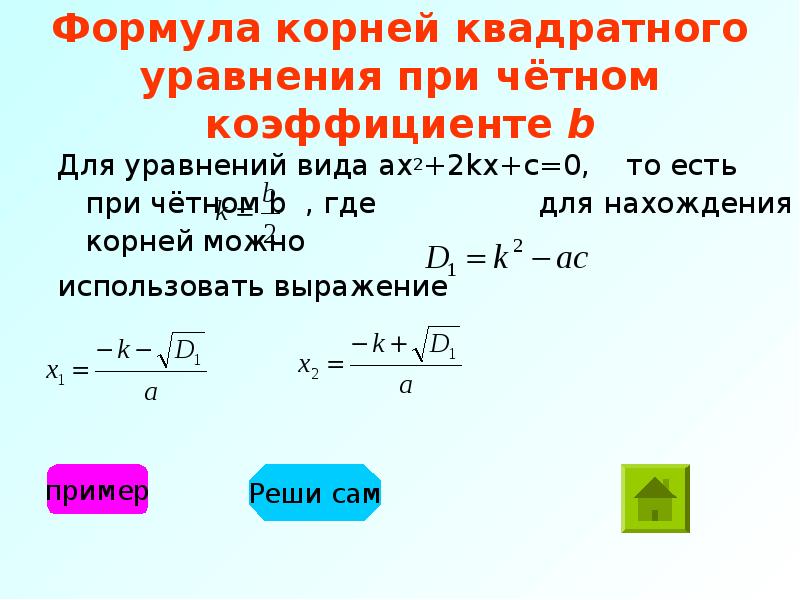 На это также указывает график, который мы построили выше. Затем мы можем использовать квадратное выражение, чтобы напрямую вычислить эти значения. корни следующим образом: 𝑥=−𝑏±√Δ2𝑎=−4±√322×4=−1±√22.

Мы можем проверить, что эти два реальных решения численно соответствуют решениям, показанным на графике выше.

Рассмотрим другой пример, на этот раз для квадратичного 4𝑥+1+4𝑥=0, что означает, что мы установили 𝑔(𝑥)=4𝑥+4𝑥+1, которая является квадратичной функцией, где 𝑎=4, 𝑏=4 и 𝑐=1. По сравнению с функция 𝑓(𝑥), функция 𝑔(𝑥) будет иметь ровно та же фигура после переноса на две единицы в положительном вертикальном направлении. График этой функции выглядит следующим образом:

выглядит как , как будто существует только одно действительное решение этого уравнения при 𝑥=−12, которое, как мы покажем, равно точно так же, как с использованием дискриминанта. Рассчитываем дискриминант следующим образом: Δ=𝑏−4𝑎𝑐=4−4×4×1=0. 

Тот факт, что Δ=0 означает, что существует один действительный (повторяющийся) корень, как видно из графика нанесено выше. Затем по квадратичной формуле вычисляются решения как 𝑥=−𝑏±√Δ2𝑎=−4±√02×4=−12.

В этом случае член ± не имеет значения, поскольку добавление нуля равносильно вычитанию нуля. в отличие от В предыдущем сценарии нет необходимости выполнять дальнейшие вычисления, чтобы найти (повторяющийся) действительный корень.

Последний пример, который мы приведем, будет для квадратного уравнения, у которого нет действительных решений. Мы возьмем предыдущий пример и немного изменить его, чтобы получить квадратное уравнение 3+4𝑥+4𝑥=0. Чтобы помочь в нашем процессе, мы определим функцию ℎ(𝑥)=4𝑥+4𝑥+3, которая является квадратичной функцией с 𝑎=4, 𝑏=4 и 𝑐=3. Этот график ℎ(𝑥) совпадает с графиком 𝑔(𝑥), переведенным на две единицы в положительном вертикальном направлении, результат которого показан ниже.

Из этого графика видно, что действительных решений квадратного уравнения нет, что мы можем показать, вычислив дискриминант следующим образом: Δ=𝑏−4𝑎𝑐=4−4×4×3=−32.

Это показывает, что Δ0, что означает отсутствие реальных решений, тем самым подтверждая наш прогноз после построения графика. Попытка использовать формулу квадратного корня даст следующую работу: 𝑥=−𝑏±√Δ2𝑎=−4±√−322×4.

Эта работа показывает, что мы пытаемся вычислить квадратный корень из отрицательного числа, что не дает результата это реальное число. Это означает, что не существует реальных решений исходного квадратного уравнения, как это предсказывает формула значение дискриминанта. В этой ситуации для понимания решений потребуется понимание воображаемых и комплексные числа, которые выходят за рамки этого объяснения.

Теперь давайте рассмотрим несколько примеров того, как дискриминант используется для определения числа действительных корней квадратного уравнения. уравнение.

Пример 1. Использование знака дискриминанта для определения числа комплексных корней квадратного уравнения

Сколько невещественных корней будет иметь квадратное уравнение, если его дискриминант отрицательный?

Ответ

Напомним, что если у нас есть квадратное уравнение 𝑎𝑥+𝑏𝑥+𝑐=0, где 𝑎, 𝑏, и 𝑐 — действительные числа и 𝑎≠0, то мы знаем, что формула квадратного корня 𝑥=−𝑏±√𝑏−4𝑎𝑐2𝑎, что дает нам корни квадратного. Дискриминант определяется как Δ=𝑏−4𝑎𝑐, что позволяет формула квадратного корня вместо этого должна быть записана как 𝑥=−𝑏±√Δ2𝑎.

Если дискриминант отрицательный, то мы попытаемся вычислить квадратный корень из отрицательного числа, которое имеет нет решений в действительных числах. Это означает, что у данного квадратного уравнения нет действительных решений, т.е. означает, что должно быть два невещественных корня.

Пример 2. Использование знака дискриминанта для определения числа комплексных корней квадратного уравнения

Какое условие является правильным для квадратного уравнения 𝑎𝑥+𝑏𝑥+𝑐=0 с действительными коэффициентами не иметь невещественных корней?

1. Дискриминант 𝑏−4𝑎𝑐 положителен.
2. Дискриминант 𝑏−4𝑎𝑐 равен нулю.
3. Дискриминант 𝑏−4𝑎𝑐 отрицателен.
4. Дискриминант 𝑏−4𝑎𝑐 неотрицательный.
5. Дискриминант 𝑏−4𝑎𝑐 является целым числом.

Ответ

При работе с квадратным числом мы помним, что знак дискриминанта говорит нам о количестве действительных корней. Существует три возможных количества действительных корней:

• Два действительных корня, когда Δ=𝑏−4𝑎𝑐>0
• Один действительный (повторяющийся) корень, когда Δ=𝑏−4𝑎𝑐=0
• Нет действительных корней, когда Δ=𝑏−4𝑎𝑐0

Нам говорят, что мы ищем, чтобы не было недействительных корней задан квадратичный. Это означает, что должны быть по крайней мере одно действительное решение квадратного уравнения, максимум два. Чтобы было одно реальное решение, мы требуем, чтобы дискриминант был равен нулю, а для того, чтобы было два действительных решения, мы требуем, чтобы дискриминант положителен. Для выполнения любого из этих условий требуется, чтобы дискриминант был больше больше или равно нулю. Это соответствует варианту D из приведенного выше списка, означающему, что дискриминант должен быть неотрицательным.

Два приведенных выше примера демонстрируют, как можно классифицировать количество корней, просто используя дискриминант. При попытке найти точные корни квадратного уравнения, поэтому полезным упреждающим шагом является вычисление дискриминанта, а затем используйте это, чтобы понять количество корней, прежде чем мы их вычислим. Например, если дискриминант квадратичного числа равен отрицательно, то действительных корней нет и, следовательно, нет необходимости использовать квадратную формулу для их нахождения. мы дадим пример этого в следующем вопросе.

Пример 3. Нахождение дискриминанта квадратного уравнения и его использование для определения числа действительных корней

1. Найдите дискриминант квадратного уравнения 2𝑥+3𝑥+4=0.
2. Сколько действительных корней имеет уравнение 2𝑥+3𝑥+4=0?
3. Следовательно, решите, сколько раз график 𝑦=2𝑥+3𝑥+4 пересечет ось 𝑥.

Ответ

Часть 1

Начнем с того, что приведенное выше квадратное уравнение можно классифицировать обычным способом, записав коэффициенты как 𝑎=2, 𝑏=3 и 𝑐=4. Напомним, что дискриминант квадратичного уравнения равен Δ=𝑏−4𝑎𝑐, которое мы можем вычислить для этого квадратичного уравнения следующим образом: Δ=𝑏−4𝑎𝑐=3−4×2×4=−23,

Часть 2

Напомним, что знак дискриминанта квадратного числа говорит нам о количестве действительных корней, которое имеет квадратное число. В частности, если его знак отрицательный, то действительных корней нет. Учитывая, что ∆0, это означает, что у данного квадратного уравнения нет действительных корней, поэтому ответ равен нулю действительных корней.

Часть 3

Функция имеет корень, когда график этой функции пересекает ось 𝑥. Учитывая, что эта функция имеет нет действительных корней, это означает, что график функции не пересекает ось 𝑥. Это может быть подтверждено графически с использованием приведенного ниже графика функции 𝑓(𝑥)=2𝑥+3𝑥+4.

Мы видим, что график функции никогда не пересечет ось 𝑥, как и предсказывалось.

Мы уже видели, что формула квадратного корня может быть выражена через дискриминант как 𝑥=−𝑏±√Δ2𝑎.

Прежде чем вычислять корни квадратного числа, нам нужно будет вычислить квадратный корень из дискриминанта Δ. Это означает, что если Δ является квадратным числом, то квадратный корень вернет целое число. При условии, что 𝑎 и 𝑏 оба рациональны, в этом конкретном случае значения 𝑥, следовательно, будет рациональным. Однако, как правило, Δ не является квадратное число, что означает, что квадратный корень этого значения будет иррациональным числом. Когда это так, будет подразумевают, что значения 𝑥 будут иррациональными, поскольку они будут комбинацией иррационального числа и два рациональных числа с помощью сложения и деления. Заметим, что это свойство имеет место только в предположении, что 𝑎 и 𝑏 оба рациональны. Если они оба не рациональны, то нам нужно будет рассмотреть вопрос несколько более деликатный, как мы увидим в следующем примере.

Пример 4. Определение рациональности корней квадратного уравнения с помощью дискриминанта

Определить, рациональны или нет корни уравнения 𝑥−√5𝑥−1=0, не решая его.

Ответ

Зададим коэффициенты этого квадратного уравнения стандартным образом, зафиксировав 𝑎=1, 𝑏=−√5 и 𝑐=−1. Напомним, что дискриминант квадратичного 𝑎𝑥+𝑏𝑥+𝑐=0 равен Δ=𝑏−4𝑎𝑐, и квадратичная формула говорит нам, что корни этого квадратного числа равны 𝑥=−𝑏±√Δ2𝑎.

Затем мы можем вычислить дискриминант квадратичного уравнения следующим образом: Δ=𝑏−4𝑎𝑐=−√5−4×1×(−1)=5+4=9.

Мы знаем, что, поскольку это число положительное, существует два действительных корня. Мы также можем видеть, что в квадратичной формуле 2𝑎 рационально, и √Δ=√9=3 также рационально. Однако −𝑏 иррационально; следовательно, корни будут иррациональными.

В нашем следующем примере мы исследуем поведение квадратичных уравнений, рассматривая коэффициент 𝑐 быть параметром.

Пример 5. Нахождение интервала, которому принадлежит переменная в квадратном уравнении, зная тип его корней содержит 𝑘.

Ответ

Начнем с того, что обработаем этот квадрат обычным образом. Обозначим параметры как 𝑎=4, 𝑏=−12, и 𝑐=𝑘. Напомним, что знак дискриминанта квадратичного числа 𝑎𝑥+𝑏𝑥+𝑐=0 дает нам количество корней квадратного. В этом вопросе нам нужны два различных действительных корня, что происходит, когда дискриминант положительный. Мы вычисляем дискриминант Δ следующим образом: Δ=𝑏−4𝑎𝑐=(−12)−4×4×𝑘=144−16𝑘=16(9−𝑘).

Вопрос просил нас найти все возможные значения 𝑘, которые гарантируют, что корни квадратичного настоящие и разные. Другими словами, нас просят найти возможные значения 𝑘 такие, что два действительных корня, а это означает, что ∆>0.