Дисперсия как найти: Дисперсия случайной величины, дисперсия что это такое

alexxlab / / Разное

18. Дисперсия дискретной случайной величины

Зная лишь математическое ожидание случайной величины, еще нельзя судить ни о том, какие возможные значения она принимает, ни о том, как они рассеяны вокруг математического ожидания.

Рассмотрим, например, дискретные случайные величины X и Y , заданные следующими законами распределения:


X

-0,001

0,001

P

0,5

0,5

Y

-1000

1000

P

0,5

0,5

Математические ожидания этих величин

Другими словами, математическое ожидание полностью случайную величину не характеризует. По этой причине наряду с математическим ожиданием вводят и другие числовые характеристики.

Определение7.1: Отклонением называют разность между случайной величиной и ее математическим ожиданием: X – M(X).

Свойство отклонения: Математическое ожидание отклонения равно нулю:

M[X – M(X)] = 0.

Доказательство: Пользуясь свойствами математического ожидания и тем, что M(X)- Постоянная величина, имеем

M[X – M(X)] = M(X) – M[M(X)] = M(X) –M(X)= 0.

Замечание: Наряду с термином “отклонение” используют термин “центрированная величина”. Центрированной случайной величиной Называют разность между случайной величиной и ее математическим ожиданием: = X – M(X).

Определение7.2:Дисперсией (рассеянием) дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

D(X) = M[X – M(X)]2.

Пусть дискретная случайная величина задана рядом распределения

X

x1

X2

X3

…..

Xn

P

p1

P2

P3

…..

Pn

Тогда

D(X) = M[X – M(X)]2 = [x1-M(X)]2p1+ [x2-M(X)]2p2+…+ [Xn-M(X)]2Pn.

Таким образом, Чтобы найти дисперсию, достаточно вычислить сумму произведений возможных значений квадрата отклонения на их вероятности.

Пример.

Найти дисперсию случайной величины X , которая задана следующим рядом распределения:

X

1

2

5

P

0,3

0,5

0,2

Решение: Математическое ожидание M(X) = 1∙0,3+2∙0,5+5∙0,2 = 2,3.

Тогда D(X) = (1 — 2,3)2∙0,3 + (2 — 2,3)2∙0,5 + (5 — 2,3)2∙0,2 = 1,69 ∙ 0,3 + 0,09 ∙ 0,5 + 7,29 ∙ 0,2 = 2,01.

Для вычисления дисперсии часто удобно пользоваться другой формулой:

D(X) = M(X2) – [M(X)]2.

Доказательство:

D(X) = M[X – M(X)]2=M[X2 — 2X∙M(X) + M2(X)]= M(X2) – 2M(X)

∙M(X) + M2(X) =

= M(X2) – 2M2(X)+ M2(X) = M(X2)- M2(X).

Таким образом, Дисперсия равна разности между математическим ожиданием квадрата случайной величины и квадратом ее математического ожидания.

Пример. Найти дисперсию случайной величины X , которая задана следующим рядом распределения:

X

2

3

5

P

0,1

0,6

0,3

Решение: Математическое ожидание M(X) = 2∙0,1+3∙0,6+5∙0,3 = 3,5. Тогда M(X2) = 22∙0,1+32∙0,6+52∙0,3 = 13,3. Дисперсия D(X) = M(X2) – [M(X)]2=13,3 – (3,5)2=1,05.

< Предыдущая   Следующая >

Найти общую дисперсию. Дисперсия и стандартное отклонение в MS EXCEL

Дисперсия в статистике находится как индивидуальных значений признака в квадрате от . В зависимости от исходных данных она определяется по формулам простой и взвешенной дисперсий:

1. (для несгруппированных данных) вычисляется по формуле:

2. Взвешенная дисперсия (для вариационного ряда):

где n — частота (повторяемость фактора Х)

Пример нахождения дисперсии

На данной странице описан стандартный пример нахождения дисперсии, также Вы можете посмотреть другие задачи на её нахождение

Пример 1. Имеются следующие данные по группе из 20 студентов заочного отделения. Нужно построить интервальный ряд распределения признака, рассчитать среднее значение признака и изучить его дисперсию

Построим интервальную группировку.

Определим размах интервала по формуле:

где X max– максимальное значение группировочного признака;
X min–минимальное значение группировочного признака;
n – количество интервалов:

Принимаем n=5. Шаг равен: h = (192 — 159)/ 5 = 6,6

Составим интервальную группировку

Для дальнейших расчетов построим вспомогательную таблицу:

X’i– середина интервала. (например середина интервала 159 – 165,6 = 162,3)

Среднюю величину роста студентов определим по формуле средней арифметической взвешенной:

Определим дисперсию по формуле:

Формулу дисперсии можно преобразовать так:

Из этой формулы следует, что дисперсия равна разности средней из квадратов вариантов и квадрата и средней.

Дисперсия в вариационных рядах с равными интервалами по способу моментов может быть рассчитана следующим способом при использовании второго свойства дисперсии (разделив все варианты на величину интервала). Определении дисперсии

, вычисленной по способу моментов, по следующей формуле менее трудоемок:

где i — величина интервала;
А — условный ноль, в качестве которого удобно использовать середину интервала, обладающего наибольшей частотой;
m1 — квадрат момента первого порядка;
m2 — момент второго порядка

(если в статистической совокупности признак изменяется так, что имеются только два взаимно исключающих друг друга варианта, то такая изменчивость называется альтернативной) может быть вычислена по формуле:

Подставляя в данную формулу дисперсии q =1- р, получаем:

Виды дисперсии

Общая дисперсия измеряет вариацию признака по всей совокупности в целом под влиянием всех факторов, обуславливающих эту вариацию. Она равняется среднему квадрату отклонений отдельных значений признака х от общего среднего значения х и может быть определена как простая дисперсия или взвешенная дисперсия.

характеризует случайную вариацию, т.е. часть вариации, которая обусловлена влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Такая дисперсия равна среднему квадрату отклонений отдельных значений признака внутри группы X от средней арифметической группы и может быть вычислена как простая дисперсия или как взвешенная дисперсия.

Таким образом, внутригрупповая дисперсия измеряет вариацию признака внутри группы и определяется по формуле:

где хi — групповая средняя;
ni — число единиц в группе.

Например, внутригрупповые дисперсии, которые надо определить в задаче изучения влияния квалификации рабочих на уровень производительности труда в цехе показывают вариации выработки в каждой группе, вызванные всеми возможными факторами (техническое состояние оборудования, обеспеченность инструментами и материалами, возраст рабочих, интенсивность труда и т.

д.), кроме отличий в квалификационном разряде (внутри группы все рабочие имеют одну и ту же квалификацию).

Средняя из внутри групповых дисперсий отражает случайную , т. е. ту часть вариации, которая происходила под влиянием всех прочих факторов, за исключением фактора группировки. Она рассчитывается по формуле:

Характеризует систематическую вариацию результативного признака, которая обусловлена влиянием признака-фактора, положенного в основание группировки. Она равняется среднему квадрату отклонений групповых средних от общей средней. Межгрупповая дисперсия рассчитывается по формуле:

Правило сложения дисперсии в статистике

Согласно правилу сложения дисперсий общая дисперсия равна сумме средней из внутригрупповых и межгрупповых дисперсий:

Смысл этого правила заключается в том, что общая дисперсия, которая возникает под влиянием всех факторов, равняется сумме дисперсий, которые возникают под влиянием всех прочих факторов, и дисперсии, возникающей за счет фактора группировки.

2 раз.

.

Обратно, если — неотрицательная п.в. функция, такая что , то существует абсолютно непрерывная вероятностная мера на такая, что является её плотностью.

,

где любая борелевская функция, интегрируемая относительно вероятностной меры .

Дисперсия, виды и свойства дисперсии Понятие дисперсии

Дисперсия в статистике находится как среднее квадратическое отклонение индивидуальных значений признака в квадрате от средней арифметической. В зависимости от исходных данных она определяется по формулам простой и взвешенной дисперсий:

1. Простая дисперсия (для несгруппированных данных) вычисляется по формуле:

2. Взвешенная дисперсия (для вариационного ряда):

где n — частота (повторяемость фактора Х)

Пример нахождения дисперсии

На данной странице описан стандартный пример нахождения дисперсии, также Вы можете посмотреть другие задачи на её нахождение

Пример 1. Определение групповой, средней из групповой, межгрупповой и общей дисперсии

Пример 2. Нахождение дисперсии и коэффициента вариации в группировочной таблице

Пример 3. Нахождение дисперсии в дискретном ряду

Пример 4. Имеются следующие данные по группе из 20 студентов заочного отделения. Нужно построить интервальный ряд распределения признака, рассчитать среднее значение признака и изучить его дисперсию

Построим интервальную группировку. Определим размах интервала по формуле:

где X max– максимальное значение группировочного признака; X min–минимальное значение группировочного признака; n – количество интервалов:

Принимаем n=5. Шаг равен: h = (192 — 159)/ 5 = 6,6

Составим интервальную группировку

Для дальнейших расчетов построим вспомогательную таблицу:

X»i– середина интервала. (например середина интервала 159 – 165,6 = 162,3)

Среднюю величину роста студентов определим по формуле средней арифметической взвешенной:

Определим дисперсию по формуле:

Формулу можно преобразовать так:

Из этой формулы следует, что дисперсия равна разности средней из квадратов вариантов и квадрата и средней.

Дисперсия в вариационных рядах с равными интервалами по способу моментов может быть рассчитана следующим способом при использовании второго свойства дисперсии (разделив все варианты на величину интервала). Определении дисперсии , вычисленной по способу моментов, по следующей формуле менее трудоемок:

где i — величина интервала; А — условный ноль, в качестве которого удобно использовать середину интервала, обладающего наибольшей частотой; m1 — квадрат момента первого порядка; m2 — момент второго порядка

Дисперсия альтернативного признака (если в статистической совокупности признак изменяется так, что имеются только два взаимно исключающих друг друга варианта, то такая изменчивость называется альтернативной) может быть вычислена по формуле:

Подставляя в данную формулу дисперсии q =1- р, получаем:

Виды дисперсии

Общая дисперсия измеряет вариацию признака по всей совокупности в целом под влиянием всех факторов, обуславливающих эту вариацию. Она равняется среднему квадрату отклонений отдельных значений признака х от общего среднего значения х и может быть определена как простая дисперсия или взвешенная дисперсия.

Внутригрупповая дисперсия характеризует случайную вариацию, т.е. часть вариации, которая обусловлена влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Такая дисперсия равна среднему квадрату отклонений отдельных значений признака внутри группы X от средней арифметической группы и может быть вычислена как простая дисперсия или как взвешенная дисперсия.

Таким образом, внутригрупповая дисперсия измеряет вариацию признака внутри группы и определяется по формуле:

где хi — групповая средняя; ni — число единиц в группе.

Например, внутригрупповые дисперсии, которые надо определить в задаче изучения влияния квалификации рабочих на уровень производительности труда в цехе показывают вариации выработки в каждой группе, вызванные всеми возможными факторами (техническое состояние оборудования, обеспеченность инструментами и материалами, возраст рабочих, интенсивность труда и т. д.), кроме отличий в квалификационном разряде (внутри группы все рабочие имеют одну и ту же квалификацию).

Средняя из внутри групповых дисперсий отражает случайную вариацию, т. е. ту часть вариации, которая происходила под влиянием всех прочих факторов, за исключением фактора группировки. Она рассчитывается по формуле:

Межгрупповая дисперсия характеризует систематическую вариацию результативного признака, которая обусловлена влиянием признака-фактора, положенного в основание группировки. Она равняется среднему квадрату отклонений групповых средних от общей средней. Межгрупповая дисперсия рассчитывается по формуле:

Теория вероятности — особый раздел математики, который изучают только студенты высших учебных заведений. Вы любите расчёты и формулы? Вас не пугают перспективы знакомства с нормальным распределением, энтропией ансамбля, математическим ожиданием и дисперсией дискретной случайной величины? Тогда этот предмет вам будет очень интересен. Давайте познакомимся с несколькими важнейшими базовыми понятиями этого раздела науки.

Вспомним основы

Даже если вы помните самые простые понятия теории вероятности, не пренебрегайте первыми абзацами статьи. Дело в том, что без четкого понимания основ вы не сможете работать с формулами, рассматриваемыми далее.

Итак, происходит некоторое случайное событие, некий эксперимент. В результате производимых действий мы можем получить несколько исходов — одни из них встречаются чаще, другие — реже. Вероятность события — это отношение количества реально полученных исходов одного типа к общему числу возможных. Только зная классическое определение данного понятия, вы сможете приступить к изучению математического ожидания и дисперсии непрерывных случайных величин.

Среднее арифметическое

Ещё в школе на уроках математики вы начинали работать со средним арифметическим. Это понятие широко используется в теории вероятности, и потому его нельзя обойти стороной. Главным для нас на данный момент является то, что мы столкнемся с ним в формулах математического ожидания и дисперсии случайной величины.

Мы имеем последовательность чисел и хотим найти среднее арифметическое. Всё, что от нас требуется — просуммировать всё имеющееся и разделить на количество элементов в последовательности. Пусть мы имеем числа от 1 до 9. Сумма элементов будет равна 45, и это значение мы разделим на 9. Ответ: — 5.

Дисперсия

Говоря научным языком, дисперсия — это средний квадрат отклонений полученных значений признака от среднего арифметического. Обозначается одна заглавной латинской буквой D. Что нужно, чтобы её рассчитать? Для каждого элемента последовательности посчитаем разность между имеющимся числом и средним арифметическим и возведем в квадрат. Значений получится ровно столько, сколько может быть исходов у рассматриваемого нами события. Далее мы суммируем всё полученное и делим на количество элементов в последовательности. Если у нас возможны пять исходов, то делим на пять.

У дисперсии есть и свойства, которые нужно запомнить, чтобы применять при решении задач. Например, при увеличении случайной величины в X раз, дисперсия увеличивается в X в квадрате раз (т. е. X*X). Она никогда не бывает меньше нуля и не зависит от сдвига значений на равное значение в большую или меньшую сторону. Кроме того, для независимых испытаний дисперсия суммы равна сумме дисперсий.

Теперь нам обязательно нужно рассмотреть примеры дисперсии дискретной случайной величины и математического ожидания.

Предположим, что мы провели 21 эксперимент и получили 7 различных исходов. Каждый из них мы наблюдали, соответственно, 1,2,2,3,4,4 и 5 раз. Чему будет равна дисперсия?

Сначала посчитаем среднее арифметическое: сумма элементов, разумеется, равна 21. Делим её на 7, получая 3. Теперь из каждого числа исходной последовательности вычтем 3, каждое значение возведем в квадрат, а результаты сложим вместе. Получится 12. Теперь нам остается разделить число на количество элементов, и, казалось бы, всё. Но есть загвоздка! Давайте её обсудим.

Зависимость от количества экспериментов

Оказывается, при расчёте дисперсии в знаменателе может стоять одно из двух чисел: либо N, либо N-1. Здесь N — это число проведенных экспериментов или число элементов в последовательности (что, по сути, одно и то же). От чего это зависит?

Если количество испытаний измеряется сотнями, то мы должны ставить в знаменатель N. Если единицами, то N-1. Границу ученые решили провести достаточно символически: на сегодняшний день она проходит по цифре 30. Если экспериментов мы провели менее 30, то делить сумму будем на N-1, а если более — то на N.

Задача

Давайте вернемся к нашему примеру решения задачи на дисперсию и математическое ожидание. Мы получили промежуточное число 12, которое нужно было разделить на N или N-1. Поскольку экспериментов мы провели 21, что меньше 30, выберем второй вариант. Итак, ответ: дисперсия равна 12 / 2 = 2.

Математическое ожидание

Перейдем ко второму понятию, которое мы обязательно должны рассмотреть данной статье. Математическое ожидание — это результат сложения всех возможных исходов, помноженных на соответствующие вероятности. Важно понимать, что полученное значение, как и результат расчёта дисперсии, получается всего один раз для целой задачи, сколько бы исходов в ней не рассматривалось.

Формула математического ожидания достаточно проста: берем исход, умножаем на его вероятность, прибавляем то же самое для второго, третьего результата и т. д. Всё, связанное с этим понятием, рассчитывается несложно. Например, сумма матожиданий равна матожиданию суммы. Для произведения актуально то же самое. Такие простые операции позволяет с собой выполнять далеко не каждая величина в теории вероятности. Давайте возьмем задачу и посчитаем значение сразу двух изученных нами понятий. Кроме того, мы отвлекались на теорию — пришло время попрактиковаться.

Ещё один пример

Мы провели 50 испытаний и получили 10 видов исходов — цифры от 0 до 9 — появляющихся в различном процентном отношении. Это, соответственно: 2%, 10%, 4%, 14%, 2%,18%, 6%, 16%, 10%, 18%. Напомним, что для получения вероятностей требуется разделить значения в процентах на 100. Таким образом, получим 0,02; 0,1 и т.д. Представим для дисперсии случайной величины и математического ожидания пример решения задачи.

Среднее арифметическое рассчитаем по формуле, которую помним с младшей школы: 50/10 = 5.

Теперь переведем вероятности в количество исходов «в штуках», чтобы было удобнее считать. Получим 1, 5, 2, 7, 1, 9, 3, 8, 5 и 9. Из каждого полученного значения вычтем среднее арифметическое, после чего каждый из полученных результатов возведем в квадрат. Посмотрите, как это сделать, на примере первого элемента: 1 — 5 = (-4). Далее: (-4) * (-4) = 16. Для остальных значений проделайте эти операции самостоятельно. Если вы всё сделали правильно, то после сложения всех вы получите 90.

Продолжим расчёт дисперсии и математического ожидания, разделив 90 на N. Почему мы выбираем N, а не N-1? Правильно, потому что количество проведенных экспериментов превышает 30. Итак: 90/10 = 9. Дисперсию мы получили. Если у вас вышло другое число, не отчаивайтесь. Скорее всего, вы допустили банальную ошибку при расчётах. Перепроверьте написанное, и наверняка всё встанет на свои места.

Наконец, вспомним формулу математического ожидания. Не будем приводить всех расчётов, напишем лишь ответ, с которым вы сможете свериться, закончив все требуемые процедуры. Матожидание будет равно 5,48. Напомним лишь, как осуществлять операции, на примере первых элементов: 0*0,02 + 1*0,1… и так далее. Как видите, мы просто умножаем значение исхода на его вероятность.

Отклонение

Ещё одно понятие, тесно связанное с дисперсией и математическим ожиданием — среднее квадратичное отклонение. Обозначается оно либо латинскими буквами sd, либо греческой строчной «сигмой». Данное понятие показывает, насколько в среднем отклоняются значения от центрального признака. Чтобы найти её значение, требуется рассчитать квадратный корень из дисперсии.

Если вы построите график нормального распределения и захотите увидеть непосредственно на нём квадратичного отклонения, это можно сделать в несколько этапов. Возьмите половину изображения слева или справа от моды (центрального значения), проведите перпендикуляр к горизонтальной оси так, чтобы площади получившихся фигур были равны. Величина отрезка между серединой распределения и получившейся проекцией на горизонтальную ось и будет представлять собой среднее квадратичное отклонение.

Программное обеспечение

Как видно из описаний формул и представленных примеров, расчеты дисперсии и математического ожидания — не самая простая процедура с арифметической точки зрения. Чтобы не тратить время, имеет смысл воспользоваться программой, используемой в высших учебных заведениях — она называется «R». В ней есть функции, позволяющие рассчитывать значения для многих понятий из статистики и теории вероятности.

Например, вы задаете вектор значений. Делается это следующим образом: vector

В заключение

Дисперсия и математическое ожидание — это без которых сложно в дальнейшем что-либо рассчитать. В основном курсе лекций в вузах они рассматриваются уже в первые месяцы изучения предмета. Именно из-за непонимания этих простейших понятий и неумения их рассчитать многие студенты сразу начинают отставать по программе и позже получают плохие отметки по результатам сессии, что лишает их стипендии.

Потренируйтесь хотя бы одну неделю по полчаса в день, решая задания, схожие с представленными в данной статье. Тогда на любой контрольной по теории вероятности вы справитесь с примерами без посторонних подсказок и шпаргалок.

Во многих случаях возникает необходимость ввести ещё одну числовую характеристику для измерения степени рассеивания, разброса значений , принимаемых случайной величиной ξ , вокруг её математического ожидания.

Определение. Дисперсией случайной величины ξ называется число.

D ξ = M(ξ-M ξ) 2 . (1)

Другими словами, дисперсия есть математическое ожидание квадрата отклонения значений случайной величины от её среднего значения.

называется средним квадратичным отклонением

величины ξ .

Если дисперсия характеризует средний размер квадрата отклонения ξ oт Mξ , то число можно рассматривать как некоторую среднюю характеристику самого отклонения, точнее, величины | ξ-Mξ |.

Из определения (1) вытекают следующие два свойства дисперсии.

1. Дисперсия постоянной величины равна нулю. Это вполне соответствует наглядному смыслу дисперсии, как «меры разброса».

Действительно, если

ξ = С, то Mξ = C и, значит Dξ = M(C-C ) 2 = M 0 = 0.

2. При умножении случайной величины ξ на постоянное число С её дисперсия умножается на C 2

D(Cξ ) = C 2 Dξ . (3)

Действительно

D(Cξ) = M(C

= M(C .

3. Имеет место, следующая формула для вычисления дисперсии:

. (4)

Доказательство этой формулы следует из свойств математического ожидания.

Мы имеем:

4. Если величины ξ 1 и ξ 2 независимы, то дисперсия их суммы равна сумме их дисперсий:

Доказательство . Для доказательства используем свойства математического ожидания. Пусть Mξ 1 = m 1 , Mξ 2 = m 2 , тогда.

Формула (5) доказана.

Так как дисперсия случайной величины есть по определению математическое ожидание величины (ξ -m ) 2 , где m = Mξ , то для вычисления дисперсии можно воспользоваться формулами, полученными в §7 гл.II.

Так, если ξ есть ДСВ с законом распределения

x 1x 2…
p 1p 2…

то будем иметь:

. (7)

Если ξ непрерывна случайная величина с плотностью распределения p(x) , тогда получим:

Dξ = . (8)

Если использовать формулу (4) для вычисления дисперсии, то можно получить другие формулы, а именно:

, (9)

если величина ξ дискретна, и

Dξ = , (10)

если ξ распределена с плотностью p (x ).

Пример 1 . Пусть величина ξ равномерно распределена на отрезке [a,b ]. Воспользовавшись формулой (10) получим:

Можно показать, что дисперсия случайной величины , распределенной по нормальному закону с плотностью

p(x) = , (11)

равна σ 2 .

Тем самым выясняется смысл параметра σ, входящего в выражение плотности (11) для нормального закона; σ ecть среднее квадратичное отклонение величины ξ .

Пример 2 . Найти дисперсию случайной величины ξ , распределенной по биномиальному закону.

Решение . Воспользовавшись представлением ξ в виде

ξ = ξ 1 + ξ 2 + ξ n (см. пример 2 §7 гл. II) и применяя формулу сложения дисперсий для независимых величин, получим

Dξ = Dξ 1 + Dξ 2 + Dξ n .

Дисперсия любой из величин ξ i (i = 1,2, n ) подсчитывается непосредственно:

Dξ i = M(ξ i ) 2 — (Mξ i ) 2 = 0 2 · q + 1 2 p — p 2 = p (1-p ) = pq .

Окончательно получаем

Dξ = npq , где q = 1 — p .

На данной странице описан стандартный пример нахождения дисперсии, также Вы можете посмотреть другие задачи на её нахождение

Пример 1. Определение групповой, средней из групповой, межгрупповой и общей дисперсии

Пример 2. Нахождение дисперсии и коэффициента вариации в группировочной таблице

Пример 3. Нахождение дисперсии в дискретном ряду

Пример 4. Имеются следующие данные по группе из 20 студентов заочного отделения. Нужно построить интервальный ряд распределения признака, рассчитать среднее значение признака и изучить его дисперсию

Построим интервальную группировку. Определим размах интервала по формуле:

где X max– максимальное значение группировочного признака;
X min–минимальное значение группировочного признака;
n – количество интервалов:

Принимаем n=5. Шаг равен: h = (192 — 159)/ 5 = 6,6

Составим интервальную группировку

Для дальнейших расчетов построим вспомогательную таблицу:

X»i– середина интервала. (например середина интервала 159 – 165,6 = 162,3)

Среднюю величину роста студентов определим по формуле средней арифметической взвешенной:

Определим дисперсию по формуле:

Формулу можно преобразовать так:

Из этой формулы следует, что дисперсия равна разности средней из квадратов вариантов и квадрата и средней.

Дисперсия в вариационных рядах с равными интервалами по способу моментов может быть рассчитана следующим способом при использовании второго свойства дисперсии (разделив все варианты на величину интервала). Определении дисперсии , вычисленной по способу моментов, по следующей формуле менее трудоемок:

где i — величина интервала;
А — условный ноль, в качестве которого удобно использовать середину интервала, обладающего наибольшей частотой;
m1 — квадрат момента первого порядка;
m2 — момент второго порядка

Дисперсия альтернативного признака (если в статистической совокупности признак изменяется так, что имеются только два взаимно исключающих друг друга варианта, то такая изменчивость называется альтернативной) может быть вычислена по формуле:

Подставляя в данную формулу дисперсии q =1- р, получаем:

Виды дисперсии

Общая дисперсия измеряет вариацию признака по всей совокупности в целом под влиянием всех факторов, обуславливающих эту вариацию. Она равняется среднему квадрату отклонений отдельных значений признака х от общего среднего значения х и может быть определена как простая дисперсия или взвешенная дисперсия.

Внутригрупповая дисперсия характеризует случайную вариацию, т.е. часть вариации, которая обусловлена влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Такая дисперсия равна среднему квадрату отклонений отдельных значений признака внутри группы X от средней арифметической группы и может быть вычислена как простая дисперсия или как взвешенная дисперсия.

Таким образом, внутригрупповая дисперсия измеряет вариацию признака внутри группы и определяется по формуле:

где хi — групповая средняя;
ni — число единиц в группе.

Например, внутригрупповые дисперсии, которые надо определить в задаче изучения влияния квалификации рабочих на уровень производительности труда в цехе показывают вариации выработки в каждой группе, вызванные всеми возможными факторами (техническое состояние оборудования, обеспеченность инструментами и материалами, возраст рабочих, интенсивность труда и т. д.), кроме отличий в квалификационном разряде (внутри группы все рабочие имеют одну и ту же квалификацию).

Формула дисперсии

— что такое формула дисперсии? Примеры

Прежде чем изучать формулу дисперсии, вспомним, что такое дисперсия. Дисперсия ( σ 2 ) — это квадрат отклонения значений ( X i ) случайной величины ( X ) от ее среднего значения ( μ ). Формула дисперсии позволяет нам измерить этот разброс по среднему значению случайной величины. Формула дисперсии отличается для генеральной совокупности и выборки. Давайте теперь посмотрим на формулу дисперсии ниже. 92}{Н-1}\)

где

  • \(\bar{X}\) среднее значение
  • \(M_i\) — это середина i -го -го интервала.

Примечание:  

  1. Для несгруппированных данных \(\bar{X}\) = \(\dfrac{\Sigma x_i}{N} \)
  2. Для сгруппированных данных  \(\bar{X}\) = \( \dfrac{\Sigma M_i f}{\Sigma f} \)

 

Есть вопросы по основным математическим понятиям?

Станьте чемпионом по решению проблем, используя логику, а не правила.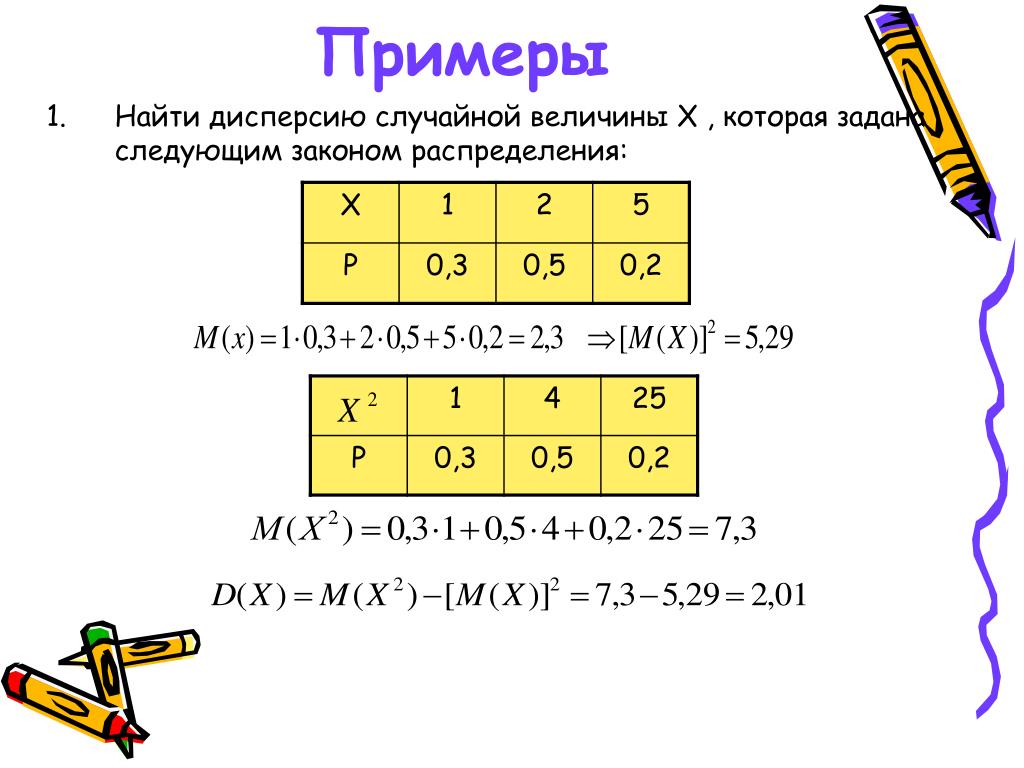 Узнайте, почему стоит математика, с нашими сертифицированными экспертами.

Примеры с использованием формулы дисперсии

Пример 1. Найдите дисперсию следующих данных с помощью формулы дисперсии: 24, 53, 53, 36, 21, 84, 64, 34, 77, 54

Решение:

Численность населения (N) = 10

x i (x i — x̄)           (x i — x̄) 2
24 -26 676
53 3 9
53 3 9
36 -14 196
21 -29 841
84 34 1156
64 14 196
34 -16 256
77 27
}{10} = \frac{4084}{10} \) = 408,4 единицы 2

Ответ:  Дисперсия заданных данных составляет 408,4 единицы 2

Пример 2:  Найдите среднее значение и дисперсию для следующих данных.

Класс 10-20 20-30 30-40 40-50 50-60 60-70 70-80 80-90 90-100
частота (f) 2 3 6 8 5 3 6 1 4

Решение:

Пусть d = (M i  — Середина)/10, для упрощения делится на 10. (ч =10)

Класс ф Середина интервала классов i th (M i )   М и ж   д   d 2     д 2 е   дф
10-20 2 15 30 -4 16 32 -8
20-30 3 25 75 -3 9 27 -9
30-40 6 35 210 -2 4 24 -12
40-50 8 45 360 -1 1 8 -8
50-60 5 55 275 0 0 0 0
60-70 3 65 195 1 1 3 3
70-80 6 75 450 2 4 24 12
80-90 1 85 85 3 9 9 3
90-100 4 95 380 4 16 64 16
  \(\Сигма f = 38\) Середина = 55 \(\Сигма M_i f = 2060 \) 92 \)

= \( (\dfrac{191 — 0,2368}{38}) 100 \) = 502 единицы 2

Ответ: Среднее значение этих данных = 54,21 единицы, а дисперсия этих данных = 502 единицы 2

Пример 3. {2}}\) 

Что лучше использовать: формулу дисперсии или формулу стандартного отклонения?

У каждого из них разные цели. Стандартное стандартное отклонение обычно более полезно для описания изменчивости данных, в то время как дисперсия обычно гораздо полезнее с математической точки зрения. Например, сумма некоррелированных распределений (случайных величин) также имеет дисперсию, которая является суммой дисперсий этих распределений.

Как найти дисперсию с помощью Python

Дисперсия — это мощный статистический показатель, используемый в анализе данных и машинном обучении. Это один из четырех основных показателей изменчивости наряду с диапазоном, межквартильным диапазоном (IQR) и стандартным отклонением. Понимание дисперсии важно, потому что оно дает вам представление о разбросе ваших данных и может использоваться для сравнения различий в группах образцов или выявления важных функций моделирования. Дисперсия также используется в машинном обучении, чтобы понять изменения в производительности модели из-за использования разных выборок обучающих данных.

Что такое дисперсия?

Дисперсия — это статистика, которая измеряет дисперсию. Низкая дисперсия указывает на то, что значения в целом схожи и не сильно отличаются от среднего, в то время как высокая дисперсия указывает на более широкий разброс значений от среднего. Вы можете использовать дисперсию либо для набора выборки, либо для всей совокупности, поскольку при расчете учитываются все точки данных в данном наборе. Хотя расчет немного отличается, когда вы смотрите на выборку по сравнению с генеральной совокупностью, вы можете рассчитать дисперсию как среднее квадратов отличий от среднего.

С помощью Python легко вычислить дисперсию. Прежде чем погрузиться в код Python, я сначала объясню, что такое дисперсия и как ее можно вычислить. К концу этого руководства вы лучше поймете, почему дисперсия является важной статистикой, а также несколько методов ее расчета с помощью Python.

Другие учебные пособия по науке о данныхКак найти выбросы с помощью IQR с использованием Python

 

Что такое дисперсия?

Дисперсия — это статистика, которая измеряет дисперсию. Низкая дисперсия указывает на то, что значения в целом схожи и не сильно отличаются от среднего, в то время как высокая дисперсия указывает на более широкий разброс значений от среднего. Вы можете использовать дисперсию либо для набора выборки, либо для всей совокупности, поскольку при расчете учитываются все точки данных в данном наборе. Хотя расчет немного отличается, когда вы смотрите на выборку по сравнению с генеральной совокупностью, вы можете рассчитать дисперсию как среднее квадратов отличий от среднего.

Поскольку дисперсия представляет собой квадрат значения, ее может быть трудно интерпретировать по сравнению с другими мерами изменчивости, такими как стандартное отклонение. Несмотря на это, анализ дисперсии может быть полезен; это поможет вам решить, какие статистические тесты использовать с вашими данными. В зависимости от статистических тестов неравномерная дисперсия между выборками может привести к искажению или смещению результатов.

Как найти дисперсию?

Расчет дисперсии для набора данных может различаться в зависимости от того, является ли набор полной совокупностью или выборкой совокупности. Формула расчета дисперсии всей совокупности выглядит так: σ² = ∑ (Xᵢ— μ)²/N

Один из популярных статистических тестов, применяющих дисперсию, называется тестом дисперсионного анализа (ANOVA). Тест ANOVA используется для оценки того, существенно ли отличаются какие-либо средние группы друг от друга при анализе категориальной независимой переменной и количественной зависимой переменной. Например, вы хотите проанализировать, влияет ли использование социальных сетей на продолжительность сна. Вы можете разбить использование социальных сетей на разные категории, такие как низкое использование , среднее использование и high используют , затем проводят тест ANOVA, чтобы определить, существуют ли статистические различия между средними группами. Тест может показать, объясняются ли результаты групповыми или индивидуальными различиями.

Еще от встроенных специалистов по данным Расчет квартилей: пошаговое объяснение

 

Как найти дисперсию?

Расчет дисперсии для набора данных может различаться в зависимости от того, является ли набор полной совокупностью или выборкой совокупности.

Формула расчета дисперсии всей совокупности выглядит так:

σ² = ∑ (Xᵢ— μ)² / N

Пояснение к формуле:

  • σ² 90 2 дисперсия 4 σ = Сумма…
  • χᵢ = каждое значение
  • μ = Среднее значение
  • ν = количество значений. расчет шаг за шагом.

    Пример диапазона чисел: 8, 6, 12, 3, 13, 9

    Найдите среднее значение совокупности ( μ ):

     (8+ 6+12+ 3+ 13+ 9) / 6
= 51/6
= 8,5

    Рассчитать отклонения от среднего путем вычитания среднего из каждого значения.

     8–8,5 = -0,5
6–8,5 = -2,5
12–8,5 = 3,5
3–8,5 = -5,5
13–8,5 = 4,5
9–8,5 = 0,5

    Возведите каждое отклонение в квадрат, чтобы получить положительное число.

     -0,5² = 0,25
-2,5² = 6,25
3,5² = 12,25
-5,5² = 30,25
4,5² = 20,25
0,5² = 0,25

    Суммируйте квадраты значений.

     0,25 + 6,25 + 12,25 + 30,25 + 20,25 + 0,25
= 69,5

    Разделите сумму квадратов на N или n-1 .

    Поскольку мы работаем со всем населением, разделим на N . Если бы мы работали с выборкой населения, мы бы разделили на n-1 .

    69,5/6 = 11,583

    Вот и все! Дисперсия нашего населения составляет 11,583 .

     

    Зачем использовать n-1 при расчете выборочной дисперсии?

    Применение n-1 к формуле называется поправкой Бесселя, названной в честь Фридриха Бесселя. При использовании выборок нам необходимо рассчитать предполагаемую дисперсию для совокупности. Если бы мы использовали N вместо n-1 для выборки, оценка была бы смещенной, потенциально недооценивая дисперсию генеральной совокупности. Использование n-1 сделает оценку дисперсии больше, переоценивая изменчивость в выборках, тем самым уменьшая систематические ошибки.

    Давайте пересчитаем дисперсию, предполагая, что значения взяты из выборки:

     69,5 / (6–1)
= 69,5/5
= 13,9

    Как видим, дисперсия больше!

    Еще от ЭрикаКак практиковать Word2Vec для НЛП с помощью Python

     

    Вычисление дисперсии с помощью Python скучный. К счастью, Python может легко обрабатывать очень большие данные. Мы рассмотрим два метода с использованием Python: 

    • Напишите нашу собственную функцию расчета дисперсии
    • Используйте встроенную функцию Pandas
     

    Написание функции дисперсии

    Когда мы начинаем писать функцию для расчета дисперсии, вспомните шаги, которые мы предприняли расчет вручную. Мы хотим, чтобы функция принимала два параметра:

    • население : массив чисел
    • is_sample : логическое значение для изменения расчета в зависимости от того, работаем ли мы с выборкой или с популяцией

    Начните с определения функции, которая принимает два параметра.

     def calculate_variance(population, is_sample = False):

    Затем добавьте логику для вычисления среднего значения совокупности.

     #рассчитать среднее
   среднее значение = (сумма (население) / len (население))

    После вычисления среднего значения найдите отличия от среднего для каждого значения. Это можно сделать в одной строке, используя генератор списка.

     # вычислить разницу
   diff = [(v - среднее значение) для v в популяции]

    Затем возведите в квадрат разности и просуммируйте их.

     #Квадратные разности и сумма
   sqr_diff = [d**2 для d в diff]
   sum_sqr_diff = сумма (sqr_diff)

    Наконец, рассчитайте дисперсию. Используя оператор If/Else , мы можем использовать параметр is_sample . Если is_sample истинно, вычислите дисперсию, используя ( n-1 ). Если оно ложно (по умолчанию), используйте N :

     #рассчитать дисперсию
   если is_sample == Истина:
       дисперсия = sum_sqr_diff/(len(население) - 1)
   еще:
       дисперсия = sum_sqr_diff/(len(население))
  
   возвратная дисперсия
Полная функция calculate_variance будет выглядеть так:
def calculate_variance (население, is_sample = False):
   #рассчитать среднее
   среднее значение = (сумма (население) / len (население))
  
   #рассчитать разницу
   diff = [(v - среднее значение) для v в популяции]
  
   #Квадратные разности и сумма
   sqr_diff = [d**2 для d в diff]
   sum_sqr_diff = сумма (sqr_diff)
  
   #рассчитать дисперсию
   если is_sample == Истина:
       дисперсия = sum_sqr_diff/(len(население) - 1)
   еще:
       дисперсия = sum_sqr_diff/(len(население))
  
   возвратная дисперсия

    Мы можем проверить вычисление, используя диапазон чисел, которые мы обработали вручную:

    Тестирование функции calculate_variance Как найти дисперсию

     

    дисперсии менее чем в 10 строках кода, есть еще более простой способ найти дисперсию. Вы можете сделать это в одной строке кода, используя Pandas. Давайте загрузим некоторые данные и рассмотрим реальный пример поиска дисперсии.

     

    Загрузка данных примера

    В примере Pandas используется набор данных BMW Price Challenge от Kaggle, который можно загрузить бесплатно. Начните с импорта библиотеки Pandas, а затем прочтите CSV-файл во фрейм данных Pandas:

     #import dependencies
импортировать панд как pd
# прочитать CSV-файл в фреймворк данных
bmw_df = bmw_df = pd.read_csv("bmw_pricing_challenge.csv")

    Мы можем подсчитать количество строк в наборе данных и отобразить первые пять строк, чтобы убедиться, что все загружено правильно:

     #распечатать количество строк
печать (длина (bmw_df))
#4843 строки
#проверить, что кадр данных соответствует ожиданиям
bmw_df. head()
    Отображение первых строк с помощью bmw_df.head()

     

    Поиск дисперсии для данных BMW

    Поскольку набор данных BMW состоит из 4843 строк, вычисление этого вручную было бы… неинтересным. Вместо этого мы можем просто вставить столбец из фрейма данных в нашу функцию calculate_variance и вернуть дисперсию. Найдем дисперсию для числовых столбцов пробег , двигатель мощность и цена .

    Дисперсия для числовых столбцов во фрейме данных BMW

     

    Использование функции Pandas var()

    На случай, если мы забудем расчет дисперсии и не сможем написать собственную функцию, в Pandas есть встроенная функция для расчета дисперсии с именем вар() . По умолчанию предполагается выборочная совокупность и в расчетах используется n-1 ; однако вы можете скорректировать расчет, передав ddof=0 аргумент.

     bmw_df[['mileage', 'engine_power', 'price']].var()
    Pandas var() function

    Как мы видим, функция Var() соответствует значениям, полученным нашим calculate_variance  функция , и это всего одна строка кода. Просматривая результаты, мы видим, что пробег имеет высокую дисперсию, что означает, что значения имеют тенденцию сильно отличаться от среднего значения. Это имеет смысл, потому что многие факторы влияют на расстояние, которое нужно проехать человеку. Для сравнения, engine_power имеет низкую дисперсию, что указывает на то, что значения не сильно отличаются от среднего.

    Что вы хотите узнать дальше? Как использовать Float в Python (с примером кода!)

     

    Выводы

    Понимание дисперсии может быть важной частью анализа данных и машинного обучения, потому что вы можете ее использовать оценить групповые различия.

    No related posts.

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *

    © 2015 - 2019 Муниципальное казённое общеобразовательное учреждение «Таловская средняя школа»

    Карта сайта