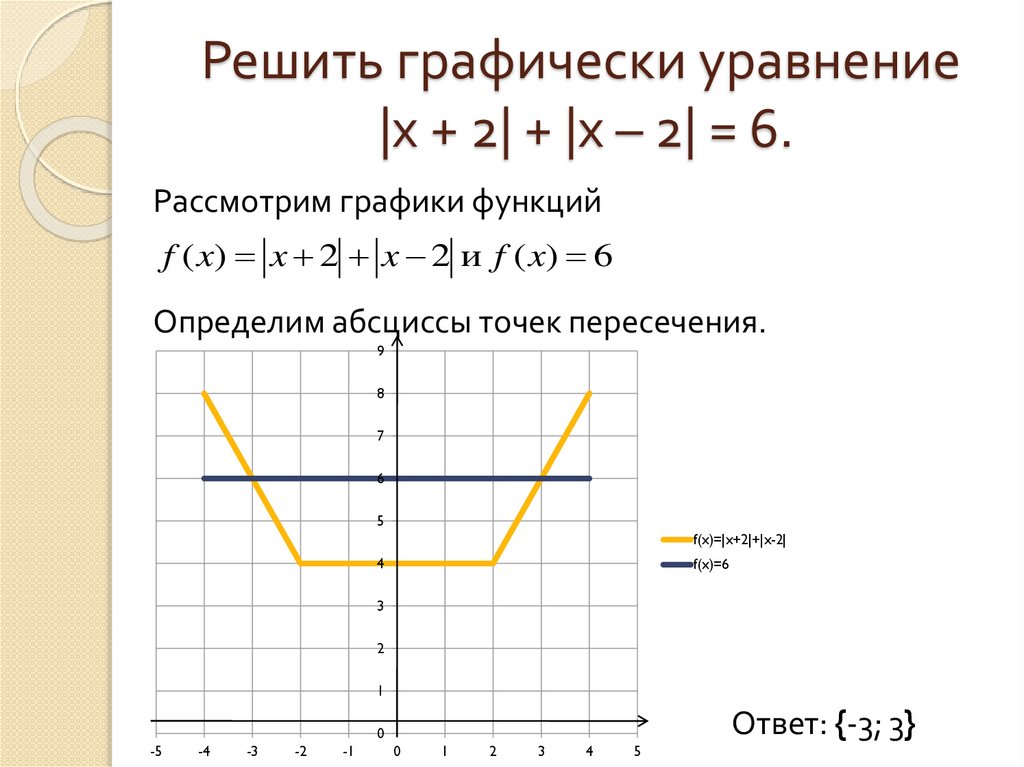
Задание №22 ОГЭ по математике
функции и их свойства, графики функций
Первичный бал: 2 Сложность (от 1 до 3): 3 Среднее время выполнения: 15 мин.
В данном задании анализируем функции и их графики.
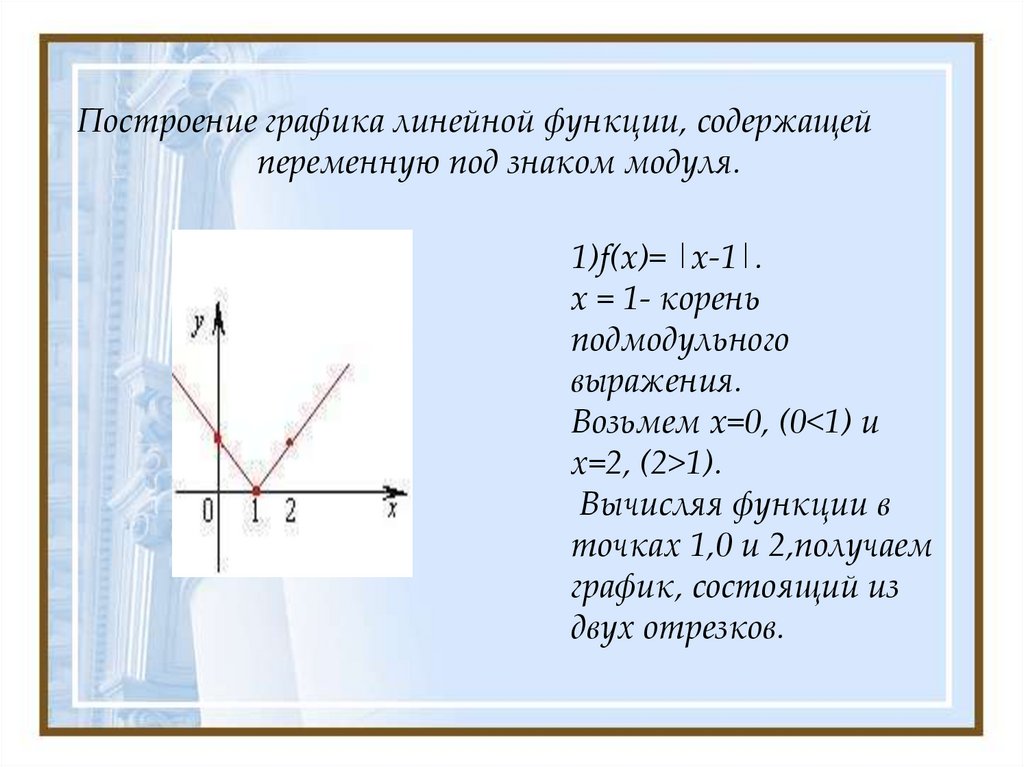
Задание 22OM21R Постройте график функции:у=х2 — |2x +1|
Определите, при каких значениях m прямая у= m имеет с графиком ровно три общие точки.Раскроем модуль:
{.у=х2−2х−1, при х≥−12….у=х2+2х+1, при х<−12…)
Для построения графика найдем вершины каждой параболы:
у=х2 – 2х – 1
х0=−b2a..=22..=1
у0=12 -2-1=-2
Итак, вершина первой параболы (1; -2)
Возьмем дополнительные точки, где х ≥−12..
| х | -0,5 | 0 | 2 | 3 |
| у | 0,25 | -1 | -1 | 2 |
у=х2 + 2х + 1
Аналогично найдем вершину второй параболы: х0=-1, у0=0
Вершина второй параболы (-1;0)
Дополнительные точки при х<−0. 5
5
| х | -2 | -0,5 |
| у | 1 | 0,25 |
Изобразим параболы в системе координат:
Теперь нам нужно ответить на вопрос задания: «Определите, при каких значениях m прямая у= m имеет с графиком ровно три общие точки?»
Для этого построим такие прямые (одна желтая, вторая зеленая), откуда видно, что первая прямая совпадает с осью х, т.е. у=0; вторая имеет с графиком три общие точки при у=0,25.
Ответ: при m равных 0; 0,25
Ответ: см. решениеpазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM2306o Постройте график функциии определите, при каких значениях с прямая y = c имеет с графиком ровно одну общую точку. В ответ запишите наибольшее число.
Разложим числитель дроби на множители: При x ≠2 и x ≠ 3 функция принимает вид: её график — парабола, из которой выколоты точки ( -2; -4) и ( 3; 6).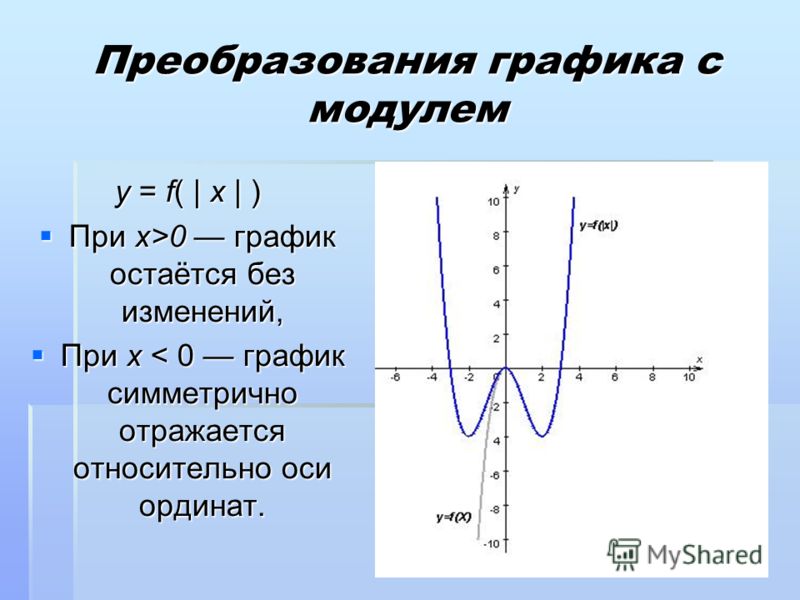
Прямая y = c имеет с графиком ровно одну общую точку либо тогда, когда проходит через вершину параболы, либо тогда, когда пересекает параболу в двух точках, одна из которых — выколотая. Вершина параболы имеет координаты ( -0,5; -6,25 ). Поэтому c = – 6,25, c = – 4 или c = 6.
Ответ: 6pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM2305o Постройте график функцииОпределите, при каких значениях k прямая y = kx не имеет с графиком общих точек. В ответ запишите наибольшее число.
Алгоритм решения:
- Раскрываем модуль и преобразовываем формул функции.
- Определяем вид функции на каждом промежутке и находим дополнительные точки графика.
- Строим график.
- Определяем искомые значения k.
- Записываем ответ.
Решение:
1. Раскрываем модуль и для каждого случая. Если x < 0, то определена при и представляет собой часть гиперболы. Дополнительные точки для построения:
Дополнительные точки для построения:| x | -5 | -4 | -3 | -2 | -1 |
| y | -1/5 | -1/4 | -1/3 | -1/2 | -1 |
| x | 1 | 2 | 3 | 4 | 5 |
| y | -1 | -1/2 | -1/3 | -1/4 | -1/5 |
Прямая y=kx не имеет общих точек с графиком данной функции, когда k=-16; 0 и 16. Тогда прямые проходят черед точки с абсциссами ¼ и – ¼ . На рисунке эти прямые изображены красным. При k = 0 прямая совпадает с осью абсцисс. Она тоже не имеет общих точек с графиком.
Ответ: 16pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM2304o Постройте график функцииОпределите, при каких значениях k прямая у = kx не имеет с графиком общих точек.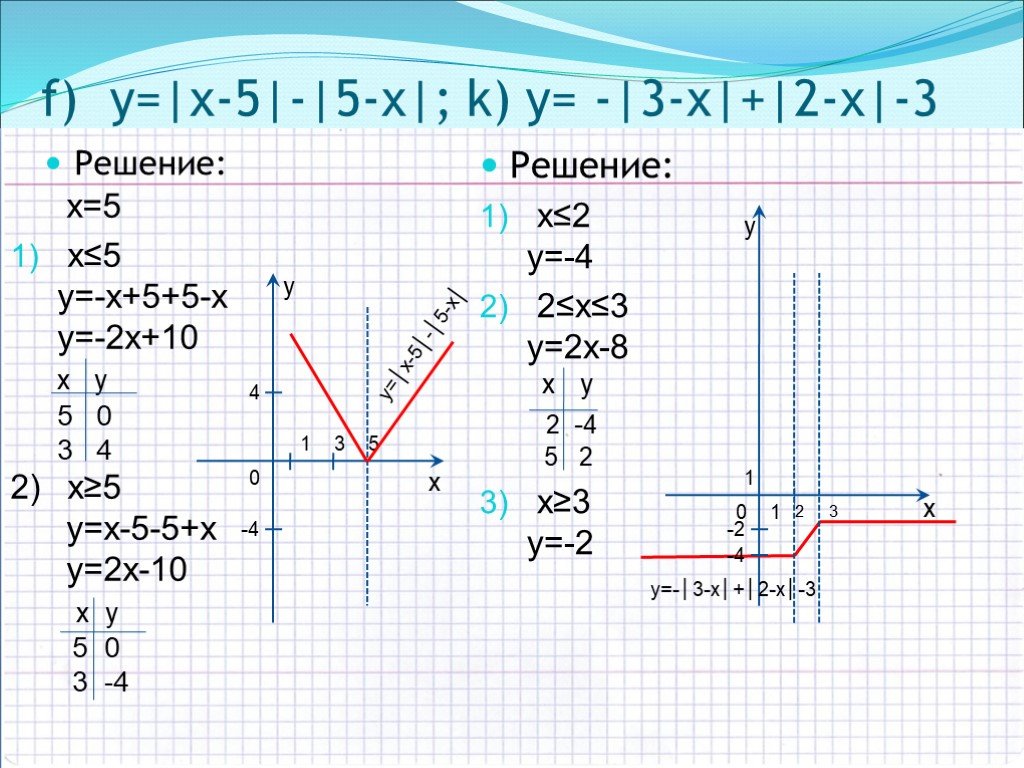 В ответ запишите наибольшее число.
В ответ запишите наибольшее число.
Алгоритм решения:
- Раскрываем модуль и преобразовываем формул функции.
- Определяем вид функции на каждом промежутке и находим дополнительные точки графика.
- Строим график.
- Определяем искомые значения k.
- Записываем ответ.
Решение:
1. Если x < 0, то Дробь, получившаяся в результате, определена . График представляет собой часть гиперболы. Точки для построения графика:| x | -5 | -4 | -3 | -2 |
| y | -1/5 | -1/4 | -1/3 | -1/2 |
| x | 2 | 3 | 4 | 5 |
| y | -1/2 | -1/3 | -1/4 | -1/5 |
4.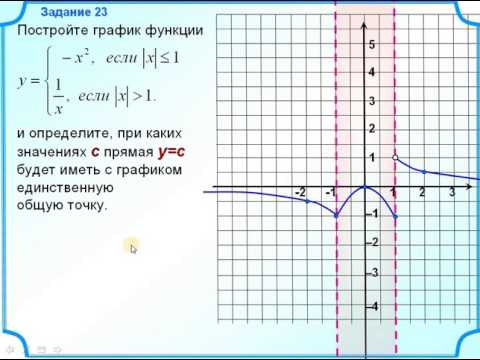 Прямая y=kx не имеет общих точек с графиком, при k=-1; 0 и 1, потому как тогда прямая проходит через точки, не входящие в область определения заданной функции.
Прямая y=kx не имеет общих точек с графиком, при k=-1; 0 и 1, потому как тогда прямая проходит через точки, не входящие в область определения заданной функции.
На графике прямые для k=-1; 1 изображены красным. При k = 0 прямая совпадает с осью абсцисс и тоже не имеет общих точек с графиком функции.
Ответ: 1pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM2303o Постройте график функцииОпределите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки. В ответ запишите наибольшее число.
Алгоритм решения:
- Преобразуем формулу, которая задает функцию.
- Определяем вид и характерные точки функции на каждом промежутке.
- Изображаем график на координатной плоскости.
- Делаем вывод относительно количества точек пересечения.
- Записываем ответ.
Решение:
1. Преобразуем формулу функции в зависимости от знака переменной 2.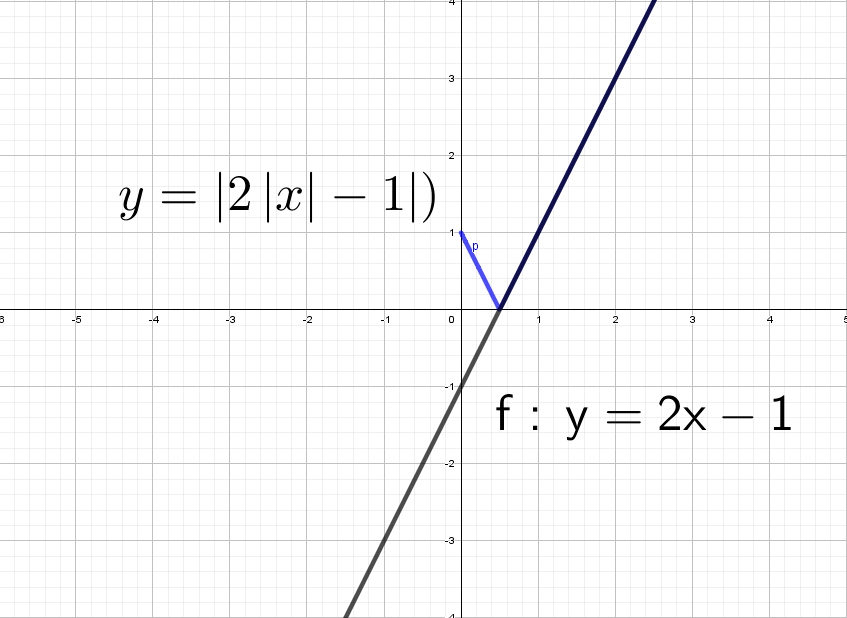 Определяем вид функции и находим дополнительные точки для каждого участка графика.
График при – часть парабола, ветви которой направлены вниз. Потому как коэффициент
Определяем вид функции и находим дополнительные точки для каждого участка графика.
График при – часть парабола, ветви которой направлены вниз. Потому как коэффициент Из построения видно, что прямая y=m имеет только 2 общие точки с графиком функции в случаях, когда m=-4 или m=9. На рисунке прямые изображены красным цветом.
Ответ: 9pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM2302o Постройте график функцииОпределите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки. В ответ запишите наибольшее из чисел.
Алгоритм решения:
- Преобразуем формулу, которая задает функцию.

- Определяем вид и характерные точки функции на каждом промежутке.
- Изображаем график на координатной плоскости.
- Делаем вывод относительно количества точек пересечения.
- Записываем ответ.
Решение:
1. Преобразуем формулу в зависимости от знака переменной х:2. Графиком функции является парабола, ветви которой направлены вниз.
Вершина ее находится в точке :
Найдем нули функции: График проходит через начало координат и точку (0;4).
Графиком второй функции является парабола, ветви которой направлены вверх.
Вершина ее находится в точке:
Определим нули параболы
3. Изображаем график на координатной плоскости:
Из изображения видно, что прямая y= m имеет с графиком только две общих точки, когда m=-9 или m=4. На графике прямая изображена красной линией при каждом значении m.
Ответ:pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM2301o Постройте график функцииОпределите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.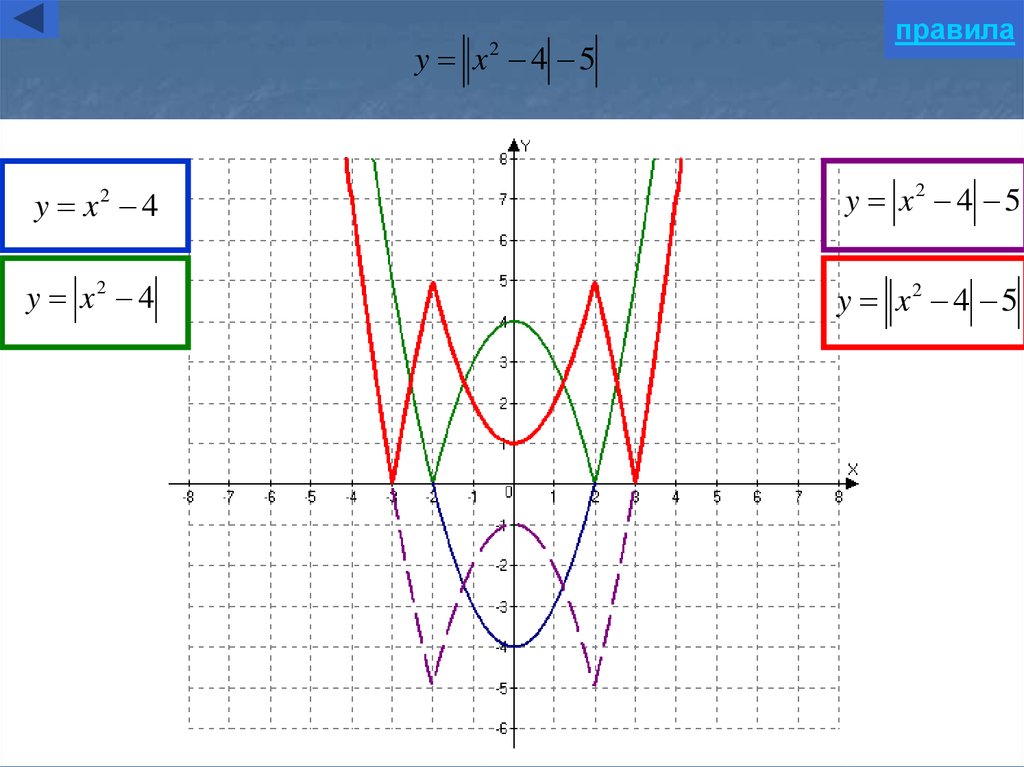 В ответ запишите наибольшее число.
В ответ запишите наибольшее число.
Алгоритм решения:
- Преобразуем формулу, которая задает функцию.
- Определяем вид и характерные точки функции на каждом промежутке.
- Изображаем график на координатной плоскости.
- Делаем вывод относительно количества точек пересечения.
- Записываем ответ.
Решение:
1. Преобразуем функцию в зависимости от знака переменной х.
Если .
Если
2. График функции заданных значениях х – часть параболы, ветви которой направлены вниз.
Вершина расположена в точке с координатами:
Найдем нули функции: График проходит через начало координат и точку (-2;-7).
Графиком второй функции является парабола, ветви которой направлены вверх.
Вершина ее находится в точке:
Определим нули параболы
3. Изображаем график функции на координатной плоскости:
4. Из построения легко видно, что прямая y = m имеет с графиком ровно две точки, когда проходит через вершину одной из парабол, образующих график данной функции.
Значит, две общие точки функция и прямая имеют при m = -2,25 или m = 12,25.
Ответ: 12,25pазбирался: Даниил Романович | обсудить разбор | оценить
👀 20.1k |
Решение №2157 На рисунке изображён график функции вида f(x)=ax + |bx + c| + d, где числа a, b, c и d — целые.
На рисунке изображён график функции вида f(x) = ax + |bx + c| + d, где числа a, b, c и d – целые. Найдите корень уравнения ax + d = 0.
Источники: Александр Иванов, решуегэ.рф.
Решение:
На графике представлена кусочно-линейная функция, раскроем модуль по определению:
f(x) = ax + |bx + c| + d
Уравнение прямой имеет вид:
y = kx + l
Найдём вид каждой из прямых:
Найдём k и l левой прямой:
k – тангенс угла (α) наклона прямой, по отношению к оси х.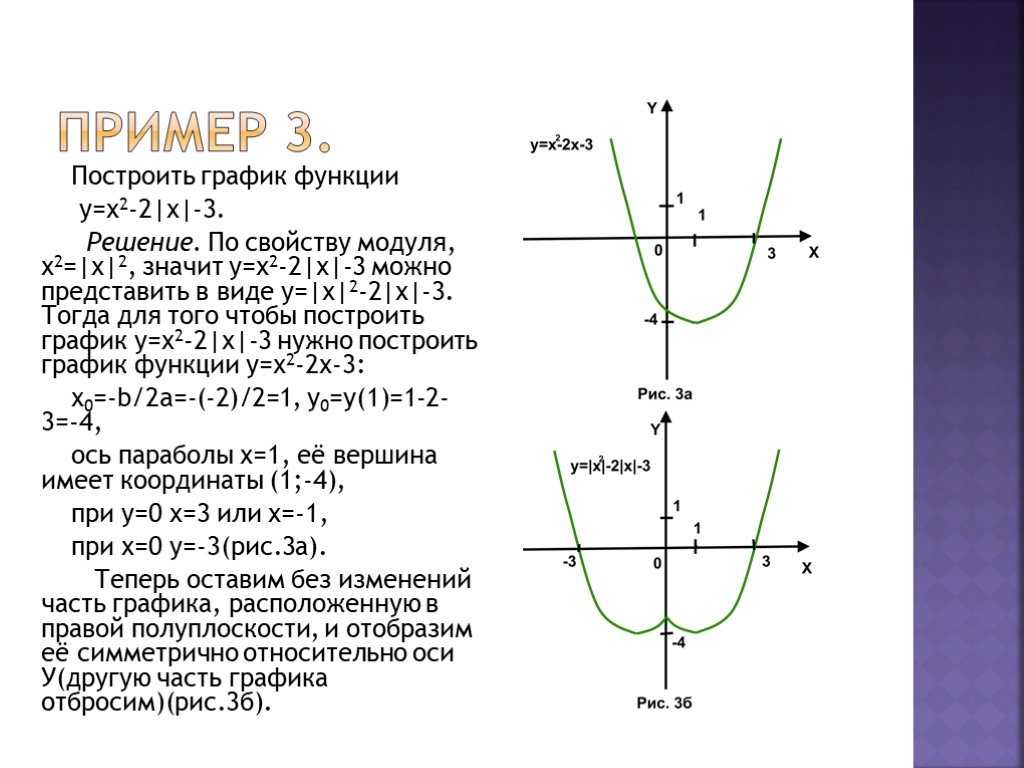 Тангенс – это отношение противолежащего катета, к прилежащему катету. Тангенсы смежных углов равны по модулю, но противоположны по знаку.
Тангенс – это отношение противолежащего катета, к прилежащему катету. Тангенсы смежных углов равны по модулю, но противоположны по знаку.
Найдём тангенс угла β, смежного к искомому углу:
l – сдвиг прямой по оси у, по графику видим, прямая сдвинута от 0 на 3.
l = 3
Уравнение прямой слева имеет вид:
y = –1·x + 3
Найдём k и l прямой справа:
Подставим координаты точки (3;4), принадлежащие прямой и k = 3, найдём l:
4 = 3·3 + b
4 – 9 = b
l = –5
Уравнение прямой справа имеет вид:
y = 3x – 5
Соотнеся коэффициенты k (а ± b) и l (±c + d) уравнений после раскрытия модуля и коэффициенты k и l уравнения прямых получаем систему уравнений (cоотнести можно в любом порядке, нужные нам коэффициенты a и d находятся вне модуля (f(x)=ax+|bx+c|+d), на их значения это не повлияет):
Сложим 1-е со 3-м уравнением и 2-е с 4-м уравнением:
Найдём корень искомого уравнения:
ax + d = 0
1·x – 1 = 0
х = 1
Ответ: 1.
Графики и комбинаторика — MAST9950 — Модули
Обзор
Комбинаторика — это область математики, изучающая дискретные, обычно конечные структуры, такие как графы. Он не только играет важную роль во многих областях математики, но и имеет практическое применение. В частности, он лежит в основе различных вычислительных процессов, используемых в цифровых технологиях и при проектировании вычислительного оборудования.
Кроме того, для учащихся 7 уровня модуль будет охватывать сложные темы комбинаторики, такие как: задачи экстремальной теории множеств; перечислительные задачи; принцип включения и исключения; теория Рамсея; вычислительная сложность; проблема P против NP.
Детали
Время контакта
Всего часов контакта: 42
Часы индивидуального обучения: 108
Всего учебных часов: 150
Метод оценивания
80% Экзамен, 20% Курсовая работа
Ориентировочное чтение
P. Cameron, Combinatorics, Topics, Techniques Algorithms, Cambridge Press, (1994)
Ловаш Л., Пеликан Дж., Вестергомби К. Дискретная математика: элементарная и не только. Спрингер-Верлаг, (2003).
Д. Б. Уэст, Введение в теорию графов, Прентис Холл, (1996).
Р.Дж. Уилсон, Введение в теорию графов, четвертое издание. Лонгман, Харлоу (1996).
Дж.А. Бонди и U.S.R. Мурти, Теория графов, Текст для выпускников по математике. 244, Springer-Verlag, (2008).
B. Ballobas, Modern Graph Theory, Graduate Text in Math., 184, Springer-Verlag, 1998.
См. список чтения в библиотеке для этого модуля (Кентербери)
Результаты обучения
Предполагаемые результаты обучения по конкретному предмету.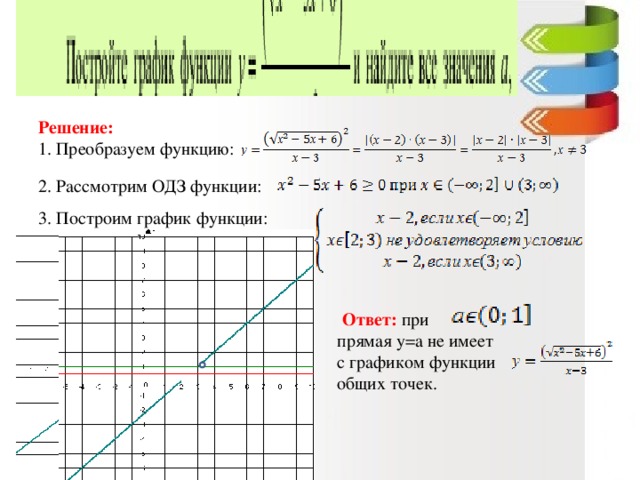 Успешно завершив модуль 7 уровня, студенты смогут:
Успешно завершив модуль 7 уровня, студенты смогут:
1 продемонстрировать систематическое понимание графов и комбинаторики;
2 продемонстрировать способность решать сложные задачи, используя очень хороший уровень навыков расчета и обработки материала в следующих областях: деревья, кратчайшие
задачи о путях, прогулки по графам, раскраски и вложения графов, потоки и паросочетания, матрицы и графы;
3 применять ряд концепций и принципов теории графов и комбинаторики в нечетко определенных контекстах, проявляя здравый смысл при выборе и применении инструментов
и техники.
Предполагаемые общие результаты обучения. Успешно завершив модуль 7 уровня, студенты смогут:
1 работать грамотно и самостоятельно, осознавать свои сильные стороны и понимать, когда нужна помощь;
2 продемонстрировать высокий уровень способности разрабатывать и оценивать логические аргументы;
3 уверенно сообщать аргументы с эффективной и точной передачей выводов;
4 управлять своим временем и использовать свои организаторские способности для планирования и внедрения эффективных и результативных режимов работы;
5 решать задачи, связанные с качественной и количественной информацией;
6 эффективно использовать навыки информационных технологий, таких как онлайн-ресурсы (Moodle), интернет-коммуникации;
7 эффективно передавать технические материалы;
8 демонстрируют повышенный уровень навыков счета и вычислений;
9 демонстрируют приобретение учебных навыков, необходимых для непрерывного профессионального развития.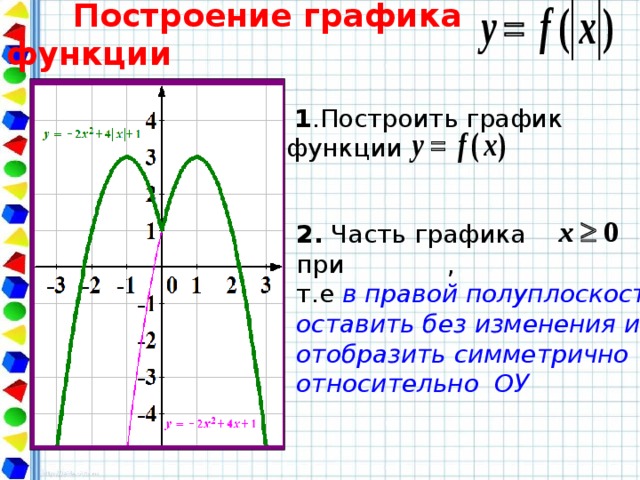
Кентский университет прилагает все усилия, чтобы обеспечить точность информации о модуле для соответствующей академической сессии и предоставить образовательные услуги, как описано. Однако курсы, услуги и другие вопросы могут быть изменены. Пожалуйста, прочитайте наш полный отказ от ответственности.
Модуль скорости и графиков.
Модуль скорости и графиков.ВВЕДЕНИЕ:
Понятие скорости важно во многих областях математики и наука. Эта концепция также дает возможность изучить и использовать некоторые из основных навыков и идей алгебры. Во многих случаях учащиеся сталкиваются с задачами «скорость-время». которые, как правило, решаются механическими процедурами, а не изучением реальные ситуации, в которых процедуры, необходимые для решения задача должна разрабатываться заново для каждой ситуации. это только в упражнения устанавливаются в конце урока в учебнике, где все из проблем имеют одинаковую настройку.
Этот модуль посвящен скорости.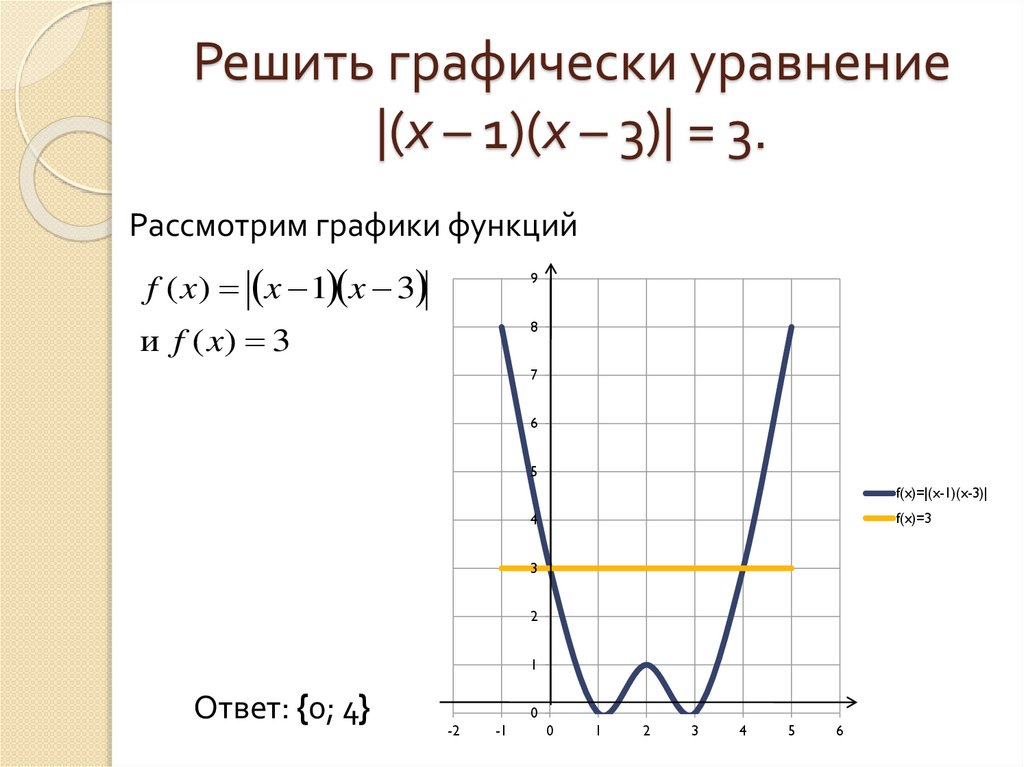 Студенты будут
исследовать скорость объекта, а также думать о
скорости во многих ситуациях. Цель – получить хороший
качественное понимание взаимосвязи между
положение объекта в данный момент времени и его скорость.
студенты также узнают, как измерить среднюю скорость и
они исследуют, как получить более точные измерения
скорость объекта. Акцент будет сделан на построении графиков для
показать скорость в зависимости от времени, с формой графика
больше интереса, чем фактические цифры на данный момент. Этот урок был
первоначально разработан для класса алгебры восьмого класса.
у учеников в классе был очень сильный курс предварительной алгебры, который
включал многие из основных навыков манипулирования символами
и написание выражений. Они не потратили много времени
графические функции.
Студенты будут
исследовать скорость объекта, а также думать о
скорости во многих ситуациях. Цель – получить хороший
качественное понимание взаимосвязи между
положение объекта в данный момент времени и его скорость.
студенты также узнают, как измерить среднюю скорость и
они исследуют, как получить более точные измерения
скорость объекта. Акцент будет сделан на построении графиков для
показать скорость в зависимости от времени, с формой графика
больше интереса, чем фактические цифры на данный момент. Этот урок был
первоначально разработан для класса алгебры восьмого класса.
у учеников в классе был очень сильный курс предварительной алгебры, который
включал многие из основных навыков манипулирования символами
и написание выражений. Они не потратили много времени
графические функции.
ПРЕДПОСЫЛКИ:
Минимальные предпосылки — это базовое понимание
система координат (оси, зависимые и независимые переменные,
нахождение и построение точек) и хорошие арифметические навыки —
особенно дробь и десятичная арифметика. Знакомство с
графические калькуляторы или графические утилиты были бы полезны для
расширения этих видов деятельности, но этот модуль не предполагает
доступ к этим инструментам. Этот модуль развивает некоторые идеи о
единиц измерения и интерпретации графиков довольно быстро.
Знакомство с
графические калькуляторы или графические утилиты были бы полезны для
расширения этих видов деятельности, но этот модуль не предполагает
доступ к этим инструментам. Этот модуль развивает некоторые идеи о
единиц измерения и интерпретации графиков довольно быстро.
Мотивацией для остальной части этого урока будет видео показывающее движение цилиндра, протаскиваемого через резервуар с вода. Это видео было записано в инженерной лаборатории в г. Университет штата Вашингтон. Лазерный световой лист используется для освещают один слой воды, а отражающие частицы равномерно распределяется по воде. Отражение лазера световой лист позволяет изучать движение жидкости за цилиндром. Мы будем использовать это видео для расследования скорость цилиндра.
Основное движение состоит из постоянного ускорения в течение короткого
время, за которым следует период с постоянной скоростью (т. е. нулевой
ускорение), и, наконец, происходит торможение до нуля.
скорость. Фаза замедления прямо противоположна
фаза разгона.
Фаза замедления прямо противоположна
фаза разгона.
Основная проблема, которую мы будем исследовать, состоит в том, как получить график скорость против времени.
ПРОЦЕДУРА:
- Спросите класс, что означает слово «скорость».
Попросите дать столько ответов, сколько сможет собрать класс — примите
предложения без замечаний, либо внести положительный,
прием комментариев по каждому предложению.
Вебстерс Словарь New World Dictionary определяет скорость следующим образом: 1. быстрота или быстрота движения или действия; скорость 2. скорость изменения положения по отношению ко времени; курс движение в определенном направлении во времени.
Так как это будет первое исследование скорости для многих студентов формальные или строгие определения не являются необходимый. В этот момент вам не нужно беспокоиться о представления о том, как измерять скорость или в каких единицах она должны быть измерены.
 В частности, понятие скорости
как вектор с величиной и направлением не
нужный. В начале нас интересует просто
скорость. Хорошее определение в обсуждении с классом
может быть «скорость — это мера того, насколько быстро
что-то движется.»
В частности, понятие скорости
как вектор с величиной и направлением не
нужный. В начале нас интересует просто
скорость. Хорошее определение в обсуждении с классом
может быть «скорость — это мера того, насколько быстро
что-то движется.»После того, как класс достигает приемлемого определения или скорость, спросите, сделает ли «отрицательная скорость» любое чувство. Даже при наивном определении скорости учащиеся должны уметь воспринимать отрицательную скорость как «скорость движения назад».
- Скажите классу, что вы что-то измерили и обнаружили, что это
отмерил «сорок два». Пауза. Спросите класс, если
что-то кажется неправильным в том, что вы только что сказали. Класс
следует указать, что вы не сказали, какие единицы измерения, т.е.
«сорок два что такое ?» Возможно, у вас есть
измерил вес вашей собаки как 42 фунта, или ваш
рост ребенка должен быть 42 дюйма.
 Спросите класс, сколько
вещи, которые могли бы быть, и какое измерение, и
какие единицы.
Спросите класс, сколько
вещи, которые могли бы быть, и какое измерение, и
какие единицы.Если класс не происходит по скорости в качестве измерения предположите, что вы, возможно, имели в виду скорость в какой-то момент по дороге в школу составляла 42 мили в секунду. час. Спросите, кажется ли это разумным: эта скорость могла бы измеряться в милях в час. Спросите, могут ли они придумать другие единицы измерения скорости, например: дюймы в секунду, футы в минуту, мили в сутки, сантиметры в секунду. Предложите классу придумать как можно больше.
Изобретение единиц скорости должно привести к открытие, что все единицы включают единицу длины в единицу времени. При необходимости сделайте это явным для ученики. Это может быть добавлено к определению класса скорость.
- Имея под рукой определение скорости класса, спросите
класс, чтобы предположить, кто может быть заинтересован в скорости.
 В каких профессиях люди будут заинтересованы в скорости, и
скорость когда-либо играет роль в их повседневной жизни.
Ответы и комментарии могут сильно различаться. Не беспокойся
с нахождением какого-либо конкретного набора ответов; осознание
цель с этим вопросом.
В каких профессиях люди будут заинтересованы в скорости, и
скорость когда-либо играет роль в их повседневной жизни.
Ответы и комментарии могут сильно различаться. Не беспокойся
с нахождением какого-либо конкретного набора ответов; осознание
цель с этим вопросом. - Покажите видео, время от времени останавливаясь, чтобы описать
ситуации, включая проводимые исследования. В этом
исследования, необходимо знать скорость
цилиндр. Спросите учащихся, как они могут определить
скорость цилиндра за один из его ходов. Дайте
подсказки по мере необходимости, чтобы помочь им придумать некоторые идеи или
идеи. В этот момент средняя скорость равна
иметь самый интуитивный смысл. Общее расстояние поездки
деленное на время дает среднюю скорость. Проверьте, чтобы
посмотреть, есть ли у студентов какие-либо мысли относительно того, почему это
можно назвать «средней скоростью».
 Быть уверенным
они правильно рассчитали среднюю скорость для одного
путешествие.
Быть уверенным
они правильно рассчитали среднюю скорость для одного
путешествие. - Спросить, полностью ли вычислена средняя скорость описывает скорость цилиндра для этой поездки. В другими словами, двигался ли цилиндр с такой скоростью за всю поездку? Это очевидно в большинстве ситуаций что цилиндр ускоряется и замедляется. Таким образом средняя скорость не говорит всего о скорости. Обсудите это в контексте вождения автомобиля: если поездка от, скажем, Стивенсона до реки Худ, на расстоянии примерно 30 миль, занимает 32 минуты, это значит скорость во все времена была 56,25 миль в час? Нет. Как с цилиндром, скорость изменяется во времени.
- Сообщите учащимся, что для целей исследования
с участием цилиндра, инженеры должны знать
точную скорость цилиндра в любой момент времени.
средней скорости просто не хватает для их работы. Просить
если у кого-нибудь есть идеи, как дать лучшее представление о
скорость цилиндра.

Это намеренно открытый вопрос — не только для студентов, но и также для учителя. Одна из возможностей для улучшения картина скорости будет определять среднюю скорости за меньшие промежутки времени, например, средняя скорость за одну половину пути или один четвертая часть пути. Все это можно определить из видео. Когда учащиеся сравнивают их со своим первым средняя скорость, они могут продолжать делать это с меньшими интервалами времени, чтобы дать достаточно точную описание скорости. Если это не выходит из свою работу, предлагайте ее, но не форсируйте ее.
Пока ученики бьются над вопросом, как дают очень хорошее представление о том, как изменяется скорость во время движение цилиндра, постановка основных задач для этого расследования может появиться. Когда студенты готово, может быть сформулировано утверждение: «Как может скорость цилиндра можно описать так, чтобы мы знали точную скорость в любой момент во время его путешествия?»
- Оставьте на время вопрос о цилиндре.
 Следующим действием является интерпретация графиков скорости. Настоящее время
следующую картинку ученикам и скажите им, что это
график, показывающий скорость во времени. Попросите их
«расскажи историю», описывающую ситуацию.
Следующим действием является интерпретация графиков скорости. Настоящее время
следующую картинку ученикам и скажите им, что это
график, показывающий скорость во времени. Попросите их
«расскажи историю», описывающую ситуацию.Повторите для следующих графиков.
- Обратный процесс от действия 7. Прочтите следующее
«рассказ» детям и попросить их нарисовать
график, представляющий скорость во времени.
«Я прыгнул в моем Subaru и взлетел так быстро, как я мог. Я сделал от нуля до шестидесяти миль в час за 10 секунд. Затем я увидел государство Патрульная машина и быстро сбросила скорость до 55. Я добрался до Стивенсон и поехал прямо через город со скоростью 25 миль в час. я остановился в магазине на окраине города, чтобы возьми немного Fritos и Mountain Dew.
 »
»«Я гулял с собакой. Мы шли не слишком быстро. Затем моя собака увидела кролика и начала тянуть изо всех сил. он мог, так что мы шли быстрее в течение нескольких минут. Затем Джордж (моя собака) должен был остановиться и «напоить куста». Это заняло много времени. Потом мы пошли дальше исходной скорости, пока мы не приблизились к дому. Мы провели в последний раз перед остановкой дома.»
«В крупных городах почтальоны доставляют почту от двери к двери, останавливаясь для доставки почты, затем переходя к следующий дом»
«Йо-йо».
При обмене картинками для этих историй слова «ускорение» и «торможение» должны быть введены надлежащим образом. Поощряйте использование этих условия там, где это уместно.
- Теперь учащиеся готовы нарисовать график
скорость цилиндра в зависимости от времени. Как и выше, количественная оценка
графики (прикрепление цифр и масштаба) не важны
на данном этапе.
 Попросите их нарисовать график, который будет работать
для «истории» цилиндра. В другом
словами, вы просите их нарисовать зависимость скорости от времени
график для цилиндра. Делитесь и обсуждайте эти фотографии
для достижения общего понимания между
ученики.
Попросите их нарисовать график, который будет работать
для «истории» цилиндра. В другом
словами, вы просите их нарисовать зависимость скорости от времени
график для цилиндра. Делитесь и обсуждайте эти фотографии
для достижения общего понимания между
ученики. - Теперь, когда учащиеся имеют общую форму графика,
они могут начать добавлять числа. На данный момент это
полезно знать, сколько времени цилиндр тратит
ускорение. Сообщите эту информацию учащимся и
спросите их, как они могут использовать эту информацию.
С момента ускорение и торможение равномерны и симметричны, теперь график можно построить достаточно точно. Поскольку скорость, конечно, постоянна между ускорением и замедление, любая средняя скорость, вычисленная в этом временной интервал будет представлять точную скорость цилиндр для этого интервала.
- К этому моменту класс будет готов рассмотреть другие
ситуации.
 Настройка устройства для определения времени приличия
мяч или другой предмет, катящий модель автомобиля или мяч вниз
склоне или любой другой ситуации, в которой скорость
изменения со временем послужили бы отличными расширениями.
Позвольте учащимся рассмотреть основную форму
график перед нанесением чисел. Это будет способствовать росту
интуитивное понимание скорости.
Настройка устройства для определения времени приличия
мяч или другой предмет, катящий модель автомобиля или мяч вниз
склоне или любой другой ситуации, в которой скорость
изменения со временем послужили бы отличными расширениями.
Позвольте учащимся рассмотреть основную форму
график перед нанесением чисел. Это будет способствовать росту
интуитивное понимание скорости.Другие расширения может включать рассмотрение положения в зависимости от времени. Идти через процесс, указанный выше, рисование общих графиков позиции в зависимости от времени для подгонки «истории» или Подгонка рассказа к графику. Нарисуйте и сравните положение графики и графики скоростей. Добавление графиков, показывающих ускорение во времени покажет учащимся все аспекты движения. Взаимосвязь этих трех величин есть важный аспект изучения исчисления и физики. Некоторый качественное понимание этих вопросов будет доступны для студентов из такого рода исследований.


 В частности, понятие скорости
как вектор с величиной и направлением не
нужный. В начале нас интересует просто
скорость. Хорошее определение в обсуждении с классом
может быть «скорость — это мера того, насколько быстро
что-то движется.»
В частности, понятие скорости
как вектор с величиной и направлением не
нужный. В начале нас интересует просто
скорость. Хорошее определение в обсуждении с классом
может быть «скорость — это мера того, насколько быстро
что-то движется.» Спросите класс, сколько
вещи, которые могли бы быть, и какое измерение, и
какие единицы.
Спросите класс, сколько
вещи, которые могли бы быть, и какое измерение, и
какие единицы.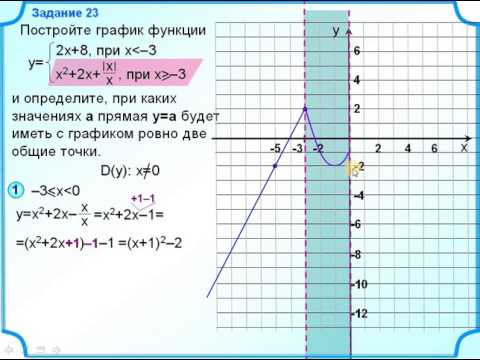 В каких профессиях люди будут заинтересованы в скорости, и
скорость когда-либо играет роль в их повседневной жизни.
Ответы и комментарии могут сильно различаться. Не беспокойся
с нахождением какого-либо конкретного набора ответов; осознание
цель с этим вопросом.
В каких профессиях люди будут заинтересованы в скорости, и
скорость когда-либо играет роль в их повседневной жизни.
Ответы и комментарии могут сильно различаться. Не беспокойся
с нахождением какого-либо конкретного набора ответов; осознание
цель с этим вопросом.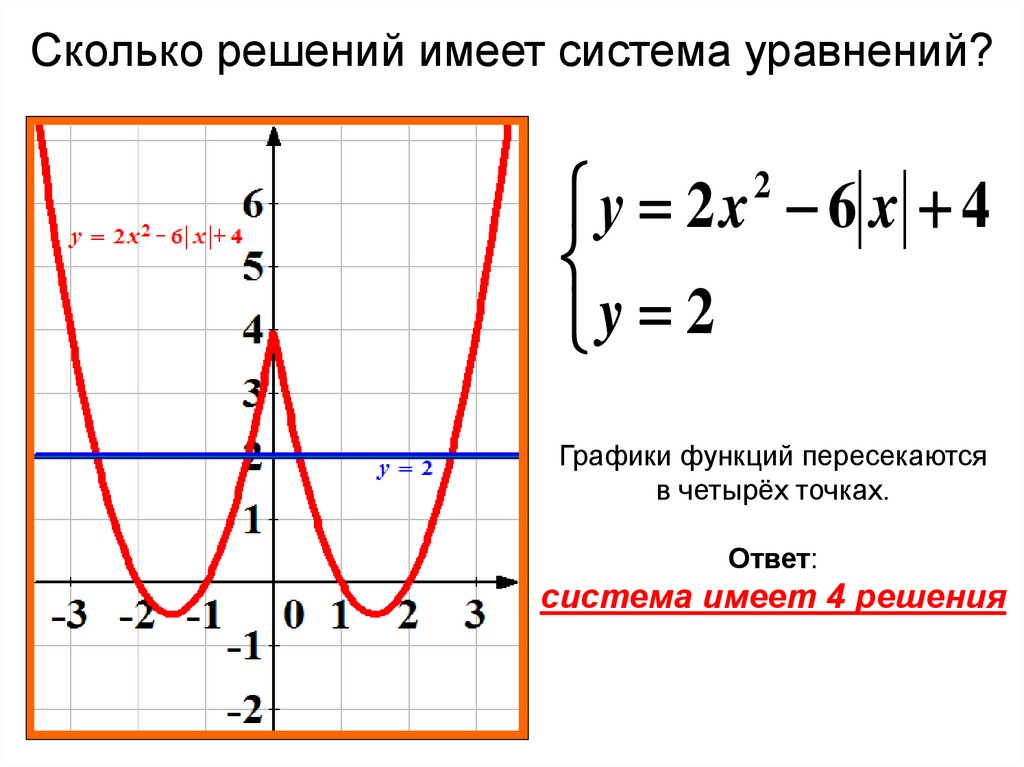 Быть уверенным
они правильно рассчитали среднюю скорость для одного
путешествие.
Быть уверенным
они правильно рассчитали среднюю скорость для одного
путешествие.
 Следующим действием является интерпретация графиков скорости. Настоящее время
следующую картинку ученикам и скажите им, что это
график, показывающий скорость во времени. Попросите их
«расскажи историю», описывающую ситуацию.
Следующим действием является интерпретация графиков скорости. Настоящее время
следующую картинку ученикам и скажите им, что это
график, показывающий скорость во времени. Попросите их
«расскажи историю», описывающую ситуацию. »
» Попросите их нарисовать график, который будет работать
для «истории» цилиндра. В другом
словами, вы просите их нарисовать зависимость скорости от времени
график для цилиндра. Делитесь и обсуждайте эти фотографии
для достижения общего понимания между
ученики.
Попросите их нарисовать график, который будет работать
для «истории» цилиндра. В другом
словами, вы просите их нарисовать зависимость скорости от времени
график для цилиндра. Делитесь и обсуждайте эти фотографии
для достижения общего понимания между
ученики.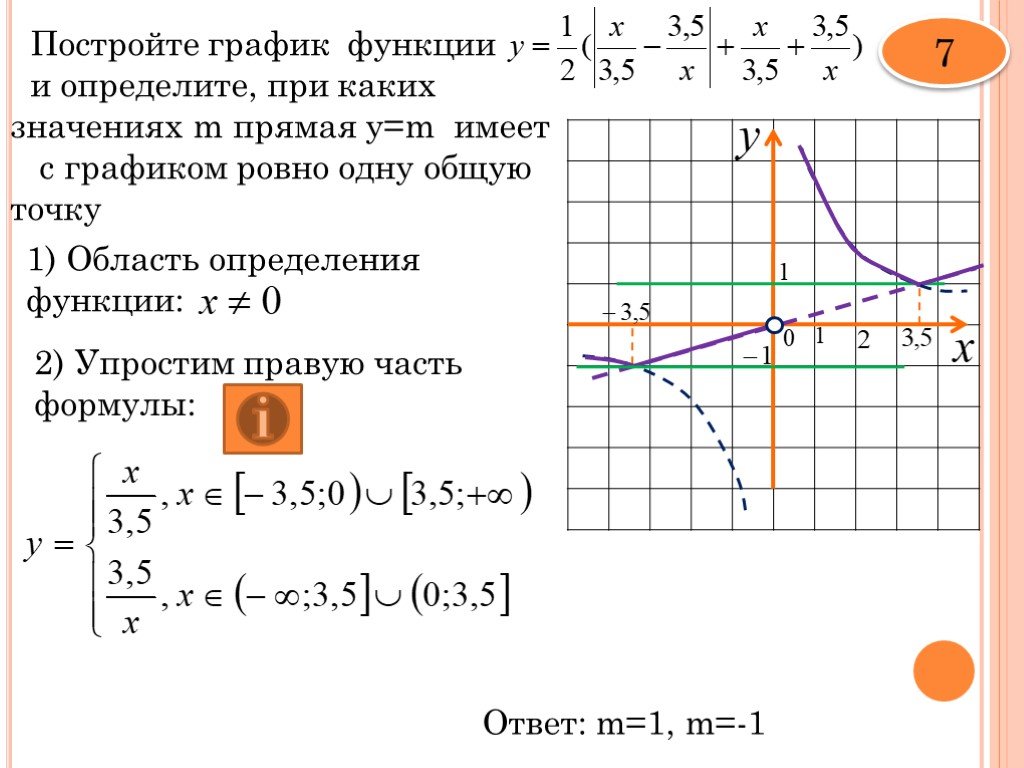 Настройка устройства для определения времени приличия
мяч или другой предмет, катящий модель автомобиля или мяч вниз
склоне или любой другой ситуации, в которой скорость
изменения со временем послужили бы отличными расширениями.
Позвольте учащимся рассмотреть основную форму
график перед нанесением чисел. Это будет способствовать росту
интуитивное понимание скорости.
Настройка устройства для определения времени приличия
мяч или другой предмет, катящий модель автомобиля или мяч вниз
склоне или любой другой ситуации, в которой скорость
изменения со временем послужили бы отличными расширениями.
Позвольте учащимся рассмотреть основную форму
график перед нанесением чисел. Это будет способствовать росту
интуитивное понимание скорости.