Дисперсия, формула дисперсии, виды дисперсии, простая дисперсия, взвешенная дисперсия
Понятие дисперсии
Дисперсия в статистике находится как среднее квадратическое отклонение индивидуальных значений признака в квадрате от средней арифметической. В зависимости от исходных данных она определяется по формулам простой и взвешенной дисперсий:
1. Простая дисперсия (для несгруппированных данных) вычисляется по формуле:
2. Взвешенная дисперсия (для вариационного ряда):
где n — частота (повторяемость фактора Х)
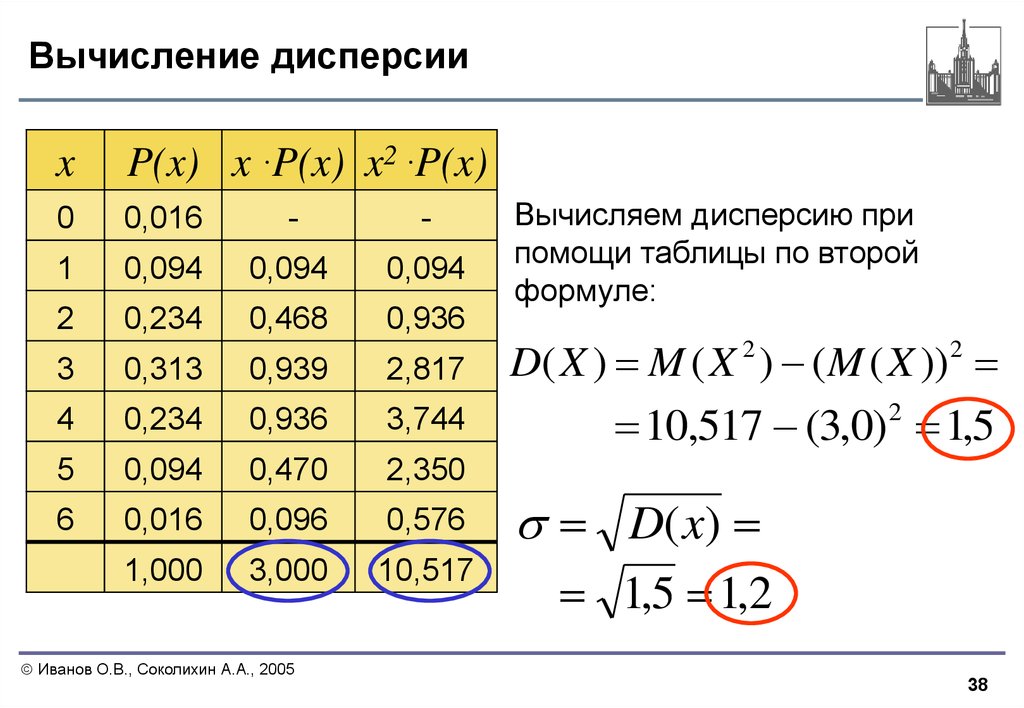
Пример нахождения дисперсии
На данной странице описан стандартный пример нахождения дисперсии, также Вы можете посмотреть другие задачи на её нахождение
Пример 1. Имеются следующие данные по группе из 20 студентов заочного отделения. Нужно построить интервальный ряд распределения признака, рассчитать среднее значение признака и изучить его дисперсию
Построим интервальную группировку.
где X max– максимальное значение группировочного признака;
X min–минимальное значение группировочного признака;
n – количество интервалов:
Принимаем n=5. Шаг равен: h = (192 — 159)/ 5 = 6,6
Составим интервальную группировку
Для дальнейших расчетов построим вспомогательную таблицу:
X’i– середина интервала. (например середина интервала 159 – 165,6 = 162,3)
Среднюю величину роста студентов определим по формуле средней арифметической взвешенной:
Определим дисперсию по формуле:
Пример 2. Определение групповой, средней из групповой, межгрупповой и общей дисперсии
Пример 3. Нахождение дисперсии и коэффициента вариации в группировочной таблице
Пример 4.
Нахождение дисперсии в дискретном ряду
Формулу дисперсии можно преобразовать так:
Из этой формулы следует, что дисперсия равна разности средней из квадратов вариантов и квадрата и средней.
Дисперсия в вариационных рядах с равными интервалами по способу моментов может быть рассчитана следующим способом при использовании второго свойства дисперсии (разделив все варианты на величину интервала). Определении дисперсии, вычисленной по способу моментов, по следующей формуле менее трудоемок:
где i — величина интервала;
А — условный ноль, в качестве которого удобно использовать середину интервала, обладающего наибольшей частотой;
m1 — квадрат момента первого порядка;
m2 — момент второго порядка
Дисперсия альтернативного признака
Подставляя в данную формулу дисперсии q =1- р, получаем:
Виды дисперсии
Общая дисперсия измеряет вариацию признака по всей совокупности в целом под влиянием всех факторов, обуславливающих эту вариацию.
Она равняется среднему квадрату отклонений отдельных значений признака х от общего среднего значения х и может быть определена как простая дисперсия или взвешенная дисперсия.
Внутригрупповая дисперсия характеризует случайную вариацию, т.е. часть вариации, которая обусловлена влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Такая дисперсия равна среднему квадрату отклонений отдельных значений признака внутри группы X от средней арифметической группы и может быть вычислена как простая дисперсия или как взвешенная дисперсия.
Таким образом, внутригрупповая дисперсия измеряет вариацию признака внутри группы и определяется по формуле:
где хi — групповая средняя;
ni — число единиц в группе.
Например, внутригрупповые дисперсии, которые надо определить в задаче изучения влияния квалификации рабочих на уровень производительности труда в цехе показывают вариации выработки в каждой группе, вызванные всеми возможными факторами (техническое состояние оборудования, обеспеченность инструментами и материалами, возраст рабочих, интенсивность труда и т.
д.), кроме отличий в квалификационном разряде (внутри группы все рабочие имеют одну и ту же квалификацию).
Средняя из внутри групповых дисперсий отражает случайную вариацию, т. е. ту часть вариации, которая происходила под влиянием всех прочих факторов, за исключением фактора группировки. Она рассчитывается по формуле:
Межгрупповая дисперсия характеризует систематическую вариацию результативного признака, которая обусловлена влиянием признака-фактора, положенного в основание группировки. Она равняется среднему квадрату отклонений групповых средних от общей средней. Межгрупповая дисперсия рассчитывается по формуле:
Правило сложения дисперсии в статистике
Согласно правилу сложения дисперсий общая дисперсия равна сумме средней из внутригрупповых и межгрупповых дисперсий:
Смысл этого правила заключается в том, что общая дисперсия, которая возникает под влиянием всех факторов, равняется сумме дисперсий, которые возникают под влиянием всех прочих факторов, и дисперсии, возникающей за счет фактора группировки.
2 раз.
Источник: Балинова B.C. Статистика в вопросах и ответах: Учеб. пособие. — М.: ТК. Велби, Изд-во Проспект, 2004. — 344 с.
Дисперсия, среднеквадратичное (стандартное) отклонение, коэффициент вариации в Excel
Из предыдущей статьи мы узнали о таких показателях, как размах вариации, межквартильный размах и среднее линейное отклонение. В этой статье изучим дисперсию, среднеквадратичное отклонение и коэффициент вариации.
Дисперсия
Дисперсия случайной величины – это один из основных показателей в статистике. Он отражает меру разброса данных вокруг средней арифметической.
Сейчас небольшой экскурс в теорию вероятностей, которая лежит в основе математической статистики. Как и матожидание, дисперсия является важной характеристикой случайной величины. Если матожидание отражает центр случайной величины, то дисперсия дает характеристику разброса данных вокруг центра.
Формула дисперсии в теории вероятностей имеет вид:
То есть дисперсия — это математическое ожидание отклонений от математического ожидания.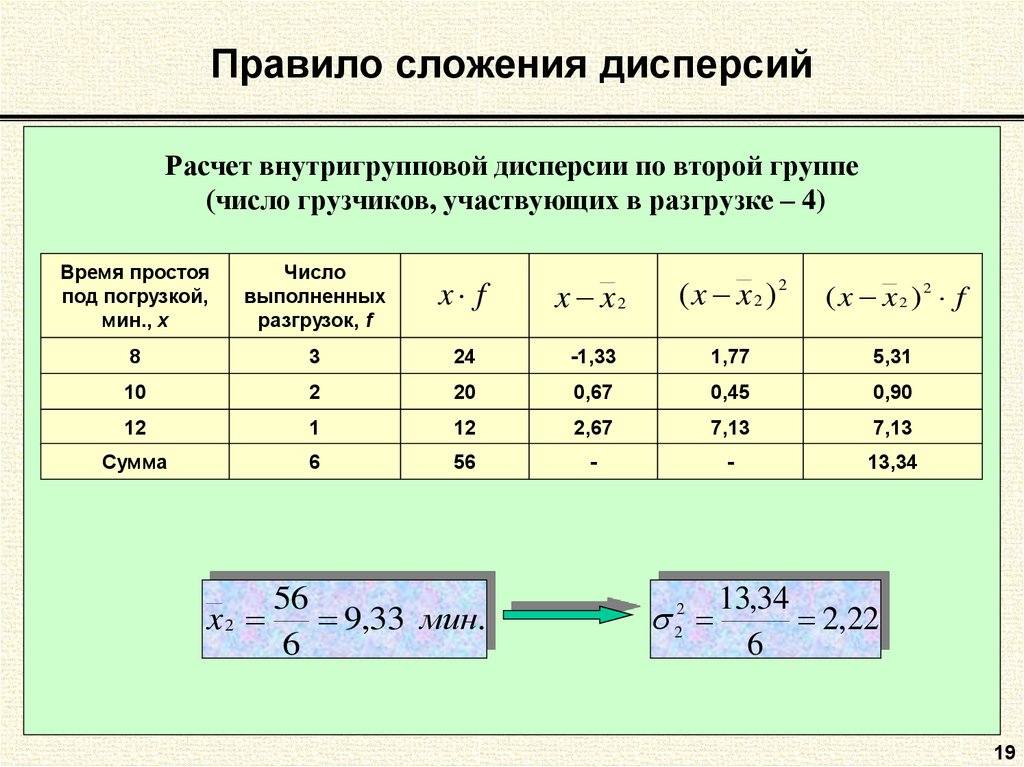
На практике при анализе выборок математическое ожидание, как правило, не известно. Поэтому вместо него используют оценку – среднее арифметическое. Расчет дисперсии производят по формуле:
где
s2 – выборочная дисперсия, рассчитанная по данным наблюдений,
X – отдельные значения,
X̅– среднее арифметическое по выборке.
Стоит отметить, что у такого расчета дисперсии есть недостаток – она получается смещенной, т.е. ее математическое ожидание не равно истинному значению дисперсии. Подробней об этом здесь. Однако при увеличении объема выборки она все-таки приближается к своему теоретическому аналогу, т.е. является асимптотически не смещенной.
Простыми словами дисперсия – это средний квадрат отклонений. То есть вначале рассчитывается среднее значение, затем берется разница между каждым исходным и средним значением, возводится в квадрат, складывается и затем делится на количество значений в данной совокупности.
Разница между отдельным значением и средней отражает меру отклонения. В квадрат возводится для того, чтобы все отклонения стали исключительно положительными числами и чтобы избежать взаимоуничтожения положительных и отрицательных отклонений при их суммировании. Затем, имея квадраты отклонений, просто рассчитываем среднюю арифметическую. Средний – квадрат – отклонений. Отклонения возводятся в квадрат, и считается средняя. Теперь вы знаете, как найти дисперсию.
Расчет дисперсии в Excel
Генеральную и выборочную дисперсии легко рассчитать в Excel. Есть специальные функции: ДИСП.Г и ДИСП.В соответственно.
В чистом виде дисперсия не используется. Это вспомогательный показатель, который нужен в других расчетах. Например, в проверке статистических гипотез или расчете коэффициентов корреляции. Отсюда неплохо бы знать математические свойства дисперсии.
Свойства дисперсии
Свойство 1. Дисперсия постоянной величины A равна 0 (нулю).
D(A) = 0
Свойство 2. Если случайную величину умножить на постоянную А, то дисперсия этой случайной величины увеличится в А2 раз. Другими словами, постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат.
D(AX) = А2 D(X)
Свойство 3. Если к случайной величине добавить (или отнять) постоянную А, то дисперсия останется неизменной.
D(A + X) = D(X)
Свойство 4. Если случайные величины X и Y независимы, то дисперсия их суммы равна сумме их дисперсий.
D(X+Y) = D(X) + D(Y)
Свойство 5. Если случайные величины X и Y независимы, то дисперсия их разницы также равна сумме дисперсий.
D(X-Y) = D(X) + D(Y)
Среднеквадратичное (стандартное) отклонение
Если из дисперсии извлечь квадратный корень, получится среднеквадратичное (стандартное) отклонение (сокращенно СКО).
Встречается название среднее квадратичное отклонение и сигма (от названия греческой буквы). Общая формула стандартного отклонения в математике следующая:
На практике формула стандартного отклонения следующая:
Как и с дисперсией, есть и немного другой вариант расчета. Но с ростом выборки разница исчезает.
Расчет cреднеквадратичного (стандартного) отклонения в Excel
Для расчета стандартного отклонения достаточно из дисперсии извлечь квадратный корень. Но в Excel есть и готовые функции: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В (по генеральной и выборочной совокупности соответственно).
Среднеквадратичное отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому является сопоставимым с исходными данными.
Коэффициент вариации
Значение стандартного отклонения зависит от масштаба самих данных, что не позволяет сравнивать вариабельность разных выборках.
Чтобы устранить влияние масштаба, необходимо рассчитать коэффициент вариации по формуле:
По нему можно сравнивать однородность явлений даже с разным масштабом данных. В статистике принято, что, если значение коэффициента вариации менее 33%, то совокупность считается однородной, если больше 33%, то – неоднородной. В реальности, если коэффициент вариации превышает 33%, то специально ничего делать по этому поводу не нужно. Это информация для общего представления. В общем коэффициент вариации используют для оценки относительного разброса данных в выборке.
Расчет коэффициента вариации в Excel
Расчет коэффициента вариации в Excel также производится делением стандартного отклонения на среднее арифметическое:
=СТАНДОТКЛОН.В()/СРЗНАЧ()
Коэффициент вариации обычно выражается в процентах, поэтому ячейке с формулой можно присвоить процентный формат:
Коэффициент осцилляции
Еще один показатель разброса данных на сегодня – коэффициент осцилляции.
Это соотношение размаха вариации (разницы между максимальным и минимальным значением) к средней. Готовой формулы Excel нет, поэтому придется скомпоновать три функции: МАКС, МИН, СРЗНАЧ.
Коэффициент осцилляции показывает степень размаха вариации относительно средней, что также можно использовать для сравнения различных наборов данных.
Таким образом, в статистическом анализе существует система показателей, отражающих разброс или однородность данных.
Ниже видео о том, как посчитать коэффициент вариации, дисперсию, стандартное (среднеквадратичное) отклонение и другие показатели вариации в Excel.
Поделиться в социальных сетях:
Дисперсия свойства, формула вычисления дисперсии дискретной случайной величины, виды, правило и примеры расчетов, онлайн-калькулятор » Kupuk.
netВ различных научных дисциплинах словосочетание «дисперсия это» характеризует мало схожие понятия. С латыни «dispersio» переводится как «рассеяние».
В физике, например, означает связь фазовой скорости волны с частотой. В химии описывает несмешиваемые субстанции. В биологии – многообразие признаков популяции.
В данной статье речь пойдет о математической трактовке. Рассматривается как одно из свойств случайных величин.
Статистика, в частности, оперирует рядами данных, характеризующих какой-либо признак, явление. Интересует их изменение.
Вариация представляет собой отличие величин одинакового показателя у разных предметов. Ее изучение позволит понять причины отклонений от нормы, анализировать их и в какой-то мере прогнозировать. Также станет возможным выявить факторы, влияющие на значения, отсеяв случайные.
Характеристики равномерного распределения представлены на картинке:
При значительном объеме статистики, средняя величина очевидно близка к нормальной.
Об этом говорят и законы распределения. Отклонения от нее будут являться объективной характеристикой.
Только вот отрицательные значения этих разбросов будут сбивать с толку при расчетах, погашая положительные. А оставлять лишь модули – для математика не корректно. Напрашивается возвести в четную степень, а именно – во вторую.
Решение оказалось не только удобным. Оно открыло бо́льшие возможности в изучении отклонений. А важны именно они, поскольку сама по себе средняя мало что дает.
В качестве одного из важных показателей вариации, вводится понятие «дисперсия» – усредненный квадрат отклонений численных значений каких-либо событий от средней величины.
Кратко записывается D[X] в русскоязычных источниках и Var[X] (от «variance») в английских. В статистических выкладках используется σ2.
Никакого наглядного смысла величина не несет. Другое дело, среднее квадратическое отклонение – корень квадратный из дисперсии.
)» src=»https://www.youtube.com/embed/7Kx7SsGnuH0?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture»>Виды дисперсии дискретной случайной величины
Для анализа данных цифр в таком виде недостаточно. Гораздо больше можно выжать из последовательности, если разбить ее на группы по определенному признаку.
Общая дисперсия
Как можно заметить, вычисленная по приведенному выше определению величина характеризует отклонения в целом. Без учета определяющих вариацию факторов. Вернее, с учетом всех, включая совершенно случайные. Поэтому и называется «общей» и рассчитывается по формулам, указанным ниже.
Простая дисперсия, без разделения на группы:
Или в несколько преобразованном виде:
Взвешенная дисперсия, для вариационного ряда:
где xi – значение из ряда;
fi – частота, количество повторений;
k – групп;
n – число вариантов.
Черта сверху указывает на среднюю величину.
Межгрупповая дисперсия
Характеризует систематическое отклонение, возникающее из-за фактора, по которому производилось выделение признаков в группы. Поэтому также называется «факторной».
Как найти данную дисперсию? По формуле:
где k – количество групп;
nj – элементов в группе с индексом j.
Внутригрупповая дисперсия
Возникает по хаотичной причине, не связанной с причиной сделанной выборки. Неучтенный фактор. Еще обозначается как «остаточная».
Например, рассматривается количество выпущенных деталей за месяц каждым фрезеровщиком цеха.
В качестве критерия отбора в группу выбираем возраст оборудования. Он-то и не будет влиять на производительность внутри подборки: там станки у всех практически одинаковые.
Если вычислить среднюю величину от всех групповых,
то получим характеристику случайного разброса. Иными словами, составляющую вариации, зависящую от чего угодно, кроме фактора отбора.
Взаимосвязь
В соответствии с правилом сложения, общая D[X] включает средние выражения остаточной и факторной. И это логично, поскольку учитывает и случайное изменение в группе, и систематическое в факторной.
Свойства дисперсии
Опишем основные:
Если последовательность состоит из одинаковых чисел, то D[X] будет нулевой.
Уменьшение всех значений на постоянную величину на дисперсию не влияет. Иначе говоря, рассчитать σ2 можно по отклонениям от фиксированного числа.
Уменьшение всех цифр в k раз приведет к падению D[X] в k2 раз. Можно, например, иметь в виду значения в метрах, а результат вычислить в футах. Достаточно учесть один раз то, на что следует умножить.
Средний квадрат отклонений от постоянной величины X отличается в большую сторону от того же с использованием среднего значения. Разница составит (Xcр – X)2.
Показатели вариаций
Кроме размаха (разницы максимального и минимального значений), среднего линейного и дисперсии, изменения описываются коэффициентом вариации:
Оценить масштаб разброса проще по относительной величине. Тем более, что измеряются в одних единицах.
Пример расчета дисперсии
Компания объявила конкурсный отбор для приема сотрудников. В качестве критерия принят стаж работы по специальности. Приведем исходные данные и расчеты.
Усредненный стаж:
Дисперсия:
По альтернативной формуле:
Среднеквадратическое:
Коэффициент вариации:
youtube.com/embed/uK8MxzBGvEQ?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture»>Заключение
Статистика оперирует значительными объемами данных. Вариация, как одно из основных понятий – не исключение. И дисперсия в качестве основной характеристики.
Для упрощения расчетов существует масса онлайн калькуляторов. Имеется упомянутый инструмент в MS Excel.
Стандартное отклонение — что это, расчёт, использование, дисперсия
Стандартное отклонение (англ. Standard Deviation) — простыми словами это мера того, насколько разбросан набор данных.
Вычисляя его, можно узнать, являются ли числа близкими к среднему значению или далеки от него.
Если точки данных находятся далеко от среднего значения, то в наборе данных имеется большое отклонение; таким образом, чем больше разброс данных, тем выше стандартное отклонение.
Стандартное отклонение обозначается буквой σ (греческая буква сигма).
Стандартное отклонение также называется:
- среднеквадратическое отклонение,
- среднее квадратическое отклонение,
- среднеквадратичное отклонение,
- квадратичное отклонение,
- стандартный разброс.
Использование и интерпретация величины среднеквадратического отклонения
Стандартное отклонение используется:
- в финансах в качестве меры волатильности,
- в социологии в опросах общественного мнения — оно помогает в расчёте погрешности.
Пример:
Рассмотрим два малых предприятия, у нас есть данные о запасе какого-то товара на их складах.
| День 1 | День 2 | День 3 | День 4 | |
|---|---|---|---|---|
Пред. А | 19 | 21 | 19 | 21 |
| Пред.Б | 15 | 26 | 15 | 24 |
В обеих компаниях среднее количество товара составляет 20 единиц:
- А -> (19 + 21 + 19+ 21) / 4 = 20
- Б -> (15 + 26 + 15+ 24) / 4 = 20
Однако, глядя на цифры, можно заметить:
- в компании A количество товара всех четырёх дней очень близко находится к этому среднему значению 20 (колеблется лишь между 19 ед. и 21 ед.),
- в компании Б существует большая разница со средним количеством товара (колеблется между 15 ед. и 26 ед.).
Если рассчитать стандартное отклонение каждой компании, оно покажет, что
- стандартное отклонение компании A = 1,
- стандартное отклонение компании Б ≈ 5.
Стандартное отклонение показывает эту волатильность данных — то, с каким размахом они меняются; т.е. как сильно этот запас товара на складах компаний колеблется (поднимается и опускается).
Расчет среднеквадратичного (стандартного) отклонения
Формулы вычисления стандартного отклонения
Где:σ — стандартное отклонение,
xi — величина отдельного значения выборки,
μ — среднее арифметическое выборки,
n — размер выборки.
Эта формула применяется, когда анализируются все значения выборки.Где:
S — стандартное отклонение,
n — размер выборки,
xi — величина отдельного значения выборки,
xср — среднее арифметическое выборки.
Эта формула применяется, когда присутствует очень большой размер выборки, поэтому на анализ обычно берётся только её часть.
Единственная разница с предыдущей формулой: “n — 1” вместо “n”, и обозначение «xср» вместо «μ».
Разница между формулами S и σ («n» и «n–1»)
Состоит в том, что мы анализируем — всю выборку или только её часть:
- только её часть – используется формула S (с «n–1»),
- полностью все данные – используется формула σ (с «n»).
Как рассчитать стандартное отклонение?
Пример 1 (с σ)
Рассмотрим данные о запасе какого-то товара на складах Предприятия Б.
| День 1 | День 2 | День 3 | День 4 | |
| Пред.Б | 15 | 26 | 15 | 24 |
Если значений выборки немного (небольшое n, здесь он равен 4) и анализируются все значения, то применяется эта формула:
Применяем эти шаги:
1. Найти среднее арифметическое выборки:
μ = (15 + 26 + 15+ 24) / 4 = 20
2. От каждого значения выборки отнять среднее арифметическое:
x1 — μ = 15 — 20 = -5
x2 — μ = 26 — 20 = 6
x3 — μ = 15 — 20 = -5
x4 — μ = 24 — 20 = 4
3. Каждую полученную разницу возвести в квадрат:
(x1 — μ)² = (-5)² = 25
(x2 — μ)² = 6² = 36
(x3 — μ)² = (-5)² = 25
(x4 — μ)² = 4² = 16
4. Сделать сумму полученных значений:
Σ (xi — μ)² = 25 + 36+ 25+ 16 = 102
5. Поделить на размер выборки (т.е. на n):
(Σ (xi — μ)²)/n = 102 / 4 = 25,5
6. Найти квадратный корень:
√((Σ (xi — μ)²)/n) = √ 25,5 ≈ 5,0498
Пример 2 (с S)
Задача усложняется, когда существуют сотни, тысячи или даже миллионы данных.
В этом случае берётся только часть этих данных и анализируется методом выборки.
У Андрея 20 яблонь, но он посчитал яблоки только на 6 из них.
Популяция — это все 20 яблонь, а выборка — 6 яблонь, это деревья, которые Андрей посчитал.
| Яблоня 1 | Яблоня 2 | Яблоня 3 | Яблоня 4 | Яблоня 5 | Яблоня 6 |
| 9 | 2 | 5 | 4 | 12 | 7 |
Так как мы используем только выборку в качестве оценки всей популяции, то нужно применить эту формулу:
Математически она отличается от предыдущей формулы только тем, что от n нужно будет вычесть 1. Формально нужно будет также вместо μ (среднее арифметическое) написать X ср.
Применяем практически те же шаги:
1. Найти среднее арифметическое выборки:
Xср = (9 + 2 + 5 + 4 + 12 + 7) / 6 = 39 / 6 = 6,5
2. От каждого значения выборки отнять среднее арифметическое:
X1 – Xср = 9 – 6,5 = 2,5
X2 – Xср = 2 – 6,5 = –4,5
X3 – Xср = 5 – 6,5 = –1,5
X4 – Xср = 4 – 6,5 = –2,5
X5 – Xср = 12 – 6,5 = 5,5
X6 – Xср = 7 – 6,5 = 0,5
3.
Каждую полученную разницу возвести в квадрат:
(X1 – Xср)² = (2,5)² = 6,25
(X2 – Xср)² = (–4,5)² = 20,25
(X3 – Xср)² = (–1,5)² = 2,25
(X4 – Xср)² = (–2,5)² = 6,25
(X5 – Xср)² = 5,5² = 30,25
(X6 – Xср)² = 0,5² = 0,25
4. Сделать сумму полученных значений:
Σ (Xi – Xср)² = 6,25 + 20,25+ 2,25+ 6,25 + 30,25 + 0,25 = 65,5
5. Поделить на размер выборки, вычитав перед этим 1 (т.е. на n–1):
(Σ (Xi – Xср)²)/(n-1) = 65,5 / (6 – 1) = 13,1
6. Найти квадратный корень:
S = √((Σ (Xi – Xср)²)/(n–1)) = √ 13,1 ≈ 3,6193
Дисперсия и стандартное отклонение
Стандартное отклонение равно квадратному корню из дисперсии (S = √D). То есть, если у вас уже есть стандартное отклонение и нужно рассчитать дисперсию, нужно лишь возвести стандартное отклонение в квадрат (S² = D).
Дисперсия — в статистике это «среднее квадратов отклонений от среднего». Чтобы её вычислить нужно:
- Вычесть среднее значение из каждого числа
- Возвести каждый результат в квадрат (так получатся квадраты разностей)
- Найти среднее значение квадратов разностей.
Ещё расчёт дисперсии можно сделать по этой формуле:
Где:S² — выборочная дисперсия,
Xi — величина отдельного значения выборки,
Xср (может появляться как X̅) — среднее арифметическое выборки,
n — размер выборки.
Правило трёх сигм
Это правило гласит: вероятность того, что случайная величина отклонится от своего математического ожидания более чем на три стандартных отклонения (на три сигмы), почти равна нулю.
Глядя на рисунок нормального распределения случайной величины, можно понять, что в пределах:
- одного среднеквадратического отклонения заключаются 68,26% значений (Xср ± 1σ или μ ± 1σ),
- двух стандартных отклонений — 95,44% (Xср ± 2σ или μ ± 2σ),
- трёх стандартных отклонений — 99,72% (Xср ± 3σ или μ ± 3σ).
Это означает, что за пределами остаются лишь 0,28% — это вероятность того, что случайная величина примет значение, которое отклоняется от среднего более чем на 3 сигмы.
Стандартное отклонение в excel
Вычисление стандартного отклонения с «n – 1» в знаменателе (случай выборки из генеральной совокупности):
1.
Занесите все данные в документ Excel.
2. Выберите поле, в котором вы хотите отобразить результат.
3. Введите в этом поле «=СТАНДОТКЛОНА(«
4. Выделите поля, где находятся данные, потом закройте скобки.
5. Нажмите Ввод (Enter).
В случае если данные представляют всю генеральную совокупность (n в знаменателе), то нужно использовать функцию СТАНДОТКЛОНПА.
Коэффициент вариации
Коэффициент вариации — отношение стандартного отклонения к среднему значению, т.е. Cv = (S/μ) × 100% или V = (σ/X̅) × 100%.
Стандартное отклонение делится на среднее и умножается на 100%.
Можно классифицировать вариабельность выборки по коэффициенту вариации:
- при <10% выборка слабо вариабельна,
- при 10% – 20 % — средне вариабельна,
- при >20 % — выборка сильно вариабельна.
Узнайте также про:
- Корреляции,
- Метод Крамера,
- Метод наименьших квадратов,
- Теорию вероятностей
- Интегралы.
Дисперсия и ее оценка
Определение дисперсии случайных величин
Определение 1Дисперсия – норма, отражающая, с точки зрения теории, ожидаемое отклонение случайной величины от ее математического ожидания.
В математической статистике она определяется в качестве центрального момента второго порядка. Приведем формулу дисперсии:
где М(х) – математическое ожидание, а D(х) – дисперсия.
На основе данной формулы можно вывести другую, которая дает оценку дисперсии:
где S2— оценка дисперсии, Xi— наблюдаемые значения, n – объем собранных эмпирических значений, X—— оценка математического ожидания.
В первой формуле оценка математического ожидания не смещена, но во второй формуле дисперсия является выборочной. Т.е. эта оценка дает характеристику величине дисперсии данной выборки, не для популяции данных.
Обычно для эксперимента необходимо оценить популяционный характер математического ожидания и дисперсию.
Так как вторая формула предполагает сравнение эмпирических знаний не с истинной величиной, а с оценочной, то происходит смещение оценки дисперсии. Способами дифференциального исчисления определено: ожидаемая величина оценки дисперсии по второй формуле описывает соотношение:
Данная формула отражает выборочную дисперсию. Из нее следует, что при наличии 10 выборочных значений случайной величины идет занижение значения. Получается 9/10 дисперсий анализируемой величины для генеральной совокупности. Если увеличить объем в десять раз, то уменьшиться величина смещения до одной сотой, и при этому полученный результат будет отличаться от ожидаемого значения. При помощи третьей формулы можно рассчитать несмещенную оценку дисперсии:
Данная формула называется популяционной дисперсией, или дисперсией генеральной совокупности. Эту формулу используют для расчета генеральной совокупности, третью – для определения вариантов внутри выборки и выход за пределы имеющихся значений, который не предполагается теорией.
Характеристика оценивания стандартного отклонения
Иногда для оценивания важна не сама дисперсия, а оценка стандартного отклонения. Эти две величины связаны однозначным соотношением. Оценивание стандартного отклонения также применяется для выборки и генеральной совокупности, как и дисперсия. Оценка данной величины является предпочтительной, так как она удобна для восприятия из-за своей размерности. Помимо этого, эту величину используют для вычисления стандартной ошибки. Формула выглядит следующим образом:
где SE – стандартная ошибка.
Данная статистика необходима для интервальной оценки исследуемой случайной величины.
Характеристика оценки полумежквартильного интервала
Это еще один способ оценивания вариантов в распределении случайной величины. Ее обозначают Q. Она используется в качестве альтернативы стандартного отклонения, несмотря на то, что они связаны соотношением Q = 0,67σ.
Определение 2Квартиль – это вариант названия квантиля распределения.
При соответствии медианы с половиной распределения, то квартиль равен четверти. Т.е. первая четверть – это первый квартиль, половина – второй квартиль, три четвертых – третий, общая сумма величины – четвертый квартиль. Формула межквартильного интервала выглядит следующим образом:
Данную оценку используют, например, в сенсорной психофизике при оценивании порога способом констант.
Характеристика ковариации
Иногда необходимо оценить не одну дисперсию, а две (х,у). Такая статистика называется ковариацией. Ее формула выглядит следующим образом:
Она определяет степень связи между двумя переменами. Отличительная особенность ковариации – это ее выражение и в положительных и в отрицательных числах. Так как ковариация зависит от размерности, то оценить степень между переменными невозможно. Поэтому в качестве меры двух переменных используют термин «корреляция». Ее величина может быть определена за счет деления ковариации на произведение стандартных отклонений двух случайных величин, между которыми вычисляют ковариацию.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Автор: Анна Коврова
Преподаватель факультета психологии кафедры общей психологии. Кандидат психологических наук
Дисперсия и стандартное отклонение
Полное руководство для понимания дисперсии и стандартного отклонения
Описательная статистика используется для описания основной информации о данных. Они помогают нам понять некоторые особенности данных, давая краткое изложение выборки. Это похоже на первое впечатление от того, что показывают нам данные. Вкратце, описательная статистика — это метрики и количественный анализ для краткого описания нашей выборки. И они разбиты на меры центральной тенденции и меры изменчивости.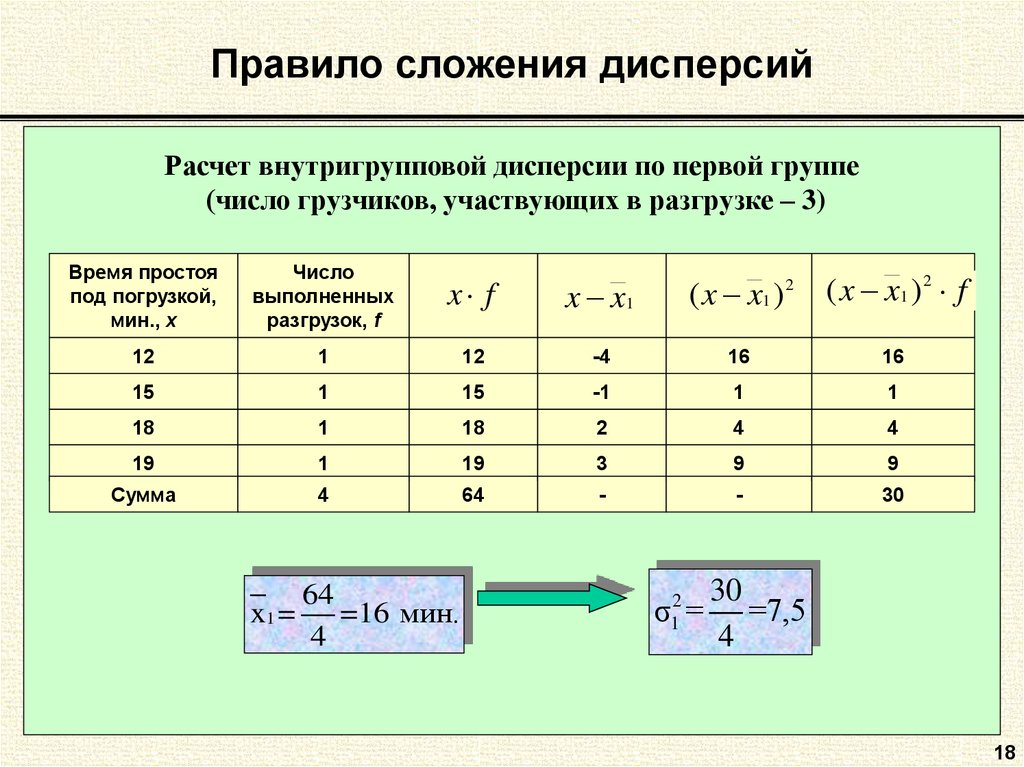
В этой статье мы обсудим последнее и рассмотрим известные вопросы о дисперсии и стандартном отклонении.
Дисперсия
Определение
Предположим, что у нас есть случайная величина, по определению она может принимать разные значения. Распределение этой случайной величины определяет ее диапазон и вариацию. Теперь мы хотим иметь метрику для измерения степени изменения этой переменной. Это то, что мы называем дисперсией: это показатель, описывающий разброс между набором данных от его среднего значения. Его также можно рассматривать как меру ширины распределения, но это больше связано с нормальным распределением, чем для других распределений.
Математически в совокупности мы можем рассчитать это как: среднее квадратическое расстояние между каждой точкой и средним значением, это коррелирует с тем, насколько далеко каждая точка в наборе данных находится от среднего.
Эта формула может быть выражена более широко и прямо следующим образом, потому что ожидаемое значение случайной величины в генеральной совокупности — это просто ее среднее значение.
Есть еще одна формула дисперсии, еще один взгляд на то, как мы воспринимаем понятие дисперсии, более простой и элегантный.
В нем говорится: Дисперсия — это разница между ожидаемым значением квадрата входных данных и квадратом ожидаемого значения входных данных.
Несмотря на то, что эта формула проста, она менее интерпретируема, чем первая. Мы можем рассматривать это как упрощение другого.
Среднеквадратичное отклонение
Многие люди думают, что дисперсия — это раздражающий шаг при вычислении стандартного отклонения, и они в чем-то правы, потому что мы обычно думаем о нормальном распределении, поскольку оно повсеместно встречается в вероятности, статистике и нашей жизни. Другой аргумент заключается в том, что стандартное отклонение помогает нам построить доверительный интервал с учетом среднего значения в нормальном распределении.
Теперь следующий шаг после вычисления дисперсии — это квадратный корень, и на сцену выходит знаменитая сигма.
Эта формула дает нам своего рода среднее значение того, насколько далеко точка от среднего значения. Но вы думаете, о чем я думаю:
Почему извлекают квадратный корень из суммы квадратов, а не из абсолютного значения?
На самом деле, это законный вопрос, и я должен признать, что мне потребовалось много времени, чтобы разобраться в этом вопросе, и я до сих пор вижу, что статистики не уделяют достаточно времени, чтобы понять его и, таким образом, объяснить его.
Во-первых, это дебаты столетней давности. Он называется стандартным отклонением (SD) против среднего отклонения (MD), и есть два аргумента в пользу того, почему статистики используют SD, а не MD.
- Первый — это то, на что указал Фишер в 1920 при идеальных обстоятельствах. Фишер доказал, что эти две статистики достаточно хороши для описания отклонения генеральной совокупности, но он обнаружил, что стандартное отклонение более эффективно в том смысле, что имеет наименьшую вероятную ошибку в качестве оценки параметра совокупности. Конкретно, имея дело с повторяющимися большими выборками, он обнаруживает, что стандартное отклонение средних отклонений на 14% больше, чем стандартное отклонение стандартных отклонений [1]. Следовательно, SD более последовательна, чем MD, и поэтому предпочтение отдается статистической теории.
- Второй аргумент заключается в том, что MD довольно сложно манипулировать алгебраически, однако возведение в квадрат значительно упрощает работу с алгеброй и предлагает свойства, которых нет в MD. Возьмем для примера нормальное распределение: мы можем довольно точно указать процент распределения, лежащий в пределах каждого стандартного отклонения от среднего. Есть очень большая теория и сложная форма статистики, основанная на стандартном отклонении, например: регрессия наименьших квадратов, дисперсионный анализ, центральная предельная теорема и так далее.
Конкретно, имея дело с повторяющимися большими выборками, он обнаруживает, что стандартное отклонение средних отклонений на 14% больше, чем стандартное отклонение стандартных отклонений [1]. Следовательно, SD более последовательна, чем MD, и поэтому предпочтение отдается статистической теории.Следует отметить, что на SD очень сильно влияет ненормальность, в частности, на него влияют чрезвычайно высокие и чрезвычайно низкие значения.
Некоторые исследования показали, что MD эффективен в реальных условиях и для распределений, отличных от совершенно нормальных, и, в конце концов, MD легче понять. Таким образом, можно сказать, что выбор зависит от данных.
Еще один момент для интерпретации SD и ознакомления с ней — это рассматривать наши данные как многомерное пространство, где каждое наблюдение представляет собой значение в другом измерении. Это согласуется с независимостью наблюдений от евклидова пространства. Итак, согласно теореме Пифагора, расстояние между двумя векторами равно:
а стандартное отклонение — это расстояние, нормированное числом наблюдений, при условии, что вектор y является средним вектором.
Оценка дисперсии
Теперь предположим, что у нас есть выборка, и мы хотим оценить истинную дисперсию генеральной совокупности. Мы можем наивно оценить это как исходную формулу:
На самом деле это смещенная оценка истинной дисперсии. Фактически, мы недооцениваем дисперсию этой формулы, и у нас есть:
Давайте докажем, почему эта формула верна при любом значении среднего.
Другими словами, различия между данными и средним значением выборки обычно меньше, чем данные и среднее значение генеральной совокупности, если только среднее значение выборки не совпадает со средним значением генеральной совокупности, а этого практически никогда не происходит. Таким образом, различия в среднем значении генеральной совокупности приведут к большему значению, и это большее значение и есть то, что мы должны оценить. Однако мы недооцениваем это. Итак, чтобы компенсировать эту недооценку, нам нужно разделить на n-1 для измерения расстояний от образца, и новая формула:
Почему деление на n-1, а не на n-2 или n-1,5?
Другой закономерный вопрос: почему деление на точное число является своего рода калибровкой нашей оценки?
В статистике мы оцениваем качество оценщика, проверяя, является ли он беспристрастным. Это означает, что ожидаемое значение оценщика равно истинному значению. Например, оценка среднего несмещена.
Теперь давайте проделаем ту же самую проверку дисперсии и посмотрим, объективна ли ее оценка.
Заключение
Что вам нужно убрать из этой статьи:
- Дисперсия измеряет разброс данных с акцентом на экстремально низкие и высокие значения.
- Стандартное отклонение — это показатель отклонения данных, который измеряет в среднем, насколько далеко точка от среднего значения.
- Мы используем стандартное отклонение по сравнению со средним отклонением, потому что первое более согласовано, а второе трудно поддается алгебраическим манипуляциям.
- Мы делим оценку на n-1, потому что при делении на n мы недооцениваем ее, что означает, что погружение на n делает оценку смещенной.
[1] Стивен Горард, Возвращаясь к дебатам 90-летней давности: преимущества среднего отклонения (2004 г.), Почему мы используем стандартное отклонение?
Что такое дисперсия? | Определение, примеры и формулы
Опубликован в
24 сентября 2020 г.
по
Прита Бхандари.
Отредактировано
22 мая 2022 г.
Дисперсия является мерой изменчивости. Он рассчитывается путем взятия среднего квадрата отклонений от среднего.
Дисперсия говорит вам о степени разброса в вашем наборе данных. Чем более разбросаны данные, тем больше дисперсия по отношению к среднему значению.
Содержание
- Дисперсия по сравнению со стандартным отклонением
- Популяция по сравнению с дисперсией по выборке
- Этапы расчета дисперсии
- Почему дисперсия имеет значение?
- Часто задаваемые вопросы о дисперсии
Дисперсия против стандартного отклонения
Стандартное отклонение выводится из дисперсии и показывает, в среднем, насколько далеко каждое значение отстоит от среднего. Это квадратный корень из дисперсии.
Обе меры отражают изменчивость распределения, но их единицы различаются:
- Стандартное отклонение выражается в тех же единицах, что и исходные значения (например, в метрах).
- Дисперсия выражается в более крупных единицах (например, в квадратных метрах)
Поскольку единицы дисперсии намного больше, чем единицы типичного значения набора данных, сложнее интуитивно интерпретировать число дисперсии. Вот почему стандартное отклонение часто предпочитают в качестве основной меры изменчивости.
Однако дисперсия более информативна в отношении изменчивости, чем стандартное отклонение, и она используется для статистических выводов.
Население и выборочная дисперсия
Различные формулы используются для расчета дисперсии в зависимости от того, есть ли у вас данные из всей совокупности или выборки.
Дисперсия населения
Когда вы соберете данные о каждом интересующем вас члене совокупности, вы сможете получить точное значение дисперсии совокупности.
Формула дисперсии населения выглядит следующим образом:
| Формула | Объяснение |
|---|---|
|
Выборочная дисперсия
При сборе данных из выборки выборочная дисперсия используется для оценок или выводов о дисперсии генеральной совокупности.
формула выборочной дисперсии выглядит так:
| Формула | Пояснение |
|---|---|
|
Для выборок мы используем n – 1 в формуле, потому что использование n дало бы нам смещенную оценку, которая последовательно занижает изменчивость. Выборочная дисперсия, как правило, ниже, чем реальная дисперсия генеральной совокупности.
Уменьшение выборки n до n – 1 делает дисперсию искусственно большой, давая вам объективную оценку изменчивости: лучше переоценить, чем недооценить изменчивость в выборках.
Важно отметить, что то же самое с формулами стандартного отклонения не приводит к полностью объективным оценкам. Поскольку квадратный корень не является линейной операцией, такой как сложение или вычитание, беспристрастность формулы выборочной дисперсии не распространяется на формулу выборочного стандартного отклонения.
Предотвратите плагиат, запустите бесплатную проверку.
Попробуй бесплатноШаги для расчета дисперсии
Дисперсия обычно рассчитывается автоматически любым программным обеспечением, которое вы используете для статистического анализа. Но вы также можете рассчитать его вручную, чтобы лучше понять, как работает формула.
Существует пять основных шагов для нахождения дисперсии вручную. Мы будем использовать небольшой набор данных из 6 баллов, чтобы пройти по шагам.
| Набор данных | |||||
|---|---|---|---|---|---|
| 46 | 69 | 32 | 60 | 52 | 41 |
Чтобы найти среднее, сложите все баллы, а затем разделите их на количество баллов.
| Среднее () |
|---|
| = (46 + 69 + 32 + 60 + 52 + 41) 6 = 50 |
Вычтите среднее из каждой оценки, чтобы получить отклонения от среднего.
Поскольку x̅ = 50, отнимите 50 от каждого результата.
| Оценка | Отклонение от среднего |
|---|---|
| 46 | 46 – 50 = -4 |
| 69 | 69 – 50 = 19 |
| 32 | 32 – 50 = -18 |
| 60 | 60 – 50 = 10 |
| 52 | 52 – 50 = 2 |
| 41 | 41 – 50 = -9 |
Умножить каждое отклонение от среднего само на себя. Это приведет к положительным числам.
| Квадрат отклонения от среднего |
|---|
| (-4) 2 = 4 × 4 = 16 |
| 19 2 = 19 × 19 = 361 |
| (-18) 2 = -18 × -18 = 324 |
| 10 2 = 10 × 10 = 100 |
| 2 2 = 2 × 2 = 4 |
| (-9) 2 = -9 × -9 = 81 |
Сложите все квадраты отклонений.
Это называется сумма квадратов.
| Сумма квадратов |
|---|
| 16 + 361 + 324 + 100 + 4 + 81 = 886 |
Разделить сумму квадратов на n – 1 (для выборки) или N (для генеральной совокупности).
Так как мы работаем с образцом, мы будем использовать n – 1, где n = 6.
| Разница |
|---|
| 886 (6 – 1) = 886 5 = 177,2 |
Почему дисперсия имеет значение?
Разница имеет значение по двум основным причинам:
- Параметрические статистические тесты чувствительны к дисперсии.
- Сравнение дисперсии выборок помогает оценить групповые различия.
Однородность дисперсии в статистических тестах
Важно учитывать дисперсию перед выполнением параметрических тестов.
Эти тесты требуют равных или близких дисперсий, также называемых однородностью дисперсии или гомоскедастичностью, при сравнении разных выборок.
Неравномерная дисперсия между образцами приводит к смещенным и искаженным результатам теста. Если у вас неравномерная дисперсия по выборкам, более подходящими являются непараметрические тесты.
Использование дисперсии для оценки групповых различий
Статистические тесты, такие как дисперсионные тесты или дисперсионный анализ (ANOVA), используют выборочную дисперсию для оценки групповых различий. Они используют дисперсии выборок, чтобы оценить, отличаются ли друг от друга совокупности, из которых они взяты.
Пример исследования Как исследователь в области образования вы хотите проверить гипотезу о том, что разная частота проведения тестов приводит к разным итоговым баллам студентов колледжей. Вы собираете окончательные баллы от трех групп по 20 студентов в каждой, которые часто, нечасто или редко участвовали в викторинах в течение семестра.
- Образец A: один раз в неделю
- Образец B: один раз в 3 недели
- Образец C: один раз в 6 недель
Чтобы оценить групповые различия, вы выполняете дисперсионный анализ.
Основная идея дисперсионного анализа состоит в том, чтобы сравнить дисперсии между группами и дисперсии внутри групп, чтобы увидеть, лучше ли результаты объясняются групповыми различиями или индивидуальными различиями.
Если дисперсия между группами выше, чем внутригрупповая дисперсия, то группы, вероятно, будут отличаться в результате вашего лечения. Если нет, то вместо этого результаты могут быть получены из индивидуальных различий членов выборки.
Пример исследованияВаш дисперсионный анализ оценивает, обусловлены ли различия в средних итоговых баллах между группами различиями в частоте опросов или индивидуальными различиями учащихся в каждой группе. Для этого вы получаете соотношение межгрупповой дисперсии окончательных баллов и внутригрупповой дисперсии окончательных баллов — это F-статистика.
При большой F-статистике вы найдете соответствующее значение p и сделаете вывод, что группы значительно отличаются друг от друга.
Часто задаваемые вопросы о дисперсии
- В чем разница между стандартным отклонением и дисперсией?
Дисперсия — это среднеквадратичное отклонение от среднего значения, а стандартное отклонение — это квадратный корень из этого числа. Обе меры отражают изменчивость распределения, но их единицы различаются:
- Стандартное отклонение выражается в тех же единицах, что и исходные значения (например, минуты или метры).
- Дисперсия выражается в более крупных единицах (например, в квадратных метрах).
Хотя единицы дисперсии труднее интуитивно понять, дисперсия важна в статистических тестах.
- Что такое гомоскедастичность?
Гомоскедастичность или однородность дисперсий — это предположение о равных или подобных дисперсиях в разных сравниваемых группах.
Это важное допущение параметрических статистических тестов, поскольку они чувствительны к любым различиям. Неравномерные отклонения в выборках приводят к необъективным и искаженным результатам испытаний.
Полезна ли эта статья?
Вы уже проголосовали. Спасибо 🙂
Ваш голос сохранен 🙂
Обработка вашего голоса.
..
Прита имеет академическое образование в области английского языка, психологии и когнитивной нейробиологии. Как междисциплинарный исследователь, она любит писать статьи, объясняющие сложные исследовательские концепции для студентов и ученых.
Стандартное отклонение и дисперсия
Отклонение просто означает, насколько далеко от нормы
Стандартное отклонениеСтандартное отклонение является мерой того, насколько наши номера есть.
Его символ σ (греческая буква сигма)
Формула проста: это квадратный корень из Дисперсия. Итак, теперь вы спрашиваете: «Что такое дисперсия?»
Дисперсия
Дисперсия определяется как:
Среднее в квадрате отличий от среднего.
Чтобы рассчитать дисперсию, выполните следующие действия:
- Расчет среднего (простое среднее из номеров)
- Затем для каждого числа: вычтите среднее значение и возведите результат в квадрат
(разность в квадрате ).
- Затем определите среднее значение этих квадратов разностей. (Почему Квадрат?)
Пример
Вы и ваши друзья только что измерили рост ваших собак. (в миллиметрах):
Высота (в плечах): 600 мм, 470 мм, 170 мм, 430 мм. и 300мм.
Узнайте среднее значение, дисперсию и стандартное отклонение.
Ваш первый шаг — найти среднее значение:
Ответ:
| Среднее | = | 600 + 470 + 170 + 430 + 300 5 |
| = | 1970 5 | |
| = | 394 |
, поэтому средняя (средняя) высота составляет 394 мм. Нанесем это на график:
Теперь мы вычисляем разницу каждой собаки от среднего значения:
Чтобы рассчитать дисперсию, возьмите каждую разницу, возведите ее в квадрат и затем усреднить результат:
| Разница | ||
| о 2 | = | 206 2 + 76 2 + (−224) 2 + 36 2 + (−94) 2 5 6 |
| = | 42436 + 5776 + 50176 + 1296 + 8836 5 | |
| = | 108520 5 | |
| = | 21704 | |
Итак, дисперсия равна 21 704
Стандартное отклонение — это всего лишь квадратный корень из дисперсии, так:
| Стандартное отклонение | ||
| о | = | √21704 |
| = | 147,32. .. | |
| = | 147 (с точностью до миллиметра) | |
Стандартное отклонение хорошо тем, что оно полезно. Теперь мы можем показать, какие высоты находятся в пределах одного стандартного отклонения. (147мм) Среднее:
Таким образом, используя стандартное отклонение, мы имеем «стандарт» способ узнать, что является нормальным, а что сверхбольшим или сверхнормативным маленький.
Ротвейлеры — это высоких собак. А таксы немного коротко, да?
Использование
Мы можем ожидать, что около 68% значений будут в пределах плюс-минус. 1 стандартное отклонение.
Прочтите стандартное нормальное распределение, чтобы узнать больше.
Также попробуйте Калькулятор стандартного отклонения.
Но..
. есть небольшое изменение с Sample DataНаш пример был для Популяции (5 собак — единственные собаки, которые нас интересуют).
Но если данные представляют собой выборку (выборку, взятую из большей совокупности), то расчет меняется!
Если у вас есть «N» значений данных, которые являются:
- Население : разделите на N при расчете дисперсии (как у нас)
- A Образец : разделить на N-1 при расчете дисперсии
Все остальные расчеты остаются прежними, включая то, как мы вычисляли среднее значение.
Пример: если наши 5 собак являются просто выборкой большей популяции собак, мы делим на 4 вместо 5 следующим образом: Отклонение = √27 130 = 165 (с точностью до мм)
Думайте об этом как об «исправлении», когда ваши данные являются лишь образцом.
Формулы
Вот две формулы, объясненные в разделе Формулы стандартного отклонения, если вы хотите узнать больше:
«Стандартное отклонение населения «: | ||
| « Образец Стандартное отклонение «: |
Выглядит сложно, но важным изменением является деление
на N-1 (вместо N ) при расчете выборочного стандартного отклонения.
*Сноска: Почему квадратные различия?
Если мы просто сложим отличия от среднего… отрицательные числа отменят положительные:
| 4 + 4 — 4 — 4 4 = 0 |
Так что это не сработает. Как насчет того, чтобы использовать абсолютные значения?
| |4| + |4| + |−4| + |−4| 4 = 4 + 4 + 4 + 4 4 = 4 |
Это выглядит хорошо (и это среднее отклонение), но как насчет этого случая:
| |7| + |1| + |−6| + |−2| 4 = 7 + 1 + 6 + 2 4 = 4 |
О нет! Это также дает значение 4,
Даже если различия более распространены.
Итак, попробуем возвести каждую разность в квадрат (и извлечь в конце квадратный корень):
| √( 4 2 + 4 2 + (-4) 2 + (-4) 2 4 ) = √( 64 4 ) = 4 | ||
| √( 7 2 + 1 2 + (-6) 2 + (-2) 2 4 ) = √( 90 4 ) = 4,74… |
Как хорошо! Стандартное отклонение больше, когда различия более разбросаны … как раз то, что нам нужно.
На самом деле этот метод аналогичен расстоянию между точками, только применяется по-другому.
И алгебру проще использовать с квадратами и квадратными корнями, чем с абсолютными значениями, что упрощает использование стандартного отклонения в других областях математики.
Вернуться к началу
699, 1472, 1473, 3068, 3069, 3070, 3071, 1474, 3804, 3805
Формулы стандартного отклонения
Отклонение просто означает, насколько далеко от нормы
Стандартное отклонениеСтандартное отклонение является мерой того, как наши номера .
Вы могли бы прочитать эту более простую страницу о стандартном отклонении в первую очередь.
Но здесь мы объясним формулы .
Стандартное отклонение обозначается символом σ (греческая буква сигма).
Это формула стандартного отклонения:
Что сказать? Пожалуйста, объясните!
ОК. Давайте объясним это шаг за шагом.
Скажем, у нас есть набор чисел вроде 9, 2, 5, 4, 12, 7, 8, 11.
Чтобы вычислить стандартное отклонение этих чисел:
- 1. Определите среднее (простое среднее из номеров)
- 2. Затем для каждого числа: вычтите среднее значение и возведите результат в квадрат
- 3. Затем вычислите среднее значение этих квадратов разностей.
- 4. Извлеките из этого квадратный корень, и готово!
Затем для каждого числа: вычтите среднее значение и возведите результат в квадратФормула на самом деле говорит все это, и я покажу вам, как это сделать.
Объяснение формулы
Во-первых, давайте возьмем несколько значений для примера:
Пример: у Сэма 20 кустов роз.
Количество цветков на каждом кусте
9, 2, 5, 4, 12, 7, 8, 11, 9, 3, 7, 4, 12, 5, 4, 10, 9, 6, 9, 4
Определите стандартное отклонение.
Шаг 1. Вычислите среднее значение
В приведенной выше формуле μ (греческая буква «мю») — это среднее значение всех наших значений…
Пример: 9, 2, 5, 4, 12, 7, 8, 11, 9, 3, 7, 4, 12, 5, 4, 10, 9, 6, 9, 4
Среднее значение:
9+2+5+4+12+7+8+11+9+3+7+4+12+5+4+10+9+6+9+4 20
= 140 20 = 7
Итак, мк = 7
Шаг 2.
Затем для каждого числа: вычтите среднее значение и возведите результат в квадратЭто часть формулы, которая говорит:
Так что же такое х 9?1035 я ? Это отдельные значения x 9, 2, 5, 4, 12, 7 и т. д….
Другими словами, x 1 = 9, x 2 = 2, x 3 = 5 и т. д.
Итак, он говорит: «для каждого значения вычтите среднее значение и возведите результат в квадрат», вот так
Пример (продолжение):
(9 — 7) 2 = (2) 2 = 4
(2 — 7) 2 = (-5) 5 4 2 0475
(5 — 7) 2 = (-2) 2 = 4
(4 — 7) 2 = (-3) 2 =
9000 3 2 . 7) 2 = (5) 2 = 25(7 — 7) 2 = (0) 2 = 0
(8 -7) 2 .
0
(8 -7) 2 2 = 1 . ) 2 = 1
… и т.д…
И получаем такие результаты:
4, 25, 4, 9, 25, 0, 1, 16, 4, 16, 0, 9 , 25, 4, 9, 9, 4, 1, 4, 9
Шаг 3. Затем определите среднее значение этих квадратов разностей.
Чтобы вычислить среднее значение, сложите все значения , затем разделите на сколько .
Сначала сложите все значения из предыдущего шага.
Но как мы говорим «сложить их все» в математике? Используем «Сигму»: Σ
Удобная сигма-нотация предлагает суммировать столько терминов, сколько мы хотим:
Сигма-нотация
Мы хотим сложить все значения от 1 до N, где в нашем случае N=20, потому что значений 20:
Пример (продолжение):
Что означает: просуммируйте все значения от (x 1 -7) 2 до (x N -7) 2
3 уже вычислено 1 -7) 2 =4 и т.
д. в предыдущем шаге, так что просто суммируйте их:= 4+25+4+9+25+0+1+16+4+16+0+9+ 25+4+9+9+4+1+4+9 = 178
Но это еще не среднее, нам нужно разделить на сколько , что делается путем умножения на 1/N (то же, что деление на N):
Пример (продолжение):
Среднее квадратов разностей = (1/20) × 178 = 8,9
(Примечание: это значение называется «дисперсией»)
Шаг 4. Извлеките из этого квадратный корень:
Пример (завершение):
σ = √(8.9) = 2,983…
ГОТОВО!
Стандартное отклонение выборки
Но подождите, есть еще…
…иногда наши данные — это только выборка всего населения.
Пример: Сэм имеет
20 кустов роз, но посчитал цветы только на 6 из них !«Население» — это все 20 розовых кустов,
, а «образец» — это 6 кустов, у которых Сэм насчитал цветы.
Скажем, количество цветов Сэма:
9, 2, 5, 4, 12, 7
Мы все еще можем оценить стандартное отклонение.
Но когда мы используем выборку как оценку всего населения , формула стандартного отклонения изменяется на это:
Формула для Стандартное отклонение выборки :
Важным изменением является «N-1» вместо «N» (что называется «поправкой Бесселя»).
Символы также меняются, чтобы показать, что мы работаем с выборкой, а не со всей совокупностью:
- Среднее значение теперь равно x (называется «x-bar») для выборочное среднее вместо μ для среднего значения генеральной совокупности,
- И ответ s (для выборочного стандартного отклонения) вместо σ .
Но на расчеты не влияют. Только N-1 вместо N меняет расчеты.
Хорошо, давайте теперь воспользуемся стандартным отклонением образца :
.
Шаг 1. Вычислите среднее значение
Пример 2: Использование выборочных значений 9, 2, 5, 4, 12, 7
Среднее значение равно (9+2+5+4+12+7) / 6 = 39/6 = 6,5
Итак:
x = 6,5
Шаг 2. Затем для каждого числа: вычтите среднее значение и возведите результат в квадрат
Пример 2 (продолжение):
(9 — 6,5) 2 = (2,5) 2 = 6,25
(2 — 6,5) 2 = (-4,5) 2 = 20,25
(5) 2 = 20,25
(-4,5) 2 = 20,25
(-4,5) — 6,5) 2 = (-1,5) 2 = 2,25
(4 — 6,5) 2 = (-2,5) 2 = 6,25
(12 — 6,5) 2 = (5,5) 2 = 30,25
(7 — 6,5) 2 = (0,5) 2 = 0,25
Шаг 3. Затем определите среднее значение этих квадратов разностей.
Чтобы вычислить среднее значение, сложите все значения , затем разделите на сколько .
Но подождите… мы вычисляем стандартное отклонение выборки , поэтому вместо деления на сколько (N) мы будем делить на N-1
Example 2 (continued):
Sum = 6.25 + 20.25 + 2.25 + 6.25 + 30.25 + 0.25 = 65.5
Divide by N-1 : (1/5) × 65.5 = 13.1
( Это значение называется «Выборочная дисперсия»)
Шаг 4. Извлеките из этого квадратный корень:
Пример 2 (завершение):
s = √(13.1) = 3,619…
ГОТОВО!
Сравнение
Использование целых населения мы получили: Среднее значение = 7 , стандартное отклонение = 2,983…
Используя выборку , мы получили: Среднее значение выборки = 6,5 , Стандартное отклонение выборки = 3,619…
Наше выборочное среднее было ошибочным на 7%, а наше выборочное стандартное отклонение было ошибочным на 21%.
Зачем брать пробу?
В основном потому, что это проще и дешевле.
Представьте, что вы хотите знать, что думает вся страна… вы не можете спросить миллионы людей, поэтому вместо этого вы спросите, может быть, 1000 человек.
Есть хорошая цитата (возможно, Сэмюэля Джонсона):
«Не обязательно есть животное целиком, чтобы понять, что мясо жесткое.»
Это основная идея выборки. Чтобы узнать информацию о популяции (такую как среднее значение и стандартное отклонение), нам не нужно смотреть на всех членов популяции; нам нужен только образец.
Но когда мы берем образец, мы теряем некоторую точность.
Поиграйте с этим в симуляторе нормального распространения.
Резюме
Популяция Стандартное отклонение: | ||
| Образец Стандартное отклонение: |
699, 1472, 1473, 1474
Дисперсия: определение, формулы и расчеты
Дисперсия — это мера изменчивости в статистике.
Он оценивает среднеквадратичную разницу между значениями данных и средним значением. В отличие от некоторых других статистических показателей изменчивости, он включает в свои расчеты все точки данных, сопоставляя каждое значение со средним значением.
Если в выборке нет вариабельности, все значения одинаковы, а дисперсия равна нулю. По мере дальнейшего распространения значений данных изменчивость увеличивается.
Например, эти два распределения имеют одно и то же среднее значение. Однако набор данных справа имеет большую изменчивость и, следовательно, более высокую дисперсию.
В этом посте вы узнаете, как рассчитать как популяционную, так и выборочную дисперсию и как их интерпретировать.
Связанный пост : Показатели изменчивости
Формулы дисперсии
Существуют две формулы для дисперсии. Правильная формула зависит от того, работаете ли вы со всей совокупностью или используете выборку для оценки значения совокупности.
Другими словами, решите, какую формулу использовать, в зависимости от того, выполняете ли вы описательную или выводную статистику.
Уравнения приведены ниже, а затем я работаю над примером нахождения дисперсии, чтобы воплотить ее в жизнь.
Формула дисперсии населения
Используйте форму уравнения для населения, когда у вас есть значения для всех членов интересующей группы. В этом случае вы не используете выборку для оценки генеральной совокупности. Вместо этого вы измерили всех людей или предметы и нуждаетесь в дисперсии для этой конкретной группы. Например, если вы измерили результаты тестов для всех членов класса и вам нужно узнать значение для этого класса, используйте формулу дисперсии генеральной совокупности.
Формула дисперсии всей совокупности выглядит следующим образом:
В формуле дисперсии населения:
- σ 2 — дисперсия населения.
- X i — это точка данных i th .
- µ — среднее значение генеральной совокупности.
- n — количество наблюдений.
Чтобы найти дисперсию, возьмите точку данных, вычтите среднее значение генеральной совокупности и возведите эту разницу в квадрат. Повторите этот процесс для всех точек данных. Затем суммируйте все эти квадраты значений и разделите на количество наблюдений. Следовательно, это среднеквадратическая разница.
Формула выборочной дисперсии
Используйте формулу выборочной дисперсии, когда вы используете выборку для оценки значения генеральной совокупности. Например, если вы взяли случайную выборку студентов-статистиков, записали их результаты тестов и хотите использовать эту выборку в качестве оценки совокупности студентов-статистиков, используйте формулу выборочной дисперсии.
Формула генеральной совокупности имеет тенденцию недооценивать изменчивость, когда вы используете ее с выборкой. Приведенная ниже примерная формула исправляет это смещение.
В формуле выборочной дисперсии:
- s 2 — выборочная дисперсия.
- X i — это точка данных i th .
- x̅ — выборочное среднее.
- n–1 — степени свободы.
Процесс расчета выборки очень похож на метод популяции. Однако вы работаете с выборкой, а не с популяцией, и делите на n–1. Этот знаменатель противодействует систематической ошибке, когда выборки имеют тенденцию занижать значение генеральной совокупности.
Давайте рассмотрим пример расчета!
Как найти дисперсию
Вот пример расчета дисперсии с использованием формулы образца. Набор данных содержит 17 наблюдений в таблице ниже. Цифры в скобках соответствуют столбцам таблицы.
Чтобы вычислить статистику, возьмите каждое значение данных (1) и вычтите среднее значение (2), чтобы вычислить разницу (3), а затем возведите разницу в квадрат (4).
Внизу рабочего листа я суммирую квадраты значений и делю их на 17 – 1 = 16, потому что мы находим выборочное значение.
Дисперсия для этого набора данных равна 201.
Интерпретация дисперсии
Дисперсия в статистике представляет собой средний квадрат расстояния между точками данных и средним значением. Поскольку в нем используются квадратные единицы, а не натуральные единицы данных, интерпретация менее интуитивна. Более высокие значения указывают на большую изменчивость, но для конкретных значений нет интуитивной интерпретации. Несмотря на этот недостаток, некоторые проверки статистических гипотез используют его в своих расчетах. Например, почитайте о F-тесте и ANOVA.
Выравнивание различий служит нескольким целям.
Возведение разностей в квадрат не позволяет значениям выше и ниже среднего отменять друг друга. Следовательно, дисперсия всегда больше или равна нулю. Это почти всегда положительное значение, потому что только наборы данных, содержащие одно повторяющееся значение (например, все значения равны 15), имеют нулевое значение.
Кроме того, возведение в квадрат различий непропорционально увеличивает влияние точек данных, которые находятся дальше от среднего значения.
Этот дополнительный вес отражает свойства нормального распределения, при котором выбросы значительно менее вероятны. Экстремальные значения не убывают линейно.
Если вы возьмете квадратный корень из дисперсии, вы получите стандартное отклонение, которое использует интуитивно понятные натуральные единицы измерения данных. Среднее абсолютное отклонение — еще одна мера изменчивости, в которой также используются натуральные единицы, но ее формула не возводит разности в квадрат.
Определение отклонения
Оглавление
Содержание
Что такое дисперсия?
Понимание дисперсии
Преимущества и недостатки
Пример
Часто задаваемые вопросы
Часто задаваемые вопросы о различиях
По
Адам Хейс
Полная биография
Адам Хейс, доктор философии, CFA, финансовый писатель с более чем 15-летним опытом работы на Уолл-стрит в качестве трейдера деривативов.
Помимо своего обширного опыта торговли деривативами, Адам является экспертом в области экономики и поведенческих финансов. Адам получил степень магистра экономики в Новой школе социальных исследований и докторскую степень. из Университета Висконсин-Мэдисон по социологии. Он является обладателем сертификата CFA, а также лицензий FINRA Series 7, 55 и 63. В настоящее время он занимается исследованиями и преподает экономическую социологию и социальные исследования финансов в Еврейском университете в Иерусалиме.
Узнайте о нашем редакционная политика
Обновлено 06 июля 2022 г.
Рассмотрено
Майкл Дж. Бойл
Рассмотрено Майкл Дж. Бойл
Полная биография
Майкл Бойл — опытный специалист в области финансов, более 10 лет занимающийся финансовым планированием, деривативами, акциями, фиксированным доходом, управлением проектами и аналитикой.
Узнайте о нашем Совет финансового контроля
Факт проверен
Викки Веласкес
Факт проверен Викки Веласкес
Полная биография
Викки Веласкес — исследователь и писатель, которая руководила, координировала и руководила различными общественными и некоммерческими организациями.
Она провела углубленное исследование по социальным и экономическим вопросам, а также пересмотрела и отредактировала учебные материалы для района Большого Ричмонда.
Узнайте о нашем редакционная политика
Инвестопедия / Алекс Дос Диас
Что такое дисперсия?
Термин дисперсия относится к статистическому измерению разброса между числами в наборе данных. В частности, дисперсия измеряет, насколько далеко каждое число в наборе от среднего (среднего) и, следовательно, от любого другого числа в наборе. Дисперсия часто обозначается этим символом: σ 2 . Он используется как аналитиками, так и трейдерами для определения волатильности и безопасности рынка.
Квадратный корень из дисперсии представляет собой стандартное отклонение (SD или σ), которое помогает определить постоянство доходности инвестиций в течение определенного периода времени.
Ключевые выводы
- Дисперсия — это измерение разброса между числами в наборе данных.
- В частности, он измеряет степень разброса данных относительно среднего значения выборки.
- Инвесторы используют дисперсию, чтобы увидеть, насколько рискованно вложение и будет ли оно прибыльным.
- Дисперсия также используется в финансах для сравнения относительной эффективности каждого актива в портфеле для достижения наилучшего распределения активов.
- Квадратный корень из дисперсии является стандартным отклонением.
Смотреть сейчас: что такое дисперсия?
Понимание разницы
В статистике дисперсия измеряет отклонение от среднего или среднего значения. Он рассчитывается путем взятия разностей между каждым числом в наборе данных и средним значением, затем возведения в квадрат разностей, чтобы сделать их положительными, и, наконец, деления суммы квадратов на количество значений в наборе данных.
Дисперсия рассчитывается по следующей формуле:
о 2 знак равно ∑ я знак равно 1 н ( Икс я − Икс ‾ ) 2 Н куда: Икс я знак равно Каждое значение в наборе данных Икс ‾ знак равно Среднее значение всех значений в наборе данных Н знак равно Количество значений в наборе данных \begin{align}&\sigma^2 = \frac { \sum_{i = 1} ^ { n } \big (x_i — \overline { x } \big ) ^ 2 }{ N } \\&\textbf{ где:} \\&x_i = \text{Каждое значение в наборе данных} \\&\overline { x } = \text{Среднее значение всех значений в наборе данных} \\&N = \text{Количество значений в наборе данных набор данных} \\\end{выровнено} σ2=N∑i=1n(xi−x)2где:xi=Каждое значение в наборе данныхx=Среднее значение всех значений в наборе данныхN=Количество значений в наборе данных
Вы также можете использовать приведенную выше формулу для расчета дисперсии в других областях, кроме инвестиций и торговли, с некоторыми небольшими изменениями.
Например, при расчете выборочной дисперсии для оценки дисперсии совокупности знаменатель уравнения дисперсии становится равным N — 1, так что оценка является несмещенной и не занижает дисперсию совокупности.
Преимущества и недостатки вариантов
Статистики используют дисперсию, чтобы увидеть, как отдельные числа соотносятся друг с другом в наборе данных, а не используют более широкие математические методы, такие как распределение чисел по квартилям. Преимущество дисперсии в том, что она рассматривает все отклонения от среднего значения как одинаковые, независимо от их направления. Квадраты отклонений не могут в сумме равняться нулю и вообще не создают видимость изменчивости данных.
Однако одним из недостатков дисперсии является то, что она придает дополнительный вес выбросам. Это цифры, далекие от среднего. Возведение этих чисел в квадрат может исказить данные. Еще одна ловушка использования дисперсии заключается в том, что ее нелегко интерпретировать. Пользователи часто используют его в первую очередь для извлечения квадратного корня из его значения, которое указывает на стандартное отклонение данных.
Как отмечалось выше, инвесторы могут использовать стандартное отклонение, чтобы оценить, насколько постоянна доходность с течением времени.
В некоторых случаях риск или волатильность могут быть выражены в виде стандартного отклонения, а не дисперсии, поскольку первое часто легче интерпретировать.
Пример отклонения по финансам
Вот гипотетический пример, демонстрирующий, как работает дисперсия. Допустим, доходность акций компании ABC составляет 10 % в первый год, 20 % в год 2 и −15 % в год 3. Среднее значение этих трех доходностей составляет 5 %. Различия между каждым доходом и средним значением составляют 5%, 15% и -20% за каждый последующий год.
Возведение этих отклонений в квадрат дает 0,25%, 2,25% и 4,00% соответственно. Если мы сложим эти квадраты отклонений, то получим в сумме 6,5%. Когда вы делите сумму 6,5% на единицу меньше количества возвратов в наборе данных, поскольку это выборка (2 = 3-1), это дает нам дисперсию 3,25% (0,0325). Извлечение квадратного корня из дисперсии дает стандартное отклонение 18% (√0,0325 = 0,180) для доходности.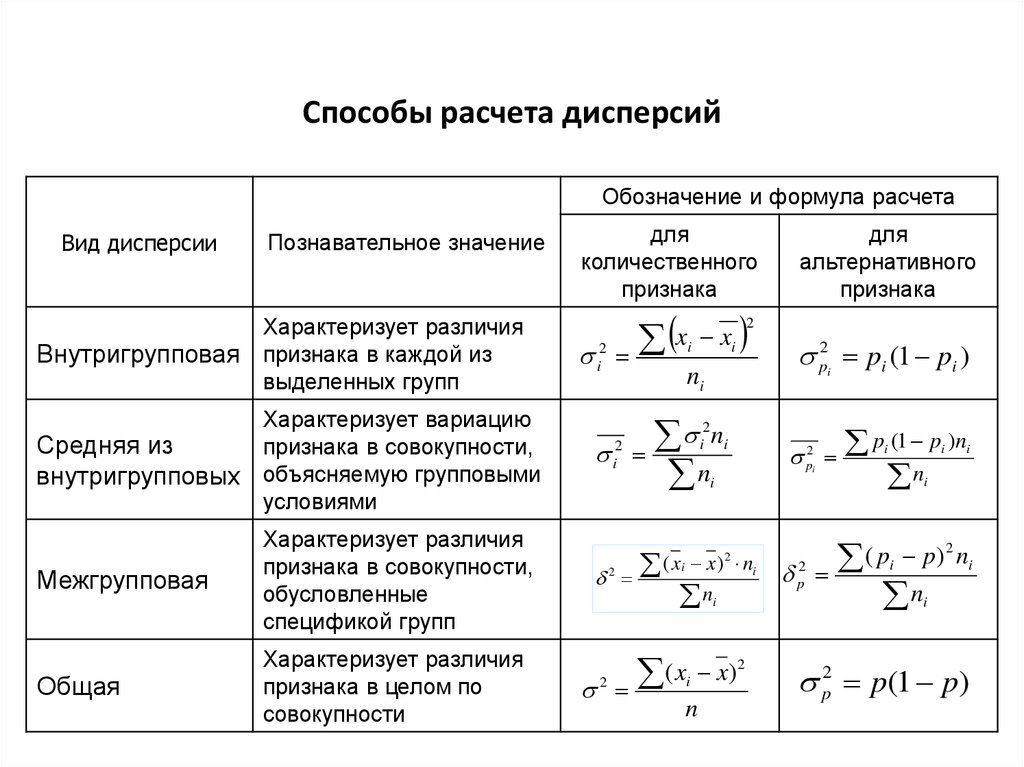
Часто задаваемые вопросы
Как рассчитать дисперсию?
Чтобы вычислить дисперсию, выполните следующие действия:
- Вычислите среднее значение данных.
- Найдите отличие каждой точки данных от среднего значения.
- Возведение в квадрат каждого из этих значений.
- Сложите все квадраты значений.
- Разделите эту сумму квадратов на n – 1 (для выборки) или N (для генеральной совокупности).
Для чего используется дисперсия?
Дисперсия — это, по сути, степень разброса в наборе данных относительно среднего значения этих данных. Он показывает количество вариаций, существующих между точками данных. Визуально, чем больше дисперсия, тем «жирнее» будет распределение вероятностей. В финансах, если что-то вроде инвестиций имеет большую дисперсию, это может быть интерпретировано как более рискованное или волатильное.
Почему стандартное отклонение часто используется больше, чем дисперсия?
Стандартное отклонение — это квадратный корень из дисперсии.
Иногда это более полезно, так как при извлечении квадратного корня единицы измерения удаляются из анализа. Это позволяет проводить прямое сравнение между разными вещами, которые могут иметь разные единицы измерения или разные величины. Например, если сказать, что увеличение X на одну единицу увеличивает Y на два стандартных отклонения, это позволяет понять взаимосвязь между X и Y независимо от того, в каких единицах они выражены.
Дисперсия — определение, формула, примеры, свойства
Дисперсия — это статистическое измерение, которое используется для определения разброса чисел в наборе данных по отношению к среднему значению или среднему значению. Квадрат стандартного отклонения даст нам дисперсию. Используя дисперсию, мы можем оценить, насколько растянуто или сжато распределение.
В статистике могут быть два типа дисперсии, а именно выборочная дисперсия и дисперсия генеральной совокупности. Символ дисперсии задается σ 2 . Дисперсия широко используется при проверке гипотез, проверке соответствия и выборке методом Монте-Карло.
Чтобы проверить, насколько сильно различаются отдельные точки данных по отношению к среднему значению, мы используем дисперсию. В этой статье мы рассмотрим определение, примеры, формулы, приложения и свойства дисперсии.
| 1. | Что такое дисперсия? |
| 2. | Формула дисперсии |
| 3. | Дисперсия и стандартное отклонение |
| 4. | Как найти дисперсию? |
| 5. | Дисперсия и ковариация |
| 6. | Свойства отклонения |
| 7. | Часто задаваемые вопросы о дисперсии |
Что такое дисперсия?
Дисперсия является мерой дисперсии. Мера дисперсии — это величина, которая используется для проверки изменчивости данных о среднем значении. Данные могут быть двух типов — сгруппированные и разгруппированные. Когда данные выражаются в виде интервалов классов, они называются сгруппированными данными.
С другой стороны, если данные состоят из отдельных точек данных, они называются несгруппированными данными. Выборочная и генеральная дисперсия может быть определена для обоих типов данных.
Дисперсия Определение
Дисперсия населения — Все члены группы известны как население. Когда мы хотим выяснить, как каждая точка данных в данной совокупности изменяется или распределяется, мы используем дисперсию совокупности. Он используется для получения квадрата расстояния каждой точки данных от среднего значения генеральной совокупности.
Выборочная дисперсия — Если размер генеральной совокупности слишком велик, трудно учесть каждую точку данных. В таком случае из совокупности берется определенное количество точек данных, чтобы сформировать выборку, которая может описать всю группу. Таким образом, выборочная дисперсия может быть определена как среднее квадратов расстояний от среднего. Дисперсия всегда рассчитывается относительно среднего значения выборки.
Общее определение дисперсии состоит в том, что она представляет собой ожидаемое значение квадратов отличий от среднего значения.
Пример дисперсии
Предположим, у нас есть набор данных {3, 5, 8, 1}, и мы хотим найти дисперсию генеральной совокупности. Среднее дается как (3 + 5 + 8 + 1) / 4 = 4,25. Тогда, используя определение дисперсии, мы получаем [(3 — 4,25) 2 + (5 — 4,25) 2 + (8 — 4,25) 2 + (1 — 4,25) 2 ] / 4 = 6,68 . Таким образом, дисперсия = 6,68.
9{2}}{n}\), где \(\overline{X}\) означает среднее, \(M_{i}\) — середина интервала i th , \(X_{i }\) — это точка данных i th , N — сумма всех частот, а n — количество наблюдений.
Среднее значение для сгруппированных данных = \(\frac{\sum M_{i}f_{i}}{\sum f_{i}}\)
Общая формула дисперсии задается как
Var (X) = E[( X – μ) 2 ]
Дисперсия и стандартное отклонение
Когда мы берем квадрат стандартного отклонения, мы получаем дисперсию заданных данных.
Интуитивно мы можем думать о дисперсии как о числовом значении, которое используется для оценки изменчивости данных о среднем значении. Это означает, что дисперсия показывает, насколько далеко каждая отдельная точка данных от среднего, а также друг от друга. Когда мы хотим найти дисперсию точек данных относительно среднего значения, мы используем стандартное отклонение. Другими словами, когда мы хотим увидеть, как наблюдения в наборе данных отличаются от среднего, используется стандартное отклонение. о 2 — это символ, обозначающий дисперсию, а σ представляет собой стандартное отклонение. Дисперсия выражается в квадратных единицах, в то время как стандартное отклонение имеет ту же единицу, что и совокупность или выборка.
Как найти дисперсию?
Для нахождения дисперсии разгруппированных данных можно использовать следующие шаги:
- Найти среднее значение наблюдений. Это можно сделать, разделив сумму всех наблюдений на количество наблюдений.
- Вычесть среднее значение из каждого наблюдения.
- Возведение в квадрат каждого из этих значений.
- Сложите все значения, полученные на предыдущем шаге.
- Разделите значение из шага 4 на n (для дисперсии генеральной совокупности) или n — 1 (для дисперсии выборки).
Дисперсия биномиального распределения
Биномиальное распределение определяется как дискретное распределение вероятностей, в котором указывается количество успешных результатов при проведении биномиального эксперимента n раз. Каждый раз, когда результат эксперимента может быть только 0 или 1. Допустим, у нас есть биномиальный эксперимент, который состоит из n испытаний, и вероятность успеха в каждом испытании определяется p, тогда дисперсия биномиального распределения дается как:
σ 2 = np (1 — p).
Здесь np также равно среднему значению.
Дисперсия распределения Пуассона
Распределение Пуассона — это еще один тип дискретного распределения вероятностей, который дает вероятность определенного количества событий, происходящих в течение определенного периода времени.
Параметр распределения Пуассона определяется как λ. В этом распределении среднее значение и дисперсия равны. Дисперсия распределения Пуассона определяется как:
σ 2 = λ
Дисперсия равномерного распределения
Равномерное распределение является типом непрерывного распределения вероятностей. Это также известно как прямоугольное распределение, поскольку результат эксперимента будет лежать между минимальной и максимальной границей. Если a — минимальная граница, а b — максимальная граница, то дисперсия равномерного распределения будет следующей: (б + а) / 2.
Дисперсия и ковариация
Дисперсия используется для описания разброса набора данных и определения того, насколько далеко каждая точка данных находится от среднего значения. Ковариация показывает нам, как две случайные величины будут связаны друг с другом. Он измеряет, как одна переменная будет затронута из-за изменения другой случайной переменной. Если у нас есть положительная ковариация, это означает, что обе переменные движутся в одном направлении.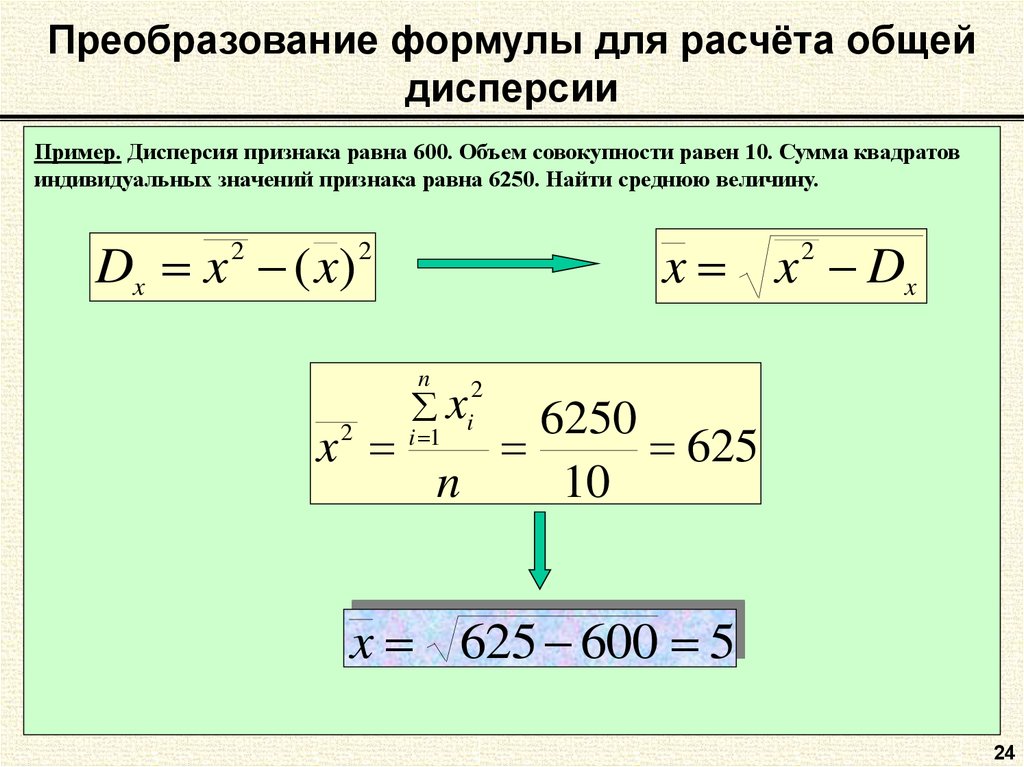
Однако если у нас отрицательная ковариация, это означает, что обе переменные движутся в противоположных направлениях. Предположим, у нас есть две случайные величины x и y. Здесь x — зависимая переменная, а y — независимая переменная. Пусть n — количество точек данных в выборке, \(\overline{x}\) — среднее значение x, а \(\overline{y}\) — среднее значение y, тогда формула для ковариации приведена ниже. : 9{n}(x_{i} — \overline{x})(y_{i} — \overline{y})}{n — 1}\)
Свойства отклонения
Ниже приведены некоторые свойства дисперсии, которые могут помочь в решении как простых, так и сложных задач на суммы.
- Если значение дисперсии равно 0, это означает, что все точки данных в наборе данных имеют одинаковое значение.
- Большая дисперсия означает, что данные более сильно разбросаны по сравнению со средним значением. Точно так же небольшая дисперсия показывает, что значения точек данных ближе друг к другу и сгруппированы вокруг среднего значения.
- Var(X + C) = Var(X), где X — случайная величина, а C — константа.
- Var(aX + b) = a 2 , здесь a и b — константы.
- Вар(СХ) = С 2
Var(X), C — константа. - Var(X 1 + X 2 +……+ X n ) = Var(X 1 ) + Var(X 2 ) +……..+Var(X n ) где X 1 , X 2 ,……, X n — независимые случайные величины.
Статьи по теме:
- Калькулятор дисперсии
- Средний
- Вероятность
Важные примечания о дисперсии
- Дисперсия является мерой изменчивости данных и описывает, как точки данных распределены по отношению к среднему значению.
- Может быть два типа дисперсии — выборочная дисперсия и дисперсия генеральной совокупности.
- Могут быть два вида данных — сгруппированные и разгруппированные. Таким образом, мы можем иметь сгруппированную выборочную дисперсию, негруппированную выборочную дисперсию, сгруппированную дисперсию совокупности и негруппированную дисперсию совокупности.
- Дисперсия представляет собой квадрат стандартного отклонения.
- Ковариация описывает, как зависимая и независимая случайные величины связаны друг с другом.
Часто задаваемые вопросы о Variance
Что такое дисперсия в статистике?
Дисперсия в статистике — это мера дисперсии, указывающая на изменчивость точек данных по отношению к среднему значению. Выборочная дисперсия и дисперсия населения — это два типа дисперсии.
Как рассчитать дисперсию?
Дисперсия разгруппированных данных может быть рассчитана с помощью следующих шагов:
- Найдите среднее значение и вычтите его из каждой точки данных.
- Проведите суммирование квадратов значений, полученных на шаге 1.
- Разделите это значение на n(количество наблюдений) или n — 1, если необходимо рассчитать дисперсию генеральной совокупности или выборки соответственно.
Что дисперсия говорит вам о данных?
Дисперсия говорит нам, насколько разбросаны данные по отношению к среднему значению.