Как считается длина окружности. Задачи на площадь круга
Окружностью называется ряд равноудалённых точек от одной точки, которая, в свою очередь, является центром этой окружности. Окружность имеет также свой радиус, равный расстоянию этих точек от центра.
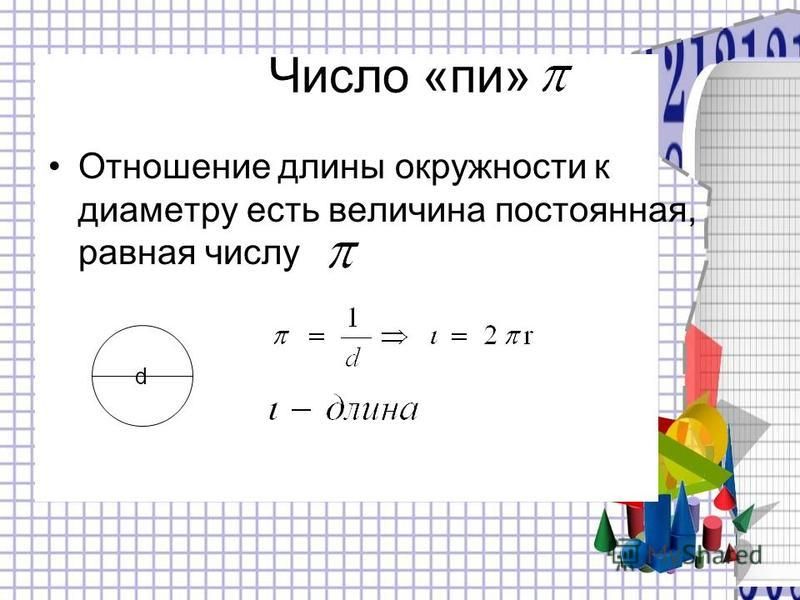
Отношение длины, какой либо окружности к её диаметру, для всех окружностей одинаково. Это отношение есть число, являющееся математической константой, которое обозначается греческой буквой π .
Определение длины окружности
Произвести расчёт окружности можно по следующей формуле:
L = π D = 2 π r
r — радиус окружности
D — диаметр окружности
L — длина окружности
π — 3.14
Задача:
Вычислить длину окружности , имеющей радиус 10 сантиметров.
Решение:
Формула для вычисления дины окружности имеет вид:
L = π D = 2 π r
где L – длина окружности, π – 3,14 , r – радиус окружности, D – диаметр окружности.
Таким образом, длина окружности, имеющей радиус 10 сантиметров равна:
L = 2 × 3,14 × 10 = 62,8 сантиметра
Окружность представляет собой геометрическую фигуру, являющуюся совокупностью всех точек на плоскости, удаленных от заданной точки, которая называется ее центром, на некоторое расстояние, не равное нулю и именуемое радиусом. Определять ее длину с различной степенью точности ученые умели уже в глубокой древности: историки науки считают, что первая формула для вычисления длины окружности была составлена примерно в 1900 году до нашей эры в древнем Вавилоне.
С такими геометрическими фигурами, как окружности, мы сталкиваемся ежедневно и повсеместно. Именно ее форму имеет внешняя поверхность колес, которыми оснащаются различные транспортные средства. Эта деталь, несмотря на свою внешнюю простоту и незатейливость, считаются одним из величайших изобретений человечества, причем интересно, что аборигены Австралии и американские индейцы вплоть до прихода европейцев совершенно не имели понятия о том, что это такое.
По всей вероятности, самые первые колеса представляли собой отрезки бревен, которые насаживались на ось. Постепенно конструкция колеса совершенствовалась, их конструкция становилась все более и более сложной, а для их изготовления требовалось использовать массу различных инструментов. Сначала появились колеса, состоящие из деревянного обода и спиц, а затем, для того, чтобы уменьшить износ их внешней поверхности, ее стали обивать металлическими полосами. Для того чтобы определить длины этих элементов, и требуется использовать формулу расчета длины окружности (хотя на практике, вероятнее всего, мастера это делали «на глаз» или просто опоясывая колесо полосой и отрезая требуемый ее участок).
Следует заметить, что колесо используется отнюдь не только в транспортных средствах. Например, его форму имеет гончарный круг, а также элементы шестеренок зубчатых передач, широко применяемых в технике. Издавна колеса использовались в конструкциях водяных мельниц (самые древние из известных ученым сооружений такого рода строились в Месопотамии), а также прялок, применявшихся для изготовления нитей из шерсти животных и растительных волокон.
Окружности нередко можно встретить и в строительстве. Их форму имеют достаточно широко распространенные круглые окна, очень характерные для романского архитектурного стиля. Изготовление этих конструкций – дело весьма непростое и требует высокого мастерства, а также наличия специального инструмента. Одной из разновидностей круглых окон являются иллюминаторы, устанавливаемые в морских и воздушных судах.
Таким образом, решать задачу определения длины окружности часто приходится инженерам-конструкторам, разрабатывающим различные машины, механизмы и агрегаты, а также архитекторам и проектировщикам. Поскольку число π , необходимое для этого, является бесконечным, то с абсолютной точностью определить этот параметр не представляется возможным, и поэтому при вычислениях учитывается та ее степень, которая в том или ином конкретном случае является необходимой и достаточной.
Окружностью называют кривую линию, которая ограничивает собой круг. В геометрии фигуры плоские, поэтому определение относится к двухмерному изображению. Предполагается, что все точки этой кривой удалены от центра круга на равное расстояние.
Предполагается, что все точки этой кривой удалены от центра круга на равное расстояние.
У окружности есть несколько характеристик, на основе которых производят расчеты, связанные с этой геометрической фигурой. В их число входит: диаметр, радиус, площадь и длина окружности. Эти характеристики взаимосвязаны, то есть для их вычисления достаточно информации хотя бы об одной из составляющих. Например, зная только радиус геометрической фигуры по формуле можно найти длину окружности, диаметр, и ее площадь.
- Радиус окружности – это отрезок внутри окружности, соединённый с ее центром.
- Диаметр – это отрезок внутри окружности, соединяющий ее точки и проходящий через центр. По сути, диаметр – это два радиуса. Именно так выглядит формула для его вычисления: D=2r.
- Есть еще одна составляющая окружности – хорда. Эта прямая, которая соединяет две точки окружности, но не всегда проходит через центр. Так вот ту хорду, которая через него проходит, тоже называют диаметром.

Как узнать длину окружности? Сейчас выясним.
Длина окружности: формула
Для обозначения этой характеристики выбрана латинская буква p. Еще Архимед доказал, что отношение длины окружности к ее диаметру является одним и тем же числом для всех окружностей: это число π, которое приблизительно равно 3,14159. Формула для вычисления π выглядит так: π = p/d. Согласно этой формуле, величина p равна πd, то есть длина окружности: p= πd. Поскольку d (диаметр) равен двум радиусам, то эту же формулу длины окружности можно записать как p=2πr.Рассмотрим применение формулы на примере простых задач:
Задача 1
У основания царь-колокола диаметр равен 6,6 метров. Какова длина окружности основания колокола?
- Итак, формула для вычисления окружности — p= πd
- Подставляем имеющееся значение в формулу: p=3,14*6,6= 20,724
Ответ: длина окружности основания колокола 20,7 метра.
Задача 2
Искусственный спутник Земли вращается на расстоянии 320 км от планеты. Радиус Земли – 6370 км. Какова длина круговой орбиты спутника?
Радиус Земли – 6370 км. Какова длина круговой орбиты спутника?
- 1.Вычислим радиус круговой орбиты спутника Земли: 6370+320=6690 (км)
- 2.Вычислим длину круговой орбиты спутника по формуле: P=2πr
- 3.P=2*3,14*6690=42013,2
Ответ: длина круговой орбиты спутника Земли 42013,2 км.
Способы измерения длины окружности
Вычисление длины окружности на практике используется не часто. Причиной тому приблизительное значение числа π. В быту для поиска длины круга используют специальный прибор – курвиметр. На окружности отмечают произвольную точку отсчета и ведут от нее прибор строго по линии, пока опять не дойдут до этой точки.
Как найти длину окружности? Нужно просто держать в голове незамысловатые формуля для вычислений.
Окружность состоит из множества точек, которые находятся на равном расстоянии от центра. Это плоская геометрическая фигура, и найти ее длину не составит труда. С окружностью и кругом человек сталкивается ежедневно независимо от того, в какой сфере он работает. Многие овощи и фрукты , устройства и механизмы, посуда и мебель имеют круглую форму. Кругом называют то множество точек, которое находится в границах окружности. Поэтому длина фигуры равна периметру круга.
Многие овощи и фрукты , устройства и механизмы, посуда и мебель имеют круглую форму. Кругом называют то множество точек, которое находится в границах окружности. Поэтому длина фигуры равна периметру круга.
Характеристики фигуры
Кроме того, что описание понятия окружности достаточно простое, её характеристики также несложные для понимания. С их помощью можно вычислить её длину. Внутренняя часть окружности состоит из множества точек, среди которых две — А и В — можно увидеть под прямым углом. Этот отрезок называют диаметром, он состоит из двух радиусов.
В пределах окружности имеются точки Х такие , что не изменяется и не равняется единице отношение АХ/ВХ. В окружности это условие обязательно соблюдается, в ином случае эта фигура не имеет форму круга. На каждую точку, из которых состоит фигура, распространяется правило: сумма квадратов расстояний от этих точек до двух других всегда превышает половину длины отрезка между ними.
Основные термины окружности
Для того чтобы уметь находить длину фигуры, необходимо знать основные термины, касающиеся её. Основные параметры фигуры — это диаметр, радиус и хорда . Радиусом называют отрезок, соединяющий центр круга с любой точкой на её кривой. Величина хорды равна расстоянию между двумя точками на кривой фигуры. Диаметр — расстояние между точками , проходящее через центр фигуры.
Основные параметры фигуры — это диаметр, радиус и хорда . Радиусом называют отрезок, соединяющий центр круга с любой точкой на её кривой. Величина хорды равна расстоянию между двумя точками на кривой фигуры. Диаметр — расстояние между точками , проходящее через центр фигуры.
Основные формулы для вычислений
Параметры используются в формулах вычислений величин окружности:
Диаметр в формулах вычисления
В экономике и математике нередко появляется необходимость поиска длины окружности. Но и в повседневной жизни можно столкнуться с этой надобностью, к примеру, во время постройки забора вокруг бассейна круглой формы. Как рассчитать длину окружности по диаметру? В этом случае используют формулу C = π*D, где С — это искомая величина, D — диаметр.
Например, ширина бассейна равна 30 метрам, а столбики забора планируют поставить на расстоянии десяти метров от него. В этом случае формула расчёта диаметра: 30+10*2 = 50 метров. Искомая величина (в этом примере — длина забора): 3,14*50 = 157 метров. Если столбики забора будут стоять на расстоянии трёх метров друг от друга, то всего их понадобится 52.
Если столбики забора будут стоять на расстоянии трёх метров друг от друга, то всего их понадобится 52.
Расчёты по радиусу
Как вычислить длину окружности по известному радиусу? Для этого используется формула C = 2*π*r, где С — длина, r — радиус. Радиус в круге меньше диаметра в два раза, и это правило может пригодиться в повседневной жизни. К примеру, в случае приготовления пирога в раздвижной форме.
Для того чтобы кулинарное изделие не испачкалось, необходимо использовать декоративную обёртку. А как вырезать бумажный круг подходящего размера?
Те, кто немного знаком с математикой, понимают, что в этом случае нужно умножить число π на удвоенный радиус используемой формы. Например, диаметр формы равен 20 сантиметрам, соответственно, её радиус составляет 10 сантиметров. По этим параметрам находится необходимый размер круга: 2*10*3, 14 = 62,8 сантиметра.
Подручные способы вычисления
Если найти длину окружности по формуле нет возможности, то стоит воспользоваться подручными методами расчёта этой величины:
- При небольших размерах круглого предмета его длину можно найти с помощью верёвки, обёрнутой вокруг один раз.

- Величину большого предмета измеряют так: на ровной плоскости раскладывают верёвку, и по ней прокатывают круг один раз.
- Современные студенты и школьники для расчётов используют калькуляторы. В режиме онлайн по известным параметрам можно узнавать неизвестные величины.
Круглые предметы в истории человеческой жизни
Первое изделие круглой формы, которое изобрёл человек — это колесо. Первые конструкции представляли собой небольшие округлые бревна, насаженные на оси. Затем появились колёса, сделанные из деревянных спиц и обода. Постепенно в изделие добавляли металлические детали для уменьшения износа. Именно для того, чтобы узнать длину металлических полос для обивки колёса, учёные прошлых веков искали формулу расчёта этой величины.
Форму колеса имеет гончарный круг , большинство деталей в сложных механизмах, конструкциях водяных мельниц и прялок. Нередко встречаются круглые предметы в строительстве — рамки круглых окон в романском архитектурном стиле, иллюминаторы в суднах. Архитекторы, инженеры, учёные, механики и проектировщики ежедневно в сфере своей профессиональной деятельности сталкиваются с надобностью расчёта размеров окружности.
Архитекторы, инженеры, учёные, механики и проектировщики ежедневно в сфере своей профессиональной деятельности сталкиваются с надобностью расчёта размеров окружности.
Множество предметов в окружающем мире имеют круглую форму. Это колеса, круглые оконные проемы, трубы, различная посуда и многое другое. Подсчитать, чему равна длина окружности, можно, зная ее диаметр или радиус.
Существует несколько определений этой геометрической фигуры.
- Это замкнутая кривая, состоящая из точек, которые располагаются на одинаковом расстоянии от заданной точки.
- Это кривая, состоящая из точек А и В, являющихся концами отрезка, и всех точек, из которых А и В видны под прямым углом. При этом отрезок АВ – диаметр.
- Для того же отрезка АВ эта кривая включает все точки С, такие, что отношение АС/ВС неизменно и не равняется 1.
- Это кривая, состоящая из точек, для которых справедливо следующее: если сложить квадраты расстояний от одной точки до двух данных других точек А и В, получится постоянное число, большее 1/2 соединяющего А и В отрезка.
 Это определение выводится из теоремы Пифагора.
Это определение выводится из теоремы Пифагора.
Обратите внимание! Есть и другие определения. Круг – это область внутри окружности. Периметр круга и есть ее длина. По разным определениям круг может включать или не включать саму кривую, являющуюся его границей.
Определение окружности
Формулы
Как вычислить длину окружности через радиус? Это делается по простой формуле:
где L – искомая величина,
π – число пи, примерно равное 3,1413926.
Обычно для нахождения нужной величины достаточно использовать π до второго знака, то есть 3,14, это обеспечит нужную точность. На калькуляторах, в частности инженерных, может быть кнопка, которая автоматически вводит значение числа π.
Обозначения
Для нахождения через диаметр существует следующая формула:
Если L уже известно, можно легко узнать радиус или диаметр. Для этого L нужно поделить на 2π или на π соответственно.
Если уже дана круга, нужно понимать, как найти длину окружности по этим данным. Площадь круга равняется S = πR2. Отсюда находим радиус: R = √(S/π). Тогда
Площадь круга равняется S = πR2. Отсюда находим радиус: R = √(S/π). Тогда
L = 2πR = 2π√(S/π) = 2√(Sπ).
Вычислить площадь через L также несложно: S = πR2 = π(L/(2π))2 = L2/(4π)
Резюмируя, можно сказать, что существует три основных формулы:
- через радиус – L = 2πR;
- через диаметр – L = πD;
- через площадь круга – L = 2√(Sπ).
Число пи
Без числа π решить рассматриваемую задачу не получится. Число π впервые и было найдено как отношение длины окружности к ее диаметру. Это сделали еще древние вавилоняне, египтяне и индийцы. Нашли они его довольно точно – их результаты отличались от известного сейчас значения π не больше, чем на 1%. Постоянную приближали такими дробями как 25/8, 256/81, 339/108.
Далее значение этой постоянной считали не только с позиции геометрии, но и с точки зрения математического анализа через суммы рядов. Обозначение этой константы греческой буквой π впервые использовал Уильям Джонс в 1706 году, а популярно оно стало после работ Эйлера.
Сейчас известно, что эта постоянная представляет собой бесконечную непериодическую десятичную дробь, она иррациональна, то есть ее нельзя представить в виде отношения двух целых чисел. С помощью вычислений на суперкомпьютерах в 2011 году узнали 10-триллионный знак константы.
Это интересно! Для запоминания нескольких первых знаков числа π были придуманы различные мнемонические правила. Некоторые позволяют хранить в памяти большое число цифр, например, одно французское стихотворение поможет запомнить пи до 126 знака.
Если вам необходима длина окружности, онлайн-калькулятор поможет в этом. Таких калькуляторов существует множество, в них нужно только ввести радиус или диаметр. У некоторых из них есть обе эти опции, другие вычисляют результат только через R. Некоторые калькуляторы могут рассчитать искомую величину с разной точностью, нужно указать число знаков после запятой. Также с помощью онлайн-калькуляторов можно посчитать площадь круга.
Такие калькуляторы легко найти любым поисковиком. Также существуют мобильные приложения, которые помогут решить задачу, как найти длину окружности.
Полезное видео: длина окружности
Практическое применение
Решать такую задачу чаще всего необходимо инженерам и архитекторам, но и в быту знание нужных формул тоже может пригодиться. Например, требуется обернуть бумажной полоской торт, испеченный в форме с поперечником 20 см. Тогда не составит труда найти длину этой полоски:
L = πD = 3,14 * 20 = 62,8 см.
Другой пример: нужно построить забор вокруг круглого бассейна на определенном расстоянии. Если радиус бассейна 10 м, а забор нужно поставить на расстоянии 3 м, то R для полученной окружности будет 13 м. Тогда ее длина равна:
L = 2πR = 2 * 3,14 * 13 = 81,68 м.
Полезное видео: круг — радиус, диаметр, длина окружности
Итог
Периметр круга легко рассчитать по простым формулам, включающим диаметр или радиус. Также можно найти искомую величину через площадь круга. Решить эту задачу помогут онлайн-калькуляторы или мобильные приложения, в которые нужно ввести единственное число – диаметр или радиус.
Решить эту задачу помогут онлайн-калькуляторы или мобильные приложения, в которые нужно ввести единственное число – диаметр или радиус.
Сначала разберемся в отличии между кругом и окружностью. Чтобы увидеть эту разницу, достаточно рассмотреть, чем являются обе фигуры. Это бесчисленное количество точек плоскости, располагающиеся на равном расстоянии от единственной центральной точки. Но, если круг состоит и из внутреннего пространства, то окружности оно не принадлежит. Получается, что круг это и окружность, ограничивающая его (о-кру(г)жность), и бесчисленное число точек, что внутри окружности.
Для любой точки L , лежащей на окружности, действует равенство OL=R . (Длина отрезка OL равняется радиусу окружности).
Отрезок, который соединяет две точки окружности, является ее хордой .
Хорда, проходящая прямо через центр окружности, является диаметром этой окружности (D) . Диаметр можно вычислить по формуле: D=2R
Длина окружности вычисляется по формуле: C=2\pi R
Площадь круга : S=\pi R^{2}
Дугой окружности называется та ее часть, которая располагается между двух ее точек. {\circ}}
{\circ}}
Диаметр, что перпендикулярен хорде, делит хорду и стянутые ею дуги пополам.
В случае, если хорды AB и CD окружности имеют пересечение в точке N , то произведения отрезков хорд, разделенные точкой N , равны между собой.
AN\cdot NB = CN \cdot ND
Касательная к окружности
Касательной к окружности принято называть прямую, у которой имеется одна общая точка с окружностью.
Если же у прямой есть две общие точки, ее называют секущей .
Если провести радиус в точку касания, он будет перпендикулярен касательной к окружности.
Проведем две касательные из этой точки к нашей окружности. Получится, что отрезки касательных сравняются один с другим, а центр окружности расположится на биссектрисе угла с вершиной в этой точке.
AC = CB
Теперь к окружности из нашей точки проведем касательную и секущую. Получим, что квадрат длины отрезка касательной будет равен произведению всего отрезка секущей на его внешнюю часть. {\circ}
{\circ}
\angle ADB = \angle AEB = \angle AFB
На одной окружности находятся вершины треугольников с тождественными углами и заданным основанием.
Угол с вершиной внутри окружности и расположенный между двумя хордами тождественен половине суммы угловых величин дуг окружности, которые заключаются внутри данного и вертикального углов.
\angle DMC = \angle ADM + \angle DAM = \frac{1}{2} \left (\cup DmC + \cup AlB \right)
Угол с вершиной вне окружности и расположенный между двумя секущими тождественен половине разности угловых величин дуг окружности, которые заключаются внутри угла.
\angle M = \angle CBD — \angle ACB = \frac{1}{2} \left (\cup DmC — \cup AlB \right)
Вписанная окружность
Вписанная окружность — это окружность, касающаяся сторон многоугольника.
В точке, где пересекаются биссектрисы углов многоугольника, располагается ее центр.
Окружность может быть вписанной не в каждый многоугольник.
Площадь многоугольника с вписанной окружностью находится по формуле:
S = pr ,
p — полупериметр многоугольника,
r — радиус вписанной окружности.
Отсюда следует, что радиус вписанной окружности равен:
r = \frac{S}{p}
Суммы длин противоположных сторон будут тождественны, если окружность вписана в выпуклый четырехугольник. И наоборот: в выпуклый четырехугольник вписывается окружность, если в нем суммы длин противоположных сторон тождественны.
AB + DC = AD + BC
В любой из треугольников возможно вписать окружность. Только одну единственную. В точке, где пересекаются биссектрисы внутренних углов фигуры, будет лежать центр этой вписанной окружности.
Радиус вписанной окружности вычисляется по формуле:
r = \frac{S}{p} ,
где p = \frac{a + b + c}{2}
Описанная окружность
Если окружность проходит через каждую вершину многоугольника, то такую окружность принято называть описанной около многоугольника . {\circ}
{\circ}
Около любого треугольника можно описать окружность, причем одну-единственную. Центр такой окружности будет расположен в точке, где пересекаются серединные перпендикуляры сторон треугольника.
Радиус описанной окружности можно вычислить по формулам:
R = \frac{a}{2 \sin A} = \frac{b}{2 \sin B} = \frac{c}{2 \sin C}
R = \frac{abc}{4 S}
a , b , c — длины сторон треугольника,
S — площадь треугольника.
Теорема Птолемея
Под конец, рассмотрим теорему Птолемея.
Теорема Птолемея гласит, что произведение диагоналей тождественно сумме произведений противоположных сторон вписанного четырехугольника.
AC \cdot BD = AB \cdot CD + BC \cdot AD
Длина окружности. Площадь круга
Представим себе такую историю…
– Паша, чем ты занимаешься? – спросил у друга Саша.
–
Решил обновить шины на моём велосипеде, – ответил Паша. – Чтобы купить новые,
мне нужно знать размер колеса.
– И как же ты узнаешь этот размер? – решил уточнить Саша.
– Для этого мне нужно измерить длину шины велосипедного колеса, – ответил Паша.
– А как измерить эту длину? – удивился Саша. – Ты же не будешь для этого резать шину?
– Да это же совсем просто! – улыбнулся Паша. – Я взял сантиметровую ленту у мамы и ей измерил длину шины.
– И точно, всё просто! – согласился Саша. – И что же у тебя вышло?
– Длина шины моего колеса равна 189 сантиметрам.
– Это значит, размер твоего велосипедного колеса 189 сантиметров? – решил уточнить Саша.
– Нет, – ответил Паша, – а вот чтобы выяснить размер велосипедного колеса, нужно как-то из длины шины выразить диаметр. А как это сделать, я не знаю.
– Ну чего же ты расстраиваешься?! – воскликнул Саша. – Давай спросим у Мудряша. Он точно сможет нам помочь.
–
Ребята, прежде чем я отвечу на ваш вопрос, давайте немного разомнёмся и
выполним устные задания, – предложил Мудряш.
– Давайте сверимся! – сказал Мудряш. — Посмотрите, что у вас должно было получиться!
– Ну а теперь вернёмся к вашему вопросу, – начал Мудряш. – Всё правильно. Чтобы выяснить, какой размер у велосипедного колеса, нужно знать его диаметр. Но для начала давайте определим, какую форму имеет велосипедное колесо.
– Велосипедное колесо имеет форму окружности, – ответили мальчишки.
– Верно! – согласился Мудряш. – Зная длину окружности, можно вычислить её диаметр.
– А как измерить длину окружности? – решили спросить мальчишки. – Ведь длину окружности не измеряешь сантиметровой лентой. Да и разрезать её не получится, чтобы измерить линейкой.
–
Изобретательный ум человека придумал много способов решения этой задачи, –
начал Мудряш. – Обозначим длину окружности буквой l.
Несложно догадаться, что длина l
окружности зависит от длины её диаметра d,
а именно: чем больше диаметр, тем больше будет длина окружности. Другими
словами, длина окружности прямо пропорциональна её диаметру.
Другими
словами, длина окружности прямо пропорциональна её диаметру.
Но, оказывается, для всех окружностей отношение длины окружности к её диаметру является одним и тем же числом .
Это число обозначают греческой буквой. Читают эту букву . Это начальная буква греческого слова perimetron, которое и означает «окружность». Запомните! Отношение длины окружности к её диаметру равно числу . Отсюда можем записать, что длину окружности можно вычислить по формуле . Вы уже знаете, что диаметр в 2 раза больше радиуса, следовательно, можно получить ещё одну формулу для вычисления длины окружности: .
– Тогда получается, чтобы выразить диаметр окружности, а в моём случае — диаметр велосипедного колеса, – начал Паша, – нужно длину окружности разделить на это число ?
– Правильно! – ответил Мудряш.
– Но разве можно разделить число на букву? – спросил Паша. – Или это загадочное число имеет какое-то значение?
–
Давайте немного коснёмся истории, – предложил Мудряш. – Ещё в Древнем Египте
было замечено, что длина окружности примерно в 3 раза больше её диаметра, то
есть древние египтяне считали, что число .
Затем древние учёные установили, что число .
Позднее выяснилось, что –
это достаточно точное, но всё-таки приблизительное значение числа .
Со временем великий древнегреческий учёный Архимед доказал, что число .
Французский математик Франсуа Виет вычислил значение числа с
девятью правильными знаками после запятой ().
А вот уже в 18 веке математики установили, что число относится
к таким числам, точное значение которых записать невозможно ни с помощью
обыкновенных, ни с помощью десятичных дробей, то есть число нельзя
представить в виде конечной десятичной дроби или бесконечной периодической
десятичной дроби. Оно выражается бесконечной непериодической десятичной дробью.
Учёные до сих пор проявляют большой интерес к числу .
С появлением современных компьютеров можно вычислить число с
огромной точностью.
– Ещё в Древнем Египте
было замечено, что длина окружности примерно в 3 раза больше её диаметра, то
есть древние египтяне считали, что число .
Затем древние учёные установили, что число .
Позднее выяснилось, что –
это достаточно точное, но всё-таки приблизительное значение числа .
Со временем великий древнегреческий учёный Архимед доказал, что число .
Французский математик Франсуа Виет вычислил значение числа с
девятью правильными знаками после запятой ().
А вот уже в 18 веке математики установили, что число относится
к таким числам, точное значение которых записать невозможно ни с помощью
обыкновенных, ни с помощью десятичных дробей, то есть число нельзя
представить в виде конечной десятичной дроби или бесконечной периодической
десятичной дроби. Оно выражается бесконечной непериодической десятичной дробью.
Учёные до сих пор проявляют большой интерес к числу .
С появлением современных компьютеров можно вычислить число с
огромной точностью. Так, например, в 1987 году благодаря расчётам на компьютере
братья Чудновские вывели число с
миллионом символов после запятой. В 2009 году учёные из Японии рассчитали на
суперкомпьютере значение числа с
двумя с половиной миллионами знаков после запятой. В этом же году программист
из Франции Фабрис Беллар с помощью компьютера получил 2 699 999 990 000
символов после запятой. Только представьте себе, его расчёты длились 131 день.
Так, например, в 1987 году благодаря расчётам на компьютере
братья Чудновские вывели число с
миллионом символов после запятой. В 2009 году учёные из Японии рассчитали на
суперкомпьютере значение числа с
двумя с половиной миллионами знаков после запятой. В этом же году программист
из Франции Фабрис Беллар с помощью компьютера получил 2 699 999 990 000
символов после запятой. Только представьте себе, его расчёты длились 131 день.
– Ого! – воскликнули ребята. – Это число такое большущее!
– Не пугайтесь числа , – продолжил Мудряш. – При вычислениях мы чаще всего будем использовать приближённое значение числа с точностью до сотых, то есть .
– Тогда получается, что диаметр моего велосипедного колеса равен 189 разделить на 3,14, – начал считать Паша, – и приближённо равен 60 сантиметрам.
–
Молодец! – похвалил Пашу Мудряш. – Кстати, с помощью нашего интересного числа можно
вычислить ещё и площадь круга. Запомните! Площадь круга радиуса
вычисляется
по формуле: .
Для вывода этой формулы наших математических знаний пока ещё недостаточно. Как
получают эту формулу, вы узнаете в старших классах. Поэтому пока для решения
задач мы будем использовать готовую формулу.
Запомните! Площадь круга радиуса
вычисляется
по формуле: .
Для вывода этой формулы наших математических знаний пока ещё недостаточно. Как
получают эту формулу, вы узнаете в старших классах. Поэтому пока для решения
задач мы будем использовать готовую формулу.
– А теперь, ребята, давайте посмотрим, как вы всё поняли, и выполним несколько заданий.
Задание первое: найдите длину окружности, если известно, что: её радиус равен 24 сантиметрам; её диаметр равен 9,5 дециметра. Число округлите до сотых.
Решение: мы знаем, что длина окружности вычисляется по формуле . Подставим наши значения в формулу. Посчитаем. Получим, что длина окружности приближённо равна 150,72 сантиметра.
Перейдём
к следующему условию. Нам известен диаметр окружности. Мы знаем, что длину
окружности можно вычислить по формуле .
Подставим наши значения. Посчитаем. И получим, что длина окружности приближённо
равна 29,83 дециметра.
Задание второе: найдите диаметр колеса велосипеда, если известно, что на расстоянии 450 метров оно сделало 150 оборотов. Число округлите до сотых. Результат округлите до сотых метра.
Решение: для начала вычислим, чему равна длина окружности колеса. Так как на расстоянии 450 метров колесо сделало 150 оборотов, то 1 оборот колеса равен 3 метрам. Полный оборот колеса – это и есть длина окружности. А теперь вычислим диаметр колеса. Из формулы длины окружности выразим диаметр . Подставим наши значения. Получим, что диаметр колеса примерно равен 0,955 метра. В условии задачи сказано, что ответ нужно округлить со сотых. Так как после округляемого разряда стоит цифра 5, то к разряду сотых добавим 1. Получим, что диаметр колеса приближённо равен 0,96 метра. Запишем ответ.
Задание
третье: вычислите площадь круга, если его диаметр равен 6
сантиметрам. Число округлите
до сотых.
Решение: мы знаем, что площадь круга можно вычислить по формуле . Диаметр круга в 2 раза больше его радиуса. Следовательно, радиус нашего круга равен 3 сантиметрам. Подставим наши значения в формулу площади круга. Посчитаем. Получим, что площадь круга приближённо равна 28,26 см2.
И последнее задание: Сторона квадрата равна 8 сантиметрам. Найдите площадь закрашенной части круга. Число округлите до целых.
Решение: по
рисунку видно, что сторона квадрата является диаметром круга. Значит, диаметр
круга равен 8 сантиметрам. Мы знаем, что площадь круга можно вычислить по
формуле .
Так как диаметр круга в 2 раза больше его радиуса, то радиус нашего круга равен
4 сантиметрам. Подставим наши значения в формулу площади круга. Посчитаем.
Получим, что площадь всего круга приближённо равна 48 см2. По
условию задачи нам нужно выяснить, чему равна площадь закрашенной части круга. Нетрудно заметить, что эта закрашенная часть составляет половину круга. Значит,
площадь закрашенной части круга приближённо равна 24 см2. Не забудем
записать ответ.
Нетрудно заметить, что эта закрашенная часть составляет половину круга. Значит,
площадь закрашенной части круга приближённо равна 24 см2. Не забудем
записать ответ.
Оценка вашего веса | Здоровый вес, питание и физическая активность
Калькулятор ИМТ для взрослых
Большое количество жира в организме может привести к заболеваниям, связанным с весом, и другим проблемам со здоровьем. Недостаток веса также является риском для здоровья. Индекс массы тела (ИМТ) и окружность талии являются инструментами скрининга для оценки состояния веса в связи с потенциальным риском заболевания. Однако ИМТ и окружность талии не являются инструментами диагностики риска заболевания. Обученный поставщик медицинских услуг должен проводить другие оценки состояния здоровья, чтобы оценить риск заболевания и диагностировать статус заболевания.
Как измерить и интерпретировать статус веса
Индекс массы тела взрослого человека или ИМТ
ИМТ — это вес человека в килограммах, деленный на квадрат роста в метрах. Высокий ИМТ может указывать на высокую упитанность тела, а низкий ИМТ может указывать на слишком низкую упитанность. Чтобы рассчитать свой ИМТ, см. Калькулятор ИМТ. Или определите свой ИМТ, найдя свой рост и вес в этой таблице индексов ИМТ.
Высокий ИМТ может указывать на высокую упитанность тела, а низкий ИМТ может указывать на слишком низкую упитанность. Чтобы рассчитать свой ИМТ, см. Калькулятор ИМТ. Или определите свой ИМТ, найдя свой рост и вес в этой таблице индексов ИМТ.
- Если ваш ИМТ меньше 18,5 , он попадает в диапазон недостаточного веса.
- Если ваш ИМТ составляет от 18,5 до 24,9 , он попадает в диапазон здорового веса.
- Если ваш ИМТ составляет от 25,0 до 29,9 , он попадает в диапазон избыточного веса.
- Если ваш ИМТ равен 30,0 или выше , он попадает в диапазон ожирения.
Вес, превышающий нормальный вес для данного роста, считается избыточным весом или ожирением. Вес, который ниже, чем тот, который считается здоровым для данного роста, описывается как недостаточный вес. 1
На индивидуальном уровне ИМТ можно использовать в качестве инструмента скрининга, но он не является диагностическим признаком полноты тела или здоровья человека. Обученный поставщик медицинских услуг должен проводить соответствующие оценки состояния здоровья, чтобы оценить состояние здоровья человека и риски.
Обученный поставщик медицинских услуг должен проводить соответствующие оценки состояния здоровья, чтобы оценить состояние здоровья человека и риски.
Как измерить рост и вес для расчета ИМТ
Для расчета ИМТ необходимо измерить рост и вес. Наиболее точно измерять рост в метрах, а вес в килограммах. Однако формула ИМТ была адаптирована для роста, измеряемого в дюймах, и веса, измеряемого в фунтах. Эти измерения можно провести в кабинете поставщика медицинских услуг или дома с помощью рулетки и весов.
Дополнительную информацию см. в разделе ИМТ для взрослых.
К началу страницы
Окружность талии
Чтобы правильно измерить окружность талии:
- Встаньте и поместите рулетку вокруг талии, чуть выше бедер
- Убедитесь, что лента расположена горизонтально вокруг талии
- Держите ленту плотно прилегающей к талии, но не сдавливая кожу
- Измерьте талию сразу после выдоха
Еще один способ оценить потенциальный риск заболевания — измерить окружность талии. Чрезмерный абдоминальный жир может быть серьезным, потому что он подвергает вас большему риску развития состояний, связанных с ожирением, таких как диабет 2 типа, высокое кровяное давление и ишемическая болезнь сердца. Ваша талия может говорить о том, что у вас более высокий риск развития заболеваний, связанных с ожирением, если вам 9 лет.0031 1 :
Чрезмерный абдоминальный жир может быть серьезным, потому что он подвергает вас большему риску развития состояний, связанных с ожирением, таких как диабет 2 типа, высокое кровяное давление и ишемическая болезнь сердца. Ваша талия может говорить о том, что у вас более высокий риск развития заболеваний, связанных с ожирением, если вам 9 лет.0031 1 :
- Мужчина с окружностью талии более 40 дюймов
- Небеременная женщина с окружностью талии более 35 дюймов
Окружность талии может использоваться в качестве скринингового инструмента, но не является диагностическим признаком полноты тела или здоровья человека. Обученный поставщик медицинских услуг должен проводить соответствующие оценки состояния здоровья, чтобы оценить состояние здоровья человека и риски.
Примечание : Информация на этих страницах предназначена только для взрослых мужчин и небеременных женщин. Чтобы оценить вес детей или подростков, см. Калькулятор ИМТ для детей и подростков.
Начало страницы
Оценка вашего веса и риска для здоровья
Оценка веса и риска для здоровья включает использование трех ключевых показателей:
- Индекс массы тела (ИМТ)
- Окружность талии
- Факторы риска заболеваний и состояний, связанных с ожирением
Индекс массы тела (ИМТ)
ИМТ является полезной мерой избыточного веса и ожирения. Он рассчитывается исходя из вашего роста и веса. ИМТ — это оценка телесного жира и хороший показатель риска заболеваний, которые могут возникнуть при большем количестве телесного жира. Чем выше ваш ИМТ, тем выше риск развития определенных заболеваний, таких как болезни сердца, высокое кровяное давление, диабет 2 типа, камни в желчном пузыре, проблемы с дыханием и некоторые виды рака.
Хотя ИМТ можно использовать для большинства мужчин и женщин, он имеет некоторые ограничения:
- У спортсменов и других людей с мускулистым телосложением количество жира в организме может быть завышено.

- Он может недооценивать жировые отложения у пожилых людей и других лиц, потерявших мышечную массу.
Используйте Калькулятор ИМТ или Таблицы ИМТ для оценки жировых отложений. Оценка ИМТ означает следующее:
| ИМТ | |
|---|---|
| Подвес | Менее 18,5 |
| Обычный | 18,5–24,9 |
| Избыточный вес | 25,0–29,9 |
| Ожирение | 30,0 и выше |
Окружность талии
Измерение окружности талии помогает выявить возможные риски для здоровья, связанные с избыточным весом и ожирением. Если большая часть вашего жира находится вокруг талии, а не на бедрах, вы подвергаетесь более высокому риску сердечных заболеваний и диабета 2 типа. Этот риск возрастает с размером талии более 35 дюймов для женщин или более 40 дюймов для мужчин. Чтобы правильно измерить талию, встаньте и поместите рулетку вокруг талии, чуть выше бедер. Измерьте свою талию сразу после выдоха.
Если большая часть вашего жира находится вокруг талии, а не на бедрах, вы подвергаетесь более высокому риску сердечных заболеваний и диабета 2 типа. Этот риск возрастает с размером талии более 35 дюймов для женщин или более 40 дюймов для мужчин. Чтобы правильно измерить талию, встаньте и поместите рулетку вокруг талии, чуть выше бедер. Измерьте свою талию сразу после выдоха.
Таблица Риски заболеваний, связанных с ожирением, по ИМТ и окружности талии дает вам представление о том, увеличивает ли ваш ИМТ в сочетании с окружностью талии риск развития заболеваний или состояний, связанных с ожирением.
Факторы риска для здоровья Темы, связанные с ожирением
Наряду с избыточным весом или ожирением, следующие состояния подвергают вас повышенному риску сердечных и других заболеваний:
Факторы риска
- Высокое кровяное давление (гипертония)
- Высокий уровень холестерина ЛПНП («плохой» холестерин)
- Низкий уровень холестерина ЛПВП («хороший» холестерин)
- Высокий уровень триглицеридов
- Высокий уровень глюкозы в крови (сахар)
- Семейный анамнез преждевременных сердечных заболеваний
- Отсутствие физической активности
- Курение сигарет
Людям, страдающим ожирением (ИМТ выше или равном 30) или страдающим избыточным весом (ИМТ от 25 до 29,9) и имеющим два или более факторов риска, рекомендуется похудеть.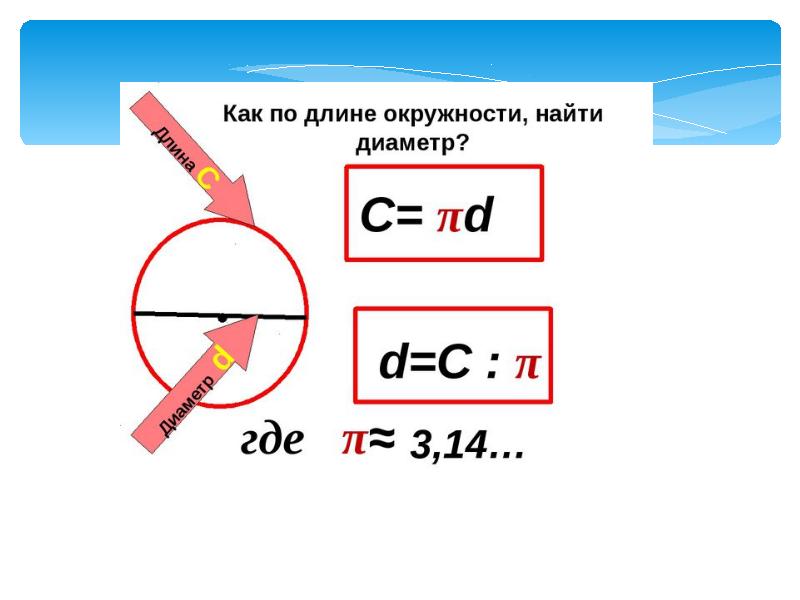


 Это определение выводится из теоремы Пифагора.
Это определение выводится из теоремы Пифагора.