Длина отрезка по координатам точек: Размещение рекламы на Studygide.ru

Как вычислить длину отрезка по координатам точек. Нахождение координат середины отрезка: примеры, решения

Определить длину отрезка возможно разными способами. Для того чтобы узнать, как найти длину отрезка, достаточно иметь в наличии линейку или знать специальные формулы для расчета.

Длина отрезка с помощью линейки

Для этого прикладываем к построенному на плоскости отрезку линейку с миллиметровыми делениями, причем начальную точку необходимо совместить с нулем шкалы линейки. Затем следует отметить на данной шкале расположение конечной точки данного отрезка. Полученное количество целых делений шкалы и будет являться длиной отрезка, выраженной в см. и мм.

Метод координат на плоскости

Если известны координаты отрезка (х1;у1) и (х2;у2), то следует рассчитать его длину следующим образом. Из координат на плоскости второй точки следует вычесть координаты первой точки. В итоге должно получиться два числа. Каждое из таких чисел необходимо возвести в квадрат, а потом найти сумму этих квадратов. Из полученного числа следует извлечь квадратный корень, который будет являться расстоянием между точками. Поскольку данные точки являются концами отрезка, то данное значение и будет его длиной.

Рассмотрим пример, как найти длину отрезка по координатам. Есть координаты двух точек (-1;2) и (4;7). При нахождении разности координат точек получаем следующие значения: х = 5, у =5. Полученные числа и будут являться координатами отрезка. Затем каждое число возводим в квадрат и находим сумму результатов, она равна 50. Из этого числа извлекаем квадратный корень. Результат таков: 5 корней из 2. Это длина отрезка.

Метод координат в пространстве

Для этого необходимо рассмотреть, как найти длину вектора. Именно он и будет являться отрезком в евклидовом пространстве. Находится он почти таким же образом, как длина отрезка на плоскости. Построение вектора происходит в разных плоскостях . Как найти длину вектора?

1. Найдите координаты вектора, для этого из координат его конечной точки нужно вычесть координаты его начальной точки.
2. После этого нужно возвести каждую координату вектора в квадрат.
3. Затем складываем квадраты координат.
4. Чтобы найти длину вектора, нужно извлечь квадратный корень из суммы квадратов координат.

Рассмотрим алгоритм вычисления на примере. Необходимо найти координаты вектора АВ. Точки А и В имеют следующие координаты: А (1;6;3) и В (3;-1;7). Начало вектора лежит в точке А, конец расположен в точке В. Таким образом, чтобы найти его координаты, необходимо вычесть координаты точки А из координат точки В: (3 — 1; -1 — 6;7 — 3) = (2;-7;4).

Теперь возводим каждую координату в квадрат и складываем их: 4+49+16=69. И наконец, извлекает квадратный корень из данного числа. Его трудно извлечь, поэтому результат записываем таким образом: длина вектора равна корню из 69.

Если же вам не важно самому высчитывать длину отрезков и векторов, а нужен просто результат, то вы можете воспользоваться онлайн-калькулятором, например, этим .

Теперь, изучив данные способы и рассмотрев представленные примеры, вы без проблем сможете найти длину отрезка в любой задаче.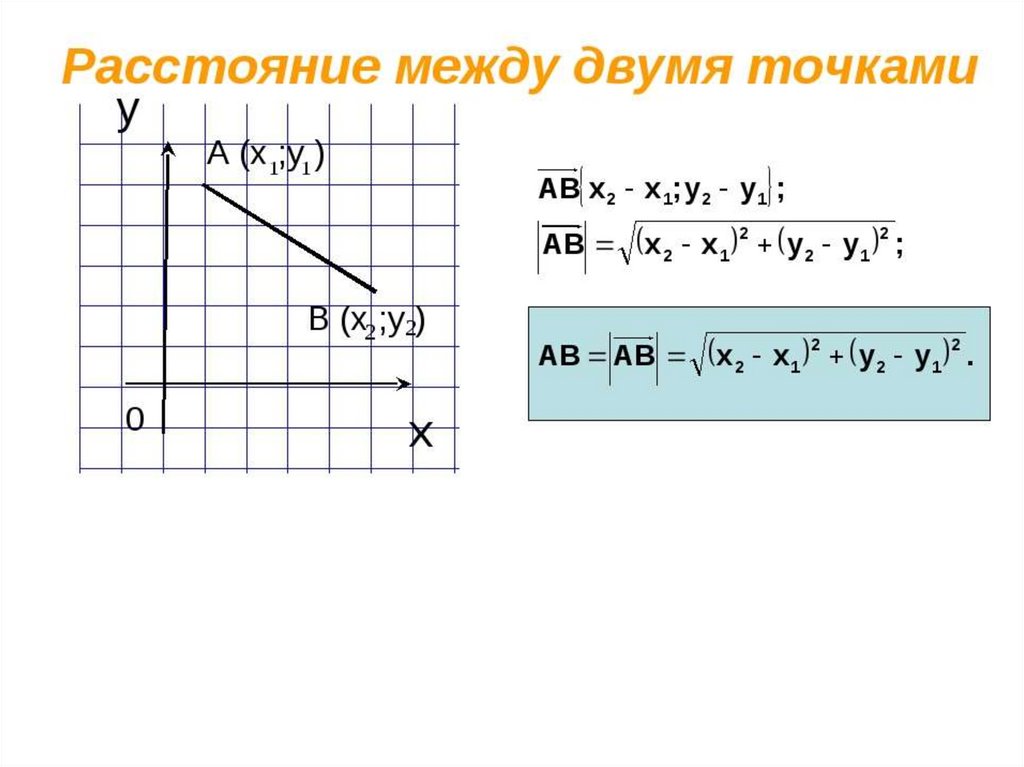

Существуют три основных системы координат, используемых в геометрии, теоретической механике, других разделах физики: декартова, полярная и сферическая. В этих системах координат вся точка имеет три координаты. Зная координаты 2-х точек, дозволено определить расстояние между этими двумя точками.

Вам понадобится

• Декартовы, полярные и сферические координаты концов отрезка

Инструкция

1. Разглядите для начала прямоугольную декартову систему координат. Расположение точки в пространстве в этой системе координат определяется координатами x,y и z. Из начала координат к точке проводится радиус-вектор. Проекции этого радиус-вектора на координатные оси и будут координатами этой точки.Пускай у вас сейчас есть две точки с координатами x1,y1,z1 и x2,y2 и z2 соответственно. Обозначьте за r1 и r2, соответственно, радиус-векторы первой и 2-й точки. Видимо, что расстояние между этими двумя точками будет равно модулю вектора r = r1-r2, где (r1-r2) – векторная разность.

2))

Видео по теме

Длина, как уже отмечалось, обозначается знаком модуля.

Если даны две точки плоскости и , то длину отрезка можно вычислить по формуле

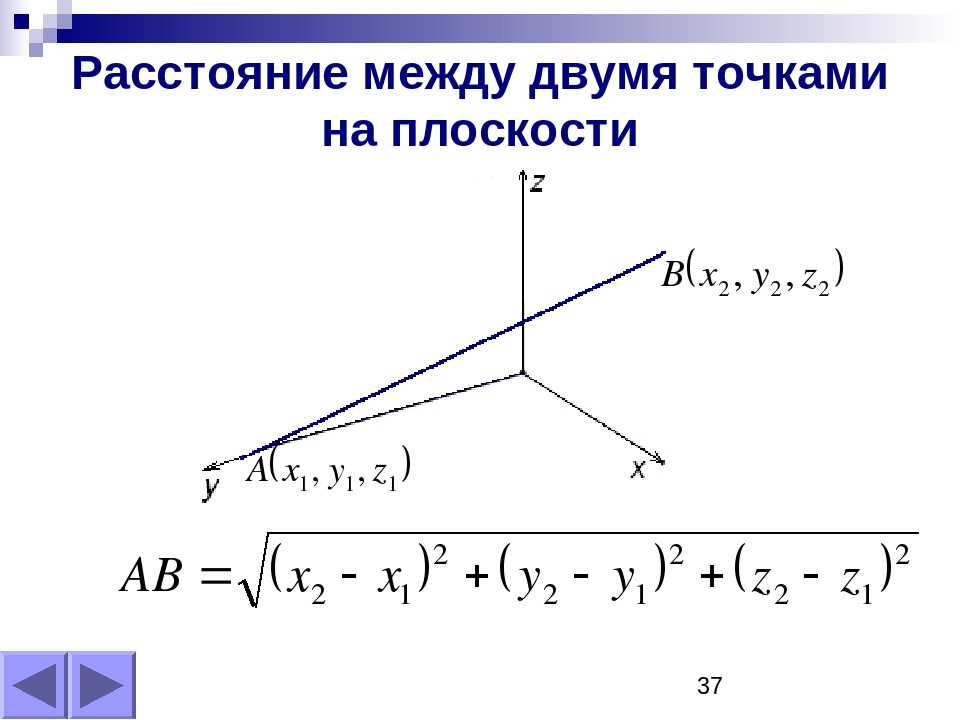
Если даны две точки пространства и , то длину отрезка можно вычислить по формуле

Примечание: Формулы останутся корректными, если переставить местами соответствующие координаты: и , но более стандартен первый вариант

Пример 3

Решение: по соответствующей формуле:

Ответ:

Для наглядности выполню чертёж

Отрезок – это не вектор , и перемещать его куда-либо, конечно, нельзя. Кроме того, если вы выполните чертеж в масштабе: 1 ед. = 1 см (две тетрадные клетки), то полученный ответ можно проверить обычной линейкой, непосредственно измерив длину отрезка.

Да, решение короткое, но в нём есть ещё пара важных моментов, которые хотелось бы пояснить:

Во-первых, в ответе ставим размерность: «единицы». В условии не сказано, ЧТО это, миллиметры, сантиметры, метры или километры. Поэтому математически грамотным решением будет общая формулировка: «единицы» – сокращенно «ед.».

Во-вторых, повторим школьный материал, который полезен не только для рассмотренной задачи:

Обратите внимание на важный технический приём – вынесение множителя из-под корня . В результате вычислений у нас получился результат и хороший математический стиль предполагает вынесение множителя из-под корня (если это возможно). Подробнее процесс выглядит так: . Конечно, оставить ответ в виде не будет ошибкой – но недочетом-то уж точно и весомым аргументом для придирки со стороны преподавателя.

Вот другие распространенные случаи:

Нередко под корнем получается достаточно большое число, например . Как быть в таких случаях? На калькуляторе проверяем, делится ли число на 4: . Да, разделилось нацело, таким образом: . А может быть, число ещё раз удастся разделить на 4? . Таким образом: . У числа последняя цифра нечетная, поэтому разделить в третий раз на 4 явно не удастся. Пробуем поделить на девять: . В результате:
Готово.

Вывод: если под корнем получается неизвлекаемое нацело число, то пытаемся вынести множитель из-под корня – на калькуляторе проверяем, делится ли число на: 4, 9, 16, 25, 36, 49 и т.д.

В ходе решения различных задач корни встречаются часто, всегда пытайтесь извлекать множители из-под корня во избежание более низкой оценки да ненужных заморочек с доработкой ваших решений по замечанию преподавателя.

Давайте заодно повторим возведение корней в квадрат и другие степени:

Правила действий со степенями в общем виде можно найти в школьном учебнике по алгебре, но, думаю, из приведённых примеров всё или почти всё уже ясно.

Задание для самостоятельного решения с отрезком в пространстве:

Пример 4

Даны точки и . Найти длину отрезка .

Решение и ответ в конце урока.

В статье ниже будут освещены вопросы нахождения координат середины отрезка при наличии в качестве исходных данных координат его крайних точек. Но, прежде чем приступить к изучению вопроса, введем ряд определений.

Yandex.RTB R-A-339285-1 Определение 1

Отрезок – прямая линия, соединяющая две произвольные точки, называемые концами отрезка. В качестве примера пусть это будут точки A и B и соответственно отрезок A B .

Если отрезок A B продолжить в обе стороны от точек A и B , мы получим прямую A B . Тогда отрезок A B – часть полученной прямой, ограниченный точками A и B . Отрезок A B объединяет точки A и B , являющиеся его концами, а также множество точек, лежащих между. Если, к примеру, взять любую произвольную точку K , лежащую между точками A и B , можно сказать, что точка K лежит на отрезке A B .

Определение 2

Длина отрезка – расстояние между концами отрезка при заданном масштабе (отрезке единичной длины). Длину отрезка A B обозначим следующим образом: A B .

Определение 3

Середина отрезка – точка, лежащая на отрезке и равноудаленная от его концов. Если середину отрезка A B обозначить точкой C , то верным будет равенство: A C = C B

Исходные данные: координатная прямая O x и несовпадающие точки на ней: A и B . Этим точкам соответствуют действительные числа

x A и x B . Точка C – середина отрезка A B: необходимо определить координату x C .

Поскольку точка C является серединой отрезка А В, верным будет являться равенство: | А С | = | С В | . Расстояние между точками определяется модулем разницы их координат, т.е.

| А С | = | С В | ⇔ x C — x A = x B — x C

Тогда возможно два равенства: x C — x A = x B — x C и x C — x A = — (x B — x C)

Из первого равенства выведем формулу для координаты точки C: x C = x A + x B 2 (полусумма координат концов отрезка).

Из второго равенста получим: x A = x B , что невозможно, т.к. в исходных данных — несовпадающие точки. Таким образом, формула для определения координат середины отрезка A B с концами A (x A) и B (x B):

Полученная формула будет основой для определения координат середины отрезка на плоскости или в пространстве.

Исходные данные: прямоугольная система координат на плоскости О x y , две произвольные несовпадающие точки с заданными координатами A x A , y A и B x B , y B .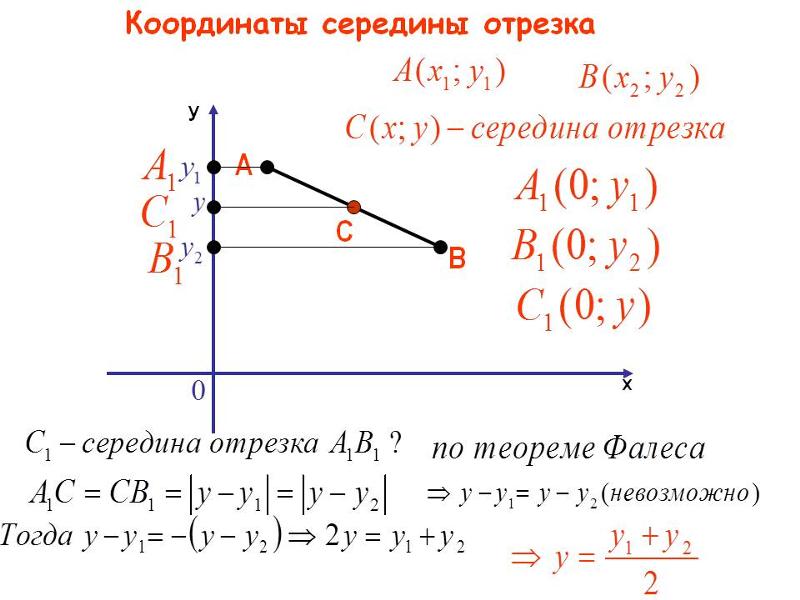

Точка C – середина отрезка A B . Необходимо определить координаты x C и y C для точки C .

Возьмем для анализа случай, когда точки A и B не совпадают и не лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. A x , A y ; B x , B y и C x , C y — проекции точек A , B и C на оси координат (прямые О х и О y).

Согласно построению прямые A A x , B B x , C C x параллельны; прямые также параллельны между собой. Совокупно с этим по теореме Фалеса из равенства А С = С В следуют равенства: А x С x = С x В x и А y С y = С y В y , и они в свою очередь свидетельствуют о том, что точка С x – середина отрезка А x В x , а С y – середина отрезка А y В y . И тогда, опираясь на полученную ранее формулу, получим:

x C = x A + x B 2 и y C = y A + y B 2

Этими же формулами можно воспользоваться в случае, когда точки A и B лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. Проводить детальный анализ этого случая не будем, рассмотрим его лишь графически:

Резюмируя все выше сказанное, координаты середины отрезка A B на плоскости с координатами концов A (x A , y A) и B (x B , y B) определяются как :

(x A + x B 2 , y A + y B 2)

Исходные данные: система координат О x y z и две произвольные точки с заданными координатами A (x A , y A , z A) и B (x B , y B , z B) . Необходимо определить координаты точки C , являющейся серединой отрезка A B .

A x , A y , A z ; B x , B y , B z и C x , C y , C z — проекции всех заданных точек на оси системы координат.

Согласно теореме Фалеса верны равенства: A x C x = C x B x , A y C y = C y B y , A z C z = C z B z

Следовательно, точки C x , C y , C z являются серединами отрезков A x B x , A y B y , A z B z соответственно. Тогда, для определения координат середины отрезка в пространстве верны формулы:

x C = x A + x B 2 , y c = y A + y B 2 , z c = z A + Z B 2

Полученные формулы применимы также в случаях, когда точки A и B лежат на одной из координатных прямых; на прямой, перпендикулярной одной из осей; в одной координатной плоскости или плоскости, перпендикулярной одной из координатных плоскостей.

Определение координат середины отрезка через координаты радиус-векторов его концов

Формулу для нахождения координат середины отрезка также можно вывести согласно алгебраическому толкованию векторов.

Исходные данные: прямоугольная декартова система координат O x y , точки с заданными координатами A (x A , y A) и B (x B , x B) . Точка C – середина отрезка A B .

Согласно геометрическому определению действий над векторами верным будет равенство: O C → = 1 2 · O A → + O B → . Точка C в данном случае – точка пересечения диагоналей параллелограмма, построенного на основе векторов O A → и O B → , т.е. точка середины диагоналей.Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: O A → = (x A , y A) , O B → = (x B , y B) . Выполним некоторые операции над векторами в координатах и получим:

O C → = 1 2 · O A → + O B → = x A + x B 2 , y A + y B 2

Следовательно, точка C имеет координаты:

x A + x B 2 , y A + y B 2

По аналогии определяется формула для нахождения координат середины отрезка в пространстве:

C (x A + x B 2 , y A + y B 2 , z A + z B 2)

Примеры решения задач на нахождение координат середины отрезка

Среди задач, предполагающих использование полученных выше формул, встречаются, как и те, в которых напрямую стоит вопрос рассчитать координаты середины отрезка, так и такие, что предполагают приведение заданных условий к этому вопросу: зачастую используется термин «медиана», ставится целью нахождение координат одного из концов отрезка, а также распространены задачи на симметрию, решение которых в общем также не должно вызывать затруднений после изучения настоящей темы. Рассмотрим характерные примеры.

Пример 1

Исходные данные: на плоскости – точки с заданными координатами А (- 7 , 3) и В (2 , 4) . Необходимо найти координаты середины отрезка А В.

Решение

Обозначим середину отрезка A B точкой C . Координаты ее буду определяться как полусумма координат концов отрезка, т.е. точек A и B .

x C = x A + x B 2 = — 7 + 2 2 = — 5 2 y C = y A + y B 2 = 3 + 4 2 = 7 2

Ответ : координаты середины отрезка А В — 5 2 , 7 2 .

Пример 2

Исходные данные: известны координаты треугольника А В С: А (- 1 , 0) , В (3 , 2) , С (9 , — 8) . Необходимо найти длину медианы А М.

Решение

1. По условию задачи A M – медиана, а значит M является точкой середины отрезка B C . В первую очередь найдем координаты середины отрезка B C , т.е. точки M:

x M = x B + x C 2 = 3 + 9 2 = 6 y M = y B + y C 2 = 2 + (- 8) 2 = — 3

1. Поскольку теперь нам известны координаты обоих концов медианы (точки A и М), можем воспользоваться формулой для определения расстояния между точками и посчитать длину медианы А М:

A M = (6 — (- 1)) 2 + (- 3 — 0) 2 = 58

Ответ: 58

Пример 3

Исходные данные: в прямоугольной системе координат трехмерного пространства задан параллелепипед A B C D A 1 B 1 C 1 D 1 . Заданы координаты точки C 1 (1 , 1 , 0) , а также определена точка M , являющаяся серединой диагонали B D 1 и имеющая координаты M (4 , 2 , — 4) . Необходимо рассчитать координаты точки А.

Решение

Диагонали параллелепипеда имеют пересечение в одной точке, которая при этом является серединой всех диагоналей. Исходя из этого утверждения, можно иметь в виду, что известная по условиям задачи точка М является серединой отрезка А С 1 . Опираясь на формулу для нахождения координат середины отрезка в пространстве, найдем координаты точки А: x M = x A + x C 1 2 ⇒ x A = 2 · x M — x C 1 = 2 · 4 — 1 + 7 y M = y A + y C 1 2 ⇒ y A = 2 · y M — y C 1 = 2 · 2 — 1 = 3 z M = z A + z C 1 2 ⇒ z A = 2 · z M — z C 1 = 2 · (- 4) — 0 = — 8

Ответ: координаты точки А (7 , 3 , — 8) .

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Существует целая группа заданий (входящих в экзаменационные типы задач), связанная с координатной плоскостью.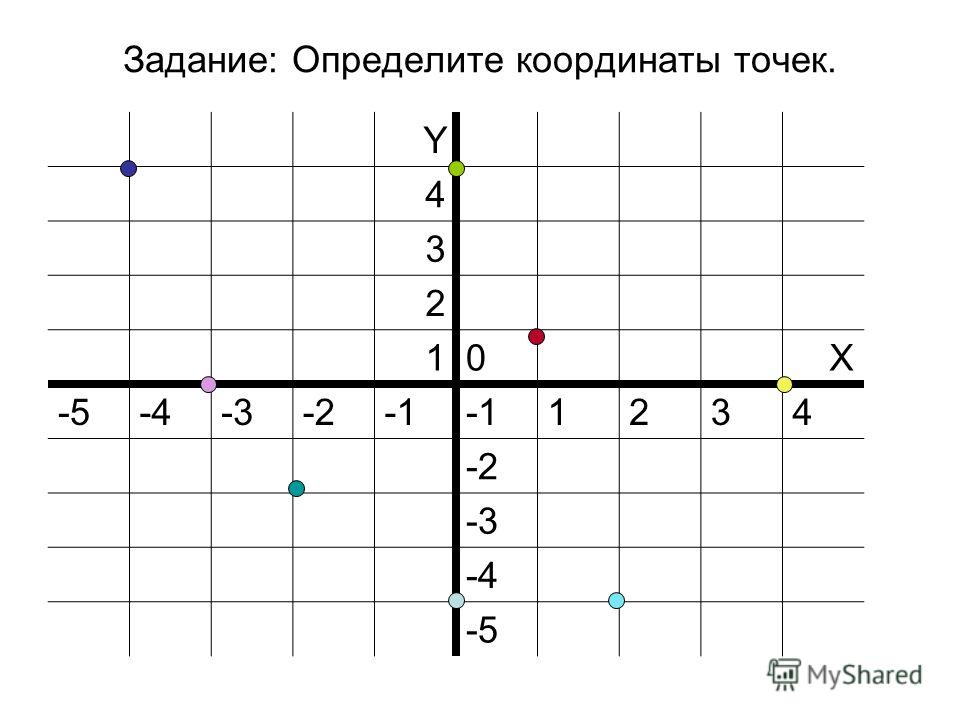 Это задачи начиная с самых элементарных, которые решаются устно (определение ординаты или абсциссы заданной точки, либо точки симметричной заданной и другие), заканчивая задачами в которых требуется качественное знание, понимание и хорошие навыки (задачи связанные с угловым коэффициентом прямой).

Постепенно мы с вами рассмотрим все их. В этой статье начнём с элементарных. Это простые задачи на определение: абсциссы и ординаты точки, длинны отрезка, середины отрезка, синуса или косинуса угла наклона прямой. Большинству эти задания будут не интересны. Но изложить их считаю необходимым.

Дело в том, что не все учатся в школе. Очень многие сдают ЕГЭ спустя 3-4 и более лет после её окончания и что такое абсцисса и ордината помнят смутно. Будем разбирать и другие задачи, связанные с координатной плоскостью, не пропустите, подпишитесь, на обновление блога. Теперь н емного теории.

Построим на координатной плоскости точку А с координатами х= 6, y=3.

Говорят, что абсцисса точки А равна шести, ордината точки А равна трём.

Если выразиться просто, то ось ох это ось абсцисс, ось оу это ость ординат.

То есть, абсцисса это точка на оси ох в которую проецируется точка заданная на координатной плоскости; ордината это точка на оси оу в которую проецируется оговоренная точка.

Длина отрезка на координатной плоскости

Формула для определения длины отрезка, если известны координаты его концов:

Как вы видите, длина отрезка — это длина гипотенузы в прямоугольными треугольнике с катетами равными

Х В – Х А и У В – У А

* * *

Середина отрезка. Её Координаты.

Формула для нахождения координат середины отрезка:

Уравнение прямой проходящей через две данные точки

Формула уравнения прямой походящей через две данные точки имеет вид:

где (х 1 ;у 1 ) и (х 2 ;у 2 ) координаты заданных точек.

Подставив значения координат в формулу, она приводится к виду:

y = kx + b , где k — это угловой коэффициент прямой

Эта информация нам понадобиться при решении другой группы задач связанных с координатной плоскостью. Статья об этом будет, не пропустите!

Что ещё можно добавить?

Угол наклона прямой (или отрезка) это угол между осью оХ и этой прямой, лежит в пределах от 0 до 180 градусов.

Рассмотрим задачи.

Из точки (6;8) опущен перпендикуляр на ось ординат. Найдите ординату основания перпендикуляра.

Основание перпендикуляра опущенного на ось ординат будет иметь координаты (0;8). Ордината равна восьми.

Ответ: 8

Найдите расстояние от точки A с координатами (6;8) до оси ординат.

Расстояние от точки А до оси ординат равно абсциссе точки А.

Ответ: 6.

A (6;8) относительно оси Ox .

Точка симметричная точке А относительно оси оХ имеет координаты (6;– 8).

Ордината равна минус восьми.

Ответ: – 8

Найдите ординату точки, симметричной точке A (6;8) относительно начала координат.

Точка симметричная точке А относительно начала координат имеет координаты (– 6;– 8).

Её ордината равна – 8.

Ответ: –8

Найдите абсциссу середины отрезка, соединяющего точки O (0;0) и A (6;8).

Для того, решить поставленную задачу необходимо найти координаты середины отрезка. Координаты концов нашего отрезка (0;0) и (6;8).

Вычисляем по формуле:

Получили (3;4). Абсцисса равна трём.

Ответ: 3

*Абсциссу середины отрезка можно определить без вычисления по формуле, построив данный отрезок на координатной плоскости на листе в клетку. Середину отрезка несложно будет определить по клеткам.

Найдите абсциссу середины отрезка, соединяющего точки A (6;8) и B (–2;2).

Для того, решить поставленную задачу необходимо найти координаты середины отрезка. Координаты концов нашего отрезка (–2;2) и (6;8).

Вычисляем по формуле:

Получили (2;5). Абсцисса равна двум.

Ответ: 2

*Абсциссу середины отрезка можно определить без вычисления по формуле, построив данный отрезок на координатной плоскости на листе в клетку.

Найдите длину отрезка, соединяющего точки (0;0) и (6;8).

Длина отрезка при данных координатах его концов вычисляется по формуле:

в нашем случае имеем О(0;0) и А(6;8). Значит,

*Порядок координат при вычитании не имеет значения. Можно из абсциссы и ординаты точки О вычесть абсциссу и ординату точки А:

Ответ:10

Найдите косинус угла наклона отрезка, соединяющего точки O (0;0) и A (6;8), с осью абсцисс.

Угол наклона отрезка – это угол между этим отрезком и осью оХ.

Из точки А опустим перпендикуляр на ось оХ:

То есть, угол наклона отрезка это угол ВОА в прямоугольном треугольнике АВО.

Косинусом острого угла в прямоугольном треугольнике является

отношение прилежащего катета к гипотенузе

Необходимо найти гипотенузу ОА.

По теореме Пифагора: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Таким образом, косинус угла наклона равен 0,6

Ответ: 0,6

Из точки (6;8) опущен перпендикуляр на ось абсцисс. Найдите абсциссу основания перпендикуляра.

Через точку (6;8) проведена прямая, параллельная оси абсцисс. Найдите ординату ее точки пересечения с осью оУ .

Найдите расстояние от точки A с координатами (6;8) до оси абсцисс.

Найдите расстояние от точки A с координатами (6;8) до начала координат.

Онлайн калькулятор. Длина отрезка. Расстояние между точками. Как найти длину отрезка

Автор Historian Просмотров 448 Опубликовано 19.07.2022

Если отрезок перпендикулярен оси, то его проекцией является точка. В декартовых системах координат одно из положений вектора имеет нулевое значение. Например, AB (0; 1) или AB (-3; 0). Так называемые единичные векторы используются для определения направления в пространстве.

Содержание

1. Формула длины отрезка в координатах. Нахождение координат середины отрезка, примеры, решения
2. Точки a и b введены! Решение:
3. Вам понадобится
4. Равные отрезки
5. Сравнение отрезков
6. Примеры решения задач с пояснениями
7. Примеры решения задач
8. Использование онлайн-калькулятора
9. Геометрия 7 класс. Урок 5. Решение задач по теме «Измерение отрезков»
10. Рефлексия учебной деятельности

Формула длины отрезка в координатах. Нахождение координат середины отрезка, примеры, решения

Ниже приведен подробный пример определения длины отрезка при заданной координате с помощью онлайн-сервиса Контрольная работа Ru.

Предположим, вам нужно найти длину отрезка на плоскости

(В пространстве это можно вычислить по аналогии, изменяя только точки в трех измерениях).

Сегмент AB имеет концы A (1, 2) и B (3, 4).

Чтобы рассчитать длину отрезка AB, выполните следующие действия

1. перейдите на служебную страницу и найдите расстояние между двумя точками в интернете.

Это можно использовать, так как длина отрезка в координатах точно равна расстоянию между точками A и B.

Чтобы установить правильные размеры точки A, перетащите правый нижний край влево, как показано на рисунке.

После ввода координат первой точки A (1, 2) нажмите кнопку Точка A.

3. на втором этапе необходимо ввести координаты второй точки B, как показано на следующем рисунке.

Точки a и b введены! Решение:

Найдите расстояние между точками (s)

Отрезок — это сегмент прямой линии, состоящий из всех точек на линии между двумя определенными точками (называемыми краями отрезка).

Рассмотрим первый пример. Пусть отрезок прямой задан двумя точками в координатной плоскости. Его длину можно найти, применив теорему Пифагора.

Таким образом, в системе координат отрезок рисуется путем указания координат ребер (x1; y1) и (x2; y2). Проведем от края отрезка перпендикулярно осям x и y. Отметьте красным цветом участок, который является проекцией исходного участка на координатные оси. Затем переместите проектируемый участок параллельно краю участка. （Получается треугольник (прямоугольный). Гипотенуза этого треугольника — отрезок АВ, а перенесенная проекция — его катет.

Вычислите длину этих видов. Таким образом, длина проекции на ось y равна y2-y1, а длина проекции на ось x равна x2-x1. Применим теорему Пифагора: || AB |²= (y2-y1)²+ (x2-x1)². В данном случае|AB| — это длина отрезка.

Если вы используете эту диаграмму для расчета длины отрезка, вам даже не нужно создавать этот отрезок. Затем рассчитывается длина отрезка с использованием координат (1; 3) и (2; 5). Применяя теорему Пифагора, получаем. | AB |²= (2-1)²+ (5-3)²= 1 + 4= 5. Это означает, что длина отрезка равна 5:1/2.

Чтобы найти длину отрезка, воспользуйтесь следующим методом. Для этого необходимо знать координаты двух точек в системе. Рассмотрим этот вариант, применив двухмерную декартову систему координат.

Таким образом, двумерная система координат дает координаты конечных точек отрезка. Если провести через эти точки прямую, которая должна быть перпендикулярна оси координат, то получится прямоугольный треугольник. Первая часть — это косая сторона получившегося треугольника. Катет треугольника образует отрезок, длина которого равна проекции гипотенузы на оси координат. Учитывая теорему Пифагора, мы заключаем, что Чтобы найти длину конкретного отрезка, нужно найти длину его проекции на две координатные оси.

Найдем длины проекций (X и Y) исходного отрезка на координатные оси. Вычислите их, найдя разность между координатами точки на другой оси: X = X2-X1, Y = Y2-Y1.

Вычислите длину отрезка A, найдя следующий квадратный корень

A =√(X²+Y²)=√((X2-X1)²+(Y2-Y1)²).

Если координаты находятся между точками 2;4 и 4;1, то их длины равны √((4-2)²+(1-4)²) = √13≈3.61 соответственно.

Существуют три основные системы координат, используемые в геометрии, теоретической инженерии и других отраслях физики. 2)).

Если отрезок задан двумя точками в координатной плоскости, его длина может быть найдена с помощью теоремы Пифагора.

Если отрезок перпендикулярен оси, то его проекцией является точка. В декартовых системах координат одно из положений вектора имеет нулевое значение. Например, AB (0; 1) или AB (-3; 0). Так называемые единичные векторы используются для определения направления в пространстве.

Геометрия изучается в начале 7 класса, где впервые вводятся основные понятия: точки, прямые, плоскости, радиусы и отрезки. Если провести прямую линию и поставить на ней две точки, то отрезок между ними станет одним отрезком.

Равные отрезки

Равные отрезки — это отрезки одинаковой длины. Когда равные сегменты накладываются друг на друга, их края перекрываются.

Пример. Возьмите две секции CD и LM.

Расположите отрезки параллельно друг другу так, чтобы точка C находилась над точкой L, а точка D — над точкой M.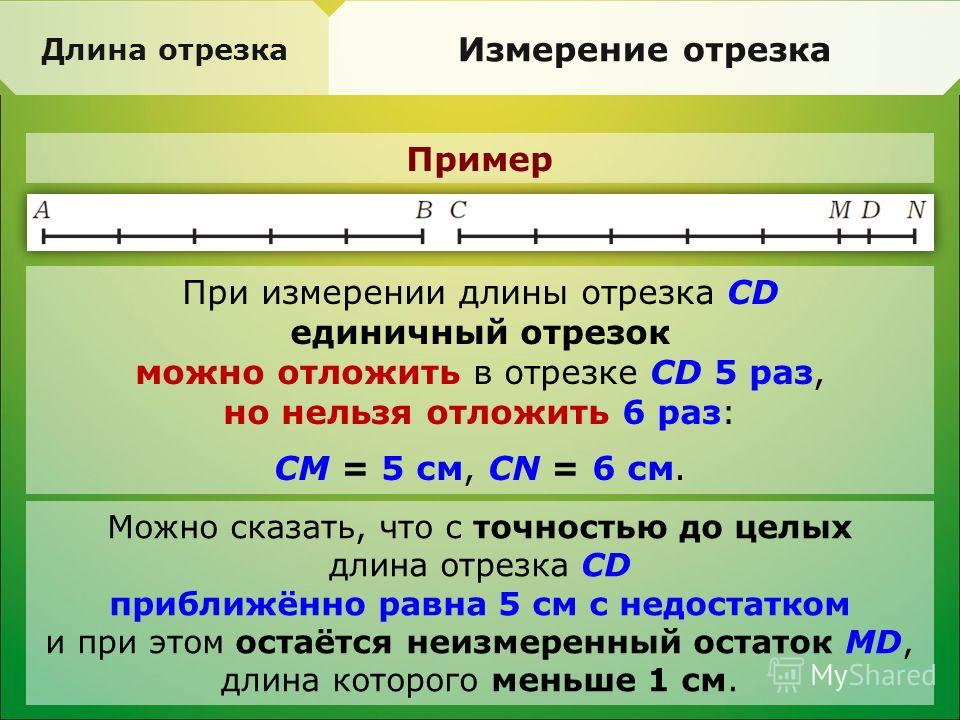

Поэтому, поскольку длины отрезков равны, CD = LM.

Сравнение отрезков

Сравнение двух отрезков означает определение того, равны ли они или один из них больше другого.

Вы можете сравнить два отрезка, проведя прямую линию из одной и той же точки к одной и той же стороне обоих отрезков. Для этого можно использовать компас.

Чтобы разместить прямой участок, совпадающий с определенным участком, сначала установите ножки компаса так, чтобы его кончик находился в конце участка. Затем, не меняя раствора компаса, переместите его так, чтобы оба конца были прямыми. .

Чтобы сравнить два сегмента, можно получить один из следующих результатов. Сегменты равны, первый сегмент больше второго или первый сегмент меньше второго.

Пример. Если два линейных отрезка CA и CB добавлены из точки C, а точка A находится между C и B, то CA меньше CB (или CB больше CA).

Если точка B находится между C и A, то отрезок CA больше, чем отрезок CB (или CB меньше, чем отрезок CA):.

CA>CB или CB

Если точки A и B совпадают, то отрезки CA и CB равны.

Отрезки равны, если концы отрезков совпадают при их пересечении.

Измеряйте и сравнивайте длины отрезков: чем больше отрезок, тем больше отрезок.

Пример. Сравните длины отрезков AB и AC.

Отрезок AB больше отрезка AG, потому что

Если длины отрезков AB и AC равны, то

При измерении отрезков, если их длины равны, то отрезки равны.

Длина участка может быть определена несколькими способами. Чтобы знать, как найти длину прямой линии, достаточно иметь линейку или знать специальную формулу для ее вычисления.

Примеры решения задач с пояснениями

Дано: четыре отрезка лежат на одной прямой. AN = NB, BK = KS и AC = 5 см.

Решение: длина отрезка AC равна сумме длин составляющих его компонентов. AS = AN + NB +VC+X. Если AN = NB, BK = KS и AC = 5 см, то 2NB + 2VC = 5 (см), 2- (NB + VC) = 5 (см), NB + VC = 2,5 (см), NB + VC = NK ⇒ NK = 2,5 (см).

Дано: точки Ο, Α и Β лежат на прямой, ΟΑ = 12 см, ΟΒ = 9 см.

Поиск: расстояние между средними точками отрезков OA и OB.

Пусть M — среднее значение отрезка OA, а N — среднее значение отрезка OB.

Длина отрезка MN равна расстоянию между средними точками отрезков OA и OB, MN = MO + ON = 6 (см) + 4,5 (см) = 10,5 (см).

Если координаты находятся между точками 2;4 и 4;1, то их длины равны √((4-2)²+(1-4)²) = √13≈3.61 соответственно.

Примеры решения задач

В большинстве случаев несложно найти длину вектора с помощью координат или просто вычислить положение отрезка на плоскости. Однако, поскольку проекции очень часто используются при проверке различных физических процессов, вам необходимо уметь выполнять эти действия.

В 7 классе средней школы даны типовые вопросы для самостоятельной работы. Научившись редактировать их и находить ответы, вы сможете претендовать на знание предмета. Ниже приведены примеры различных уровней сложности.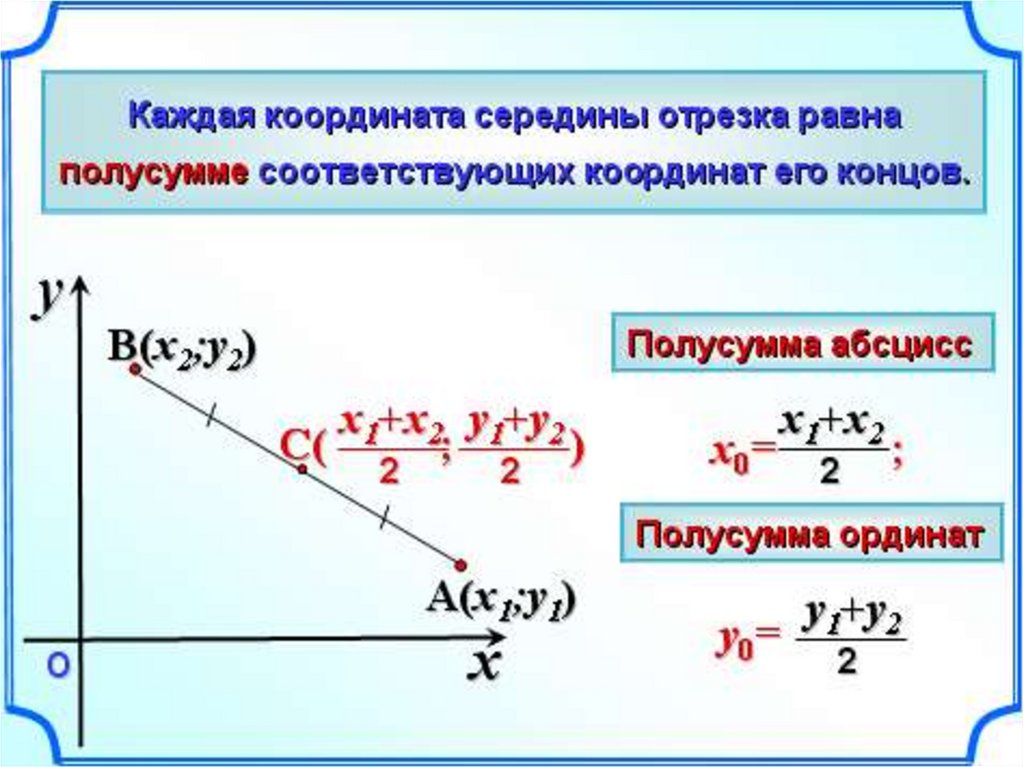

Вот более сложные вопросы. На уровне есть две точки. Первые координаты — L (1, 5), вторые — J (2, 7). Найдите длину отрезка, соединяющего их. Чтобы понять суть проблемы, можно составить план этих двух точек и линий, которые нужно провести, соединяя их. Далее необходимо построить две вертикальные линии этих координат и пересечь их. Их пересечения записываются. Пусть будет буква Т.

На рисунке видно, что полученная фигура — не что иное, как прямоугольный треугольник. Мы видим, что секции LT и JT являются катетами. Поэтому достаточно найти их длину по модулю и применить теорему Пифагора. Таким образом, длины:| LT | = x2-x1 = 7-5 = 2, | JT | = 2 —1 = 1. Из формулы для нахождения диагоналей искомая длина равна: d=√LT2+ JT2=√22+12=√5.

Поэтому все задачи на нахождение длины или положения отрезка решаются с использованием координатного типа. Не имеет значения, какой регион исследуется. Это относится как к двумерному, так и к n-мерному пространству.

Использование онлайн-калькулятора

На практике решение задач почти всегда связано с поиском параметров в пространстве. Это особенно верно в физике, где изучаются электромагнетизм и движение. Во многих случаях точки должны быть нанесены на координатные оси, что в конечном итоге приводит к сложной геометрии. Таким образом, даже незначительные на первый взгляд ошибки могут привести к неправильным ответам.

Гораздо эффективнее использовать так называемые онлайн-компьютеры. Это обычные сайты со специальными программами для вычисления математических задач. Ими может пользоваться любой человек, имеющий доступ в Интернет и установленный интернет-браузер. Все, что нужно сделать пользователю, это ввести исходные данные в предложенную форму и нажать на интерактивную кнопку, которая часто обозначается как «Рассчитать». Приложение запускается автоматически, и ответ приходит в течение нескольких секунд. Нет необходимости беспокоиться о его точности. Кроме того, программное обеспечение использует алгоритм, основанный на математических формулах.

Среди наиболее популярных сервисов, предлагающих бесплатный доступ к своим услугам, можно назвать следующие

• ru.onlinemschool;
• ru.solverbook;
• math.semestr;
• geleot;
• mathonline.um-razum.

Эти услуги доступны на русском языке и имеют простой и понятный пользовательский интерфейс. Их услуги привлекательны не только для студентов, но и для инженеров, выполняющих сложные расчеты. В первом случае это экономит время и дает точные результаты, а во втором — очень помогает в их исследованиях. Это связано с тем, что на этих сайтах содержится весь необходимый теоретический материал, включая примеры расчетов. Кроме того, программа не только предоставляет расчеты, но и показывает пошаговые решения с пояснениями ключевых моментов.

Таким образом, учащиеся учатся самостоятельно вычислять ответы после попытки решить некоторые задачи, даже если они ничего не понимают. Векторные формулы идеально подходят для автоматических расчетов. Поэтому использование электронного калькулятора для вычисления координат вектора имеет большой полевой смысл.

Алгебраические свойства рассеяния, формулы для вычисления дисперсии дискретных случайных величин, выражения, правила и примеры расчета, онлайн калькулятор

Градиентное векторное произведение алгебраических множеств, основные свойства, формулы и условия, примеры решения задач, онлайн калькулятор

Расположите отрезки параллельно друг другу так, чтобы точка C находилась над точкой L, а точка D — над точкой M.

Геометрия 7 класс. Урок 5. Решение задач по теме «Измерение отрезков»

Основные образовательные цели курса: развить умение решать задачи и находить длину части пространства или всего пространства — научить приемам логического мышления — проверить предметные знания и изученные навыки решения задач.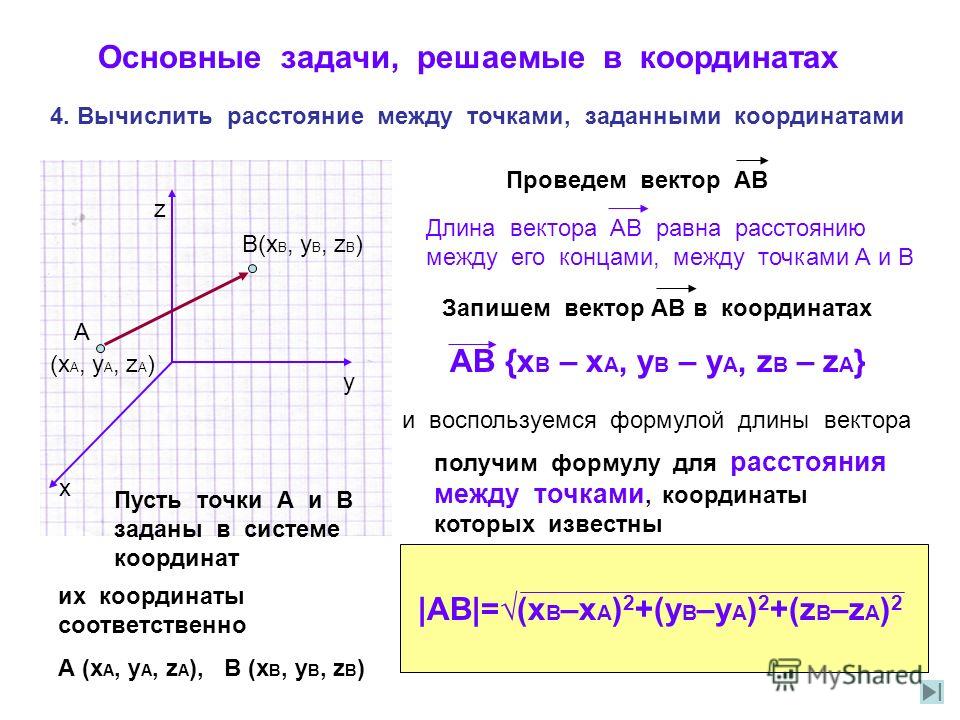

Проверить решение дополнительной домашней задачи. (Справившийся с заданием учащийся заранее записывает решение на доске.)

Дано: AF = FB, B K = KC, AC = 5 см (рис. 1.53). Поиск: FK. решение: из условий задачи, AF = FB, BK = KS, тогда AF + FB + BK + KS = AC, 2FB + 2K = 5 см, FB + BK = 2,5 см, FB + BK = FK, тогда FK = 2,5 см. ответ: fk = 2,5 см.

(a) BC = 2,5 см (рис. 1.54). Поиск: ac. (Ответ: ac = 5 см.) б) ad = 42 см, bc = 11 см (рис. 1.55). Найдите: ab. (Ответ: ab = 20 см.) c) as = 18 дм. AB: AC = 5:4 (рис. 1.56). Поиск: ab. (Ответ: ab = 10 дм.).

Вопрос # 38 Дано, что: o, a и b — прямые линии, oa = 2 см, ob = 9 см. Поиск: расстояние между средними точками отрезков o и ob равно a) ∈ Ab, b) ∉ab. Решение: либо в середине отрезка OA, либо в середине отрезка ob. Возможны два случая (рис. 1.57): а) отрезок o ab, где mo = ao: 2 = 6 см, n = b: 2 = 4,5 см. Расстояние между средними точками отрезков OA и OB равно длине отрезка, a = Mo + on = 6 см + 4,5 см = 10,5 см. (b) Если точка O не лежит на отрезке ab, то Mo = AO: 2 = 6 см, ON = BO: 2 = 4,5 см. mn = MO -ON = 6 см -4,5 см = 1,5 см. (Ответ: a) 10,5 см — b) 1,5 см).

Вопрос # 40 дано: ab = 28 см, c, d ∈ Ab, m — среда ac, n — среда db. Mn = 16 см. поиск: cd. решение: ab = am + mn + nb, nb = 28 см -16 см = 12 см. так как m — среда ac, am = mc, n — среда bd, bn = nd. так как am + nb = 12 см, bn = nd, mc + dn = 12 см. Mn = MC + CD + DN = 16 см, MC + DN = 12 см, CD = MN-(MC + DN) = 16 см -12 см = 4 см (рис. 1.58). (Ответ: 4 см.)

Инструкция к вопросу: — От точек m, n, c, d отделены несколько отрезков отрезка AB. — Что вы можете сказать об этих разделах? Являются ли какие-либо из этих разделов равными? — Их длина составляет 16 см? — Какова общая длина AM и NB? Какова общая длина MC и DN? — Как найти длину отрезка компакт-диска?

Рефлексия учебной деятельности

1. Как найти длину отрезка, если точка делит его на два отрезка, длины которых известны?
2. Как определить, какая из трех точек лежит на прямой между двумя другими, если известны длины всех трех образовавшихся отрезков? Например, точки А, В и С лежат на одной прямой, АВ = 6 см, АС = 4 см, ВС = 10 см.
3. Каким может быть взаимное расположение точек А, В и С на прямой? Как найти длину отрезка АВ в каждом случае? Например, АС = 7 см, ВС = 5 см.

1. Решить задачи № 35, 36, 37, 39 из учебника.
2. Решить дополнительную задачу . Длина отрезка АВ = 6 см. Внутри отрезка взята точка М. Найдите длину отрезка ВМ, если: а) АМ = 2ВМ; б) 2АМ = 3ВМ; в) АМ : ВМ = 1 : 5; г) AM : ВМ = 3 : 4; д) AM – ВМ = 2; е) 2ВМ + 3АМ = 14.

Смотреть: геометрия 7 класс. Урок 5. Решение задач и работа дома №1 «Измерение сектора». Цель — работа с основным руководством. Для руководства приведены цитаты из пособия «План курса геометрии.7 класс / Гаврилова Н.Ф.-М.: Вако.

Нахождение длины и середины отрезка — Криста Кинг Математика

Что такое середина отрезка?

В этом уроке мы рассмотрим, как алгебраически найти длину отрезка прямой, когда у нас есть информация и измерения частей отрезка прямой.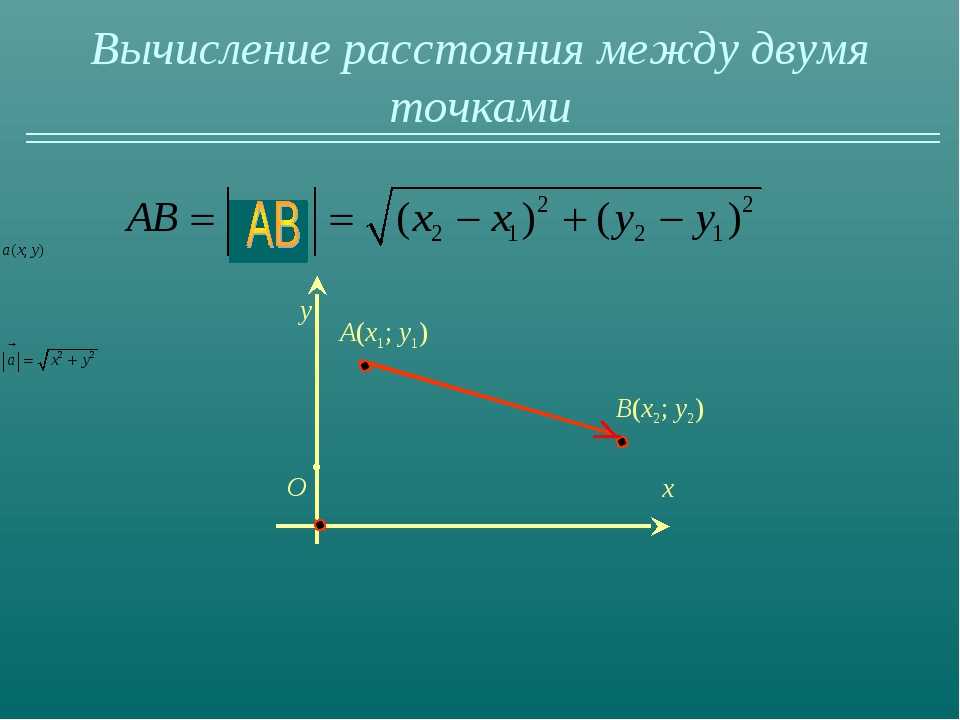

Помните, что отрезок — это конечный отрезок линии, названный по его концам. Например, отрезок ???\overline{AB}??? может выглядеть так:

Привет! Я Криста.

Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.

Отрезки и расстояние

Расстояние между двумя точками на отрезке называется длиной отрезка. Обычно мы используем тот же символ для длины отрезка, что и для самого отрезка. Итак ???\overline{AB}??? может использоваться для представления самого сегмента, а также длины сегмента.

В этом примере расстояние между точками ???A??? и ???Б???

???\overline{AB}=|3-(-2)|???

???\overline{AB}=|3+2|???

???\overline{AB}=|5|???

???\overline{AB}=5???

В этом примере вы также можете считать от ???A??? в ???Б??? и получить расстояние ???5???. Как видите, иногда бывает полезно нарисовать числовую линию, чтобы визуализировать длину отрезка.

Нахождение длины отрезка, а затем его середины

Пройти курс

Хотите узнать больше о геометрии? У меня есть пошаговый курс для этого. 🙂

Учить больше

Использование числовой прямой для решения задачи о средней точке

Пример

Точки ???S???, ???T???, ???U???, ???V???, и ???В??? лежат по порядку на числовой прямой. Точка ???U??? находится в ???-2???. Где находятся остальные точки?

???\overline{ST}=2???

???\overline{TU}=1???

???\overline{UV}=3???

???\overline{VW}=2???

Если мы нанесем точку ???U??? в ???-2???, затем ???S???, ???T???, ???U???, ???V???, и ???W?? ? должно быть нанесено таким образом:

Мы знаем точку ???U??? находится на ???-2??? и ???\overline{TU}=1???. Это позволяет нам найти точку ???T??? в 3???. Теперь мы можем использовать ???\overline{ST}=2??? найти, что ???S=-5??? и ???\overline{UV}=3??? найти, что ???V=1???. Теперь мы можем найти точку ???W??? используя ???\overline{VW}=2???, поэтому ???W=3???.

Давайте посмотрим на другой пример.

Расстояние между двумя точками на отрезке называется длиной отрезка.

Пример

Найти ???\overline{AB}???, если ???\overline{AC}=12??? и ???\overline{BC}=7???.

Мы знаем, что ???\overline{AC}=12??? и ???\overline{BC}=7???. Из диаграммы мы также знаем, что ???\overline{AB}??? является частью ???\overline{AC}???.

Мы видим, что ???\overline{AC}-\overline{BC}=\overline{AB}???, поэтому имеем ???\overline{AB}=12-7=5??? .

Давайте посмотрим на последний пример.

Пример

Расположение четырех точек на числовой прямой: ???A=2???, ???B=4???, ???C=-3???, и ? ??D=-6???. Каково значение ???\overline{AB}+\overline{CD}????

Мы можем нарисовать числовую линию, чтобы решить задачу.

Теперь мы видим, что ???\overline{AB}=|4-2|=2??? единицы и ???\overline{CD}=|-3-(-6)|=3??? единицы. Итак, ???\overline{AB}+\overline{CD}=2 + 3 = 5??? единицы.

Получить доступ к полному курсу геометрии

Начать

Изучайте математикуКриста Кинг 24 декабря 2020 г. математика, учитесь онлайн, онлайн-курс, онлайн-математика, геометрия, отрезок, длина отрезка, середина отрезка, середина, числовая линия, расстояние между точками на прямой

0 лайков

Разделение сегмента в заданном соотношении

Предположим, у вас есть отрезок PQ¯ на координатной плоскости, и вам нужно найти точку на отрезке 13 пути от P до Q.

Давайте сначала рассмотрим простой случай, когда P находится в начале координат, а линия сегмент горизонтальный.

Длина прямой составляет 6 единиц, и точка на отрезке 13 пути от P до Q будет на расстоянии 2 единиц от P и 4 единиц от Q и будет в (2,0).

Рассмотрим случай, когда отрезок не является горизонтальной или вертикальной линией.

Компоненты направленного отрезка PQ¯ равны 〈6,3〉  и нам нужно найти точку, скажем, X на отрезке 13 пути из P в Q.

Тогда компоненты отрезка PX ¯ суть 〈(13)(6),(13)(3)〉=〈2,1〉.

Поскольку начальная точка отрезка находится в начале координат, координаты точки X задаются как (0+2,0+1)=(2,1).

Теперь давайте решим более сложную задачу, где ни P, ни Q не находятся в начале координат.

Используйте конечные точки отрезка PQ¯ для записи компонентов направленного отрезка.

ϩ (x2 -x1), (y2 -y1) á = ϩ (7–1), (2–6) ás = ϩ 6, −4 

теперь аналогичным образом, компоненты сегмента px ¯  где X — точка на отрезке 13 пути из P в Qare 〈(13)(6),(13)(−4)〉=〈2,−1,25〉.

Чтобы найти координаты точки X, прибавьте компоненты отрезка PX¯ к координатам начальной точки P.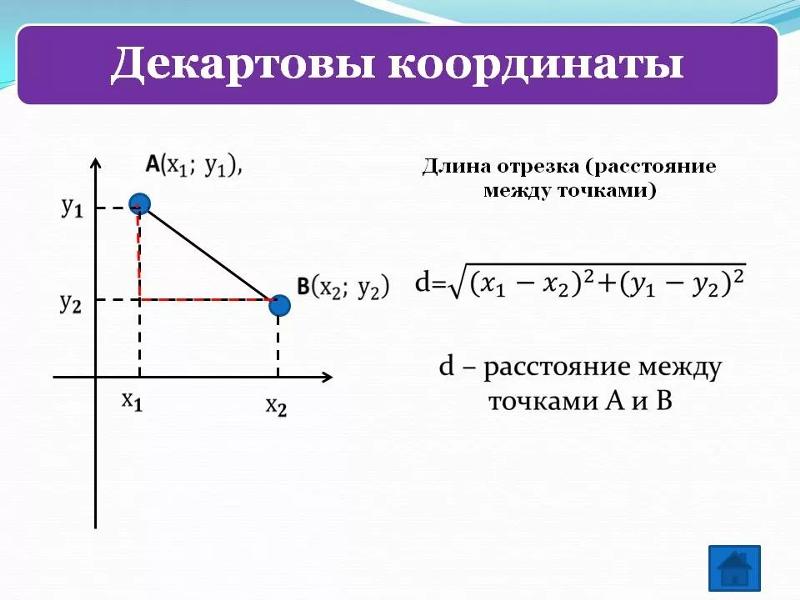

Итак, координаты точки X равны (1+2,6−1,25)=(3,4,75).

Обратите внимание, что получившиеся сегменты PX¯ и XQ¯ имеют длины в соотношении 1:2.

В общем: что если вам нужно найти точку на отрезке, которая делит его на два отрезка с длинами в отношении a:b?

Рассмотрим направленный отрезок XY¯ с координатами концов как X(x1,y1) и Y(x2,y2).

Предположим, что точка Z разделила отрезок в отношении a:b, тогда точка представляет собой aa+b пути из X в Y.

Итак, обобщая имеющийся у нас метод, компоненты отрезка XZ¯ равны 〈(aa+b(x2−x1)),(aa+b(y2−y1))〉.

Затем X-координата точки Z составляет

x1+aa+b (x2-x1) = x1 (a+b)+a (x2-x1) a+b = bx1+ax2a+b.

Аналогично, Y-координата составляет

Y1+AA+B (Y2-Y1) = Y1 (A+B)+A (Y2-Y1) A+B = BY1+AY2A+B.

Следовательно, координаты точки Z равны (bx1+ax2a+b,by1+ay2a+b).

Пример 1:

Найдите координаты точки, которая делит направленный отрезок MN¯ с координатами концов в M(−4,0)  и M(0,4) в отношении 3:1?

Пусть L — точка, которая делит MN¯  в отношении 3:1.