Длина векторов по координатам: Модуль вектора. Длина вектора.

примеры и решения, формулы и теоремы

Длина вектора — основные формулы

Длину вектора a→ будем обозначать a→. Данное обозначение аналогично модулю числа, поэтому длину вектора также называют модулем вектора.

Для нахождения длины вектора на плоскости по его координатам, требуется рассмотреть прямоугольную декартову систему координат Oxy. Пусть в ней задан некоторый вектор a→ с координатами ax;ay. Введем формулу для нахождения длины (модуля) вектора a→ через координаты ax и ay.

От начала координат отложим вектор OA→=a→. Определим соответственные проекции точки A на координатные оси как Ax и Ay . Теперь рассмотрим прямоугольник OAxAAy с диагональю OA.

Из теоремы Пифагора следует равенство OA2=OAx2+OAy2, откуда OA=OAx2+OAy2. Из уже известного определения координат вектора в прямоугольной декартовой системе координат получаем, что OAx2=ax2 и OAy2=ay2, а по построению длина OA равна длине вектора OA→, значит, OA→=OAx2+OAy2.

Отсюда получается, что формула для нахождения длины вектора a→=ax;ay имеет соответствующий вид: a→=ax2+ay2.

Если вектор a→ дан в виде разложения по координатным векторам a→=ax·i→+ay·j→, то вычислить его длину можно по той же формуле a→=ax2+ay2, в данном случае коэффициенты ax и ay выступают в роли координат вектора a→ в заданной системе координат.

Пример 1

Вычислить длину вектора a→=7;e, заданного в прямоугольной системе координат.

Решение

Чтобы найти длину вектора, будем использовать формулу нахождения длины вектора по координатамa→=ax2+ay2: a→=72+e2=49+e

Ответ: a→=49+e.

Формула для нахождения длины вектора a→=ax;ay;az по его координатам в декартовой системе координат Oxyz в пространстве, выводится аналогично формуле для случая на плоскости (см. рисунок ниже)

В данном случае OA2=OAx2+OAy2+OAz2 (так как ОА – диагональ прямоугольного параллелепипеда), отсюда OA=OAx2+OAy2+OAz2. Из определения координат вектора можем записать следующие равенства OAx=ax; OAy=ay; OAz=az; , а длина ОА равна длине вектора, которую мы ищем, следовательно, OA→=OAx2+OAy2+OAz2.

Отсюда следует, что длина вектора a→=ax;ay;az равна a→=ax2+ay2+az2.

Пример 2

Вычислить длину вектора a→=4·i→-3·j→+5·k→, где i→,j→,k→ — орты прямоугольной системы координат.

Решение

Дано разложение вектора a→=4·i→-3·j→+5·k→, его координаты равны a→=4,-3,5. Используя выше выведенную формулу получим a→=ax2+ay2+az2=42+(-3)2+52=52.

Ответ:a→=52.

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание

Длина вектора через координаты точек его начала и конца

Выше были выведены формулы, позволяющие находить длины вектора по его координатам. Мы рассмотрели случаи на плоскости и в трехмерном пространстве. Воспользуемся ими для нахождения координат вектора по координатам точек его начала и конца.

Итак, даны точки с заданными координатами A(ax;ay) и B(bx;by), отсюда вектор AB→ имеет координаты (bx-ax; by-ay)значит, его длина может быть определена по формуле: AB→=(bx-ax)2+(by-ay)2

А если даны точки с заданными координатами A(ax;ay;az) и B(bx;by;bz) в трехмерном пространстве, то длину вектора AB→ можно вычислить по формуле

AB→=(bx-ax)2+(by-ay)2+(bz-az)2

Пример 3

Найти длину вектора AB→, если в прямоугольной системе координат A1, 3, B-3, 1.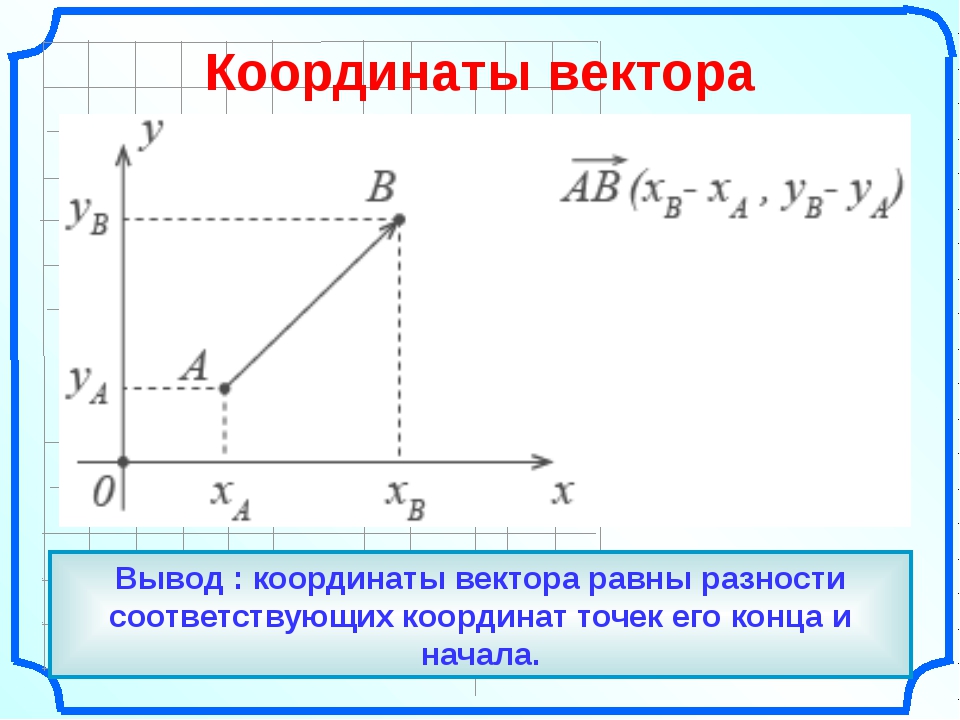

Решение

Используя формулу нахождения длины вектора по координатам точек начала и конца на плоскости, получим AB→=(bx-ax)2+(by-ay)2: AB→=(-3-1)2+(1-3)2=20-23.

Второй вариант решения подразумевает под собой применение данных формул по очереди: AB→=(-3-1; 1-3)=(-4; 1-3); AB→=(-4)2+(1-3)2=20-23.-

Ответ: AB→=20-23.

Пример 4

Определить, при каких значениях  длина вектора AB→ равна 30, еслиA(0, 1, 2); B(5, 2, λ2) .

Решение

Для начала распишем длину вектора AB→ по формуле: AB→=(bx-ax)2+(by-ay)2+(bz-az)2=(5-0)2+(2-1)2+(λ2-2)2=26+(λ2-2)2

Затем полученное выражение приравняем к 30, отсюда найдем искомые λ:

 26+(λ2-2)2=3026+(λ2-2)2=30(λ2-2)2=4λ2-2=2 или λ2-2=-2  λ1=-2, λ2=2, λ3=0.

Ответ: λ1=-2, λ2=2, λ3=0.

Нахождение длины вектора по теореме косинусов

Увы, но в задачах не всегда бывают известны координаты вектора, поэтому рассмотрим другие способы нахождения длины вектора.

Пусть заданы длины двух векторов AB→, AC→ и угол между ними (или косинус угла), а требуется найти длину вектора BC→ или CB→. В таком случае, следует воспользоваться теоремой косинусов в треугольнике △ABC, вычислить длину стороны BC, которая и равна искомой длине вектора.

Рассмотрим такой случай на следующем примере.

Пример 5

Длины векторов AB→ и AC→ равны 3 и 7 соответственно, а угол между ними равен π3. Вычислить длину вектора BC→.

Решение

Длина вектора BC→ в данном случае равна длине стороны BC треугольника △ABC. Длины сторон AB и AC треугольника известны из условия (они равны длинам соответствующих векторов), также известен угол между ними, поэтому мы можем воспользоваться теоремой косинусов:BC2=AB2+AC2-2·AB·AC·cos∠(AB,→AC→)=32+72-2·3·7·cosπ3=37 ⇒BC=37 Таким образом, BC→=37.

Ответ:BC→=37.

Итак, для нахождения длины вектора по координатам существуют следующие формулы a→=ax2+ay2 или a→=ax2+ay2+az2, по координатам точек начала и конца вектора AB→=(bx-ax)2+(by-ay)2 или AB→=(bx-ax)2+(by-ay)2+(bz-az)2, в некоторых случаях следует использовать теорему косинусов.

Модуль вектора. Длина вектора.

Навигация по странице:

Определение длины вектора

Определение.

Длина направленного отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора AB.

Для обозначения длины вектора используются две вертикальные линии слева и справа |AB|.

Основное соотношение. Длина вектора |a| в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат.

Формулы длины вектора

Формула длины вектора для плоских задач

В случае плоской задачи модуль вектора a = {a_x ; a_y} можно найти воспользовавшись следующей формулой:

Формула длины вектора для пространственных задач

В случае пространственной задачи модуль вектора a = {a_x ; a_y ; a_z} можно найти воспользовавшись следующей формулой:

Формула длины n -мерного вектора

В случае n-мерного пространства модуль вектора a = {a

1 ; a₂; . .. ; a_n} можно найти воспользовавшись следующей формулой:

|a| = (	n	ai2)1/2
	Σ
	i=1

Примеры задач на вычисление длины вектора

Примеры вычисления длины вектора для плоских задачи

Пример 1. Найти длину вектора a = {2; 4}.

Решение: |a| = √2² + 4² = √4 + 16 = √20 = 2√5.

Пример 2. Найти длину вектора a = {3; -4}.

Решение: |a| = √3² + (-4)² = √9 + 16 = √25 = 5.

Примеры вычисления длины вектора для пространственных задачи

Пример 3. Найти длину вектора a = {2; 4; 4}.

Решение: |a| = √2² + 4² + 4² = √4 + 16 + 16 = √36 = 6.

Пример 4. Найти длину вектора a = {-1; 0; -3}.

Решение: |a| = √(-1)² + 0² + (-3)² = √1 + 0 + 9 = √10.

Примеры вычисления длины вектора для пространств с размерностью большей 3

Пример 5. Найти длину вектора a = {1; -3; 3; -1}.

Решение: |a| = √1² + (-3)² + 3² + (-1)² = √1 + 9 + 9 + 1 = √20 = 2√5

Пример 6. Найти длину вектора a = {2; 4; 4; 6 ; 2}.

Решение: |a| = √2² + 4² + 4² + 6² + 2² = √4 + 16 + 16 + 36 + 4 = √76 = 2√19.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

вектор длина

Вы искали вектор длина? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и вычисление длины вектора, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «вектор длина».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как вектор длина,вычисление длины вектора,вычисление длины вектора по его координатам,вычисление длины вектора по его координатам доказательство,вычислить длину вектора,длина вектор,длина вектора,длина вектора c,длина вектора в пространстве,длина вектора как найти,длина вектора как обозначается,длина вектора модуль вектора,длина вектора определение,длина вектора по двум точкам,длина вектора по его координатам,длина вектора по координатам,длина вектора по координатам начала и конца,длина вектора по координатам точек,длина вектора по координатам формула,длина вектора равна,длина вектора равна квадратному корню из суммы его координат,длина вектора формула,длина вектора формула по координатам,длина вектора через координаты,длина вектора это,длина векторов,длина векторов по координатам,длина через координаты вектора,длину вектора,длины векторов,длины векторов как найти,как в прямоугольнике найти длины векторов,как вычислить длину вектора,как вычислить длину вектора по координатам,как зная координаты вектора найти его длину,как зная координаты найти длину вектора,как найти длина вектора,как найти длину вектора,как найти длину вектора ав,как найти длину вектора если известны его координаты,как найти длину вектора если известны координаты вектора,как найти длину вектора зная его координаты,как найти длину вектора зная его координаты начала и конца,как найти длину вектора зная координаты,как найти длину вектора зная координаты его начала и конца,как найти длину вектора и координаты,как найти длину вектора по двум точкам,как найти длину вектора по его координатам,как найти длину вектора по координатам,как найти длину вектора по координатам двух точек,как найти длину вектора по координатам начала и конца,как найти длину вектора формула,как найти длину вектора через координаты,как найти длину векторов,как найти длину и координаты вектора,как найти длины векторов,как найти длины векторов по координатам,как найти квадрат длины вектора,как найти координаты вектора если известна длина вектора,как найти координаты вектора зная длину,как найти координаты вектора зная его длину,как найти координаты вектора зная его длину и координаты начала,как найти координаты вектора и длину,как найти координаты вектора через длину,как найти координаты и длину вектора,как находить длину вектора,как обозначается длина вектора,как определить длину вектора,как определить длину вектора по координатам,как узнать длину вектора,как узнать длину вектора по координатам,квадрат длины вектора формула,координаты вектора длина вектора,модуль вектора длина вектора,модуль вектора определение,найдите длину и координаты вектора,найдите длины векторов,найти длину вектора,найти длину вектора по координатам,найти длину вектора по координатам точек,найти длину и координаты вектора,найти длину по координатам точек вектора,найти длины векторов,найти координаты вектора и длину,найти координаты и длину вектора,нахождение длины вектора,нахождение длины вектора по его координатам,определение вектора длина вектора,определение вектора длины,определение вектора длины вектора,определение длина вектора,определение длины вектора,определение модуль вектора,по координатам точек найти длину вектора,формула вычисления длины вектора,формула вычисления длины вектора по его координатам,формула длина вектора,формула длины вектора,формула длины вектора по его координатам,формула для вычисления длины вектора по его координатам,формула для нахождения длины вектора,формула как найти длину вектора,формула квадрат длины вектора,формула модуля вектора,формула нахождения длины,формула нахождения длины вектора,формула нахождения длины вектора по его координатам,чему равна длина вектора,что такое длина вектора.

На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и вектор длина. Просто введите задачу в окошко и нажмите «решить» здесь (например, вычисление длины вектора по его координатам).

Где можно решить любую задачу по математике, а так же вектор длина Онлайн?

Решить задачу вектор длина вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Длина вектора. Модуль вектора | Калькулятор

Вектором называется направленный отрезок AB; точка A — начало, точка B — конец вектора
Вектор обозначается либо двумя большими буквами — своим началом и концом: AB либо одной малой буквой: a.
Длину вектора a будем обозначать ∣a∣. Данное обозначение аналогично модулю числа, поэтому длину вектора также называют модулем вектора.

Определение длины вектора

• Длина направленного отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора AB.
• Длиной (модулем) вектора AB называется неотрицательное число, равное расстоянию между его началом и концом, то есть длина вектора — это длина отрезка AB. Длина AB обозначается |AB|
• Основное соотношение. Длина вектора |a| в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат.

Длина нулевого вектора 0 равна нулю. Длина единичного вектора e равна единице.

Длина вектора, заданного координатами, равна корню квадратному из суммы квадратов его координат.

Формула длины вектора для плоских задач

В случае плоской задачи модуль вектора a = {a_x ; a_y} можно найти воспользовавшись следующей формулой:

|a| = √a_x² + a_y²

Формула длины вектора в трехмерном пространстве

В случае пространственной задачи модуль вектора a = {a_x ; a_y ; a_z} можно найти воспользовавшись следующей формулой:

|a| = √a_x² + a_y² + a_z²

Примеры задач на вычисление длины вектора

Пример 1.

Вектор

ОА имеет начальную точку в начале координат О (0; 0; 0) и конечную точку в А (4; 6; 10). Найдите длину вектора.
Решение:
|ОА| = √4²+6²+10²
|ОА| = √152
|ОА| = 12,32

Пример 2.

Найти длину вектора a = {2; 4}.
Решение:
|a| = √2² + 4²
|a| = √4 + 16
|a| = √20
|a| = 2√5
|a| = 4.47213595499958

Пример 3.

Найти длину вектора a = {-1; 0; -3}.
Решение:
|a| = √(-1)² + 0² + (-3)²
|a| = √1 + 0 + 9
|a| = √10

Полезен ли материал?

#Векторы #Калькуляторы

Характеристики вектора: длина, направление, координаты

У любого вектора есть 2 главные характеристики:

• длина (математики говорят «модуль вектора»)
• направление (в какую сторону вектор на рисунке направлен)

Третья характеристика вектора – это его координаты.

Примечание:

Зная координаты вектора, можно найти его длину и направление. Поэтому, задавать информацию о векторе можно двояко: либо указав его длину и направление, либо его координаты.

Что такое координаты вектора

Координаты вектора – это длины его теней на осях координат (его проекции на оси).

Координаты вектора указывают так:

\[\vec{a} = \left\{ a_{x}; a_{y} \right\}\]

\( a_{x} \) – это  «x» координата вектора, проекция вектора \( \vec{a} \) на ось Ox;

\( a_{y} \) — это  «y» координата вектора, проекция вектора \( \vec{a} \) на ось Oy;

Рис. 1. Обозначения вектора и его проекций на координатные оси

Координаты вектора можно получить из координат его начальной и конечной точек:

«координата вектора» = «конец» — «начало»

 

Пример:

\( A \left( 1;1 \right) \) — начальная точка,

\( B \left( 4;3 \right) \) — конечная точка,

Рис. {2} } \]

Как указать направление вектора

Указать направление вектора можно с помощью его координат. Так как в его координатах уже содержится информация о длине и направлении вектора.

Бывает так, что координаты вектора неизвестны, а известна только лишь его длина. Тогда направление можно указать с помощью угла между вектором и какой-либо осью.

Для двумерного вектора

Если вектор двумерный, то для указания направления (см. рис. 10) можно использовать один из двух углов:

• угол \( \alpha \) между вектором и горизонталью (осью Ox),
• или угол \( \beta \) вежду вектором и вертикалью (осью Oy).

Рис. 6. Углы между вектором и осями на плоскости

Словами указать направление вектора можно так:

• вектор длиной 5 единиц направлен под углом 30 градусов к горизонтали;
• Или же: вектор длиной 5 единиц направлен под углом 60 градусов к вертикали.

Такой способ указания координат используют в полярной системе координат.

Для трехмерного вектора

Когда вектор располагается в трехмерном пространстве, чтобы указать, куда вектор направлен, используют два угла.

• угол между вектором и осью Oz;
• и один из углов: между вектором и осью Oy, или между вектором и осью Ox;

Такой способ указания координат используют в сферической системе координат.

Считаем Землю шаром. Расположим ее центр в начале трехмерной системы координат – точке (0 ; 0 ; 0).

Тогда координаты любой точки на поверхности планеты можно указать с помощью радиус-вектора этой точки.

Для указания сферических координат принято использовать:

• длину вектора,
• угол между осью Ox и вектором и
• угол между осью Oz и вектором.

Длина вектора по координатам с примером решения

Содержание:

 

1. Сложение векторов
2. Разность векторов
3. Умножение вектора на число

Пусть вектор задан своими проекциями: Перенесем его параллельно себе так, чтобы его начало совпало с началом координат. Получим Из рис. 1.9 видно, что

Согласно (1.5) аналогично и Эти числа подставим в предыдущую формулу и получим Извлечем квадратный корень и найдем длину вектора:

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Пример с решением

Задача:

Пусть в пространстве Oxyz точки А и В заданы координатами (рис. 1.10). Нужно найти расстояние между ними.

Так как координаты точки равны проекциям на оси координат радиус-вектора этой точки, то Согласно (1.8) Значит, — Отсюда видно, что проекции вектора на оси координат равны разностям соответствующих координат его конца и начала. Зная проекции , по формуле (1.10) найдем длину вектора следовательно, и расстояние между точками А и В:

Скалярной называется величина, которая полностью определяется своим численным значением. Примерами скалярных величин являются длина, площадь, объем, масса. Вектором называется направленный отрезок прямой, соединяющий две точки в пространстве (рис. 1.4). Если А и В — начало и конец вектора, то он обозначается или

Возможно вам будут полезны данные страницы:

Длиной (модулем) вектора называется число, равное длине отрезка, соединяющего начало и конец вектора. Длина вектора обозначается Если начало вектора совпадает с концом, то вектор называется нулевым и обозначается Рис. 1.4 Ненулевые векторы называются коллинеарными, если они расположены на одной прямой или на параллельных прямых. Векторы называют равными (в этом случае пишут ), если:

— равны их длины

— они коллинеарны;

— они сонаправлены.

Следовательно, при параллельном переносе вектора получим вектор, равный исходному.

Сложение векторов

Даны векторы Вектор перенесем параллельно самому себе и поместим его начало в конец вектора Тогда вектор, начало которого совпадает с началом вектора а конец — с концом вектора Ь, называется суммой векторов и обозначается Ясно, что сумму двух векторов можно получить иначе: построить с началом в общей точке, затем достроить на этих векторах, как на сторонах, параллелограмм. Тогда его диагональ, выходящая из общего начала, будет суммой исходных векторов (рис. 1.5). Указанный метод легко распространяется на случаи трех

и большего числа векторов: от конца первого строим второй, от конца второго — третий и т. д., тогда вектор, начало которого совпадает с началом первого, а конец — с концом последнего, и будет суммой рассматриваемых векторов (рис. 1.6).

Свойства сложения векторов: Эти свойства проверяются с помощью построения.

Разность векторов

Даны векторы Построим эти векторы с началом в общей точке. Тогда вектор, начало которого совпадает с концом вектора а конец — с концом вектора , называется разностью векторов и обозначается (рис. 1.7). Из рисунка видно, что

Умножение вектора на число

Даны ненулевой вектор и число Произведением вектора на число называется вектор который:

— коллинеарен

— имеет длину

— направлен так же, как и при , и противоположно при

Свойства умножения вектора на число:

Эти свойства доказываются построением.

Вычисление длины вектора по его координатам правило. Как найти координаты вектора. Как найти координаты вектора онлайн

Длину вектора a → будем обозначать a → . Данное обозначение аналогично модулю числа, поэтому длину вектора также называют модулем вектора.

Для нахождения длины вектора на плоскости по его координатам, требуется рассмотреть прямоугольную декартову систему координат O x y . Пусть в ней задан некоторый вектор a → с координатами a x ; a y . Введем формулу для нахождения длины (модуля) вектора a → через координаты a x и a y .

От начала координат отложим вектор O A → = a → . Определим соответственные проекции точки A на координатные оси как A x и A y . Теперь рассмотрим прямоугольник O A x A A y с диагональю O A .

Из теоремы Пифагора следует равенство O A 2 = O A x 2 + O A y 2 , откуда O A = O A x 2 + O A y 2 . Из уже известного определения координат вектора в прямоугольной декартовой системе координат получаем, что O A x 2 = a x 2 и O A y 2 = a y 2 , а по построению длина O A равна длине вектора O A → , значит, O A → = O A x 2 + O A y 2 .

Отсюда получается, что формула для нахождения длины вектора a → = a x ; a y имеет соответствующий вид: a → = a x 2 + a y 2 .

Если вектор a → дан в виде разложения по координатным векторам a → = a x · i → + a y · j → , то вычислить его длину можно по той же формуле a → = a x 2 + a y 2 , в данном случае коэффициенты a x и a y выступают в роли координат вектора a → в заданной системе координат.

Пример 1

Вычислить длину вектора a → = 7 ; e , заданного в прямоугольной системе координат.

Решение

Чтобы найти длину вектора, будем использовать формулу нахождения длины вектора по координатам a → = a x 2 + a y 2: a → = 7 2 + e 2 = 49 + e

Ответ: a → = 49 + e .

Формула для нахождения длины вектора a → = a x ; a y ; a z по его координатам в декартовой системе координат Oxyz в пространстве, выводится аналогично формуле для случая на плоскости (см. рисунок ниже)

В данном случае O A 2 = O A x 2 + O A y 2 + O A z 2 (так как ОА – диагональ прямоугольного параллелепипеда), отсюда O A = O A x 2 + O A y 2 + O A z 2 . Из определения координат вектора можем записать следующие равенства O A x = a x ; O A y = a y ; O A z = a z ; , а длина ОА равна длине вектора, которую мы ищем, следовательно, O A → = O A x 2 + O A y 2 + O A z 2 .

Отсюда следует, что длина вектора a → = a x ; a y ; a z равна a → = a x 2 + a y 2 + a z 2 .

Пример 2

Вычислить длину вектора a → = 4 · i → — 3 · j → + 5 · k → , где i → , j → , k → — орты прямоугольной системы координат.

Решение

Дано разложение вектора a → = 4 · i → — 3 · j → + 5 · k → , его координаты равны a → = 4 , — 3 , 5 . Используя выше выведенную формулу получим a → = a x 2 + a y 2 + a z 2 = 4 2 + (- 3) 2 + 5 2 = 5 2 .

Ответ: a → = 5 2 .

Длина вектора через координаты точек его начала и конца

Выше были выведены формулы, позволяющие находить длины вектора по его координатам. Мы рассмотрели случаи на плоскости и в трехмерном пространстве. Воспользуемся ими для нахождения координат вектора по координатам точек его начала и конца.

Итак, даны точки с заданными координатами A (a x ; a y) и B (b x ; b y) , отсюда вектор A B → имеет координаты (b x — a x ; b y — a y) значит, его длина может быть определена по формуле: A B → = (b x — a x) 2 + (b y — a y) 2

А если даны точки с заданными координатами A (a x ; a y ; a z) и B (b x ; b y ; b z) в трехмерном пространстве, то длину вектора A B → можно вычислить по формуле

A B → = (b x — a x) 2 + (b y — a y) 2 + (b z — a z) 2

Пример 3

Найти длину вектора A B → , если в прямоугольной системе координат A 1 , 3 , B — 3 , 1 .

Решение

Используя формулу нахождения длины вектора по координатам точек начала и конца на плоскости, получим A B → = (b x — a x) 2 + (b y — a y) 2: A B → = (- 3 — 1) 2 + (1 — 3) 2 = 20 — 2 3 .

Второй вариант решения подразумевает под собой применение данных формул по очереди: A B → = (- 3 — 1 ; 1 — 3) = (- 4 ; 1 — 3) ; A B → = (- 4) 2 + (1 — 3) 2 = 20 — 2 3 . —

Ответ: A B → = 20 — 2 3 .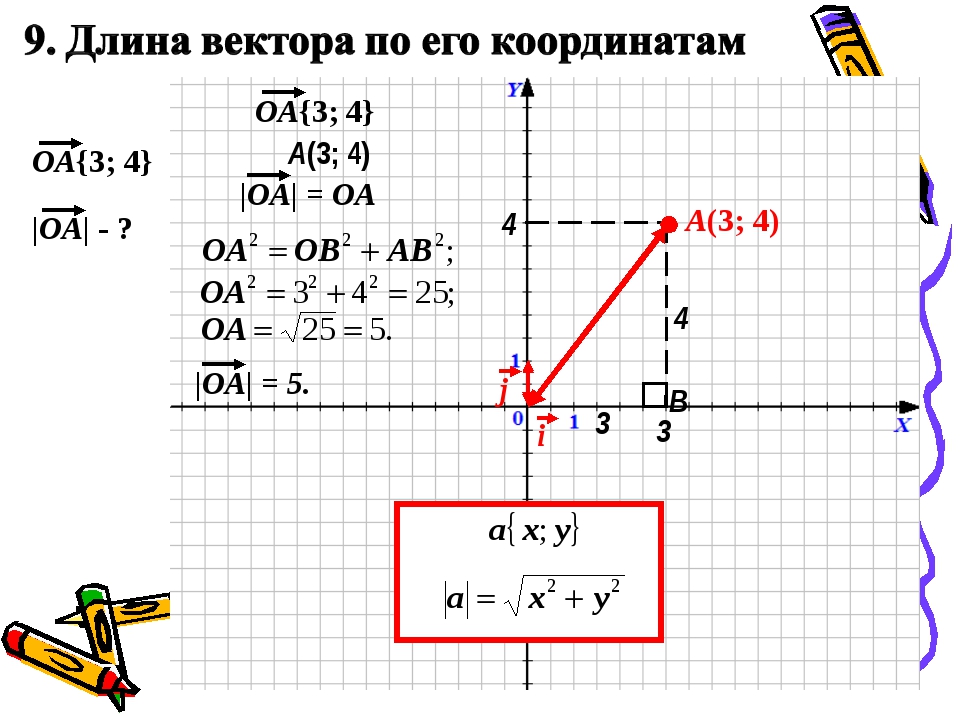

Пример 4

Определить, при каких значениях длина вектора A B → равна 30 , если A (0 , 1 , 2) ; B (5 , 2 , λ 2) .

Решение

Для начала распишем длину вектора A B → по формуле: A B → = (b x — a x) 2 + (b y — a y) 2 + (b z — a z) 2 = (5 — 0) 2 + (2 — 1) 2 + (λ 2 — 2) 2 = 26 + (λ 2 — 2) 2

Затем полученное выражение приравняем к 30 , отсюда найдем искомые λ:

26 + (λ 2 — 2) 2 = 30 26 + (λ 2 — 2) 2 = 30 (λ 2 — 2) 2 = 4 λ 2 — 2 = 2 и л и λ 2 — 2 = — 2 λ 1 = — 2 , λ 2 = 2 , λ 3 = 0 .

Ответ: λ 1 = — 2 , λ 2 = 2 , λ 3 = 0 .

Нахождение длины вектора по теореме косинусов

Увы, но в задачах не всегда бывают известны координаты вектора, поэтому рассмотрим другие способы нахождения длины вектора.

Пусть заданы длины двух векторов A B → , A C → и угол между ними (или косинус угла), а требуется найти длину вектора B C → или C B → . В таком случае, следует воспользоваться теоремой косинусов в треугольнике △ A B C , вычислить длину стороны B C , которая и равна искомой длине вектора.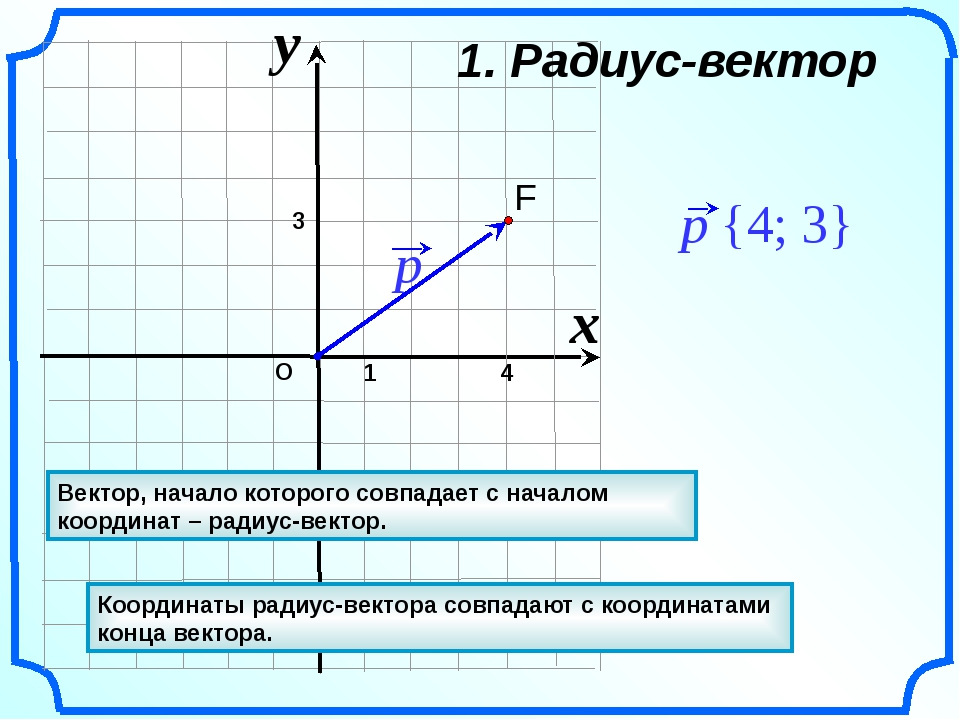

Рассмотрим такой случай на следующем примере.

Пример 5

Длины векторов A B → и A C → равны 3 и 7 соответственно, а угол между ними равен π 3 . Вычислить длину вектора B C → .

Решение

Длина вектора B C → в данном случае равна длине стороны B C треугольника △ A B C . Длины сторон A B и A C треугольника известны из условия (они равны длинам соответствующих векторов), также известен угол между ними, поэтому мы можем воспользоваться теоремой косинусов: B C 2 = A B 2 + A C 2 — 2 · A B · A C · cos ∠ (A B , → A C →) = 3 2 + 7 2 — 2 · 3 · 7 · cos π 3 = 37 ⇒ B C = 37 Таким образом, B C → = 37 .

Ответ: B C → = 37 .

Итак, для нахождения длины вектора по координатам существуют следующие формулы a → = a x 2 + a y 2 или a → = a x 2 + a y 2 + a z 2 , по координатам точек начала и конца вектора A B → = (b x — a x) 2 + (b y — a y) 2 или A B → = (b x — a x) 2 + (b y — a y) 2 + (b z — a z) 2 , в некоторых случаях следует использовать теорему косинусов.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

6.4. Некоторые приложения скалярного произведения

11. Выражение скалярного произведения вектора через координаты сомножителей. Теорема.

12. Длина вектора, длина отрезка, угол между векторами, условие перпендикулярности векторов.

13. Векторное произведение векторов, его свойства. Площадь параллелограмма.

14. Смешанное произведение векторов, его свойства. Условие компланарности вектора. Объем параллелепипеда. Объём пирамиды.

15. Способы задания прямой на плоскости.

16. Нормальное уравнение прямой на плоскости (вывод). Геометрический смысл коэффициентов.

17. Уравнение прямой на плоскости в отрезках (вывод).

Приведение общего уравнения плоскости к уравнению плоскости в отрезках.

18. Уравнение прямой на плоскости с угловым коэффициентом (вывод).

19. Уравнение прямой на плоскости, проходящей через две точки (вывод).

20. Угол между прямыми на плоскости (вывод).

21. Расстояние от точки до прямой на плоскости (вывод).

22. Условия параллельности и перпендикулярности прямых на плоскости (вывод).

23. Уравнение плоскости. Нормальное уравнение плоскости (вывод). Геометрический смысл коэффициентов.

24. Уравнение плоскости в отрезках (вывод).

25. Уравнение плоскости, проходящей через три точки (вывод).

26. Угол между плоскостями (вывод).

27. Расстояние от точки до плоскости (вывод).

28. Условия параллельности и перпендикулярности плоскостей (вывод).

29. Уравнения прямой в r3. Уравнения прямой, проходящей через две фиксированные точки (вывод).

30. Канонические уравнения прямой в пространстве (вывод).

Составление канонических уравнений прямой в пространстве.

Частные случаи канонических уравнений прямой в пространстве.

Канонические уравнения прямой проходящей через две заданные точки пространства.

Переход от канонических уравнений прямой в пространстве к другим видам уравнений прямой.

31. Угол между прямыми (вывод).

32. Расстояние от точки до прямой на плоскости (вывод).

Расстояние от точки до прямой на плоскости – теория, примеры, решения.

Первый способ нахождения расстояния от заданной точки до заданной прямой на плоскости.

Второй способ, позволяющий найти расстояние от заданной точки до заданной прямой на плоскости.

Решение задач на нахождение расстояния от заданной точки до заданной прямой на плоскости.

Расстояние от точки до прямой в пространстве – теория, примеры, решения.

Первый способ нахождения расстояния от точки до прямойaв пространстве.

Второй способ, позволяющий находить расстояние от точки до прямойaв пространстве.

33. Условия параллельности и перпендикулярности прямых в пространстве.

34. Взаимное расположение прямых в пространстве и прямой с плоскостью.

35. Классическое уравнение эллипса (вывод) и его построение. Каноническое уравнение эллипса имеет вид, где– положительные действительные числа, причём.Как построить эллипс?

36. Классическое уравнение гиперболы (вывод) и его построение. Асимптоты.

37. Каноническое уравнение параболы (вывод) и построение.

38. Функция. Основные определения. Графики основных элементарных функций.

39. Числовые последовательности. Предел числовой последовательности.

40. Бесконечно малые и бесконечно большие величины. Теорема о связи между ними, свойства.

41. Теоремы о действиях над переменными величинами, имеющими конечные пределы.

42. Число e.

Содержание

Способы определения

Свойства

История

Приближения

43. Определение предела функции. Раскрытие неопределённостей.

44. Замечательные пределы, их вывод. Эквивалентные бесконечно малые величины.

Содержание

Первый замечательный предел

Второй замечательный предел

45. Односторонние пределы. Непрерывность и разрывы функции. Односторонние пределы

Левый и правый пределы функции

Точка разрыва первого рода

Точка разрыва второго рода

Точка устранимого разрыва

46. Определение производной. Геометрический смысл, механический смысл производной. Уравнения касательной и нормали к кривой и точке.

47. Теоремы о производной обратной, сложной функций.

48. Производные простейших элементарных функций.

49. Дифференцирование параметрических, неявных и степенно-показательных функций.

21. Дифференцирование неявных и параметрически заданных функций

21.1. Неявно заданная функция

21.2. Функция, заданная параметрически

50. Производные высших порядков. Формула Тейлора.

51. Дифференциал. Применение дифференциала к приближенным вычислениям.

52. Теоремы Ролля, Лагранжа, Коши. Правило Лопиталя.

53. Теорема о необходимом и достаточном условиях монотонности функции.

54. Определение максимума, минимума функции. Теоремы о необходимом и достаточном условиях существования экстремума функции.

Теорема (необходимое условие экстремума)

55. Выпуклость и вогнутость кривых. Точки перегиба. Теоремы о необходимом и достаточном условиях существования точек перегиба.

Доказательство

57. Определители n-ого порядка, их свойства.

58. Матрицы и действия над ними. Ранг матрицы.

Определение

Связанные определения

Свойства

Линейное преобразование и ранг матрицы

59. Обратная матрица. Теорема о существовании обратной матрицы.

60. Системы линейных уравнений. Матричное решение систем линейных уравнений. Правило Крамера. Метод Гаусса. Теорема Кронекера-Капелли.

Решение систем линейных алгебраических уравнений, методы решения, примеры.

Определения, понятия, обозначения.

Решение элементарных систем линейных алгебраических уравнений.

Решение систем линейных уравнений методом Крамера.

Решение систем линейных алгебраических уравнений матричным методом (с помощью обратной матрицы).

Решение систем линейных уравнений методом Гаусса.

Решение систем линейных алгебраических уравнений общего вида.

Теорема Кронекера – Капелли.

Метод Гаусса для решения систем линейных алгебраических уравнений общего вида.

Запись общего решения однородных и неоднородных систем линейных алгебраических с помощью векторов фундаментальной системы решений.

Решение систем уравнений, сводящихся к слау.

Примеры задач, сводящихся к решению систем линейных алгебраических уравнений.

Вектором называется направленный отрезок. Длиной или модулем вектора называется длина соответствующего направленного отрезка.

Модуль вектора a обозначается . Векторa называется единичным, если . Векторы называются коллинеарными, если они параллельны одной прямой. Векторы называются компланарными, если они параллельны одной плоскости.

2. Умножение вектора на число. Свойства операции.

Умножение вектора на число, даёт противоположно направленный вектор в длиной враз больше. Умножение вектора на число в координатной форме производится умножением всех координат на это число:

Исходя из определения получается выражение для модуля вектора, умноженного на число:

Аналогично как и числами, операции сложение вектора с самим с собой можно записать через умножение на число:

А вычитание векторов можно переписать через сложение и умножение:

Исходя из того, что умножение на не меняет длины вектора, а меняет только направление и учитывая определение вектора, получаем:

3. Сложение векторов, вычитание векторов.

В координатном представлении вектор суммы получается суммированием соответствующих координат слагаемых:

Для геометрического построения вектора суммы используют различные правила (методы), однако они все дают одинаковый результат.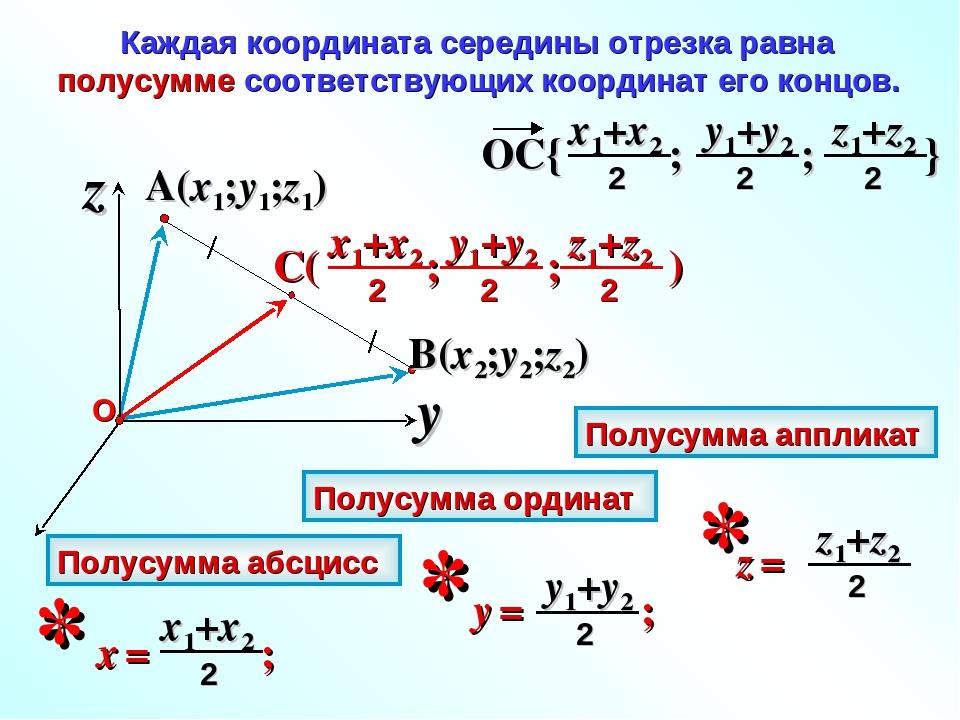 Использование того или иного правила обосновывается решаемой задачей.

Правило треугольника

Правило треугольника наиболее естественно следует из понимания вектора как переноса. Ясно, что результат последовательного применения двух переносов инекоторой точки будет тем же, что применение сразу одного переноса, соответствующего этому правилу. Для сложения двух векторовипо правилутреугольника оба эти вектора переносятся параллельно самим себе так, чтобы начало одного из них совпадало с концом другого. Тогда вектор суммы задаётся третьей стороной образовавшегося треугольника, причём его начало совпадает с началом первого вектора, а конец с концом второго вектора.

Это правило прямо и естественно обобщается для сложения любого количества векторов, переходя в правило ломаной :

Правило многоугольника

Начало второго вектора совмещается с концом первого, начало третьего — с концом второго и так далее, сумма же векторов есть вектор, с началом, совпадающим с началом первого, и концом, совпадающим с концом-го (то есть изображается направленным отрезком, замыкающим ломаную). Так же называется правилом ломаной.

Правило параллелограмма

Для сложения двух векторов ипо правилупараллелограмма оба эти векторы переносятся параллельно самим себе так, чтобы их начала совпадали. Тогда вектор суммы задаётся диагональю построенного на них параллелограмма, исходящей из их общего начала. (Легко видеть, что эта диагональ совпадает с третьей стороной треугольника при использовании правила треугольника).

Правило параллелограмма особенно удобно, когда есть потребность изобразить вектор суммы сразу же приложенным к той же точке, к которой приложены оба слагаемых — то есть изобразить все три вектора имеющими общее начало.

Модуль суммы векторов

Модуль суммы двух векторов можно вычислить, использую теорему косинусов :

Где — косинус угла между векторамии.

Если векторы изображены в соответствии с правилом треугольника и берется угол по рисунку — между сторонами треугольника — что не совпадает с обычным определением угла между векторами, а значит и с углом в приведенной формуле, то последний член приобретает знак минус, что соответствует теореме косинусов в ее прямой формулировке.

Для суммы произвольного количества векторов применима аналогичная формула, в которой членов с косинусом больше: по одному такому члену существует для каждой пары векторов из суммируемого набора. Например, для трех векторов формула выглядит так:

Вычитание векторов

Два вектора и вектор их разности

Для получения разности в координатной форме надо вычесть соответствующие координаты векторов:

Для получения вектора разности начала векторов соединяются и началом векторабудет конец, а концом — конец. Если записать, используя точки векторов, то.

Модуль разности векторов

Три вектора , как и при сложении, образуют треугольник, и выражение для модуля разности получается аналогичным:

где — косинус угла между векторамии

Отличие от формулы модуля суммы в знаке перед косинусом, при этом надо хорошо следить, какой именно угол берется (вариант формулы модуля суммы с углом между сторонами треугольника при суммировании по правилу треугольника по виду не отличается от данной формулы для модуля разности, но надо иметь в виду, что для тут берутся разные углы: в случае суммы берётся угол, когда вектор переносится к концу вектора, когда же ищется модель разности, берётся угол между векторами, приложенными к одной точке; выражение для модуля суммы с использованием того же угла, что в данном выражении для модуля разности, отличается знаком перед косинусом).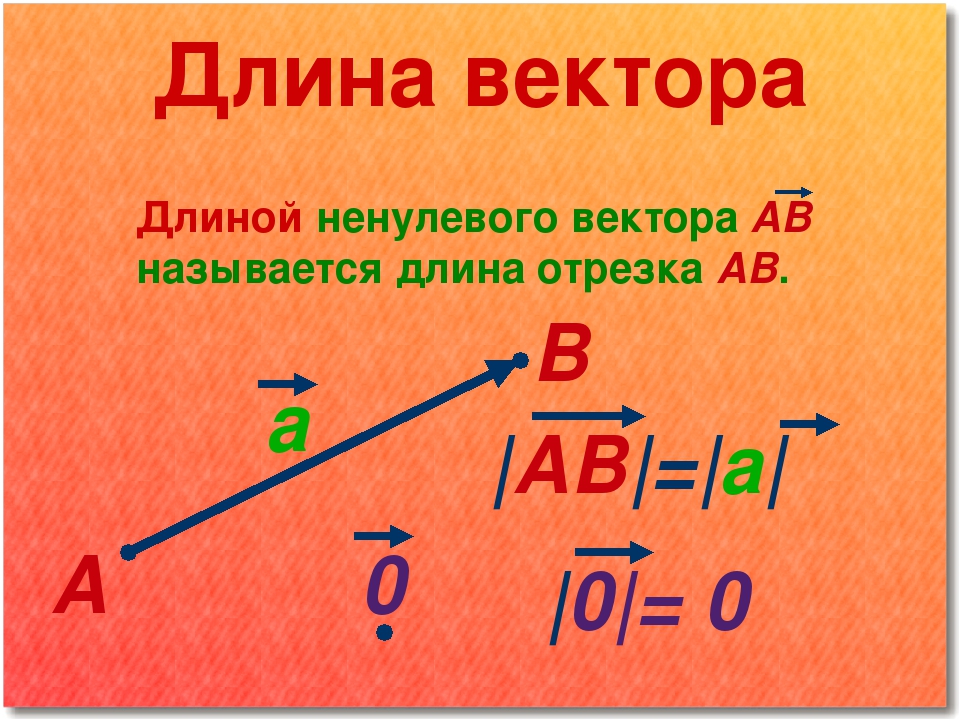

Прежде всего надо разобрать само понятие вектора. Для того, чтобы ввести определение геометрического вектора вспомним, что такое отрезок . Введем следующее определение.

Определение 1

Отрезком будем называть часть прямой, которая имеет две границы в виде точек.

Отрезок может иметь 2 направления. Для обозначения направления будем называть одну из границ отрезка его началом, а другую границу — его концом. Направление указывается от его начала к концу отрезка.

Определение 2

Вектором или направленным отрезком будем называть такой отрезок, для которого известно, какая из границ отрезка считается началом, а какая его концом.

Обозначение: Двумя буквами: $\overline{AB}$ – (где $A$ его начало, а $B$ – его конец).

Одной маленькой буквой: $\overline{a}$ (рис. 1).

Введем теперь, непосредственно, понятие длин вектора.

Определение 3

Длиной вектора $\overline{a}$ будем называть длину отрезка $a$.

Обозначение: $|\overline{a}|$

Понятие длины вектора связано, к примеру, с таким понятием, как равенство двух векторов.

Определение 4

Два вектора будем называть равными, если они удовлетворяют двух условиям: 1. Они сонаправлены; 1. Их длины равны (рис. 2).

Для того, чтобы определять векторы вводят систему координат и определяют координаты для вектора во введенной системе. Как мы знаем, любой вектор можно разложить в виде $\overline{c}=m\overline{i}+n\overline{j}$, где $m$ и $n$ – действительные числа, а $\overline{i}$ и $\overline{j}$ — единичные векторы на оси $Ox$ и $Oy$, соответственно.

Определение 5

Коэффициенты разложения вектора $\overline{c}=m\overline{i}+n\overline{j}$ будем называть координатами этого вектора во введенной системе координат. Математически:

$\overline{c}={m,n}$

Как найти длину вектора?

Для того, чтобы вывести формулу для вычисления длины произвольного вектора по данным его координатам рассмотрим следующую задачу:

Пример 1

Дано: вектор $\overline{α}$, имеющий координаты ${x,y}$. Найти: длину этого вектора.

Введем на плоскости декартову систему координат $xOy$.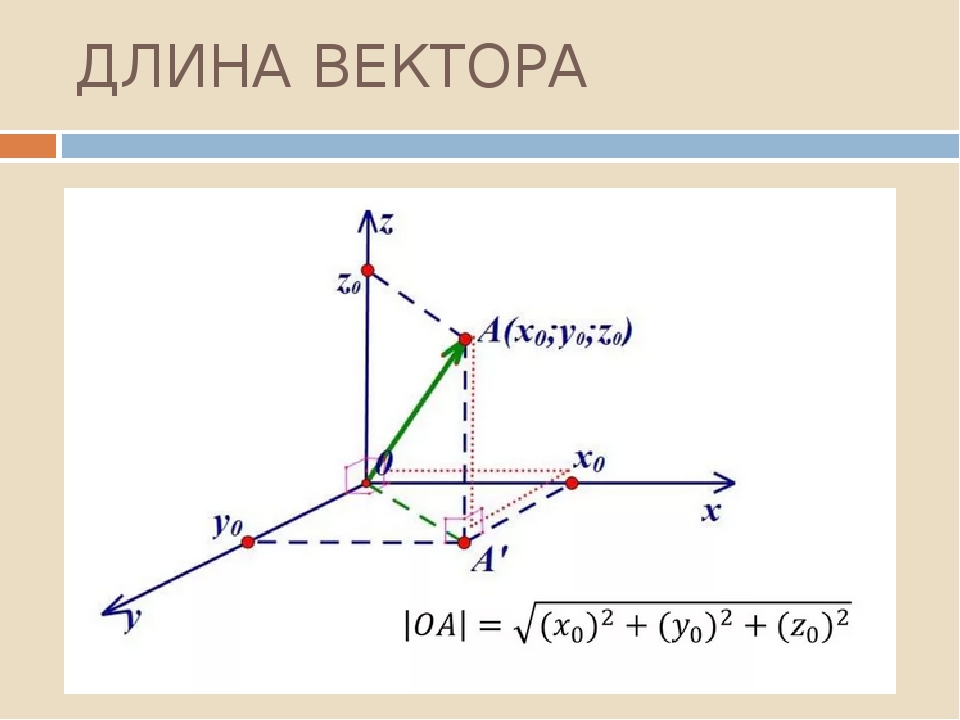 2}$.

Вывод: Чтобы найти длину вектора, у которого задан его координаты, необходимо найти корень из квадрата суммы этих координат.

Пример задач

Пример 2

Найдите расстояние между точками $X$ и $Y$, которые имеют следующие координаты: $(-1,5)$ и $(7,3)$, соответственно.

Любые две точки можно легко связать с понятием вектора. Рассмотрим, к примеру, вектор $\overline{XY}$. Как мы уже знаем, координаты такого вектора можно найти, вычтя из координат конечной точки ($Y$) соответствующие координаты начальной точки ($X$). Получим, что

Oxy

О А ОА .

, откуда ОА .

Таким образом, .

Рассмотрим пример.

Пример.

Решение.

:

Ответ:

Oxyz в пространстве.

А ОА будет диагональю.

В этом случае (так как ОА ОА .

Таким образом, длина вектора .

Пример.

Вычислите длину вектора

Решение.

, следовательно,

Ответ:

Прямая на плоскости

Общее уравнение

Ax + By + C ( > 0).

Вектор = (А; В) — нормальный вектор прямой.

В векторном виде: + С = 0 , где — радиус-вектор произвольной точки на прямой (рис. 4.11).

Частные случаи:

1) By + C = 0 — прямая параллельна оси Ox ;

2) Ax + C = 0 — прямая параллельна оси Oy ;

3) Ax + By = 0 — прямая проходит через начало координат;

4) y = 0 — ось Ox ;

5) x = 0 — ось Oy .

Уравнение прямой в отрезках

где a, b — величины отрезков, отсекаемых прямой на осях координат.

Нормальное уравнение прямой (рис. 4.11)

где — угол, образуемый нормально к прямой и осью Ox ; p — расстояние от начала координат до прямой.

Приведение общего уравнения прямой к нормальному виду:

Здесь — нормируемый множитель прямой; знак выбирается противоположным знаку C , если и произвольно, если C = 0 .

Нахождение длины вектора по координатам.

Длину вектора будем обозначать . Из-за такого обозначения длину вектора часто называют модулем вектора.

Начнем с нахождения длины вектора на плоскости по координатам.

Введем на плоскости прямоугольную декартову систему координат Oxy . Пусть в ней задан вектор и он имеет координаты . Получим формулу, позволяющую находить длину вектора через координаты и .

Отложим от начала координат (от точки О ) вектор . Обозначим проекции точки А на координатные оси как и соответственно и рассмотрим прямоугольник с диагональю ОА .

В силу теоремы Пифагора справедливо равенство , откуда . Из определения координат вектора в прямоугольной системе координатмы можем утверждать, что и , а по построению длина ОА равна длине вектора , следовательно, .

Таким образом, формула для нахождения длины вектора по его координатам на плоскости имеет вид .

Если вектор представлен в виде разложения по координатным векторам , то его длина вычисляется по этой же формуле , так как в этом случае коэффициенты и являются координатами вектора в заданной системе координат.

Рассмотрим пример.

Пример.

Найдите длину вектора , заданного в декартовой системе координат.

Решение.

Сразу применяем формулу для нахождения длины вектора по координатам :

Ответ:

Теперь получим формулу для нахождения длины вектора по его координатам в прямоугольной системе координат Oxyz в пространстве.

Отложим от начала координат вектор и обозначим проекции точки А на координатные оси как и . Тогда мы можем построить на сторонах и прямоугольный параллелепипед, в котором ОА будет диагональю.

В этом случае (так как ОА – диагональ прямоугольного параллелепипеда), откуда .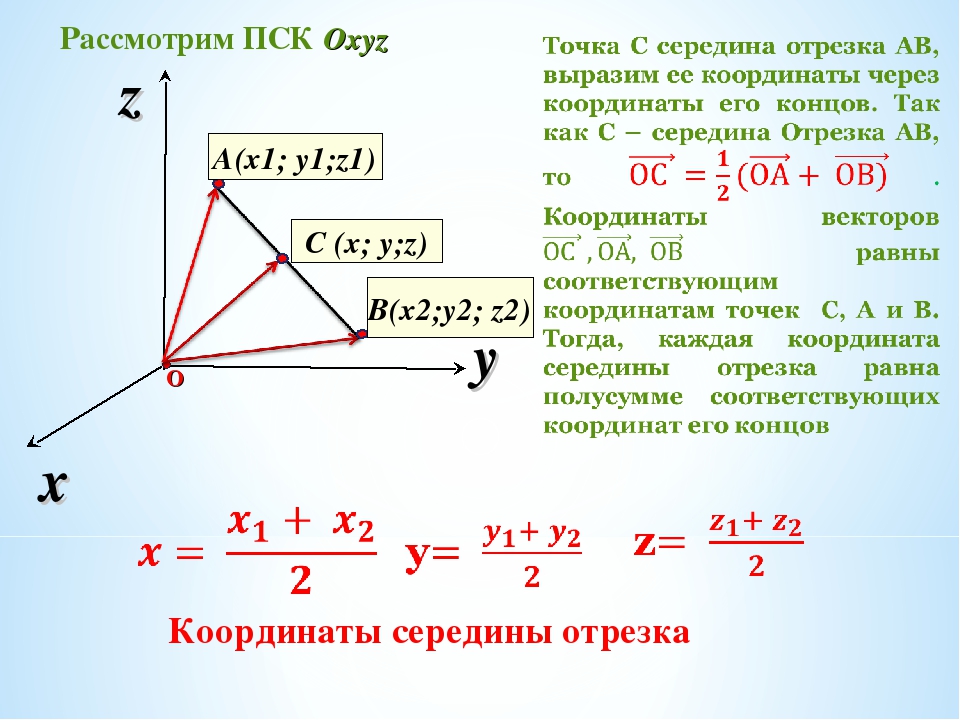 Определение координат вектора позволяет нам записать равенства , а длина ОА равна искомой длине вектора, следовательно, .

Таким образом, длина вектора в пространстве равна корню квадратному из суммы квадратов его координат , то есть, находится по формуле .

Пример.

Вычислите длину вектора , где — орты прямоугольной системы координат.

Решение.

Нам дано разложение вектора по координатным векторам вида , следовательно, . Тогда по формуле нахождения длины вектора по координатам имеем .

Прежде всего надо разобрать само понятие вектора. Для того, чтобы ввести определение геометрического вектора вспомним, что такое отрезок . Введем следующее определение.

Определение 1

Отрезком будем называть часть прямой, которая имеет две границы в виде точек.

Отрезок может иметь 2 направления. Для обозначения направления будем называть одну из границ отрезка его началом, а другую границу — его концом. Направление указывается от его начала к концу отрезка.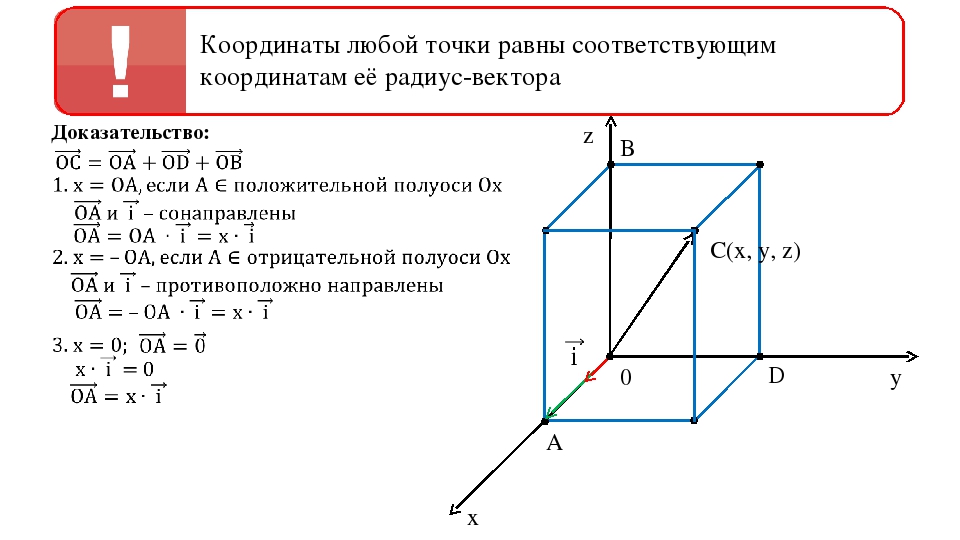

Определение 2

Вектором или направленным отрезком будем называть такой отрезок, для которого известно, какая из границ отрезка считается началом, а какая его концом.

Обозначение: Двумя буквами: $\overline{AB}$ – (где $A$ его начало, а $B$ – его конец).

Одной маленькой буквой: $\overline{a}$ (рис. 1).

Введем теперь, непосредственно, понятие длин вектора.

Определение 3

Длиной вектора $\overline{a}$ будем называть длину отрезка $a$.

Обозначение: $|\overline{a}|$

Понятие длины вектора связано, к примеру, с таким понятием, как равенство двух векторов.

Определение 4

Два вектора будем называть равными, если они удовлетворяют двух условиям: 1. Они сонаправлены; 1. Их длины равны (рис. 2).

Для того, чтобы определять векторы вводят систему координат и определяют координаты для вектора во введенной системе. Как мы знаем, любой вектор можно разложить в виде $\overline{c}=m\overline{i}+n\overline{j}$, где $m$ и $n$ – действительные числа, а $\overline{i}$ и $\overline{j}$ — единичные векторы на оси $Ox$ и $Oy$, соответственно.

Определение 5

Коэффициенты разложения вектора $\overline{c}=m\overline{i}+n\overline{j}$ будем называть координатами этого вектора во введенной системе координат. Математически:

$\overline{c}={m,n}$

Как найти длину вектора?

Для того, чтобы вывести формулу для вычисления длины произвольного вектора по данным его координатам рассмотрим следующую задачу:

Пример 1

Дано: вектор $\overline{α}$, имеющий координаты ${x,y}$. Найти: длину этого вектора.

Введем на плоскости декартову систему координат $xOy$. От начал введенной системы координат отложим $\overline{OA}=\overline{a}$. Построим проекции $OA_1$ и $OA_2$ построенного вектора на оси $Ox$ и $Oy$, соответственно (рис. 3).

Построенный нами вектор $\overline{OA}$ будет радиус вектором для точки $A$, следовательно, она будет иметь координаты ${x,y}$, значит

$=x$, $[ OA_2]=y$

Теперь мы легко можем найти искомую длину с помощью теоремы Пифагора, получим

$|\overline{α}|^2=^2+^2$

$|\overline{α}|^2=x^2+y^2$

$|\overline{α}|=\sqrt{x^2+y^2}$

Ответ: $\sqrt{x^2+y^2}$.

Вывод: Чтобы найти длину вектора, у которого задан его координаты, необходимо найти корень из квадрата суммы этих координат.

Пример задач

Пример 2

Найдите расстояние между точками $X$ и $Y$, которые имеют следующие координаты: $(-1,5)$ и $(7,3)$, соответственно.

Любые две точки можно легко связать с понятием вектора. Рассмотрим, к примеру, вектор $\overline{XY}$. Как мы уже знаем, координаты такого вектора можно найти, вычтя из координат конечной точки ($Y$) соответствующие координаты начальной точки ($X$). Получим, что

Величина и направление векторов

Величина вектора

Величина вектора п Q → это расстояние между начальной точкой п и конечная точка Q . В символах величина п Q → записывается как | п Q → | .

Если заданы координаты начальной и конечной точек вектора, то Формула расстояния можно использовать для определения его величины.

| п Q → | знак равно ( Икс 2 — Икс 1 ) 2 + ( у 2 — у 1 ) 2

Пример 1:

Найдите величину вектора п Q → чья начальная точка п Я сидел ( 1 , 1 ) и конечная точка находится в Q Я сидел ( 5 , 3 ) .

Решение:

Используйте формулу расстояния.

Подставьте значения Икс 1 , у 1 , Икс 2 , а также у 2 .

| п Q → | знак равно ( 5 — 1 ) 2 + ( 3 — 1 ) 2 знак равно 4 2 + 2 2 знак равно 16 + 4 знак равно 20 ≈ 4. 5

Величина п Q → около 4.5 .

Направление вектора

Направление вектора — это мера угла, который он образует с горизонтальная линия .

Для определения направления вектора можно использовать одну из следующих формул:

загар θ знак равно у Икс , где Икс горизонтальное изменение и у это вертикальное изменение

или же

загар θ знак равно у 2 — у 1 Икс 2 — Икс 1 , где ( Икс 1 , у 1 ) начальная точка и ( Икс 2 , у 2 ) конечная точка.

Пример 2:

Найдите направление вектора п Q → чья начальная точка п Я сидел ( 2 , 3 ) и конечная точка находится в Q Я сидел ( 5 , 8 ) .

Даны координаты начальной и конечной точек.Подставьте их в формулу загар θ знак равно у 2 — у 1 Икс 2 — Икс 1 .

загар θ знак равно 8 — 3 5 — 2 знак равно 5 3

Найдите обратный загар и воспользуйтесь калькулятором.

θ знак равно загар — 1 ( 5 3 ) ≈ 59 °

Вектор п Q → имеет направление около 59 ° .

Нахождение координат точек с помощью векторов? (См. Рисунок)

Чтобы найти координаты A B C , нам нужно найти пересечение векторных линий.Это можно сделать, приравняв каждую пару векторных линий.

Для поиска точки A воспользуемся векторными линиями AB и AC . См. Диаграмму.

#AB = AC #

# ((0), (2)) + r ((2), (1)) = ((0), (5)) + t ((1), (- 1)) #

# цвет (белый) (->) 2r = t #
# 2 + r = 5-t #

Решение для # r # и # t #:

# г = 3-т #

# 2 (3-t) = t => t = 2 #

# 2r = 2 => r = 1 #

Использование их в #AB = AC #

# ((0), (2)) + 1 ((2), (1)) = ((0), (5)) + 2 ((1), (- 1)) #

# ((2), (3)) = ((2), (3)) #

Координата A : # цвет (белый) (8) (2 цвета (белый) (1), 3) #

Для поиска точки B воспользуемся векторными линиями AB и BC .

#AB = BC #

# ((0), (2)) + r ((2), (1)) = ((8), (6)) + s ((- 1), (- 2)) #

# цвет (белый) (888) 2r = 8-s #
# 2 + r = 6-2s #

# г = 4-2с #

# 2 (4-2s) = 8-s => s = 0 #
# 2 + r = 6-2 (0) => r = 4 #

Используя их в #AB = BC #

# ((0), (2)) + 4 ((2), (1)) = ((8), (6)) + 0 ((- 1), (- 2)) #

# ((8), (6)) = ((8), (6)) #

Координата B : # цвет (белый) (8) (8 цвет (белый) (1), 6) #

Для нахождения точки C воспользуемся векторными линиями AC и BC .

# AC = BC #

# ((0), (5)) + t ((1), (- 1)) = ((8), (6)) + s ((- 1), (- 2)) #

# цвет (белый) (8888) t = 8-s #
# 5-t = 6-2s #

# 5- (8-с) = 6-2с => s = 3 #
# t = 8-3 => t = 5 #

Использование их в #AC = BC #

# ((0), (5)) + 5 ((1), (- 1)) = ((8), (6)) + 3 ((- 1), (- 2)) #

# ((5), (0)) = ((5), (0)) #

Координата C : # цвет (белый) (8) (5 цвет (белый) (1), 0) #

Чтобы вычислить длины сторон, мы могли бы использовать формулу расстояния или найти векторы #vec (AB), vec (AC) и vec (CB) # и найти их величину. 2)) = sqrt (45) = 3sqrt (5) #

Стороны AB и BC имеют одинаковую длину.

Координаты:

# A = (2, 3) #
# B = (8, 6) #
# C = (5, 0) #

Длина сторон:

# AB = 3sqrt (5) #
# BC = 3sqrt (5) #
# AC = 3sqrt (2) #

Как сложить и вычесть векторы алгебраически

Введение

В этой статье мы рассмотрим вектор. Векторы — в отличие от простых чисел (скаляров), которые имеют только величину — имеют как величину (длину), так и направление.Мы рассмотрим, как представлять векторные величины, а также как их складывать и вычитать.

Ключевые термины

Скаляр

Вектор

Нулевой вектор

Цели

Количественное определение векторов с использованием системы координат

Сложение и вычитание векторов графически и алгебраически

Отдельные числа, то есть значения, имеющие только (положительную или отрицательную) величину, называются скалярами . Числа 0, –3, π, i, 1,3, e, и т. Д. — все это примеры скаляров. Другой тип значения, который часто используется в математике, — это вектор. Вектор — это величина, которая имеет направление как величины , так и направления . В этой статье мы рассмотрим некоторые математические характеристики векторов. Векторы имеют широкое применение, например, в физике.

Введение в векторы

Чтобы понять разницу между скаляром и вектором, полезно вспомнить физические примеры.Рассмотрим, например, температуру. Вы можете использовать термометр для измерения температуры воздуха в разных местах. В каждом случае вы получите некоторое число (и единицу) — скажем, 65 ° F. Это величина, но с ней не связано никакого направления; таким образом, это скалярная величина. Теперь рассмотрим измерения ветра в тех же местах. Когда вы измеряете ветер, вы, вероятно, измеряете и скорость, и направление. Таким образом, ваши измерения ветра составляют вектор. Мы могли бы выразить этот вектор в виде стрелки, указывающей в направлении ветра, причем длина стрелки пропорциональна скорости ветра.Ниже показаны два измерения ветра, сделанные в разных точках; стрелки представляют векторы, связанные с этими измерениями.

Векторы имеют величину и направление, но сами по себе не имеют назначенного местоположения. То есть, пока сохраняется направление и длина «стрелки», мы можем перемещать ее куда угодно, не меняя ее. Это важная характеристика, которая позволит нам активно работать с векторами.

Представление векторов

Наша первая задача — найти способ четко и последовательно представлять векторы. Графически это просто: поскольку мы можем перемещать вектор куда угодно, давайте всегда располагаем «хвост» вектора в начале координатной плоскости. (Обратите внимание, что «голова» и «хвост» вектора определены, как показано ниже.)

Теперь, когда хвост вектора помещен в начало координат (помните, мы можем перемещать вектор куда угодно, если сохраняем его направление и длину), мы можем количественно определить его как координаты головы.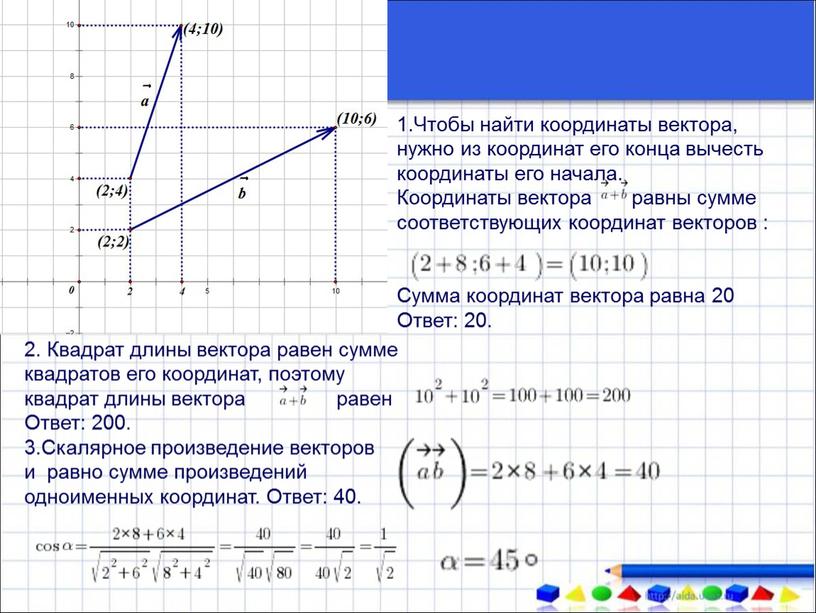 Пример показан ниже для вектора v . (Обратите внимание: чтобы отличать символы, представляющие векторы, от символов, представляющих скаляры, мы используем полужирный шрифт. Другой распространенный метод — использовать небольшую стрелку над символом: например, вектор.)

Таким образом, вектор v — это просто координаты точки в (2, 3). Обратите внимание, что все векторы, показанные ниже, равны (2, 3) — наше соглашение заключается в том, что вектор описывается координатами точки в его голове только , когда его хвост расположен в начале координат.

Хотя мы показали вектор только в двух измерениях, этот подход можно обобщить на любое количество измерений. Например, в трех измерениях вектор будет иметь форму ( x, y, z ). Все свойства двумерных векторов можно легко расширить до трех измерений.

Но как нам «переместить» вектор с числовой точки зрения? Например, скажем, вектор v имеет голову в (3, 2) и хвост в (1, 4).

Ответ заключается в перемещении (или перемещении) головы и хвоста на эквивалентное расстояние и в одном направлении. Это преобразование должно привести к тому, что хвост вектора переместится в начало координат — простой процесс, который включает вычитание каждой координаты хвоста из себя. В приведенном выше примере результат (3–3, 2–2) = (0, 0). Чтобы перевести голову, аналогичным образом вычтите координаты хвоста из координат головы — это удовлетворяет нашему критерию, что перевод имеет фиксированное расстояние и направление.Таким образом, голову нужно двигать следующим образом: (1 — 3, 4 — 2) = (–2, 2). Таким образом, в общем, чтобы найти значение произвольно расположенного вектора, вычтите координаты хвоста из координат головы. Этот процесс проиллюстрирован ниже.

Обратите внимание, что вектор (0, 0), иногда называемый нулевым вектором , имеет длину 0, но не имеет определенного направления. (То есть независимо от того, какое направление вы выберете, нулевой вектор будет одинаковым.)

Практическая задача: Определите значение каждого вектора, показанного на графике ниже.

Решение: В каждом случае можно найти координатное выражение для вектора, вычитая координаты хвоста из соответствующих координат головы. Это работает, даже если хвост находится в начале координат, имеющем координаты (0, 0). Но если хвост находится в начале координат, вектор также просто равен координатам головы. Если это вам поможет, перерисуйте векторы так, чтобы хвосты располагались в начале координат.

a = (–1, 4)

b = (–3, –3)

с = (3 — 3, 2 — 0) = (0, 2)

d = (3 — 2, –4 — [–1]) = (1, –3)

Сложение и вычитание векторов

Как и в случае со скалярами, мы можем складывать и вычитать векторы. Процесс аналогичен, но с одной или двумя оговорками. Чтобы сложить или вычесть два вектора a и b , добавьте или вычтите соответствующие координаты вектора.То есть, где a и b определены следующим образом, вот правила для сложения и вычитания.

Обратите внимание, что, как и в случае со скалярами, сложение векторов коммутативно, а вычитание — нет. Графически мы складываем два вектора a и b , помещая хвост b в голову a и затем создавая новый вектор, начиная с хвоста a и заканчивая в голове b. .Координаты этого нового вектора определяются так же, как и раньше: путем размещения его хвоста в начале координат. Этот процесс проиллюстрирован ниже для векторов a = (4, 1) и b = (-1, 2).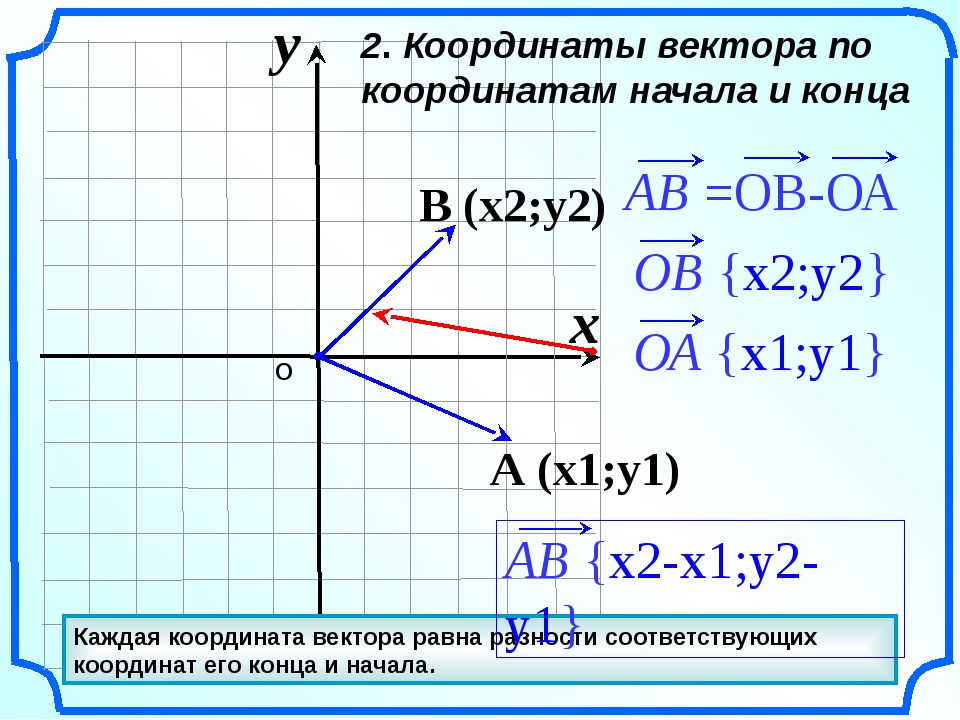

Обратите внимание, что

Вычитание векторов следует в основном той же процедуре, что и сложение, за исключением того, что вычитаемый вектор «меняет направление» на противоположное.Рассмотрим те же векторы a _{и b , как указано выше, за исключением того, что мы вычислим a — b. (Обратите внимание, что это то же самое, что и , где — b имеет ту же длину, что и b , но имеет противоположное направление.)}

Практическая задача: Выполните следующие векторные операции.

а. (3, 2) — (4, 5) б.(-1, 5) + (10, -6) с. (-1, 0) — (0, 0)

Решение: В каждом случае сложите или вычтите соответствующие координаты, чтобы найти результат. Один из полезных способов проверить свой ответ — нарисовать векторы на графике, показывая сложение или вычитание и сравнивая ваши результаты.

а. (-1, -3) б. (9, -1) с. (-1, 0)

Вектор положения

— объяснение и примеры

Мы можем использовать вектор положения , чтобы сообщить нам положение одного объекта относительно другого.В частности, вектор позиции:

«Вектор, который указывает местоположение или положение данной точки относительно произвольной контрольной точки, такой как начало координат».

В этой теме мы обсудим следующие аспекты векторов позиций:

• Что такое вектор положения?
• Как найти вектор положения

Что такое вектор положения?

Часто векторы, которые начинаются в начале координат и заканчиваются в любой произвольной точке, называются векторами положения.Они используются для определения положения точки относительно начала координат.

Направление вектора положения указывает от начала координат к данной точке. В c \ декартовой системе координат, если точка O — начало координат, а Q — некоторая точка (x1, y1), то вектор положения, направленный из точки O в точку Q, представляется как OQ . В трехмерном пространстве, если O = (0,0,0) и Q = (x1, y1, z1), то вектор положения r точки Q представлен следующим образом:

г = x1i + y1j + z1k

Предположим, у нас есть два вектора, A, и B, с векторами положения a = (2,4) и b = (3, 5) соответственно.Затем мы можем записать координаты векторов A и B как:

A = (2,4), B = (3, 5)

Как найти вектор положения

Перед определением вектора положения точки нам сначала нужно определить координаты этой точки. Предположим, у нас есть две точки, M и N, где M = (x1, y1) и N = (x2, y2). Затем мы хотим найти вектор положения из точки M в точку N, вектор MN . Чтобы определить этот вектор положения, мы вычитаем соответствующие компоненты M из N :

.

MN = (x2-x1, y2-y1)

Формула вектора положения

Используя информацию выше, мы можем обобщить формулу, которая будет определять вектор положения между двумя точками, если бы мы знали положение точек в плоскости xy.

Например, рассмотрим точку P, которая имеет координаты (xk, yk) в плоскости xy, и другую точку Q, которая имеет координаты (xk + 1, yk + 1). Формула для определения вектора положения от P до Q:

PQ = ((xk + 1) -xk, (yk + 1) -yk)

Помните, что вектор положения PQ относится к вектору, который начинается в точке P и заканчивается в точке Q. Точно так же, если мы хотим найти вектор положения из точки Q в точку P, мы можем написать:

КП = (xk — (xk + 1), yk — (yk + 1))

Примеры

В этом разделе мы обсудим некоторые примеры задач вектора положения и их пошаговые решения. Это поможет глубже понять векторы позиций.

Пример 1

Учитывая две точки A = (-4, 6) и B = (5, 12), определите вектор положения AB. Затем , вычисляют величину вектора AB .

Раствор

Учитывая две точки в системе координат xy, мы можем использовать следующую формулу, чтобы найти вектор положения AB :

AB = (x2-x1, y2-y1)

Где x1, y1 представляют координаты точки A, а x2, y2 представляют координаты точки B.Таким образом, просто подставляя значения точек A и B в приведенное выше уравнение, мы можем найти вектор положения AB :

AB = (5 — (- 4), 12-6)

AB = ((5+ 4), 12-6)

AB = (9, 6)

Таким образом, вектор положения AB эквивалентен вектору, который начинается в начале координат и направлен в точку на 9 единиц вправо по оси x и на 6 единиц вверх по оси y. 2

| AB | = √81 + 36

| AB | = √117

| AB | = 3√13

Пример 2

По двум точкам A = (-4, 6) и B = (5, 12) определить вектор положения BA. Затем вычислите величину вектора BA и опишите взаимосвязь между вектором положения AB и вектором положения BA .

Раствор

Учитывая две точки в системе координат xy, мы можем использовать следующую формулу, чтобы найти вектор положения BA :

BA = (x1-x2, y1-y2)

Где x1, y1 представляют координаты точки A, а x2, y2 представляют координаты точки B.Обратите внимание, что вектор положения BA представляет собой вектор, направленный от точки B к точке A. Он отличается от вектора положения AB, , который направлен от A к B. Таким образом, просто помещая значения точек A и B в приведенном выше уравнении мы можем найти вектор положения BA:

BA = (-4-5), 6-12)

BA = (-9, -6)

Таким образом, вектор положения BA эквивалентен вектору, который начинается в начале координат и направлен в точку на 9 единиц влево по оси x и на 6 единиц вниз по оси y. 2

| BA | = √81 + 36

| BA | = √117

| BA | = 3√13

Напомним, что в первом примере мы нашли вектор положения AB, для тех же точек, а в этом примере мы определили вектор положения BA. Два вектора положения имеют одинаковую величину. Поскольку они имеют противоположные направления, соотношение между ними составляет:

.

BA = -1 * (9, 6)

BA = -1 * AB

BA = — AB

Таким образом, два вектора положения параллельны друг другу и противоположны друг другу.То есть они отрицания друг друга.

Пример 3

Учитывая, что вектор положения точки, S1, равен OS1 = (2, 3), и что вектор S1S2 = (-3, 6), определить вектор положения точки S2, OS2 .

Раствор

Сначала мы строим вектор OS1 с его начальной точкой в ​​начале координат (0,0) и конечной точкой в ​​точке (2,3). Мы также строим вектор OS2, , который начинается в начале координат и заканчивается в точке S2.Обозначим неизвестное положение S2 произвольными координатными точками (x, y). Поскольку мы знаем вектор положения S1S2 и знаем, что он дает связь между S1 и S2, мы также можем нарисовать S1S2. Это направленный вектор, начальная точка которого находится в S1 и направлен на три единицы влево и на шесть единиц вверх. Из изображения ниже видно, что у нас есть треугольник 0S1S2. Таким образом, теперь мы можем использовать закон треугольника (или правило «голова к хвосту») сложения векторов для определения координат точки S2 следующим образом:

S1S2 = OS1 + OS2

OS2 = S1S2 — OS1

Подставляя указанные значения в это уравнение, мы получаем:

OS2 = (-3, 6) — (2, 3)

OS2 = (-3, 6) + (-2, -3)

OS2 = (-3-2, 6-3)

OS2 = (-5, 3)

Таким образом, OS2 = (- 5, 3) — вектор положения для точки S2.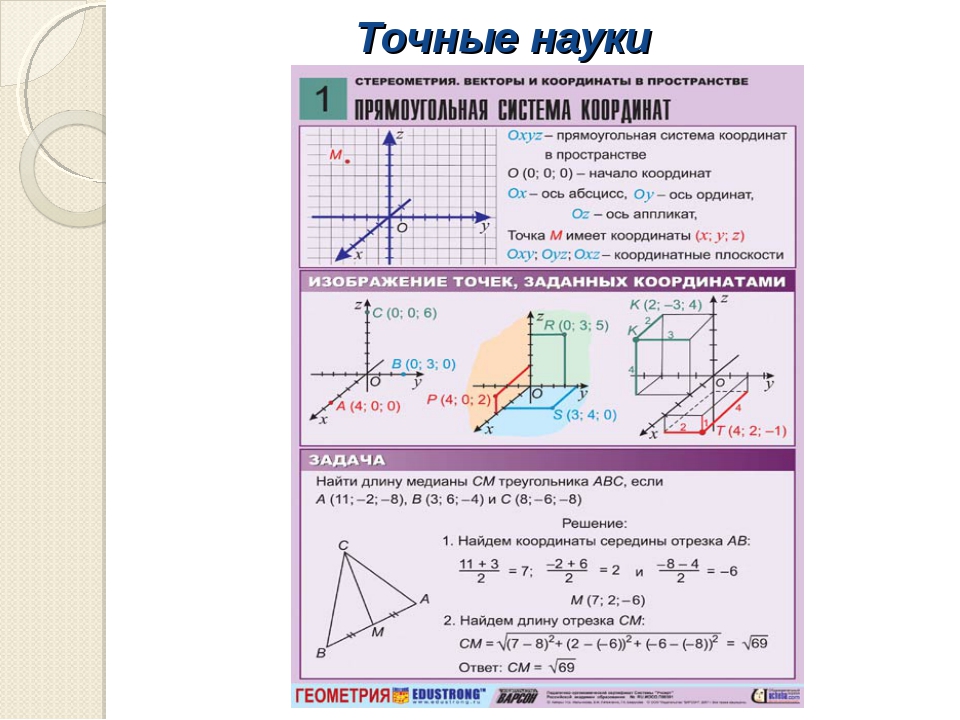

Пример 4

По двум точкам M = (4, m) и Q = (-n, -3) определить вектор положения QM.

Раствор

Учитывая две точки в системе координат xy, мы можем использовать следующую формулу для определения вектора положения Q :

QM = (-n-4, -3-m).

Поскольку нам неизвестны координаты QM или значения n и m, мы не можем упростить уравнение.2

| R | = √100 + 25 + 9

| R | = √100 + 25 + 9

| R | = √134

Пример 6

Учитывая точки, c = 5i + 6j + 3k и d = 2i + 5j — 2k в ортогональной системе, определите вектор положения между этими двумя точками, CD.

Раствор

Учитывая две точки, мы можем использовать следующую формулу для определения вектора положения CD :

CD = (2-5, 5-5, -2-3)

CD = (-3, 0, -5)

CD = -3i + 0j -5k

Практические вопросы

1. Пусть u = (-1, 4) и v = (2, 5). Определите вектор положения, представленный UV .
2. Пусть u = (-1, 4) и v = (2, 5). Определите вектор положения, представленный VU .
3. Пусть v = (3, 5) и VM = (-6, 3). Найдите вектор положения точки m.
4. Для данного b = (3,2,5) определите его вектор положения, R. Затем найдите длину вектора
5. Пусть вектор AB начинается с a = (1, 2) и заканчивается на b = (2, 3). Определите его вектор положения и его длину.
6. Пусть вектор OB начинается с o = (0,0) и заканчивается на b = (-2, 6). Определите его вектор положения.

Ответы

1. УФ = (3,1). Направление UV на 3 единицы вправо по оси x и на 1 единицу вверх.
2. VU = (-3, -1). Направление VU — на 3 единицы влево по оси x и на 1 единицу вниз. Два вектора UV, и VU, противоположны по направлению.
3. Вектор положения точки m может быть задан OM = (-9, -2)
4. R = 3i + 2j + 5k — вектор положения, длина | R | = √38
5. Вектор положения — AB = (1,1), и его длина | AB | = √2
6. Вектор положения: OB = (-2,6), и его длина | OB | = √40

Предыдущий урок | Главная страница | Следующий урок

Калькулятор величины вектора [2D, 3D, 4D, 5D]

Этот калькулятор величины вектора — простой инструмент, который помогает вам оценить величину на основе компонентов вектора.В тексте вы узнаете, как найти величину вектора и привыкнете к общей величине векторной формулы. В конце текста вы можете прочитать о некоторых физических величинах, которые являются векторами, и о том, что нам говорят их величины.

Как найти величину вектора?

Вектор можно определить как упорядоченный набор чисел. Количество компонентов вектора зависит от размерности пространства. На практике мы обычно имеем дело с трехмерными векторами с тремя различными компонентами.В декартовых координатах мы можем использовать значения компонентов x , y и z .

Когда мы переключаемся на сферические координаты, удобно использовать значения двух углов, θ и φ , и звездную величину , которая представляет собой длину вектора в самом чистом смысле. Другими словами, это трехмерное расстояние между начальной и конечной точкой вектора.

Компоненты вектора также могут быть комплексными числами.

Величина векторной формулы

Величина вектора | V | можно оценить разными способами, в зависимости от размерности векторного пространства. Нас:

• | V | = √ (x² + y²) в 2-м пространстве
• | V | = √ (x² + y² + z²) в трехмерном пространстве
• | V | = √ (x² + y² + z² + t²) в 4-м пространстве
• | V | = √ (x² + y² + z² + t² + w²) в 5-мерном пространстве и так далее . ..

Как вы можете видеть в формуле для величины вектора, величина — это квадратный корень из суммы компонентов вектора во второй степени во всех случаях.В этом калькуляторе величин вектора вы можете установить размерность вашего вектора, чтобы выбрать правильную формулу. В результате величина величины всегда положительна, и поэтому мы можем измерить ее в любом эксперименте, где мы имеем дело с векторными величинами.

Величину вектора можно также вычислить как квадратный корень из скалярного произведения вектора на себя:

| V | = √ (В · В)

По определению, величина единичного вектора равна 1 .

Как пользоваться калькулятором величины вектора?

Давайте посмотрим на этот вычислительный пример, чтобы узнать, как найти величину вектора в 4-мерном пространстве. Компоненты вектора: x = 3 , y = -1 , z = 2 , t = -3 .

1. Оцените квадраты каждого компонента вектора: x² = 9 , y² = 1 , z² = 4 , t² = 9
2. Сложите все вместе: x² + y² + z² + t² = 9 + 1 + 4 + 9 = 23
3. Вычислите величину вектора как квадратный корень из этих значений: | V | = √23 = 4.796

Примеры векторов в жизни

Многие физические величины (например, сила, ускорение и скорость) являются векторами. В этих случаях величина вектора — это абсолютное значение измеряемой величины, подобно тому, как скорость является величиной скорости.

Вы можете создавать другие, более сложные, вычисляя перекрестное произведение двух векторов. Крутящий момент — это произведение векторов расстояния и силы.

Векторная алгебра:

ВЕКТОРНЫЕ МЕТОДЫ

Приоритетные направления:

1. Векторы и векторное сложение
2. Единичные векторы
3. Базовые векторы и компоненты вектора
4. прямоугольный координаты в 2-D
5. прямоугольный координаты в 3-D
6. Вектор соединение двух точек
7. Точечный продукт
8. Перекрестное произведение
9. Трехместный товар
10. Трехместный векторный продукт

Векторы и векторное сложение:

Скаляр — это величина, такая как масса или температура, которая имеет только величину. » на жирном символе (т.е.,). Следовательно,

Любой вектор можно превратить в единичный вектор, разделив его на длину.

Любой вектор можно полностью представить, указав его величину и единицу измерения. вектор по его направлению.

Базовые векторы и компоненты вектора:

Базовые векторы — это набор векторов, выбранных в качестве базовых для представления всех остальных векторы.Идея состоит в том, чтобы построить каждый вектор из сложения векторов по базовым направлениям. Например, вектор на рисунке можно записать как сумма трех векторов u ₁ , u ₂ и u ₃ , каждый по направлению одного из базовых векторов e ₁ , e ₂ и e ₃ , так что

Каждый из векторов u ₁ , u ₂ и u ₃ параллельна одному из базовых векторов и может быть записана как скалярное кратное эта база.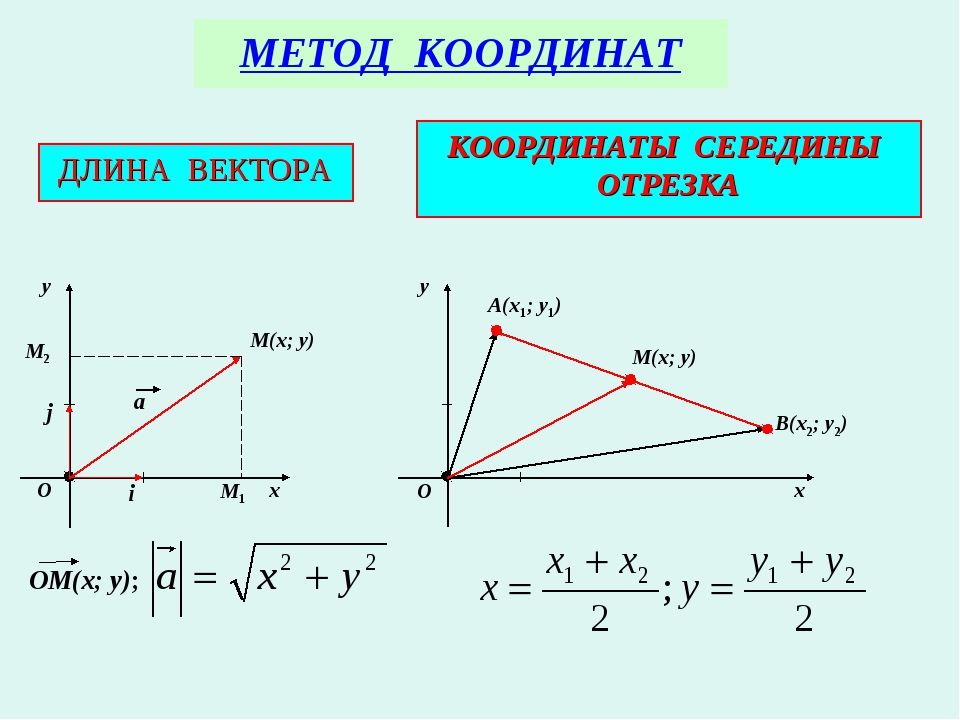 Пусть u ₁ , u ₂ , а u ₃ обозначим эти скалярные множители так, чтобы получилось

Оригинальный вектор u банка теперь будет записано как

Скалярные множители u ₁ , u ₂ и u ₃ известны как компоненты и в базе, описанной базой векторы e ₁ , e ₂ и e ₃ .Если базовые векторы являются единичными векторами, то компоненты представляют собой длины соответственно трех векторов u ₁ , u ₂ , и u ₃ . Если базовые векторы являются единичными векторами и взаимно ортогонально, то основание называется ортонормированным, евклидовым или декартовым база.

Вектор может быть разрешен по любым двум направлениям в плоскости, содержащей его. На рисунке показано, как правило параллелограмма используется для построения векторов и . и b , что в сумме дает c .

В трех измерениях вектор может быть разрешен вдоль любых трех некомпланарных линий. На рисунке показано, как можно разрешить вектор по трем направлениям. сначала найдя вектор в плоскости двух направлений, а затем разрешение этого нового вектора по двум направлениям на плоскости.

Когда векторы представлены в терминах базовых векторов и компонентов, сложение двух векторов приводит к сложению компонентов векторы.Следовательно, если два вектора A и B представлены как

тогда,

прямоугольный компоненты в 2-D:

Базовые векторы прямоугольной системы координат x-y задаются формулой единичные векторы и вдоль x и y направления соответственно.

Используя базовые векторы, можно представить любой вектор F как

В силу ортогональности базисов имеют место следующие соотношения.

прямоугольный координаты в 3-D:

Базовые векторы прямоугольной системы координат задаются набором три взаимно ортогональных единичных вектора, обозначенных,, и что расположены вдоль координатных направлений x , y и z , соответственно, как показано на рисунке.

Показанная система является системой для правой руки, поскольку большой палец правой руки указывает в направлении z , если пальцы таковы, что представляют вращение вокруг оси z от x до y . Эта система может можно превратить в левостороннюю систему, изменив направление любого из координатные линии и связанный с ними базовый вектор.

В прямоугольной системе координат компонентами вектора являются проекции вектора вдоль x , y и z направления. Например, на рисунке проекции вектора A вдоль направлений x, y, и z задаются A _x , A _y , и A _z соответственно.

В результате теоремы Пифагора и ортогональности базы векторов, величина вектора в прямоугольной системе координат может быть рассчитано по

Направляющий косинус:

Направляющие косинусы определены как

где углы, и — углы показаны на рисунке.Как показано на рисунке, направляющие косинусы представляют собой косинусы углов между вектором и тремя координаты направления.

Направляющие косинусы могут быть вычислены из компоненты вектора и его величина через отношения

Три направляющих косинуса не являются независимыми и должно удовлетворять соотношению

Эти результаты формируют тот факт, что

Единичный вектор может быть построен вдоль вектора используя направляющие косинусы в качестве компонентов вдоль x , y и z направление.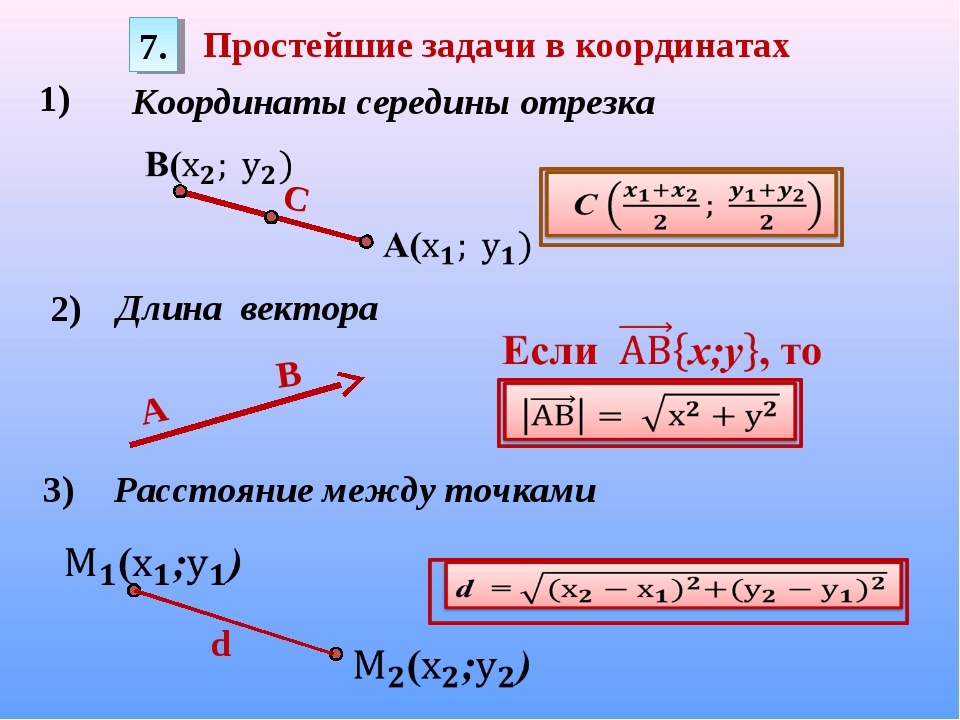 Например, единичный вектор вдоль вектора A получается из

Следовательно,

Вектор соединение двух точек:

Вектор, соединяющий точку A с точкой B дается

Единичный вектор вдоль линии A-B может быть получен из

Вектор F по линии A-B и величиной F может таким образом получается из соотношения

Точечный продукт:

Скалярное произведение обозначается «» между двумя векторами.В скалярное произведение векторов A и B приводит к скаляру, заданному отношение

где — угол между двумя векторами. Порядок не важен в скалярное произведение, как видно из определения скалярных произведений. В результате один получает

Скалярное произведение имеет следующие свойства.

Поскольку косинус 90 ^o равен нулю, скалярное произведение двух ортогональные векторы приведут к нулю.

Поскольку угол между вектором и самим собой равен нулю, а косинус нуля единица, величина вектора может быть записана в терминах скалярного произведения используя правило

Прямоугольные координаты:

При работе с векторами, представленными в прямоугольная система координат по составляющим

, то скалярное произведение может быть оценено из отношение

Это можно проверить прямым умножением векторы и отмечая, что из-за ортогональности базовых векторов прямоугольная система

Проекция вектора на линию:

Ортогональная проекция вектора вдоль прямой получается перемещением одного конца вектора на линию и опусканием перпендикулярно линии от другого конца вектора. Результирующий отрезок на прямой — это ортогональная проекция вектора или просто его проекция.

Скалярная проекция вектора A вдоль единичный вектор — длина ортогональной проекции A вдоль линии, параллельной, и может быть оценен с помощью скалярного произведения. В отношение для проекции

Векторная проекция А вдоль агрегата. вектор просто умножает скалярную проекцию на единичный вектор, чтобы получить вектор вместе.Это дает соотношение

Крест товар:

Перекрестное произведение векторов a и b — вектор, перпендикулярный к обоим a и b и имеет величину, равную площади параллелограмм, полученный из a и b . Направление креста продукт определяется правилом правой руки.Перекрестное произведение обозначается «» между векторами

Порядок важен в перекрестном произведении. Если порядок операций изменится в перекрестном произведении направление результирующего вектора меняется на противоположное. То есть

Перекрестное произведение имеет следующие свойства.

Прямоугольные координаты:

При работе в прямоугольных системах координат, перекрестное произведение векторов a и b , заданных

можно оценить с помощью правила

Можно также использовать прямое умножение основания векторов с использованием соотношений

Тройной товар:

Тройное произведение векторов a , b и c равно

Стоимость тройного произведения равна объему параллелепипеда. построенный из векторов. Это видно из рисунка с

г.

Тройной продукт имеет следующие свойства

Прямоугольные координаты:

Рассмотрим векторы, описанные в прямоугольной форме. система координат как

Тройное произведение можно оценить с помощью отношение

Тройной вектор товар:

Произведение тройного вектора имеет свойства

3D векторов | Суперпроф

Мы живем в трехмерном мире, что означает, что у нас есть 3 оси в качестве ориентира.Эти оси — ось x, ось y и ось z. Векторное знание применимо в реальной жизни, что в конечном итоге означает, что применяются все векторные законы, но в предыдущих источниках мы были привязаны к 2-мерному, изменяет ли 3-мерный мир все законы? Абсолютно! но неужели это изменение слишком велико? Нет, все, что вам нужно сделать, это добавить третье измерение (ось z) ко всем этим законам. Трехмерный вектор — это отрезок прямой в трехмерном пространстве, проходящий от точки A (хвост) до точки B (голова).

Каждый вектор имеет величину (или длину) и направление.Помните, что основы не изменятся, потому что мы просто добавляем здесь еще одно измерение. Это не означает, что то, что вы изучали раньше, будет полностью изменено, всего несколько изменений в формуле, но концепция останется прежней. Если у вас есть хорошее понимание предыдущих законов, то понимание законов в трехмерном пространстве не будет для вас проблемой.

Компоненты трехмерного вектора

Когда мы работаем в трехмерном пространстве, мы всегда рассматриваем все три базы координат, которые являются осью x, осью y и осью z.Например, у нас есть две точки в трехмерном пространстве, и это точка A и точка B. Координаты точек A и B будут записаны (в трехмерном пространстве) следующим образом:

и. Ваш учитель также попросил вас найти вектор, но как вы это будете делать в трехмерном пространстве? Та же голова без хвоста? Да точно так же! Вам нужно вычесть координату головы из координаты хвоста.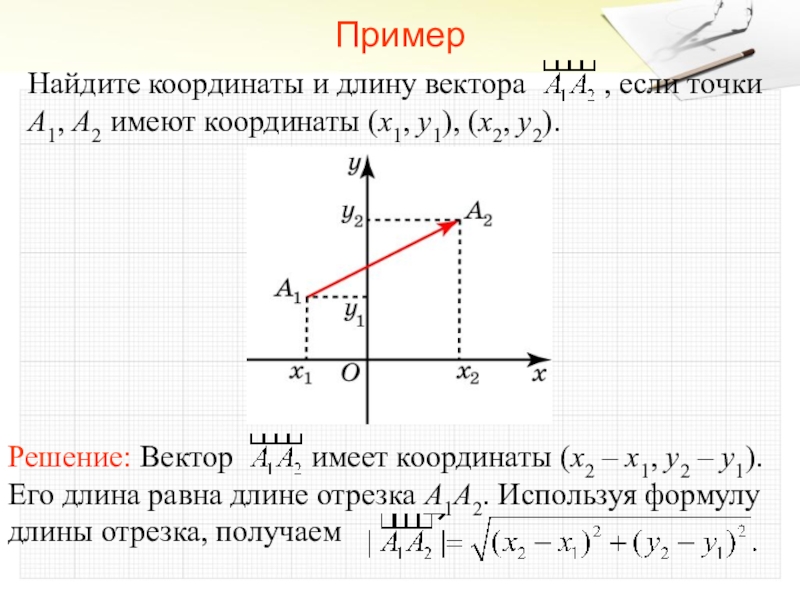

Вычислите компоненты векторов, которые можно нарисовать в треугольнике с вершинами

и.

Не забывайте, что вектор состоит из двух вещей: одна — это направление, а другая — величина. Если вы перевернете направление, это означает, что все координаты вектора также будут перевернуты:

Лучшие доступные репетиторы по математике

Первый урок бесплатно

Величина или длина вектора

Величина — ключ элемент вектора и вектор без величины — это просто направление без мощности.Величина вектора равна длине отрезка линии, который его определяет. Величина вектора всегда представлена ​​положительным числом, и только нулевой вектор имеет величину ноль .

Расчет величины для определения ее компонентов

Возможно, вы знакомы с формулой величины, которая равна

, но с третьим новым измерением все будет немного иначе. Чтобы найти величину трехмерного вектора, вам нужно просуммировать все возведенные в квадрат компоненты различных осей, а затем извлечь квадратный корень из ответа.

Ниже решенный вопрос для уточнения.

Учитывая векторы

и, найдите величины и ·

Расчет модуля, зная координаты точек

Чтобы вычислить величину, мы воспользуемся формулой расстояния, но с небольшим изменением. Возможно, вы раньше сталкивались с проблемами двух измерений, поэтому в то время вы использовали только компоненты x и y, но теперь все изменилось.На этот раз вы будете использовать три компонента, но не волнуйтесь, если вы хорошо понимаете формулу расстояния, это будет для вас кусок пирога. Например, у вас есть две точки A и B. Координаты точки A равны

, а координаты точки B равны.

Первый шаг — вычесть компонент хвоста из компонента головы, как вы делали это раньше. Найдите разницу для всех компонентов, а затем возьмите квадрат всех этих ответов. Сложите все эти квадраты ответов, а затем извлеките квадратный корень из полученного ответа, и это будет ваша величина из двух разных векторов, или вы можете использовать приведенную ниже формулу и просто подставить значения и найти ответ всего за один шаг.

Расстояние между двумя точками

Формула для расстояния между двумя точками аналогична найденной величине двух векторов.

ПРИМЕР

Найдите расстояние между точками

и.

Единичный вектор

Векторы бывают самых разных форм и размеров, но как мы описываем эти векторы? С помощью единичного вектора. Определение единичного вектора довольно просто, это вектор с величиной

.Это означает, что любой вектор, величина которого равна единице, независимо от направления, называется единичным вектором. Один из наиболее распространенных терминов, которые мы используем в главе, посвященной векторам, называется нормализация. Нормализация означает получение другого единичного вектора в том же направлении.

No related posts.