Задачи на расстояние от точки до кривой. Видеоурок. Алгебра 10 Класс
Тема: Производная
Урок: Задачи на расстояние от точки до кривой
Что такое расстояние от точки докривой? Точку можно соединить со многими точками кривой. Каждый раз будут получаться разные расстояния. Среди них нужно найти наименьшее. Это расстояние и будет называться расстоянием от точки до кривой. На кривой надо найти такую точку , чтобы расстояние было наименьшим (см. рис. 1).
Рис. 1. Расстояние от точки до кривой.
Видим, что задача на расстояние – это задача на экстремум, на минимум, то есть без производной не обойтись.
Вспомним, что расстояние от точки до прямой – это длина перпендикуляра (см. рис.2).
Рис. 2. Расстояние от точки до прямой.
Расстояние между прямыми – это тоже длина перпендикуляра (см. рис.3).
Рис. 3. Расстояние между прямыми.
Расстояние от точки до окружности легко найти. Нужно соединить центр с точкой , в результате получится точка . – искомое расстояние (см. рис.4).
Рис. 4. Расстояние от точки до окружности.
Расстояние между двумя окружностями, которые не пересекаются. Нужно соединить центры, получим две точки и . – искомое расстояние (см. рис.5).
Рис. 5. Расстояние между двумя окружностями.
Сформулируем задачу в общем виде и напомним, каким образом ее решать. Мы повторили, что такое расстояние. Вспомним формулу расстояния между двумя заданными точками. Предположим, что на координатной плоскости даны две точки и (см. рис.6).
Рис. 6. Расстояние между двумя заданными точками.
Расстояние между точками вычисляется по формуле
.
Таким образом, находится расстояние между точками, если известны координаты этих точек.
На параболе найти точки ближайшие к началу координат, то есть к точке .
Рис. 7. График функции.
Решение.
Из простейшего анализа задачи можно увидеть, что задача имеет два решения, в силу симметрии графика функции относительно оси Y (см. рис.7).
Координаты искомой точки: . По соответствующей формуле можем найти квадрат расстояния:
. Это расстояние должно быть наименьшим. Упростим эту формулу и получим:
или
.
Можно сразу использовать производную для решения задачи, но пока попытаемся воспользуемся свойствами биквадратной функции. С помощью замены переменной , получим:
. Задача свелась к нахождению минимума следующей квадратичной функции . Найдем абсциссу вершины (см. рис.8).
Рис. 8. Абсцисса вершины параболы.
Задача практически решена. Наименьшее значение этой функции будет тогда, когда . Вычислим . Значит, функция ведет себя следующим образом (см. рис.9):
Рис. 9. Схематический график функции .
Без производной, с помощью свойств квадратичной функции, решили задачу. Если , то , отсюда , . Если значения координат известны, вычислим значения . ; Получили ответ ; .
Итак, была задача: найти точки на кривой, которые бы отстояли от начала координат на наименьшее расстояние. Такие точки найдены. Первая точка — , вторая точка – .
Напомним ход решения задачи. Точка зависит только от , ее координаты – . При выражении квадрата расстояния, получили функцию от . Можно с помощью производной найти минимум. Можно сделать проще. Если сделать замену , получим квадратичную функцию и можно найти наименьшее значение данной квадратичной функции.
Ответ: .
На графике функции найти точку , ближайшую к данной точке . Решение.
Сделаем рисунок (см. рис.10).
Рис. 10. График функции .
Заданы координаты двух точек: и .
Найдем расстояние АМ:
.
или .
— квадратичная функция от . Вспомним, что нужно найти минимальное значение, то есть . Графиком этой функции является парабола, ветвями направленная вверх, значит, минимум находится в вершине. Выделим полный квадрат и получим:
. Выяснилось, что . Равенство достигается, когда принимает самое минимальное значение. Это будет в случае, когда . Таким образом, получили ответ , а . Значит, координаты точки .
Ответ: .
Итак, мы рассмотрели задачи на расстояние от точки до кривой. Можно находить само это расстояние, можно искать точки, которые обеспечивают минимум этого расстояния. Повторили, что такое расстояние между фигурами. Расстояние от точки до кривой – это наименьшее из расстояний, которое получается, когда точка на кривой пробегает все возможные значения. Например, точка может пробегать все значения на кривой , но наименьшее расстояние будет тогда, когда точка имеет координаты . Для этого нужно, во-первых, вспомнить, что такое расстояние, и во-вторых, каким образом ищется расстояние между точками, если известны координаты. И, наконец, надо записать квадрат расстояния и проанализировать полученную функцию. Если не удается это сделать элементарными средствами, с помощью свойств квадратичной функции, то надо использовать производную и искать наименьшее значение функции .
Список рекомендованной литературы
1. Алгебра и начала анализа, 10 класс (в двух частях). Учебник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2009.
2. Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.
3. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики).-М.: Просвещение, 1996.
4. Галицкий М.Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение алгебры и математического анализа.-М.: Просвещение, 1997.
5. Сборник задач по математике для поступающих во ВТУЗы (под ред. М.И.Сканави).-М.:Высшая школа, 1992.
6. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебраический тренажер.-К.: А.С.К., 1997.
7. ЗвавичЛ.И., Шляпочник Л.Я., Чинкина Алгебра и начала анализа. 8-11 кл.: Пособие для школ и классов с углубленным изучением математики (дидактические материалы).-М.: Дрофа, 2002.
8. Саакян С.М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.
9. Карп А.П. Сборник задач по алгебре и началам анализа : учеб. пособие для 10-11 кл. с углубл. изуч. математики.-М.: Просвещение, 2006.
10. Глейзер Г.И. История математики в школе. 9-10 классы (пособие для учителей).-М.: Просвещение, 1983
Дополнительные веб-ресурсы
1. Интернет-портал Mathematics.ru (Источник).
2. Портал Естественных Наук (Источник).
3. Интернет-портал Exponenta.ru (Источник).
Сделай дома
№ 46.52 (а) (Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.)
interneturok.ru
Задачи на расстояние от точки до кривой. Патриотическое воспитание
Дополнительные сочиненияНа уроке по теме «Задачи на расстояние от точки до кривой» вначале повторяются основные понятия, связанные с решением задачи на расстояние от точки до кривой. При решении подобных задач обычно применяется производная. Методика решения задачи объясняется на конкретных примерах.
Тема: Производная
Урок: Задачи на расстояние от точки до кривой
1. Опорные факты
Что такое расстояние от точкидокривой? Точку можно соединить со многими точками кривой. Каждый раз будут получаться разные расстояния. Среди них нужно найти наименьшее. Это расстояние и будет называться расстоянием от точки до кривой. На кривой надо найти такую точку , чтобы расстояние было наименьшим (см. рис. 1).
Рис. 1. Расстояние от точки до кривой.
Видим, что задача на расстояние – это задача на экстремум, на минимум, то есть без производной не обойтись.
Вспомним, что расстояние от точки до прямой – это длина перпендикуляра (см. рис.2).
Рис. 2. Расстояние от точки до прямой.
Расстояние между прямыми – это тоже длина перпендикуляра (см. рис.3).
Рис. 3. Расстояние между прямыми.
Расстояние от точки до окружности легко найти. Нужно соединить центр с точкой , в результате получится точка . – искомое расстояние (см. рис.4).
Рис. 4. Расстояние от точки до окружности.
Расстояние между двумя окружностями, которые не пересекаются. Нужно соединить центры, получим две точки и . – искомое расстояние (см. рис.5).
Рис. 5. Расстояние между двумя окружностями.
Сформулируем задачу в общем виде и напомним, каким образом ее решать. Мы повторили, что такое расстояние. Вспомним формулу расстояния между двумя заданными точками. Предположим, что на координатной плоскости даны две точки и (см. рис.6).

Рис. 6. Расстояние между двумя заданными точками.
Расстояние между точками вычисляется по формуле
.
Таким образом, находится расстояние между точками, если известны координаты этих точек.
2. Задача 1
На параболе найти точки ближайшие к началу координат, то есть к точке .
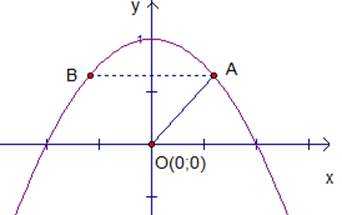
Рис. 7. График функции.
Решение.
Из простейшего анализа задачи можно увидеть, что задача имеет два решения, в силу симметрии графика функции относительно оси Y (см. рис.7).
Координаты искомой точки: . По соответствующей формуле можем найти квадрат расстояния:
. Это расстояние должно быть наименьшим. Упростим эту формулу и получим:
или
.
Можно сразу использовать производную для решения задачи, но пока попытаемся воспользуемся свойствами биквадратной функции. С помощью замены переменной , получим:
. Задача свелась к нахождению минимума следующей квадратичной функции . Найдем абсциссу вершины (см. рис.8).
Рис. 8. Абсцисса вершины параболы.
Задача практически решена. Наименьшее значение этой функции будет тогда, когда . Вычислим . Значит, функция ведет себя следующим образом (см. рис.9):
Рис. 9. Схематический график функции .
Без производной, с помощью свойств квадратичной функции, решили задачу. Если , то , отсюда , . Если значения координат известны, вычислим значения . ; Получили ответ ; .
Итак, была задача: найти точки на кривой, которые бы отстояли от начала координат на наименьшее расстояние. Такие точки найдены. Первая точка — , вторая точка – .
Напомним ход решения задачи. Точка зависит только от , ее координаты – . При выражении квадрата расстояния, получили функцию от . Можно с помощью производной найти минимум. Можно сделать проще. Если сделать замену , получим квадратичную функцию и можно найти наименьшее значение данной квадратичной функции.
Ответ: .
3. Задача 2
На графике функции найти точку , ближайшую к данной точке . Решение.
Сделаем рисунок (см. рис.10).
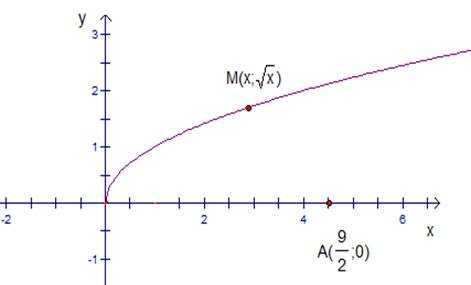
Рис. 10. График функции .
Заданы координаты двух точек: и .
Найдем расстояние АМ:
.
или .
— квадратичная функция от . Вспомним, что нужно найти минимальное значение, то есть . Графиком этой функции является парабола, ветвями направленная вверх, значит, минимум находится в вершине. Выделим полный квадрат и получим:
. Выяснилось, что . Равенство достигается, когда принимает самое минимальное значение. Это будет в случае, когда . Таким образом, получили ответ , а . Значит, координаты точки .
Ответ: .
4. Итог урока
Итак, мы рассмотрели задачи на расстояние от точки до кривой. Можно находить само это расстояние, можно искать точки, которые обеспечивают минимум этого расстояния. Повторили, что такое расстояние между фигурами. Расстояние от точки до кривой – это наименьшее из расстояний, которое получается, когда точка на кривой пробегает все возможные значения. Например, точка может пробегать все значения на кривой , но наименьшее расстояние будет тогда, когда точка имеет координаты . Для этого нужно, во-первых, вспомнить, что такое расстояние, и во-вторых, каким образом ищется расстояние между точками, если известны координаты. И, наконец, надо записать квадрат расстояния и проанализировать полученную функцию. Если не удается это сделать элементарными средствами, с помощью свойств квадратичной функции, то надо использовать производную и искать наименьшее значение функции .
Список рекомендованной литературы
1. Алгебра и начала анализа, 10 класс (в двух частях). Учебник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2009.
2. Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.
3. Виленкин Н. Я., Ивашев-Мусатов О. С., Шварцбурд С. И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики).-М.: Просвещение, 1996.
4. Галицкий М. Л., Мошкович М. М., Шварцбурд С. И. Углубленное изучение алгебры и математического анализа.-М.: Просвещение, 1997.
5. Сборник задач по математике для поступающих во ВТУЗы (под ред. М. И.Сканави).-М.:Высшая школа, 1992.
6. Мерзляк А. Г., Полонский В. Б., Якир М. С. Алгебраический тренажер.-К.: А. С.К., 1997.
7. ЗвавичЛ. И., Шляпочник Л. Я., Чинкина Алгебра и начала анализа. 8-11 кл.: Пособие для школ и классов с углубленным изучением математики (дидактические материалы).-М.: Дрофа, 2002.
8. Саакян С. М., Гольдман А. М., Денисов Д. В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.
9. Карп А. П. Сборник задач по алгебре и началам анализа : учеб. пособие для 10-11 кл. с углубл. изуч. математики.-М.: Просвещение, 2006.
10. Глейзер Г. И. История математики в школе. 9-10 классы (пособие для учителей).-М.: Просвещение, 1983
Дополнительные веб-ресурсы
1. Интернет-портал Mathematics. ru .
2. Портал Естественных Наук .
3. Интернет-портал Exponenta. ru .
Сделай дома
№ 46.52 (а) (Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.)
dp-adilet.kz
10 класс. Алгебра. Типовые задачи на производную. Расстояние от точки до кривой. Иррациональные функции. — Типовые задачи на производную. Расстояние от точки до кривой. Иррациональные функции.
Комментарии преподавателя
Задачи на расстояние от точки до кривой
Что такое расстояние от точки докривой? Точку можно соединить со многими точками кривой. Каждый раз будут получаться разные расстояния. Среди них нужно найти наименьшее. Это расстояние и будет называться расстоянием от точки до кривой. На кривой надо найти такую точку , чтобы расстояние было наименьшим (см. рис. 1).
Рис. 1. Расстояние от точки до кривой.
Видим, что задача на расстояние – это задача на экстремум, на минимум, то есть без производной не обойтись.
Вспомним, что расстояние от точки до прямой – это длина перпендикуляра (см. рис.2).
Рис. 2. Расстояние от точки до прямой.
Расстояние между прямыми – это тоже длина перпендикуляра (см. рис.3).
Рис. 3. Расстояние между прямыми.
Расстояние от точки до окружности легко найти. Нужно соединить центр с точкой , в результате получится точка . – искомое расстояние (см. рис.4).
Рис. 4. Расстояние от точки до окружности.
Расстояние между двумя окружностями, которые не пересекаются. Нужно соединить центры, получим две точки и . – искомое расстояние (см. рис.5).
Рис. 5. Расстояние между двумя окружностями.
Сформулируем задачу в общем виде и напомним, каким образом ее решать. Мы повторили, что такое расстояние. Вспомним формулу расстояния между двумя заданными точками. Предположим, что на координатной плоскости даны две точки и (см. рис.6).
Рис. 6. Расстояние между двумя заданными точками.
Расстояние между точками вычисляется по формуле
.
Таким образом, находится расстояние между точками, если известны координаты этих точек.
На параболе найти точки ближайшие к началу координат, то есть к точке .
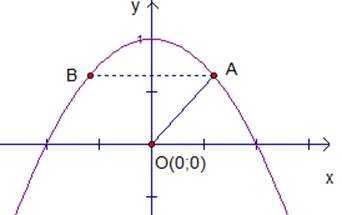
Рис. 7. График функции.
Решение.
Из простейшего анализа задачи можно увидеть, что задача имеет два решения, в силу симметрии графика функции относительно оси Y (см. рис.7).
Координаты искомой точки: . По соответствующей формуле можем найти квадрат расстояния:
. Это расстояние должно быть наименьшим. Упростим эту формулу и получим:
или
.
Можно сразу использовать производную для решения задачи, но пока попытаемся воспользуемся свойствами биквадратной функции. С помощью замены переменной , получим:
. Задача свелась к нахождению минимума следующей квадратичной функции . Найдем абсциссу вершины (см. рис.8).
Рис. 8. Абсцисса вершины параболы.
Задача практически решена. Наименьшее значение этой функции будет тогда, когда . Вычислим . Значит, функция ведет себя следующим образом (см. рис.9):
Рис. 9. Схематический график функции .
Без производной, с помощью свойств квадратичной функции, решили задачу. Если , то , отсюда
www.kursoteka.ru
10 класс. Алгебра. Типовые задачи на производную. Расстояние от точки до кривой. Иррациональные функции. — Типовые задачи на производную. Расстояние от точки до кривой. Иррациональные функции.
Комментарии преподавателя
Задачи на расстояние от точки до кривой
Что такое расстояние от точки докривой? Точку можно соединить со многими точками кривой. Каждый раз будут получаться разные расстояния. Среди них нужно найти наименьшее. Это расстояние и будет называться расстоянием от точки до кривой. На кривой надо найти такую точку , чтобы расстояние было наименьшим (см. рис. 1).
Рис. 1. Расстояние от точки до кривой.
Видим, что задача на расстояние – это задача на экстремум, на минимум, то есть без производной не обойтись.
Вспомним, что расстояние от точки до прямой – это длина перпендикуляра (см. рис.2).
Рис. 2. Расстояние от точки до прямой.
Расстояние между прямыми – это тоже длина перпендикуляра (см. рис.3).
Рис. 3. Расстояние между прямыми.
Расстояние от точки до окружности легко найти. Нужно соединить центр с точкой , в результате получится точка . – искомое расстояние (см. рис.4).
Рис. 4. Расстояние от точки до окружности.
Расстояние между двумя окружностями, которые не пересекаются. Нужно соединить центры, получим две точки и . – искомое расстояние (см. рис.5).
Рис. 5. Расстояние между двумя окружностями.
Сформулируем задачу в общем виде и напомним, каким образом ее решать. Мы повторили, что такое расстояние. Всп
www.kursoteka.ru
10 класс. Алгебра. Типовые задачи на производную. Расстояние от точки до кривой. Иррациональные функции. — Типовые задачи на производную. Расстояние от точки до кривой. Иррациональные функции.
Комментарии преподавателя
Задачи на расстояние от точки до кривой
Что такое расстояние от точки докривой? Точку можно соединить со многими точками кривой. Каждый раз будут получаться разные расстояния. Среди них нужно найти наименьшее. Это расстояние и будет называться расстоянием от точки до кривой. На кривой надо найти такую точку , чтобы расстояние было наименьшим (см. рис. 1).
Рис. 1. Расстояние от точки до кривой.
Видим, что задача на расстояние – это задача на экстремум, на минимум, то есть без производной не обойтись.
Вспомним, что расстояние от точки до прямой – это длина перпендикуляра (см. рис.2).
Рис. 2. Расстояние от точки до прямой.
Расстояние между прямыми – это тоже длина перпендикуляра (см. рис.3).
Рис. 3. Расстояние между прямыми.
Расстояние от точки до окружности легко найти. Нужно соединить центр с точкой , в результате получится точка . – искомое расстояние (см. рис.4).
Рис. 4. Расстояние от точки до окружности.
Расстояние между двумя окружностями, которые не пересекаются. Нужно соединить центры, получим две точки и . – искомое расстояние (см. рис.5).
Рис. 5. Расстояние между двумя окружностями.
Сформулируем задачу в общем виде и напомним, каким образом ее решать. Мы повторили, что такое расстояние. Вспомним формулу расстояния между двумя заданными точками. Предположим, что на координатной плоскости даны две точки и (см. рис.6).
Рис. 6. Расстояние между двумя заданными точками.
Расстояние между точками вычисляется по формуле
.
Таким образом, находится расстояние между точками, если известны координаты этих точек.
На параболе найти точки ближайшие к началу координат, то есть к точке .

Рис. 7. График функции.
Решение.
Из простейшего анализа задачи можно увидеть, что задача имеет два решения, в силу симметрии графика функции относительно оси Y (см. рис.7).
Координаты искомой точки: . По соответствующей формуле можем найти квадрат расстояния:
. Это расстояние должно быть наименьшим. Упростим эту формулу и получим:
или
.
Можно сразу использовать производную для решения задачи, но пока попытаемся воспользуемся свойствами биквадратной функции. С помощью замены переменной , получим:
. Задача свелась к нахождению минимума следующей квадратичной функции . Найдем абсциссу вершины (см. рис.8).
Рис. 8. Абсцисса вершины параболы.
Задача практически решена. Наименьшее значение этой функции будет тогда, когда . Вычислим . Значит, функция ведет себя следующим образом (см. рис.9):
Рис. 9. Схематический график функции .
Без производной, с помощью свойств квадратичной функции, решили задачу. Если , то , отсюда ,
www.kursoteka.ru
10 класс. Алгебра. Производная. Типовые задачи на производную. — Типовые задачи на производную. Расстояние от точки до кривой. Иррациональные функции.
Комментарии преподавателя
Задачи на расстояние от точки до кривой
Что такое расстояние от точки докривой? Точку можно соединить со многими точками кривой. Каждый раз будут получаться разные расстояния. Среди них нужно найти наименьшее. Это расстояние и будет называться расстоянием от точки до кривой. На кривой надо найти такую точку , чтобы расстояние было наименьшим (см. рис. 1).
Рис. 1. Расстояние от точки до кривой.
Видим, что задача на расстояние – это задача на экстремум, на минимум, то есть без производной не обойтись.
Вспомним, что расстояние от точки до прямой – это длина перпендикуляра (см. рис.2).
Рис. 2. Расстояние от точки до прямой.
Расстояние между прямыми – это тоже длина перпендикуляра (см. рис.3).
Рис. 3. Расстояние между прямыми.
Расстояние от точки до окружности легко найти. Нужно соединить центр с точкой , в результате получится точка . – искомое расстояние (см. рис.4).
Рис. 4. Расстояние от точки до окружности.
Расстояние между двумя окружностями, которые не пересекаются. Нужно соединить центры, получим две точки и
www.kursoteka.ru
Определение расстояния от точки до кривой поверхности
На рис. 32 показана зависимость коэффициента увеличения тяги от отношения расстояния до поверхности удара струи к диаметру струи. Коэф- фициент увеличения тяги но определению равен отношению значений тяги на данном расстоянии от сопла до и после удаления отклоняющей пластины. Сплошное кольцевое сечение создает сплошную пелену жидкости, в то время как прерывистое кольцо образовано отдельными щелевыми струями, расположенными по кольцу. Кривая для такого прерывистого кольца имеет плавную форму и достигает значения коэффициента усиления тяги, равного единице, при отношении расстояния до омываемой поверхности к диаметру [c.324]Для практического исполнения анодной защиты предварительно на лабораторной установке снимают анодные поляризационные потенциостатические кривые, характеризующие анодное поведение металла в данной среде. По ним определяют диапазон защитных потенциалов, критическую плотность тока / р и плотность тока полной пассивации / . Аппаратурное оформление и методика снятия поляризационных кривых описаны в [14]. При высокой электропроводности промышленной среды расположение катодов в аппарате мало влияет на пассивацию поверхности. При низкой электропроводности среды, вследствие возникновения большого градиента потенциала вдоль защищаемой- поверхности, на определенном расстоянии от катода стенки аппарата остаются в активном состоянии и подвергаются коррозии, в то время как вблизи катода потенциал удерживается в области устойчивой пассивности. Поэтому предварительные сведения о дальнодействии анодной защиты или ее рассеивающей способности имеют [c.263]
Определение расстояния от точки до кривой поверхности [c.77]
Сущность волнового движения можно выразить синусоидальной кривой, приведенной на рис. 3.12. Эта кривая может относиться, например, к контуру волн на поверхности океана в определенный момент. Расстояние между двумя соседними гребнями называется длиной волны и обычно обозначается Я (греческая буква лямбда ). Высота гребня (равная в то же время углублению между гребнями) по отношению к среднему уровню волны называется амплитудой волны. Если волны движутся со скоростью с м-с , то частота волн, обозначаемая символом V (греческая буква ню ), равна сД частота выражает число волн, проходящих во времени (1 с) через фиксированную точку. Размерность длины волны та же, что и размерность длины. Размерность частоты — [c.62]
Часто, однако, трудно подобрать такую молекулу сравнения группы А, которая давала бы близкую к исследуемой молекуле групп В ж Ъ теплоту адсорбции на неспецифическом адсорбенте. Для удобства интерполяции QA B) или QA D) в этих случаях в [6] предложено пользоваться графиком зависимости ряда сходных молекул группы А от их электронной поляризуемости а (рис. 2). Константы неспецифических дисперсионного и индукционного взаимодействий увеличиваются с ростом а (см. ]3, 4]). Для определения вклада AQ при адсорбции производных алканов, относящихся к группе В или I), в качестве молекул сравнения группы А удобно взять к-алканы [1], потому что расстояния от поверхности СНд, СНз и многих групп заместителей одинаковы или близки. Так как специфическое взаимодействие также увеличивается с ростом а, на том же графике наносят величины и Разности между этими величинами и соответствующими точками (при тех же а) на кривой зависимости от а дают вклады А Q специфических взаимодействий молекул групп 5 или В в теплоту их адсорбции. Найденные из этого графика величины AQ отмечены на рис. 2. Различие величин AQ для (СаНа зО, найденных таким способом и приведенных в табл. 1, составляет не более 15%. Для молекул группы В величина AQ в общем увеличивается с ростом квадрупольного (т) и диполь- [c.135]
На рис. 36 показаны три различные по форме барьера [44в, 46, 47]. При той же самой величине поля Р и работе выхода ф плотности эмиссии различаются более чем на порядок и все же наклон прямых Фаулера — Нордхейма пропорционален ф в пределах точности обычных измерений ( 1%)- При условии, что приложенное поле не слишком сильное, т. е. что толщина барьера еще превышает несколько атомных диаметров, изменения площади под потенциальной кривой, вызванные приложенным полем, сконцентрированы в тех областях, где потенциал является линейной функцией расстояния. Таким образом, особенности барьера вблизи поверхности не будут влиять на определение работы выхода. [c.168]
На рис. 4.1,а представлены поляризационные кривые при постоянной силе тока на катоде, расположенном в центре цилиндра. При значениях силы тока 5—10 А потенциал быстро возрастает до (+0,4) —(+0,7) В. Таким же методом получены данные для катода, расположенного на расстоянии 1,27 см от стенки сосуда (рис. 4.1,6). Капиллярный каломельный электрод сравнения был расположен между катодом и стенкой сосуда. Из рис. 4.1, в видно, что время, необходимое для образования пассивной пленки (катод расположен на расстоянии 5,08 см от стенки сосуда), мало отличается от времени при катоде, расположенном ближе к стенке. На рис. 4.1,г показано время пассивации для точки, расположенной в противоположной стороне от катода. Сравнение данных рис. 4.1 показывает, что пассивация начинается вблизи катода и через определенное время распространяется по всей поверхности. [c.74]
Сущность волнового движения можно выразить синусоидальной кривой, показанной на рис. 3.15. Эта кривая может представлять, например, контур волн на поверхности океана в определенный момент. Расстояние между двумя соседними гребнями называется длиной волны и обычно обозначается Я (греческая буква лямбда ). Высота гребня (равная в то же время углублению между гребнями) по отношению к среднему уровню волны называется амплитудой волны. Если волны движутся со скоростью с м.с 1, то частота волн, обозначаемая символом v (греческая буква ню ), равна с/Я частота выражает число волн, проходящих в определенное время (в 1 с) через фиксированную точку. Размерность длины волны та же, что и размерность длины. Размерность частоты — число волн в секунду (время» ]. Нетрудно понять, что произведение длины волны на частоту Xv — [длина] [время 1] имеет размерность скорости. Длина волны Я, частота v и скорость с связаны уравнением [c.61]
Метод отнесения расчетов коэффициентов диффузии по степенным рядам к срединной точке кинетической кривой хотя и нивелирует до некоторой степени влияние на диффузионную константу слоя красителя, отложившегося на поверхности волокна и не проникшего внутрь полимера, но не всегда дает возможность исключить из расчетов эту долю красителя полностью. С учетом сказанного лучший способ определения действительных коэффициентов диффузии красителей в волокнистых материалах состоит в применении различных вариантов микро-фотометрического анализа распределения окрашенных зон в поперечном сечении волокна. Для расчета коэффициента диффузии в данном случае содержание красителя в волокне выражают как функцию расстояния X, на которое он проник в полимер, и пользуются зависи- [c.166]
На рис. 141 изображена диаграмма напряжений в образцах с надрезами. Ординаты кривых выражают напряжения в точках, расположенных на различном расстоянии от
www.chem21.info
