Решение целых и дробно рациональных уравнений
Давайте познакомимся с рациональными и дробными рациональными уравнениями, дадим их определение, приведем примеры, а также разберем наиболее распространенные типы задач.
Рациональное уравнение: определение и примеры
Знакомство с рациональными выражениями начинается в 8 классе школы. В это время на уроках алгебры учащиеся все чаще начинают встречать задания с уравнениями, которые содержат рациональные выражения в своих записях. Давайте освежим в памяти, что это такое.
Определение 1Рациональное уравнение – это такое уравнение, в обеих частях которого содержатся рациональные выражения.
В различных пособиях можно встретить еще одну формулировку.
Определение 2Рациональное уравнение – это такое уравнение, запись левой части которого содержит рациональное выражение, а правая – нуль.
Определения, которые мы привели для рациональных уравнений, являются равнозначными, так как говорят об одно и том же.
А теперь обратимся к примерам.
Пример 1Рациональные уравнения:
x=1, 2·x−12·x2·y·z3=0, xx2+3·x-1=2+27·x-a·(x+2), 12+34-12x-1=3.
Рациональные уравнения точно также, как и уравнения других видов, могут содержать любое количество переменных от 1 до нескольких. Для начала мы рассмотрим простые примеры, в которых уравнения будут содержать только одну переменную. А затем начнем постепенно усложнять задачу.
Рациональные уравнения делятся на две большие группы: целые и дробные. Посмотрим, какие уравнения будут относиться к каждой из групп.
Определение 3Рациональное уравнение будет являться целым в том случае, если в записи левой и правой его частей содержатся целые рациональные выражения.
Определение 4Рациональное уравнение будет являться дробным в том случае, если одна или обе его части содержат дробь.
Дробно рациональные уравнения в обязательном порядке содержат деление на переменную или же переменная имеется в знаменателе. В записи целых уравнений такого деления нет.
Пример 23·x+2=0 и (x+y)·(3·x2−1)+x=−y+0,5 – целые рациональные уравнения. Здесь обе части уравнения представлены целыми выражениями.
1x-1=x3 и x:(5·x3+y2)=3:(x−1):5 – это дробно рациональные уравнения.
К числу целых рациональных уравнений можно отнести линейные и квадратные уравнения.
Решение целых уравнений
Решение таких уравнений обычно сводится к преобразованию их в равносильные алгебраические уравнения. Достичь этого можно путем проведения равносильных преобразований уравнений в соответствии со следующим алгоритмом:
- сначала получим ноль в правой части уравнения, для этого на необходимо перенести выражение, которое находится в правой части уравнения, в его левую часть и поменять знак;
- затем преобразуем выражение в левой части уравнения в многочлен стандартного вида.

Мы должны получить алгебраическое уравнение. Это уравнение будет равносильным по отношению к исходному уравнению. Легкие случаи позволяют нам для решения задачи свести целое уравнение с линейному или квадратному. В общем случае мы решаем алгебраическое уравнение степени n.
Пример 3Необходимо найти корни целого уравнения 3·(x+1)·(x−3)=x·(2·x−1)−3.
Решение
Проведем преобразование исходного выражения с целью получить равносильное ему алгебраическое уравнение. Для этого произведем перенос выражения, содержащегося в правой части уравнения, в левую часть и заменим знак на противоположный. В итоге получим: 3·(x+1)·(x−3)−x·(2·x−1)+3=0.
Теперь проведем преобразование выражения, которое находится в левой части в многочлен стандартного вида и произведем необходимые действия с этим многочленом:
3·(x+1)·(x−3)−x·(2·x−1)+3=(3·x+3)·(x−3)−2·x2+x+3==3·x2−9·x+3·x−9−2·x2+x+3=x2−5·x−6
У нас получилось свести решение исходного уравнения к решению квадратного уравнения вида x2−5·x−6=0. Дискриминант этого уравнения положительный: D=(−5)2−4·1·(−6)=25+24=49. Это значит, действительных корней будет два. Найдем их, воспользовавшись формулой корней квадратного уравнения:
Дискриминант этого уравнения положительный: D=(−5)2−4·1·(−6)=25+24=49. Это значит, действительных корней будет два. Найдем их, воспользовавшись формулой корней квадратного уравнения:
x=—5±492·1,
x1=5+72 или x2=5-72,
x1=6 или x2=-1
Проверим верность корней уравнения, которые мы нашли в ходе решения. Для этого числа, которые мы получили, подставим в исходное уравнение: 3·(6+1)·(6−3)=6·(2·6−1)−3
Ответ: 6, −1.
Давайте разберем, что значит «степень целого уравнения». С этим термином мы будем часто встречаться в тех случаях, когда нам надо будет представить целое уравнение в виде алгебраического. Дадим определение понятию.
Определение 5Степень целого уравнения – это степень алгебраического уравнения, равносильного исходному целому уравнению.
Если посмотреть на уравнения из примера, приведенного выше, можно установить: степень данного целого уравнения вторая.
Если бы наш курс ограничивался решением уравнений второй степени, то рассмотрение темы на этом можно было бы закончить. Но все не так просто. Решение уравнений третьей степени сопряжено с трудностями. А для уравнений выше четвертой степени и вовсе не существует общих формул корней. В связи с этим решение целых уравнений третьей, четвертой и других степеней требует от нас применения целого ряда других приемов и методов.
Чаще прочих используется подход к решению целых рациональных уравнений, который основан на методе разложения на множители. Алгоритм действий в этом случае следующий:
- переносим выражение из правой части в левую с тем, чтобы в правой части записи остался нуль;
- представляем выражение в левой части как произведение множителей, а затем переходим к совокупности нескольких более простых уравнений.
Найдите решение уравнения (x2−1)·(x2−10·x+13)=2·x·(x2−10·x+13).
Решение
Переносим выражение из правой части записи в левую с противоположным знаком:
Намного проще пойти другим путем: вынесем за скобки общий множитель x2−10·x+13. Так мы придем к уравнению вида (x2−10·x+13)·(x2−2·x−1)=0. Теперь заменим полученное уравнение совокупностью двух квадратных уравнений x2−10·x+13=0 и x2−2·x−1=0 и найдем их корни через дискриминант: 5+2·3, 5-2·3, 1+2, 1-2.
Ответ: 5+2·3, 5-2·3, 1+2, 1-2.
Точно также мы можем использовать метод введения новой переменной. Этот метод позволяет нам переходить к равносильным уравнениям со степенями ниже, чем были степени в исходном целом уравнении.
Есть ли корни у уравнения (x2+3·x+1)2+10=−2·(x2+3·x−4)?
Решение
Если мы сейчас попробуем свести целое рациональное уравнение к алгебраическому, то получим уравнение 4 степени, которое не имеет рациональных корней. Потому нам будет проще пойти другим путем: ввести новую переменную у, которая заменит в уравнении выражение x2+3·x.
Теперь мы будем работать с целым уравнением (y+1)2+10=−2·(y−4). Перенесем правую часть уравнения в левую с противоположным знаком и проведем необходимые преобразования. Получим: y2+4·y+3=0. Найдем корни квадратного уравнения: y=−1 и y=−3.
Теперь проведем обратную замену. Получим два уравнения x2+3·x=−1 и x2+3·x=−3. Перепишем их как x2+3·x+1=0 и x2+3·x+3=0. Используем формулу корней квадратного уравнения для того, чтобы найти корни первого уравнения из полученных: -3±52 . Дискриминант второго уравнения отрицательный. Это значит, что действительных корней у второго уравнения нет.
Ответ: -3±52
Целые уравнения высоких степеней попадаются в задачах достаточно часто. Пугаться их не нужно. Нужно быть готовым применить нестандартный метод их решения, в том числе и ряд искусственных преобразований.
Решение дробно рациональных уравнений
Начнем рассмотрение этой подтемы мы с алгоритма решения дробно рациональных уравнений вида p(x)q(x)=0 , где p(x) и q(x) – целые рациональные выражения. Решение остальных дробно рациональных уравнений всегда можно свести к решению уравнений указанного вида.
В основу наиболее употребимого метода решения уравнений p(x)q(x)=0 положено следующее утверждение: числовая дробь uv, где v – это число, которое отлично от нуля, равна нулю только в тех случаях, когда числитель дроби равен нулю. Следуя логике приведенного утверждения мы можем утверждать, что решение уравнения p(x)q(x)=0 может быть сведено в выполнению двух условий: p(x)=0 и q(x)≠0. На этом построен алгоритм решения дробных рациональных уравнений вида p(x)q(x)=0 :
- находим решение целого рационального уравнения p(x)=0;
- проверяем, выполняется ли для корней, найденных в ходе решения, условие q(x)≠0.

Если это условие выполняется, то найденный корень является корнем исходного уравнения. Если нет, то корень не является решением задачи.
Пример 6Найдем корни уравнения 3·x-25·x2-2=0 .
Решение
Мы имеем дело с дробным рациональным уравнением вида p(x)q(x)=0, в котором p(x)=3·x−2, q(x)=5·x2−2=0. Приступим к решению линейного уравнения 3·x−2=0. Корнем этого уравнения будет x=23.
Проведем проверку найденного корня, удовлетворяет ли он условию 5·x2−2≠0
Условие выполняется. Это значит, что x=23 является корнем исходного уравнения.
Ответ: 23.
Есть еще один вариант решения дробных рациональных уравнений p(x)q(x)=0. Вспомним, что это уравнение равносильно целому уравнению p(x)=0 на области допустимых значений переменной x исходного уравнения. Это позволяет нам использовать следующий алгоритм в решении уравнений p(x)q(x)=0 :
- решаем уравнение p(x)=0;
- находим область допустимых значений переменной x;
- берем корни, которые лежат в области допустимых значений переменной x, в качестве искомых корней исходного дробного рационального уравнения.

Решите уравнение x2-2·x-11×2+3·x=0.
Решение
Для начала решим квадратное уравнение x2−2·x−11=0. Для вычисления его корней мы используем формулу корней для четного второго коэффициента. Получаем D1=(−1)2−1·(−11)=12, и x=1±23.
Теперь мы можем найти ОДЗ переменной x для исходного уравнения. Это все числа, для которых x2+3·x≠0. Это то же самое, что x·(x+3)≠0, откуда x≠0, x≠−3.
Теперь проверим, входят ли полученные на первом этапе решения корни x=1±23 в область допустимых значений переменной x. Мы видим, что входят. Это значит, что исходное дробное рациональное уравнение имеет два корня x=1±23.
Ответ: x=1±23
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать заданиеВторой описанный метод решения проще первого в случаях, когда легко находится область допустимых значений переменной x, а корни уравнения p(x)=0 иррациональные. Например, 7±4·269. Корни могут быть и рациональными, но с большим числителем или знаменателем. Например, 1271101 и −3159. Это позволяет сэкономить время на проведении проверки условия q(x)≠0 : намного проще исключить корни, которые не подходят, по ОДЗ.
Например, 7±4·269. Корни могут быть и рациональными, но с большим числителем или знаменателем. Например, 1271101 и −3159. Это позволяет сэкономить время на проведении проверки условия q(x)≠0 : намного проще исключить корни, которые не подходят, по ОДЗ.
В тех случаях, когда корни уравнения p(x)=0 целые, целесообразнее использовать первый из описанных алгоритмов решения уравнений вида p(x)q(x)=0. Быстрее сразу находить корни целого уравнения p(x)=0, после чего проверять, выполняется ли для них условие q(x)≠0, а не находить ОДЗ, после чего решать уравнение p(x)=0 на этой ОДЗ. Это связано с тем, что в таких случаях сделать проверку обычно проще, чем найти ОДЗ.
Пример 8Найдите корни уравнения (2·x-1)·(x-6)·(x2-5·x+14)·(x+1)x5-15·x4+57·x3-13·x2+26·x+112=0.
Решение
Начнем с рассмотрения целого уравнения (2·x−1)·(x−6)·(x2−5·x+14)·(x+1)=0 и нахождения его корней. Для этого применим метод решения уравнений через разложение на множители. Получается, что исходное уравнение равносильно совокупности четырех уравнений 2·x−1=0, x−6=0, x2−5·x+14=0, x+1=0, из которых три линейных и одно квадратное. Находим корни: из первого уравнения x=12, из второго – x=6, из третьего – x=7, x=−2, из четвертого – x=−1.
Получается, что исходное уравнение равносильно совокупности четырех уравнений 2·x−1=0, x−6=0, x2−5·x+14=0, x+1=0, из которых три линейных и одно квадратное. Находим корни: из первого уравнения x=12, из второго – x=6, из третьего – x=7, x=−2, из четвертого – x=−1.
Проведем проверку полученных корней. Определить ОДЗ в данном случае нам сложно, так как для этого придется провести решение алгебраического уравнения пятой степени. Проще будет проверить условие, по которому знаменатель дроби, которая находится в левой части уравнения, не должен обращаться в нуль.
По очереди подставим корни на место переменной х в выражение x5−15·x4+57·x3−13·x2+26·x+112и вычислим его значение:
125−15·124+57·123−13·122+26·12+112==132−1516+578−134+13+112=122+132≠0;
65−15·64+57·63−13·62+26·6+112=448≠0;
75−15·74+57·73−13·72+26·7+112=0;
(−2)5−15·(−2)4+57·(−2)3−13·(−2)2+26·(−2)+112=−720≠0;
(−1)5−15·(−1)4+57·(−1)3−13·(−1)2+26·(−1)+112=0.
Проведенная проверка позволяет нам установить, что корнями исходного дробного рацинального уравнения являются 12, 6 и −2.
Ответ: 12, 6, -2
Пример 9Найдите корни дробного рационального уравнения 5·x2-7·x-1·x-2×2+5·x-14=0 .
Решение
Начнем работу с уравнением (5·x2−7·x−1)·(x−2)=0. Найдем его корни. Нам проще представить это уравнение как совокупность квадратного и линейного уравнений 5·x2−7·x−1=0 и x−2=0.
Используем формулу корней квадратного уравнения для поиска корней. Получаем из первого уравнения два корня x=7±6910 , а из второго x=2.
Подставлять значение корней в исходное уравнение для проверки условий нам будет достаточно сложно. Проще будет определить ОДЗ переменной x. В данном случае ОДЗ переменной x – это все числа, кроме тех, для которых выполняется условие x2+5·x−14=0. Получаем: x∈-∞, -7∪-7, 2∪2, +∞.
Теперь проверим, принадлежат ли найденные нами корни к области допустимых значений переменной x.
Корни x=7±6910 — принадлежат, поэтому, они являются корнями исходного уравнения, а x=2 – не принадлежит, поэтому, это посторонний корень.
Ответ: x=7±6910.
Разберем отдельно случаи, когда в числителе дробного рационального уравнения вида p(x)q(x)=0 находится число. В таких случаях, если в числителе находится число, отличное от нуля, то уравнение не будет иметь корней. Если это число будет равно нулю, то корнем уравнения будет любое число из ОДЗ.
Пример 10Решите дробное рациональное уравнение -3,2×3+27=0.
Решение
Данное уравнение не будет иметь корней, так как в числителе дроби из левой части уравнения находится отличное от нуля число. Это значит, что ни при каких значениях x значение приведенной в условии задачи дроби не будет равняться нулю.
Ответ: нет корней.
Пример 11Решите уравнение 0x4+5·x3=0.
Решение
Так как в числителе дроби находится нуль, решением уравнения будет любое значение x из ОДЗ переменной x.
Теперь определим ОДЗ. Оно будет включать все значения x, при которых x4+5·x3≠0. Решениями уравнения x4+5·x3=0являются 0 и −5, так как, это уравнение равносильно уравнению x3·(x+5)=0, а оно в свою очередь равносильно совокупности двух уравнений x3=0 и x+5=0, откуда и видны эти корни. Мы приходим к тому, что искомой областью допустимых значений являются любые x, кроме x=0 и x=−5.
Решениями уравнения x4+5·x3=0являются 0 и −5, так как, это уравнение равносильно уравнению x3·(x+5)=0, а оно в свою очередь равносильно совокупности двух уравнений x3=0 и x+5=0, откуда и видны эти корни. Мы приходим к тому, что искомой областью допустимых значений являются любые x, кроме x=0 и x=−5.
Получается, что дробное рациональное уравнение 0x4+5·x3=0 имеет бесконечное множество решений, которыми являются любые числа кроме нуля и -5.
Ответ: -∞, -5∪(-5, 0∪0, +∞
Теперь поговорим о дробных рациональных уравнениях произвольного вида и методах их решения. Их можно записать как r(x)=s(x), где r(x) и s(x) – рациональные выражения, причем хотя бы одно из них дробное. Решение таких уравнений сводится к решению уравнений вида p(x)q(x)=0.
Мы уже знаем, что мы можем получить равносильное уравнение при переносе выражения из правой части уравнения в левое с противоположным знаком. Это значит, что уравнение r(x)=s(x) равносильно уравнение r(x)−s(x)=0. Также мы уже разобрали способы преобразования рационального выражения в рациональную дробь. Благодаря этому мы без труда можем преобразовать уравнение r(x)−s(x)=0 в тождественную ему рациональную дробь вида p(x)q(x).
Это значит, что уравнение r(x)=s(x) равносильно уравнение r(x)−s(x)=0. Также мы уже разобрали способы преобразования рационального выражения в рациональную дробь. Благодаря этому мы без труда можем преобразовать уравнение r(x)−s(x)=0 в тождественную ему рациональную дробь вида p(x)q(x).
Так мы переходим от исходного дробного рационального уравнения r(x)=s(x) к уравнению вида p(x)q(x)=0, решать которые мы уже научились.
Следует учитывать, что при проведении переходов от r(x)−s(x)=0 к p(x)q(x)=0 , а затем к p(x)=0 мы можем не учесть расширения области допустимых значений переменной x.
Вполне реальна ситуация, когда исходное уравнение r(x)=s(x) и уравнение p(x)=0 в результате преобразований перестанут быть равносильными. Тогда решение уравнения p(x)=0 может дать нам корни, которые будут посторонними для r(x)=s(x). В связи с этим в каждом случае необходимо проводить проверку любым из описанных выше способов.
Чтобы облегчить вам работу по изучению темы, мы обобщили всю информацию в алгритм решения дробного рационального уравнения вида r(x)=s(x):
- переносим выражение из правой части с противоположным знаком и получаем справа нуль;
- преобразуем исходное выражение в рациональную дробь p(x)q(x), последовательно выполняя действия с дробями и многочленами;
- решаем уравнение p(x)=0;
- выявляем посторонние корни путем проверки их принадлежности ОДЗ или методом подстановки в исходное уравнение.
Визуально цепочка действий будет выглядеть следующим образом:
r(x)=s(x)→r(x)-s(x)=0→p(x)q(x)=0→p(x)=0→отсеиваниепостороннихкорней
Пример 12Решите дробное рациональное уравнение xx+1=1x+1.
Решение
Перейдем к уравнению xx+1-1x+1=0. Преобразуем дробное рациональное выражение в левой части уравнения к виду p(x)q(x).
Для этого нам придется привести рациональные дроби к общему знаменателю и упростить выражение:
xx+1-1x-1=x·x-1·(x+1)-1·x·(x+1)x·(x+1)==x2-x-1-x2-xx·(x+1)=-2·x-1x·(x+1)
Для того, чтобы найти корни уравнения -2·x-1x·(x+1)=0, нам необходимо решить уравнение −2·x−1=0. Получаем один корень x=-12.
Получаем один корень x=-12.
Нам осталось выполнить проверку любым из методов. Рассмотрим их оба.
Подставим полученное значение в исходное уравнение. Получим -12-12+1=1-12+1. Мы пришли к верному числовому равенству −1=−1. Это значит, что x=−12 является корнем исходного уравнения.
Теперь проведем проверку через ОДЗ. Определим область допустимых значений переменной x. Это будет все множество чисел, за исключением −1 и 0 (при x=−1 и x=0 обращаются в нуль знаменатели дробей). Полученный нами корень x=−12 принадлежит ОДЗ. Это значит, что он является корнем исходного уравнения.
Ответ: −12.
Пример 13Найдите корни уравнения x1x+3-1x=-23·x.
Решение
Мы имеем дело с дробным рациональным уравнением. Следовательно, будем действовать по алгоритму.
Перенесем выражение из правой части в левую с противоположным знаком: x1x+3-1x+23·x=0
Проведем необходимые преобразования: x1x+3-1x+23·x=x3+2·x3=3·x3=x.
Приходим к уравнению x=0. Корень этого уравнения – нуль.
Проверим, не является ли этот корень посторонним для исходного уравнения. Подставим значение в исходное уравнение: 010+3-10=-23·0. Как видите, полученное уравнение не имеет смысла. Это значит, что 0 – это посторонний корень, а исходное дробное рациональное уравнение корней не имеет.
Ответ: нет корней.
Если мы не включили в алгоритм другие равносильные преобразования, то это вовсе не значит, что ими нельзя пользоваться. Алгоритм универсален, но он создан для того, чтобы помогать, а не ограничивать.
Пример 14Решите уравнение 7+13+12+15-x2=7724
Решение
Проще всего будет решить приведенное дробное рациональное уравнение согласно алгоритму. Но есть и другой путь. Рассмотрим его.
Отнимем от правой и левой частей 7, получаем: 13+12+15-x2=724 .
Отсюда можно заключить, что выражение в знаменателе левой части должно быть равно числу, обратному числу из правой части, то есть, 3+12+15-x2=247.
Вычтем из обеих частей 3: 12+15-x2=37. По аналогии 2+15-x2=73, откуда 15-x2=13, и дальше 5-x2=3, x2=2, x=±2
Проведем проверку для того, чтобы установить, являются ли найденные корни корнями исходного уравнения.
Ответ: x=±2
Дробно рациональные уравнения. Решения
Уравнение которые можно свести к дроби f(x)/g(x)=0 называется дробно рациональным уравнением.
Решение дробно рациональных уравнений не слишком сложная задача если Вы знаете методику, а она достаточно проста.
Если уравнение имеет несколько слагаемых то переносим их по одну сторону знака равенства и сводим к общему знаменателю. В результате получим дробную функцию f(x)/g(x), которая равна нулю
Следующим шагом находим корни числителя. Отвергаем среди них те, которые не принадлежат области допустимых значений (нули знаменателя) и записываем правильный ответ.
В теории все просто, однако на практике и у школьников и у студентов возникают проблемы при сведены к общему знаменателю, отыскании корней и т. д. Для ознакомления с решением рассмотрим несколько распространенных задач.
д. Для ознакомления с решением рассмотрим несколько распространенных задач.
Примеры дробно рациональных уравнений
Пример 1. Найти корни уравнения
Решение: По методике переносим слагаемые и сводим к общему знаменателю
Приравниваем числитель и знаменатель к нулю и находим корни. Первое уравнение можем решить по теореме Виета
Второе раскладываем на множители
Если от корней числителя отбросить нули знаменателя то получим только одно решение x=-7.
Внимание: Всегда проверяйте совпадают ли корни числителя и знаменателя. Если такие есть то не учитывайте их в ответе.
Ответ: х=-7.
————————————
Пример 2. Решить уравнение
Решение: Задано дробное рациональное уравнение. Находим сначала корни числителя, для этого решаем квадратное уравнение
Вычисляем дискриминант
и корни уравнения
Получили три нуля числителя .
Квадратное уравнение в знаменателе проще и можем решить по теореме Виета
Числитель и знаменатель не имеют общих корней поэтому все три найденные значения будут решениями.
————————————
Пример 3. Найти корни уравнения
Решение: Переносим слагаемое за знак равенства
и сводим к общему знаменателю
Раскрываем в числителе скобки и сводим к квадратному уравнению
Полученное дробно рациональное уравнение эквивалентно системе двух уравнений
Корни первого вычисляем через дискриминант
Нули второго находим без проблем
Исключаем из решений числителя значение и получим.
Ответ: х=3.
————————————
Задачи на движение
Задача 4. Вертолет пролетел по ветру расстояние 120 км и обратно вернулся, потратив на весь путь 6 час. Найдите скорость ветра если скорость в штиль составляет 45 км/час.
Решение:
Обозначим скорость ветра через х км/час. Тогда за ветром скорость вертолета составит (45+х) км/час, и в обратном направлении (45-х) км/час. По условию задачи вертолет потратил 6 часов на дорогу.
Разделив расстояние на скорость и просуммировав получим время
Получили дробно рациональное уравнение схема решения которого неоднократно повторялась
Решением второго уравнения будут значения x=-45; x=45.
Корни числителя найдем после упрощений
С физических соображений первое решение отвергаем.
Ответ: скорость ветра 15 км/час.
————————————
Задачи о совместной работе
Задача 2. Два лесорубы работая вместе выполнили норму вырубки за 4 дня. Сколько дней нужно на выполнение этой работы каждому лесорубу отдельно если первому для вырубки нормы нужно на 6 дней меньше чем другому?
Решение: Пусть первый лесоруб выполняет норму по х дней. Тогда второму необходимо (х+6) дней.
Это означает что за один день первый выполнит , а второй — часть всей нормы. По условию выполняют норму за 4 дня, то есть оба в день могут выполнить нормы.
Составляем и решаем уравнение
Данное дробно рациональное уравнение эквивалентно системе двух уравнений
Одно решение не соответствует физической сути задачи. Время второго лесоруба
х+6=6+6=12 (дней)
Ответ: Работу первый лесоруб выполнит за 6 дней, а второй за 12.
————————————
Подобных дробно рациональных уравнений можно рассмотреть множество, схема их решения неизменна. В теоретических задачах правильно составляйте уравнение и не заблуждайтесь при сведении к общему знаменателю. Все остальное сводится к решению преимущественно линейных или квадратных уравнений.
Рациональные уравнения (ЕГЭ — 2021)
А вот еще одно уравнение \( \displaystyle \frac{5}{x+1}+\frac{4{x}-6}{(x+1)\cdot (x+3)}=3\). Это уравнение целое? НЕТ!!! Тут есть деление на переменную \( \displaystyle x\), а это говорит о том, что уравнение не целое. Тогда какое же оно? Это дробно рациональное уравнение.
Дробно-рациональное уравнение – рациональное (без знака корня) уравнение, в котором левая или правая части являются дробными выражениями.
На первый взгляд особой разницы не видно, ну давай попробуем решать его как мы решали целое (линейное) уравнение.
Для начала найдем наименьший общий знаменатель, это будет \( \displaystyle (x+1)\cdot (x+3)\). {2}}+3x=0.\end{array}\)
{2}}+3x=0.\end{array}\)
Ну как, это уже попроще выглядит, чем в начале было?
Выносим за скобку общий множитель: \( \displaystyle 3x\cdot (x+1)=0\)
У этого уравнения два решения, его левая сторона принимает нулевое значение при \( \displaystyle x=0\) и \( \displaystyle x=-1\).
Вроде бы все, ну ладно давайте напоследок подставим корни \( \displaystyle x=0\) и \( \displaystyle x=-1\) в исходное уравнение, чтобы проверить, нет ли ошибок. Сначала подставим \( \displaystyle 0\), получается \( \displaystyle 3=3\) –нет претензий?
С ним все нормально. А теперь \( \displaystyle -1\), и тут же видим в знаменателе первого члена \( \displaystyle -1+1\)!
Но ведь это же будет ноль!
На ноль делить нельзя, это все знают, в чем же дело???
Дело в ОДЗ! (если забыл что это, повтори тему «ОДЗ»!) Области Допустимых Значений.
Всякий раз когда ты видишь уравнение, где есть переменные (\( \displaystyle x,y\) и т.д.) в знаменателе, прежде всего, нужно найти ОДЗ, найти какие значения может принимать икс, хотя удобнее в ОДЗ написать, чему икс НЕ может быть равен, ведь таких значений не так много, как правило.
Просто запомни, что на ноль делить нельзя! И перед тем как решать наше уравнение нам следовало сделать так:
ОДЗ: \( \displaystyle x+1\ne 0\) и \( \displaystyle x+3\ne 0\) \( \displaystyle \Rightarrow x\ne -1\) и \( \displaystyle x\ne -3\).
Если бы мы сразу так написали, то заранее бы знали, что эти ответы стоит исключить и так, из полученных нами \( \displaystyle x=0\) и \( \displaystyle x=-1\) мы смело исключаем \( \displaystyle x=-1\), т.к. он противоречит ОДЗ.
Значит, какой ответ будет у решенного уравнения?
В ответ стоит написать только один корень, \( \displaystyle x=0\).
Стоит заметить, что ОДЗ не всегда сказывается на ответе, возможны случаи, когда корни, которые мы получили, не попадают под ограничения ОДЗ.
Но писать ОДЗ в дробно рациональных уравнениях стоит всегда – так просто спокойнее, что ты ничего не упустил и да,
ВСЕГДА по окончании решения сверяй свои корни и область допустимых значений!
Урок 3.
 квадратные уравнения, неравенства и их системы — Алгебра и начала математического анализа — 10 класс
квадратные уравнения, неравенства и их системы — Алгебра и начала математического анализа — 10 классАлгебра и начала математического анализа, 10 класс
Урок №3. Квадратные уравнения, неравенства и их системы.
Перечень вопросов, рассматриваемых в теме:
- систематизация знаний учащихся о решении квадратных уравнений и неравенств;
- установление зависимости количества и расположения корней квадратного уравнения от его коэффициентов и значения дискриминанта;
- способы решения квадратных уравнений и неравенств с параметрами.
Глоссарий по теме:
Параметр — (от греч. parametron — отмеривающий) в математике, величина, числовые значения которой позволяют выделить определенный элемент из множества элементов того же рода.
Основная литература:
Колягин Ю. М., Ткачева М. В., Фёдорова Н.Е. и др. Алгебра и начала математического анализа. 10 класс. Базовый и углублённый уровни. — М. : Просвещение, 2017.
: Просвещение, 2017.
Ткачева М. В., Федорова Н. Е. Алгебра и начала математического анализа. Тематические тесты. 10 класс. Базовый и профильный уровни. 2016.
Шабунин М. И., Ткачева М. В., Фёдорова Н.Е. и др. Алгебра и начала математического анализа. Дидактические материалы. 10 класс. Профильный уровень. 2016.
Теоретический материал для самостоятельного изучения
В курсе средней школы будут рассматриваться показательные, логарифмические, тригонометрические уравнения и неравенства. Чтобы облегчить дальнейшее изучение специальных уравнений, нужно уметь решать квадратные уравнения и неравенства, устанавливать и объяснять зависимость вида решения от его коэффициентов и дискриминанта, представлять геометрическую интерпретацию задач.
Квадратные уравнения.
На уроке будем рассматривать различные способы решения квадратных уравнений.
Как определить, сколько корней имеет уравнение, подскажет дискриминант.
Дискриминант – это число, которое находим по формуле
Если D <0 корней нет, если D = 0 один корень, если D> 0 два корня.
Если дискриминант D> 0 , корни можно найти по формуле:
Если D = 0 , то
Рассмотрите пример. Решить уравнение
Шаг 1. Выпишем коэффициенты a, b, c.
Шаг 2. Найдем дискриминант. D=16.
Шаг 3. Запишем формулу корней и подставим значения. Вычислим значения корней:
Заметим:
1.Перед решением квадратного уравнения привести его к стандартному виду.
2. Избавьтесь от минуса перед . Для этого надо умножить всё уравнение на -1.
3. Если в уравнении есть дробные коэффициенты, умножьте уравнение на общий знаменатель.
4. Проверяйте корни по теореме Виета. Это просто, когда a=1.
Рассмотрите другие формулы:
, где второй коэффициент b=2k – четное число.
Приведенное квадратное уравнение , старший коэффициент равен a= 1, проще решать по теореме Виета.
Уравнение (х-3) (х+5) =0 является квадратным. Для его решения воспользуйтесь свойством: произведение равно 0, когда один из множителей равен 0.
Осталось вспомнить, как решаются неполные квадратные уравнения. Неполные — значит один или два коэффициента равны нулю.
Для решения систем уравнений применяются все методы решения: подстановки, сложения, графический.
Рассмотрим несколько примеров:
Пример 1.
Если из одного из уравнений можно выразить х или у, применяем метод подстановки. Выразите х из первого уравнения и подставьте во второе. Решите и найдите корни.
Пример 2.
Применяем метод сложения. Выполнив сложение, получаем уравнение , далее x= ±5. Находим у= ±2. Составляем возможные пары чисел.
Записываем ответ: (5; 2), (5; -2), (-5; 2), (- 5; -2).
Пример 3. Иногда проще ввести новые переменные.
Пусть xy=u, x+y=v. Тогда систему можно записать в более простом виде:
Решение смотри в примере 1.
Часть 2. Квадратные неравенства.
Теперь, когда мы разобрали решение квадратных уравнений, переходим к решению квадратных неравенств
ax^2+ bx + c больше или меньше нуля.
Шаг 1. Запишем соответствующее неравенству квадратное уравнение и найдем его корни. Отметим корни на оси OХ и схематично покажем расположение ветвей параболы «вверх» или «вниз».
Шаг 2. Расставим на оси знаки, соответствующие знаку квадратичной функции: там, где парабола выше оси, ставим +, а там, где ниже –.
Шаг 3. Выписываем интервалы, соответствующие знаку неравенства. Если неравенство нестрогое, корни входят в интервал, если строгое не входят.
Вспомните возможные случаи расположения корней на оси и ветвей параболы в зависимости от коэффициента а и дискриминанта.
Метод интервалов упрощает схему решения. По-прежнему находим корни квадратного трехчлена, расставляем на числовой прямой. Определяем знаки на интервалах + или – по схеме:
если а>0 + — +, если а <0 — + -. Или путём подстановки произвольного значения квадратный трехчлен.
Рассмотрим несколько примеров:
D=0 все точки параболы выше оси и только одна х=2 на оси ОХ -нет решений.
D<0 коэффициент а=2>0 ветви вверх. Парабола выше оси, все значения положительны, значит х- любое число. Неравенство не имеет решений.
Далее рассмотрим схему решения системы неравенств.
Алгоритм решения системы неравенств.
1.Решить первое неравенство системы, изобразить его графически на оси x.
2.Решить второе неравенство системы, изобразить его графически на оси x.
3.Выбрать в ответ те участки, в которых решение первого и второго неравенств пересекаются. Записать ответ.
Часть 3
Теперь, когда мы разобрали решение квадратных уравнений и неравенств переходим к решению самых сложных заданий с параметрами. Если в уравнении или неравенстве некоторые коэффициенты заданы не числовыми значениями, а обозначены буквами, то они называются параметрами, а само уравнение или неравенство параметрическим.
Первый шаг в решении — найти особое значение параметра.
Второй шаг – определить допустимые значения.
Если в задаче требуется определить знаки корней квадратного уравнения, то, как правило, удобнее использовать теорему Виета.
Но прежде, чем применять теорему Виета, обязательно нужно проверить, что уравнение имеет корни! Для этого вычисляем дискриминант.
Рассмотрите примеры решения неравенства с параметром.
Графический метод решения обладает несомненным преимуществом – можно представить решение наглядно.
Для любого свойства, сформулированного на алгебраическом языке, нужно уметь давать геометрическую интерпретацию и, наоборот, по поведению графика параболы дать общую оценку коэффициентов квадратного трехчлена и его корней.
Например, если старший коэффициент квадратного трехчлена меньше 0, то ветви параболы направлены вниз. Если дискриминант больше 0, то трехчлен имеет различные действительные корни и парабола пересекает ось абсцисс в двух точках и т.д.
Мы рассмотрели лишь некоторые примеры, иллюстрирующие применение графического метода к решению квадратных уравнений и неравенств. Более подробно с методами решения квадратных уравнений, неравенств, их систем вы можете, поработав с интерактивными моделями.
Более подробно с методами решения квадратных уравнений, неравенств, их систем вы можете, поработав с интерактивными моделями.
Задания тренировочного модуля с разбором.
Пример 1.
При каких значениях параметра, а квадратное уравнение
имеет только один корень?
Находим дискриминант D=25-4∙2∙5a=25-40a. Уравнение имеет один корень, если D=0, т.е. 25-40a=0, а=5/8.
Пример 2.
Определите, на каком интервале значения квадратного трехчлена отрицательны?
Решаем неравенство: . Находим дискриминант квадратного трехчлена D= 1-4∙2∙ (-1) =1+8=9. Находим корни . Расставляем точки на числовой прямой.
Старший коэффициент а=2 ветви параболы вверх. Знаки чередуются + — +. Записываем ответ: — 0,5< х <1.
Методы решения квадратных и дробно-рациональных уравнений
Исследования методов решений квадратных и дробно рациональных уравнений
Выполнили:
Аббасов Руслан
Землянский Руслан
Голубцов Артур
Содержание
- Из истории
- Определение
- Классификация
- Способы решения
- Теорема Виета
- Проверка знаний
- Решение дробно рациональных уравнений
- Выдающаяся личность Виет
О математика. В веках овеяна ты славой, Светило всех земных светил. Тебя царицей величавой Недаром Гаусс окрестил. Строга, логична, величава, Стройна в полете, как стрела, Твоя немеркнущая слава В веках бессмертье обрела. Мы славим разум человека, Дела его волшебных рук, Надежду нынешнего века, Царицу всех земных наук. Поведать мы сегодня вам хотим Историю возникновения Того, что каждый школьник должен знать – Историю квадратных уравнений.
В веках овеяна ты славой, Светило всех земных светил. Тебя царицей величавой Недаром Гаусс окрестил. Строга, логична, величава, Стройна в полете, как стрела, Твоя немеркнущая слава В веках бессмертье обрела. Мы славим разум человека, Дела его волшебных рук, Надежду нынешнего века, Царицу всех земных наук. Поведать мы сегодня вам хотим Историю возникновения Того, что каждый школьник должен знать – Историю квадратных уравнений.
Из истории
Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до нашей эры вавилоняне. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и такие, например, полные квадратные уравнения:
Из истории
Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает по существу с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены. Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.
Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены. Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.
ОПРЕДЕЛЕНИЕ
Квадратным уравнением называется уравнение вида где a , b, c , d – заданные числа, x – переменная. Числа a, b, c носят следующие названия: a — первый коэффициент, b второй коэффициент, с — свободный член.
КЛАССИФИКАЦИЯ
Полные: ax 2 + bx + c =0 ,
где коэффициенты b и с отличны от нуля ;
Неполные: ax 2 + bx =0, ax 2 + c =0 или ax 2 =0
т.е. хотя бы один из коэффициентов b или c равен нулю;
Приведенные: x 2 + bx + c =0 ,
т. е. уравнение, первый коэффициент которого равен единице (а=1).
е. уравнение, первый коэффициент которого равен единице (а=1).
СПОСОБЫ РЕШЕНИЯ
- Решение полных квадратных уравнений
- Дискриминант
- Решение неполных квадратных уравнений
- Решение приведенного квадратного уравнения
- Графический метод решения квадратных уравнений
- Решение биквадратных уравнений
Решение полных квадратных уравнений
По формуле корней квадратного уравнения: a x 2 + b x + c =0 ,
Дискриминант
Дискриминант
при
квадратное уравнение имеет два корня
Дискриминант
при
квадратное уравнение имеет один корень
Дискриминант
при
квадратное уравнение не имеет корней
Формулы корней
Решение неполных квадратных уравнений
Если хотя бы один из коэффициентов c или b равен нулю, то квадратное уравнение называется неполным квадратным уравнением .
1.Если c =0 и b =0 , то уравнение ax 2 =0 имеет один корень x =0 ;
2.Если c =0 , то уравнение ax 2 + bx =0 имеет два корня:
3.Если b =0 , то уравнение ax 2 + c =0
при не имеет корней,
при имеет два корня
Решение приведенного квадратного уравнения
3. По теореме обратной теореме Виета
x 2 + bx + c =0
х 1 +х 2 =- b,
x 1 ×x 2 =c .
1.По формуле корней квадратного уравнения
2. Метод выделения полного квадрата
Пример . x 2 +2x-3=0
x 2 +2x=3,
x 2 +2x+1=3+1
(x+1) 2 =4
x+1=2 или x+1=-2
x 1 =1 , x 2 =-3
Графический метод решения квадратных уравнений
Чтобы получить решение квадратного уравнения графическим способом Квадратное уравнение разделяют на две функции, линейную и квадратичную. 2
2
y 2 =-(bx+c)
Графический метод решения квадратных уравнений
- Функция y1 это парабола. Функция y2 это прямая линия. Решением, корнями квадратного уравнения являются точки пересечения этих функций.
- При решении могут представиться три варианта:
- Функции имеют две точки пересечения — два корня квадратного уравнения действительны и различны между собой.
- Функции имеют одну точку пересечения — квадратное уравнение имеет только один действительный корень.
- Функции не имеют ни одной точки пересечения — тогда оба корня квадратного уравнения мнимые, комплексные числа.
Решение биквадратного уравнения
Определение : уравнение вида ax 4 + bx 2 + c =0 называют биквадратным .
- Определение : уравнение вида ax 4 + bx 2 + c =0 называют биквадратным .
- Определение : уравнение вида ax 4 + bx 2 + c =0 называют биквадратным .

Пример . 9 x 4 +5 x 2 -4=0
Обозначим x 2 = t . Тогда данное уравнение примет вид
9 t 2 +5 t -4=0
Откуда t 1 =9/4, t 2 =-1.
Уравнение x 2 =4/9 имеет корни x 1 =2/3, x 2 =-2/3 ,
а уравнение x 2 =-1 не имеет действительных корней.
Решение квадратных уравнений
Если все коэффициенты квадратного уравнения отличны от нуля, то находим дискриминант.
Если квадратное уравнение является приведенным, то можем его решить с помощью теоремы Виета.
Теорема Виета.
Если x 1 и х 2 – корни приведенного квадратного уравнения х 2 +рх+ q =0 , то х 1 +х 2 = — р , х 1 . х 2 = q .
Если коэффициент при квадрате переменной равен 1, то уравнение называется приведенным.
Решите?
1.
2.
3.
4.
5.
Проверим…
1.
так как получили число меньше нуля, следовательно, уравнение корней не имеет
Проверим…
2.
Проверим…
3.
Проверим…
4.
найдем дискриминант
так как дискриминант меньше нуля, следовательно, квадратное уравнение не имеет корней
Проверим…
5.
Решение дробно рациональных уравнений
- При решении уравнений, содержащих переменную в знаменателе дроби сначала нужно избавиться от дроби. Для этого находят наименьший общий знаменатель, и обе части уравнения умножают на этот знаменатель. Далее полученное выражение упрощают, и получается обыкновенное линейное или квадратное уравнение.
- Только нужно найти область допустимых значений выражения (ОДЗ). После того, как найдены корни уравнения, обязательно проверяем, входят ли они в ОДЗ.

- Вспомним два правила решения уравнений:
- 1) Если обе части уравнения разделить или умножить на одно и то же число, корни уравнения не изменятся.
- 2) Слагаемые можно переносить из одной части уравнения в другую с противоположным знаком .
Выдающаяся личность Виет
Франсуа Виет родился в 1540 году в городе Фонтене ле-Конт провинции Пуату. Получив юридическое образование, он в 19 лет успешно занимался адвокатской практикой в родном городе. Как адвокат Виет пользовался у населения авторитетом и уважением. Он был широко образованным человеком. В 1571 году Виет переехал в Париж и там познакомился с математиком Пьером Рамусом. Благодаря своему таланту и, отчасти, благодаря браку своей бывшей ученицы с принцем де Роганом, Виет сделал блестящую карьеру и стал советником Генриха III, а после его смерти — Генриха IV. В последние годы жизни Виет занимал важные посты при дворе короля Франции. Умер он в Париже в самом начале семнадцатого столетия. Есть подозрения, что он был убит.
Есть подозрения, что он был убит.
Квадратные уравнения: приведённые уравнения, формулы корней
Квадратное уравнение или уравнение второй степени с одним неизвестным — это уравнение, которое после преобразований может быть приведено к следующему виду:
ax2 + bx + c = 0 — квадратное уравнение,
где x — это неизвестное, а a, b и c — коэффициенты уравнения. В квадратных уравнениях a называется первым коэффициентом (a ≠ 0), b называется вторым коэффициентом, а c называется известным или свободным членом.
Уравнение:
ax2 + bx + c = 0
называется полным квадратным уравнением. Если один из коэффициентов b или c равен нулю, или нулю равны оба эти коэффициента, то уравнение представляют в виде неполного квадратного уравнения.
Приведённое квадратное уравнение
Полное квадратное уравнение можно привести к более удобному виду, разделив все его члены на a, то есть на первый коэффициент:
Затем можно избавиться от дробных коэффициентов, обозначив их буквами p и q:
| если | b | = p, а | c | = q, |
| a | a |
то получится x2 + px + q = 0.
Уравнение x2 + px + q = 0 называется приведённым квадратным уравнением. Следовательно, любое квадратное уравнение, в котором первый коэффициент равен 1, можно назвать приведённым.
Например, уравнение:
x2 + 10x — 5 = 0
является приведённым, а уравнение:
-3x2 + 9x — 12 = 0
можно заменить приведённым уравнением, разделив все его члены на -3:
x2 — 3x + 4 = 0.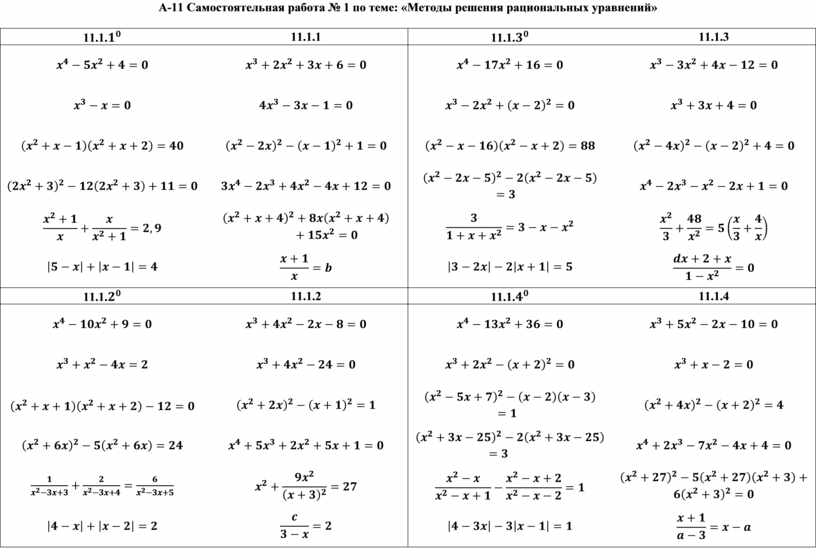
Решение квадратных уравнений
Чтобы решить квадратное уравнение, надо привести его к одному из следующих видов:
ax2 + bx + c = 0;
ax2 + 2kx + c = 0;
x2 + px + q = 0.
Для каждого вида уравнения есть своя формула нахождения корней:
| Вид уравнения | Формула корней | ||||
|---|---|---|---|---|---|
| ax2 + bx + c = 0 | |||||
| ax2 + 2kx + c = 0 | |||||
| x2 + px + q = 0 |
|
Обратите внимание на уравнение:
ax2 + 2kx + c = 0
это преобразованное уравнение ax2 + bx + c = 0, в котором коэффициент b — четный, что позволяет его заменить на вид 2k. Поэтому формулу нахождения корней для этого уравнения можно упростить, подставив в неё 2k вместо b:
Поэтому формулу нахождения корней для этого уравнения можно упростить, подставив в неё 2k вместо b:
Пример 1. Решить уравнение:
3x2 + 7x + 2 = 0.
Так как в уравнении второй коэффициент не является чётным числом, а первый коэффициент не равен единице, то искать корни будем по самой первой формуле, называемой общей формулой нахождения корней квадратного уравнения. Сначала определим, чему равны коэффициенты:
a = 3, b = 7, c = 2.
Теперь, для нахождения корней уравнения, просто подставим значения коэффициентов в формулу:
| x1 = | -2 | = — | 1 | , x2 = | -12 | = -2 |
| 6 | 3 | 6 |
Пример 2:
x2 — 4x — 60 = 0.
Определим, чему равны коэффициенты:
a = 1, b = -4, c = -60.
Так как в уравнении второй коэффициент — чётное число, то будем использовать формулу для квадратных уравнений с чётным вторым коэффициентом:
x1 = 2 + 8 = 10, x2 = 2 — 8 = -6
Ответ: 10, -6.
Пример 3.
y2 + 11y = y — 25.
Приведём уравнение к общему виду:
y2 + 11y = y — 25;
y2 + 11y — y + 25 = 0;
y2 + 10y + 25 = 0.
Определим, чему равны коэффициенты:
a = 1, p = 10, q = 25.
Так как первый коэффициент равен 1, то будем искать корни по формуле для приведённых уравнений с чётным вторым коэффициентом:
Ответ: -5.
Пример 4.
x2 — 7x + 6 = 0.
Определим, чему равны коэффициенты:
a = 1, p = -7, q = 6.
Так как первый коэффициент равен 1, то будем искать корни по формуле для приведённых уравнений с нечётным вторым коэффициентом:
x1 = (7 + 5) : 2 = 6,
x2 = (7 — 5) : 2 = 1.
Ответ: 6, 1.
Линейные и квадратные уравнения
Определение
Уравнение (с одной переменной) — это некоторое равенство двух выражений, содержащее неизвестную (переменную). \[f(x)=g(x) \qquad \qquad (1)\]Пусть для определенности все дальнейшие уравнения содержат переменную, обозначенную буквой \(x\).
Замечание
Заметим, что \(x\) — это просто некоторое число, значение которого неизвестно.
Определение
Областью определения (или областью допустимых значений, сокращенно ОДЗ) любого уравнения вида \((1)\) будем называть множество значений переменной \(x\), при которых определены (то есть не теряют смысла) функции \(f(x)\) и \(g(x)\).
Пример
Уравнение \(\dfrac {10}{x-1}=5\) определено при всех значениях переменной \(x\), кроме \(x=1\), потому что в этом случае знаменатель дроби в левой части равенства обращается в ноль. Значит, ОДЗ уравнения \(x\in (-\infty;1)\cup(1;+\infty)\).
Определение
Корнем уравнения называется то числовое значение \(x\), при котором уравнение обращается в верное равенство.
Иногда корни уравнения называют решением этого уравнения.
Например, корнем уравнения из предыдущего примера является число \(x=3\), потому как тогда уравнение принимает вид \(\dfrac{10}{3-1}=5\) или, что то же самое, \(5=5\), что является верным равенством.
Замечание
1) Заметим, что уравнение может как иметь корни, так и не иметь корней. Например, уравнение \(\dfrac 1x=0\) ни при каких значениях \(x\) не может быть верным, потому что дробь равна нулю, когда ее числитель равен нулю, а знаменатель при этом не теряет смысла. 3=64\) является \(x=4\).
3=64\) является \(x=4\).
РЕШЕНИЕ КВАДРАТИЧЕСКИХ УРАВНЕНИЙ
Примечание:
- Квадратное уравнение — это полиномиальное уравнение степени 2.
- П-образный график квадратичной кривой называется параболой.
- Квадратное уравнение имеет два решения. Либо два разных реальных решения, одно двойное действительное решение или два мнимых решения.
- Есть несколько методов, которые вы можете использовать для решения квадратного уравнения:
- Факторинг
- Завершение площади
- Квадратичная формула
- Графики
- Все методы начинаются с установки уравнения равным нулю.
Решите относительно x в следующем уравнении.
Пример 1:
Уравнение уже обнулено.
Если вы забыли, как манипулировать дробями, нажмите «Дроби» для просмотра.
Удалите все дроби, записав уравнение в эквивалентной форме
без дробных коэффициентов. В этой задаче это можно сделать с помощью
умножение обеих частей уравнения на 2.
В этой задаче это можно сделать с помощью
умножение обеих частей уравнения на 2.
Метод 1: Факторинг
Уравнение нелегко разложить на множители.Следовательно, мы не будем использовать этот метод.
Метод 2: Завершение квадрата
Добавьте 10 к обеим частям уравнения
Добавьте к обеим сторонам уравнения:
Разложите левую сторону на множители и упростите правую:
Извлеките квадратный корень из обеих частей уравнения:
Добавьте 16 к обеим сторонам уравнения:
Метод 3: квадратичная формула
Квадратичная формула:
В уравнении a — это коэффициент члена, b — коэффициент члена x , и c — постоянная.Замените 1 на a , -32 на b и -10 на c в квадратная формула и упростить.
Метод 4: построение графиков
Изобразите левую часть уравнения,
и изобразите правую часть уравнения.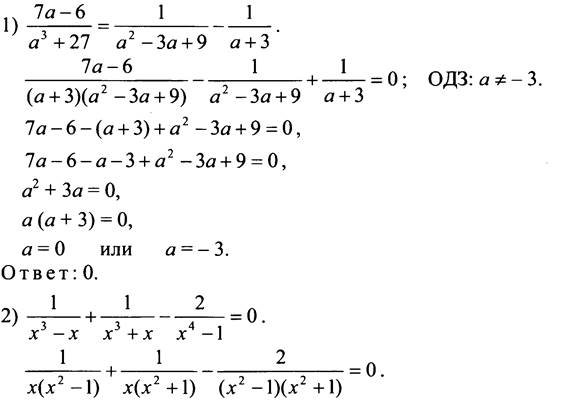 График представляет собой не что иное, как ось абсцисс. Итак, что вы будете искать
где график пересекает
ось абсцисс. Другими словами, точки пересечения по оси x — это
решения этого уравнения.
График представляет собой не что иное, как ось абсцисс. Итак, что вы будете искать
где график пересекает
ось абсцисс. Другими словами, точки пересечения по оси x — это
решения этого уравнения.
На графике видно, что есть два пересечения по оси x, одно на 32.309506 и один -0.309506.
Ответы: 32.309506, и эти ответы могут или могут не быть решениями исходных уравнений. Вы должны убедиться, что эти ответы — это решения.
Отметьте эти ответы в исходном уравнении.
Проверьте решение x = 32,309506, заменив 32,309506 в исходном
уравнение для x. Если левая часть уравнения
равна правой сторону уравнения после подстановки, вы нашли правильный отвечать.
Поскольку левая часть исходного уравнения равна правой части исходное уравнение после того, как мы подставим значение 32.309506 вместо x, тогда x = 32,309506 — это решение. Проверьте решение x = -0,309506, заменив -0,309506 в исходном
уравнение для x. Если левая часть уравнения равна правой
сторону уравнения после подстановки, вы нашли правильный
отвечать.
Если левая часть уравнения равна правой
сторону уравнения после подстановки, вы нашли правильный
отвечать.
Решения уравнения
равны 32,309506 и — 0,309506.
Комментарий: вы можете использовать точные решения, чтобы разложить исходное уравнение на множители.
С
С
Продукт
С
тогда мы могли бы сказать
Однако произведение первых членов множителей не равно
Умножение
Давайте проверим,
Если вы хотите проработать другой пример, нажмите «Пример».
Если вы хотите проверить себя, решив некоторые задачи, подобные этой
Например, нажмите «Проблема»
Если вы хотите вернуться к оглавлению уравнения, щелкните
СОДЕРЖАНИЕ
С. Домашняя страница O.S MATHematics
Домашняя страница O.S MATHematics
Вам нужна дополнительная помощь? Пожалуйста, разместите свой вопрос на нашем S.O.S. Математика CyberBoard.
Как решить это квадратное уравнение (где $ x $ представлен дробью, содержащей квадратный корень)?
Как решить это квадратное уравнение (где $ x $ представлен дробью, содержащей квадратный корень)? — Обмен математическими стекамиСеть обмена стеков
Сеть Stack Exchange состоит из 177 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.
Посетить Stack Exchange- 0
- +0
- Авторизоваться Зарегистрироваться
Mathematics Stack Exchange — это сайт вопросов и ответов для людей, изучающих математику на любом уровне, и профессионалов в смежных областях. Регистрация займет всего минуту.
Регистрация займет всего минуту.
Кто угодно может задать вопрос
Кто угодно может ответить
Лучшие ответы голосуются и поднимаются наверх
Спросил
Просмотрено 247 раз
$ \ begingroup $Если $ x- \ frac {4} {5} = \ pm \ frac {\ sqrt {31}} {5} $, как я могу найти значения a и b в следующем уравнении?
$$ 5x ^ 2 + ax + b = 0? $$
Я попытался заменить $ (\ frac {4} {5} \ pm \ frac {\ sqrt {31}} {5}) $ на $ x $ и совершенно запутался.
Создан 30 дек.
блестящий66155 серебряных знаков1010 бронзовых знаков
$ \ endgroup $ 1 $ \ begingroup $Возведите в квадрат обе стороны, умножьте обе стороны на 5 долларов, затем переместите все члены влево.2-8 х — 3 = 0. \ end {align}
Итак, $ a = -8 $ и $ b = -3 $.
Создан 30 дек.
$ \ endgroup $ 3 $ \ begingroup $ $ (x- \ frac 4 5) ^ {2} = \ frac {31} {25} $ можно записать как $ 5x ^ {2} -8x-3 = 0 $. 2-sx + p = 0 $$
с ненулевым множителем, из общеизвестного результата средней школы.2-20a}} {5} = \ frac {\ sqrt {31}} {5}
2-sx + p = 0 $$
с ненулевым множителем, из общеизвестного результата средней школы.2-20a}} {5} = \ frac {\ sqrt {31}} {5}
Из первого $ a = -8 $ и заменив во втором: $ b = -3 $
Создан 30 дек.
Маттео4,81511 золотых знаков55 серебряных знаков2121 бронзовый знак
$ \ endgroup $Не тот ответ, который вы ищете? Посмотрите другие вопросы с метками квадратичность или задайте свой вопрос.
Mathematics Stack Exchange лучше всего работает с включенным JavaScriptВаша конфиденциальность
Нажимая «Принять все файлы cookie», вы соглашаетесь с тем, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в отношении файлов cookie.
Принимать все файлы cookie Настроить параметры
10.3 Решение квадратных уравнений с использованием квадратной формулы — элементарная алгебра 2e
Цели обучения
К концу этого раздела вы сможете:
- Решать квадратные уравнения с использованием формулы корней квадратного уравнения
- Используйте дискриминант, чтобы предсказать количество решений квадратного уравнения
- Определите наиболее подходящий метод решения квадратного уравнения
Будьте готовы 10.7
Прежде чем начать, пройдите тест на готовность.
Упростить: −20−510−20−510.
Если вы пропустили эту проблему, просмотрите Пример 1.74.
Будьте готовы 10,8
Упростить: 4 + 1214 + 121.
Если вы пропустили эту проблему, просмотрите Пример 9.29.
Будьте готовы 10.9
Упростить: 128128.
Если вы пропустили эту проблему, просмотрите Пример 9.12.
Когда мы решали квадратные уравнения в последнем разделе, завершая квадрат, мы каждый раз предпринимали одни и те же шаги.К концу набора упражнений вы, возможно, задавались вопросом: «А нет ли более простого способа сделать это?» Ответ — «да». В этом разделе мы выведем и воспользуемся формулой, чтобы найти решение проблемы. квадратное уровненеие.
Мы уже видели, как решить формулу для конкретной переменной «в целом», чтобы мы проделали алгебраические шаги только один раз, а затем использовали новую формулу, чтобы найти значение конкретной переменной. Теперь мы рассмотрим этапы завершения квадрата в целом, чтобы решить квадратное уравнение для x .Может быть полезно взглянуть на один из примеров в конце последнего раздела, где мы решали уравнение вида ax2 + bx + c = 0ax2 + bx + c = 0, когда вы читаете алгебраические шаги ниже, так что вы см. их как с числами, так и «в целом».
их как с числами, так и «в целом».
| Начнем со стандартной формы квадратного уравнения и решим его для x , заполнив квадрат. | ax2 + bx + c = 0a ≠ 0ax2 + bx + c = 0a ≠ 0 |
| Изолируйте переменные члены с одной стороны. | ax2 + bx = −cax2 + bx = −c |
| Делим старший коэффициент равным 1, разделив на a. | ax2a + bax = −caax2a + bax = −ca |
| Упростить. | x2 + bax = −cax2 + bax = −ca |
| Чтобы завершить квадрат, найдите (12 · ba) 2 (12 · ba) 2 и добавьте его к обеим сторонам уравнения.  (12ba) 2 = b24a2 (12ba) 2 = b24a2 (12ba) 2 = b24a2 (12ba) 2 = b24a2 | x2 + bax + b24a2 = −ca + b24a2x2 + bax + b24a2 = −ca + b24a2 |
| Левая часть представляет собой полный квадрат, разложите его на множители. | (х + b2a) 2 = −ca + b24a2 (x + b2a) 2 = −ca + b24a2 |
| Найдите общий знаменатель правой части и запишите эквивалентных дробей с общим знаменателем. | (x + b2a) 2 = b24a2 − c · 4aa · 4a (x + b2a) 2 = b24a2 − c · 4aa · 4a |
| Упростить. | (х + b2a) 2 = b24a2−4ac4a2 (x + b2a) 2 = b24a2−4ac4a2 |
| Объедините в одну фракцию. | (х + b2a) 2 = b2−4ac4a2 (x + b2a) 2 = b2−4ac4a2 |
Используйте свойство квадратного корня. | х + b2a = ± b2−4ac4a2x + b2a = ± b2−4ac4a2 |
| Упростить. | х + b2a = ± b2−4ac2ax + b2a = ± b2−4ac2a |
| Добавьте −b2a − b2a к обеим частям уравнения. | х = −b2a ± b2−4ac2ax = −b2a ± b2−4ac2a |
| Объедините термины с правой стороны. | x = −b ± b2−4ac2ax = −b ± b2−4ac2a |
Последнее уравнение — квадратичная формула.
Квадратичная формула
Решения квадратного уравнения вида ax2 + bx + c = 0ax2 + bx + c = 0, a ≠ 0a ≠ 0 даются формулой:
x = −b ± b2−4ac2ax = −b ± b2−4ac2a Чтобы использовать квадратичную формулу, мы подставляем значения a, b, иca, b иc в выражение в правой части формулы.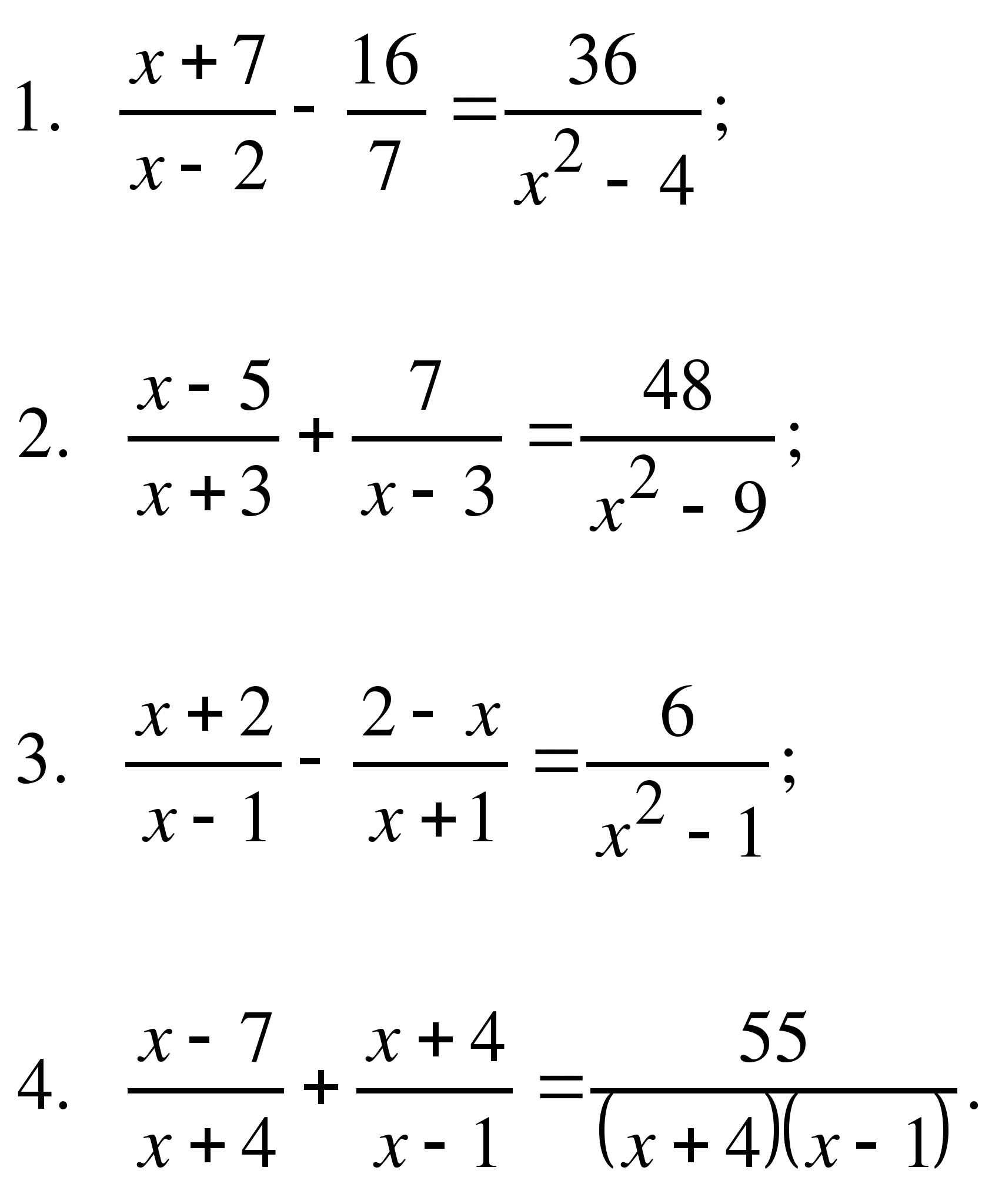 Затем мы делаем все математические вычисления, чтобы упростить выражение. Результат дает решение (я) квадратного уравнения.
Затем мы делаем все математические вычисления, чтобы упростить выражение. Результат дает решение (я) квадратного уравнения.
Пример 10.28
Как решить квадратное уравнение с помощью квадратной формулы
Решите 2×2 + 9x − 5 = 02×2 + 9x − 5 = 0, используя дискриминант.
Попробовать 10,55
Решите 3y2−5y + 2 = 03y2−5y + 2 = 0, используя дискриминант.
Попробуйте 10,56
Решите 4z2 + 2z − 6 = 04z2 + 2z − 6 = 0, используя дискриминант.
How To
Решите квадратное уравнение, используя квадратичную формулу.
- Шаг 1. Запишите квадратную формулу в стандартной форме. Определите значения aa, bb и cc.
- Шаг 2. Напишите квадратичную формулу. Затем подставьте значения aa, bb и c.c.
- Шаг 3. Упростите.
- Шаг 4. Проверьте решения.
Если вы произносите формулу во время написания каждой задачи, вы быстро запомните ее. И помните, квадратная формула — это уравнение.Убедитесь, что вы начали с «x = x =».
И помните, квадратная формула — это уравнение.Убедитесь, что вы начали с «x = x =».
Пример 10.29
Решите x2−6x + 5 = 0x2−6x + 5 = 0, используя дискриминант.
Попробуйте 10,57
Решите a2−2a − 15 = 0a2−2a − 15 = 0, используя дискриминант.
Попробовать 10,58
Решите b2 + 10b + 24 = 0b2 + 10b + 24 = 0, используя дискриминант.
Когда мы решали квадратные уравнения с помощью свойства квадратного корня, мы иногда получали ответы с радикалами. То же самое может случиться и при использовании квадратичной формулы.Если в качестве решения мы получаем радикал, окончательный ответ должен иметь радикал в его упрощенной форме.
Пример 10.30
Решите 4y2−5y − 3 = 04y2−5y − 3 = 0, используя дискриминант.
Решение
Мы можем использовать квадратичную формулу, чтобы найти переменную в квадратном уравнении, независимо от того, называется ли оно « x ».
Попробуйте 10,59
Решите 2p2 + 8p + 5 = 02p2 + 8p + 5 = 0, используя квадратичную формулу.
Попробовать 10.60
Решите 5q2−11q + 3 = 05q2−11q + 3 = 0, используя дискриминант.
Пример 10.31
Решите 2×2 + 10x + 11 = 02×2 + 10x + 11 = 0, используя квадратичную формулу.
Попробуйте 10.61
Решите 3m2 + 12m + 7 = 03m2 + 12m + 7 = 0, используя квадратичную формулу.
Попробуйте 10.62
Решите 5n2 + 4n − 4 = 05n2 + 4n − 4 = 0, используя дискриминант.
Мы не можем извлечь квадратный корень из отрицательного числа. Итак, когда мы подставляем aa, bb и cc в квадратную формулу, если величина внутри радикала отрицательна, квадратное уравнение не имеет реального решения.Мы увидим это в следующем примере.
Пример 10.32
Решите 3p2 + 2p + 9 = 03p2 + 2p + 9 = 0, используя квадратичную формулу.
Попробуйте 10.63
Решите 4a2−3a + 8 = 04a2−3a + 8 = 0, используя дискриминант.
Попробуйте 10.64
Решите 5b2 + 2b + 4 = 05b2 + 2b + 4 = 0, используя квадратичную формулу.
Квадратные уравнения, которые мы решили до сих пор в этом разделе, были записаны в стандартной форме: ax2 + bx + c = 0ax2 + bx + c = 0. Иногда нам нужно сделать некоторую алгебру, чтобы привести уравнение в стандартную форму, прежде чем мы сможем использовать квадратичную формулу.
Пример 10.33
Решите x (x + 6) + 4 = 0x (x + 6) + 4 = 0, используя дискриминант.
Попробуйте 10.65
Решите x (x + 2) −5 = 0x (x + 2) −5 = 0, используя дискриминант.
Попробуйте 10.66
Решите y (3y − 1) −2 = 0y (3y − 1) −2 = 0, используя дискриминант.
Когда мы решали линейные уравнения, если в уравнении было слишком много дробей, мы «очищали дроби», умножая обе части уравнения на ЖК-дисплей. Это дало нам возможность решить эквивалентное уравнение — без дробей.Мы можем использовать ту же стратегию с квадратными уравнениями.
Пример 10.34
Решите 12u2 + 23u = 1312u2 + 23u = 13, используя дискриминант.
Попробуйте 10.67
Решите 14c2−13c = 11214c2−13c = 112, используя дискриминант.
Попробуйте 10.68
Решите 19d2−12d = −1219d2−12d = −12, используя дискриминант.
Подумайте об уравнении (x − 3) 2 = 0 (x − 3) 2 = 0. Мы знаем из принципа нулевого произведения, что это уравнение имеет только одно решение: x = 3x = 3.
В следующем примере мы увидим, как использование квадратичной формулы для решения уравнения с полным квадратом также дает только одно решение.
Пример 10.35
Решите 4×2−20x = −254×2−20x = −25, используя дискриминант.
Решение
Вы узнали, что 4×2−20x + 254×2−20x + 25 — это полный квадрат?
Попробуйте 10.69
Решите r2 + 10r + 25 = 0r2 + 10r + 25 = 0, используя квадратичную формулу.
Попробовать 10. 70
70
Решите 25t2−40t = −1625t2−40t = −16, используя дискриминант.
Использование дискриминанта для предсказания числа решений квадратного уравнения
Когда мы решали квадратные уравнения в предыдущих примерах, иногда мы получали два решения, иногда одно решение, иногда нет реальных решений. Есть ли способ предсказать количество решений квадратного уравнения, не решая его на самом деле?
Да, количество внутри корня квадратной формулы позволяет нам легко определить количество решений.Эта величина называется дискриминантом.
Дискриминант
В квадратной формуле x = −b ± b2−4ac2ax = −b ± b2−4ac2a величина b2−4acb2−4ac называется дискриминантом.
Давайте посмотрим на дискриминант уравнений в Примере 10.28, Примере 10.32 и Примере 10.35, а также на количество решений этих квадратных уравнений.
| Квадратное уравнение (в стандартной форме) | Дискриминант b2−4acb2−4ac | Знак Дискриминанта | Количество реальных решений | |
|---|---|---|---|---|
Пример 10. 28 28 | 2×2 + 9x − 5 = 02×2 + 9x − 5 = 0 | 92−4 · 2 (−5) = 12192−4 · 2 (−5) = 121 | + | 2 |
| Пример 10.35 | 4×2−20x + 25 = 04×2−20x + 25 = 0 | (−20) 2−4 · 4 · 25 = 0 (−20) 2−4 · 4 · 25 = 0 | 0 | 1 |
| Пример 10.32 | 3п2 + 2п + 9 = 03п2 + 2п + 9 = 0 | 22−4 · 3 · 9 = −10422−4 · 3 · 9 = −104 | – | 0 |
Когда дискриминант положительный (x = −b ± + 2a) (x = −b ± + 2a) квадратное уравнение имеет два решения .
Когда дискриминант ноль (x = −b ± 02a) (x = −b ± 02a) квадратное уравнение имеет одно решение .
Когда дискриминант отрицательный (x = −b ± −2a) (x = −b ± −2a) квадратное уравнение не имеет реальных решений .
How To
Используйте дискриминант b2−4acb2−4ac, чтобы определить количество решений квадратного уравнения.
Для квадратного уравнения вида ax2 + bx + c = 0ax2 + bx + c = 0, a ≠ 0a ≠ 0,
- , если b2−4ac> 0b2−4ac> 0, уравнение имеет два решения.
- , если b2−4ac = 0b2−4ac = 0, уравнение имеет одно решение.
- , если b2−4ac <0b2−4ac <0, уравнение не имеет реальных решений.
Пример 10.36
Определите количество решений каждого квадратного уравнения:
ⓐ 2v2−3v + 6 = 02v2−3v + 6 = 0 ⓑ 3×2 + 7x − 9 = 03×2 + 7x − 9 = 0 ⓒ 5n2 + n + 4 = 05n2 + n + 4 = 0 ⓓ 9y2−6y + 1 = 09y2−6y + 1 = 0
Решение
Чтобы определить количество решений каждого квадратного уравнения, мы посмотрим на его дискриминант.
ⓐ
| 2v2−3v + 6 = 02v2−3v + 6 = 0 | |
| Уравнение в стандартной форме, укажите a , b , c . | a = 2, b = −3, c = 6a = 2, b = −3, c = 6 |
| Запишите дискриминант. | b2−4acb2−4ac |
| Подставить значения a , b , c . | (3) 2−4 · 2 · 6 (3) 2−4 · 2 · 6 |
| Упростить. | 9−48−399−48−39 |
| Поскольку дискриминант отрицательный, реальных решений уравнения отсутствуют.  |
Ⓑ
| 3×2 + 7x − 9 = 03×2 + 7x − 9 = 0 | |
| Уравнение в стандартной форме, укажите a , b , c . | a = 3, b = 7, c = −9a = 3, b = 7, c = −9 |
| Запишите дискриминант. | b2−4acb2−4ac |
| Подставить значения a , b , c . | (7) 2−4 · 3 · (−9) (7) 2−4 · 3 · (−9) |
Упростить. | 49 + 10815749 + 108157 |
| Поскольку дискриминант положительный, существует два решения уравнения. |
Ⓒ
| 5n2 + n + 4 = 05n2 + n + 4 = 0 | |
| Уравнение в стандартной форме, укажите a , b , c . | a = 5, b = 1, c = 4a = 5, b = 1, c = 4 |
| Запишите дискриминант. | b2−4acb2−4ac |
Подставить значения a , b , c . | (1) 2−4 · 5 · 4 (1) 2−4 · 5 · 4 |
| Упростить. | 1-80-791-80-79 |
| Поскольку дискриминант отрицательный, реальных решений уравнения отсутствуют. |
Ⓓ
| 9y2−6y + 1 = 09y2−6y + 1 = 0 | |
| Уравнение в стандартной форме, укажите a , b , c . | a = 9, b = −6, c = 1a = 9, b = −6, c = 1 |
| Запишите дискриминант. | b2−4acb2−4ac |
Подставить значения a , b , c . | (−6) 2−4 · 9 · 1 (−6) 2−4 · 9 · 1 |
| Упростить. | 36−36036−360 |
| Поскольку дискриминант равен 0, существует одно решение уравнения. |
Попробуйте 10.71
Определите количество решений каждого квадратного уравнения:
ⓐ 8m2−3m + 6 = 08m2−3m + 6 = 0 ⓑ 5z2 + 6z − 2 = 05z2 + 6z − 2 = 0 ⓒ 9w2 + 24w + 16 = 09w2 + 24w + 16 = 0 ⓓ 9u2−2u + 4 = 09u2−2u + 4 = 0
Попробовать 10.72
Определите количество решений каждого квадратного уравнения:
ⓐ b2 + 7b − 13 = 0b2 + 7b − 13 = 0 ⓑ 5a2−6a + 10 = 05a2−6a + 10 = 0 ⓒ 4r2−20r + 25 = 04r2−20r + 25 = 0 ⓓ 7t2−11t + 3 = 07t2−11t + 3 = 0
Определите наиболее подходящий метод для решения квадратного уравнения
Мы использовали четыре метода для решения квадратных уравнений:
- Факторинг
- Свойство с квадратным корнем
- Завершение площади
- Квадратичная формула
Вы можете решить любое квадратное уравнение с помощью квадратичной формулы, но это не всегда самый простой метод.
Как сделать
Определите наиболее подходящий метод для решения квадратного уравнения.
- Шаг 1. Сначала попробуйте Факторинг . Если квадратичные множители легко, этот метод очень быстрый.
- Шаг 2. Далее попробуйте применить свойство квадратного корня . Если уравнение соответствует форме ax2 = kax2 = k или a (x − h) 2 = ka (x − h) 2 = k, его можно легко решить, используя свойство квадратного корня.
- Шаг 3. Используйте квадратичную формулу . Любое квадратное уравнение можно решить с помощью квадратной формулы.
А как насчет метода завершения квадрата? Большинство людей считают этот метод громоздким и предпочитают не использовать его. Нам нужно было включить его в эту главу, потому что мы завершили квадрат в целом, чтобы получить квадратную формулу. Вы также будете использовать процесс завершения квадрата в других областях алгебры.
Пример 10.37
Определите наиболее подходящий метод для решения каждого квадратного уравнения:
ⓐ 5z2 = 175z2 = 17 ⓑ 4×2−12x + 9 = 04×2−12x + 9 = 0 ⓒ 8u2 + 6u = 118u2 + 6u = 11
Решение
ⓐ 5z2 = 175z2 = 17
Поскольку уравнение находится в виде ax2 = kax2 = k, наиболее подходящим методом является использование свойства квадратного корня.
ⓑ 4×2−12x + 9 = 04×2−12x + 9 = 0
Мы понимаем, что левая часть уравнения представляет собой трехчлен полного квадрата, поэтому факторинг будет наиболее подходящим методом.
ⓒ 8u2 + 6u = 118u2 + 6u = 11
Приведите уравнение в стандартную форму. 8u2 + 6u − 11 = 08u2 + 6u − 11 = 0
В то время как наша первая мысль может заключаться в том, чтобы попробовать факторинг, размышления обо всех возможностях проб и ошибок приводят нас к выбору квадратичной формулы как наиболее подходящего метода
Попробовать 10.73
Определите наиболее подходящий метод для решения каждого квадратного уравнения:
x2 + 6x + 8 = 0x2 + 6x + 8 = 0 ⓑ (n − 3) 2 = 16 (n − 3) 2 = 16 ⓒ 5p2−6p = 95p2−6p = 9
Попробовать 10,74
Определите наиболее подходящий метод для решения каждого квадратного уравнения:
ⓐ 8a2 + 3a − 9 = 08a2 + 3a − 9 = 0 ⓑ 4b2 + 4b + 1 = 04b2 + 4b + 1 = 0 ⓒ 5c2 = 1255c2 = 125
Раздел 10.3. Упражнения
Практика ведет к совершенству
Решите квадратные уравнения с помощью квадратичной формулы
В следующих упражнениях решите, используя квадратичную формулу.
105.r2−8r − 33 = 0r2−8r − 33 = 0
113.v (v + 5) −10 = 0 v (v + 5) −10 = 0
114.3w (w − 2) −8 = 03w (w − 2) −8 = 0
118.25d2−60d + 36 = 025d2−60d + 36 = 0
121.p2−6p − 27 = 0p2−6p − 27 = 0
129.2×2 + 12x − 3 = 02×2 + 12x − 3 = 0
Использование дискриминанта для прогнозирования числа решений квадратного уравнения
В следующих упражнениях определите количество решений каждого квадратного уравнения.
131.- ⓐ 4×2−5x + 16 = 04×2−5x + 16 = 0
- ⓑ 36y2 + 36y + 9 = 036y2 + 36y + 9 = 0
- ⓒ 6м2 + 3м − 5 = 06м2 + 3м − 5 = 0
- ⓓ 18n2−7n + 3 = 018n2−7n + 3 = 0
- ⓐ 9v2−15v + 25 = 09v2−15v + 25 = 0
- ⓑ 100w2 + 60w + 9 = 0100w2 + 60w + 9 = 0
- ⓒ 5c2 + 7c − 10 = 05c2 + 7c − 10 = 0
- ⓓ 15d2−4d + 8 = 015d2−4d + 8 = 0
- ⓐ r2 + 12r + 36 = 0r2 + 12r + 36 = 0
- ⓑ 8t2−11t + 5 = 08t2−11t + 5 = 0
- ⓒ 4u2−12u + 9 = 04u2−12u + 9 = 0
- ⓓ 3v2−5v − 1 = 03v2−5v − 1 = 0
- ⓐ 25p2 + 10p + 1 = 025p2 + 10p + 1 = 0
- ⓑ 7q2−3q − 6 = 07q2−3q − 6 = 0
- ⓒ 7у2 + 2у + 8 = 07у2 + 2у + 8 = 0
- ⓓ 25z2−60z + 36 = 025z2−60z + 36 = 0
Определите наиболее подходящий метод для решения квадратного уравнения
В следующих упражнениях определите наиболее подходящий метод (разложение на множители, квадратный корень или квадратная формула) для решения каждого квадратного уравнения. Не решай.
135.ⓐ x2−5x − 24 = 0x2−5x − 24 = 0 ⓑ (y + 5) 2 = 12 (y + 5) 2 = 12 ⓒ 14m2 + 3m = 1114m2 + 3m = 11
136.ⓐ (8v + 3) 2 = 81 (8v + 3) 2 = 81 ⓑ w2−9w − 22 = 0w2−9w − 22 = 0 ⓒ 4n2−10 = 64n2−10 = 6
137.ⓐ 6a2 + 14 = 206a2 + 14 = 20 ⓑ (x − 14) 2 = 516 (x − 14) 2 = 516 ⓒ y2−2y = 8y2−2y = 8
138.ⓐ 8b2 + 15b = 48b2 + 15b = 4 ⓑ 59v2−23v = 159v2−23v = 1 ⓒ (w + 43) 2 = 29 (w + 43) 2 = 29
Повседневная математика
139.Ракета запускается прямо с корабля в море. Решите уравнение 16 (t2−13t + 40) = 016 (t2−13t + 40) = 0 для tt, количества секунд, которое потребуется, чтобы ракета достигла высоты 640 футов.
140.Архитектор проектирует холл гостиницы. Она хочет иметь треугольное окно, выходящее в атриум, с шириной окна на 6 футов больше высоты. Из-за ограничений по энергопотреблению площадь окна должна составлять 140 квадратных футов. Решите уравнение 12h3 + 3h = 14012h3 + 3h = 140 для hh, высоты окна.
Письменные упражнения
141. Решите уравнение x2 + 10x = 200×2 + 10x = 200
ⓐ, заполнив квадрат
ⓑ с помощью квадратичной формулы
ⓒ Какой метод вы предпочитаете? Почему?
Решите уравнение 12y2 + 23y = 2412y2 + 23y = 24
ⓐ, заполнив квадрат
ⓑ с помощью квадратичной формулы
ⓒ Какой метод вы предпочитаете? Почему?
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела.
ⓑ Что этот контрольный список говорит вам о вашем мастерстве в этом разделе? Какие шаги вы предпримете для улучшения?
Решите квадратные уравнения по квадратичной формуле — элементарная алгебра
Цели обучения
К концу этого раздела вы сможете:
- Решите квадратные уравнения по формуле корней квадратного уравнения
- Используйте дискриминант, чтобы предсказать количество решений квадратного уравнения
- Определите наиболее подходящий метод решения квадратного уравнения
Прежде чем начать, пройдите тест на готовность.
- Упростить:.
Если вы пропустили эту проблему, просмотрите (рисунок). - Упростить:.
Если вы пропустили эту проблему, просмотрите (рисунок). - Упростить:.
Если вы пропустили эту проблему, просмотрите (рисунок).
Когда мы решали квадратные уравнения в последнем разделе, завершая квадрат, мы каждый раз предпринимали одни и те же шаги. К концу набора упражнений вы, возможно, задавались вопросом: «А нет ли более простого способа сделать это?» Ответ — «да». В этом разделе мы выведем и воспользуемся формулой, чтобы найти решение проблемы. квадратное уровненеие.
Мы уже видели, как решить формулу для конкретной переменной «в целом», чтобы мы проделали алгебраические шаги только один раз, а затем использовали новую формулу, чтобы найти значение конкретной переменной. Теперь мы рассмотрим этапы завершения квадрата в целом, чтобы решить квадратное уравнение для x . Может быть полезно взглянуть на один из примеров в конце последнего раздела, где мы решали уравнение формы, когда вы читаете алгебраические шаги ниже, поэтому вы видите их как с числами, так и со словом «в целом».’
Последнее уравнение — квадратичная формула.
Квадратичная формула
Решения квадратного уравнения вида даются формулой:
Чтобы использовать квадратичную формулу, мы подставляем значения в выражение в правой части формулы. Затем мы делаем все математические вычисления, чтобы упростить выражение. Результат дает решение (я) квадратного уравнения.
Как решить квадратное уравнение с помощью квадратной формулы
Решите, используя дискриминант.
Решите, используя дискриминант.
Решите, используя дискриминант.
Если вы произносите формулу во время написания каждой задачи, вы быстро запомните ее. И помните, квадратная формула — это уравнение. Обязательно начинайте с «».
Решите, используя дискриминант.
Решите, используя дискриминант.
Решите, используя дискриминант.
Когда мы решали квадратные уравнения с помощью свойства квадратного корня, мы иногда получали ответы с радикалами. То же самое может случиться и при использовании квадратичной формулы. Если в качестве решения мы получаем радикал, окончательный ответ должен иметь радикал в его упрощенной форме.
Решите, используя дискриминант.
Решение
Мы можем использовать квадратичную формулу, чтобы найти переменную в квадратном уравнении, независимо от того, называется ли оно « x ».
Решите, используя дискриминант.
Решите, используя дискриминант.
Решите, используя дискриминант.
Решите, используя дискриминант.
Решите, используя дискриминант.
Мы не можем извлечь квадратный корень из отрицательного числа. Итак, когда мы подставляем, и в квадратную формулу, если величина внутри радикала отрицательна, квадратное уравнение не имеет реального решения.Мы увидим это в следующем примере.
Решите, используя дискриминант.
Решите, используя дискриминант.
Решите, используя дискриминант.
Все квадратные уравнения, которые мы решили до сих пор в этом разделе, были записаны в стандартной форме,. Иногда нам нужно сделать некоторую алгебру, чтобы привести уравнение в стандартную форму, прежде чем мы сможем использовать квадратичную формулу.
Решите, используя дискриминант.
Решите, используя дискриминант.
Решите, используя дискриминант.
Когда мы решали линейные уравнения, если в уравнении было слишком много дробей, мы «очищали дроби», умножая обе части уравнения на ЖК-дисплей. Это дало нам возможность решить эквивалентное уравнение — без дробей. Мы можем использовать ту же стратегию с квадратными уравнениями.
Решите, используя дискриминант.
Решите, используя дискриминант.
Решите, используя дискриминант.
Подумайте об уравнении. Мы знаем из принципа нулевого произведения, что это уравнение имеет только одно решение:.
В следующем примере мы увидим, как использование квадратичной формулы для решения уравнения с полным квадратом также дает только одно решение.
Решите, используя дискриминант.
Решение
Вы узнали, что это идеальный квадрат?
Решите, используя дискриминант.
Решите, используя дискриминант.
Использование дискриминанта для предсказания числа решений квадратного уравнения
Когда мы решали квадратные уравнения в предыдущих примерах, иногда мы получали два решения, иногда одно решение, иногда нет реальных решений. Есть ли способ предсказать количество решений квадратного уравнения, не решая его на самом деле?
Да, количество внутри корня квадратной формулы позволяет нам легко определить количество решений.Эта величина называется дискриминантом.
Дискриминант
В квадратичной формуле величина называется дискриминантом.
Давайте посмотрим на дискриминант уравнений на (Рисунок), (Рисунок) и (Рисунок), а также на количество решений этих квадратных уравнений.
Когда дискриминант положительный квадратное уравнение имеет два решения .
Когда дискриминант ноль квадратное уравнение имеет одно решение .
Когда дискриминант отрицательный квадратное уравнение не имеет реальных решений .
Определите количество решений каждого квадратного уравнения:
ⓐⓑⓒⓓ
ⓐ нет реальных решений ⓑ 2 ⓒ 1 ⓓ нет реальных решений
Определите количество решений каждого квадратного уравнения:
ⓐⓑⓒⓓ
ⓐ 2 ⓑ нет реальных решений ⓒ 1 ⓓ 2
Определите наиболее подходящий метод для решения квадратного уравнения
Мы использовали четыре метода для решения квадратных уравнений:
- Факторинг
- Свойство с квадратным корнем
- Завершение площади
- Квадратичная формула
Вы можете решить любое квадратное уравнение с помощью квадратичной формулы, но это не всегда самый простой метод.
Определите наиболее подходящий метод решения квадратного уравнения.
- Сначала попробуйте Факторинг . Если квадратичные множители легко, этот метод очень быстрый.
- Далее попробуйте применить свойство квадратного корня . Если уравнение соответствует форме или, его можно легко решить с помощью свойства квадратного корня.
- Используйте квадратичную формулу . Любое квадратное уравнение можно решить с помощью квадратной формулы.
А как насчет метода завершения квадрата? Большинство людей считают этот метод громоздким и предпочитают не использовать его.Нам нужно было включить его в эту главу, потому что мы завершили квадрат в целом, чтобы получить квадратную формулу. Вы также будете использовать процесс завершения квадрата в других областях алгебры.
Определите наиболее подходящий метод для решения каждого квадратного уравнения:
ⓐⓑⓒ
Решение
ⓐ
Так как уравнение находится в, наиболее подходящим методом является использование свойства квадратного корня.
ⓑ
Мы понимаем, что левая часть уравнения представляет собой трехчлен полного квадрата, поэтому факторинг будет наиболее подходящим методом.
ⓒ
Приведите уравнение в стандартную форму.
В то время как наша первая мысль может заключаться в том, чтобы попробовать факторинг, размышления обо всех возможностях проб и ошибок приводят нас к выбору квадратичной формулы как наиболее подходящего метода
Определите наиболее подходящий метод для решения каждого квадратного уравнения:
ⓐⓑⓒ
коэффициент ⓑ Свойство квадратного корня ⓒ Квадратичная формула
Определите наиболее подходящий метод для решения каждого квадратного уравнения:
ⓐⓑⓒ
ⓐ Квадратичная формула ⓑ факторинг ⓒ Свойство квадратного корня
Практика ведет к совершенству
Решите квадратные уравнения с помощью квадратичной формулы
В следующих упражнениях решите, используя квадратичную формулу.
Использование дискриминанта для прогнозирования числа решений квадратного уравнения
В следующих упражнениях определите количество решений каждого квадратного уравнения.
ⓐ нет реальных решений ⓑ 1
ⓒ 2 ⓓ нет реальных решений
ⓐ 1 ⓑ нет реальных решений
ⓒ 1 ⓓ 2
Определите наиболее подходящий метод для решения квадратного уравнения
В следующих упражнениях определите наиболее подходящий метод (разложение на множители, квадратный корень или квадратная формула) для решения каждого квадратного уравнения. Не решай.
коэффициент ⓑ квадратный корень
ⓒ Квадратичная формула
коэффициент ⓑ квадратный корень
коэффициент
Повседневная математика
Ракета запускается прямо с корабля в море.Решите уравнение для количества секунд, в течение которых ракета будет находиться на высоте 640 футов.
Архитектор проектирует холл гостиницы. Она хочет иметь треугольное окно, выходящее в атриум, с шириной окна на 6 футов больше высоты. Из-за ограничений по энергопотреблению площадь окна должна составлять 140 квадратных футов. Решите уравнение для высоты окна.
Письменные упражнения
Решите уравнение
ⓐ, заполнив квадрат
ⓑ с помощью квадратичной формулы
ⓒ Какой метод вы предпочитаете? Почему?
ⓐⓑ
ⓒ ответы будут отличаться
Решите уравнение
ⓐ, заполнив квадрат
ⓑ с помощью квадратичной формулы
ⓒ Какой метод вы предпочитаете? Почему?
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела.
ⓑ Что этот контрольный список говорит вам о вашем мастерстве в этом разделе? Какие шаги вы предпримете для улучшения?
Глоссарий
- дискриминант
- В квадратной формуле величина называется дискриминантом.
Решение рациональных уравнений — ChiliMath
Рациональное уравнение — это тип уравнения, в котором используется по крайней мере одно рациональное выражение, причудливое название для дроби .Лучший подход к решению этого типа уравнения — исключить все знаменатели, используя идею ЖК-дисплея (наименьшего общего знаменателя). Таким образом, оставшееся уравнение, с которым приходится иметь дело, обычно либо линейное, либо квадратичное.
В этом уроке я хочу рассмотреть более десяти (10) рабочих примеров с разным уровнем сложности. Я считаю, что большинство из нас изучает математику, глядя на множество примеров. Вот так!
Примеры решения рациональных уравнений
Пример 1: Решите приведенное ниже рациональное уравнение и проверьте свои ответы на наличие посторонних значений.
Было бы неплохо, если бы знаменателей не было? Что ж, мы не можем просто стереть их без какого-либо правильного алгебраического шага. Подход состоит в том, чтобы найти наименьший общий знаменатель (также известный как наименьшее общее кратное) и использовать его для умножения обеих сторон рационального уравнения. Это приводит к удалению знаменателей, оставляя нам регулярные уравнения, которые мы уже знаем, как решать, такие как линейные и квадратичные. В этом суть решения рациональных уравнений.
- ЖК-дисплей 6x.Я умножу обе части рационального уравнения на 6x, чтобы избавиться от знаменателей. В любом случае, это наша цель — сделать нашу жизнь намного проще.
- У вас должно получиться примерно такое после раздачи жк.
- Я решил оставить переменную x справа. Поэтому удалите -5x слева, добавив обе стороны по 5x.
- Упростить. Теперь очевидно, как решить это одношаговое уравнение. Разделите обе стороны на коэффициент 5x.
- Ага! Окончательный ответ — x = 2 после проверки его в исходном рациональном уравнении. Это дает правдивое заявление.
Всегда возвращайте свои «решенные ответы» в исходное уравнение, чтобы исключить посторонние решения. Это критический аспект общего подхода при решении таких проблем, как рациональные уравнения и радикальные уравнения.
Пример 2: Решите приведенное ниже рациональное уравнение и проверьте свои ответы на наличие посторонних значений.
Первым шагом в решении рационального уравнения всегда является поиск «серебряной пули», известной как ЖКД. Итак, для этой проблемы найти ЖК-дисплей просто.
Поехали.
Попытайтесь выразить каждый знаменатель как уникальных степеней простых чисел, переменных и / или членов.
Умножьте вместе единицы с наивысшими показателями для каждого уникального простого числа , переменной и / или членов, чтобы получить требуемый ЖК-дисплей.
- ЖК-дисплей 9x.Распределите его по обеим сторонам уравнения, чтобы избавиться от знаменателей.
- Чтобы переменные оставались слева, вычтите обе части на 63.
- Полученное уравнение представляет собой одношаговое уравнение. Разделите обе части на коэффициент при x.
- Вот и все! Верните значение x = — \, 39 обратно в основное рациональное уравнение, и оно должно убедить вас в том, что оно работает.
Пример 3: Решите приведенное ниже рациональное уравнение и проверьте свои ответы на наличие посторонних значений.
Похоже жк уже выдан. У нас есть единственный и общий член \ left ({x — 3} \ right) для обоих знаменателей. Число 9 имеет тривиальный знаменатель 1, поэтому я не буду его учитывать. Следовательно, ЖК-дисплей должен быть \ влево ({x — 3} \ right).
- ЖК-дисплей здесь \ left ({x — 3} \ right). Используйте его как множитель к обеим сторонам рационального уравнения.
- Надеюсь, вы получите это линейное уравнение после некоторых отмен.
Распределите константу 9 в \ left ({x — 3} \ right).
- Объедините константы в левой части уравнения.
- Переместите все числа вправо, прибавив 21 к обеим сторонам.
- Неплохо. Снова возьмите за привычку проверять решенный «ответ» из исходного уравнения.
Он должен работать, так что да, окончательный ответ — x = 2.
Пример 4: Решите приведенное ниже рациональное уравнение и проверьте свои ответы на наличие посторонних значений.
Я надеюсь, что теперь вы сможете определить, какой ЖК-дисплей для этой проблемы, осмотрев. Если нет, все будет хорошо. Просто продолжайте повторять несколько примеров, и в дальнейшем это будет иметь больше смысла.
Попытайтесь выразить каждый знаменатель как уникальных степеней простых чисел, переменных и / или членов.
Умножьте вместе единицы с наивысшими показателями для каждого уникального простого числа , переменной и / или членов, чтобы получить требуемый ЖК-дисплей.
- ЖК-дисплей расположен на 4 \ влево ({x + 2} \ вправо).Умножьте на него каждую часть уравнения.
- После тщательного преобразования ЖК-дисплея в рациональное уравнение, я надеюсь, что у вас тоже есть это линейное уравнение.
Краткое примечание : Если вы когда-либо сталкивались с остатками знаменателя после умножения, это означает, что у вас неправильный ЖК-дисплей.
Теперь распределите константы в скобках с обеих сторон.
- Объедините константы в левой части, чтобы упростить его.
- На этом этапе примите решение, где сохранить переменную.
- Удерживая x слева, мы вычитаем обе части на 4.
- Вот и все. Проверьте свой ответ, чтобы убедиться в его достоверности.
Пример 5: Решите приведенное ниже рациональное уравнение и проверьте свои ответы на наличие посторонних значений.
Ориентируясь по знаменателям, ЖК-дисплей должен быть 6x. Почему?
Помните, перемножайте вместе «каждую копию» простых чисел или переменных с наибольшей степенью.
- ЖК-дисплей 6x. Распределите по обе стороны данного рационального уравнения.
- Так должно выглядеть после осторожной отмены аналогичных условий.
Укажите константу в круглых скобках.
- Переменную x можно комбинировать в левой части уравнения.
- Поскольку слева только одна константа, я оставлю переменную x на противоположной стороне.
- Итак, я вычитаю обе стороны в 5 раз.2} + 4x — 5 = \ left ({x + 5} \ right) \ left ({x — 1} \ right). Не плохо?
Поиск ЖК-дисплея как и в предыдущих задачах.
Попытайтесь выразить каждый знаменатель как уникальных степеней простых чисел, переменных и / или членов. В этом случае у нас есть члены в виде двучленов.
Умножьте вместе единицы с наивысшими показателями для каждой уникальной копии простого числа, переменной и / или членов, чтобы получить требуемый ЖК-дисплей.
- Прежде чем я распределю ЖК-дисплей по рациональным уравнениям, полностью вычеркните знаменатели.
Это помогает в отмене общих условий позже.
- Умножьте каждую сторону на ЖК-дисплей.
- Вау! Удивительно, как быстро был убран «беспорядок» исходной проблемы.
- Избавьтесь от скобок перед распределительным свойством.
У вас должно получиться очень простое уравнение.
Пример 7: Решите приведенное ниже рациональное уравнение и проверьте свои ответы на наличие посторонних значений.
Поскольку знаменатели представляют собой два уникальных бинома, логично, что ЖК-дисплей — это всего лишь их продукт.
- ЖК-дисплей находится \ left ({x + 5} \ right) \ left ({x — 5} \ right). Разложите это на рациональное уравнение.
- В результате получается произведение двух биномов с обеих сторон уравнения.
Использование метода FOIL имеет большой смысл. Это звонит в колокол?
- Я расширил обе части уравнения, используя FOIL.2}.
- Задача сводится к регулярному линейному уравнению из квадратичного.
- Чтобы изолировать переменную x с левой стороны, необходимо сложить обе стороны на 6x.
- Переместите все константы вправо.
- Наконец, разделите обе стороны на 5, и все готово.
Пример 8: Решите приведенное ниже рациональное уравнение и проверьте свои ответы на наличие посторонних значений.
Это выглядит немного устрашающе.Но если мы будем придерживаться основ, например, правильно найти ЖК-дисплей и тщательно умножить его на уравнение, мы должны понять, что можем довольно легко управлять этим «зверем».
Выражение каждого знаменателя в виде уникальной степени выражений
Умножьте каждый уникальный член с наибольшей степенью, чтобы получить ЖК-дисплей
- Выносим за скобки знаменатели.
- Умножьте обе стороны на полученный выше ЖК-дисплей.
Будьте осторожны со своими отменами.
- У вас должно получиться что-то вроде этого, если все сделано правильно.
- На следующем шаге поместите константы в круглые скобки.
С каждым шагом это становится все проще!
Я бы объединил похожие термины с обеих сторон, чтобы еще больше упростить.
- Это просто многоступенчатое уравнение с переменными с обеих сторон. Легкий!
- Чтобы оставить x слева, вычтите обе стороны на 10x.
- Переместите все чистые числа вправо.
- Вычтем обе стороны на 15.
- Простое одношаговое уравнение.
- Разделите обе части на 5, чтобы получить окончательный ответ. Опять же, не забудьте вернуть значение в исходное уравнение для проверки.
Пример 9: Решите приведенное ниже рациональное уравнение и проверьте свои ответы на наличие посторонних значений.
Давайте найдем ЖК-дисплей для этой задачи и воспользуемся им, чтобы избавиться от всех знаменателей.
Выразите каждый знаменатель в виде уникальной степени выраженности.
Умножьте каждый уникальный член на наибольшую степень, чтобы определить ЖК-дисплей.
- Полностью вынести за скобки знаменатели
- Распределите найденный выше ЖК-дисплей по данному рациональному уравнению, чтобы исключить все знаменатели.
- Мы свели задачу к очень простому линейному уравнению. В этом «волшебство» использования ЖК-дисплея.
Умножьте константы в скобки.
- Держите переменную слева, вычитая x с обеих сторон.
- Держите константы справа.
- Складываем обе части на 8, чтобы найти x. Сделанный!
Пример 10: Решите приведенное ниже рациональное уравнение и проверьте свои ответы на наличие посторонних значений.
Начнем с определения ЖК-дисплея. Выразите каждый знаменатель в виде степеней уникальных терминов. Затем умножьте выражения с наивысшими показателями для каждого уникального члена , чтобы получить требуемый ЖК-дисплей.
Итак, у нас есть
- Полностью вынесите за скобки знаменатели.
- Разделите найденный выше ЖК-дисплей на рациональное уравнение, чтобы исключить все знаменатели.
- Укажите константу в круглых скобках.
- Критический этап : Здесь мы имеем дело с квадратным уравнением. Поэтому держите все (как переменные, так и константы) на одной стороне, заставляя противоположную сторону равняться нулю.2} — 5x + 4 = \ left ({x — 1} \ right) \ left ({x — 4} \ right). Вы можете проверить это методом FOIL.
- Используйте свойство нулевого произведения, чтобы найти x.
Установите каждый коэффициент равным нулю, затем решите каждое простое одношаговое уравнение.
Опять же, всегда сверяйте решенные ответы с исходными уравнениями, чтобы убедиться, что они верны.
Практика с рабочими листамиВозможно, вас заинтересует:
Сложение и вычитание рациональных выражений
Умножение рациональных выражений
Решение рациональных неравенств
% PDF-1.4 % 221 0 объект> эндобдж xref 221 108 0000000016 00000 н. 0000004576 00000 н. 0000004713 00000 н. 0000004930 00000 н. 0000004973 00000 н. 0000005177 00000 н. 0000005408 00000 н. 0000005497 00000 н. 0000009994 00000 н. 0000014647 00000 п. 0000019217 00000 п. 0000023874 00000 п. 0000028451 00000 п. 0000033053 00000 п. 0000033811 00000 п. 0000034565 00000 п. 0000035383 00000 п. 0000035787 00000 п. 0000036168 00000 п. 0000036523 00000 п. 0000036697 00000 п. 0000036784 00000 п. 0000037246 00000 п. 0000037463 00000 п. 0000037760 00000 п. 0000037829 00000 п. 0000042458 00000 п. 0000046595 00000 п. 0000050573 00000 п. 0000053586 00000 п. 0000057011 00000 п. 0000057178 00000 п. 0000057784 00000 п. 0000058390 00000 п. 0000058513 00000 п. 0000058621 00000 п. 0000059089 00000 н. 0000059556 00000 п. 0000059699 00000 н. 0000059807 00000 п. 0000059974 00000 н. 0000060443 00000 п. 0000060911 00000 п. 0000061034 00000 п. 0000061142 00000 п. 0000061628 00000 п. 0000062122 00000 п. 0000062245 00000 п. 0000062353 00000 п. 0000062988 00000 п. 0000063111 00000 п. 0000063219 00000 п. 0000063319 00000 п. 0000063390 00000 п. 0000063487 00000 п. 0000063559 00000 п. 0000063615 00000 п. 0000063718 00000 п. 0000063774 00000 п. 0000063877 00000 п. 0000063933 00000 п. 0000064098 00000 п. 0000064154 00000 п. 0000064278 00000 н. 0000064334 00000 п. 0000064452 00000 п. 0000064508 00000 п. 0000064628 00000 п. 0000064684 00000 п. 0000064822 00000 п. 0000064878 00000 п. 0000065008 00000 п. 0000065064 00000 п. 0000065189 00000 п. 0000065245 00000 п. 0000065372 00000 п. 0000065428 00000 п. 0000065539 00000 п. 0000065595 00000 п. 0000065723 00000 п. 0000065779 00000 п. 0000065926 00000 п. 0000065982 00000 п. 0000066112 00000 п. 0000066168 00000 п. 0000066284 00000 п. 0000066340 00000 п. 0000066444 00000 п. 0000066500 00000 п. 0000066552 00000 п. 0000066604 00000 п. 0000066657 00000 п. 0000066711 00000 п. 0000066763 00000 п. 0000066815 00000 п. 0000066867 00000 п. 0000066919 00000 п. 0000066971 00000 п. 0000067023 00000 п. 0000067075 00000 п. 0000067127 00000 п. 0000067179 00000 п. 0000067231 00000 п. 0000067283 00000 п. 0000067335 00000 п. 0000067383 00000 п. 0000067431 00000 п. 0000002456 00000 н. трейлер ] >> startxref 0 %% EOF 328 0 obj> поток # | LmhyOec> & ȡE6> T6h4n {F FN {30G ڭ N3h3 ؐ X a [j̷ ‘]% _f * q msldw’Z6.вуЛ! rwg̟RkuT @ CotO (u «# cB_D # f.u- @ eHQ?, EmF] b \ o.% WHrlV]} EK
Произошла ошибка при настройке вашего пользовательского файла cookie
Произошла ошибка при настройке вашего пользовательского файла cookieЭтот сайт использует файлы cookie для повышения производительности. Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка вашего браузера для приема файлов cookie
Существует множество причин, по которым cookie не может быть установлен правильно. Ниже приведены наиболее частые причины:
- В вашем браузере отключены файлы cookie.Вам необходимо сбросить настройки своего браузера, чтобы он принимал файлы cookie, или чтобы спросить вас, хотите ли вы принимать файлы cookie.
- Ваш браузер спрашивает вас, хотите ли вы принимать файлы cookie, и вы отказались. Чтобы принять файлы cookie с этого сайта, нажмите кнопку «Назад» и примите файлы cookie.
- Ваш браузер не поддерживает файлы cookie. Если вы подозреваете это, попробуйте другой браузер.
- Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г., браузер автоматически забудет файл cookie.Чтобы исправить это, установите правильное время и дату на своем компьютере.
- Вы установили приложение, которое отслеживает или блокирует установку файлов cookie. Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу.Чтобы предоставить доступ без файлов cookie потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файле cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в cookie; никакая другая информация не фиксируется.
Как правило, в cookie-файлах может храниться только информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта.Например, сайт не может определить ваше имя электронной почты, пока вы не введете его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступа к остальной части вашего компьютера, и только сайт, который создал файл cookie, может его прочитать.
.





