Для чего нужен определитель матрицы: О том, как правильно понимать определитель матрицы / Хабр

14) Определитель произведения матриц

Определи́тель (или детермина́нт) — одно из основных понятий линейной алгебры. Определитель матрицы является многочленом от элементов квадратной матрицы (то есть такой, у которой количество строк и столбцов равно). В общем случае матрица может быть определена над любым коммутативным кольцом, в этом случае определитель будет элементом того же кольца.

Определитель матрицы А обозначается как: det(A), |А| или Δ(A).

Определение через разложение по первой строке

Схема расчета определителя матрицы .

Для матрицы первого порядка детерминантом является сам единственный элемент этой матрицы:

Для матрицы детерминант определяется как

Для матрицы определитель задаётся рекурсивно:

, где — дополнительный минор к элементу . Эта формула называется разложением по строке.

В частности, формула вычисления определителя матрицы такова:

Свойства определителей

— Определитель — кососимметричная полилинейная функция строк (столбцов) матрицы. Полилинейность означает, что определитель линеен по всем строкам (столбцам): , где и т. д. — строчки матрицы, — определитель такой матрицы.

— При добавлении к любой строке (столбцу) линейной комбинации других строк (столбцов) определитель не изменится.

— Если две строки (столбца) матрицы совпадают, то её определитель равен нулю.

— Если две (или несколько) строки (столбца) матрицы линейно зависимы, то её определитель равен нулю.

— Если переставить две строки (столбца) матрицы, то её определитель умножается на (-1).

— Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя.

— Если хотя бы одна строка (столбец) матрицы нулевая, то определитель равен нулю.

— Сумма произведений всех элементов любой строки на их алгебраические дополнения равна определителю.

— Сумма произведений всех элементов любого ряда на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю.

— Определитель произведения квадратных матриц одинакового порядка равен произведению их определителей (cм. также формулу Бине-Коши).

— С использованием индексной нотации определитель матрицы 3×3 может быть определён с помощью

символа Леви-Чивита из соотношения:

17) Многочлены от одного неизвестного и операции над ними

Многочлены от одного неизвестного. Общий вид уравнения n-ной степени (где n некоторое положительное число) есть: a0xN+a1x(N-1)+…+a(n-1)x+an=0. — многочленом n-ной степени от неизвестного х. Многочленом называется лишь выражение вида: a0xN+a1x(N-1)+…+a(n-1)x+an. то есть лишь сумма целых неотрицательных степеней неизвестного x, взятых с некоторыми числовыми коэффициентами. В частности, мы не будем считать многочленами такие выражения, которые содержат неизвестное x с отрицательными или дробными показателями. Для сокращенной записи многочленов употребляются символы f(x), g(x) и так далее. Деление многочленов. Теория многочленов в определенном отношении похожа на теорию целых чисел, хотя внешне эти две теории не имеют ничего общего. Внутренняя же близость, схожесть этих теорий объясняется тем, что для многочленов, так же как и для целых чисел, можно определить деление и, что еще более важно, деление с остатком. f(x) ,g(x)/=0.q(x).Многочлен делится на многочлен , если существует такой многочлен , что выполняется равенство: f(x)=g(x)q(x). Для многочленов, как и для целых чисел, существует алгоритм деления с остатком.

Теорема о делении с остатком. Для любых двух многочленов f(x) и g(x) можно найти такие многочлены q(x) и r(x , что f(x)=g(x)q(x)+r(x), причем степень r(x) меньше степени g(x) или же r(x)=0. Многочлены q(x) и r(x), удовлетворяющие этому условию, определяются однозначно. f(x)-r1(x), s(x)=r1(x)-r(x). Если разности f(x)-r(x) и обе делятся наg(x), то их разность также делится наg(x). Если бы многочлен s(x) был ненулевым, то он имел бы степень меньшую, чем g(x), и не мог бы тогда делится наg(x). r1(x)=r(x) .Следовательно, s(x)=0, так что . В практической деятельности для нахождения частного и остатка применяют способ вычисления, называемый «деление углом». Деление многочлена на многочлен с остатком. Теорема 2.3 Для любого полинома f(x) и любого полинома g(x) = 0 существуют полиномы q(x) и r(x), удовлетворяющие двум условиям: f(x) = g(x)q(x) + r(x) и deg r(x) < deg g(x) Полиномы q(x) и r(x) определяются однозначно. Полиномы q(x) и r(x) называют соответственно частным и остатком от деления f(x) на g(x). В частности, если здесь положить g = x − λ, то r- константа и мы получаем в Теорема 2.4 (Безу) Значение полинома f(x) в точке λ равно остатку от деления f(x) на λ: f(λ) = r. На практике деление с остатком выполняют ¾уголком¿, однако част- ный случай деления многочлена p(x) = a0xn + a1xn−1 + … + an−1x + an на двучлен x−λ удобнее осуществлять по схеме Горнера, даже если нам нужен только лишь остаток от деления, то есть значение p(λ). Схема получается простым сравнением коэффициентов при одинаковых степенях при раскрытии скобок в правой части тождества a0xN + a1x(N-1) + . . . + an = (x − λ)(b0x(N−1)+ b1x(N−2) + . . . + bn−1) + r Делители многочлена .Делитель многочлена f(x) — многочлен g(x), такой, что f(x) = g(x)q(x). Наибольший общий делитель двух многочленов. Наибольший общий делитель многочленов f(x) и g(x) — такой их общий делитель d(x), который делится на любой другой их общий делитель. Алгоритм Евклида (алгоритм последовательного деления) нахождения наибольшего общего делителя многочленов f(x) и g(x): f(x)=g(x)q1(x)+r1(x), g(x)=r1(x)q2(x)+r2(x), r1(x)=r2(x)q3(x)+r3(x), ………………………………. . r(k-3)(x)=r(k-2)(x)+r(k-1)(x), r(k-2)(x)=r(k-1)(x)qk(x)+rk(x), r(k-1)(x)=rk(x)q(k+1)(x). Тогда rk(x) — наибольший общий делитель f(x) и g(x).

Гаджеты недели 13 ноября 2017 года

В этом выпуске: зубная щетка Be. не нуждается в электричестве; стакан Vocktail обманет вкусовые рецепторы; послушный термос Muggino, а также другие занимательные гаджеты.

 

Бутылка Quartz обезвредит бактерии

Если верить ученым-физиологам, то вода — это важнейшая составная часть организма, удельный вес которой достигает 70 процентов. Поэтому неудивительно то, что создаются различные гаджеты, цель которых улучшить качество потребления жидкости человеком. Вот, например, на ресурсе Kickstarter вполне успешно собирают средства для выпуска на рынок бутылки Quartz. Данный гаджет способен помощью ультрафиолетового излучения очищать воду от вредоносных бактерий. Ультрафиолетовая лампочка встроена в крышку Quartz, она испускает ультрафиолетовый свет с длиной волны 260 нанометров — этого достаточно для того, чтобы уничтожить до 99. 9999% всех известных бактерий. Для активирования лампы, достаточно нажать на специальную кнопку на крышке бутылки. После этого начнется излучение, которое продлится минуту.

Сообщается, что даже без участия человека Quartz станет автоматически обрабатывать жидкость внутри себя — каждые четыре часа. Встроенный аккумулятор прослужит примерно два месяца без подзарядки, для которой применяется USB-кабель. Вместимость Quartz составляет 525 миллилитров. Помимо обеззараживания гаджет способен выступать в роли обыкновенного термоса. Цена Quartz для участников проекта составит от $59, а вот в рознице бутылка будет стоить дороже — $100. Корпус Quartz доступен в пяти цветах: черный, синий, голубой, розовый и серый (https://www.kickstarter.com/).

 

“Послушный” термос Muggino

А вот на краудфандинговой платформе Indiegogo собирают денежные средства для создания умного термоса Muggino. Он создан в виде большой кружки высотой 21 сантиметр, оснащенной ручкой, чтобы было удобнее разливать напиток. Muggino способен не только сохранять, но и поддерживать нужную температуру налитой в него жидкости. То есть с помощью мобильного приложения владелец термоса задает определенную температуру, которая будет удерживаться до отмены команды. Диапазон возможных температур — от 0 до 99 градусов по Цельсию. Muggino даже умеет запоминать указанные ранее температуры разных видов жидкости, и для включения обогревания человеку достаточно коснуться к корпусу термоса два раза, а для активации охлаждения — три раза. Вместимость гаджета составляет 355 миллилитров.

А еще термос Muggino способен выступать в роли пауэрбанка, то есть к нему можно подключать для зарядки мобильные девайсы. Электронная часть термоса состоит из Bluetooth-модуля, аккумулятора и термоэлектрического генератора. Последний нужен для того, чтобы преобразовывать тепло от горячих жидкостей в электричество для подзарядки собственного аккумулятора. Заряжать Muggino можно через адаптер от электрической сети, используя интерфейс USB. По предзаказу термос Muggino доступен за $79, но на рынке его стоимость вырастет до $130.

 

Vocktail — безопасный обман

Продолжаем тему особенностей хранения и принятия человеком жидкостей. Сотрудники Сингапурского Национального университета показали уникальную разработку — стакан, который способен изменять органолептические свойства налитой жидкости. Его назвали очень красиво — Vocktail. Неважно, что вы налили в стакан, ведь встроенные электроды сами “определят” уровень солености либо сладости напитка, а светодиоды — цвет напитка. Кроме того, специальная трубочка, размещенная в стакане, создаст аромат и степень газированности жидкости. В результате даже простую воду можно будет пить словно газировку! Конечно, это будет обман организма, но зато безвредный, ведь не всем по состоянию здоровья допустимо потреблять сладкие и газированные напитки. Разработанное мобильное приложение позволит создавать новые вкусы, а также делиться ими с родными или близкими.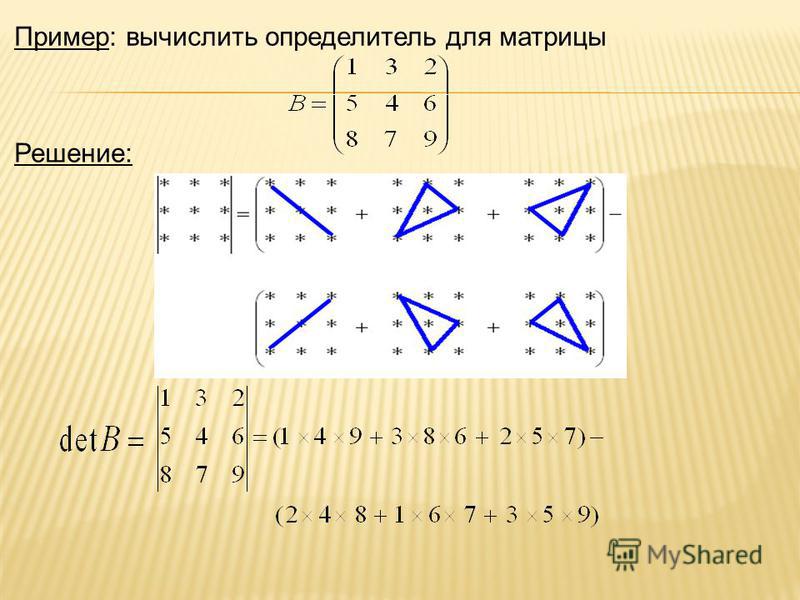 Будущее из “Матрицы” уже рядом…

 

Зубная щетка Be., свободная от электричества

После выпитой кружки кофе или стакана газированного напитка неплохо бы почистить зубы и полость рта. Поможет в этом гаджет со странным названием Be. Такое название получилось от сложения начальных букв двух английских слов: Beyond и Electriс, то есть “за пределами электричества”. И действительно, Be. представляет собой зубную щетку, которой не нужна встроенная батарея для свой работы. Для начала функционирования достаточно два раза прокрутить колесико у основания корпуса, а затем нажать на кнопку включения. Внутри Be. расположены две пружины, которые разжимаясь дают кинетическую энергию. Этой энергии хватит на 120 секунд процесса очистки на скорости 40 тысяч оборотов в минуту.

После завершения процесса чистки Be. подаст звуковой сигнал. Очень удобно, ведь данная щетка не требует ни зарядной станции, ни смены батареек… в общем, — полная свобода и возможность в любом месте быстро и легко почистить зубы. В комплекте прилагаются три сменных насадки. И еще один немаловажный момент — все компоненты Be выполнены из биоразлагаемых материалов. Отходов в виде аккумуляторных батареек тоже нет. Стоимость Be. сейчас составляет всего $49 (https://www.kickstarter.com).

 

NarcoScan: самый маленький определитель наркотиков

Завершит наш обзор изобретение финских специалистов из компании Spectral Engines. Это первый в мире компактный сканер для определения наркотических вещества. Гаджет получил название NarcoScan и его действительно можно уместить в ладони. Вес устройства составляет несколько сотен граммов, так что в сравнению с аналогами, продающимися на рынке, NarcoScan в десятки раз компактнее и, что немаловажно, дешевле. Таких показателей удалось добиться за счет того, что значительную часть работы за сканер выполняет смартфон. Именно он заменяет NarcoScan и процессор, и дисплей. Наличие наркотических веществ даже в минимальной концентрации определяется за счет инфракрасной спектроскопии. Полученная информация мгновенно поступает в облачный сервис, где обрабатывается с помощью специальных алгоритмов, разработанных Spectral Engines. После анализа данные отправляются в мобильное приложение и затем высвечиваются на экране смартфона. Сообщается, что на всё про всё NarcoScan затрачивает считанные секунды, определяя героин, кокаин или амфетамин. Список определяемых наркотических веществ будет расширяться и обновляться ( https://newatlas.com).

Линейная алгебра — интуитивно понятная математика

К настоящему моменту вы уже заметили тему во всех предыдущих разделах. Преобразование может либо сопоставить все в n-мерном пространстве где-то еще в этом n-мерном пространстве, либо сжать это n-мерное пространство в пространство более низкого измерения, такое как линия или плоскость.

Вы, вероятно, также оцените, что некоторые преобразования сжимают или расширяют пространство больше, чем другие. Для простых изменений единичных векторов довольно очевидно, сколько пространства сжимается или расширяется.

Для других преобразований не так очевидно, сколько места сжимается или расширяется.

В любом случае, однако, есть вычисление, которое мы можем сделать, чтобы выяснить, сколько места в целом сжато или расширено, независимо от других эффектов преобразования. Результат этого вычисления называется определителем.

Чтобы интерпретировать определитель, мы можем подумать о том, что происходит с квадратом 1×1 в случае 2D или с объемом 1x1x1 в случае 3D. Фактор, на который этот квадрат или объем имеет большую площадь или объем, является определителем. Поскольку преобразование является линейным, любая другая площадь или объем будут изменяться с тем же коэффициентом.

Теперь, что касается вычисления этой штуки — давайте начнем с 2D случая.

x=’ role=»presentation» tabindex=»0″>x=x=

y=’ role=»presentation» tabindex=»0″>y=y=

Когда мы имеем дело только с квадратами, это это довольно просто — это просто базовая геометрия средней школы — ширина ×’ role=»презентация» tabindex=»0″>×× высота. Определитель — это буквально площадь, определяемая масштабом каждого из двух базисных векторов.

Вы можете подумать, что выполнение более сложных действий, таких как сдвиг или вращение, усложнит задачу, но, как оказалось, это не так.

x’ role=»presentation» tabindex=»0″>xx = 1.00 y’ role=»presentation» tabindex=»0″>yy=

x’ role=»presentation» tabindex=»0″>xx = 0,00 y’ role=»presentation» tabindex=»0″>yy = 1,00

Несмотря на то, что эта форма существенно меняется, определитель преобразования по-прежнему равен 1. Причина этого в том, что мы можем представить, что единичный квадрат растягивается до прямоугольника, вдвое превышающего его размер, но затем нам нужно вычесть пустые прямоугольные треугольники на обоих концах, которые растут так же быстро, как и этот прямоугольник.

Все становится немного интереснее, когда у нас есть сдвиги в двух направлениях.

x’ role=»презентация» tabindex=»0″>xx = 1,00 y’ role=»презентация» tabindex=»0″>yy=

x’ role=»презентация» tabindex=»0″>xx= y’ role=»presentation» tabindex=»0″>yy = 1,00

При этом преобразовании сдвиг по оси x и сдвиг по оси y равен, так что преобразованные базисные векторы сходятся в точке. Обратите внимание, как при этом сама область становится все меньше и меньше, несмотря на то, что величина наших базисных векторов увеличивается. Однако, если мы масштабируем один из базисных векторов, обратите внимание, что они больше не будут сходиться в одной и той же точке:

x’ role=»presentation» tabindex=»0″>xx = 1.00 y’ role=»presentation» tabindex=»0″>yy=

x’ role=»presentation» tabindex=»0″>xx= y’ role=»presentation» tabindex=»0″>yy=

С учетом этих интуитивных представлений мы должны без труда сказать, что детерминант в двух измерениях как-то связан с соотношением между левой и правой диагональю. По мере роста произведения левой диагонали общий масштабный коэффициент для площади, затронутой преобразованием, увеличивается, потому что базисные векторы удаляются друг от друга все дальше и дальше. По мере того, как произведение правой диагонали растет, оно на самом деле сжимается, потому что базисные векторы сближаются друг с другом.

Таким образом, в целом определяющим фактором является разница между факторами роста (левая диагональ) и коэффициентами сжатия (правая диагональ).

Поэтому неудивительно, что мы можем представить определитель матрицы следующим образом:

[abcd]

‘ role=»presentation» tabindex=»0″>[abcd][abcd]

следующим образом формула:

ad−bc

‘ role=»presentation» tabindex=»0″>ad-bcad-bc

Как насчет обобщения на многомерное пространство? Для трехмерного пространства мы могли бы представить себе объем, состоящий из трех двумерных граней, одна вдоль yz’ role=»presentation» tabindex=»0″>yzyz в точке x=0′ role=»presentation» tabindex=»0 «>x=0x=0, один по xz’ role=»presentation» tabindex=»0″>xzxz по y=0′ role=»presentation» tabindex=»0″>y=0y=0 и один по xy’ роли =»презентация» tabindex=»0″>xyxy в z=0′ role=»презентация» tabindex=»0″>z=0z=0.

Вы заметили что-то странное в этой визуализации? Кажется, что плоскость вдоль их’ role=»presentation» tabindex=»0″>yzyz обращена в отрицательном направлении. Давайте посмотрим на матрицу в этот момент.

[100010001]

‘ role=»presentation» tabindex=»0″>⎡⎢⎣100010001⎤⎥⎦[100010001]

Напомним, что эта матрица 3×3 может быть описана как набор плоскостей, каждая из которых имеет двухкомпонентные базисные векторы. Если мы пройдем по первой строке, заметим, что во второй и третьей строках есть три возможных матрицы 2×2.

x=1,yz=’ роль=»презентация» tabindex=»0″>x=1,yz=x=1,yz=[1001]’ роль=»презентация» tabindex=»0″>[1001] [1001]

y=0,xz=’ роль=»презентация» tabindex=»0″>y=0,xz=y=0,xz=[0001]’ роль=»презентация» tabindex=»0″> [0001][0001]

z=0,xy=’ role=»presentation» tabindex=»0″>z=0,xy=z=0,xy=[0100]’ role=»presentation» tabindex=» 0″>[0100][0100]

Обратите внимание, что для каждого из них значение в первой строке является масштабным коэффициентом, соответствующий определитель 2×2 также является масштабным коэффициентом. Таким образом, у нас есть три разных коэффициента масштабирования, а также три разных игровых области, каждая из которых дает нам объем 3×3. Конечно, обратите внимание, что в этом случае громкость y’ role=»presentation» tabindex=»0″>yy и z’ role=»presentation» tabindex=»0″>zzvolumes равна нулю.

x=’role=»presentation» tabindex=»0″>x=x=detyz=1′ role=»presentation» tabindex=»0″>detyz=1detyz=1, →1′ role=» презентация» tabindex=»0″>→1→1

y=0′ role=»презентация» tabindex=»0″>y=0y=0, detxz=0′ role=»презентация» tabindex=»0″> detxz=0detxz=0, →0′ role=»презентация» tabindex=»0″>→0→0

z=0′ role=»презентация» tabindex=»0″>z=0z=0, detxy=0′ role=»презентация» tabindex=»0″>detxy=0detxy=0, →0′ role=»презентация» tabindex=»0″>→0→0

Что произойдет, если мы начнем масштабировать по оси, отличной от оси x’ role=»presentation» tabindex=»0″>xx? Что ж, определитель (и, следовательно, площадь) плоскости 2×2 будет увеличиваться, и поэтому объем будет увеличиваться, даже несмотря на то, что масштабный коэффициент x’ role=»presentation» tabindex=»0″>xx никогда не увеличивается.

x=1′ role=»presentation» tabindex=»0″>x=1x=1, detyz=’ role=»presentation» tabindex=»0″>detyz=detyz=1.00, →1′ роль =»презентация» tabindex=»0″>→1→1

y=0′ role=»presentation» tabindex=»0″>y=0y=0, detxz=0′ role=»presentation» tabindex=»0″>detxz=0detxz=0, →0′ role=»презентация» tabindex=»0″>→0→0

z=0′ role=»презентация» tabindex=»0″>z=0z=0, detxy=0′ role=»презентация» tabindex=» 0″>detxy=0detxy=0, →0′ role=»presentation» tabindex=»0″>→0→0

Хорошо, давайте немного усложним. Что произойдет, если мы сдвинем плоскость xz’ role=»presentation» tabindex=»0″>xzxz?

x=1′ role=»presentation» tabindex=»0″>x=1x=1, detyz=1′ role=»presentation» tabindex=»0″>detyz=1detyz=1, →1′ role=»презентация» tabindex=»0″>→1→1

y=0′ role=»презентация» tabindex=»0″>y=0y=0, detxz=0′ role=»презентация» tabindex=» 0″>detxz=0detxz=0, →0′ role=»презентация» tabindex=»0″>→0→0

z=0′ role=»презентация» tabindex=»0″>z=0z =0, detxy=0′ role=»presentation» tabindex=»0″>detxy=0detxy=0, →0′ role=»presentation» tabindex=»0″>→0→0

Как и в случае 2D, площадь единичного куба, преобразуемая здесь, не меняется. По мере того, как он растет ближе к оси x, мы просто убираем эквивалентное количество объема с каждой стороны. Это можно визуализировать ниже.

x=1′ role=»presentation» tabindex=»0″>x=1x=1, detyz=1′ role=»presentation» tabindex=»0″>detyz=1detyz=1, →1′ role=»презентация» tabindex=»0″>→1→1

y=’ role=»презентация» tabindex=»0″>y=y=0, detxz=0′ role=»презентация» tabindex=»0 «>detxz=0detxz=0, →0′ role=»презентация» tabindex=»0″>→0→0

z=0′ role=»презентация» tabindex=»0″>z=0z=0, detxy=0′ role=»презентация » tabindex=»0″>detxy=0detxy=0, →0′ role=»presentation» tabindex=»0″>→0→0

Аналогично 2D-случаю, если мы сдвигаем роль xy =»presentation» tabindex=»0″>xyxy и компонентов yx’ role=»presentation» tabindex=»0″>yxyx объем фактически начнет схлопываться во что-то очень похожее на самолет. Вы видите, почему? Посмотрите, что происходит с базисными векторами.

x=1′ role=»presentation» tabindex=»0″>x=1x=1, detyz=1′ role=»presentation» tabindex=»0″>detyz=1detyz=1, →1′ role=»презентация» tabindex=»0″>→1→1

y=’ role=»презентация» tabindex=»0″>y=y=, detxz=’ role=»презентация» tabindex=»0″> detxz=detxz=0. 00, →’ role=»презентация» tabindex=»0″>→→0.00

z=0′ role=»презентация» tabindex=»0″>z=0z=0, detxy=0′ role=»презентация» tabindex=»0 «>detxy=0detxy=0, →0′ role=»presentation» tabindex=»0″>→0→0

Однако мы еще не закончили. Что произойдет, если вы добавите сдвиг в плоскости xz’ role=»presentation» tabindex=»0″>xzxz?

x=1′ role=»presentation» tabindex=»0″>x=1x=1, detyz=1′ role=»presentation» tabindex=»0″>detyz=1detyz=1, →1′ role=»презентация» tabindex=»0″>→1→1

y=’ role=»презентация» tabindex=»0″>y=y=, detxz=’ role=»презентация» tabindex=»0″> detxz=detxz=0.00, →’ role=»презентация» tabindex=»0″>→→0.00

z=0′ role=»презентация» tabindex=»0″>z=0z=0, detxy=’ role=»презентация» tabindex=»0″ >detxy=detxy=0, →0′ role=»presentation» tabindex=»0″>→0→0

Вы заметите, что, несмотря на то, что мы добавили сдвиг на плоскости xz’ role=»presentation» tabindex=»0″>xzxz, два базиса векторы по-прежнему оказывались компланарными, а не коллинеарными. Так что у нас все-таки остался самолет.

На этот раз мы добавим дополнительный сдвиг в плоскости zx’ role=»presentation» tabindex=»0″>zxzx.

x=1′ role=»presentation» tabindex=»0″>x=1x=1, detyz=1′ role=»presentation» tabindex=»0″>detyz=1detyz=1, →1′ role=»презентация» tabindex=»0″>→1→1

y=’ role=»презентация» tabindex=»0″>y=y=, detxz=’ role=»презентация» tabindex= «0»>detxz=detxz=0.00, →’ role=»презентация» tabindex=»0″>→→0.00

z=’ role=»presentation» tabindex=»0″>z=z=, detxy=’ role=»presentation» tabindex=»0″>detxy =detxy=0, →0′ role=»presentation» tabindex=»0″>→0→0

Теперь том в конечном итоге становится перевернутой и искаженной версией самого себя, так что у него есть отрицательный объем, как бы вывернутый наизнанку.

С этими интуитивными предположениями мы должны быть в состоянии найти алгоритм для определителя 3×3 относительно приемлемым. Мы проходим через первую строку и берем субдетерминант yz’ role=»presentation» tabindex=»0″>yzyz во второй и третьей строках. Напомним, что скалярное значение в первой строке как бы придает объем области в другом измерении. Затем мы вычитаем масштабированный субдетерминант y’ role=»presentation» tabindex=»0″>yy, примененный к xy’ role=»presentation» tabindex=»0″>xyxy, поскольку это просто сворачивало пространство в плоскость. и делает общий объем меньше. Затем скалярное значение z’ role=»presentation» tabindex=»0″>zz, примененное к xy’ role=»presentation» tabindex=»0″>xyxy, снова увеличивает общий объем, поэтому мы добавляем это.

Или, в более общем случае, для матрицы 3×3 вида: −b×det(dfgi)+c×det(dehh)

‘ role=»presentation» tabindex=»0″>a×det(efhi)−b×det(dfgi)+c× det(dehh)a×det(efhi)−b×det(dfgi)+c×det(dehh)

Как оказалось, этот же алгоритм можно использовать для любой строки или столбца, применяя их к соответствующим субдетерминантам, хотя особое внимание следует обратить на то, отрицается ли этот субдетерминант в общем уравнении. Общее правило для 3×3 выглядит примерно так:

[+−+−+−+−+]

‘ role=»presentation» tabindex=»0″>⎡⎢⎣+-+-+-+-+⎤ ⎥⎦[+-+-+-+-+]

Правило для матрицы 4×4 или даже матрицы n×n’ role=»presentation» tabindex=»0″>n×nn×n очень похоже — оно просто рекурсивно определяется в терминах скаляра по сравнению с другими субдетерминантами. Что имеет смысл, если вы помните, как определяется сама размерность. Плоскость — это просто линия всех возможных вертикальных линий. Объем — это просто линия каждой возможной плоскости и так далее.

Теперь вычисление определителя таким образом для матрицы 3×3 уже достаточно утомительно и становится экспотенциально более утомительным по мере увеличения количества измерений. К счастью, есть более простой способ сделать это, используя несколько инвариантов.

Посмотрите, что происходит, когда вы пытаетесь вычислить определитель матрицы, как показано ниже, когда вы спускаетесь по первому столбцу: ⎥ ⎥ ⎥⎦[1234034500560007]

Обратите внимание на то, что, поскольку большинство масштабируемых субдетерминантов равны нулю, общая рекурсивная формула расширяется довольно хорошо: ⎟ ⎟⎠det(1234034500560007)

1×det(345056007)

‘ role=»presentation» tabindex=»0″>1×det⎛⎜⎝345056007⎞⎟⎠1×det(345056003;) 3×det(5607)

‘ role=»presentation» tabindex=»0″>1×3×det(5607)1×3×det(5607)

1×3×5× 7

‘ role=»presentation» tabindex=»0″>1×3×5×71×3×5×7

Теперь вопрос в том, как мы можем привести нашу матрицу в эту форму, чтобы мы могли выполнять вычисления в далеком будущем. более простой способ. Ответ, конечно, элементарные операции со строками. Однако элементарные операции со строками могут сохранять пространство строк, но они не сохраняют общую характеристику преобразования, включая степень, в которой оно масштабирует пространство или переворачивает пространство на себя.

Тот факт, что это не так, довольно легко увидеть, если рассмотреть конечный результат идеального исключения строк. Вы можете превратить что-то беспорядочное в то, что по сути является матрицей идентичности, которая ничего не делает с пространством. Обе матрицы имели одинаковое пространство строк, но преобразования больше не было.

Итак, когда мы выполняем операции со строками, нам нужно отслеживать некоторую дополнительную информацию, которая позволяет нам отменить изменения, влияющие на определитель.

Тип 1 Обмен строками: когда мы обмениваем две строки, мы фактически переворачиваем пространство на себя, что означает, что определитель будет отрицательным. Поэтому нам нужно отслеживать, сколько раз мы отрицаем определитель, чтобы мы могли отменить его позже.

Тип 2 Масштабирование строки: вспомните, что когда мы умножаем всю строку на скаляр, определитель масштабируется именно на эту величину. Поэтому нам нужно отследить этот скаляр на потом, так как это один из факторов, на который масштабировался детерминант с уменьшенным числом строк.

Тип 3 Правая линейная комбинация: как это ни парадоксально, добавление скалярных множителей любой строки к любой другой строке (при условии, что сама целевая строка не масштабируется как часть комбинации, отсюда и термин правая линейная комбинация), не изменит вообще определитель. Рассмотрим сдвиг, в котором мы добавляем скаляр, кратный второй строке, к первой, чтобы понять, почему это так:

Имея все это в виду, мы можем вычислить определитель 3×3 гораздо более простым способом. Наблюдайте, как меняется характер преобразования и коэффициент, на который изменяется площадь, когда мы применяем операции сокращения строк.

[1−10−1−10212]

‘ role=»presentation» tabindex=»0″>⎡⎢⎣1−10−1−10212⎤⎥⎦[1−10−1−10212 ]

Прежде чем мы начнем, обратите внимание на некоторые особенности этого преобразования. Во-первых, обратите внимание, что он инвертирует пространство по оси x’ role=»presentation» tabindex=»0″>xx. Также обратите внимание, что он также расширяет пространство.

Сначала вычитаем 2 раза первую строку из третьей. Это операция типа 3, и она не повлияет на определитель.

[1−10−1−10032]

‘ role=»presentation» tabindex=»0″>⎡⎢⎣1−10−1−10032⎤⎥⎦[1−10−1−10032]

Теперь вычтите вторую строку из первой. Это также операция типа 3 и не влияет на определитель.

[200−1−10032]

‘ role=»presentation» tabindex=»0″>⎡⎢⎣200−1−10032⎤⎥⎦[200−1−10032]

Затем добавьте половину первого ряда ко второму. Это тип 3, и als не влияет на определитель.

[2000−10032]

‘ role=»presentation» tabindex=»0″>⎡⎢⎣2000−10032⎤⎥⎦[2000−10032]

Добавить три раза вторую строку к третьей, которая также является типом 3 10002]

Теперь отсюда мы можем напрямую вычислить определитель, просто умножив его по диагонали (напомним, что определитель еще не изменился):

2×−1×2=− 4

‘ role=»presentation» tabindex=»0″>2×−1×2=−42×−1×2=−4

Для полноты картины очистим матрицу, умножив первую строку на 12. ‘ role=»presentation» tabindex=»0″>1212, вторая строка на -1 и третья строка на 12′ role=»presentation» tabindex=»0″>1212. Эти операции изменяют определитель на общий коэффициент −14’ role=»presentation» tabindex=»0″>−14−14.

[100010001]

‘ role=»presentation» tabindex=»0″>⎡⎢⎣100010001⎤⎥⎦[100010001]

Вычислить определитель этой новой матрицы с уменьшенным числом строк несложно

1×1&#x0003 1=1

‘ role=»presentation» tabindex=»0″>1×1×1=11×1×1=1

И чтобы восстановить наш первоначальный определитель, нам нужно сделать обратное изменение к определителю , то есть разделить на −14′ role=»presentation» tabindex=»0″>−14−14

1−14=−4

‘ role=»presentation» tabindex=»0″>1−14=−41−14=−4

На основании того, что мы здесь видели, следует отметить несколько моментов относительно определителя. Во-первых, должно быть довольно интуитивно понятно, что если вы масштабируете всю матрицу с помощью некоторого скаляра, вы также будете масштабировать определитель с помощью этого скаляра, возведенного в степень количества строк в этой матрице. Например, масштабирование единичной матрицы на 3 изменит определитель на 9, поскольку сначала он масштабируется на 3 по оси x, на 3 по оси y и на 3 по оси z.

detαAmn=αndeA

‘ role=»presentation» tabindex=»0″>detαAmn=αandetAdetαAmn=αndetA

Во-вторых, если рассматривать две матрицы как преобразования, определитель их произведения равен произведение определителей.

detAB=detA×detB

‘ role=»presentation» tabindex=»0″>detAB=detA×detBdetAB=detA×detB

Можно ли использовать определитель матрицы 4×4 в компьютерной графике?

спросил 4 года, 6 месяцев назад

Изменено 4 года, 6 месяцев назад

Просмотрено 954 раза

В большинстве графических библиотек, которые я видел, есть функция, которая возвращает определитель из матриц 3×3 и 4×4, но я понятия не имею, когда вам действительно нужно использовать определитель в трехмерной компьютерной графике.

Какие примеры использования определителя в программировании трехмерной графики?

• матрица
• графика
• 3d
• определители

3

Не пришло мне в голову…

Если определитель равен 0, то матрицу нельзя инвертировать, что полезно знать.

Если определитель отрицательный, то объекты, преобразованные матрицей, будут перевернуты как в зеркале (леворукость станет праворукостью и наоборот)

Для матриц 3×3 объем объекта будет умножен на определитель, когда он преобразуется матрицей. Знание этого может быть полезно для определения, например, уровня детализации/количества полигонов для использования при рендеринге объекта.

1

В трехмерной векторной графике

используются матрицы однородного преобразования 4×4, и нам нужны прямые и обратные матрицы стенда, которые можно вычислить с помощью (суб)детерминантов. Но для ортогональных матриц есть более быстрые и точные методы, такие как

• полная псевдообратная матрица.

Многие тесты пересечения используют определители (или могут быть преобразованы для их использования), особенно для квадратных уравнений (эллипсоиды,…), например:

• Повышение точности пересечения лучей и эллипсоидов

, как предложил Мэтт Тиммерманс, вы можете решить, является ли ваша матрица обратимой или левосторонней/правосторонней, что полезно для обнаружения ошибок в матрицах (ухудшение точности) или переноса скелетов между форматами или двигателями и т. д.

И я уверен, что их много. других применений для него в векторной математике (IIRC IGES использует их для вращающихся поверхностей, перекрестное произведение является определителем,…)

Критерий вписанной окружности является ключевым примитивом для вычисления диаграмм Вороного и триангуляции Делоне. Он задается знаком определителя 4×4.

(изображение с https://www.