Для чисел a и b справедливы неравенства 15 а 16: Для чисел a и b справедливы неравенства 15<=a<=16 и 4<=b<=5.Между какими ближайшими целыми числами заключено...

ГДЗ Алгебра Потапов 8 класс Дидактические Номер Вариант 3 СР-1. Числовые неравенства. Числовые промежутки

Содержание

Авторы:Потапов, Никольский, Шевкин

Изд-во:Просвещение

Вид УМК:контрольные и самостоятельные

Серия:МГУ-школе

Смотреть правильно оформленное решениe и ответ на задание Вариант 3 по алгебре 8 класс дидактические материалы автор(ы) Потапов, Никольский, Шевкин

Условие:

1. Укажите три числа, заключенные между числами 6,7(98) и 6,(798)

2. Изобразите на координатной оси числовой промежуток, соответствующий неравенствам

3. С помощью знаков ∈ и ∉ запишите, принадлежит ли данное число указанному числовому промежутку

4. Изобразите на координатной оси числовые промежутки; укажите объединение и пересечение этих промежутков

5. Для чисел a и b справедливы неравенства 14,7≤a≤15,5 и 5≤b≤7. Между какими ближайшими целыми числами заключено число

6. Докажите свойство числовых неравенств

Скачать решение

Сообщи об ошибке или поделись идеей💡

Мне не нравится на сайте, измените:Сделайте так, чтобы можно было:Решение неправильно/опечатка

Содержание

Вариант 1Вариант 2Вариант 3Вариант 4

Похожие решебники по алгебре 8 класс

• Учебник

• КИМ

• Тесты

• Контрольные

• Контрольные

• Дидактич.

• Тетрадь

• Учебник

• Учебник

• org/Book»>

  Контрольные

• Дидактич.

• Контрольные

• Контрольные

• Тетрадь

• Самостоят.

• Тесты

• Учебник

• Дидактич.

• Учебник

• Учебник

• Учебник

• Дидактич.

• Дидактич.

• org/Book»>

  Дидактич.

• Контрольные

• Контрольные

• Тетрадь

• Тетрадь

• Тетрадь

• Учебник

• Тесты

• Тесты

• Тесты

• Тесты

• Учебник

• Учебник

• Учебник

• Тетрадь

• org/Book»>

  Дидактич.

• Дидактич.

• КИМ

• Контрольные

• Контрольные

• Тетрадь

• Тетрадь

• Контрольные

• Тесты

• Тесты

Лабораторная работа n 3. — Энциклопедия современных знаний

Цели и задачи работы: изучение разветвляющихся алгоритмов, операторов выбора, программирование разветвляющегося вычислительного процесса.

Теоретические сведения о работе и примеры программ приведены в литературе [1-7], конспекте лекций, слайдах.

Задание к работе: Реализовать разветвляющийся вычислительный процесс. Самостоятельно решить задачи в соответствии с индивидуальным вариантом.

Описание используемых выполнения работы : язык программирования С, среда Visual Studio, операционная система Windows ХР/7.

Методика выполнения работы:

1. Разработать алгоритм решения задачи по индивидуальному заданию.

2. Написать и отладить программу решения задачи.

3. Протестировать работу программы на различных исходных данных.

Требования к отчету:

Отчет должен содержать титульный лист, задание, текст программы с комментариями, тесты.

Контрольные вопросы по лабораторной преподаватель задает в процессе демонстрации студентом полученных навыков работы в интегрированной среде.

Примеры индивидуальных заданий:

А. Задание 1.Базовое:

Во всех заданиях данной группы требуется вывести текст «TRUE», если приведенное высказывание для предложенных исходных данных является истинным, и текст «FALSE» в противном случае. Все числа, для которых указано количество цифр (двузначное число, трехзначное число и т. д.), считаются целыми положительными.

1. Дано целое число A. Проверить истинность высказывания: «Число A является положительным».

2. Дано целое число A. Проверить истинность высказывания: «ЧислоA является нечетным».

3. Дано целое число A. Проверить истинность высказывания: «Число A является четным».

4. Даны два целых числа: A, B. Проверить истинность высказывания: «Справедливы неравенства A 2 и B ? 3».

5. Даны два целых числа: A, B. Проверить истинность высказывания: «Справедливы неравенства A ? 0 или B ?2».

6. Даны три целых числа: A, B, C. Проверить истинность высказывания: «Справедливо двойное неравенство A B C».

7. Даны три целых числа: A, B, C. Проверить истинность высказывания: «Число B находится между числами A и C».

8. Даны два целых числа: A, B. Проверить истинность высказывания: «Каждое из чисел A и B нечетное».

9. Даны два целых числа: A, B. Проверить истинность высказывания: «Хотя бы одно из чисел A и B нечетное».

10. Даны два целых числа: A, B. Проверить истинность высказывания: «Ровно одно из чисел A и B нечетное».

11. Даны два целых числа: A, B. Проверить истинность высказывания: «Числа A и B имеют одинаковую четность».

12. Даны три целых числа: A, B, C. Проверить истинность высказывания: «Каждое из чисел A, B, C положительное».

13. Даны три целых числа: A, B, C. Проверить истинность высказывания: «Хотя бы одно из чисел A, B, C положительное».

14. Даны три целых числа: A, B, C. Проверить истинность высказывания: «Ровно одно из чисел A, B, C положительное».

15. Даны три целых числа: A, B, C. Проверить истинность высказывания: «Ровно два из чисел A, B, C являются положительными».

16. Дано целое положительное число. Проверить истинность высказывания: «Данное число является четным двузначным».

17. Дано целое положительное число. Проверить истинность высказывания: «Данное число является нечетным трехзначным».

18. Проверить истинность высказывания: «Среди трех данных целых чисел есть хотя бы одна пара совпадающих».

19. Проверить истинность высказывания: «Среди трех данных целых чисел есть хотя бы одна пара взаимно противоположных».

20. Дано трехзначное число. Проверить истинность высказывания:«Все цифры данного числа различны».

21. Даны числа x, y. Проверить истинность высказывания: «Точка с координатами (x, y) лежит во второй координатной четверти».

22. Даны числа x, y. Проверить истинность высказывания: «Точка с координатами (x, y) лежит в четвертой координатной четверти».

23. Даны числа x, y. Проверить истинность высказывания: «Точка с координатами (x, y) лежит во второй или третьей координатной четверти».

24. Даны числа x, y. Проверить истинность высказывания: «Точка с координатами (x, y) лежит в первой или третьей координатной четверти».

25. Даны числа x, y, x1, y1, x2, y2. Проверить истинность высказывания: «Точка с координатами (x, y) лежит внутри прямоугольника, левая верхняя вершина которого имеет координаты (x1, y1), правая нижняя — (x2, y2), а стороны параллельны координатным осям».

Б. Задание 2. Базовое.

1. Дано целое число. Если оно является положительным, то прибавить к нему 1; в противном случае не изменять его. Вывести полученное число.

2. Дано целое число. Если оно является положительным, то прибавить к нему 1; в противном случае вычесть из него 2. Вывести полученное число.

3. Дано целое число. Если оно является положительным, то прибавить к нему 1; если отрицательным, то вычесть из него 2; если нулевым, то заменить его на 10. Вывести полученное число.

4. Даны три целых числа. Найти количество положительных чисел в исходном наборе.

5. Даны три целых числа. Найти количество положительных и количество отрицательных чисел в исходном наборе.

6. Даны два числа. Вывести большее из них.

7. Даны два числа. Вывести порядковый номер меньшего из них.

8. Даны два числа. Вывести вначале большее, а затем меньшее из них.

9. Даны две переменные вещественного типа: A, B. Перераспределить значения данных переменных так, чтобы в A оказалось меньшее из значений, а в B — большее. Вывести новые значения переменных A и B.

10. Даны две переменные целого типа: A и B. Если их значения не равны, то присвоить каждой переменной сумму этих значений, а если равны, то присвоить переменным нулевые значения. Вывести новые значения переменных A и B.

11. Даны две переменные целого типа: A и B. Если их значения не равны, то присвоить каждой переменной большее из этих значений, а если равны, то присвоить переменным нулевые значения. Вывести новые значения переменных A и B.

12. Даны три числа. Найти наименьшее из них.

13. Даны три числа. Найти среднее из них (то есть число, расположенное между наименьшим и наибольшим).

14. Даны три числа. Вывести вначале наименьшее, а затем наибольшее из данных чисел.

15. Даны три числа. Найти сумму двух наибольших из них.

16. Даны три переменные вещественного типа: A, B, C. Если их значения упорядочены по возрастанию, то удвоить их; в противном случае заменить значение каждой переменной на противоположное. Вывести новые значения переменных A, B, C.

17. Даны три переменные вещественного типа: A, B, C. Если их значения упорядочены по возрастанию или убыванию, то удвоить их; в против- ном случае заменить значение каждой переменной на противоположное. Вывести новые значения переменных A, B, C.

18. Даны три целых числа, одно из которых отлично от двух других, равных между собой. Определить порядковый номер числа, отличного от остальных.

19. Даны четыре целых числа, одно из которых отлично от трех других, равных между собой. Определить порядковый номер числа, отличного от остальных.

20. На числовой оси расположены три точки: A, B, C. Определить, какая из двух последних точек (B или C) расположена ближе к A, и вывести эту точку и ее расстояние от точки A.

21. Даны целочисленные координаты точки на плоскости. Если точка совпадает с началом координат, то вывести 0. Если точка не совпадает с началом координат, но лежит на оси OX или OY, то вывести соответственно 1 или 2. Если точка не лежит на координатных осях, то вывести 3.

22. Даны координаты точки, не лежащей на координатных осях OX и OY. Определить номер координатной четверти, в которой находится данная точка.

23. Даны целочисленные координаты трех вершин прямоугольника, стороны которого параллельны координатным осям. Найти координаты его четвертой вершины.

24. Дано целое число. Вывести его строку-описание вида «отрицательное четное число», «нулевое число», «положительное нечетное число» и т. д.

25. Дано целое число, лежащее в диапазоне 1–999. Вывести его строку- описание вида «четное двузначное число», «нечетное трехзначное число» и т. д.

Лабораторная работа №3. Физика 9 класс. Тема: Исследование периода и частоты колебаний маятника

Похожие статьи.

• Теоретический материал к лабораторной работе №2 основы алгоритмизации

• Лабораторная работа n 2.

• Лабораторная работа №1в. сортировка методом прямого включения

• Лабораторная работа n 7.

Уравнения / Неравенства — PSAT Math

Все математические ресурсы PSAT

10 Диагностические тесты 421 практический тест Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 … 12 13 14 15 16 17 18 19 20 21 22 23 Следующая →

PSAT Math Help » Алгебра » Уравнения / Неравенства

3x ²  – 11x = –10

Какое из следующих значений является допустимым для x?

Возможные ответы:

5 /3

Ни один из других ответов

-2

3

-5 / 3

Правильный ответ:

5 /3

Объяснение:

Начнем с того, что приведем наше уравнение к следующему виду: Ax ²  + BX + C = 0:

3x ²  – 11x + 10 = 0

Теперь, если учесть левое число, можно найти ответ.

. Начните с рассмотрения двух групп. Они должны будут начинаться соответственно с 3 и 1 в качестве коэффициентов для вашего значения x. Точно так же, глядя на последний элемент, вы можете сказать, что оба должны иметь + или -, поскольку коэффициент C положительный. Наконец, поскольку коэффициент B отрицателен, мы знаем, что он должен быть равен –. Итак, мы знаем:

(3x – ?)(x – ?)

Потенциальные множители 10: 10, 1; 1, 10; 2, 5; 5, 2

5 и 2 работают:

(3x – 5)(x – 2) = 0, потому что вы можете СЛОГАТЬ (3x – 5)(x – 2) обратно в 3x ²  – 11x + 10.

Теперь остается хитрость: установить каждый из факторов равным 0, потому что если какая-либо группа равна 0, все уравнение будет равно 0:

3x – 5 = 0 → 3x = 5 → x = 5/3

x – 2 = 0 → x = 2

Следовательно, x равно 5/3 или 2. Первое представляется как ответ.

Сообщить об ошибке

Какова сумма значений x, которые удовлетворяют следующему уравнению:

16 ^x  – 10(4) ^x + 16 = 0.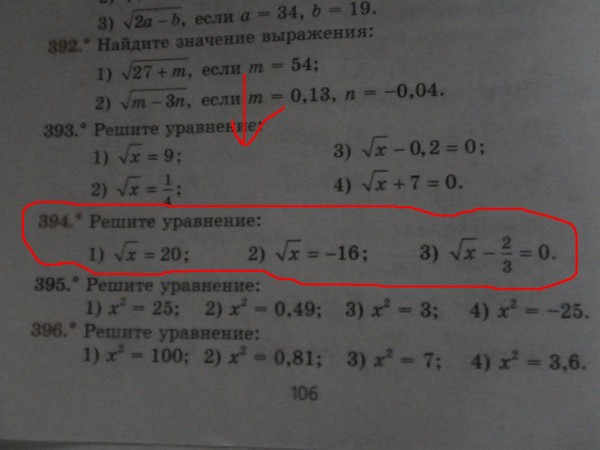

0 Возможные ответы:

2

5/2

4

3/2

1

Правильный ответ:

2

Объяснение:

Уравнение, которое нам нужно решить, 16 ^x  – 10(4) ^x  + 16 = 0,9.0005

Уравнения этого типа часто можно «преобразовать» в другие уравнения, такие как линейные или квадратные уравнения, если мы перепишем некоторые термины.

Во-первых, мы можем заметить, что 16 = 4 ² . Таким образом, мы можем записать 16 ^x как (4 ² ) ^x или как (4 ^x

) ² .

Теперь уравнение (4 ^x ) ²  – 10(4) ^x  + 16 = 0

Давайте введем переменную u и приравняем ее к 4 ^x . Преимущество этого в том, что он позволяет нам «преобразовать» исходное уравнение в квадратное уравнение.

u ²  – 10u + 16 = 0

Это уравнение знакомо нам гораздо лучше. Чтобы решить ее, нам нужно разложить ее на множители и приравнять каждый множитель к нулю. Чтобы разложить его на множители, мы должны подумать о двух числах, которые при умножении дают нам 16, а при сложении дают -10. Эти два числа -8 и -2. Таким образом, мы можем разложить u ²  – 10u + 16 = 0 следующим образом:

(u – 8)(u – 2) = 0

Далее приравняем каждый коэффициент к 0.

Прибавьте 2.

u = 2.

Таким образом, u должно равняться 2 или 8. Однако мы хотим найти x, а не u. Поскольку мы определили u равным 4

x , уравнения примут следующий вид:

4 ^x = 2 или 4 ^x = 8

Сначала решим 4 ^x = 2. Мы можем переписать 4 ^x как (2 ² ) ^x = 2 ^2x , так что основания совпадают.

2 ^2x = 2 = 2 ¹

2x = 1

x = 1/2

Наконец, мы решим 4 ^{x x 4 9 0 3 4 0 0 4 снова, давайте снова, давайте 0 2x . Мы также можем записать 8 как 2 3 .}

2 ^2x = 2 ³

2x = 3

x = 3/2

В исходном вопросе нам предлагается найти сумму значений x, которые решают уравнение. Поскольку х может быть 1/2 или 3/2, сумма 1/2 и 3/2 равна 2.

Ответ 2.

Сообщить об ошибке

Если x > 0, какие значения

x удовлетворяют неравенству x ² >

7 x

8 ?

Возможные ответы:

Все положительные реальные номера

Все идеальные квадраты

Все положительные числа

Нет значений x Сатиффиффи.0020

Все действительные числа больше единицы

Объяснение:

Есть два значения, где x ² = x , а именно x = 0 и x = 1. Все значения от 0 до 1 уменьшаются после возведения в квадрат. Все значения больше 1 становятся больше после возведения в квадрат.

Сообщить об ошибке

Пусть f ( x ) = 2 x ²  – 4 x + 1 и g ( х ) = ( х ² + 16) ^(1/2)

. Если k — отрицательное число такое, что f ( k ) = 31, то каково значение ( f ( g ( k ))?

0 Возможные ответы 0: 0

-81

5

25

-35

31

Правильный ответ:

31

Объяснение:

Чтобы найти значение f ( g ( k )), нам сначала нужно будет найти k . Нам говорят, что f ( k ) = 31, поэтому мы можем написать выражение для f ( k ) и найти k .

F ( x ) = 2 x ² — 4 x + 1

F ( K ) = 2 K ² — 4 K + 10007. = 31

Вычтите 31 с обеих сторон.

2 K ² — 4 K — 30 = 0

Разделите обе стороны на 2.

K ² — 2 K — 15 = 0

Теперь мы можем фактор. для этого нужно подумать о двух числах, которые умножаются, чтобы дать -15, и складываются, чтобы дать -2. Эти два числа равны –5 и 3.

k ²  –2 k  – 15 = ( k  – 5)( k + 3) = 0

0, чтобы найти значения для к .

k  – 5 = 0

Добавьте 5 к обеим сторонам.

k = 5

Теперь устанавливаем k + 3 = 0.

Вычитаем по 3 с обеих сторон.

k = –3

Это означает, что k может быть либо 5, либо –3. Однако нам говорят, что k — отрицательное число, что означает k = –3.

Наконец, мы можем вычислить выражение f ( g (–3)). Сначала нам нужно найти г (–3).

G ( x ) = ( x ² + 16) ^(1/2)

G (–3) = (–3) ² + 16) ^(1/2)

= (9 + 16) ^(1/2)

= 25 ^(1/2)

Возведение чего-либо в половинную степень равносильно извлечению квадратного корня .

25 ^(1/2) = 5

Теперь, когда мы знаем, что g (–3) = 5, мы должны найти f (5).

f (5) = 2(5) ²  – 4(5) + 1

= 2(25) – 20 + 1 = 31

Ответ: 31.

Сообщить об ошибке 5

I. реальный

II. рациональный

III. различное

Какое из описаний характеризует решения уравнения 2x ²  – 6x + 3 = 0?

Возможные ответы:

Только II и III

Только I

Только I и II

Только I и III

Только II

Правильный ответ:

Только I и III

Пояснение:

Уравнение в задаче квадратное, поэтому для его решения можно использовать квадратичную формулу. Если уравнение имеет вид x ² + bx + c = 0, где a , b и c — константы, то приведенная ниже квадратичная формула дает нам решения х .

В данной задаче a = 2, b = –6 и c = 3. называется дискриминантом и дает нам важную информацию о природе решений квадратного уравнения.

Если дискриминант меньше нуля, то корни недействительны, потому что нам пришлось бы брать квадратный корень из отрицательного числа, что дает мнимый результат. Дискриминант уравнения, которое нам дано, равен (–6) ²  – 4(2)(3) = 36 – 24 = 12 > 0. Поскольку дискриминант неотрицательный, решения уравнения будут вещественными. Таким образом, вариант I правильный.

Дискриминант также может сказать нам, являются ли решения уравнения рациональными или нет. Если мы возьмем квадратный корень из дискриминанта и получим рациональное число, то решения уравнения должны быть рациональными. В этой задаче нам нужно будет извлечь квадратный корень из 12. Однако 12 не является полным квадратом, поэтому извлечение его квадратного корня даст иррациональное число. Поэтому решения уравнения в задаче не могут быть рациональными. Это означает, что вариант II неверен.

Наконец, дискриминант сообщает нам, различны ли корни уравнения (отличны ли они друг от друга). Если дискриминант равен нулю, то решения x становятся (– b + 0)/2 a и (– b  – 0)/2 a , поскольку квадратный корень из нуля равно 0. Обратите внимание, что (– b + 0)/2 a совпадает с (– b  – 0)/2 a . Таким образом, если дискриминант равен нулю, то корни уравнения одинаковые, т.е. нечеткие. В этой конкретной задаче дискриминант = 12, что не равно нулю. Это означает, что два корня будут разными, т.е. различными. Следовательно, применяется вариант III.

Ответ только на варианты I и III.

Сообщить об ошибке

Решить для x .

3 x ² + 15 x — 18 = 0.

Возможные ответы:

x = 2 или x = –3

x = –6 или x = –3

x = –6 или x = –3

x = –6 или x = –3

x = –6 или x 9000 х = 1

х = 5 или х = 1

х = –2 или х = 3

х 6 или =0007 x = –1

Правильный ответ:

x = –6 или x = 1

Объяснение:

Сначала посмотрим, есть ли общий термин.

3 x ² + 15 x — 18 = 0

Мы можем вытащить 3: 3 ( x ² + 5 x — 6) = 0

Разделение обеих сторон. на 3: x ² + 5 x  – 6 = 0

Нам нужны два числа, которые в сумме дают 5 и умножаются на –6. 6 и –1 работают.

( x + 6) ( x — 1) = 0

x = –6 или x = 1

Отчет о ошибке

Выражение равно 0 и

Возможные ответы:

Правильный ответ:

Объяснение:

Разложите выражение на множители и установите каждый множитель равным 0:

Сообщить об ошибке

Произведение двух последовательных положительных чисел, кратных четырем, равно 96.  Чему равна сумма этих двух чисел?

Возможные ответы:

Правильный ответ:

Объяснение:

Пусть  = первое число и  = второе число.

Итак, уравнение для решения становится . Перед разложением на множители это квадратное уравнение необходимо умножить и приравнять к нулю. Затем приравняйте каждый множитель к нулю и решите. Правильны только положительные числа, поэтому ответ равен .

Сообщить об ошибке

Произведение двух последовательных положительных нечетных чисел равно 35. Чему равна сумма этих двух чисел?

Возможные ответы:

Правильный ответ:

Объяснение:

Пусть  = первое положительное число и  = второе положительное число.

Уравнение для решения становится

Мы умножаем это квадратное уравнение и устанавливаем его равным 0, затем делим.

Сообщить об ошибке

Произведение двух последовательных положительных чисел, кратных четырем, равно 192. Чему равна сумма этих двух чисел?

Возможные ответы:

Правильный ответ:

Объяснение:

Пусть  = первое положительное число и  = второе положительное число

Уравнение, которое нужно решить, становится

. Мы решаем это квадратное уравнение, умножая его и приравнивая его к 0. Следующий шаг – факторизация.

Сообщить об ошибке

← Назад 1 2 … 12 13 14 15 16 17 18 19 20 21 22 23 Далее →

Уведомление об авторских правах

Все математические ресурсы PSAT

100 Диагностические тесты 421 практический тест Вопрос дня Карточки Learn by Concept

Напишите неравенство, которое представляет число, умноженное на пять меньше, чем удвоенное число, равное как минимум пятнадцати, затем решите неравенство

Математическая алгебра 1 Уравнение 7 класс

Кристина Н.

спросил 18.05.19

выпускной экзамен по математике в 7 классе

Подписаться І 1

Подробнее

Отчет

1 ответ эксперта

Лучший Новейшие Самый старый

Автор: ЛучшиеНовыеСамыеСтарые

Лиза Б. ответил 24.05.19

Репетитор

5,0 (228)

Помощь учащимся в естествознании и математике в течение 20+ лет

См. таких репетиторов

Смотрите таких репетиторов

Ключ в том, чтобы перевести эту задачу шаг за шагом:

Запишите неравенство

Это говорит нам о том, что мы будем использовать >, <, ≥ или ≤ вместо = при описании двух сторон уравнение.

, что на пять меньше

Это говорит нам о том, что нам нужно отнять или вычесть 5: –5

два раза число

Мы не знаем число, поэтому назовем его х . Дважды х равно 2 х .

Затем, предыдущий шаг говорит нам, что нам нужно на пять меньше, чем удвоенное число, поэтому мы говорим 2 x –5.

то есть не менее пятнадцати

«Не менее пятнадцати» говорит нам, что первая часть уравнения может быть больше или равна 15, что означает, что нам нужен знак ≥. Если бы во фразе говорилось «более пятнадцати», мы бы использовали >.

Складываем все вместе, получаем 2 x – 5 ≥ 15.

затем решаем неравенство

Мы отменяем все действия алгебры, чтобы x решить в обратном порядке.

2 x – 5 ≥ 15 Сначала отмените вычитание, прибавив 5 к обеим сторонам.

2 x ≥ 20 Затем разделите обе части на 2.

x ≥ 10. Мы видим, что x должен быть больше или равен 10. Это означает, что мы можем выбрать любое число, 10 или больше, и подставьте его обратно в уравнение, которое мы построили, чтобы проверить наш ответ.

Дайте мне знать, если вам нужна дополнительная помощь один на один!

Голосовать за 0 Понизить голос

Подробнее

Отчет

Все еще ищете помощь? Получите правильный ответ, быстро.

Задайте вопрос бесплатно

Получите бесплатный ответ на быстрый вопрос.

No related posts.