Вариант 11.
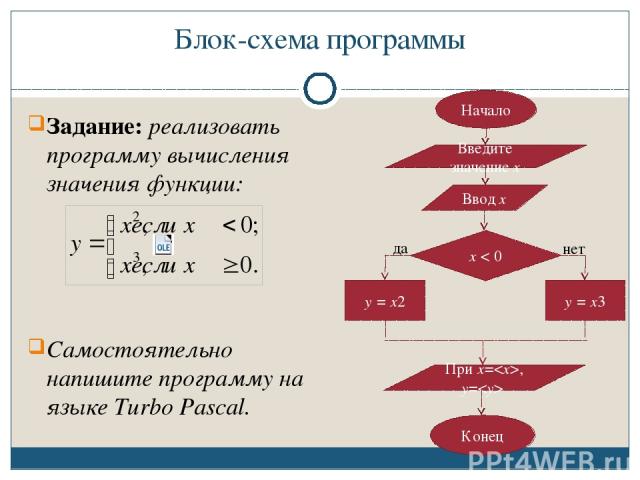
Даны целочисленные координаты точки на плоскости. Если точка совпадает с началом координат, то вывести 0. Если точка не совпадает с началом координат, но лежит на оси OX или OY, то вывести соответственно 1 или 2. Если точка не лежит на координатных осях, то вывести 3.
Дано целое число. Вывести его строку-описание вида «отрицательное четное число», «нулевое число», «положительное нечетное число» и т. д.
Арифметические действия над числами пронумерованы следующим образом: 1 — сложение, 2 — вычитание, 3 — умножение, 4 — деление. Дан номер действия N (целое число в диапазоне 1–4) и вещественные числа A и B (B не равно 0). Выполнить над числами указанное действие и вывести результат.
Даны целые числа K и N (N > 0). Вывести N раз число K.
Дано целое число N (> 1) и две вещественные точки на числовой оси: A, B (A < B).

F(A), F(A + H), F(A + 2·H), …, F(B).
Вариант 12.
Для данного вещественного x найти значение следующей функции f, принимающей вещественные значения:
f(x) = 2·sin(x), если x > 0,
6 − x, если x ≤ 0.
Для данного вещественного x найти значение следующей функции f, принимающей значения целого типа:
0, если x < 0,
f(x) = 1, если x принадлежит [0, 1), [2, 3), …,
−1,если x принадлежит [1, 2), [3, 4), … .
Единицы длины пронумерованы следующим образом: 1 — дециметр, 2 — километр, 3 — метр, 4 — миллиметр, 5 — сантиметр. Дан номер единицы длины (целое число в диапазоне 1–5) и длина отрезка в этих единицах (вещественное число).
(2·N)/((2·N)!)
(N! = 1·2·…·N). Полученное число является приближенным значением функции cos в точке X.
Дано целое число N (> 2). Последовательность целых чисел AK определяется следующим образом:
A1 = 1, A2 = 2, A3 = 3, AK = AK−1 + AK−2 − 2·AK−3, K= 4, 5,… .
Вывести элементы A1, A2, …, AN.
Функция f(x), определенная для вещественного числа, обладает тем свойством, что \\[f\\left( {f\\left( x \\right)} \\right) \\cdot \\left( {1 + f\\left( x \\right)} \\right) = — f\\left( x \\right)\\] для всех x в области определения f. Если число 3 находится в домене и диапазоне f, вычислите значение f(3).A.$\\dfrac{{ — 3}}{4}$B.$\\dfrac{{ — 3}} {2}$C.$\\dfrac{2}{3}$D.$\\dfrac{{
Ответ
Подтверждено
273,6 тыс.+ просмотров
Подсказка: В этом вопросе нам нужно определить значение функции при значении x как 3 такое, что \[f\left( {f\left( x \right)} \right) \cdot \left( {1 + f\left( x \right)} \right) = — f\left( x \right)\] должно быть выполнено.
 Для этого мы будем использовать простые арифметические операции и перестановки данного выражения, чтобы получить результат.
Для этого мы будем использовать простые арифметические операции и перестановки данного выражения, чтобы получить результат.Полный пошаговый ответ:
Данное выражение равно \[f\left( {f\left( x \right)} \right) \cdot \left( {1 + f\left( x \right)} \right) = — f\left( x \right)\]
Перенос члена \[\left( {1 + f\left( x \right)} \right)\] вправо- стороны, мы получаем
\[
\Rightarrow f\left( {f\left( x \right)} \right) \cdot \left( {1 + f\left( x \right)} \right) = — f\left( x \right) \\
\Rightarrow f\left( {f\left( x \right)} \right) = \dfrac{{ — f\left( x \right)}}{{1 + f\left( x \right)}} — — — — (i) \\
\]
В соответствии с вопросом функция f(x) была определена для действительного числа, поэтому пусть функция f(x) равна ‘x’, такому что x принадлежит множеству действительных чисел.
Подставляя значение функции f(x) вместо x в уравнение (i), получаем
\[
\Rightarrow f\left( {f\left( x \right)} \right) = \dfrac{{ — f\left( x \right)}}{{1 + f\left( x \right)}} \\
\Rightarrow f(x) = \dfrac{{ — x}}{{1 + x}} — — — — (ii) \\
\]
Теперь нас попросили определить значение функции при x=3. Итак, подставьте x=3 в уравнение (ii), чтобы оценить значение функции.
Итак, подставьте x=3 в уравнение (ii), чтобы оценить значение функции.
\[
\Стрелка вправо f(x) = \dfrac{{ — x}}{{1 + x}} \\
\Стрелка вправо f(3) = \dfrac{{ — 3}}{{1 + 3} } \\
\]
Упрощая вышеприведенное уравнение, получаем
\[
\Rightarrow f(3) = \dfrac{{ — 3}}{{1 + 3}} \\
= \dfrac{{ — 3 }}{4} \\
\]
Следовательно, значение функции f(x) при x=3 задается как \[\dfrac{{ — 3}}{4}\] так, что функция f( x) был определен на действительных числах и \[f\left( {f\left( x \right)} \right) \cdot \left( {1 + f\left( x \right)} \right) = — ж\влево(х\вправо)\].
Вариант А правильный.Примечание: Здесь интересно отметить, что диапазон и область определения функции включают 3, поэтому наши результаты должны попадать только в заданный диапазон. Действительные числа состоят из нуля (0), положительных и отрицательных целых чисел (-3, -1, 2, 4) и всех дробных и десятичных значений между ними (0,4, 3,1415927, 1/2).
 Действительные числа делятся на рациональные и иррациональные числа.
Действительные числа делятся на рациональные и иррациональные числа. Дата последнего обновления: 20 апреля 2023 г.
•
Всего просмотров: 273,6 тыс.
•
Просмотров сегодня: 4,43 тыс.
Домен и набор функций Rational
домен из функция ф Икс это набор всех значений, для которых определена функция, и диапазон функции – это множество всех значений, которые ф берет.
Область определения рациональной функции состоит из всех действительных чисел Икс за исключением тех, для которых знаменатель равен 0 .
 Чтобы найти эти
Икс
значений, подлежащих исключению из области определения рациональной функции, приравнять знаменатель к нулю и найти
Икс
.
Чтобы найти эти
Икс
значений, подлежащих исключению из области определения рациональной функции, приравнять знаменатель к нулю и найти
Икс
.Например, домен родительская функция ф Икс «=» 1 Икс множество всех действительных чисел, кроме Икс «=» 0 . Или область определения функции ф Икс «=» 1 Икс − 4 множество всех действительных чисел, кроме Икс «=» 4 .
Теперь рассмотрим функцию ф Икс «=» Икс + 1 Икс − 2 Икс − 2 . При упрощении, когда Икс ≠ 2 становится линейной функцией ф Икс «=» Икс + 1 .
 Но исходная функция не определена в
Икс
«=»
2
. Это оставляет график с дырой, когда
Икс
«=»
2
.
Но исходная функция не определена в
Икс
«=»
2
. Это оставляет график с дырой, когда
Икс
«=»
2
.Один из способов найти диапазон рациональной функции — найти область определения обратной функции.
Другой способ — набросать график и определить диапазон.
Снова рассмотрим родительскую функцию ф Икс «=» 1 Икс . Мы знаем, что функция не определена, когда Икс «=» 0 .
Как Икс → 0 по обе стороны от нуля, ф Икс → ∞ . Точно так же, как Икс → ± ∞ , ф Икс → 0 .
График приближается Икс -ось как Икс стремится к положительной или отрицательной бесконечности, но никогда не касается Икс -ось. То есть функция может принимать все действительные значения, кроме 0 .

Итак, областью действия функции является множество действительных чисел, кроме 0 .
Пример 1:
Найдите область определения и диапазон функции у «=» 1 Икс + 3 − 5 .
Чтобы найти исключенное значение в области определения функции, приравняйте знаменатель к нулю и найдите Икс .
Икс + 3 «=» 0 ⇒ Икс «=» − 3
Таким образом, областью определения функции является множество действительных чисел, кроме − 3 .
Диапазон функции такой же, как и область определения обратной функции. Итак, чтобы найти диапазон, определите обратную функцию.
Обменять Икс и у .
Икс «=» 1 у + 3 − 5
Решение для у Вы получаете,
Икс + 5 «=» 1 у + 3 ⇒ у + 3 «=» 1 Икс + 5 ⇒ у «=» 1 Икс + 5 − 3
Итак, обратная функция ф − 1 Икс «=» 1 Икс + 5 − 3 .

Исключенное значение в области определения обратной функции можно определить, приравняв знаменатель к нулю и решив для Икс .
Икс + 5 «=» 0 ⇒ Икс «=» − 5
Итак, областью определения обратной функции является множество действительных чисел, кроме − 5 . То есть областью действия данной функции является множество действительных чисел, кроме − 5 .
Следовательно, область определения данной функции равна { Икс е ℝ | Икс ≠ − 3 } и диапазон { у е ℝ | у ≠ − 5 } .

Пример 2:
Найдите область определения и диапазон функции у «=» Икс 2 − 3 Икс − 4 Икс + 1 .
Используйте графический калькулятор, чтобы построить график функции.
Когда вы факторизуете числитель и отменяете ненулевые общие множители, функция сводится к линейной функции, как показано.у «=» Икс + 1 Икс − 4 Икс + 1 «=» Икс + 1 Икс − 4 Икс + 1 «=» Икс − 4
Итак, граф линейный с дыркой в точке Икс «=» − 1 .

Используйте график, чтобы определить домен и диапазон.
Функция не определена для Икс «=» − 1 . Итак, домен { Икс е ℝ | Икс ≠ − 1 } или − ∞ , − 1 ∪ − 1 , ∞ .
Диапазон функции { у е ℝ | у ≠ к где у − 1 «=» к } .
Для Икс ≠ − 1 , функция упрощается до у «=» Икс − 4 .
 Функция не определена в
Икс
«=»
−
1
или функция не принимает значение
−
1
−
4
«=»
−
5
. То есть,
к
«=»
−
5
.
Функция не определена в
Икс
«=»
−
1
или функция не принимает значение
−
1
−
4
«=»
−
5
. То есть,
к
«=»
−
5
.Следовательно, область действия функции { у е ℝ | у ≠ − 5 } или − ∞ , − 5 ∪ − 5 , ∞ .
Ан асимптота это линия, к которой график функции приближается, но никогда не касается. В родительской функции ф Икс «=» 1 Икс , оба Икс — и у -оси являются асимптотами.
 График родительской функции будет приближаться к асимптотам, но никогда не будет касаться их.
График родительской функции будет приближаться к асимптотам, но никогда не будет касаться их.Чтобы найти вертикальную асимптоту рациональной функции, приравняйте знаменатель к нулю и найдите Икс .
Если степень многочлена в числителе меньше степени знаменателя, то горизонтальной асимптотой является Икс -ось или у «=» 0 .
Функция ф Икс «=» а Икс , а ≠ 0 имеет тот же домен, диапазон и асимптоты, что и ф Икс «=» 1 Икс .
Теперь график функции ф Икс «=» а Икс − б + с , а ≠ 0 является гиперболой, симметричной относительно точки б , с . Вертикальная асимптота функции равна Икс «=» б а горизонтальная асимптота равна у «=» с .

В более общем виде функция ф Икс «=» а Икс + б с Икс + г имеет вертикальную асимптоту при Икс «=» − г с и горизонтальная асимптота при у «=» а с . В более общем случае, если и числитель, и знаменатель имеют одинаковую степень, то горизонтальная асимптота будет у «=» к где к есть отношение старшего коэффициента числителя к коэффициенту знаменателя.
Если степень знаменателя на единицу меньше степени числителя, то функция имеет наклонную асимптоту.
Пример 3:
Найдите вертикальную и горизонтальную асимптоты функции ф Икс «=» 5 Икс − 1 .
Чтобы найти вертикальную асимптоту, приравняйте знаменатель к нулю и найдите Икс .




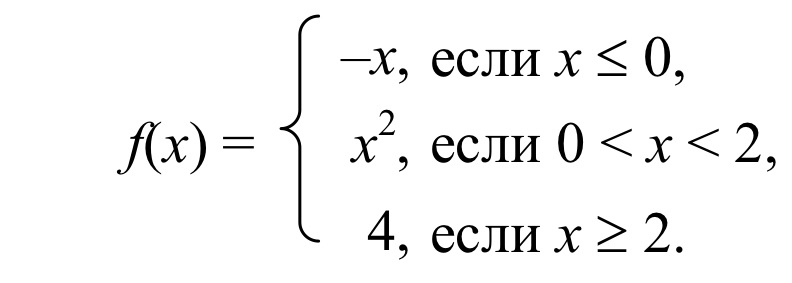 Для этого мы будем использовать простые арифметические операции и перестановки данного выражения, чтобы получить результат.
Для этого мы будем использовать простые арифметические операции и перестановки данного выражения, чтобы получить результат. Итак, подставьте x=3 в уравнение (ii), чтобы оценить значение функции.
Итак, подставьте x=3 в уравнение (ii), чтобы оценить значение функции.  Действительные числа делятся на рациональные и иррациональные числа.
Действительные числа делятся на рациональные и иррациональные числа.  Чтобы найти эти
Икс
значений, подлежащих исключению из области определения рациональной функции, приравнять знаменатель к нулю и найти
Икс
.
Чтобы найти эти
Икс
значений, подлежащих исключению из области определения рациональной функции, приравнять знаменатель к нулю и найти
Икс
. Но исходная функция не определена в
Икс
«=»
2
. Это оставляет график с дырой, когда
Икс
«=»
2
.
Но исходная функция не определена в
Икс
«=»
2
. Это оставляет график с дырой, когда
Икс
«=»
2
.



 Функция не определена в
Икс
«=»
−
1
или функция не принимает значение
−
1
−
4
«=»
−
5
. То есть,
к
«=»
−
5
.
Функция не определена в
Икс
«=»
−
1
или функция не принимает значение
−
1
−
4
«=»
−
5
. То есть,
к
«=»
−
5
. График родительской функции будет приближаться к асимптотам, но никогда не будет касаться их.
График родительской функции будет приближаться к асимптотам, но никогда не будет касаться их.