Днф квайна: Метод Квайна.

6.2. Сокращённая днф. Метод Квайна.

Определение 1. Элементарным произведением называется конъюнкт, в который любая переменная входит не более одного раза. Формула (х₁, х₂, … х_п) называется импликантой формулы (х₁, х₂, … х_п), если   элементарное произведение и для соответствующих формулам  и  функций f_ и f_ справедливо неравенство f_f_. Формула (х₁, х₂, … х_п) называется импликантой функции f, если 

 импликанта совершенной ДНФ, представляющей функцию f. Импликанта (х₁, х₂, … х_п)=формулы называется простой, если после отбрасывания любой литеры из  не получается формула, являющаяся импликантой формулы . Дизъюнкция всех простых импликант данной формулы (функции) называется сокращённой ДНФ.

Пример 6.1. Найдем все импликанты, простые импликанты и сокращённую ДНФ функции ху. Всевозможные элементарные произведения от переменных х и у  это в точности следующие: х, у, ,,ху, у, х,. Построим для самой функции и для этих элементарных произведений таблицу истинности:

х	у	ху	х	у			ху	у	х
0	0	0	0	0	1	1	0	0	0	1
0	1	1	0	1	1	0	0	1	0	0
1	0	1	1	0	0	1	0	0	1	1
1	1	1	1	1	0	0	1	0	0	0

Сравнивая значения элементарных произведений со значениями функции ху, заключаем, что импликантами этой функции являются в точности х, у, ху, у, х, так как для всех них выполнено условиехуf_, где f_  одна из х, у, ху, у, х(например,хух). Из этих импликант простыми являются толькох

и у. Действительно, удаление одной из литеры в импликантах ху, у, хведёт к получению других, а именно х или у. Таким образом, сокращённой ДНФ функции является ху (что, впрочем, следует из определения самой функции).

В качестве другого примера отметим, что всевозможными импликантами функции ху являются у, х, из которых все являются простыми, и, следовательно, сокращённой ДНФ являетсяух.

Ясно, что с помощью таблицы истинности при большом числе переменных построение сокращённой ДНФ становится проблематичной. Существуют специальные методы, позволяющие избегать работы с таблицами истинности. Они основаны на следующих операциях замены подформул, формул, выражающих функции, им эквивалентными подформулами:

Ах

АА  операция полного склеивания;

АхАААхА операция неполного склеивания;

Ах^АА  операция элементарного поглощения (0, 1)

Упражнение 6. 1.Найти сокращённые ДНФ функций из упражнения 5.1.

Решение. а) Применим к СДНФ функции сначала операцию неполного склеивания, а затемэлементарного поглощения:

zyxzzzyxzz

y.

В результате получили сокращённую ДНФ функции.

(1) К паре конъюнктов zиxz(точнее, к их дизъюнкции) применили операцию неполного склеивания:zxzz. Больше пар, к которым можно применить эту операцию, нет.

(2) К парам (z,z) и (z,xz) применили операцию элементарного поглощения: zzzи zxzz. .

Ответ: z

y.

6.3. Минимальная ДНФ. Таблица Квайна. Рассмотрим ещё

Пример 6.2. Пусть функция f(x, y, z) задана совершенной ДНФ f(x, y, z)=zxxy. Производя над ней операции склеивания и элементарного поглощения, получаем её сокращённую ДНФf(x, y, z)=x. Построив её таблицу истинности, можно убедиться, что импликантуможно удалить, то естьf(x, y, z)=x, и сокращённую ДНФ функции можно упрощать дальше, удаляя лишние импликанты.

Определение 2. Тупиковой ДНФ называется ДНФ, которая получается из сокращённой ДНФ удалением всех лишних импликант, не меняя таблицу истинности.

Минимальной ДНФ функции называется её тупиковая ДНФ с наименьшим числом вхождений переменных.

Одним из способов получения минимальной ДНФ из сокращённой ДНФ является использование так называемой таблицы Квайна (ТК). Заголовками столбцов ТК являются конституенты единицы СДНФ, а заголовками строк  простые импликанты из сокращённой ДНФ. Таблица заполняется знаками «+» на пересечениях тех строк и столбцов, для которых конъюнкт, стоящий в заголовке строки, входит в конституенту единицы, являющейся заголовком столбца. В тупиковую ДНФ выбирается минимальное число тех простых импликант, знаки «+» при которых охватывают все столбцы ТК.

ТК для функции примера 6.2 имеет вид

		z	x	xy
	+	+
	+		+
x			+	+

Минимальное число простых импликант, знаки «+» при которых охватывают все столбцы, образуют импликанты первой и третьей строки, то есть иx. Поэтомуxявляется МДНФ функции.

Упражнение 6.2.Найти все тупиковые и минимальные ДНФ функций упражнения 5.1.

6.4. Метод Квайна-Мак-Класки. При больших п (порядка 4) метод Квайна становится громоздким. Существует ряд модификаций метода, позволяющих технически упростить данный метод. Опишем один из методов, называемых методом Квайна-Мак-Класки.

Сначала заметим, что при операции склеивания склеиваются элементарные произведения, отличающиеся только одной литерой. Это и положено в основу модификации. Алгоритм метода  следующий:

1. Представим каждую конституенту булевой функции в виде двоичного набора длины п.

2. Сгруппируем наборы так, чтобы в каждую группу попали те и только те наборы, которые имеют одинаковое число единиц, располагая их в порядке возрастания числа единиц.

3. Сравнивая наборы из соседних групп, выделяем пары, отличающиеся только в одной позиции (тем самым выделяем конституенты, отличающиеся только одной литерой).

4. В обоих выделенных наборах пар заменяем отличающиеся символы (0 и 1) на «-» (тем самым из двух различных наборов получаем один и тот же набор из 0, 1 и «-», что соответствует тому, что два одинаковых элементарных произведения склеили по отличающейся литере, при этом знак «-» соответствует тому, что соответствующая литера в полученном элементарном произведении будет отсутствовать).

Если в результате склеивания получается уже имеющийся набор, то результат склеивания (то есть полученный набор) опускается (это соответствует тому, что согласно закона идемпотентности одинаковые элементарные произведения сливаются в одну). Если в результате склеивания получаются наборы, отличающиеся только в одной позиции, причём в соответствующей позиции одного стоит знак «-» (у других  0 или 1), то остальные опускаются (что соответствует элементарному поглощению)

5. После всевозможных склеиваний на очередном этапе, переходим к пункту 2.

Процесс продолжается до тех пор, пока склеивать будет нечего. Простыми импликантами являются те элементарные произведения, которые не участвовали в процессе склейки на очередном шаге.

Пример 6.3. Проиллюстируем метод на примере функции, имеющей систему равенств f(0, 1, 0)=f(0, 1, 1)=f(1, 0, 1)=f(1, 1, 0)=f(1, 1, 1)=1 примера 6.2. Располагать группы и результаты всех шагов удобно в таблице. Кроме того, наборы, участвующие при склейке на очередном шаге, будем как-то помечать, например, знаком «*». Тогда после конечного шага все наборы, не участвовавшие при склейке на очередном шаге, останутся непомеченными.

В

	I шаг	II шаг
010*	01-* -10*	-1-
011* 101* 110*	-11* 1-1 11-*
111*

результате первого шага мы склеили: 1) наборы 010 и 011, получили 01-; 2) наборы 010 и 110, получили -10; 3) наборы 011 и 111, получили -11; 4) 101 и 111, получили 1-1; 5) наборы 110 и 111, получили 11-. Во втором шаге склеиваются: 1) наборы 01- и 11-, получается -1-; 2) наборы -10 и -11, получается -1- (который уже есть). После второго шага склеивать нечего. В итоге непомеченными оказываются -1- и 1-1. Это означает, что соответствующие им элементарные произведенияу и хz являются простыми импликантами функции. Таким образом, сокращённой ДНФ данной функции является ухz.

Заметим, что для удобства в таблице Квайна при обозначении элементарных произведений также удобно использование наборов из 0 и 1. Так, таблица Квайна для нашего примера выглядит следующим образом:

	010	011	101	110	111
-1-	+	+		+	+
1-1			+		+

Из таблицы видим, что полученная сокращённая ДНФ является минимальной, и даже тупиковой.

Упражнение 6.3.Найти все тупиковые и минимальные ДНФ функций упражнения 5.2.

Решение. б) Применяя модификацию метода Квайна, находим сокращённую ДНФ.

	Iшаг	IIшаг
0000*	-000 000-
0001* 1000*	10-0* 1-00*	1—0
0110* 1010* 1100*	011-* -110* 1-10* 11-0*	-11-
0111* 1110*	-111* 111-*
1111*

Она же оказыется тупиковой и минимальной, в чем легко убедиться, построив таблицу Квайна:

	0000	0001	0110	0111	1000	1010	1100	1110	1111
1—0					+	+	+	+
-11-			+	+				+	+
-000	+				+
0001		+

Минимизация логических функций методом Квайна

• Нахождение простых импликант
• Составление импликантной матрицы и расстановка меток избыточности
• Нахождение существенных импликант и ислючение связанных с ними строк и столбцов
• Выбор минимального элемента
• Определение и запись минимальной нормальной формы

Метод Квайна по своей сути идентичен как по отношению к дизъюнктивной нормальной форме, так и к конъюнктивной нормальной форме, поэтому рассмотрим его на примере дизъюнктивной формы. В основе метода лежит использование двух основных законов алгебры логики — закона склеивания и закона поглощения. Процедура минимизации проводится в несколько этапов. Рассмотрим её на примере функции, приведённой в таблице ниже (таблица 1).

Таблица 1. Таблица истинности к примеру

Номер набора	x1	x2	x3	x4	f
0	0	0	0	0	1
1	0	0	0	1	1
2	0	0	1	0	1
3	0	0	1	1	0
4	0	1	0	0	0
5	0	1	0	1	1
6	0	1	1	0	1
7	0	1	1	1	1
8	1	0	0	0	1
9	1	0	0	1	1
10	1	0	1	0	1
11	1	0	1	1	0
12	1	1	0	0	0
13	1	1	0	1	0
14	1	1	1	0	1
15	1	1	1	1	0

Перебирают все пары минтермов исходной совершенной дизъюнктивной нормальной формы, склеивая те из них, для которых эта операция возможна. При составлении пар любой из минтермов может быть испоользован многократно. Процедура повторяется и над полученными импликантами — опять проводятся операции склеивания. Процесс повторяется до тех пор, пока не останется ни одной импликанты, допускающей склеивания с другими. Такие импликанты называются простыми. Участовавшие в склеивании элементарные конъюнкции помечаются каким-либо символом, например, «*».

Наличие такого символа означает, что данная элементарная конъюнкция уже учтена в какой-то из импликант, полученных в результате склеивания, и поглощается последней. Если какой-либо из минтермов изначально не удалось склеить ни с одним другим, то он уже сам по себе является простой импликантой. Дизъюнктивная нормальная форма, составленная из всех простых импликант, полученных в результате описанной процедуры, представляет собой сокращённую ДНФ, эквивалентную исходной СДНФ. Данный этап иллюстирует таблица ниже (таблица 2).

Таблица 2. Склеивание минтермов совершенной ДНФ

Номер набора	Минтермы
0	*
1	*
2	*
5	*
6	*
7	*
8	*
9	*
10	*
14	*

Склеиваемые наборы	Минтермы
0, 1
0, 2
0, 8
1, 5
1, 9
2, 6
2, 10
5, 7
6, 7
6, 14
8, 9
8, 10
10, 14

В левой части таблицы показаны минтермы исходной совершенной ДНФ.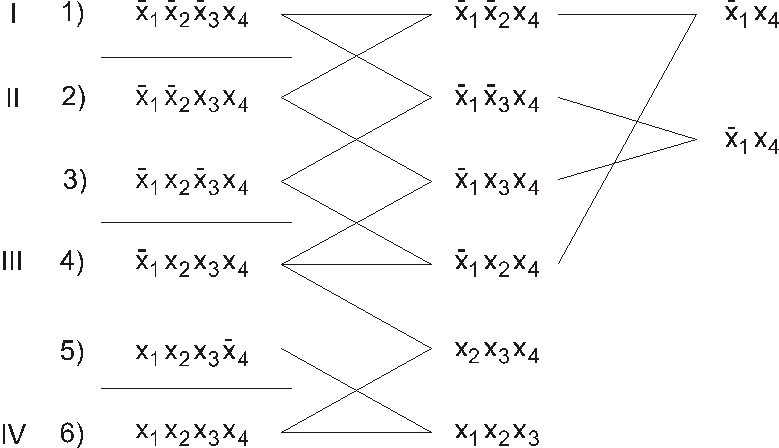 Анализируюются все возможные пары минтермов, и, если это возможно, производится их склеивание. Минтермы, участовавшие в операции склеивания, помечаются символом «*». Результаты склеивания с указанием номеров «склеенных» минтермов показаны в правой части таблицы 2.

В результате первого этапа склеивания получены 13 импликант ранга 3. Поскольку помеченными оказались все минтермы, среди них простых импликант нет, тем самым в 13 импликантах содержится вся исходная информация, и, ДНФ, составленная из этих импликант, полностью эквивалентна исходной совершенной ДНФ. Далее повторим процедуру попарного склеивания применительно к полученным 13 импликантам. Это показано в таблице 3.

Таблица 3. Склеивание импликант ранга 3

Склеиваемые наборы	Минтермы
0, 1	*
0, 2	*
0, 8	*
1, 5
1, 9	*
2, 6	*
2, 10	*
5, 7
6, 7
6, 14	*
8, 9	*
8, 10	*
10, 14	*

Склеиваемые наборы	Импликанты
0, 1, 8, 9
0, 2, 8, 10
0, 8, 1, 9
0, 8, 2, 10
2, 6, 10, 14
2, 10, 6, 14

Из таблицы видно, что импликанты, обозначенные как 1,5; 5,7 и 6,7 остались непомеченными. Это означает, что они не были склеены ни с одной другой импликантой, поэтому являются простыми и должны учитываться на последующих этапах минимизации. В ходе склеивания образовались три пары импликант ранга 2. В соответсвии с теоремой идемпотентности из нескольких одинаковых импликант можно составить только одну. Нетрудно заметить, что дальнейшее склеивание трёх оставшихся импликант ранга 2 невозможно, то есть эти импликанты простые. Таким образом, в дополнение к трём простым импликантам ранга 3: , и получены ещё три простые импликанты ранга 2: , и . Логическая сумма перечисленных простых импликант представляет собой сокращённую ДНФ:

Этот и последующие шаги имеют целью убрать из сокращённой ДНФ все лишние простые импликанты, тем самым перейти от сокращённой ДНФ к тупиковым формам, а затем и к минимальным. Задача решается с помощью специальной импликантной матрицы. Каждая строка такой матрицы соответствует одной из простых импликант, входящих в сокращённую ДНФ, иными словами, количество строк в матрице равно числу простых импликант в сокращённой ДНФ. Столбцы матрицы представляют минтермы исходной СДНФ, при этом каждому из них соответствует свой столбец.

Если минтерм в столбце импликантной матрицы содержит в себе простую импликанту из какой-либо строки матрицы, то на пересечении данного столбца и данной строки ставится метка избыточности. Это означает, что данная простая импликанта поглощает соответсвующий минтерм и способна заменить его в окончательном логическом выражении.

Таблица 4. Импликантная матрица Квайна

0, 1, 8, 9
0, 2, 8, 10
2, 6, 10, 14
1, 5
5, 7
6, 7

0	1	2	5	6	7	8	9	10	14
√	√					√	√
√		√				√		√
		√		√				√	√
	√		√
			√		√
				√	√

Импликантная матрица для рассматриваемого примера (таблица 4) содержит 6 строк (по числу простых импликант) и 10 столбцов (по числу минтермов исходной СДНФ). В матрице минтермы обозначены своими номерами, а слева от простых импликант перечислены номера минтермов, из которых эти импликанты были получены. Расставим в ней метки в тех позициях, где простая импликанта, указанная в левом столбце, покрывает минтерм, записанный в верхней строке.

Присутствие в столбце только одной метки означает, что простая импликанта строки, где стоит эта метка, является существенной или базисной импликантой, то есть обязательно войдёт в минимальную ДНФ. Строка, содержащая существенную импликанту, а также столбцы, на пересечении с которыми в этой строке стоит метка избыточности, вычёркиваются. Это позволяет упростить последующие шаги минимизации. Если после упомянутого вычёркивания в оставшейся части таблицы появятся строки, не содержащие меток или содержащие идентично расположенные метки, то такие строки также вычёркиваются. В последнем случае оставляют одну — ту, в которой простая импликанта имеет наименьший ранг среди остальных вычёркиваемых импликант.

Таблица 5. Удаление из импликантной матрицы существенных импликант и покрываемых ими минтермов.

0, 1, 8, 9
0, 2, 8, 10
2, 6, 10, 14
1, 5
5, 7
6, 7

0	1	2	5	6	7	8	9	10	14
√	√					√	√
√		√				√		√
		√		√				√	√
	√		√
			√		√
				√	√

В нашей функции по одной метке имеют столбцы 9 и 14. Следовательно, имеют место две существенные импликанты: и . С учётом этого поиск остальных импликант минимальной ДНФ можно упростить, исключив строки с существенными импликантами, а также перекрываемые ими столбцы. Это показано в таблице . (удаляемые столбцы закрашены).

После вычёркивания существенных импликант и , а также столбцов с минтермами, которые поглощаются этими импликантами, получим сокращённую матрицу (таблица 6).

Таблица 6. Сокращённая импликантная матрица

		5	7
0, 2, 8, 10
1, 5		√
5, 7		√	√
6, 7			√

Первая строка не содержит меток избыточности, поэтому её можно удалить. (таблица 7)

Таблица 7. Сокращённая импликантная матрица после исключения пустых строк.

		5	7
1, 5		√
5, 7		√	√
6, 7			√

В сокращённой импликантной матрице (таблица 7) нужно выбрать минимально возможную совокупность строк, которая включает метки во всех столбцах («покрывает» все оставшиеся в таблице минтермы). Дизъюнкция простых импликант, соответствующих строкам этой совокупности, а также ранее вычеркнутых существенных импликант, образует тупиковую ДНФ. В общем случае полных покрытий с одинаковым числом строк, а значит, и тупиковых ДНФ может быть несколько.

Из матрицы (таблица 7) видно, что минимальное покрытие не исключённых ранее минтермов обеспечивает простая импликанта либо пара импликант и . С учётом ранее выявленных существенных импликант получаем две тупиковые ДНФ:

;

.

В случае нескольких тупиковых форм предпочтение отдаётся той из них, которая имеет наименьший коэффициент сложности. Если получилась лишь одна тупиковая ДНФ, то она одновременно является и минимальной.

Коэффициент сложности первой из двух получившихся тупиковых форм равен 10, а второй — 14. По этой причине минимальной ДНФ следует признать первое выражение:

.

Нет времени вникать в решение? Можно заказать работу!

Пройти тест по теме Математическая логика

К началу страницы

Минимизация ПФ методом Квайна

Идея минимизации ПФ методом Квайна заключается в применении двух соотношений:

1) – соотношение (неполного) склеивания;

2) – соотношение поглощения.

Справедливость этих соотношений можно проверить при помощи элементарных преобразований или по таблицам истинности.

Теорема Квайна. Если в совершенной дизъюнктивной нормальной форме ПФ провести все операции неполного склеивания и затем все операции поглощения, то в результате получится сокращенная ДНФ исходной ПФ, т.е. дизъюнкция всех ее простых импликант.

Доказательство этой теоремы приводится, например, в [7], при этом используется операция развертывания, обратная операции склеивания:

.

Из формулировки теоремы Квайна следует, что в качестве исходной формы представления ПФ должна использоваться СДНФ. Если функция задана в произвольной форме, то вначале ее следует преобразовать к СДНФ. При этом переход от произвольной ДНФ к СДНФ осуществляется путем применения операции развертывания.

Практическое применение метода Квайна можно условно разделить на два этапа. На первом этапе минимизации производятся все возможные склеивания и поглощения по заданной СДНФ минимизируемой функции. В результате получается сокращенная ДНФ.

На втором этапе для получения минимальной ДНФ необходимо исключить из сокращенной ДНФ все лишние простые импликанты. Это делается с помощью так называемой импликантной матрицы Квайна, которая представляет собой таблицу, столбцы которой отмечаются простыми импликантами, т.е. дизъюнктивными членами полученной на предыдущем этапе сокращенной ДНФ, а строки – членами СДНФ минимизируемой ПФ. При этом в ячейке импликантной матрицы на пересечении i-й строки и j-го столбца ставится отметка, если соответствующая этому столбцу импликанта является частью члена СДНФ, которому соответствует j-я строка.

Минимальная ДНФ строится по импликантной матрице следующим образом. Анализируются все возможные совокупности простых импликант (столбцы матрицы), накрывающие все члены СДНФ (строки матрицы). Простая импликанта накрывает член СДНФ, если на пересечении соответствующей строки и столбца матрицы имеется отметка. Одна импликанта может накрывать несколько строк. Из этих совокупностей выбирается одна (или несколько) с наименьшим числом членов (простых импликант), которая определяет минимальную ДНФ.

Для сокращения перебора можно пользоваться следующим подходом. Вначале по возможности определяются строки импликантной матрицы, в которых имеется только одна отметка. Простые импликанты, которым соответствуют эти отметки, называются базисными и обязательно входят в минимальную ДНФ функции, так как только эти простые импликанты в минимальной ДНФ представляют члены исходной СДНФ, записанные в найденных строках. Остальные строки импликантной матрицы должны быть накрыты минимальным числом простых импликант. В некоторых случаях базисные импликанты могут накрывать все строки.

Рассмотрим пример.

Пусть ПФ задана картой Карно (табл. 4.6). Ее СДНФ имеет вид

На первом этапе выполним все склеивания конституент 1 по одной переменной. При этом будет получена совокупность элементарных произведений, являющихся импликантами и представляющих собой общие части склеиваемых конституент. Для удобства присвоим каждому получаемому элементарному произведению порядковый номер. Не участвовавшие в очередном склеивании конституенты 1 или импликанты должны входить в последующие совокупности импликант в неизмененном виде.

Повторим процедуру склеивания по одной переменной над каждой парой элементов совокупности импликант, полученных на предыдущем шаге. Будем повторять эту процедуру до тех пор, пока остаются элементарные произведения, между которыми возможно склеивание. Каждому элементу новой совокупности поставим в соответствие индекс, составленный из индексов импликант, участвующих в склеивании.

Полученную совокупность необходимо дополнить определенной на предыдущем этапе импликантой с порядковым номером 5, так как эта импликанта не участвовала в последующем склеивании (является простой).

Над полученной совокупностью элементарных произведений необходимо выполнить процедуру поглощения. В рассматриваемом примере совокупность элементарных произведений не содержит элементов, способных поглощать другие элементы, за исключением повторяющихся.

Окончательно, после исключения повторяющихся элементов, совокупность импликант запишется в следующем виде:

Дальнейшее выполнение склеиваний и поглощений невозможно.

Запишем сокращенную ДНФ минимизируемой функции:

Построим импликантную матрицу Квайна (табл. 4.9).

Таблица 4.9

№	Конституенты 1	Простые импликанты
		+	+
		+			+
		+
		+	+
			+	+
			+	+
				+
				+
					+

 

Поставим отметки в ячейках импликантной матрицы, находящихся на пересечении таких строк и столбцов, в которых простая импликанта является частью соответствующей конституенты 1.

Отыщем минимальное покрытие столбцами всех строк таблицы. Столбец импликантной матрицы, которому соответствует простая импликанта , обязательно должен войти в минимальное покрытие, поскольку только эта импликанта накрывает строки 7 и 8 матрицы.

Кроме того, простая импликанта может представлять в минимальной совокупности еще две конституенты 1, находящиеся в строках 5 и 6.

Аналогичные рассуждения можно провести в отношении простой импликанты , поскольку только она может представлять в минимальной совокупности простых импликант строку 9 импликантной матрицы. Отметим, что эта импликанта также накрывает конституенту 1, записанную в строке 2.

Таким образом, задача упростилась и заключается в нахождении минимального покрытия оставшихся трех конституент 1 (строки 1, 3, 4) оставшимися простыми импликантами.

Очевидно, что простая импликанта накрывает оставшиеся три строки матрицы. Следовательно, простая импликанта оказалась лишней и в минимальную ДНФ не входит.

Окончательно минимальная ДНФ запишется в виде

.

Метод Квайна является базовым методом минимизации ПФ.

---

Дата добавления: 2020-02-05; просмотров: 352; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

---

William & Mary Colonial Relays — Статистика

Бейсбол Бейсбол: Facebook Бейсбол: Твиттер Бейсбол: Инстаграм Бейсбол: Расписание Бейсбол: состав Бейсбол: Новости Баскетбол Баскетбол: Facebook Баскетбол: Твиттер Баскетбол: Инстаграм Баскетбол: Расписание Баскетбол: состав Баскетбол: Новости Напрямик По пересеченной местности: Facebook По пересеченной местности: Твиттер Кросс-кантри: Инстаграм Кросс-кантри: Расписание Кросс-кантри: состав Кросс-кантри: Новости Футбол Футбол: Фейсбук Футбол: Твиттер Футбол: Инстаграм Футбол: Расписание Футбол: состав Футбол: Новости Гольф Гольф: Фейсбук Гольф: Твиттер Гольф: Инстаграм Гольф: Расписание Гольф: состав Гольф: Новости Лакросс Лакросс: Facebook Лакросс: Твиттер Лакросс: Инстаграм Лакросс: Расписание Лакросс: состав Лакросс: Новости Футбольный Футбол: Фейсбук Футбол: Твиттер Футбол: Инстаграм Футбол: Расписание Футбол: Состав Футбол: Новости Плавание и дайвинг Плавание и дайвинг: Facebook Плавание и дайвинг: Твиттер Плавание и дайвинг: Instagram Плавание и дайвинг: Расписание Плавание и дайвинг: состав Плавание и дайвинг: Новости Большой теннис Теннис: Facebook Теннис: Твиттер Теннис: Инстаграм Теннис: Расписание Теннис: состав Теннис: Новости Легкая атлетика Легкая атлетика: Facebook Легкая атлетика: Твиттер Легкая атлетика: Instagram Легкая атлетика: Расписание Легкая атлетика: состав Легкая атлетика: Новости Водное поло Водное поло: Facebook Водное поло: Твиттер Водное поло: Инстаграм Водное поло: Расписание Водное поло: Состав Водное поло: Новости Борьба Борьба: Facebook Борьба: Твиттер Борьба: Инстаграм Борьба: Расписание Борьба: состав Борьба: Новости Баскетбол Баскетбол: Facebook Баскетбол: Твиттер Баскетбол: Инстаграм Баскетбол: Расписание Баскетбол: состав Баскетбол: Новости Напрямик По пересеченной местности: Facebook По пересеченной местности: Твиттер Кросс-кантри: Инстаграм Кросс-кантри: Расписание Кросс-кантри: Состав Кросс-кантри: Новости Хоккей на траве Хоккей на траве: Facebook Хоккей на траве: Твиттер Хоккей на траве: Instagram Хоккей на траве: Расписание Хоккей на траве: Состав Хоккей на траве: Новости Гольф Гольф: Фейсбук Гольф: Твиттер Гольф: Инстаграм Гольф: Расписание Гольф: состав Гольф: Новости Лакросс Лакросс: Facebook Лакросс: Твиттер Лакросс: Инстаграм Лакросс: Расписание Лакросс: Состав Лакросс: Новости Гребля Гребля: Facebook Гребля: Твиттер Гребля: Инстаграм Гребля: Расписание Гребля: состав Гребля: Новости Футбольный Футбол: Фейсбук Футбол: Твиттер Футбол: Инстаграм Футбол: Расписание Футбол: Состав Футбол: Новости Софтбол Софтбол: Facebook Софтбол: Твиттер Софтбол: Инстаграм Софтбол: Расписание Софтбол: состав Софтбол: Новости Плавание и дайвинг Плавание и дайвинг: Facebook Плавание и дайвинг: Твиттер Плавание и дайвинг: Instagram Плавание и дайвинг: Расписание Плавание и дайвинг: состав Плавание и дайвинг: Новости Большой теннис Теннис: Facebook Теннис: Твиттер Теннис: Инстаграм Теннис: Расписание Теннис: Состав Теннис: Новости Легкая атлетика Легкая атлетика: Facebook Легкая атлетика: Твиттер Легкая атлетика: Instagram Легкая атлетика: Расписание Легкая атлетика: Состав Легкая атлетика: Новости Волейбол Волейбол: Facebook Волейбол: Твиттер Волейбол: Инстаграм Волейбол: Расписание Волейбол: Состав Волейбол: Новости Водное поло Водное поло: Facebook Водное поло: Твиттер Водное поло: Инстаграм Водное поло: Расписание Водное поло: Состав Водное поло: Новости Обогащение студентов-спортсменов Студент-спортсмен, здоровье и благополучие Имя, изображение и подобие Что значит быть бизоном Университет Бакнелла Прием и помощь Центр соответствия требованиям NCAA Имя, изображение и подобие Студент-спортсмен, здоровье и благополучие Обогащение студентов-спортсменов Удобства Спортивная подготовка и спортивная медицина Сила и кондиционирование Лига патриотов на ESPN+ Приложение нации бизонов Живая статистика Виртуальный приветственный центр Колледж искусств и наук Инженерный колледж Колледж управления Фримена Успех последипломного образования Льюисбург, Пенсильвания Приветствие от AD О клубе Бизон Пожертвовать Способы дать Bison Athletics Fund for Excellence Одно стадо, один день зал славы Юниор Бизон Клуб Стратегический план Информация о билетах Купить билеты Командный магазин TicketSmarter — официальный партнер по перепродаже билетов Лига патриотов на ESPN+ Приложение нации бизонов Живая статистика Фейсбук Инстаграм Твиттер Канал YouTube COVID-19Зрительская политика Удобства Направления Акции и события Юниор Бизон Клуб Зубр Хорошего спорта! Программа Политика задней двери Составное расписание Каталог Соответствие NCAA Атлетическая подготовка/Спортивная медицина Сила и кондиционирование Черлидинг Услуги отдыха Мужская команда Club Varsity Политика Bucknell Athletics NIL Стратегический план Чествование ученого-спортсмена зал славы Обладатели небывалых наград для пожилых людей по средам с. .. Подкаст «Тогда, сейчас, навсегда, луч» Архив историй Спонсорские возможности Вакансии

Райт лидирует на чемпионате Европы среди финнов

Пожалуйста, выберите домашнюю версию

Версия Sail-World AsiaSail-World AustraliaSail-World CanadaSail-World EuropeSail-World New ZealandSail-World United KingdomSail-World USAYachtsandYachting.comCruising Северное полушариеCruising Южное полушариеMarine Business EuropeMarine Business North AmericaMarine Business OceaniaPowerboat.World EuropeMotorboat.World North AmericaMotorboat.World OceaniaFishingBoating.World AustraliaFishingBoating .World New ZealandFishingBoating.World USANZ Boating World

by Finn media, 27 сентября 2006 г.

Эд Райт (Великобритания) Finn Class http://www.finnclass.org

Эд Райт из Британии максимально использовал второй день чемпионата Европы среди финнов, выиграв первую гонку и заняв третье место во второй. Спортсмен команды Skandia GBR сейчас лидирует в чемпионате, отставая от действующего чемпиона мира Йонаса Хёг-Кристенсена (DEN) на 6 очков в общем зачете.

Сегодняшние условия в Паламосе обеспечили отличное плавание. Солнце вышло, Tramontana дул со скоростью от 18 до 26 узлов, небольшие изменчивые волны в сочетании с формирующейся зыбью делали гонки захватывающими.

Это был отличный день и для Энтони Носситера (Австралия), который наслаждался изнурительными условиями. Матрос команды +39 разогрелся в первой гонке, заняв пятое место, прежде чем выиграть вторую стильно, пересекнув финишную черту на 40 секунд раньше испанской надежды Рафаэля Трухильо. «Я много тренировался в Валенсии на моем финне, — объяснил Носситер с широкой улыбкой на лице, — но только в ясную погоду. Такой сильный бриз — хорошая перемена, это больше похоже на Австралию!».

Средняя скорость 22 узла в первой гонке и порывы ветра до 26 узлов временами затрудняли гонку. Во второй гонке скорость снизилась до 16 узлов, однако Сорен Хольм (Дания) увидел, как его мачта сломалась и упала на первом такте.

Поскольку четыре моряка выиграли по гонке, чемпионат остается открытым в середине первой серии. Отсутствие Эмилиоса Папатанасиу, который сегодня вернулся в Грецию после того, как повредил колено во время вчерашней первой гонки, делает игры еще более открытыми.

Британец Марк Эндрюс увеличивает отставание в юниорском дивизионе после 7-го места в гонке 3. Он занимает 5 мест в общем зачете на 21-м месте. Эндрю Миллс — 34-й, а Петр Кула — 3-й юниор на 38-м месте.

Общие позиции после второго дня:

1 Великобритания 111 Эдвард Райт 2 6 1 3 12 очков
2 ДЕН 2 Йонас Хёг-Кристенсен 4 2 8 4 18
3 Хорватия 25 Марин Мишура 3 5 4 СЛ 8 25 9 0 6 25 9 0 6 Гаспер Винсек 5 3 6 12 26
5 FRA 73 Гийом Флоран 1 11 10 5 27
6 AUS 221 Энтони Носситер 3 19 5 1 28
7 ESP 100 Рафаэль Трухильо Вильяр 23 1 12 2 38
8 FRA 972 Исмаэль Бруно 6 16 20 9 51
9 CRO 524 Иван Кляквич-Гаспич 3 1 0 7 FIN1 8 14 216 Тапио Ниркко 12 23 13 7 55
11 Швеция 736 Йохан Тилландер 16 4 23 14 57
12 НОР 1 Пир Моберг 20 14 2 22 58
13 Чехия 1 Михаэль Майер 19 20 19 11 5 Sg 1 Даниэль Бирмарк 1 Даниэль Бирмарк 1 69 1 18 70
15 POL 12 Вацлав Шукель 18 21 15 16 70
16 POL 7 Рафал Шукель 15 29 4 28 76
17 AUT 271 Florian Raudaschl 9 10 31 26 26 76
18 ESP 836 Альберто Ваделл Сабатер 7 26 27 27 77 77
19 CAN 41 Крис Кук 13 18 17 30 78
20 NED 842 Pieter-Jan Postma 17 5 30 27 79
21 GBR. 88 Марк Эндрюс 25 22 7 25 79
22 NED 80 S.E. Willems 37 25 9 8 79
23 ESP 310 Pablo Arrarte 33 13 22 13 81
24 GBR 625 ED Greig 24 12 24 24 24 84
25 USA 4 Zach Railey 21 17 23 23 23 89
26 GBR 550 Matt Howard 28 24 33 10 95
27 ESP 1 Диего Фруктуозо 10 36 29 21 96
28 IRL 10 Аарон О`Грэйди 26 27 14 31 98
29 DEN 7 Сорен Холм 22 9 11 DNF 112
30 CZE 9 Michal Hruby 27 33 21 35 116
31 AUS 228 Josh Beaver 31 31 25 29 116
32 NED 64 Wietze Zetzema 29 30 43 36 138
33 IRL 5 Goodbody 40 39 16 49 144
34 GBR 634 Andrew Mills 35 32 38 42 147
35 NED 41 Karel Van Hellemond 45 35 32 37 149
36 ITA 117 Giorgio Poggi 34 34 35 46 149
37 EST 7. 151
38 POL 17 Петр Кула 32 28 39 53 152
39 GRE 8 Александрос Драгуцис 36 41 36 39152
40 GER 174 Matthias Bohn 49 47 42 20 158
41 ITA 68 Piero Romeo 41 42 34 43 160
42 ITA 101 Riccardo Cordovani 46 37 50 32 165
43 GBR 628 Nick Craig 38 49 45 33 165
44 POL 1 Krzysztof Dabkowski 39 44 57 34 174
45 SWE 6 Björn Allansson 42 38 56 41 177
46 AUS 241 Brendan Casey 53 53 37 40 183
47 GBR 99 Henry Bagnall 52 56 40 38 186
48 CZE 52 Tomas Vika 48 40 46 52 186
49 ESP 161 Мигель Фернандес Васко 43 59 47 47 196
50 CAN 115 Дерек Месс 44 50 52 50 196
51 GBR 589 Питер Дэвидсон 60 55 41 45 201
52 POL 45 PIOTR MAZUR 50 52 59 44 205
53 ITA 660 Davide Bortoletto 55 51 51 48 205
54 NED 804 CEES Scheurwater 56 46 53 56 211111135 55555555555555555555555555555555555555555555555555555555555555555 Беликзай 58 58 49 51 216
56 ITA 70 Francesco Lubrano 47 45 55 DNC 217
57 ESP 696 ALVARO ELORZA HERRA 57 57 54 54 222
58 HUSKTON PRAL 54 43 58 DNF 225
59 59 CRZE 3RILC 34 58 DNF 225
59 59 59 59 59 59 59 59 59 59 59 59 59 59 59 59. 239
60 POR 83 Нуно Эспириту Санто 51 61 60 DNC 242
61 GBR 8 Тим Карвер 62 48 DNC DNC 250
62 POR 55 Хорхе Пиньейро де Мело 59 62 61 DNC 252
63 IRL 2 Гай О’Лири 63 60 DNF DNC 263
64 POR 310 Родриго Куина 61 65 DNC DNC 266
65 ESP 5 196 DNC 3 6 DNC0 6 Пабло Лопес4 Бальдан 66 ITA 941 Paolo Cisbani 65 64 DNC DNC 269
67 ESP 190 Mauricio Luque Diaz DNF DNC DNC DNC 280
67 GRE 7 Emilios Papathanasiou DNF DNC DNC DNC 280
67 ESP 316 Francisco Javier Garcia Miura DNC DNC DNC DNC 280

Principal race офицер Рафаэль Серрано сообщил тренерам во время ежедневного разбора полетов, что завтра может быть две гонки. В ближайшие дни синоптики обещают 3-узловой ветер.

Если вы хотите сделать ссылку на эту статью, используйте этот URL-адрес: www.sail-world.com/27729.

Олимпиада – Португалия на летних Олимпийских играх 1960 года

Художественная гимнастика
Индивидуальное многоборье, мужчины	Эрменеджильдо Кандеяс	120
Вольные упражнения, мужчины	Эрменеджильдо Кандеяс	=111 r1/2
Прыжки с лошади, мужчины	Эрменеджильдо Кандеяс	129 р1/2
Брусья мужские	Эрменеджильдо Кандеяс	=116 r1/2
Турник мужской	Эрменеджильдо Кандеяс	114 р1/2
Кольца мужские	Эрменеджильдо Кандеяс	116 р1/2
Конь с шипами, мужчины	Эрменеджильдо Кандеяс	106 р1/2
Индивидуальное многоборье, женщины	Далия Саммер	109
	Эсбела да Фонсека	116
	Мария Хелена Кунья	119
Вольные упражнения, женщины	Мария Хелена Кунья	=105 r1/2
	Далия Саммер	110 р1/2
	Эсбела да Фонсека	112 р1/2
Конный прыжок, женщины	Далия Саммер	91 р1/2
	Эсбела да Фонсека	=101 r1/2
	Мария Хелена Кунья	119 р1/2
Брусья, женские	Далия Саммер	115 р1/2
	Эсбела да Фонсека	120 р1/2
	Мария Хелена Кунья	122 р1/2
Балансир женский	Далия Саммер	110 р1/2
	Мария Хелена Кунья	=113 r1/2
	Эсбела да Фонсека	117 р1/2
Легкая атлетика
5000 метров, Мужчины	Мануэль Оливейра	6 ч3 р1/2
3000 м с препятствиями, мужчины	Хоаким Феррейра	11 ч2 р1/2
Прыжки в длину, мужчины	Педро де Алмейда	28 р1/2
Метание молота, мужчины	Эдуардо Альбукерке	28 р1/2
Десятиборье, мужчины	Вилар Сантос	ДНФ
Велосипедная дорога
Шоссейная гонка, индивидуальная, мужчины	Рамиро Мартинс	ДНФ
	Хосе Пачеко	ДНФ
	Марио Сильва	ДНФ
	Франсиско Валада	ДНФ
100 километров Командная гонка на время, Мужчины	Португалия	25
	Хосе Пачеко • Марио Силва • Франсиско Валада • Рамиро Мартинс
Конная выездка
Индивидуальный, открытый	Антонио, виконт де Мозелос	10
	Луис Мена и Сильва	17
Конный спорт
Личное, Мужчины	Марио Дельгадо	35
	Хорхе Матиас	ДНФ
	Альваро Саббо	ДНФ
	Хоаким Сильва	ДНФ
Команда, Мужчины	Португалия	ДНФ
	Альваро Саббо • Хоаким Силва • Хорхе Матиас • Марио Дельгадо
Конный спорт
Индивидуальный, открытый	Энрике Кальядо	=11
	Жоао Лопес	ДНФ
	Антониу де Алмейда	ДНФ
Команда, открытая	Португалия	ДНФ
	Антониу де Алмейда • Энрике Кальядо • Жоао Лопес
Ограждение
Рапира, индивидуальная, мужчины	Мануэль Боррего	4 п11 р1/5
	Орландо Азинхайс	6 изн. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт