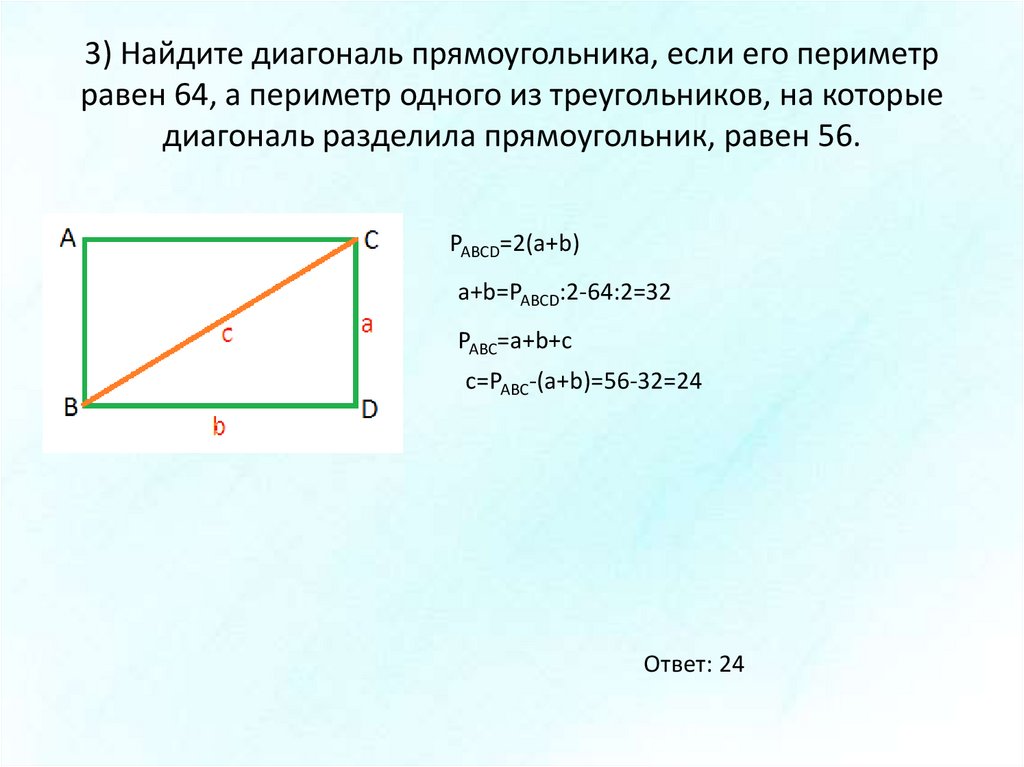
Какой периметр у равнобедренного треугольника. Периметр и площадь треугольника
Периметром треугольника , как в прочем и любой фигуры, называется сумма длин всех сторон. Довольно часто это значение помогает найти площадь или используется для расчета других параметров фигуры.
Формула периметра треугольника выглядит так:
Пример расчета периметра треугольника. Пусть дан треугольник со сторонами a = 4см, b = 6 см, c = 7 см. подставим данные в формулу: см
Формула расчета периметра равнобедренного треугольника будет выглядеть так:
Формула расчета периметра равностороннего треугольника :
Пример расчета периметра равностороннего треугольника. Когда все стороны фигуры равны, то их можно просто умножить на три. Допустим, дан правильный треугольник со стороной 5 см в таком случае: см
В общем, когда все стороны даны, найти периметр довольно просто. В остальных же ситуациях требуется найти размер недостающей стороны. В прямоугольном треугольнике можно найти третью сторону по
В прямоугольном треугольнике можно найти третью сторону по
Рассмотрим пример расчета периметра равнобедренного треугольника при условии, что мы знаем длину катетов в прямоугольном равнобедренном треугольнике.
Дан треугольник с катетами a
=b
=5 см. Найти периметр. Для начала найдем недостающую сторону с
. см
Теперь посчитаем периметр: см
Периметр прямоугольного равнобедренного треугольника будет равен 17 см.
В случае, когда известна гипотенуза и длина одного катета, можно найти недостающий по формуле:
Если в прямом треугольнике известна гипотенуза и один из острых углов, то недостающая сторона находится по формуле.
Предварительные сведения
Периметр любой плоской геометрической фигур на плоскости определяется как сумма длин всех его сторон. Исключением из этого не является и треугольник. Сначала приведем понятие треугольника, а также виды треугольников в зависимости от сторон.
Определение 1
Треугольником будем называть геометрическую фигуру, которая составлена из трех точек, соединенных между собой отрезками (рис. 1).
Определение 2
Точки в рамках определения 1 будем называть вершинами треугольника.
Определение 3
Отрезки в рамках определения 1 будем называть сторонами треугольника.
Очевидно, что любой треугольник будет иметь 3 вершины, а также три стороны.
В зависимости от отношении сторон друг к другу, треугольники делятся на разносторонние, равнобедренные и равносторонние.
Определение 4
Треугольник будем называть разносторонним, если ни одна из его сторон не равняется никакой другой.
Определение 5
Треугольник будем называть равнобедренным, если две его стороны равны друг другу, но не равняются третьей стороне.
Определение 6
Треугольник будем называть равносторонним, если все его стороны равняются друг другу.
Все виды этих треугольников Вы можете видеть на рисунке 2.
Как найти периметр разностороннего треугольника?
Пусть нам дан разносторонний треугольник, у которого длины сторон будут равняться $α$, $β$ и $γ$.
Вывод: Для нахождения периметра разностороннего треугольника надо все длин его сторон сложить между собой.
Пример 1
Найти периметр разностороннего треугольника равняются $34$ см, $12$ см и $11$ см.
$P=34+12+11=57$ см
Ответ: $57$ см.
Пример 2
Найти периметр прямоугольного треугольника, у которого катеты равняются $6$ и $8$ см.
Сначала найдем длину гипотенуз этого треугольника по теореме Пифагора. Обозначим ее через $α$, тогда
$α=10$ По правилу вычисления периметра разностороннего треугольника, получим
$P=10+8+6=24$ см
Ответ: $24$ см.
Как найти периметр равнобедренного треугольника?
Пусть нам дан равнобедренный треугольник, у которого длины боковых сторон будут равняться $α$, а длина основания равняется $β$.
По определению периметра плоской геометрической фигуры, получим, что
$P=α+α+β=2α+β$
Вывод: Для нахождения периметра равнобедренного треугольника надо удвоенную длину его сторон сложить с длиной его основания.
Пример 3
Найти периметр равнобедренного треугольника, если его боковые стороны равняются $12$ см, а основание $11$ см.
По рассмотренному выше примеру, видим, что
$P=2\cdot 12+11=35$ см
Ответ: $35$ см.
Пример 4
Найти периметр равнобедренного треугольника, если его высота, проведенная на основание, равняется $8$ см, а основание $12$ см.
Рассмотрим рисунок по условию задачи:
Так как треугольник равнобедренный, то $BD$ также является и медианой, следовательно, $AD=6$ см.
По правилу вычисления периметра равнобедренного треугольника, получим
$P=2\cdot 10+12=32$ см
Ответ: $32$ см.
Как найти периметр равностороннего треугольника?
Пусть нам дан равносторонний треугольник, у которого длины всех сторон будут равняться $α$.
По определению периметра плоской геометрической фигуры, получим, что
$P=α+α+α=3α$
Вывод: Для нахождения периметра равностороннего треугольника надо длину стороны треугольника умножить на $3$.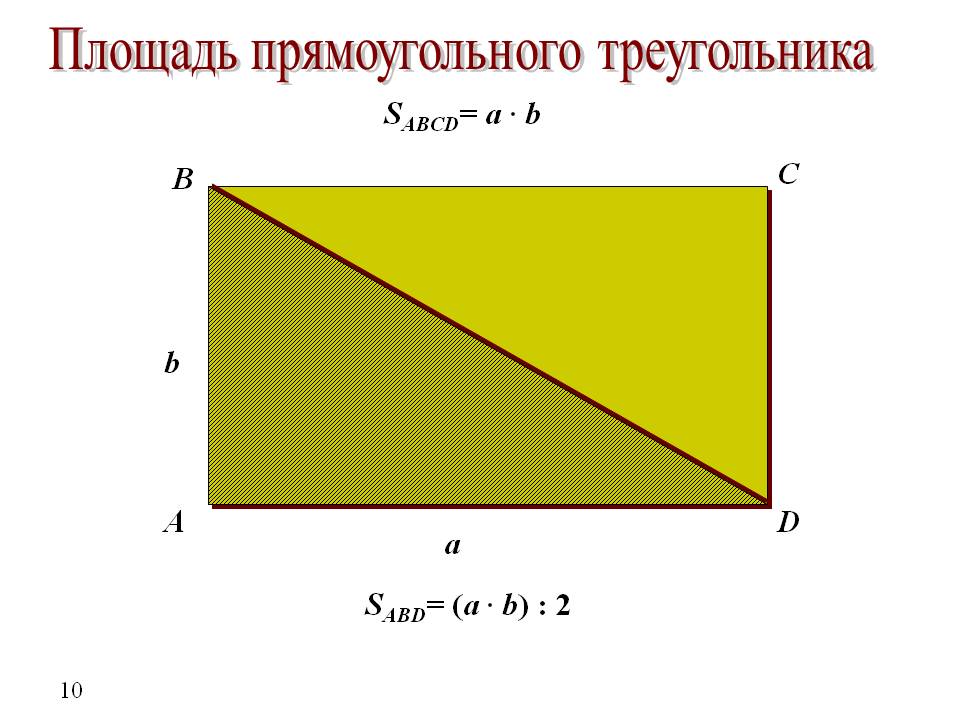
Пример 5
Найти периметр равностороннего треугольника, если его сторона равняется $12$ см.
По рассмотренному выше примеру, видим, что
$P=3\cdot 12=36$ см
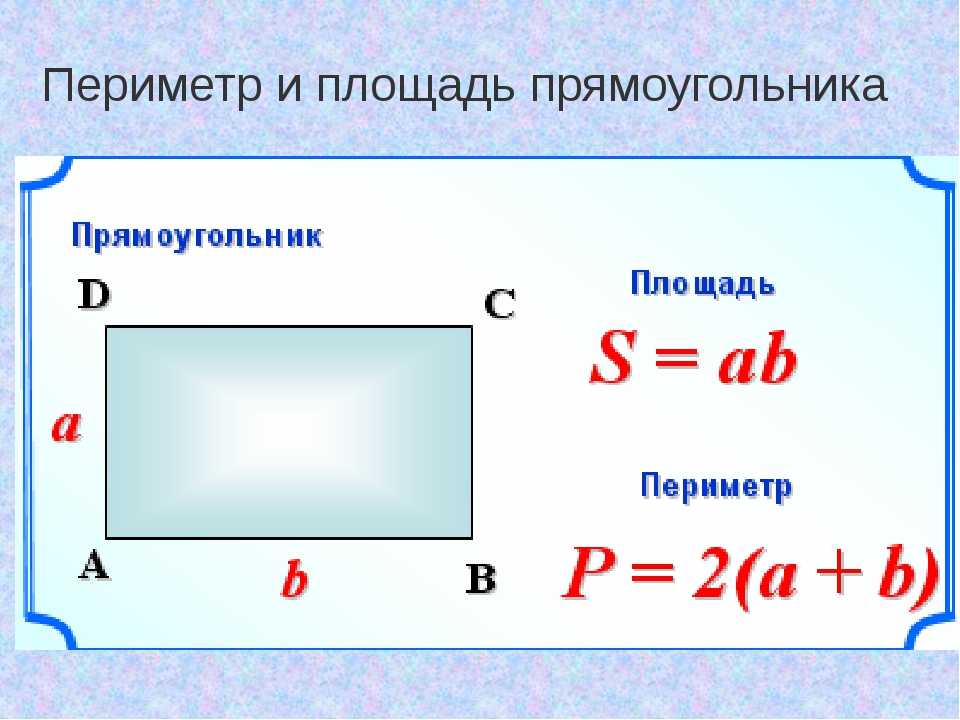
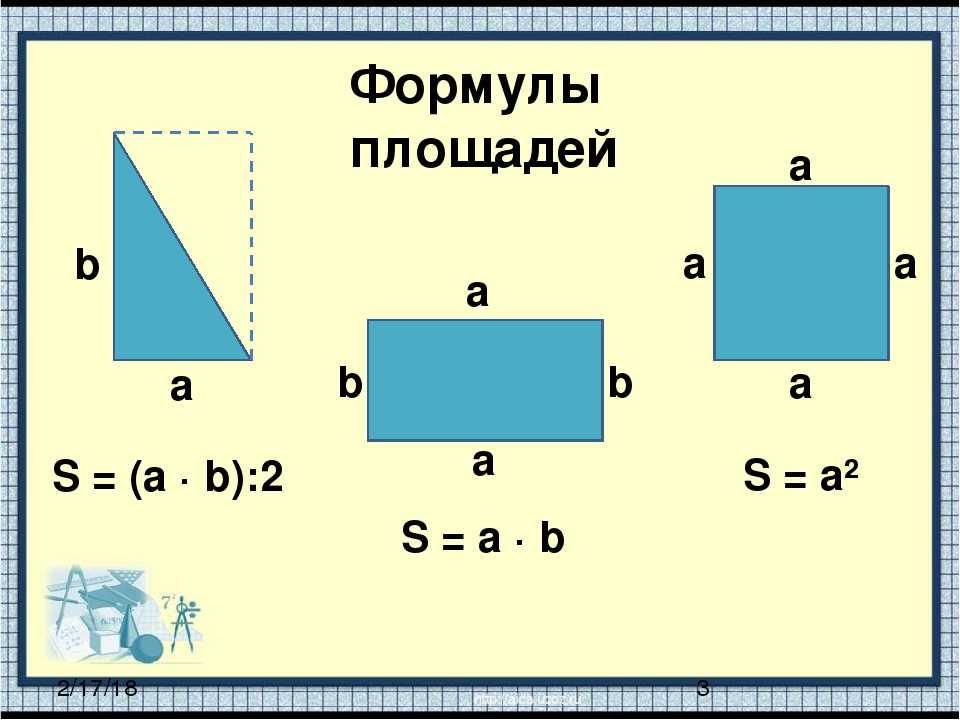
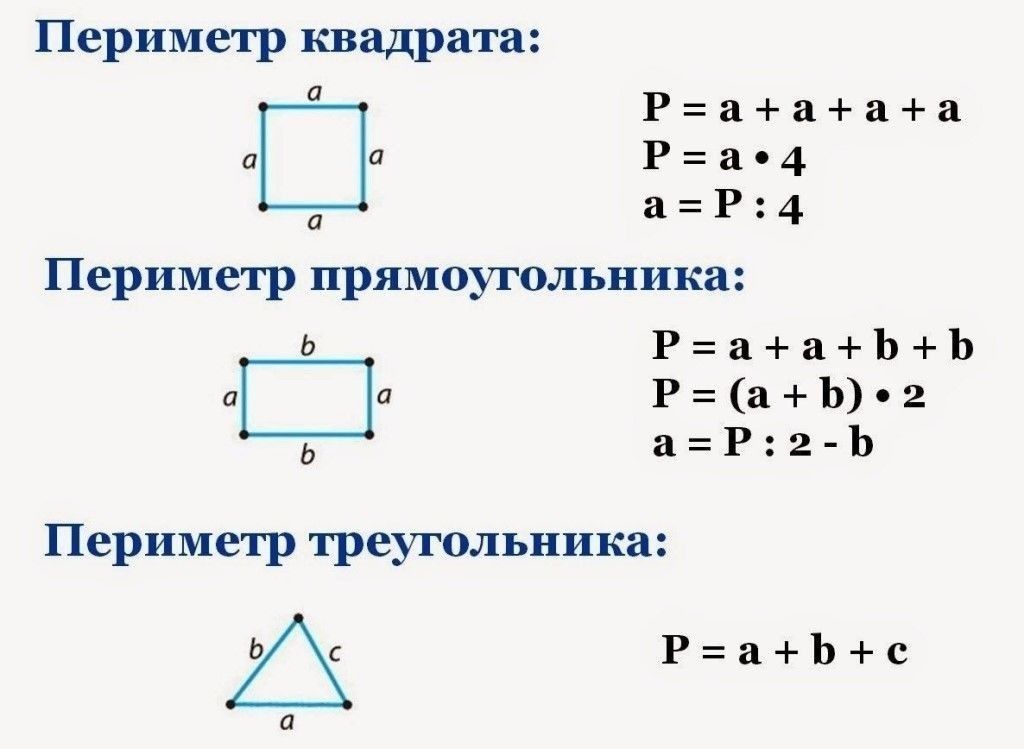
Любого треугольника равен сумме длин трёх его сторон. Общая формула для нахождения периметра треугольников:
P = a + b + c
где P — это периметр треугольника, a , b и c — его стороны.
Можно найти сложив последовательно длины его сторон или умножив длину боковой стороны на 2 и прибавив к произведению длину основания. Общая формула для нахождения периметра равнобедренных треугольников будет выглядеть так:
P = 2a + b
где P — это периметр равнобедренного треугольника, a — любая из боковых сторон, b — основание.
Можно найти сложив последовательно длины его сторон или умножив длину любой его стороны на 3. Общая формула для нахождения периметра равносторонних треугольников будет выглядеть так:
P = 3a
где P — это периметр равностороннего треугольника, 
Площадь
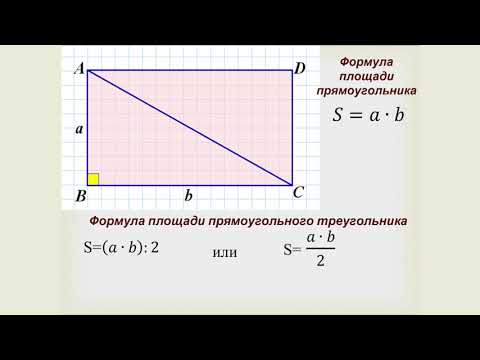
Для измерения площади треугольника можно сравнить его с параллелограммом . Рассмотрим треугольник ABC :
Если взять равный ему треугольник и приставить его так, чтобы получился параллелограмм, то получится параллелограмм с той же высотой и основанием, что и у данного треугольника:
В данном случае общая сторона сложенных вместе треугольников является диагональю образованного параллелограмма. Из свойства параллелограммов известно, что диагональ всегда делит параллелограмм на два равных треугольника, значит площадь каждого треугольника равна половине площади параллелограмма.
Так как площадь параллелограмма равна произведению его основания на высоту, то площадь треугольника будет равна половине этого произведения. Значит для ΔABC площадь будет равна
Теперь рассмотрим прямоугольный треугольник:
Два равных прямоугольных треугольника можно сложить в прямоугольник, если прислонить их друг к другу гипотенузой. Так как площадь прямоугольника равна произведению его смежных сторон, то площадь данного треугольника равна:
Так как площадь прямоугольника равна произведению его смежных сторон, то площадь данного треугольника равна:
Из это можно сделать вывод, что площадь любого прямоугольного треугольника равна произведению катетов, разделённому на 2.
Из данных примеров можно сделать вывод, что площадь любого треугольника равна произведению длин основания и высоты, опущенной на основание, разделённому на 2 . Общая формула для нахождения площади треугольников будет выглядеть так:
| S = | ah a |
| 2 |
где S — это площадь треугольника, a — его основание, h a — высота, опущенная на основание a .
Периметр – это сумма всех сторон фигуры. Эта характеристика, наравне с площадью, одинаково востребована для всех фигур. Формула периметра равнобедренного треугольника логично вытекает из его свойств, но формула не столь сложна, как получение и закрепление практических навыков.
Формула вычисления периметра
Боковые стороны равнобедренного треугольника равны между собой. Это проистекает из определения и хорошо видно даже из названия фигуры. Именно из этого свойства и проистекает формула периметра:
Это проистекает из определения и хорошо видно даже из названия фигуры. Именно из этого свойства и проистекает формула периметра:
P=2a+b, где b-это основание треугольника, a-значение боковой стороны.
Рис. 1. Равнобедренный треугольник
Из формулы видно, что для нахождения периметра достаточно знать величину основания и одной из боковых сторон. Рассмотри несколько задач на нахождение периметра равнобедренного треугольника. Задачи будем решать по мере возрастания сложности, это позволит лучше понять способ размышления, которому нужно следовать для нахождения периметра.
Задача 1
- В равнобедренном треугольнике основание равно 6, а высота, проведенная к этому основанию, равна 4. Необходимо найти периметр фигуры.
Рис. 2. Рисунок к задаче 1
Высота равнобедренного треугольника, проведенная к основанию, является также медианой и высотой. Это свойство очень часто используется при решении задач, связанных с равнобедренными треугольниками. 2}=\sqrt{9+16}=\sqrt{25}=5$$
2}=\sqrt{9+16}=\sqrt{25}=5$$
Найдем периметр: P=AC+AB*2=6+5*2=16
Задача 2
- В равнобедренном треугольнике высота, проведенная к основанию, равна 10, а острый угол при основании 30 градусам. нужно найти периметр треугольника.
Рис. 3. Рисунок к задаче 2
Эта задача осложнена отсутствием сведений о сторонах треугольника, но, зная значение высоты и угла, в прямоугольном треугольнике ABH можно найти катет AH, а после решение пойдет по тому же сценарию, что и в задаче 1.
Найдем AH через значение синуса:
$$sin (ABH)={BH\over AB}={1\over2}$$ — синус 30 градусов является табличным значением.
Выразим нужную сторону:
$$AB={{BH\over {1\over 2}}} =BH*2=10*2=20$$
Через котангенс найдем значение AH:
$$ctg(BAH)={AH\over BH}={1\over\sqrt{3}}$$
$$AH={BH\over\sqrt{3}}=10*\sqrt{3}=17,32$$ — получившееся значение округлим до сотых.
Найдем основание:
AC=AH*2=17,32*2=34,64
Теперь, когда все требуемые значения найдены, определим периметр:
P=AC+2*AB=34,64+2*20=74,64
Задача 3
- В равнобедренном треугольнике ABC известна площадь, которая равна $$16\over\sqrt{3}$$ и острый угол при основании в 30 градусов.

Значения в условии часто приводятся в виде произведения корня на число. Это делается, чтобы максимально оградить последующее решение от погрешностей. Округлять результат лучше в конце вычислений
При такой постановке задачи может показаться, что решений нет, ведь сложно выразить одну из сторон или высоту из имеющихся данных. Попробуем решить по-другому.
Обозначим высоту и половину основания латинскими буквами: BH=h и AH=a
Тогда основание будет равно: AC=AH+HC=AH*2=2a
Площадь: $$S={1\over 2}*AC*BH={1\over 2}*2a*h=ah$$
С другой стороны, значение h можно выразить из треугольника ABH через тангенс острого угла. Почему именно тангенс? Потому что в треугольнике ABH мы уже обозначили два катета a и h. Нужно выразить одно через другое. Два катета вместе связывают тангенс и котангенс. Традиционно к котангенсу и косинусу обращаются, только если не подходит тангенс или синус. Это не правило, можно решать так, как удобно, просто так принято. 2}=4,62$$
2}=4,62$$
Подставим значения в формулу периметра:
P=AB*2+AH*2=4,62*2+4*2=17,24
Что мы узнали?
Мы разобрались подробно во всех тонкостях нахождения периметра равнобедренного треугольника. Решили три задачи разного уровня сложности, показав на примере, как решаются типовые задачи на решение равнобедренного треугольника.
Тест по теме
Оценка статьи
Средняя оценка: 4.4 . Всего получено оценок: 83.
Как найти периметр прямоугольного треугольника? – Обзоры Вики
Периметр прямоугольного треугольника — это общая длина его границы или сумма длин всех трех сторон, включая гипотенузу, высоту и основание. Это рассчитывается по формуле: Р = основание + высота + гипотенуза.
com/embed/M5OzJuVgItc» frameborder=»0″ allowfullscreen=»allowfullscreen» data-original-w=»720″ data-original-h=»520″>Во-вторых, как найти периметр прямоугольного равнобедренного треугольника? Периметр равнобедренного прямоугольного треугольника можно рассчитать по формуле: Р = ч + 2л, где h — длина гипотенузы, l — длина смежных сторон.
Как найти периметр треугольника в координатной геометрии?
Чтобы вычислить периметр треугольника, прибавьте длину его сторон. Например, если у треугольника есть стороны a, b и c, тогда периметр этого треугольника будет P = a + b + c.
тогда как найти периметр треугольника с 3 координатами? Периметр= 3 + 5 + 4 = 12
Чтобы найти периметр треугольника, найдите длины каждой стороны треугольника, используя формулу расстояния. Используйте формулу расстояния, чтобы найти длину между точками A и B, B и C, C и A. Затем сложите все три длины вместе, чтобы получить периметр.
Как найти периметр? Прямоугольник имеет две равные длины и две равные ширины. Чтобы найти периметр или расстояние вокруг прямоугольника, нам нужно сложить все четыре длины сторон. Это можно сделать эффективно, просто сложив длину и ширину, а затем умножив эту сумму на два, поскольку каждой стороны по две.
Чтобы найти периметр или расстояние вокруг прямоугольника, нам нужно сложить все четыре длины сторон. Это можно сделать эффективно, просто сложив длину и ширину, а затем умножив эту сумму на два, поскольку каждой стороны по две.
Как найти периметр треугольника 45 45 90?
Как решить треугольник 45 45 90? 45 45 90 формула треугольника
- второй катет также равен а.
- гипотенуза равна a√2.
- площадь равна а²/2.
- периметр равен a(2 + √2)
Как найти периметр? Чтобы найти периметр прямоугольника, сложите длины четырех сторон прямоугольника. Если у вас есть только ширина и высота, вы можете легко найти все четыре стороны (каждая из двух сторон равна высоте, а две другие стороны равны ширине). Умножьте высоту и ширину на два и сложите результаты.
Чему равен периметр равнобедренного прямоугольного треугольника со стороной 5?
Гипотенуза этого прямоугольного треугольника, являющегося одной из двух конгруэнтных сторон равнобедренного треугольника, имеет длину 5 единиц (согласно теореме Пифагора). Общий периметр будет длина основания (6) плюс длина гипотенузы каждого прямоугольного треугольника (5).
Общий периметр будет длина основания (6) плюс длина гипотенузы каждого прямоугольного треугольника (5).
Как найти периметр треугольника, если не хватает одной стороны? Если это прямоугольный треугольник, вы можете использовать теорема Пифагора (a2 + b2 = c2) найти длину недостающей стороны. Оттуда вы можете легко рассчитать периметр. Для других типов треугольников вы можете использовать закон косинусов, чтобы найти периметр, если вы знаете 2 стороны и хотя бы 1 из углов.
Как найти периметр треугольника без данных сторон?
Существует три основных метода определения периметра прямоугольного треугольника.
- Когда указаны длины сторон, сложите их вместе.
- Найдите недостающую сторону, используя теорему Пифагора.
- Если нам известна информация о боковых углах и боковых сторонах, найдите недостающую сторону, используя закон косинусов.
Как найти периметр 4-х точек?
Чтобы найти периметр четырехугольника на графике, мы используем следующие шаги.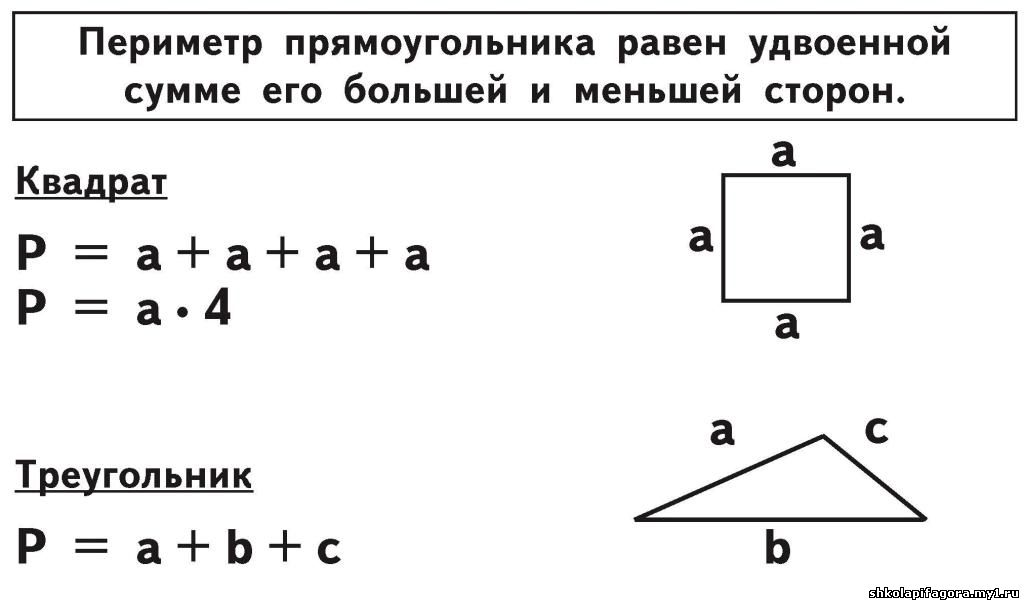
- Шаг 1: Найдите координаты вершин на графике.
- Шаг 2: Примените формулу расстояния, чтобы найти длины сторон четырехугольника.
- Шаг 3: Сложите все длины сторон, и сумма даст периметр четырехугольника.
Какая фигура имеет периметр 34 фута? периметр Прямоугольник 34 фута, а площадь 30 квадратных футов.
Как решить специальный прямоугольный треугольник 45 45 90?
Каковы стороны треугольника 45 45 90? Треугольник 45°-45°-90° — это особый прямоугольный треугольник, который имеет два угла по 45° и один угол по 90°. Длины сторон этого треугольника находятся в отношении; Сторона 1: Сторона 2: Гипотенуза = n: n: n√2 = 1: 1: √2.
Как найти гипотенузу треугольника 45 45 90?
Что такое периметр площади? Периметр. Площадь относится к пространству, занимаемому формой, предметом или поверхностью. Периметр относится к мере длины контура или границы формы, объекта или поверхности. Площадь измеряется в квадратных единицах.
Что такое периметр в математике?
CCSS.Математика: 3.MD.D.8. Периметр расстояние по краю фигуры. Узнайте, как найти периметр, сложив длины сторон различных фигур. Создано Салом Ханом.
Чему равен периметр фигуры В? Ответ: Периметр двумерной фигуры равен расстояние вокруг формы. Он находится путем сложения всех сторон (если они все равны).
Чему равен периметр равнобедренного прямоугольного треугольника, одна сторона которого равна 18?
Гипотенуза равнобедренного прямоугольного треугольника равна 18 дм, две равные стороны равны 18/√2 или 18√2/2 = 9√2 дм каждая. Периметр равнобедренного прямоугольного треугольника = 18(1+√2) дм. Площадь = основание*высота/2 = ab/2 ⟹ 20.709*7.323/2 = 75.826 квадратных единиц ответа.
Периметр равнобедренного прямоугольного треугольника = 18(1+√2) дм. Площадь = основание*высота/2 = ab/2 ⟹ 20.709*7.323/2 = 75.826 квадратных единиц ответа.
Является ли прямоугольный треугольник равнобедренным?
Вам может быть интересно, может ли прямоугольный треугольник быть равнобедренным треугольником? Да, Прямоугольный треугольник может быть равнобедренным и разносторонним треугольником но он никогда не может быть равносторонним треугольником. Равнобедренный треугольник – это треугольник, у которого хотя бы две стороны равны.
Как найти периметр прямоугольного равнобедренного треугольника? – Обзоры Вики
Периметр равнобедренного прямоугольного треугольника можно рассчитать по формуле: Р = ч + 2л, где h — длина гипотенузы, l — длина смежных сторон.
Аналогично, как найти недостающий периметр треугольника? Сложите длины трех сторон, чтобы найти периметр. Напомним, что периметр P = a + b + c. Теперь, когда вы знаете длины сторон a, b и c, вам просто нужно сложить длины вместе, чтобы найти периметр.
Напомним, что периметр P = a + b + c. Теперь, когда вы знаете длины сторон a, b и c, вам просто нужно сложить длины вместе, чтобы найти периметр.
Как найти периметр треугольника 45 45 90? Как решить треугольник 45 45 90? 45 45 90 формула треугольника
- второй катет также равен а.
- гипотенуза равна a√2.
- площадь равна а²/2.
- периметр равен a(2 + √2)
Как найти периметр? Чтобы найти периметр прямоугольника, сложите длины четырех сторон прямоугольника. Если у вас есть только ширина и высота, вы можете легко найти все четыре стороны (каждая из двух сторон равна высоте, а две другие стороны равны ширине). Умножьте высоту и ширину на два и сложите результаты.
Во-вторых, каков периметр равнобедренного прямоугольного треугольника со стороной 5? Гипотенуза этого прямоугольного треугольника, являющегося одной из двух конгруэнтных сторон равнобедренного треугольника, имеет длину 5 единиц (согласно теореме Пифагора).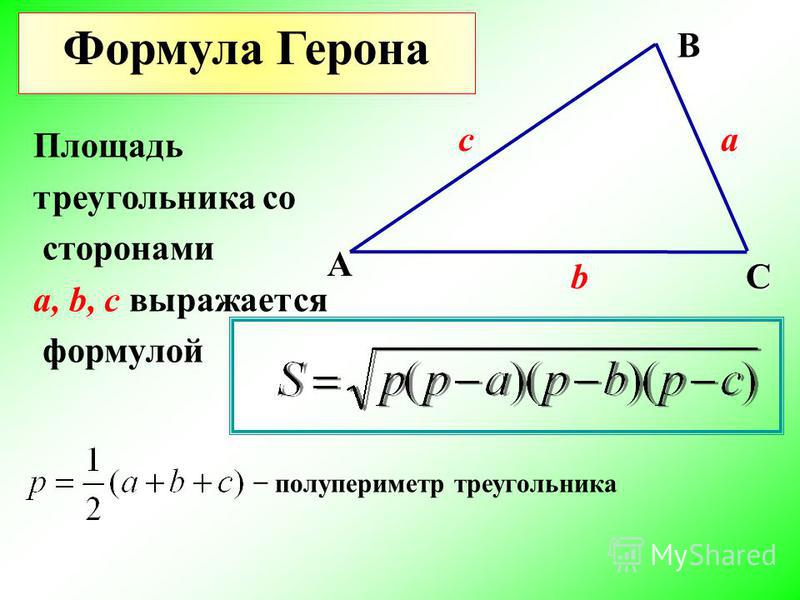 Общий периметр будет длина основания (6) плюс длина гипотенузы каждого прямоугольного треугольника (5).
Общий периметр будет длина основания (6) плюс длина гипотенузы каждого прямоугольного треугольника (5).
Какова формула периметра?
Формула периметра прямоугольника гласит, что Р = (Д + Ш) × 2, где P обозначает периметр, L обозначает длину, а W обозначает ширину. Когда вам даны размеры прямоугольной формы, вы можете просто подставить значения L и W в формулу, чтобы найти периметр.
Как решить специальный прямоугольный треугольник 45 45 90?
Каковы стороны треугольника 45 45 90? Треугольник 45°-45°-90° — это особый прямоугольный треугольник, который имеет два угла по 45° и один угол по 90°. Длины сторон этого треугольника находятся в отношении; Сторона 1: Сторона 2: Гипотенуза = n: n: n√2 = 1: 1: √2.
Длины сторон этого треугольника находятся в отношении; Сторона 1: Сторона 2: Гипотенуза = n: n: n√2 = 1: 1: √2.
Как найти гипотенузу треугольника 45 45 90?
Что такое периметр площади? Периметр. Площадь относится к пространству, занимаемому формой, предметом или поверхностью. Периметр относится к мере длины контура или границы формы, объекта или поверхности. Площадь измеряется в квадратных единицах.
Что такое периметр в математике?
CCSS.Математика: 3.MD.D.8. Периметр расстояние по краю фигуры. Узнайте, как найти периметр, сложив длины сторон различных фигур. Создано Салом Ханом.
Чему равен периметр фигуры В?
Ответ: Периметр двумерной фигуры равен расстояние вокруг формы. Он находится путем сложения всех сторон (если они все равны).
Чему равен периметр равнобедренного прямоугольного треугольника, одна сторона которого равна 18? Гипотенуза равнобедренного прямоугольного треугольника равна 18 дм, две равные стороны равны 18/√2 или 18√2/2 = 9√2 дм каждая. Периметр равнобедренного прямоугольного треугольника = 18(1+√2) дм. Площадь = основание*высота/2 = ab/2 ⟹ 20.709*7.323/2 = 75.826 квадратных единиц ответа.
Периметр равнобедренного прямоугольного треугольника = 18(1+√2) дм. Площадь = основание*высота/2 = ab/2 ⟹ 20.709*7.323/2 = 75.826 квадратных единиц ответа.
Является ли прямоугольный треугольник равнобедренным?
Вам может быть интересно, может ли прямоугольный треугольник быть равнобедренным треугольником? Да, Прямоугольный треугольник может быть равнобедренным и разносторонним треугольником но он никогда не может быть равносторонним треугольником. Равнобедренный треугольник – это треугольник, у которого хотя бы две стороны равны.
Почему мы считаем периметр? Они помогают вам количественно определить физическое пространство, а также обеспечивают основу для более сложной математики, которую можно найти в алгебре, тригонометрии и исчислении. Периметр – это измерение расстояния вокруг формы и площади дает нам представление о том, какую поверхность покрывает форма.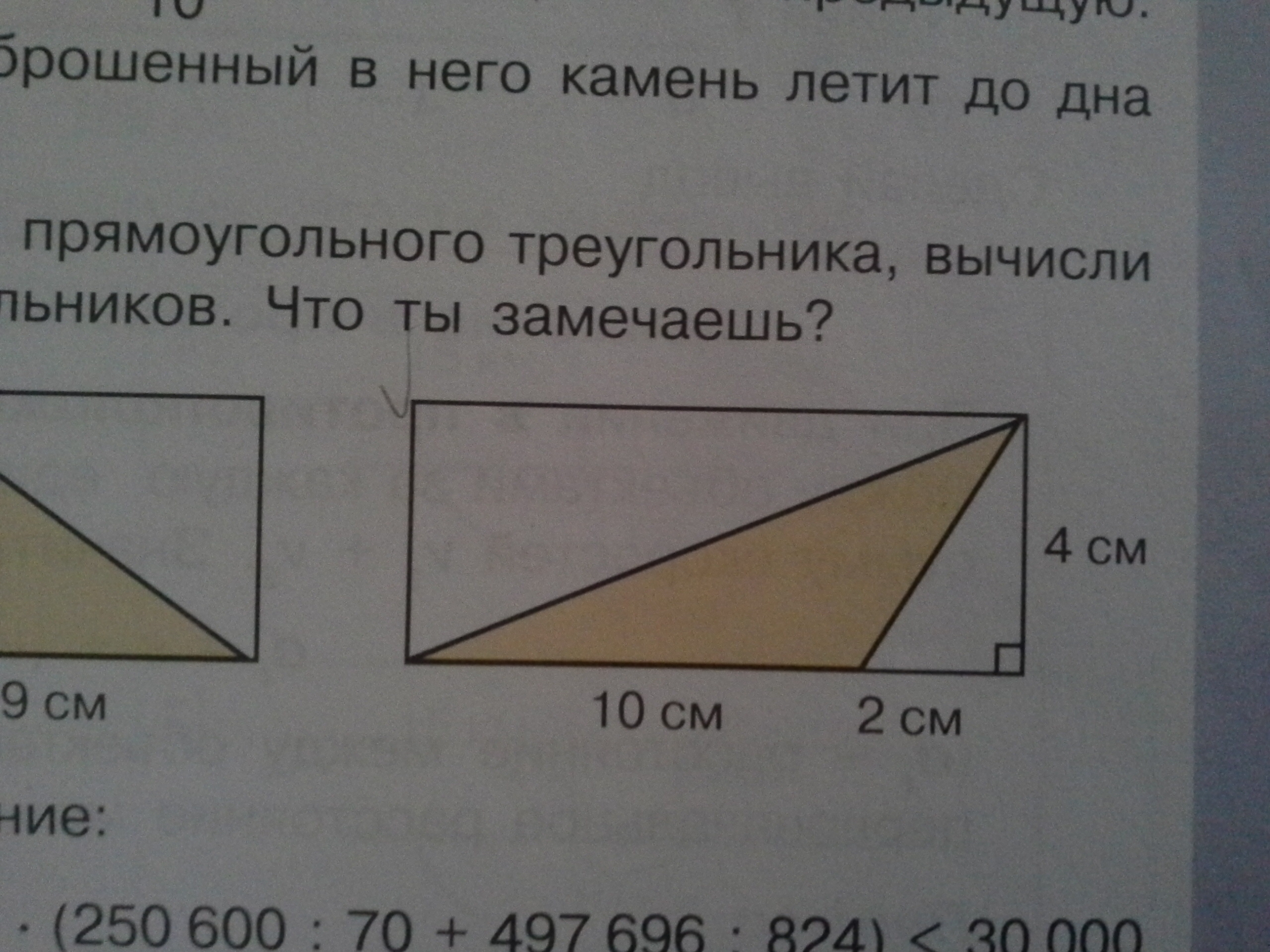
Каков периметр всех форм?
Формулы периметра
| Геометрическая форма | Формула периметра | Метрика |
|---|---|---|
| Треугольник | а + б + с | a , b и c — длины сторон |
| Прямоугольные | 2 (длина + ширина) | |
| Квадратный | 4a | a = длина стороны |
| Трапеция | а + б + с + г | a, b, c, d — стороны трапеции |
Как найти гипотенузу прямоугольного треугольника? калькулятор гипотенузы
Гипотенуза находится напротив прямого угла и может быть решена с помощью теоремы Пифагора. В прямоугольном треугольнике с катетом a и b и с гипотенузой c теорема Пифагора утверждает, что: а² + b² = с² . Чтобы найти c , возьмите квадратный корень из обеих сторон, чтобы получить c = √(b²+a²) .
Как найти стороны треугольника, если известен периметр?
com/embed/JM-nKcCDF3s» frameborder=»0″ allowfullscreen=»allowfullscreen» data-original-w=»720″ data-original-h=»520″>Сколько стоит периметр треугольника? Чтобы вычислить периметр треугольника, прибавьте длину его сторон. Например, если у треугольника есть стороны a, b и c, тогда периметр этого треугольника будет P = a + b + c.
Как найти периметр 4-х точек?
Чтобы найти периметр четырехугольника на графике, мы используем следующие шаги.
- Шаг 1: Найдите координаты вершин на графике.
- Шаг 2: Примените формулу расстояния, чтобы найти длины сторон четырехугольника.
- Шаг 3: Сложите все длины сторон, и сумма даст периметр четырехугольника.
Каков периметр PQR? Поскольку PQ равно 15, а ST равно 25, мы знаем, что пропорция между длинами сторон треугольников составляет 25/15, или 5/3. Соответствующие периметры двух треугольников, естественно, находятся в одинаковых пропорциях. Таким образом, мы можем взять периметр треугольника PQR и умножить его на 5/3, чтобы получить периметр треугольника STU, который равен 75.
Калькулятор периметра прямоугольного треугольника
Автор Komal Rafay
Отзыв от Davide Borchia
Последнее обновление: 08 октября 2022 г.
Содержание:- Что такое периметр прямоугольного треугольника
- Периметр прямоугольного треугольника калькулятор
- Формула периметра прямоугольного треугольника
- Периметр треугольника Омни калькуляторы
- Часто задаваемые вопросы
Калькулятор периметра прямоугольного треугольника — это быстрый и остроумный инструмент, который позволяет определить периметр прямоугольного треугольника на основе длина его сторон исходя из различных вариантов.
У нас есть много интересного для всех любителей геометрии:
- Каков периметр прямоугольного треугольника;
- Формула периметра прямоугольного треугольника; и
- Как вычислить периметр прямоугольного треугольника.
Если вам интересно что-либо из вышеперечисленного, приготовьтесь собрать все ответы в одном месте.
Что такое периметр прямоугольного треугольника
Как вы, возможно, уже знаете, периметр объекта или фигуры равен сумме всех его сторон. В этом случае периметр треугольника равен сумме трех его сторон.
Чем отличается периметр прямоугольного треугольника? На самом деле это не так. Это по-прежнему сумма всех трех сторон. Единственное отличие состоит в том, что треугольник характерен только для прямоугольных треугольников.
Калькулятор периметра прямоугольного треугольника
Калькулятор периметра прямоугольного треугольника — универсальный инструмент, который эффективно определяет периметр печально известного прямоугольного треугольника.
Но лучше всего то, что это можно сделать двумя способами. Один — когда у вас нет гипотенузы, а другой — когда у вас есть гипотенуза.
Инструмент дает вам выбор вверху.
Выберите формулу, которую хотите использовать,
- Учитывая катетер; или
- Даны все три стороны.
Для первого варианта, когда даны только перпендикуляр и основание, также известное как катеты, формула использует теорему Пифагора для определения гипотенузы, а затем вычисляет периметр.
- Введите перпендикуляр;
- Введите основание прямоугольного треугольника; и
- В результате получится периметр прямоугольного треугольника.
Все три стороны прямоугольного треугольника известны по второму варианту . Итак, здесь:
- Введите перпендикуляр;
- Введите базу;
- Введите гипотенузу; и
- Результат — периметр вашего прямоугольного треугольника.
Формула для определения периметра прямоугольного треугольника
Существуют две формулы, которые можно использовать для определения периметра треугольника в зависимости от сторон. 92)}P=a+b+(a2+b2)
Таким образом, использование этой формулы удобно, когда у вас нет значения гипотенузы, так как уравнение Пифагора может определить его.
2. Используя все три стороны:
P=a+b+hP = a + b + hP=a+b+h
где:
- ППС — Периметр;
- ааа — Перпендикуляр;
- bbb — Основание; и
- hhh — Гипотенуза.

Эта формула относительно проста и требует суммирования всех трех сторон. Мы можем сделать это на кончиках наших пальцев.
Эти формулы помогут вам понять, как найти периметр прямоугольного треугольника.
Калькуляторы периметра треугольника Omni
Другие инструменты Omni вычисляют периметры треугольников на основе различных типов и доступной информации.
- Калькулятор периметра треугольника;
- Калькулятор периметра треугольника с вершинами; и
- Периметр треугольника с калькулятором дробей.
Часто задаваемые вопросы
Чему равен периметр прямоугольного треугольника?
Периметр прямоугольного треугольника ничем не отличается от периметра любой другой фигуры. Это сумма всех его сторон , как и окружность. Периметр прямоугольного треугольника предназначен только для прямоугольных треугольников. Это сумма трех сторон, основания, перпендикуляра и гипотенузы .
Как вычислить периметр прямоугольного треугольника?
Периметр прямоугольного треугольника можно рассчитать двумя способами:
Если у вас есть только две стороны прямоугольного треугольника , основание и перпендикуляр, используйте формулу:
P = a + b + √(a² + b²)
три стороны прямоугольного треугольника , используем формулу:
P = a + b + h
где:
-
P— Периметр; -
и— Перпендикуляр; -
б— Основание; и -
ч— Гипотенуза.
Чему равен периметр, если катеты 8 и 9 см?
Периметр равен 29,04 см если катеты, т. е. перпендикуляр и основание, равны 8 и 9 см.
Формула для определения периметра прямоугольного треугольника, когда известны только две стороны:
P = a + b + √(a² + b²)
где:
-
P— периметр; -
и— Перпендикуляр; и -
б— Основание.
Komal Rafay
Perpendicular
Периметр
Проверьте 18 аналогичных калькуляторов треугольника 🔺
30 60 90 ТРЕЙНГИ 45 45 90 ТРИ -РАЗМЕР В ПРАВО ПРАВО ТРЕВЕНТА… 15 Еще
ПЕРИМЕТ ПРАВО ТРИАНГЕЛА — формал и примеры
ПРАВО ПРАВИ прямоугольного треугольника — это общая длина вокруг треугольника. Периметр можно найти, сложив длины всех сторон треугольника. Поскольку мы можем использовать теорему Пифагора, чтобы найти длину третьей стороны, если мы знаем длины двух сторон треугольника, нам просто нужна длина двух сторон треугольника.
Здесь мы узнаем о формуле периметра прямоугольного треугольника. Кроме того, мы сделаем обзор теоремы Пифагора, которую мы можем использовать для вычисления длин сторон. Наконец, мы увидим несколько примеров, в которых мы будем применять изученные формулы.
ГЕОМЕТРИЯ
Актуально для …
Изучение периметра прямоугольного треугольника на примерах.
См. примеры
Содержимое
ГЕОМЕТРИЯ
Актуально для …
Изучение периметра прямоугольного треугольника на примерах.
См. примеры
Формула периметра равностороннего треугольника
Периметр прямоугольного треугольника можно найти, сложив длины всех сторон треугольника. Следовательно, мы можем использовать следующую формулу:
| $латекс p=a+b+c$ |
где $латекс a, ~ b, ~ c$ — длины сторон треугольника. . 92}$
Периметр прямоугольного треугольника – Примеры с ответами
На следующих примерах вы можете попрактиковаться в решении задач, связанных с прямоугольными треугольниками. Каждый пример имеет свое решение и обоснование.
ПРИМЕР 1Каков периметр треугольника со сторонами 8 м, 9 м и 12,4 м?
Решение
Мы можем идентифицировать следующие значения:
- Сторона 1, $латекс a=8$ m
- Сторона 2, $латекс b=9$ м
- Сторона 3, $латекс c=12,4$ м
Используя формулу периметра, имеем:
$латекс p=a+b+c$
$латекс p=8+9+12,4$
$латекс p=29,4$
Периметр 29,4м.
У нас есть равносторонний треугольник со сторонами 10 м, 24 м и 26 м. Что такое периметр?
Решение
У нас есть следующее:
- Сторона 1, $латекс a=10$ м
- Сторона 2, $латекс b=24$ м
- Сторона 3, $латекс c=26$ м
Используя формулу периметра, имеем:
$латекс p=a+b+c$
$латекс p=10+24+26$
$ латекс p=60$
Периметр 60м.
ПРИМЕР 3Каков периметр прямоугольного треугольника со сторонами 11 см, 12 см и 16,28 см?
Решение
У нас есть следующие длины:
- Сторона 1, $латекс a=11$ см
- Сторона 2, $латекс b=12$ см
- Сторона 3, $латекс c=16,28$ см
Заменим эти значения в формуле периметра:
$латекс p=a+b+c$
$латекс p=11+12+16,28$
$латекс p=39.28$
Периметр 39,28см.
ПРИМЕР 4Каков периметр прямоугольного треугольника со сторонами 5 м и 12 м?
Solution
У нас есть следующие стороны:
- Сторона 1, $латекс a=5$ м
- Сторона 2, $латекс b=12$ м 92}=169$
$latex c=13$
Теперь мы можем использовать формулу периметра со следующими длинами:
$latex p=a+b+c$
$latex p=5+12+13 $
$латекс p=30$
Периметр 30м.
ПРИМЕР 5
Стороны прямоугольного треугольника равны 8 м и 11 м. Что такое периметр?
Solution
У нас есть следующие длины:
- Сторона 1, $латекс a=8$ м
- Сторона 2, $латекс b=11$ м 92}=185$
- Площадь прямоугольного треугольника – формулы и примеры
- Гипотенуза прямоугольного треугольника – формулы и примеры
- Каковы характеристики прямоугольных треугольников?
- Равнобедренный прямоугольный треугольник – формулы и примеры
- Равносторонний треугольник
- Равнобедренный треугольник
- Разносторонний треугольник
$латекс c=13,6$
Используем эти длины для нахождения периметра:
$латекс p=a+b+c$
$латекс p=8+11+13,6$
$latex p=32.6$
Периметр 32,6 м.
Периметр прямоугольного треугольника. Практические задачи
Примените на практике то, что вы узнали о периметре прямоугольного треугольника и теореме Пифагора, чтобы решить следующие задачи. Если вам нужна помощь с этими проблемами, вы можете посмотреть решенные примеры выше.
Каков периметр треугольника со сторонами 7 м, 9 м, 11,4 м?
Выберите ответ
$латекс p=25.4m$
$латекс p=27м$
$латекс p=27.4m$
$latex p=29.4m$
Каков периметр треугольника со сторонами 11м, 15м, 18,6м?
Выберите ответ
$латекс p=41.
 6м$
6м$$латекс p=42.6м$
$латекс p=43.6m$
$latex p=44.6m$
Длина сторон треугольника 9м и 12м. Что такое периметр?
Выберите ответ
$латекс p=32м$
$латекс p=34m$
$латекс p=36м$
$latex p=38m$
Каков периметр треугольника со сторонами 3м и 4м?
Выберите ответ
$латекс p=12м$
$латекс p=13м$
$латекс р=14м$
$latex p=15m$
См. также
Хотите узнать больше о прямоугольных треугольниках? Взгляните на эти страницы:
Изучайте математику с помощью наших дополнительных ресурсов по различным темам
УЗНАТЬ БОЛЬШЕ
Периметр треугольника – объяснение и примеры
Периметр треугольника можно определить как общую длину всех границ треугольника.

Пусть длины трех сторон треугольника равны $a$, $b$ и $c$, как показано на рисунке выше. С этой информацией периметр рассчитывается как :
$Периметр = a + b + c$
Треугольник представляет собой геометрическую фигуру с тремя сторонами , и его можно дополнительно разделить на различные типы в зависимости от размеров его сторон и углов. Немного изменим формулу периметра для каждого типа треугольника. В этой теме мы обсудим, как вычислить периметр различных типов треугольников.
Вообще говоря, периметр дает вам общую длину любого полигона. Периметр вычисляется простым сложением всех сторон многоугольника . Для треугольника не обязательно, чтобы все стороны и углы были равны. Соотношение между углами и сторонами зависит от типа треугольника, поэтому формула периметра будет различаться в зависимости от типа треугольника.
Каков периметр треугольника?
Периметр треугольника равен сумме длин его сторон .
 Чтобы вычислить периметр треугольника, мы должны вычислить общую длину по границам треугольника. Поскольку периметр вычисляется путем сложения, это делает периметр линейной мерой.
Чтобы вычислить периметр треугольника, мы должны вычислить общую длину по границам треугольника. Поскольку периметр вычисляется путем сложения, это делает периметр линейной мерой.Следовательно, единицы периметра те же , что и единицы данных сторон, т. е. сантиметры, метры, дюймы и т. д.
Как найти периметр треугольника
Чтобы вычислить периметр треугольника, сложите все три стороны треугольника, как мы обсуждали ранее.
Рассмотрим изображение треугольника, приведенное ниже:
Здесь стороны треугольника равны $7$, $8$ и $9$ см соответственно. Следовательно, периметр этого треугольника будет равен:
Периметр = 7 + 8+ 9 = 24$ см
Формула периметра треугольника
Формула для периметра треугольника будет зависят от типа треугольника . Давайте обсудим типы треугольников и как вывести их формулы.
Типы треугольников
Существует три различных типа треугольников s в зависимости от отношения между его сторонами.

– Равносторонний треугольник
Треугольник считается равносторонним, если длины всех трех сторон равны . Для равностороннего треугольника градусная мера каждого внутреннего угла будет равна 60 градусам. Ниже приведена фигура равностороннего треугольника.
Периметр равностороннего треугольника
Равносторонний треугольник — это треугольник с тремя равными сторонами. Итак, если стороны равны $a$, $b$ и $c$, то мы запишем периметр треугольника как
Периметр равностороннего треугольника $= a + b + c$
Поскольку мы знаем, что $a = b = c$, следовательно,
Периметр равностороннего треугольника $= 3a = 3b = 3c$
Пример 1:
Если значение одной стороны равностороннего треугольника равно 6 см, каков будет периметр треугольника?
Решение:Нам дано значение одной стороны равностороннего треугольника, но, как мы знаем, все три стороны равностороннего треугольника равны .
 Отсюда периметр треугольника будет вычисляться следующим образом:
Отсюда периметр треугольника будет вычисляться следующим образом:Периметр равностороннего треугольника $= 3\times a$
Периметр равностороннего треугольника $= 3\times 6$
Периметр равностороннего треугольника $= 18см$
– Равнобедренный треугольник
Треугольник называется равнобедренным, если длины и углы двух сторон равны друг другу, а третья сторона отличается от остальных. Ниже показана фигура равнобедренного треугольника.
Периметр равнобедренного треугольника
Равнобедренный треугольник — это треугольник с двумя равными сторонами. Итак, если стороны равны $a$, $b$ и $c$ и $a = b$, то периметр треугольника запишем как 9.0003
Периметр треугольника $= a + b + c$
Периметр равнобедренного треугольника $= a + a + c$
Периметр равнобедренного треугольника $= 2a + c$
Пример 2:
длина треугольника 40 см, а длина двух его сторон по 8 см, какова будет длина третьей стороны треугольника? Решение:Нам дано значение двух сторон треугольника, равных ; следовательно, это равнобедренный треугольник.

Периметр равнобедренного треугольника $= 2a + b$
$48 = (2\times 8) + b $
$b = \dfrac{48}{16} $
$b = 3 см $
– Разносторонний треугольник
Треугольник называется разносторонним, если длина всех трех сторон отлична друг от друга . Это означает, что ни одна сторона не будет равна любой другой стороне. Например, рисунок разностороннего треугольника ниже показывает, что ни одна из его сторон не равна.
Периметр разностороннего треугольника
Разносторонний треугольник – это треугольник, у которого три разные стороны. Поскольку все стороны различны, мы не можем изменить формулу для периметра треугольника, как мы это сделали для равностороннего и равнобедренного треугольников. Следовательно, формула остается такой же, как и стандартная, т. е.
Периметр треугольника $= a + b + c$.
Пример 3:
Если длина трех сторон треугольника равна 5 см, 6 см и 4 см соответственно, каков будет периметр треугольника?
Решение:Поскольку длины всех трех сторон треугольника различны , это разносторонний треугольник.
 Формула периметра разностороннего треугольника дается как
Формула периметра разностороннего треугольника дается какP $= a + b+ c$
$P = 5+6+4 $
$P = 15см $
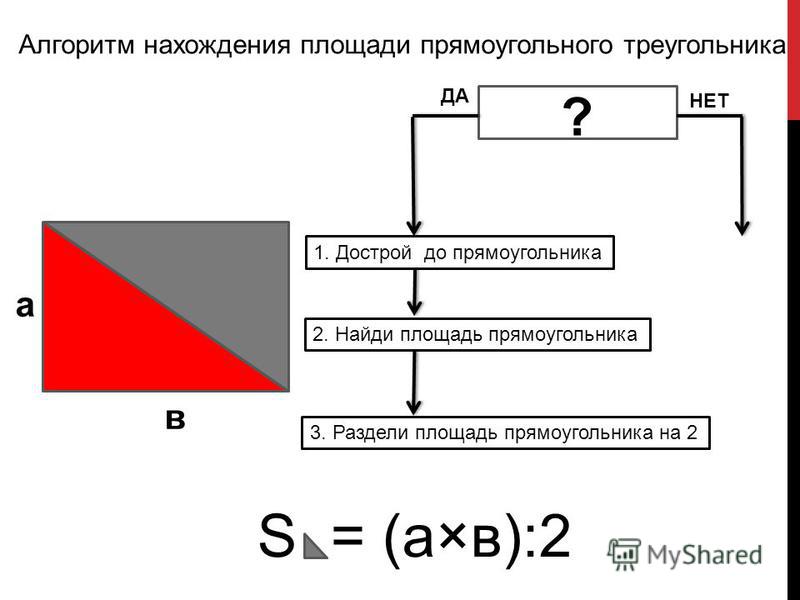
Периметр прямоугольного треугольника
Треугольник называется прямоугольным , если один из его углов прямой . Это означает, что один из углов треугольника равен 9$.{о}$. Периметр такого треугольника также рассчитывается путем сложения всех сторон треугольника, поэтому, если длина одной из сторон недоступна, мы можем использовать теорему Пифагора, чтобы найти это значение. Например, рассмотрим прямоугольный треугольник, приведенный ниже.
Здесь «b» — основание, «a» — перпендикуляр , а «c» — гипотенуза .
В соответствии с определением теоремы Пифагора квадрат гипотенузы равен сумме квадратов основания и перпендикуляра. 9{2})}$
$AC = \sqrt{64+36}$
$AC = \sqrt{100}$
$AC = 10 см$
Периметр $= AB + BC+ AC $
$ Периметр = 8+6+10 $
$ Периметр = 24 см $
Периметр равнобедренного прямоугольного треугольника
Треугольник называется равнобедренным прямоугольным, если две стороны и два угла равны, а третий угол прямой угол .
Решение: Например, рассмотрим изображение равнобедренного прямоугольного треугольника, приведенное ниже. 9{o}$ каждый. Чему будет равен периметр треугольника?
Например, рассмотрим изображение равнобедренного прямоугольного треугольника, приведенное ниже. 9{o}$ каждый. Чему будет равен периметр треугольника?Мы знаем, что прямоугольный треугольник, у которого две стороны и два внутренних угла равны, называется равнобедренным прямоугольным треугольником. Для вычисления периметра треугольника нам нужно знать длину третьей стороны . Длину третьей стороны «BC» можно рассчитать по формуле:
$BC = \sqrt{2}\times AB $
$BC = 1,414 \times 8 $
$BC = 11,31 $ ок.
Периметр треугольника будет:
Периметр $= 8 + 8 + 11,31 = 27,31 см$ прибл.
Практические вопросы1. Рассмотрим треугольник со сторонами $5см$, $6см$ и $8см$. Чему будет равен периметр треугольника?
2. Если три стороны треугольника равны $7 см$, каков будет периметр треугольника?
3. Натан проектирует треугольный сад. Помогите Натану рассчитать периметр сада, используя данные, приведенные ниже: 9{o}$ каждый.

- Длина двух сторон равна 6 см$ и 8 см$. Следовательно, один угол треугольника является прямым углом.
- Значение длин двух сторон $= 6 см$ каждая, а длина третьей стороны $10 см$
4. Алексу дан провод треугольной формы длиной $99 см$ .
- Вычислите длины сторон треугольника, если треугольник равносторонний.
- Рассчитайте длину третьей стороны, если длина двух оставшихся сторон составляет $30 см$ каждая
1. Мы знаем формулу периметра треугольника:
Периметр треугольника $= a+b+c$
Периметр треугольника $= 5см + 6см + 8см$
Периметр треугольника $= 19 см$
2. Мы знаем формулу периметра треугольника, когда все стороны равны задается как:
Периметр $= 3\times a$
Периметр $= 3\times 7$
Периметр $= 21 см$. 9{2})}$
$c = \sqrt{25+64}$
$c =\sqrt{89}$
$c = 9,43 см$ прибл.
Периметр $= a + b+ c $
Периметр $= 5+ 8 + 9,43 $
Периметр $= 22,43 см $ прибл.
- Длины двух сторон треугольника одинаковы, а длина третьей стороны различна, поэтому треугольник равнобедренный. Пусть стороны «a» и «b» $= 6 см$, а сторона «c» $= 10 см$.
Мы можем вычислить периметр, используя формулу :
Периметр треугольника $ = a+b+c $
Здесь a = b
Периметр треугольника $ = 2a +c $
Периметр треугольника $ = (2 х 6) + 10$
Периметр треугольника $ = 12 + 10$
Периметр треугольника $ = 22 см$
4.
- Нам дана общая длина провода треугольной формы , поэтому периметр треугольной фигуры равен 99 см.
Если все стороны треугольника равны, то это равносторонний треугольник. Периметр равностороннего треугольника равен:
Периметр $ = 3\times a $
99 $ = 3\times a $
a $ = \dfrac{99}{3} $
a $ = 33 см $
Таким образом, длина всех стороны треугольника по 33см.
- Нам дана общая длина провода треугольной формы и длины двух сторон треугольника.



 6м$
6м$
 Чтобы вычислить периметр треугольника, мы должны вычислить общую длину по границам треугольника. Поскольку периметр вычисляется путем сложения, это делает периметр линейной мерой.
Чтобы вычислить периметр треугольника, мы должны вычислить общую длину по границам треугольника. Поскольку периметр вычисляется путем сложения, это делает периметр линейной мерой.
 Отсюда периметр треугольника будет вычисляться следующим образом:
Отсюда периметр треугольника будет вычисляться следующим образом: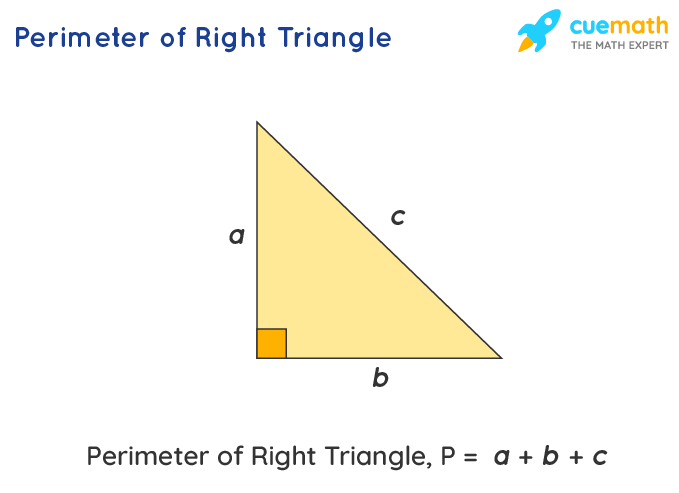
 Формула периметра разностороннего треугольника дается как
Формула периметра разностороннего треугольника дается как Например, рассмотрим изображение равнобедренного прямоугольного треугольника, приведенное ниже. 9{o}$ каждый. Чему будет равен периметр треугольника?
Например, рассмотрим изображение равнобедренного прямоугольного треугольника, приведенное ниже. 9{o}$ каждый. Чему будет равен периметр треугольника?