Избранные параграфы из книги «Математика, 5. учебник-собеседник»
Избранные параграфы из книги «Математика, 5. учебник-собеседник»Л.Шеврин, А.Гейн,
И.Коряков, М.Волков,
г. Екатеринбург
§ 53. Математика событий. Перечисляем варианты размещения по порядку
В § 42 вы решали задачи 1 и 2 о Гришиных гостях и о гвоздиках в вазах2. Перечитайте еще раз те задачи. В них было неважно, в каком порядке перечисляются предметы: гости в одном рейсе, или гвоздики в одной вазе. Например, если в хрустальной вазе гвоздика вишневого цвета, а две другие – в фарфоровой вазе, то можно сказать: «алая и белая в фарфоровой» или «белая и алая в фарфоровой» – это будет один и тот же вариант. Но часто бывает важно указать, в каком именно порядке располагаются или следуют друг за другом предметы. Так, важен порядок, в котором идут цифры в записи числа, буквы в слове: 12 и 21 – разные числа, НО и ОН – разные слова.
! Приведите и вы
какие-нибудь примеры того, когда важно указать
порядок расположения предметов.
В § 15 мы специально обсуждали разные варианты расположения по порядку одних и тех же предметов (помните?). Порядок может оказаться важен и при перечислении вариантов событий. Решим такую задачу.
Задача. Алеша, Боря, Витя и Гриша на даче Гришиного дедушки решили устроить соревнование по бегу. Дедушка объявил, что он установил два приза: за 1-е место – большую шоколадку, за 2-е – маленькую. Надо перечислить все варианты распределения бегунов по призовым местам.
Рисунок: Алеша, Боря, Витя и Гриша бегут по направлению к дедушке, который держит в руках две шоколадки – большую и маленькую.
Чтобы решить задачу, давайте рассуждать. Кто-то из четверых станет победителем соревнования; сколько здесь возможностей? Каждому ясно, что 4. Ведь обязательно произойдет одно из четырех событий: 1-м прибежит Алеша, 1-м прибежит…
! Продолжите список этих событий.
При каждом победителе
кто-нибудь из оставшихся троих станет 2-м
призером. Например, если 1-й призер – Алеша, то 2-м
призером может оказаться Боря, Витя или Гриша. Чтобы записать все варианты, договоримся
обозначить участников соревнования первыми
буквами их имен и писать буквы в порядке
занимаемых мест. Например, запись БА означает,
что 1-й призер Боря, 2-й – Алеша. Тогда получаются
варианты:
Чтобы записать все варианты, договоримся
обозначить участников соревнования первыми
буквами их имен и писать буквы в порядке
занимаемых мест. Например, запись БА означает,
что 1-й призер Боря, 2-й – Алеша. Тогда получаются
варианты:
АБ, АВ, АГ, если 1-й призер – Алеша;
БА, БВ, БГ, если 1-й призер – Боря;
ВА, ВБ, ВГ, если 1-й призер – Витя;
ГА, ГБ, ГВ, если 1-й призер – Гриша.
Видим, что здесь возможны 12 вариантов.
- А если располагать по порядку занятых мест не двоих призеров, а всех участников соревнования, то сколько получится вариантов?
Это разумный вопрос. И его можно задать не только для четырех участников, но и для любого их числа. И не обязательно интересоваться только участниками какого-либо соревнования. И даже не обязательно интересоваться именно людьми. Располагать по порядку можно любые предметы, и ответ на вопрос «Сколькими вариантами можно расположить по порядку
 В 6-м классе мы найдем формулу, дающую
ответ на него. А в этом параграфе обсудим случаи,
когда n = 2 и n = 3.
В 6-м классе мы найдем формулу, дающую
ответ на него. А в этом параграфе обсудим случаи,
когда n = 2 и n = 3.__________
Начнем со случая n = 2. Представьте, например, очередь из двух человек. Сколько вариантов их размещения в очереди? Каждому ясно, что таких вариантов 2 .
2 варианта размещения двух человек – мужчины и женщины – в очереди у окошка кассы.
Конечно, вместо людей в очереди можно размещать друг за другом (реально или мысленно) любые предметы, например, две разные буквы или две разные цифры. Ответ всегда будет один и тот же: 2 варианта. В начале параграфа мы уже приводили примеры таких вариантов для букв Н, О и цифр 1, 2.
Теперь обсудим случай, когда n = 3.
! Подумайте и скажите, сколькими вариантами можно разместить по порядку 3 предмета.
Нетрудно перечислить все возможные варианты. Их 6.
Рисунок: 6 вариантов размещения по порядку трех матрешек разного размера.
Чтобы записать эти варианты,
проще всего, пожалуй, размещать по порядку 3
разные буквы или 3 разные цифры. Используем,
например, буквы А, Б и В (можно представить, что,
как и раньше, ими обозначены Алеша, Боря и Витя,
финиширующие в соревнованиях по бегу или стоящие
друг за другом в очереди). Тогда получаются
следующие варианты:
Используем,
например, буквы А, Б и В (можно представить, что,
как и раньше, ими обозначены Алеша, Боря и Витя,
финиширующие в соревнованиях по бегу или стоящие
друг за другом в очереди). Тогда получаются
следующие варианты:
Будем называть цепочкой знаков всякую запись, в которой какие-то знаки (например,
буквы или цифры) расположены в определенном
порядке. Записывать цепочкой можно, конечно, не
только знаки, но и названия предметов, имена
людей и многое другое. Во всех таких случаях мы
ради краткости будем говорить просто
«цепочка». Если в цепочке все знаки
встречаются по одному разу, т. е. не повторяются,
то такую цепочку назовем цепочкой без
повторений.
Так, интересующие нас варианты размещения по порядку трех предметов записаны выше в виде шести трехбуквенных цепочек без повторений. Если же для ответа на тот же вопрос использовать, например, цифры 1, 2 и 3, то получатся записи в виде шести цепочек из трех цифр:
123, 132, 213, 231, 312, 321 .
L Это перечислены трехзначные числа с цифрами
1, 2 и 3?Да, эти записи можно прочитать и как записи чисел, но не всех трехзначных чисел с цифрами 1, 2, 3, а только тех, где каждая цифра используется по одному разу. Но когда интересуются просто цепочками цифр, принято читать такие записи: один-два-три, один-три-два, … .
! Продолжите чтение этих шести вариантов для цифр 1, 2, 3.
Конечно, записывая варианты размещения по порядку трех предметов, не обязательно использовать именно эти цифры или именно эти буквы.
! Назовите такие же варианты размещения цифр 2, 5, 7. Запишите все трехбуквенные цепочки без повторений из букв Б, В, Г.
Теперь можно было бы обсудить случай n = 4. Но мы отложим это до § 65, где обсудим одно полезное общее правило подсчета числа вариантов.
Вопросы и задания
53.1. Что такое цепочка
знаков? Какая цепочка называется цепочкой без
повторений?
53.
53.3. а) У Ани и ее родителей такой обычай: кто-то
из них заваривает чай, причем утренний и вечерний
«дежурные» различны. Члены этой семьи
договорились менять каждый день вариант
распределения обязанностей утреннего и
вечернего дежурных. Смогут ли они не повторять
такие варианты в течение недели?
Для подкрепления ответа запишите все такие варианты (например, обозначив Аню буквой А, а ее родителей – буквами О и М).
б) Изменим условие задачи а), добавив к нему, что в чаепитии принимает участие приехавшая погостить Анина бабушка, и она тоже будет одним из дежурных. Смогут ли члены семьи при этом условии не повторять варианты в течение 10 дней?
Рисунок: стол, за которым Аня, ее родители и бабушка пьют чай.
Для подкрепления ответа запишите все такие варианты, используя подходящие буквы.
в) (У) Младший брат
Смекалкина решил задачу а) и придумал задачу с
измененным условием: Аня и ее родители
устраивают чаепитие трижды в день и дежурные по
чаю за день не повторяются. Он предложил
Смекалкину написать все варианты распределения
обязанностей утренних, дневных и вечерних
дежурных. Смекалкин сказал, что можно не
записывать эти варианты, а воспользоваться тем,
что было сделано в объяснительном тексте. Там
говорилось точно о таком же распределении, когда
перечислялись варианты размещения по порядку
трех предметов. И все полученные варианты были
записаны там несколько раз: при помощи разных
букв и разных цифр.
Он предложил
Смекалкину написать все варианты распределения
обязанностей утренних, дневных и вечерних
дежурных. Смекалкин сказал, что можно не
записывать эти варианты, а воспользоваться тем,
что было сделано в объяснительном тексте. Там
говорилось точно о таком же распределении, когда
перечислялись варианты размещения по порядку
трех предметов. И все полученные варианты были
записаны там несколько раз: при помощи разных
букв и разных цифр.
Посмотрите еще раз объяснительный текст этого параграфа и убедитесь в правоте Смекалкина. Какие буквы и какие цифры использовались там для записи вариантов? Придумайте сами задачу, которая решалась бы записью тех же вариантов.
53.4. Дача Гришиного дедушки
находится недалеко от пруда. У дедушки есть
лодка, в которой могут разместиться все четверо
друзей: Алеша, Боря, Витя и Гриша. Дедушка
разрешил им покататься на лодке. Один из
мальчиков будет гребцом, один – рулевым. Друзья
захотели перепробовать все варианты
распределения между ними ролей гребца и
рулевого.
Рисунок: пруд; четыре мальчика (Алеша, Боря, Витя и Гриша) плавают на лодке: один гребет, один – рулевой, двое – пассажиры.
а) Успеют ли мальчики осуществить свое намерение, если им разрешено кататься 1 час, а на каждый вариант они решили отвести 5 минут?
б) (У) Младший брат Смекалкина стал решать задачу а) и начал записывать варианты распределения двух ролей между Алешей, Борей, Витей и Гришей. Но Смекалкин сказал, что записывать варианты для этой задачи вовсе не обязательно. Ведь в ней получаются точно такие же варианты, что и в задаче из объяснительного текста; надо только заменить 1-го призера гребцом, а 2-го – рулевым. Так что сразу ясно, что всех вариантов здесь тоже 12.
Обдумайте эту догадку Смекалкина, а потом решите устно похожую задачу с измененным условием: Гриша повредил руку и не может быть гребцом, и мальчики решили отвести на каждый вариант 8 минут; успеют ли они перебрать все такие варианты за 1 час?
в)* (У) Представьте, что
Гриша не может быть гребцом, а Алеша не хочет быть
рулевым. Успеют ли мальчики осуществить все
варианты, возможные при этих условиях, если им
разрешено кататься полтора часа и на каждый
вариант они решили отвести 12 минут?
Успеют ли мальчики осуществить все
варианты, возможные при этих условиях, если им
разрешено кататься полтора часа и на каждый
вариант они решили отвести 12 минут?
53.5. В объяснительном тексте появились трехбуквенные цепочки. Точно так же можно говорить о двухбуквенных цепочках, четырехбуквенных и т. д. Двухбуквенные цепочки без повторений из букв А, О, М вы записали, выполняя задание 53.3 а).
а) Сколько всего двухбуквенных цепочек без повторений из букв В, О, П, Т ? Догадайтесь, как можно узнать ответ, не записывая эти цепочки. (Совет: сравните это задание с задачей из объяснительного текста.) Затем запишите эти цепочки. Сколько среди них оказалось слов русского языка? Подчеркните их.
б) Найдите как можно больше пар букв, для которых каждая из двухбуквенных цепочек без повторений – слово русского языка. Сравните ваш список таких пар со списком, составленным соседом по парте. Оказались ли у кого-нибудь из вас слова, которые не нашел другой?
53. 6. Из букв Л, Ш, Ю можно
составить 6 трехбуквенных цепочек без
повторений:
6. Из букв Л, Ш, Ю можно
составить 6 трехбуквенных цепочек без
повторений:
ЛШЮ, ЛЮШ, ШЛЮ, ШЮЛ, ЮЛШ, ЮШЛ.
Как вы видите, из них одна цепочка (ШЛЮ) – это слово русского языка.
а) Запишите все трехбуквенные цепочки без повторений из букв К, О, Т. Сколько среди них слов русского языка? Подчеркните их.
б) Подберите такие 3 буквы, чтобы среди трехбуквенных цепочек без повторений из этих букв было 2 слова русского языка. Проверьте, правильно ли выполнил это задание сосед по парте.
в) (У) Укажите такие 3 буквы, чтобы среди трехбуквенных цепочек без повторений из этих букв не было ни одного слова русского языка.
53.7. В очереди в школьный буфет стоят ученики в таком порядке: Боря, Галя, Аня, Дима, Витя.
а) Трое учеников ушли из
очереди. Кто за кем остался стоять в очереди?
Перечислите все варианты возможного ответа. (Совет:
как и раньше, для краткости записи вариантов
можно обозначить учеников первыми буквами их
имен. )
)
б) Двое учеников ушли из очереди. Кто за кем остался стоять в очереди? Перечислите все варианты возможного ответа.
Задания из рабочей тетради
53.8о. а) Аля, Боря и Витя рассаживаются вокруг круглого стола. На приведенных ниже рисунках укажите все возможные варианты их размещения за круглым столом, вписав в прямоугольные рамочки первые буквы имен каждого из них.
б) Если интересоваться только тем, кто у каждого из ребят будет соседом слева, а кто – соседом справа, то вариантов окажется меньше. Выполнив задание а), отметьте на рисунке 53.2 одним и тем же номером те варианты, которые не отличаются взаимным расположением соседей. Сколько оказалось номеров?
Ответ: _______________________ .
Комментарии к вопросам и заданиям из § 53
53.1. Ответ на этот вопрос
легко получить из соответствующего абзаца
объяснительного текста параграфа. Он может
звучать так: цепочкой знаков называется
всякая запись, в которой какие-то знаки
расположены в определенном порядке. Если в
цепочке все знаки встречаются по одному разу, т.
е. не повторяются, то она называется цепочкой
без повторений.
Если в
цепочке все знаки встречаются по одному разу, т.
е. не повторяются, то она называется цепочкой
без повторений.
53.2. Ответы на оба вопроса даны в объяснительном тексте. Здесь может быть 2 случая: учитель удовлетворен только указанием количества вариантов, либо потребует развернутого объяснения, как это количество получается.
53.3. а) Ответ: не смогут. В неделе 7 дней, а вариантов распределения утреннего и вечернего дежурств только шесть: АМ, МА, АО, ОА, МО, ОМ.
б) Ответ: смогут. Имеется 12 вариантов распределения утреннего и вечернего дежурств: АМ, МА, АО, ОА, МО, ОМ, АБ, БА, ОБ, БО, МБ, БМ.
53.4. а) Ответ: успеют. Имеется 12 вариантов распределения роли гребца и рулевого. В этом проще всего убедиться, если воспользоваться предложением Смекалкина из пункта б) этого задания.
б) В этом пункте сначала
обсуждается принципиально важное положение, что
перечисление вариантов не зависит от того, что
именно фигурирует в этих вариантах – призовые
места или роли в лодочном экипаже. Как отмечено в
комментарии к заданию 42.7, такое обсуждение
формирует у учащихся важное понятие, которое в
математике принято называть комбинаторной
схемой.
Как отмечено в
комментарии к заданию 42.7, такое обсуждение
формирует у учащихся важное понятие, которое в
математике принято называть комбинаторной
схемой.
Ответ на задание, содержащееся во второй части этого пункта, отрицателен: не успеют. Легко подсчитать, что в данных условиях имеется 9 вариантов распределения ролей гребца и рулевого. Для этого нужно догадаться, что требуемые варианты получаются из вариантов, записанных при выполнении пункта а), вычеркиванием тех из них, где гребцом выступает Гриша. Таких вариантов 3. Если подобное рассуждение будет трудно восприниматься школьниками, можно попросить их выписать все возможные в данных условиях варианты. Вот перечень этих вариантов: АБ, АВ, АГ, БА, БВ, БГ, ВА, ВБ, ВГ.
в) Ответ: успеют. Действительно, в этом случае будет только 7 нужных вариантов – их список получается из перечня вариантов, составленного в пункте б), вычеркиванием тех вариантов, в которых Алеша выступает рулевым. Таких вариантов два: БА и ВА.
53. 5. а) Ответ: 12 цепочек.
Вот их список: ВО, ОВ, ВП,ПВ, ВТ, ТВ, ОП, ПО, ОТ, ТО, ПТ, ТП. Подчеркнуты слова русского языка,
их 4.
5. а) Ответ: 12 цепочек.
Вот их список: ВО, ОВ, ВП,ПВ, ВТ, ТВ, ОП, ПО, ОТ, ТО, ПТ, ТП. Подчеркнуты слова русского языка,
их 4.
б) Мы можем указать 12 таких пар:
АД и ДА, АЗ и ЗА, АН и НА, АХ и ХА, ИЛ и ЛИ, ИМ и МИ, ИН и НИ, ОН и НО, ОТ и ТО, УС и СУ, УФ и ФУ, ЯЛ и ЛЯ.
Комментировать большинство слов предъявленного списка нет нужды; напомним лишь, что СУ – мелкая французская монета, ИН – это (согласно «Толковому словарю русского языка» С.И. Ожегова и Н.Ю. Шведовой, 4-е изд. – М., 1998) то же самое, что АН, а АН – противительный союз, указывающий на то, что происходит нечто неожиданное, противоположное тому, что ожидалось.
53.6. а) КОТ, КТО, ОКТ, ОТК, ТКО, ТОК. Подчеркнуты 3 слова русского языка.
б) Можно взять, например, буквы Н, О, С. Среди трехбуквенных цепочек без повторений из этих букв будет 2 слова русского языка: СОН и НОС.
в) Можно взять, например, любые 3 согласные.
53. 7. а) Возможны 10 вариантов:
БГ, БА, БД, БВ, ГА, ГД, ГВ, АД, АВ, ДВ.
7. а) Возможны 10 вариантов:
БГ, БА, БД, БВ, ГА, ГД, ГВ, АД, АВ, ДВ.
б) И здесь возможны 10 вариантов: БГА, БГД, БГВ, БАД, БАВ, БДВ, ГАД, ГАВ, ГДВ, АДВ.
Сильным учащимся можно предложить подумать над тем, почему число вариантов в пунктах а) и б) оказалось одинаковым. Можно ли было предвидеть это до перечисления всех вариантов? Ответ – да, так как и в том, и в другом случае речь идет о числе способов выбора двух учеников из пяти: при этом можно считать, что в задании а) выбираемая пара учеников остается в очереди, а в задании б) такая пара из очереди уходит.
Полезно также сопоставить эту задачу с задачей 42.3.
53.8. а) Уже не раз учащиеся видели, что имеется 6 вариантов расположения трех предметов по порядку. В данном случае эти 6 вариантов вписываются в прямоугольные рамочки, заготовленные на рис. 53.2.
б) Разглядывая отмеченные в
пункте а) варианты, легко убедиться, что имеются 2
различных расположения, отвечающих условиям из
б). Они задаются цепочками АБВ и АВБ. Ответ:
потребуются 2 номера.
Ответ:
потребуются 2 номера.
§ 54. Математика событий. Цепочки, в которых знаки могут повторяться
В предыдущем параграфе мы перечисляли цепочки без повторений, состоящие из букв или цифр. Но нередко приходится иметь дело с цепочками, в которых одинаковые знаки могут повторяться. Например, в слове оно буква О встречается дважды; в слове мама каждая из двух букв встречается дважды.
! Укажите несколько слов, в которых какая-то буква встречается трижды.
Конечно, и среди чисел есть много таких, в записи которых одинаковые цифры встречаются более одного раза.
Цепочки, в которых одинаковые знаки могут повторяться, появляются при решении многих задач на перечисление вариантов. Вот одна из самых простых таких задач.
Задача 1. Перечислите все двузначные числа, в записи которых используются цифры 1, 2 и 3.
Числа, о которых говорится в
задаче, можно разбить на 3 группы: начинающиеся с
цифры 1, начинающиеся с цифры 2, начинающиеся с
цифры 3. Числа в каждой группе легко перечислить:
в первой группе – 11, 12, 13; во второй – … , в третьей
– …
Числа в каждой группе легко перечислить:
в первой группе – 11, 12, 13; во второй – … , в третьей
– …
! Перечислите числа во второй и третьей группах.
Список чисел, полученный при решении задачи 1, пригодится для решения следующей задачи.
Задача 2. Перечислите все трехзначные числа, в записи которых используются цифры 1, 2 и 3.
Такие числа снова можно разбить на 3 группы в зависимости от того, какая цифра стоит первой. Первая группа состоит из чисел, начинающихся с цифры 1. Рассмотрим эти числа. В записи каждого из них вторая и третья цифры составляют цепочку. Перечислить все такие цепочки – то же самое, что перечислить все двузначные числа, в записи которых участвуют цифры 1, 2 и 3. А вы уже перечислили их, когда решали задачу 1. Значит, первая группа интересующих нас чисел такова:
111, 112, 113,
121, 122, 123,
131, 132, 133.
! Перечислите числа во
второй и третьей группах.
Задания
54.1. а) Запишите все трехбуквенные цепочки из букв Л и И. Сколько среди них слов русского языка? Подчеркните их.
б) Подберите другие две буквы так, чтобы среди трехбуквенных цепочек из этих букв было 2 слова русского языка.
њ в)* Можно ли подобрать две буквы так, чтобы среди составленных из них трехбуквенных цепочек с возможными повторениями оказалось 3 слова русского языка? њ
54.2. а) Перечитайте в объяснительном тексте § 42 условие задачи о гостях, приезжающих к Грише, и посмотрите таблицу, которая там была составлена. Для решения той задачи можно составить и другую таблицу – с тремя столбцами. В клетках первого столбца будем записывать номер рейса, которым приехал Алеша, в клетках второго столбца – номер рейса, которым приехал Боря, в клетках третьего – номер рейса, которым приехал Витя. Обозначим эти столбцы буквами А, Б, В. Вот как будут выглядеть первые три строки новой таблицы, в которых записаны первые три варианта:
Таблица 28
Начертите в тетради таблицу
для всех восьми вариантов и заполните ее.
б) Перечислите все трехзначные числа, в записи которых участвуют только цифры 1 и 2.
в) Обратите внимание, как похожи решения в задачах а) и б): ведь можно сказать, что в строках таблицы из а) записаны все трехзначные числа с цифрами 1 и 2. Запишите теперь все двузначные числа с цифрами 1 и 2 и придумайте такую задачу на перечисление вариантов, чтобы в строках таблицы для ее решения «прочитывались» бы эти двузначные числа.
54.3. а) Перечислите все трехбуквенные цепочки из букв А и М, в которых нет рядом стоящих одинаковых букв.
б) Перечислите все трехзначные числа с цифрами 1 и 2, в которых нет рядом стоящих одинаковых цифр.
54.4. В записи натуральных чисел первая цифра не может быть нулем. Поэтому, например, цепочка 012 не может быть прочитана как трехзначное число.
а) Перечислите трехзначные числа, которые можно составить из цифр 0, 1, 2.
б) Каких чисел больше: трехзначных, составленных из цифр 1, 2, 3, или четырехзначных, составленных из цифр 0, 1, 2 ?
54. 5. Прочитывая номер
какого-нибудь телефона, люди обычно разбивают
цепочку цифр этого номера на группы, по 2 или 3
цифры в каждой группе. Например, шестизначный
номер 275275 можно представить в виде 27-52-75 или в
виде 275-275. При первом варианте его читают
«двадцать семь, пятьдесят два, семьдесят пять»;
при втором варианте – «двести семьдесят пять,
двести семьдесят пять».
5. Прочитывая номер
какого-нибудь телефона, люди обычно разбивают
цепочку цифр этого номера на группы, по 2 или 3
цифры в каждой группе. Например, шестизначный
номер 275275 можно представить в виде 27-52-75 или в
виде 275-275. При первом варианте его читают
«двадцать семь, пятьдесят два, семьдесят пять»;
при втором варианте – «двести семьдесят пять,
двести семьдесят пять».
Кнопочный телефонный аппарат.
Для запоминания какого-нибудь номера иногда стоит подумать, как удобнее разбить его на группы. Для номера, который мы только что рассмотрели, удобнее, конечно, второй вариант: надо просто повторить два раза одно и тоже число. А для номера 223242 удобнее, пожалуй, первый вариант: 22-32-42.
Как, по вашему мнению, удобнее разбить следующие номера, чтобы легко их запомнить?
501502; 434241; 254025; 537735
Запишите ваши варианты;
сравните их с вариантами, предложенными соседом
по парте; обсудите с ним (или с кем-нибудь из
старших) свой выбор. њ
њ
54.6*. а) Клоун объявил, что у него 6-значный номер телефона. А запоминать его незачем, потому что можно сразу назвать его, если помнить очень простое свойство цепочки цифр этого номера: она получается, если записать подряд 4 числа, из которых каждое последующее в 4 раза больше предыдущего.
Определите этот номер. Объясните, почему других 6-значных номеров с тем же свойством нет.
б) Младший брат Смекалкина отгадал загадку клоуна, а затем решил немного изменить ее: в свойстве цепочки цифр номера он заменил условие «в 4 раза больше» условием «на 4 больше». Смекалкин, поразмышляв, сказал, что у этой загадки получается несколько отгадок.
Найдите все цепочки из 6 цифр, которые могут получиться, если записать подряд 4 числа такие, что каждое последующее на 4 больше предыдущего. Объясните, почему других цепочек из 6 цифр с тем же свойством нет.
Задания из рабочей тетради
54.7о. Рассмотрите полоску из 2-х клеток.
Каждая ее клетка может быть
закрашена или не закрашена . Вот все
возможные варианты раскраски двухклеточной
полоски.
Вот все
возможные варианты раскраски двухклеточной
полоски.
а) На приведенных ниже трехклеточных полосках укажите все возможные варианты их раскраски (лишние заготовки полосок, если таковые окажутся, перечеркните).
б) Выполните то же задание, что и а), для полоски, состоящей из 4 клеток.
в) (У) Сравните количество раскрашенных полосок в задании а) с количеством трехзначных чисел, записанных с помощью цифр 1 и 2 (см. задание 54.2, б). Попытайтесь объяснить совпадения этих чисел.
54.8. Рассмотрите полоску из 3-х клеток.
Каждая ее клетка может быть закрашена или не закрашена . Вот все варианты закрашивания ее клеток так, что нет соседних закрашенных клеток и нет соседних незакрашенных клеток.
а)о На приведенных ниже
четырехклеточных полосках укажите все возможные
варианты такой же закраски клеток (лишние
заготовки полосок, если таковые окажутся,
вычеркните).
б) Выполните то же задание, что и а), для полоски, состоящей из 5 клеток.
Комментарии к заданиям из § 54
54.1. а) Вот список требуемых цепочек:
ИИИ, ИИЛ, ИЛИ, ИЛЛ, ЛИИ, ЛИЛ, ЛЛИ, ЛЛЛ.
Подчеркнуты 2 слова русского языка.
б) Годятся, например, буквы К и О; соответствующие слова КОК и ОКО. Другой пример: буквы И и М; соответствующие слова ИМИ и МИМ.
в) Нет, нельзя. Мы не считаем, что от учащихся надо требовать полное обоснование этого ответа, поскольку для такового необходим довольно большой перебор возможностей. Для читателей-энтузиастов, желающих досконально разобраться в обсуждаемом задании, оценим величину этого перебора. Искомая оценка будет основываться на следующих наблюдениях.
1) В трехбуквенном слове
русского языка, состоящем из двух букв,
обязательно одна буква гласная, а другая
согласная (буквы й, ь, ъ отсутствуют). В частности,
нет трехбуквенных слов, состоящих из одной буквы.
Это означает, что среди восьми трехбуквенных
цепочек, составленных из двух букв, только 6 могут
быть «кандидатами» в слова русского языка.
В частности,
нет трехбуквенных слов, состоящих из одной буквы.
Это означает, что среди восьми трехбуквенных
цепочек, составленных из двух букв, только 6 могут
быть «кандидатами» в слова русского языка.
2) Согласно правилам русского языка, слова не могут начинаться с буквы Ы и в них не бывает две буквы Ы подряд. Значит, букву Ы нужно исключить из рассмотрения.
3) Согласно правилам русского языка, в словах не может быть дважды буква Ё. Прямым перебором легко убедиться, что среди цепочек вида – какая-либо согласная буква, нет ни одного слова русского языка. Тем самым, букву Ё из рассмотрений нужно исключить.
4) Аналогично наблюдению 3 исключается буква Э.
5) Поскольку буквы Х, Ц, Ч, Ш, Щ в трехбуквенных словах не могут быть удвоенными, перебором их сочетаний с гласными легко убедиться, что данные буквы также нужно исключить из рассмотрения.
Теперь, когда число
рассматриваемых гласных букв сократилось до 7, а
согласных – до 15, подсчитаем число вариантов
выбора двух букв, из которых будут строиться
цепочки. По правилу произведения таких вариантов
105. Это не такое уж большое число, и если в классе
учится 30 человек, то каждому достанется
просмотреть 3–4 варианта. При этом в большинстве
вариантов не потребуется рассматривать все 6
комбинаций трехбуквенных цепочек, в которых
фигурируют обе выбранные буквы. Из первого
наблюдения вытекает, что если среди
трехбуквенных цепочек, составленных из двух
букв, встречаются 3 слова русского языка, то по
крайней мере в одном из них есть две одинаковые
рядом стоящие буквы. Поэтому в первую очередь
надо рассматривать именно такие цепочки. В
подавляющем большинстве случаев эти цепочки не
будут словами русского языка. В тех нескольких
случаях, когда получается какое-то слово
русского языка (например, РЕЕ – предложный падеж
слов РЕЙ и РЕЯ), нельзя указать два слова
требуемого типа из тех же букв.
По правилу произведения таких вариантов
105. Это не такое уж большое число, и если в классе
учится 30 человек, то каждому достанется
просмотреть 3–4 варианта. При этом в большинстве
вариантов не потребуется рассматривать все 6
комбинаций трехбуквенных цепочек, в которых
фигурируют обе выбранные буквы. Из первого
наблюдения вытекает, что если среди
трехбуквенных цепочек, составленных из двух
букв, встречаются 3 слова русского языка, то по
крайней мере в одном из них есть две одинаковые
рядом стоящие буквы. Поэтому в первую очередь
надо рассматривать именно такие цепочки. В
подавляющем большинстве случаев эти цепочки не
будут словами русского языка. В тех нескольких
случаях, когда получается какое-то слово
русского языка (например, РЕЕ – предложный падеж
слов РЕЙ и РЕЯ), нельзя указать два слова
требуемого типа из тех же букв.
Задание а) мы рекомендуем
обсудить в классе, задание б) выполнить дома.
Задание в), фигурирующее в учебнике в качестве
дополнительного, моделирует своеобразное
математико-лингвистическое исследование и
представляет собой приглашение продвинутых в
математическом отношении учащихся к
размышлениям на подобные темы. Демонстрация
таких неожиданных для них применений математики
в других областях знания повышает их
познавательную активность и способствует
развитию творческого потенциала таких учеников.
Демонстрация
таких неожиданных для них применений математики
в других областях знания повышает их
познавательную активность и способствует
развитию творческого потенциала таких учеников.
54.2. б) Вот эти числа:
111, 112, 121, 122, 211, 212, 221, 222.
в) В данном пункте еще раз обсуждается принципиальное положение, что перечисление вариантов не зависит от того, какие объекты фигурируют в этих вариантах.
Приведем список требуемых двузначных чисел: 11, 12, 21, 22. Учащимся, которым трудно придумать задачу на перечисление вариантов с таким ответом, можно предложить видоизменить задачу из объяснительного текста § 42 про Гришиных гостей.
54.3. Оба пункта этого задания мы рекомендуем выполнить в классе.
а) 2 цепочки: АМА и МАМ.
б) 2 числа: 121 и 212.
После выполнения задания
полезно обсудить, почему совпало количество
вариантов, и как варианты, перечисленные в б),
могут быть получены из вариантов, перечисленных
в а).
54.4. а) 100, 101, 102, 110, 111, 112, 120, 121, 122, 200, 201, 202, 210, 211, 212, 220, 221, 222. Всего 18 чисел.
б) Четырехзначных чисел, составленных из цифр 0, 1, 2, ровно вдвое больше: их 54; трехзначных чисел, составленных из цифр 1, 2, 3, только 27.
54.5. Удобные для запоминания разбиения таковы 501-502; 43-42-41; 25-40-25; 537-735 (в последнем случае приемлем и вариант 53-77-35).
54.6. а) Номер телефона клоуна 141664. Других 6-значных номеров с тем же свойством нет, так как если записать подряд 4 числа, из которых каждое последующее в 4 раза больше предыдущего, и начать не с 1, то получится число не менее чем из 7 цифр. Можно предложить сильным учащимся дополнительный вопрос: сколько существует 7-значных номеров с тем же свойством?
б) Все цепочки из 6 цифр с
требуемым свойством таковы: 261014, 371115, 481216, 591317.
Чтобы убедиться, что других таких цепочек из 6
цифр нет, нужно записать подряд 4 числа такие, что
каждое последующее на 4 больше предыдущего; тогда
6-значное число получится, если первые два числа
однозначные, а два других – двузначные.
54.7. а) При правильном выполнении задания останется одна лишняя заготовка.
б) Здесь останется две лишних заготовки.
в) Если закрашенную клетку полоски обозначить 1, а незакрашенную – 2, то сразу становится ясно, почему вариантов закраски полоски столько же, сколько трехзначных чисел, записанных с помощью цифр 1 и 2.
54.8. Легко понять, что раскраска полоски полностью определяется тем, закрашена ее первая клетка или нет. Поэтому в обоих пунктах задания имеется 2 варианта раскраски указанных там полосок.
| «Қостанай қаласы әкімдігі білім бөлімінің № 3 мектеп — гимназиясы» ММ ГУ «Школа — гимназия № 3 отдела образования акимата города Костаная» Программа факультативного курса по математике «Математический серпантин» 3 класс Подготовила: Марзабаева Людмила Ивановна Пояснительная записка Актуальность программы определена тем, что младшие школьники должны иметь мотивацию к обучению математики, стремиться развивать свои интеллектуальные возможности. Данная программа позволяет учащимся ознакомиться со многими интересными вопросами математики на данном этапе обучения, выходящими за рамки школьной программы, расширить целостное представление о проблеме данной науки. Решение математических задач, связанных с логическим мышлением закрепит интерес детей к познавательной деятельности, будет способствовать развитию мыслительных операций и общему интеллектуальному развитию. Не менее важным фактором реализации данной программы является и стремление развить у учащихся умений самостоятельно работать, думать, решать творческие задачи, а также совершенствовать навыки аргументации собственной позиции по определенному вопросу. Содержание программы соответствует познавательным возможностям младших школьников и предоставляет им возможность работать на уровне повышенных требований, развивая учебную мотивацию. Содержание занятий представляет собой введение в мир элементарной математики, а также расширенный углубленный вариант наиболее актуальных вопросов базового предмета – математика. Творческие работы, проектная деятельность и другие технологии, используемые в системе работы кружка, должны быть основаны на любознательности детей, которую и следует поддерживать и направлять. Данная практика поможет ему успешно овладеть не только общеучебными умениями и навыками, но и осваивать более сложный уровень знаний по предмету, достойно выступать на олимпиадах и участвовать в различных конкурсах. Все вопросы и задания рассчитаны на работу учащихся на занятии. Для эффективности работы факультатива желательно, чтобы работа проводилась в малых группах с опорой на индивидуальную деятельность, с последующим общим обсуждением полученных результатов. Факультатив создается с учетом склонностей ребят, их возможностей и интересов. Следует помнить, что помочь ученикам найти себя как можно раньше – одна из важнейших задач учителя начальных классов. Программа факультативного курса рассчитана на 1 года. Занятия 1 раз в неделю. Продолжительность каждого занятия не должна превышать 30 – 45 минут. которое забегает вперед развития». Л.С.Выготский Цель:
Задачи:
Принципы программы:
Создание условий для повышения мотивации к обучению математики, стремление развивать интеллектуальные возможности учащихся. 
Математика – учебная дисциплина, развивающая умения логически мыслить, видеть количественную сторону предметов и явлений, делать выводы, обобщения.
Курс строится от частных примеров (особенности решения отдельных примеров) к общим (решение математических задач).
Содержание занятий кружка направлено на освоение математической терминологии, которая пригодится в дальнейшей работе, на решение занимательных задач, которые впоследствии помогут ребятам принимать участие в школьных и городских олимпиадах и других математических играх и конкурсах.
Во-первых, развитие интереса к математике как науке физико-математического направления, во-вторых, успешное усвоение учебного материала на уроках и выступление на олимпиадах по математике. 
С точки зрения возможности усвоения основного содержания программы – возможно усвоение за 34 занятия.
Он осуществляет учебно-практическое знакомство со многими разделами математики, удовлетворяет познавательный интерес школьников к проблемам данной точной науки, расширяет кругозор, углубляет знания в данной учебной дисциплине. Учащиеся будут знать:
Учащиеся будут уметь:
Ожидаемые результаты: Занятия в кружке должны помочь учащимся:
Основные виды деятельности учащихся:
Содержание программы. 1. Из истории математики (3часа) Первоначальное знакомство с историей математики, со значением математики в жизни человека. Возникновение цифр и знаков. Решение занимательных заданий, связанных со счётом предметов. 2. Числа. Арифметические действия. (4часа). Познакомить с классификацией чисел. Виды систем счисления. Знакомство с интересными приёмами устного счёта, применение рациональных способов решения математических выражений. 3.Математические ребусы, игры, лабиринты.(8часов) Решение математических ребусов. Знакомство с простейшими умозаключениями на математическом уровне. Решение логических задач, требующих применения интуиции и умения проводить в уме несложные рассуждения. 4.Мир занимательных задач. (10часов). Решение задач в одно и два действия, задач шуток, задач со сказочным сюжетом с использование игрового материала. 5. Маленькие тайны математики. (5часов). Пространственные представления. Геометрические узоры. Закономерности в узорах. Симметрия. Части фигуры. Место заданной фигуры в конструкции. Расположение деталей. Выбор деталей в соответствии с заданным контуром конструкции. Поиск нескольких возможных вариантов решения. Составление и зарисовка фигур по собственному замыслу. Разрезание и составление фигур. Деление заданной фигуры на равные по площади части. Поиск заданных фигур в фигурах сложной конфигурации. Решение задач, формирующих геометрическую наблюдательность. Исторические сведения: — кто такой Архимед, Пифагор — открытия Архимеда, Пифагора — вклад в науку 6. Систематизация знаний по изученным разделам. Сбор материала и выпуск газеты по группам. Календарно – тематическое планирование факультативного курса по математике «Математический серпантин», 3 класс.
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Неделя математики в начальной школе | План-конспект занятия по математике по теме:
1 класс
«ПУТЕШЕСТВИЕ В СТРАНУ МАТЕМАТИКИ»
Цели: развивать навыки и умения логического мышления, умственные способности детей, пробуждать интерес к предмету математики через игру.
ВЕД. Добрый день, дорогие ребята! Сегодня у нас праздник, посвященный математике – царице всех наук. Математика – очень важная наука, которая любит задачи, кроссворды, ребусы, головоломки на досуге решать, хитроумные книги читать, размышлять. Без нее не обходится ни один человек независимо от возраста и профессии. Сейчас мы отправимся в путешествие в Страну математики. В этом путешествии вы встретитесь с интересными задачами, головоломками, ребусами. Открывают наше путешествие «Цифры».
Выходят ученики с карточками цифр 1, 2, 3… 7 и читают стихотворения.
1-й уч. Наш юный друг!
Сегодня ты пришел сюда,
Чтоб помечтать, подумать, отдохнуть,
Увидеть наш веселый праздник,
Умом своим на все взглянуть.
2-й уч. Математика повсюду,
Глазом только поведешь-
И примеров разных уйму
Ты вокруг себя найдешь.
3-й уч. Вот строительство большое.
Прежде чем его начать
Нужно было все подробно
Начертить и рассчитать.
4-й уч. А иначе в этом доме
Счастья нам не увидать:
Стекла будут с перекосом,
Потолок провалится.
А кому, друзья, скажите
Это может нравиться?
5-й уч. Чтоб водить корабли,
Чтобы в небо взлететь,
Надо многое знать,
Надо много уметь!
И при этом, и при этом
Вы заметьте- ка, друзья,
Очень важная наука — математика!
6-й уч. Почему корабли не садятся на мель,
А по курсу идут сквозь туман и метель?
Потому что, потому что
Вы заметьте-ка, друзья,
Капитанам помогает математика!
7-й уч. Чтоб врачом, моряком
Чтоб врачом, моряком
Или летчиком стать,
Надо, прежде всего
Математику знать!
И на свете нет профессии,
Вы заметьте-ка, друзья,
Где бы нам ни пригодилась математика!
ВЕД. А для этого рассаживайтесь поудобнее. Мы отправляемся в игру-путешествие по Стране математики на поезде. Путешествие интересное, поэтому с собой берем смелых, дружных, сообразительных и находчивых математиков. Ну а как же нам быть без Королевы Математики? Давайте ее позовем. (дети зовут Королеву Математики)
Королева Математики: Здравствуйте, ребята! Я самая интересная и занимательная наука в мире. Мое королевство не имеет границ. При прохождении станций вам необходимо:
— быть внимательными;
— активными;
— соблюдать тишину и порядок.
Сели в поезд — поехали!
РАЗМИНКА (проводит Королева)
- Какая цифра, если перевернуть сверху вниз, уменьшается на 3? (9).

- Когда мы смотрим на число 3, а говорим «пятнадцать» (часы).
- Сколько лет рыбачил старик из «Сказки о рыбаке и рыбке» А.С.Пушкина до того, как он поймал золотую рыбку? (33 года).
- Стоит в поле дуб. На дубе 3 ветки. На каждой ветке по 3 яблока. Сколько всего яблок? (Яблоки на дубе не растут).
- На грядке сидят 6 воробьев, к ним прилетели еще 5. Кот подкрался и схватил одного. Сколько воробьев осталось на грядке? (нисколько).
- Сколько раз старик ходил к морю в «Сказке о рыбаке и рыбке» А.С.Пушкина, чтобы выполнила желания старухи? (5 раз)
ВЕД. Молодцы, ребята! Пока была разминка, наш поезд подошел к первой станции.
1-я станция «Эстафетная»
На доске из чисел и знаков для 1 класса. Дети по очереди выходят и заполняют кружки.
+4 -2 +3 +1 -2 +5 -4 -1 +2
2-я станция «Ребусная»
ПО 2 Л 5, НИЦА С 3 ЖИ 7 Я 40 А 100 Л
ВЕД. Ребята, не успели мы выполнить задания на одной станции, кА на нашем пути уже другая станция, и называется она…
Ребята, не успели мы выполнить задания на одной станции, кА на нашем пути уже другая станция, и называется она…
3-Я СТАНЦИЯ «Цифроград»
Задание: вставить недостающее число.
ВЕД. А сейчас вы сразу догадаетесь, из какой сказки следующее задание. Речь в ней пойдет о маленькой, что скорлупка грецкого ореха была ей колыбелькой, голубые фиалки- периной, а лепесток розы- одеялом. Как звали эту девочку? (Дюймовочка). Вспомните, пожалуйста, сколько заплатила женщина старой колдунье за ячменное зернышко? (12 грошей). Грош- это старинная мелкая монета. Ответьте на вопрос: чему равнялся грош? Одной, двум или трем копейкам? А поможет вам в этом следующая подсказка.
На доске цепочка: 8 – 6 + 7 – 4 + 3 – 4 + 1 – 3 = ?
Итак, один грош – 2 копейки. А сколько копеек составляют 12 грошей? (24)
ВЕД. Ребята, вспомните литературные произведения, в названиях которых встречаются числа.
Молодцы, ребята! Мы подъехали к следующей станции, где понадобятся ваша смекалка и сообразительность, поэтому будьте внимательны, не спешите. А вот и станция…
А вот и станция…
4-я станция «Смекалистых»
Хитрые задачи с цветными кубиками (коробка, 2 красных и 2 зеленых кубика)
— Какое наименьшее количество кубиков надо достать, не глядя в коробку, чтобы было 2 одинаковых кубика?
ОТГАДАЙ — КА!
Вспомните название породы собаки, состоящей из 3 букв. Если это слово прочитать справа налево, то получится название промежутка времени, длящегося 12 месяцев. (дог- год).
Ежики с яблоками 15 — 4, 8, 3 18 – 5, 7, ?
ВЕД. Молодцы, ребята! Вы настоящие путешественники: смелые, сообразительные, знающие. А сейчас, ребята, мы поиграем! Игру проведет Королева Математика.
— Ребята, сколько пальчиков у вас на каждой руке? Вам надо быть внимательными и правильно называть цифру в конце предложения.
Все вы должны, ребята, знать,
Как мы любим цифру… (пять)
О чудесной цифре… (пять)
Можно многое сказать.
В воскресенье и в субботу
Мама стала отдыхать,
И рабочих дней в неделе
Остается только…(пять).
Тем, кто к звездам в высь стремится,
Космонавтом хочет стать,
Надо в школе не лениться,
Знать любой предмет на…(пять).
Надо хорошо учиться,
Надо дома помогать,
Коль работать не лениться,
Так обязательно на…(пять).
Что стоит в конце страницы,
Украшая всю тетрадь,
Чем вы можете гордиться?
Ну, конечно, цифрой…(пять).
Кто урок совсем не знает
И трудиться не желает,
Спишет у других страничку,
Тот получит…(единичку).
5 — я станция «Головоломки»
Вот из спичек составлен дом. Надо повернуть его к нам другой стороной, переложив только 2 спички.
6 – я станция «Кроссворды»
По вертикали:
- Как называется математический текст, в конце которого есть вопрос?
- Знак, с помощью которого выполняется уменьшение числа на несколько единиц.
- Число меньше 10 на 2.
- Действие, выполняемое при увеличении числа на несколько единиц.

По горизонтали:
- Действие, выполняемое при уменьшении числа на несколько единиц.
- Число меньше одного на один.
- Знак, с помощью которого увеличивают число на несколько единиц.
- Число больше 3 на 4.
ВЕД. Наше путешествие подошло к концу. Мы очень хорошо потрудились. Я очень рада, что вы осознаете, какое важное место занимает математика в жизни человека, что с честью выдержали предложенные вам испытания.
— Сейчас ребята 1 класса дадут клятву. (Клятву читает Королева Математика.)
КЛЯНЕМСЯ!
- Не опаздывать на уроки математики, прилежно вести тетрадь и всегда выполнять домашние задания.
- Принимать активное участие в олимпиадах и внеклассных мероприятиях по математике.
- Быть другом своих одноклассников, но не давать списывать.
- Всегда активно работать на уроке, при этом не мешать другим.
- Не отказывать товарищу в помощи, действуя по принципу: «Научился сам – научи другого».

- Любить, уважать и слушаться учителя математики как родную маму.
Клянемся! Клянемся! Клянемся!
ВЕД. Надеюсь, вам было весело на нашем празднике. Но думаю, что вы не только повеселились, но и вынесли для себя немало полезного и нужного, а главное, что математика – действительно Королева всех наук и что с ней надо дружить!
Математику учить! Математику любить!
С математикой навеки крепко – накрепко дружить!
Карбонильные соединения — методы и задачи
Новые C-C связи
Реакции на карбонильной группе
- Выбираем…
- Реакции карбонильных соединений с магний и литийорганикой
- Синтез кетонов и альдегидов из карбоновых кислот и их производных
- Реакция Виттига — немного освежили 15.12.21
- Синтез диенов реакцией Виттига
- Реакция с HCN
Реакции карбонильной группы с углеродными нуклеофилами
Литий и магнийорганические соединения – очень сильные нуклеофилы, чрезвычайно легко реагирующие с карбонильной группой. Это очень мощный способ синтеза спиртов всевозможных видов – от првичных до третичных.
Это очень мощный способ синтеза спиртов всевозможных видов – от првичных до третичных.
В первом приближении это очень простая реакция. Если есть альдегид или кетон, и есть литий или магниорганическое соединение, то их реакция непосредственно дает литиевый или магниевый алкоголят, разложение которого кислотой дает искомый спирт.
Метод очень хорош, потому что позволяет получить первичные, вторичные и третичные спирты. Первичные спирты получаются реакцией с формальдегидом (только нужно брать не обычный источник формальдегида формалин – раствор формальдегида в воде с добавкой метанола, а получить чистый газообразный формальдегид из полимера формальдегида, параформа, и растворить его в эфире),
вторичные спирты – реакцией с альдегидами,
третичные спирты – реакцией с кетонами.
В принципе, на этом можно было бы и остановиться. Но это – очень упрощенная картина. В реальности с этой реакцией связано много проблем, в которых неплохо было бы хотя бы слегка разобраться.
В реальности с этой реакцией связано много проблем, в которых неплохо было бы хотя бы слегка разобраться.
Первая проблема – использование кислоты для послереакционной обработки. Многие спирты, особенно третичные, и такие, в которых есть и алкилы и ароматические заместители, очень склонны к дегидратации, сопровождаемыми еще и перегруппировками. Чтобы избежать этого, для подкисления используют не сильные соляную или серную кислоты, а раствор хлорида аммония. Аммоний – сопряженная кислота аммиака, следовательно это довольно слабая кислота, не способная вызвать кислотно-катализируемую дегидратацию, и при этом результата взаимодействия точно такой же, как и с соляной кислотой – образуются легкорастворимые хлориды магния или лития.
Вторая проблема – литий и магнийорганические соединения являются очень сильными основаниями, что совершенно естественно, так они фактически представляют собой карбанионы от простых алканов (метиллитий, бутиллитий, аналогичные гриньяры) или бензола (фениллитий и т. п.).
п.).
При этом нельзя механически переносить известные pK алканов, которые просто фантастически высоки (по разным оценкам от 45 до 55) и бензола (тоже нехилая величина) на основности RLi и RMgX. Если бы это было так, то такие реагенты ничего, кроме депротонирования почти всего на свете не вызывали бы. К счастью, такие соединения нельзя представлять себе, как свободные карбанионы – оба металла очень хорошо держатся на отрицательном углероде, несмотря на то, что связи эти фактически ионные, но значительная льюисова кислотность обоих катионов создает существенный донорно-акцепторный вклад в связь. Вообще, такие металлоорганические соединения, как и вообще почти любые металлоорганические соединения правильнее рассматривать как координационные соединения, и тогда карбанионы являются лигандами, а поскольку координационной число у обоих металлов не один и не два, а, скорее всего 4, то свободные координационные места заполняются или молекулами раствoрителя, или обеспечивают димеризацию или даже образование более крупных агрегатов (агрегат – это результат взаимодействия двух или более молекул за счет всяких слабых связей типа донорно-акцепторных, водородных, электростатических, и всяких других, но точно не обычных ковалентных). В таких агрегатах отрицательный углерод хорошо прикрыт со всех сторон и не может так легко выцеплять атомы водорода слабой кислотности. Эту интересную особенность мы разберем подробнее на другой странице.
В таких агрегатах отрицательный углерод хорошо прикрыт со всех сторон и не может так легко выцеплять атомы водорода слабой кислотности. Эту интересную особенность мы разберем подробнее на другой странице.
Тем не менее основность этих соединений все же велика, и они вполне способны отщеплять протоны от енолизуемых карбонильных соединений с образованием енолятов. Как узнать, что присоединяется к карбонильной группе, а что скорее отщепит протон и будет действовать как основание? Точно узнать нельзя – нужен эксперимент, то есть либо нужно искать, не опубликована ли реакция между конкрентными кетоном и металлоорганическим соединением в литературе, либо изучать самим. Но для нас допустим облегченный подход, потому что нам нужен только прогноз. Посмотрим, что происходит при депротонировании и сравним с тем, что происходит при присоединении карбаниона к карбонильному углероду. Разница, на самом деле точно такая же, как и при конкуренции SN2 и E2, которую мы подробно разбирали. К протону легче подобраться, чем к карбонильному углероду, и в том и в этом случае стерические препятствия благоприятствуют отщеплению протона, а не атаке на электрофильный углерод.
Поэтому, когда мы имеем дело с маленькими кетонами и маленькими (в основном первичными алкиллитиями или гриньярами), преобладает присоединение и образование спирта. Если же либо кетон, либо RM разветвленные, мы будем иметь конкуренцию, и чем разветвленнее или то, или другое, тем больше будет енолята. Если же и то, и то разветвленное, то до карбонильного углерода вовсе не добраться, и образование енолята будет преобладать. До изобретения LDA превращение кетонов в еноляты (магниевые еноляты – мы к ним не привыкли, но раньше они были популярнее литиевых, да и сейчас находят некоторое применение) очень часто делали с помощью разветвленных гриньяров – изопропилмагнийхлорида или даже совсем рогатого мезитилмагнийбромида. В старых учебниках вы наверняка все это найдете, но после изобретения LDA и других разветвленных литиевых амидов все это отправилось на свалку истории и практически полностью забыто. Но – это забыто как полезная реакция генерации енолятов, но не забыто как важная побочная реакция при реакции металлоорганики с карбонильными соединениями, просто потому что, например, никаких шансов получить третичный спирт с тремя крупными и разветвленными группами (вторичными, третичными, циклоалкильными, фенильными) ) этим методом просто нет – хотя бы одна из трех групп должна быть поменьше, метилом или хотя бы просто первичным алкилом. Это важное ограничение, и очень неплохо про него знать и учитывать это в планировании синтезов. Кроме того, когда вы делаете реакцию реактива Гриньяра с кетоном в практикуме, не забывайте учитывать реакцию енолизации как побочную – это одна из важных причин невысоких выходов, потому что та часть кетона, которая превратилась в енолят, вернется обратно после обработки реакционной смеси кислотой или хлоридом аммония.
Это важное ограничение, и очень неплохо про него знать и учитывать это в планировании синтезов. Кроме того, когда вы делаете реакцию реактива Гриньяра с кетоном в практикуме, не забывайте учитывать реакцию енолизации как побочную – это одна из важных причин невысоких выходов, потому что та часть кетона, которая превратилась в енолят, вернется обратно после обработки реакционной смеси кислотой или хлоридом аммония.
Присоединение гриньяров к карбонильной группе – очень старая и заслуженная реакция, и от ее ранней истории остались в активном употреблении до сих пор “карбинольные” названия спиртов, особенно третичных. Спирты называют как замещенный метиловый спирт, а его, в свою очередь, называют старинным названием карбинол. Трет-бутиловый спирт поэтому назовут триметилкарбинолом, а, скажем, продукт взаимодействия ацетофенона с пропилмагнийбромидом – метил-н-пропилфенилкарбинолом. Это действительно очень удобно, потому что из такого названия прямо сразу видны возможные способы построения спирта, потому что карбинол соответствует карбонилу, а перечисление висящих на нем групп – тем группам, которые были в исходном карбонильном соединении и гриньяре. Но! – это несистемные названия, номенклатура ИЮПАК их не признает, и в современных статьях вы их не встретите.
Но! – это несистемные названия, номенклатура ИЮПАК их не признает, и в современных статьях вы их не встретите.
Карбоновые кислоты – тоже карбонильные соединения. И их производные – эфиры, амиды, хлорангидриды – тоже карбонильные соединения. И даже соли карбоновых кислот – тоже карбонильные соединения. И хотя подробно мы этими классами карбонильных соединений будем заниматься во втором семестре, прямо сейчас посмотрим на важные реакции, позволяющие получать разнообразные кетоны из карбоновых кислот. Все эти реакции – типичные реакции нуклеофила с карбонильной группой, и мы легко поймём, как они идут, уже отлично зная, что бывает в таких реакциях.
Смысл таких реакций простой – берём производное карбоновой кислоты и действуем на него нуклеофилом, металлоорганическим соединением. Произвольно это делать нельзя, так как продукты таких реакций очень сильно зависят от того, какую пару мы взяли. Литий и магнийорганические соединения – очень сильные основания, и они часто просто депротонируют производное карбоновой кислоты по α-положению, образуя енолят (у производных карбоновых кислот тоже есть еноизация и еноляты, подробнее поговорим в своём месте). Или мы не можем задержаться на присоединении одного эквивалента. Например, сложные эфиры совсем не годятся – они дают третичные спирты с двумя молями литий или магнийорганики, а если взять строго моль на моль, всё равно получите третичный спирт, а часть сложного эфира останется. Амиды тоже лучше не брать – они реагируют сложно. Но две комбинации работают очень хорошо. Это:
Или мы не можем задержаться на присоединении одного эквивалента. Например, сложные эфиры совсем не годятся – они дают третичные спирты с двумя молями литий или магнийорганики, а если взять строго моль на моль, всё равно получите третичный спирт, а часть сложного эфира останется. Амиды тоже лучше не брать – они реагируют сложно. Но две комбинации работают очень хорошо. Это:
- соль карбоновой кислоты и литийорганическое соединение. Если у вас простое и дешёвое литийорганическое соединение типа метиллития, бутиллития, фениллития, из тех, что продают на рынке в больших банках, можно взять исходную кислоту, а соль получить просто действием ещё одного эквивалента дешевой литийорганики. Но если литийорганика не такая тривиальная, соль лучше получить действием более дешевого основания, например, гидрида лития или даже натрия. В реакции непосредственно получается депротонированная форма гидрата кетона. После подкисления мы получили бы сам гидрат, но мы знаем, что у кетонов гидраты совсем неустойчивы, и тут же распадаются.

- хлорангидрид карбоновой кислоты и купрат. Это очень надёжная и быстрая реакция. Обычно ее проводят при низкой температуре, чтобы избежать побочных реакций образующегося кетона, хотя большиснтво кетонов, кроме самых реакционноспособных, с купратами и так не реагируют.
Этот подход отлично распространяется на альдегиды. Только не в лоб – у альдегидов много специфических черт, а карбоновая кислота, соотвествующая альдегидной функции – муравьиная кислота – просто рекордсменка по выпендрёжу, у неё всё немного не так, или сильно не так, как у других карбоновых кислот. Например, у неё нет хлорангидрида, и это мы и так уже знаем – напоролись, когда изучали ацилирование ароматических соединений. Соли у неё есть (называются не муравьяты, а формиаты), но они тоже очень противные, потому что не очень любят сильных оснований. Поэтому мы не можем просто взять один из методов для кетонов. Зато у неё есть амид, и мы его хорошо знаем – это популярный спецрастворитель диметилформамид.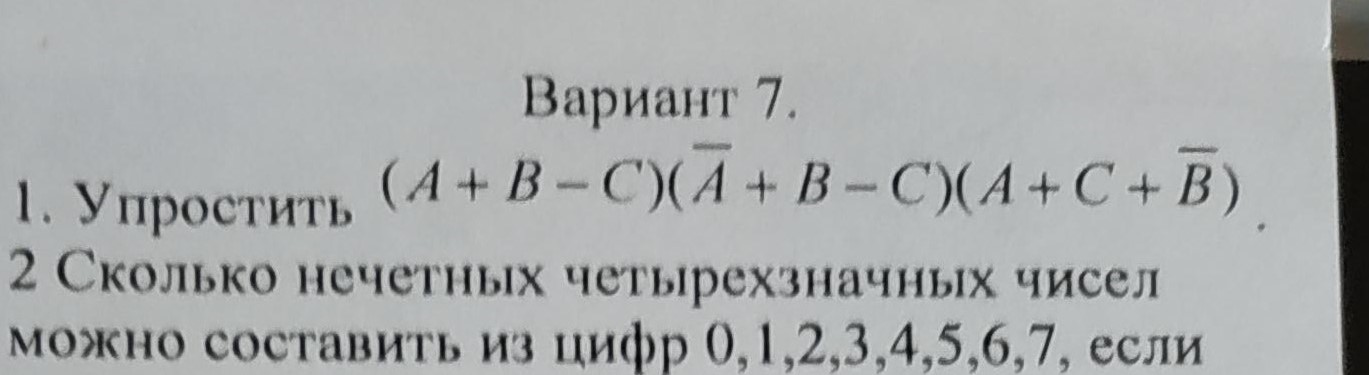 Понятно, почему нам нужно, чтобы на азоте не было водородов. И вот он хоть с литийорганикой, хоть с магнийорганикой (литийорганика обычно лучше) отлично даёт альдегиды – это, наверное, самый популярный метод синтеза альдегидов вообще, позволяющий впихнуть альдегидную (формильную) группу везде, где мы можем создать активный карбанион.
Понятно, почему нам нужно, чтобы на азоте не было водородов. И вот он хоть с литийорганикой, хоть с магнийорганикой (литийорганика обычно лучше) отлично даёт альдегиды – это, наверное, самый популярный метод синтеза альдегидов вообще, позволяющий впихнуть альдегидную (формильную) группу везде, где мы можем создать активный карбанион.
Успешность этого метода синтеза альдегидов может побудить попробовать делать и кетоны и амидов кислот. Но не стоит, плохая это реакция, она идёт, но выходы в ней низкие, и во многих случаях полно побочных.
Реакция Виттига – одна из первых реакций, с которых начался современный органический синтез, что и было отмечено половинкой Нобелевской премии (вторая пошла Герберту Брауну за гидроборирование). Реакция решает очень важную задачу синтеза – превоащение карбонильных соединений в олефины. Карбонильные соединения, как мы уже убедились, легко получаются и превращаются друг в друга миллионом разных методов, поэтому, если у нас есть способ превращения карбонильной группы в олефиновую двойную связь, мы получаем возможность синтеза огромного количества олефинов, гораздо более разнообразных, чем те, которые можно получить известными нам методами, например, элиминированием или гидрированием тройной связи. В современном синтезе таких методов, часто называемых довольно корявым словом олефинирование, многие десятки.
В современном синтезе таких методов, часто называемых довольно корявым словом олефинирование, многие десятки.
По типу реакции этот метод представляетс собой вполне обычное взаимодействие карбонильной группы с углеродным нуклеофилом, только нуклеофил не совсем обычный. Обычный, но не совсем. Обычный в том смысле, что это стабилизированный карбанион, мало ли их мы уже видели. Необычный, потому что стабилизация достигается не привычной нам мезомерной делокализацией -М заместителем, а взаимодействием с соседним атомом фосфора, да еще и положительно заряженного. Скорее всего, повышение CH-кислотности соседним атомом фосфора достигается приблизительно так же, как и соседним атомом серы, например, в тех же 1,3-дитианах: вероятно, это эффект σ-π сопряжения или обратной гиперконъюгации, возникающий из-за того, что соседний с карбанионом атом 3-го периода со своими связями имеет очень подходящие по энергии и форме пустые разрыхляющие орбитали. Это не очень наглядный эффект, и его не так просто понять, пока оставим это без доказательства, но я обязательно рано или поздно нарисую, как это работает. Дополнительный и неслабый эффект должен давать и положительный заряд на фосфоре, создающий дополнительный акцепторный индуктивный эффект, да и можно сказать, просто стабилизирующее притяжение (притяжение всегда стабилизирует, отталкивание дестабилизирует). А почему нельзя обойтись только этим, может быть, эта странная обратная гиперконъюгация даром не нужна? Нет, все-таки нужна, это серьезный эффект, проявляющийся в массе всяких молекул, и совсем делать вид, что его не существует, неправильно. Такой карбанион, стабилизированный рядом находящимся положительно заряженным атомом называют странным и не вызывающим никаких ясных ассоциаций куцым словом илид, больше похожим не на настоящее слово, а на окончание (английская версия еще хуже – ylide). Ничего, привыкнем. Реагенты Виттига в такой терминологии называются илидами фосфора. А еще бывают илиды азота, серы, селена, мышьяка, и некоторых других элементов, и у каждого из них разнообразная и интересная химия и применение в органическом синтезе.
Дополнительный и неслабый эффект должен давать и положительный заряд на фосфоре, создающий дополнительный акцепторный индуктивный эффект, да и можно сказать, просто стабилизирующее притяжение (притяжение всегда стабилизирует, отталкивание дестабилизирует). А почему нельзя обойтись только этим, может быть, эта странная обратная гиперконъюгация даром не нужна? Нет, все-таки нужна, это серьезный эффект, проявляющийся в массе всяких молекул, и совсем делать вид, что его не существует, неправильно. Такой карбанион, стабилизированный рядом находящимся положительно заряженным атомом называют странным и не вызывающим никаких ясных ассоциаций куцым словом илид, больше похожим не на настоящее слово, а на окончание (английская версия еще хуже – ylide). Ничего, привыкнем. Реагенты Виттига в такой терминологии называются илидами фосфора. А еще бывают илиды азота, серы, селена, мышьяка, и некоторых других элементов, и у каждого из них разнообразная и интересная химия и применение в органическом синтезе.
В старину, во времена Георга Виттига, считалось, что фосфор может стабилизировать соседний карбанион совсем просто, предоставляя пустую d-орбиталь, и тем самым расширяя валентные возможности сверх октета Льюиса. Формулы этих соединений писали с двойной связью P=С и называли, как и все производные 5-валентного фосфора, фосфоранами. Это нехорошая привычка, от которой стоит избавляться, и это не так просто сделать, потому что такие формулы до сих пор встречаются в учебниках и справочниках, и находят сторонников среди людей старших поколений. Никогда не спорьте с приверженцами таких структур – чувства верующих необходимо уважать, а то невзначай схлопочете двушечку. Фосфор и сера и все другие неметаллы 5-8 групп (15-18 групп в длиннопериодной таблице) не являются d-элементами и не могут использовать высоколежащие d-орбитали (d-орбитали, как и f и даже дальше безусловно есть у всех атомов, не исключая водорода, но лежат они так высоко, что почти никакого участия в образовании химических связей s- и p-элементов не принимают). Чтобы не спорить, можно принять, что форма с двойной связью – просто резонансная структура (про себя тихонько добавим – с очень малым весом). Так и волки и овцы будут и целы и сыты. Еще раз повторю – структура илида Виттига соответстует формуле с зарядами и простой связью между C и P.
Чтобы не спорить, можно принять, что форма с двойной связью – просто резонансная структура (про себя тихонько добавим – с очень малым весом). Так и волки и овцы будут и целы и сыты. Еще раз повторю – структура илида Виттига соответстует формуле с зарядами и простой связью между C и P.
Самый простой реагент Виттига получается депротонированием четвертичной соли метилтрифенилфосфония, легко получаемой SN2-реакцией трифенилфосфина (это сильный нуклеофил – вспомните SN2 и нуклеофильность) и метилиодида. Как мы уже поняли, CH-кислотность такой соли повышена, и неслабо – pK таких солей лежат рядом с 20-22. Это значит, что они несколько выше по кислотности, чем енолизуемые карбонильные соединения (pK обычно от 25 и выше), а следовательно можно отнимать протон от фосфониевой соли в присутствии карбонильного соединения, даже енолизуемого. На практике однако так обычно не делают (хотя примеров синтезов с добавлением основания прямо к смеси карбонильного соединения и илида полно, но в каждом таком случае нужно внимательно смотреть, как это сделано и почему), потому что зазор в кислотности не так велик, попасть основанием точно в одну CH-кислоту, не трогая другую непросто, и такая методика почти неизбежно приведет к побочным реакциям за счет образования енолята, например, самоконденсации. Учтите это, и по крайней мере в учебных целях всегда получайте реагент Виттига до использования в реакции с карбонильным соединением. Для предварительного получения илидов всегда используют очень сильные основания с запасом по pK минимум 10, а можно и больше – бутиллитий, амид или гидрид натрия или калия, трет-бутилат калия, LDA, и т.п. – чтобы заведомо и количественно депротонировать и не связываться с равновесиями. И еще раз повторю – не лейте их в смесь фосфониевой соли и карбонильного соединения! Еще обратите внимание на то, что илид – это карбанион, но в целом нейтральная молекула, поэтому ей не нужен внешний противоион.
Учтите это, и по крайней мере в учебных целях всегда получайте реагент Виттига до использования в реакции с карбонильным соединением. Для предварительного получения илидов всегда используют очень сильные основания с запасом по pK минимум 10, а можно и больше – бутиллитий, амид или гидрид натрия или калия, трет-бутилат калия, LDA, и т.п. – чтобы заведомо и количественно депротонировать и не связываться с равновесиями. И еще раз повторю – не лейте их в смесь фосфониевой соли и карбонильного соединения! Еще обратите внимание на то, что илид – это карбанион, но в целом нейтральная молекула, поэтому ей не нужен внешний противоион.
Так же делают и другие простые илиды из алкильных, аллильных, бензильных солей трифенилфосфина, которые можно получить SN2-замещением (трифенилфосфин – хороший нуклеофил и слабое основание, поэтому, скажем, вторичные алкилы использовать можно, но вот неопентильные – нет, потому что для этого нужен не просто хороший, а супернуклеофил, а трифенилфосфину все же далеко до этого гордого звания), и пускают их в реакцию с карбонильными соединениями.
Еще легче получаются реагенты Виттига, если в депротонируемом остатке содержатся мезомерные акцепторы – альдегидная или кето-группа, карбоксилат, циано-группа и т.п. В этом случае и SN2-замещение идет особенно быстро. Карбанион в этих случаях стабилизирован с двух сторон, и это дает pK меньше 10 – депротонировать можно даже щелочью, но осторожнее – побочные реакции ждут вас! Поэтому проще всего использовать такой чистый и безобидный реагент как гидрид натрия, даже несмотря на то, что перелет по основности будет порядков 25.
У реакции Виттига есть одна скверная особенность – она редко бывает стереоселективной (подробнее о стереоселективности и о механизме реакции Виттига посмотрите внизу в рубрике Стереоселективные реакции). По этой причине наиболее популярен самый простой реагент Виттига, действующий как стерка (в смысле ластик) буквы О в карбонильной группе. Это очень надежная реакция, и если вам нужна концевая двойная связь в самых неожиданных местах – это ваш реагент.
Если же и Виттиге есть один заместитель, и взят альдегид может получиться цис- или транс-олефин. Неплохо действует простое правило:
- если в илиде простой алкил (R’ – метил, этил, изопропил, и т.п.), то карбанион со стороны заместителя дестабилизирован индуктивным донором, то получаются в основном цис-изомеры. Транс-изомер тоже образуется, но содержание цис-изомера в смеси продуктов обычно превышает 85%. Много это или мало – достаточно, чтобы после 1-2 перекристаллизаций продукта (если он кристаллический, конечно) получить чистый цис-изомер с хорошим выходом (при перекристаллизации будут еще потери не менее 5-10%).
- если в илиде еще и сильный мезомерный акцептор, то есть карбанион сильно стабилизирован с двух сторон, то получается в основном транс-изомер, причем в этом смысле диастереомерная чистота сразу очень хорошая, то есть цис-изомер практически не образуется.
- (добавлено 15.12.21) если ни то, ни другое (например, слабый мезомерный акцептор типа фенила, или индуктивный акцептор дальше по цепи, или еще что-нибудь) получается смесь цис и транс, и это никуда не годится, если вашей целью является стереоселективный синтез чистых стереоизомеров.
 Но в реальной жизни часто придерживаются более компромиссных подходов. Во-первых, цис- и транс-изомеры часто неплохо делятся, потому что у них очень разные свойства. Транс-изомеры, например, часто более легко кристаллизуются потому что у них более симметричные молекулы, которые легче пакуются в хорошие кристаллы. Да и обычная колоночная хроматография тоже вполне неплохо делит большинство цис- и транс-изомеров. Поэтому, если для Виттига есть исходные, а это часто именно так и есть, потому что это очень простые исходные, иной раз проще замесить Виттига, и потратить немного времени на разделение изомеров. Особенно это касается получение диарилэтиленов (стильбенов) и диарилбутадиенов – это очень легко делается по Виттигу, потому что исходные бензилгалогениды и бензальдегиды или коричные альдегиды весьма легкодоступны, а сама реакция Виттига идет чрезвычайно легко и с очень высокими выходами. Не стоит забывать, что из-за мезомерного эффекта такие Виттиги можно считать стабилизированными, хоть и не в такой степени, как те, что мы рассмотрели выше – а любая дополнительная стабилизация увеличивает относительный выход транс-изомера.
Но в реальной жизни часто придерживаются более компромиссных подходов. Во-первых, цис- и транс-изомеры часто неплохо делятся, потому что у них очень разные свойства. Транс-изомеры, например, часто более легко кристаллизуются потому что у них более симметричные молекулы, которые легче пакуются в хорошие кристаллы. Да и обычная колоночная хроматография тоже вполне неплохо делит большинство цис- и транс-изомеров. Поэтому, если для Виттига есть исходные, а это часто именно так и есть, потому что это очень простые исходные, иной раз проще замесить Виттига, и потратить немного времени на разделение изомеров. Особенно это касается получение диарилэтиленов (стильбенов) и диарилбутадиенов – это очень легко делается по Виттигу, потому что исходные бензилгалогениды и бензальдегиды или коричные альдегиды весьма легкодоступны, а сама реакция Виттига идет чрезвычайно легко и с очень высокими выходами. Не стоит забывать, что из-за мезомерного эффекта такие Виттиги можно считать стабилизированными, хоть и не в такой степени, как те, что мы рассмотрели выше – а любая дополнительная стабилизация увеличивает относительный выход транс-изомера. Стабилизация проявляется ещё и в том, что для образования таких илидов не всегда нужны такие сильные основания как були, очень часто используют что-то попроще и подешевле, например, трет-бутилат или даже другие алкоголяты, или даже межфазная щёлочь – кислотность соответствующих фосфониевых солей повышена и они легче депротонируются. Многие такие реакции вообще можно вести, не получая заранее илид, а добавляя основание в смесь альдегида и фосфониевой соли, это тем более возможно потосу что бензальдегиды неенолизуемы и очень стойки к действию сильных оснований. В этих реакциях обычно образуется смесь с преобладанием транс-изомера, из которой часто этот транс-изомер просто выкристаллизовывается или прямо в реакции, или во время выделения продуктов. Про цис-изомер даже часто вообще забывают, он остается в маточнике. Поэтому в литературе полно примеров, когда такими Виттигами как будто получаются чистые транс-изомеры – авторам нужно было именно это, оно вывалилось, выход не фонтан, но, в общем, плевать на то, что остался невыделенным еще и цис-изомер, утащивший в канализацию хорошую долю выхода.
Стабилизация проявляется ещё и в том, что для образования таких илидов не всегда нужны такие сильные основания как були, очень часто используют что-то попроще и подешевле, например, трет-бутилат или даже другие алкоголяты, или даже межфазная щёлочь – кислотность соответствующих фосфониевых солей повышена и они легче депротонируются. Многие такие реакции вообще можно вести, не получая заранее илид, а добавляя основание в смесь альдегида и фосфониевой соли, это тем более возможно потосу что бензальдегиды неенолизуемы и очень стойки к действию сильных оснований. В этих реакциях обычно образуется смесь с преобладанием транс-изомера, из которой часто этот транс-изомер просто выкристаллизовывается или прямо в реакции, или во время выделения продуктов. Про цис-изомер даже часто вообще забывают, он остается в маточнике. Поэтому в литературе полно примеров, когда такими Виттигами как будто получаются чистые транс-изомеры – авторам нужно было именно это, оно вывалилось, выход не фонтан, но, в общем, плевать на то, что остался невыделенным еще и цис-изомер, утащивший в канализацию хорошую долю выхода. С точки зрения хорошего органика так делать нехорошо, но, что поделать, людям часто нужны соединения для какой-то серьёзной работы, хочется их получить хоть с каким выходом и не париться.
С точки зрения хорошего органика так делать нехорошо, но, что поделать, людям часто нужны соединения для какой-то серьёзной работы, хочется их получить хоть с каким выходом и не париться.
Тем не менее, если вы захотите подробнее разобраться в стереохимии реакции Виттига и в том, как в ней все же достигают стереоселективности, тут внизу на вкладке про стереоселективность можете посмотреть, какие ухищрения пытались использовать для улучшения стереоселективности. В принципе, это довольно бесполезная информация. В современной химии полно методов стереоселективного синтеза олефинов, и если действительно нужен чистый стереоизомер, будут использовать что-то новенькое, типа кросс-сочетания, а не модификации Виттига. Но когда-то это был высший пилотаж синтеза, и с тех пор остались сладкие воспоминания о том, как искусны некогда были органики – и вот это ровно тот материал, который даёт об этом представление. Читать это стоит только если вы увлекаетесь литературой про деяния богов и героев прошлого.
Если в Виттиге два заместителя или взят кетон, то один продукт получится только если или с той, или с другой стороны два заместителя одинаковые (например, в таком важном частном случае, когда там или там циклоалкан).
Во всех остальных случаях будет смесь E и Z-изомеров без шансов. Таких случаев обычно избегают. Также редко используют Виттига для синтеза олефинов с 4 заместителями (кетон плюс дизамещенный илид), из-за стерических проблем.
Реакция Виттига чрезвычайно популярна для синтеза сопряженных диенов и полиенов (см. на отдельной вкладке).
Слава реакции Виттига в значительной степени связана с тем, что она не против наличия двойных связей, что в илиде, что в карбонильном соединении, и даже и там, и там сразу. В результате получаются диены, в том числе сопряженные, и даже триены, тетраены, и всякие прочие многоены полиены. Это неплохо работает, образующаяся новая двойная связь обычно имеет транс-конфигурацию. Для нас это вообще единственный работающий метод синтеза разнообразных диенов, поэтому приветствуем его стоячей овацией и долгими несмолкающими аплодисментами.
Мощь этого метода оценили сразу же после появления первых статей Виттига, и уже в начале 1950-х немецкая химическая компания БАСФ, только-только выбравшаяся из-под руин нацистского концерна ИГ Фарбениндустрие, поставлявшего синильную кислоту для концлагерей, запустила промышленные процессы синтеза витамина А и идентичного природному оранжевого пигмента β-каротина. Он, например, отвечает за цвет морковки и апельсиновой Фанты, и вообще считается очень полезной пищевой добавкой – пишут, что если 18 лет подряд грызть морковку каждый день, то можно сильно поумнеть именно из-за каротина. Не знаю, не пробовал. Пить фанту 18 лет подряд почему-то не советуют. Возможности реакции Виттига в одно действие создавать огромные сопряженные системы впечатляют. Еще более занятно то, что в публикациях этих процессов обозначена в качестве основания обычная спиртовая щелочь или метилат натрия, причем реагент Виттига образуется прямо в реакционной смеси. К этому, впрочем, стоит относиться с некоторым сомнением, просто потому что эти данные взяты из патентов, а в патентах часто намеренно искажают реальные условия реакций. Поэтому впечатлимся возможностям реакции Виттига, но не будем сами использовать такие условия, а будем продолжать готовить илид отдельно действием сильного основания, и вводить его в реакцию с альдегидом.
Поэтому впечатлимся возможностям реакции Виттига, но не будем сами использовать такие условия, а будем продолжать готовить илид отдельно действием сильного основания, и вводить его в реакцию с альдегидом.
Так на заводах БАСФ начали производить простое производное витамина А – ретинол ацетат. Ацетатная защита гидроксила нужна, потому что илид обладает близкой основностью к основности алкоголятов, и без защиты были бы неизбежны потери. Убедимся, что реакция Виттига позволяет создать цепь из пяти сопряженных двойных связей с отличной стереоселективностью образующейся двойной связи – строго транс, как и нужно.
Реакция карбонильных соединений с цианидом очень удобна для того, чтобы увидеть все фокусы, которые возникают в химии карбонильной группы – обратимость, реакционную способность, активацию, катализ. И это особенно поучительно для того, чтобы посмотреть, как работают равновесия в органической химии. Поэтому остановимся поподробнее.
Если просто приосединить цианид к карбонилу, получим равновесие, причём в большиснтве случаев смещённое в сторону исходных. Само присоединение при этом экзотермично – как и в большинстве других реакций присоединения к кратным связям. Посмотрим подробнее:
Само присоединение при этом экзотермично – как и в большинстве других реакций присоединения к кратным связям. Посмотрим подробнее:
Цианистый водород (синильная кислота) к карбонилу не присоединяется. Это слабая кислота (в воде pK около 11, большая точность нам не нужна, и можно пользоваться этой величиной, так как получение циангидринов почти всегда осуществляют в водной или хотя бы протонной среде), и концентрации цианид-иона благодаря самопроизволной ионизации не хватает для обеспечения заметной скорости присоединения. Присоединяется цианид-ион, который образуется при действии оснований на HCN. При присоединении цианида получается анионный тетраэдрический интермедиат (аддукт). Эта стадия обратима, а константа очень сильно зависит от структуры карбонильного соединения. Анионный аддукт при протонировании переходит в циангидрин. При отсутствии в системе сильных оснований, это равновесие целиком сдвинуто в сторону циангидрина, и можно считать, что циангидрин является конечным продуктом реакции. Обратите внимание на первую проблему – кислотность среды. Если она велика, то в системе не будет нуклеофила, цианид-иона – реакция не пойдёт. Если наоборот, система имеет значительную основность, равновесие не дойдёт до конца, и возникнет другая проблема – циангидрин уже может начать разлагаться. Следовательно нужен некий оптимум кислотности.
Обратите внимание на первую проблему – кислотность среды. Если она велика, то в системе не будет нуклеофила, цианид-иона – реакция не пойдёт. Если наоборот, система имеет значительную основность, равновесие не дойдёт до конца, и возникнет другая проблема – циангидрин уже может начать разлагаться. Следовательно нужен некий оптимум кислотности.
Здесь впервые мы сталкиваемся с ситуацией, когда катализ требуется для двух целей: основный для того, чтобы образовался цианид-ион, и кислотный для того, чтобы вывести циангидрин из равновесия. Чтобы этого достичь нам потребуется слабая кислота, кислотность которой будет досточна для превращения анионного аддукта в циангидрин.
В таких реальных условиях реакция пойдёт не совсем так, как нарисовано на первой схеме. Само присоединение цианид-иона происходит одновременно с переносом протона от слабой кислоты. Когда в механихмах реакций что-то происходит одновременно, мы называем такой механизм согласованным, и всегда добавляем, что “одновременно” не значит совершенно синхронно. Молекулы, ионы не договариваются между собой о совместных действиях, но то, что в жидком состоянии, в растворе, всегда можно найти в непосредственной близости от событий то, что связано с растворителем (точнее, со средой реакции), в частности, если растворитель протонный и содержит слабую кислоту Бренстеда-Лоури, то найти кислый атом водорода поблизости от развивающегося в процессе реакции основного центра, например, атома кислорода с отрицательным зарядом, не проблема. Теперь анионного аддукта вообще нет, а есть переходное состояние, в котором нуклеофил вступает во взаимодействие с карбонильным углеродом, при этом атом кислорода забирает протон от слабой кислоты – это называется общим кислотным катализом – когда кислота не протонирует, потому что слаба, не может, но отдает протон через водородную связь. Еще раз обращу внимание на то, что когда рисуются стрелки обратимости до и после переходного состояния, это не значит, что переходное состояние находится в равновесии, это значит, что в равновесии находится то, что слева, и то, что справа, а переход от одного к другому, хоть вперед, хоть назад осуществляется через переходное состояние согласованной реакции.
Молекулы, ионы не договариваются между собой о совместных действиях, но то, что в жидком состоянии, в растворе, всегда можно найти в непосредственной близости от событий то, что связано с растворителем (точнее, со средой реакции), в частности, если растворитель протонный и содержит слабую кислоту Бренстеда-Лоури, то найти кислый атом водорода поблизости от развивающегося в процессе реакции основного центра, например, атома кислорода с отрицательным зарядом, не проблема. Теперь анионного аддукта вообще нет, а есть переходное состояние, в котором нуклеофил вступает во взаимодействие с карбонильным углеродом, при этом атом кислорода забирает протон от слабой кислоты – это называется общим кислотным катализом – когда кислота не протонирует, потому что слаба, не может, но отдает протон через водородную связь. Еще раз обращу внимание на то, что когда рисуются стрелки обратимости до и после переходного состояния, это не значит, что переходное состояние находится в равновесии, это значит, что в равновесии находится то, что слева, и то, что справа, а переход от одного к другому, хоть вперед, хоть назад осуществляется через переходное состояние согласованной реакции.
Из этого механизма мы видим, что циангидрин всегда должен получаться в протонной среде. Кислотность этой среды не должна при этом быть велика, так как мы не будем иметь в этой системе нуклеофила. В принципе, в качестве среды и реагента годится сам цианистый водород. Именно так впервые получил циангидрин ацетона Фридрих Урех в 1872, которого собственно и стоит считать настоящим первооткрывателем реакции образования циангидрина. С одной стороны, конечно, страшно. Но старые химики ничего не боялись, и с цианистым водородом работать очень любили.
Страшное вещество, но старые ученые не боялись. Оно известно с 18 века, и впервые его получил швед Карл Шееле действием кислоты на берлинскую лазурь. И это было еще тогда, когда настоящей химии фактически ещё не было, и техника эксперимента была практически алхимической. Жидкую HCN, кстати, впервые получили не немцы, как можно понять из её обоих тривиальных названий – синильная кислота, что является прямой калькой исходного немецкого Blausäure, и прусская кислота, как ее называют в английском и французском. Жидкую синильную кислоту впервые получил Гей-Люссак (это так у нас принято называть знаменитого француза Жозефа Луи Гэ-Люсака, ничего не поделаешь, старинная традиция, в 19 веке ещё не было депутатов государственной думы, даже настоящих). И работали с ней многие и много уже в первой половине 19 века. И ведь не травились, хотя не было тогда никаких тяг и противогазов, несмотря на высокую летучесть. Спасает, безусловно, запах – он чувствуется гораздо раньше, чем концентрация становится опасной. В общем, вполне можно работать с HCN и не погибать. Но не нужно. Вещество это любят и в промышленности, оно очень хорошо приспособлено для промышленных процессов – дешёвое, лёгкое, ничего лишнего, легколетучее, но и легкосжижаемое. Своими глазами видел на путях железнодорожную цистерну с цианистым водородом в самом ближнем Подмосковье, хотя это и было очень давно, ещё в СССР. Цистерна как цистерна. Содержавшегося в ней цианистого водорода хватило бы чтобы уморить целый город. Но, как ни странно, в промышленности почти не было серьёзных инцидентов с этим веществом за уже очень долгую историю его применения.
Жидкую синильную кислоту впервые получил Гей-Люссак (это так у нас принято называть знаменитого француза Жозефа Луи Гэ-Люсака, ничего не поделаешь, старинная традиция, в 19 веке ещё не было депутатов государственной думы, даже настоящих). И работали с ней многие и много уже в первой половине 19 века. И ведь не травились, хотя не было тогда никаких тяг и противогазов, несмотря на высокую летучесть. Спасает, безусловно, запах – он чувствуется гораздо раньше, чем концентрация становится опасной. В общем, вполне можно работать с HCN и не погибать. Но не нужно. Вещество это любят и в промышленности, оно очень хорошо приспособлено для промышленных процессов – дешёвое, лёгкое, ничего лишнего, легколетучее, но и легкосжижаемое. Своими глазами видел на путях железнодорожную цистерну с цианистым водородом в самом ближнем Подмосковье, хотя это и было очень давно, ещё в СССР. Цистерна как цистерна. Содержавшегося в ней цианистого водорода хватило бы чтобы уморить целый город. Но, как ни странно, в промышленности почти не было серьёзных инцидентов с этим веществом за уже очень долгую историю его применения. Как минимум, ее применяют в огромных количествах одном очень крупномасштабном процессе – синтезе метилметакрилата, важнейшего мономера (об этом подробнее в другом месте) и масштабы этого производства в мире огромны, масштабы измеряются сотнями тысяч тонн. Тем не менее, все живы и если и не очень здоровы, то роль синильной кислоты в этом невелика. В современных условиях синильную кислоту уже возить не принято, её обычно используют там, где получают, соединяя процессы так, чтобы ничего плохого наружу не выходило.
Как минимум, ее применяют в огромных количествах одном очень крупномасштабном процессе – синтезе метилметакрилата, важнейшего мономера (об этом подробнее в другом месте) и масштабы этого производства в мире огромны, масштабы измеряются сотнями тысяч тонн. Тем не менее, все живы и если и не очень здоровы, то роль синильной кислоты в этом невелика. В современных условиях синильную кислоту уже возить не принято, её обычно используют там, где получают, соединяя процессы так, чтобы ничего плохого наружу не выходило.
Если делать циангидрины по методу Уреха, к карбонильному соединению добавляют жидкий HCN и каталитическое количество цианида калия или просто щелочи, которая сразу даёт эквивалентное количество цианида. Фокус в том, образующийся циангидрин забирает протон с HCN, регенерируя нуклеофильный цианид-ион. Реакция экзотермична, поэтому требуется охлаждение, если это делается в больших масштабах.
Эту реакцию в огромных масштабах – сотни тысяч тонн – именно так делают в промышленности для получения ацетонциангидрина.
Но в лаборатории этот метод неудобен. Желающих работать с цианистым водородом на свете немного. Это в 19 веке химики были отмороженные и ничего не боялись. “Богатыри, не мы”. В наше время таких уж не найти. О себе скажу – если бы мне попалась методика с цианистым водородом, даже читать бы не стал – нафиг, жизнь дороже, я не Гей-Люссак. Но пугливые водились уже в начале 20 века, и голландский химик Арнольдус Ульте придумал менее нервную методику. В ней используют соль синильной кислоты, она хотя бы нелетучая, и случайно в неё не вляпаешься. К карбонильному соединению добавляют твёрдый цианид натрия или калия, воду, и при охлаждении и перемешивании прикапывают небольшой недостаток разбавленной серной кислоты. Выглядит тоже слегка нервно, но если все делать осторожно, прикапывать медленно, перемешивать и охлаждать усердно, в хорошей тяге, то проблем нет. В этом случае цианид всегда в избытке, но обратимо образующийся анионный аддукт протонируется серной кислотой и количественно выводится из равновесия. Такой метод реакция с цианидом щелочного металла при добавлении почти эквивалента кислоты называют методом Ульте.
Такой метод реакция с цианидом щелочного металла при добавлении почти эквивалента кислоты называют методом Ульте.
В литературе, даже такой, которая специально посвящена циангидринам, методы Уреха и Ульте часто путают, поэтому предупреждаю тех, кто читал об этом в других местах – я проверил это по оригинальным статьям и того, и другого, и то, что здесь написано оригинальным работам и соответствует, а что там переписывают из обзора в обзор меня не волнует.
В современной химии особенно в реакциях с очень маленькими количествами при необходимости сделать циангидрин используют триметилсилилцианид TMSCN, удобный продажный безопасный реагент (естественно, им тоже можно отравиться, потому что он при гидролизе выделяет синильную кислоту, но с тем же успехом можно отравиться и абрикосовыми косточками и пирожком из тапиоки с черникой). Это соединение чрезвычайно легко реагирует с карбонильными соединениями в присутсвии каталитических количеств кислот Льюиса или оснований. Кремниевое производное, не выделяя, гидролизуют разбавленной солянкой. Этот метод хорош не только тем, что можно повыпендриваться, использовав модные реагенты вместо старинных, но и тем, что реакция с триметилсилилцианидом необратима, поэтому так можно получать циангидрины из таких кетонов, которые по-старому просто не реагируют, так как равновесие с ними смещено в сторону исходных, например, со стерически затруднёнными или ароматическими. Об этом ниже.
Этот метод хорош не только тем, что можно повыпендриваться, использовав модные реагенты вместо старинных, но и тем, что реакция с триметилсилилцианидом необратима, поэтому так можно получать циангидрины из таких кетонов, которые по-старому просто не реагируют, так как равновесие с ними смещено в сторону исходных, например, со стерически затруднёнными или ароматическими. Об этом ниже.
И наконец есть ещё один метод, совсем тонкий. Фокус здесь в том, что в циангидрине углерод ассимметрический (если только не брать симметричный кетон). Мы обычно не обращаем на это внимания, что означает, что мы получаем рацемат циангидрина. Но в современной химии любят получать оптически активные продукты там, где это возможно. А для этого надо откуда-то взять оптическую активность, потому что сама собой она не образуется. Так как ни карбонильное соединение, ни TMSCN нехиральны, оптическую активность можно поискать в катализаторе – кислоте Льюиса, использовав какое-нибудь производное металла в виде комплекса с хиральным лигандом. Расшифровывать не буду, мы не изучаем асимметрический синтез, но о том, что он существует и без него немыслима химия 21 века, знать стоит.
Расшифровывать не буду, мы не изучаем асимметрический синтез, но о том, что он существует и без него немыслима химия 21 века, знать стоит.
Какие карбонильные соединения дают циангидрины?
Образование циангидринов – одна из самых удобных реакций для того, чтобы изучить и увидеть зависимость реакции присоединения нуклеофила к карбонильной группе ещё и от структуры карбонильного соединения. Здесь отлично работают все закономерности. Прямо как на ладони.
Во-первых, сразу скажем, что присоединение к карбонильной группе почти всегда выгодно. Мы уже не раз упоминали эту общую закономерность – кратные связи всегда богаче энергией, чем простые с участием тех же элементов. Это касается и связей С=С, но и С=О и C=N. Избыток электронной плотности на кратных связях дестабилизирует их. Поэтому реакции присоединения почти всегда экзотермичны (ΔHº < 0) и имеют и ΔGº < 0. Следовательно и константы равновесия таких реакций, когда они обратимы, больше единицы, то есть равновесия по определению почти всегда смещены в сторону аддуктов.
Но не для всех карбонильных соединений. Есть и такие, у которых константы равновесия меньше единицы, то есть равновесие смещено в обратную сторону. В общих идеях по реакционной способности карбонильных соединений в реакциях с нуклеофилами мы уже обсуждали основной фактор – стерический. И второй фактор – сопряжение карбонила с ароматическим кольцом, которое стабилизирует карбонильную группу и делает ее менее реакционноспособной. Соотвественно, две категории кетонов имеют константы меньше единицы при реакции с карбонильными соединениями –
- кетоны с крупными группами, обязательно обеими – вторичными и третичными алкилами, циклическими заместителями и тем, что на это похоже;
- один из заместителей фенил (с заместителями или без), второй может быть любым, хоть метилом
- оба заместители фенилы (с заместителями или без) или другие ароматические остатки – это самый поганый случай, константы равновесия очень малы.
В этих случаях мы не можем получить циангидрин взаимодействием кетона с цианидами или HCN. Но это не значит, что такие циангидрины невозможно получить. Один из очень надёжных способов, с помощью которого большинство этих циангидринов были получены (включая циангидрины дифенилкетонов, бензофенонов) – использование триметилсилилцианида, который присоединяется (в присутствии катализаторов, кислот Льюиса, самым популярным был и остается безводный иодид цинка) необратимо практически ко всем альдегидам и кетонам, с разложением силильного производного циангидрина сильной кислотой, обычно HCl (используют чаще всего раствор в ТГФ, эфире, спиртах и т.п.). Здесь фокус в том, что циангидрин устойчив сам по себе. Для того, чтобы включить равновесие, нужен основный катализ. Для этого годится любое более-менее сильное основание, типа щелочи, даже в очень малых количествах, поэтому катализатором разложения, то есть включения равновесия, может быть даже просто стекло, в котором хранится циангидрин. Поэтому полученные циангидрины всегда стабилизируют добавлением небольшого количества кислот, обычно уксусной, но иногда и других.
Но это не значит, что такие циангидрины невозможно получить. Один из очень надёжных способов, с помощью которого большинство этих циангидринов были получены (включая циангидрины дифенилкетонов, бензофенонов) – использование триметилсилилцианида, который присоединяется (в присутствии катализаторов, кислот Льюиса, самым популярным был и остается безводный иодид цинка) необратимо практически ко всем альдегидам и кетонам, с разложением силильного производного циангидрина сильной кислотой, обычно HCl (используют чаще всего раствор в ТГФ, эфире, спиртах и т.п.). Здесь фокус в том, что циангидрин устойчив сам по себе. Для того, чтобы включить равновесие, нужен основный катализ. Для этого годится любое более-менее сильное основание, типа щелочи, даже в очень малых количествах, поэтому катализатором разложения, то есть включения равновесия, может быть даже просто стекло, в котором хранится циангидрин. Поэтому полученные циангидрины всегда стабилизируют добавлением небольшого количества кислот, обычно уксусной, но иногда и других. В этом виде циангидрины можно хранить и использовать в реакциях, только будьте осторожны с реакциями в присутствии оснований – разложение циангидрина почти всегда произойдёт быстрее, чем та реакция, которую вы запланировали. Но, например, восстановление до аминов алюмогидридом лития, вполне рабочая реакция.
В этом виде циангидрины можно хранить и использовать в реакциях, только будьте осторожны с реакциями в присутствии оснований – разложение циангидрина почти всегда произойдёт быстрее, чем та реакция, которую вы запланировали. Но, например, восстановление до аминов алюмогидридом лития, вполне рабочая реакция.
Альдегиды (практически все) и кетоны, не относящиеся к перечисленным (“хорошие кетоны”) имеют константы равновесия реакции с HCN больше единицы и сильно больше, от двухзначных чисел у большинства хороших кетонов и ароматических альдегидов до четырёхзначных у алифатических альдегидов. О скорости реакции можно не думать – это одна из тех реакций, в которых константа равновесия важнее. Так бывает далеко не всегда. Обычно всё же мало иметь хорошую константу равновесия и экзотермичность, нужна еще и хорошая скорость реакции, а скорость, как назло, плевать хотела и на равновесие и на экзотермичность. Ну, не совсем плевать, если и константа велика и экзотермичность впечатляет, скорость прямой реакции почти всегда велика. Это прямое следствие одного из полезных качественных принципов химии, постулата Хэммонда, о котором надо бы как-нибудь вспомнить. Пока оставим, примем как данность. Здесь важно вот что: когда константа равновесия сильно больше единицы (как минимум, на порядок, то есть выражается двузначным числом) скорость реакции почти всегда (но не всегда!!) будет хороша. Проблема есть с теми реакциями, в которых константа равновесия, хоть и положительна, но не сильно больше единицы.
Это прямое следствие одного из полезных качественных принципов химии, постулата Хэммонда, о котором надо бы как-нибудь вспомнить. Пока оставим, примем как данность. Здесь важно вот что: когда константа равновесия сильно больше единицы (как минимум, на порядок, то есть выражается двузначным числом) скорость реакции почти всегда (но не всегда!!) будет хороша. Проблема есть с теми реакциями, в которых константа равновесия, хоть и положительна, но не сильно больше единицы.
С практической точки зрения, все такие простые циангидрины легко получаются одним из двух простых способов рассмотренных выше – методом Уреха или Ульте, но для кетонов покрупнее (первично-вторичных, первично-третичных) и ароматических альдегидов с сильными донорными заместителями в кольце можно тоже прибегнуть к методу с TMSCN и гидролизом силильного производного.
С заместителями можно видеть еще более тонкие эффекты. Вот, например, не совсем обычная картина зависимости константы равновесия образования циангидрина от положения нитро-группы в бензальдегидах. На первый взгляд, нитро-группа должна увеличивать электрофильность карбонильного углерода и благоприятствовать присоединению. Это так, но только для мета и орто-положения, и чем ближе, тем лучше – хорошо, мы так и думали. А вот почему пара-нитробензальдегид хуже? Да потому, что карбонил сопряжен с нитрогруппой, которая сильнее, как акцептор, значит, в этом случае карбонил – донор в цепи сопряжения. И такое сопряжение уменьшает электронную плотность на двойной связи С=О и стабилизирует её. Этот эффект оказывается сильнее увеличения электрофильности. Так, а почему тогда орто-нитробензальдегид в другой стороне? Там же тоже -M-эффект, стабилизирующий! А вот и нет. Когда мы смотрим на сопряжение, нам нужно не забывать, что сопряжение требует правильного пространственнного расположения орбиталей, и лучше всего, когда группы в плоскости, а орбитали перпендикулярны. Но в орто-расположении карбонил и нитро-группа мешают друг другу, выталкивая соседа из плоскости. Вот так они и пихаются, а страдает сопряжение, карбонил остается без стабилизации, а вот неприхотливый индуктивный эффект на месте и увеличивает электрофильность сильнее всего, потому что, чем ближе тем лучше.
На первый взгляд, нитро-группа должна увеличивать электрофильность карбонильного углерода и благоприятствовать присоединению. Это так, но только для мета и орто-положения, и чем ближе, тем лучше – хорошо, мы так и думали. А вот почему пара-нитробензальдегид хуже? Да потому, что карбонил сопряжен с нитрогруппой, которая сильнее, как акцептор, значит, в этом случае карбонил – донор в цепи сопряжения. И такое сопряжение уменьшает электронную плотность на двойной связи С=О и стабилизирует её. Этот эффект оказывается сильнее увеличения электрофильности. Так, а почему тогда орто-нитробензальдегид в другой стороне? Там же тоже -M-эффект, стабилизирующий! А вот и нет. Когда мы смотрим на сопряжение, нам нужно не забывать, что сопряжение требует правильного пространственнного расположения орбиталей, и лучше всего, когда группы в плоскости, а орбитали перпендикулярны. Но в орто-расположении карбонил и нитро-группа мешают друг другу, выталкивая соседа из плоскости. Вот так они и пихаются, а страдает сопряжение, карбонил остается без стабилизации, а вот неприхотливый индуктивный эффект на месте и увеличивает электрофильность сильнее всего, потому что, чем ближе тем лучше. .
.
Циангидрины, особенно кетонов, весьма неустойчивые соединения. Казалось бы, везде константы равновесия сильно больше единицы. Но проблема в том, что продукт распада, HCN, очень летучая вещь, а следовательно она быстро выходит из равновесия при начале разложения, и в дело вступает Ле Шателье. Бывает даже бурное разложение, почти взрывообразное. Одна вещь спасает – разложение происходит только в присутствии оснований, даже очень малых количеств (уже говорили о том, что таким может стать поверхность стекла). Поэтому, например, такая популярная и производимая в очень больших количествах циангидрин ацетона, очень опасен при хранении. В закрытой таре HCN не улетает и разложение останавливается – именно за счет повышенного давления HCN внутри – можете представить себе такой сюрприз: открываете вы баночку (или бочку), а оттуда как зашипит! Для хранения ацетонциангидрин, во-первых, очень хорошо очищают, обрабатывая кислотой, и, во-вторых, добавляют немного кислоты для стабилизации. Но штука всё равно опасная, будьте осторожны, если попадётся.
Но штука всё равно опасная, будьте осторожны, если попадётся.
Umpolung – реакции, в которых карбонильный углерод работает нуклеофилом
- Выбираем…
- Дитиановый синтез альдегидов и кетонов
- Бензоиновая конденсация
- Направленная бензоиновая конденсация и кремниевые производные циангидринов
А здесь всё наоборот: карбонильный углерод становится нуклеофилом и реагирует с углеродными электрофилами
В альдегидной группе есть один протон (а в формальдегиде даже два), который так и просится, чтобы его заменили на какой-нибудь заместитель – тогд альдегид превратился бы в кетон (а формальдегид в другой альдегид). Есть два стандартных способа выполнить такое превращение в общем случае:
а) забрать протон основанием, получив карбанион и далее использовать этот карбанион как нуклеофил в SN2-замещении;
б) заменить протон на галоген, после чего выполнить то же замещение, но с переменой реагентов местами.
В конкретных случаях бывает невозможно выполнить оба подхода – мещает или недостаточная кислотность протона, или отстутствие методов селективного галогенирования именно по этому месту. Тем не менее, как возможность оба эти способа всегда нужно иметь в виду. Интересно, что с точки зрения электрофильности и нуклеофильности предполагаемые реагенты меняются местами. Этот прием в синтезе получил странное немецкое имя Umpolung – специально выбранное так, чтобы в мало кому понятное немецкое слово впихнуть целое предложение на других языках. Слово Umpolung нельзя перевести одним русским, английским и пр. словом. Что такое Umpolung: это такой синтетический прием, в котором электрофил и нуклеофил меняются местами. Коряво получилось, не правда ли? Поэтому не переводите никогда это слово, а просто или используйте, если поняли, что это значит, или вообще забудьте.
Вернемся к задаче превратить альдегид в кетон. Карбонильный углерод, как мы знаем, по определению электрофилен, и большинство методов, основанных на замещении на карбонильном углероде используют реакцию нуклеофильного реагента с электрофильным карбонилом. Чтобы перевернуть этот подход (это как раз и был бы Umpolung) нужно было бы отщепить водород от альдегидной группы с образованием карбаниона (который в этом случае называется ацильный) – но это, оказывается невозможно. Ацильный карбанион чрезвычайно неустойчив. Понять, почему, не очень просто. Казалось бы рядом сильно-акцепторный атом кислорода и карбанион должен им стабилизироваться. Но получается все наоборот, видимо, из-за хорошо известного уже нам α-эффекта – отталкивания неподеленной пары на углероде и близких к ней пар на кислороде. Есть и другие проблемы. Высокая электрофильность карбонильного углерода в альдегидах неизбежно привела бы к тому, что даже если протон удавалось бы отрывать, образующийся карбанион немедленно присоединялся бы ко второй молекуле альдегида. Если кому-то это покажется интересным, посмотрите на хорошо известную реакцию олигомеризации формальдегида в присутствии гидроксида кальция – реакцию Бутлерова, приводящую к смесям углеводов, – там происходит нечто очень похожее.
Чтобы перевернуть этот подход (это как раз и был бы Umpolung) нужно было бы отщепить водород от альдегидной группы с образованием карбаниона (который в этом случае называется ацильный) – но это, оказывается невозможно. Ацильный карбанион чрезвычайно неустойчив. Понять, почему, не очень просто. Казалось бы рядом сильно-акцепторный атом кислорода и карбанион должен им стабилизироваться. Но получается все наоборот, видимо, из-за хорошо известного уже нам α-эффекта – отталкивания неподеленной пары на углероде и близких к ней пар на кислороде. Есть и другие проблемы. Высокая электрофильность карбонильного углерода в альдегидах неизбежно привела бы к тому, что даже если протон удавалось бы отрывать, образующийся карбанион немедленно присоединялся бы ко второй молекуле альдегида. Если кому-то это покажется интересным, посмотрите на хорошо известную реакцию олигомеризации формальдегида в присутствии гидроксида кальция – реакцию Бутлерова, приводящую к смесям углеводов, – там происходит нечто очень похожее.
Поэтому напрямую это не работает. Но можно попробовать сделать хитрее, временно превратив альдегидную группу во что-то другое, что позволило бы оторвать протон и сделать желаемое нуклеофильное замещение, а в конце вернуть на место карбонил. То есть выполнить защиту карбонила с одновременным изменением типа реакционного центра на углероде – с электрофильного на нуклеофильный. Это и будет Umpolung. Обычная защита ацеталем для этой цели не годится – атомы кислорода в ацетальных группах точно так же оказывают α-эффект, и кислотность не повышается. Но для ближайшего аналога ацеталя – тиоацеталя этой проблемы больше нет – α-эффект есть только во втором периоде, где короткие связи и компактные орбитали. Более того, оказывается что сера, а точнее ее связи с углеродом способны учствовать в делокализации отрицательного заряда карбаниона за счет эффекта, похожего на гиперконъюгацию – σ-π-сопряжения, то есть сопряжения пи-орбитали карбаниона и пустой разрыхляющей орбитали связей S-C.
Чтобы протон снимался точно с одного и правильного углерода требуется шестичленный ацеталь. Внимание – использовать в этом методе пятичленный ацеталь, похожий на тот, который мы используем в простой защите карбонильной группы ацеталем с этиленгликолем – ошибка. В пятичленном тиоацеталь протон снимается не только с правильного углерода, но и с неправильного тоже, что приводит к побочным реакциям.
Внимание – использовать в этом методе пятичленный ацеталь, похожий на тот, который мы используем в простой защите карбонильной группы ацеталем с этиленгликолем – ошибка. В пятичленном тиоацеталь протон снимается не только с правильного углерода, но и с неправильного тоже, что приводит к побочным реакциям.
Ключевое соединение метода – тиоацеталь формальдегида с 1,3-пропандитиолом, по номенклатуре гетероциклических соединений называемый 1,3-дитианом (-ан – означает насыщенный 6-членный цикл, 1,3-дитиа – два атома серы на 1 и 3 месте в цикле, нумерация всегда идет от гетероатома). Этот реагент обычно берут готовым. Если начинаем уже от монозамещенного дитиана, то берут альдегид и 1,3-пропандитиол и реагент получают отдельно. В качестве катализатора используют доступную кислоту Льюиса – трифторид бора в виде комплекса с диэтиловым эфиром, но не в каталитическом количестве, а эквимольно. Выделяющуюся воду можно при этом не удалять, как это делают при получении обычных ацеталей, так как трифторид бора ее связывает, что делает образование тиоацеталя необратимым.
Кислотность протона в 1,3-дитианах повышена (относительно циклогексана), но все равно весьма мала, поэтому для депротонирования используют очень сильные основания, чаще всего н-бутиллитий. Полученную литевую соль дитианового карбаниона алкилируют алкилгалогенидами в полном соотвествии с уже нам хорошо знакомыми закономерностями SN2-замещения. Так как нуклеофил здесь – очень сильное основание, никаких плохих субстратов (вторичных, разветвленных) использовать нельзя – ничего кроме элиминирования не будет. Ну а попытка сделать реацию с третичным субстратом считается тяжким преступлением и карается пожизненной дисквалификацией.
Из незамещенного 1,3-дитиана можно делать не только альдегиды, но и кетоны, повторив реакцию с вторым алкилирующим агентом. Хотя это делают в одной колбе без выделения продукта моноалкилирования (такие реакции называют one-pot reaction – буквально “реакция в одном горшке”), но это обязательно делают ступенчато – нельзя лить в этот самый горшок сразу два эквивалента були и оба алкилирующих агента – обязательно явно обозначьте 4 стадии, даже если оба алкилирующих реагента одинаковы (получаем симметричный кетон). И если два алкилирующих реагента разные, первым используйте тот, что похуже (первичный алкил, например), а вторым тот, что получше (метил, бензил, эпоксид и т.п.).
И если два алкилирующих реагента разные, первым используйте тот, что похуже (первичный алкил, например), а вторым тот, что получше (метил, бензил, эпоксид и т.п.).
После получения замещенного дитиана необходимо добыть оттуда карбонильную группу. Это делают почти как для обычных ацеталей – кислотным гидролизом, но с добавлением соли ртути, которая связывает выделяющийся дитиол в чрезвычайно прочный комплекс и смещает равновесие гидролиза. Ион ртути(2+) обладает чудовищным сродством к сернистым лигандам – досточно вспомнить самую обычную киноварь – HgS – одно из самых нерастворимых соединений в химии, что как раз и говорит о том, что связи Hg – S такие прочные, что разорвать их мало кому под силу.
Бензоиновая конденсация – реакция, занимающая довольно скромное место в нашем курсе. Иногда даже кажется, что это какая-то безделица, что-то очень частное и почти бесполезное, потому что в учебниках ей уделяют обычно очень скромное место, и создается впечатление, что это вообще реакция одного соединения. А такая популярная, и в общем неплохая книжка как Органикум, вообще про эту реакцию написала полную чушь, перепутав её с ацилоиновой конденсацией. Я глазам свои не поверил, когда это первый раз обнаружил, и едва не дал этой книге безапелляционную рекомендацию – фтопку, но понемногу отошёл, в ней всё же много полезного, а некоторая милая дремучесть объясняется просто – это наследие небесследно исчезнувшей и очень странной страны ГДР. К тому же я с тех пор обнаружил, что такую ошибку делает не только Органикум, так что, можно сказать, это почти узаконенное заблуждение.
А такая популярная, и в общем неплохая книжка как Органикум, вообще про эту реакцию написала полную чушь, перепутав её с ацилоиновой конденсацией. Я глазам свои не поверил, когда это первый раз обнаружил, и едва не дал этой книге безапелляционную рекомендацию – фтопку, но понемногу отошёл, в ней всё же много полезного, а некоторая милая дремучесть объясняется просто – это наследие небесследно исчезнувшей и очень странной страны ГДР. К тому же я с тех пор обнаружил, что такую ошибку делает не только Органикум, так что, можно сказать, это почти узаконенное заблуждение.
Мы путать не будем. Путают эти две реакции потому, что у них одинаковые по типу продукты – α-гидроксикетоны. У таких соединений есть еще два исторических названия по двум очень важным реакциям – ацилоины по ацилоиновой конденсации, бензоины – по бензоиновой конденсации. Удивительно, но внешнее сходство этих терминов случайно, оба термины из 19 века, бензоин вообще из самого начала, ацилоин появился немного позднее, и в те времена, когда и структур никаких никто не знал, а сходство было выяснено намного позже.
Итак, ацилоиновая конденсация – это восстановительное сдваивание сложных эфиров, происходящее под действием металлического натрия. Подробнее мы с этой реакцией разберёмся в теме Карбоновые кислоты. Сразу видим, что это реакция восстановительная – ацилоин получается восстановлением двух молекул сложного эфира натрием в неполярном апротонном растворителе. Бензоиновая конденсация – это реакция альдегидов, в классическом варианте ароматических, и происходит она при действии цианида щелочного металла. Это не окислительно-восстановительная реакция, хотя внимательный взгляд увидит, сто атомы углерода альдегидной группы в продукте изменили степени окисления, но на одинаковую величину (единицу) в разные стороны, то есть это формально диспропорционирование – одна молекула бензальдегида восстанавливает другую. Но не так, как в реакциях Каниццаро и Тищенко, где переходид водород альдегидной группы и степени окисления изменяются на 2. Но в Каниццаро этот водород переезжает в виде гидрида, с парой электронов.
И если ацилоиновая конденсация – реакция вполне общая, в неё вступаю очень многие карбоновые кислоты (в виде эфиров), то бензоиновая конденсация в оригинальном варианте просто удивительно узка – похоже, что в неё вступает только сам бензальдегид, ну и еще буквально несколько других ароматических альдегидов. Но, на самом деле, это удивительная реакция. Стоит в ней начать разбираться, как иголки буквально как из головы Страшилы, начинает вылезать множество интересных вещей, Umpolung и стабильные карбены, органокатализ, ферменты транскетолазы, витамин B1, не говоря уж об интригующих исторических следах. Подробнее я как-нибудь потом напишу, а пока разберёмся в основах.
Во первых, зададим вопрос, а что случилось с обычной реакцией альдегидов с цианидами – образования циангидрина. Почему здесь не образуется циангидрин? Бензальдегид какой-то особый альдегид? Нет, без паники, циангидрин у бензальдегида есть, он вполне устойчив, легко получается, известен уже 200 лет, и даже имеет тривилальное название – нитрил миндальной кислоты. Бензальдегид вобще неразрывно связан с миндалём, недаром его самого в начале 19 века называли не бензальдегидом, а маслом горького миндаля. Почему – обсудим отдельно и потом, это занятная история. Чтобы получить циангидрин бензальдегида нужно обязательно поставить эквивалент протонов, чтобы запротонировать отрицательный кислород. Поэтому реакцию делают в присутствии слабой кислоты, например, уксусной, но так, чтобы оставалось небольшое количество свободного цианида, иначе присоединяться будет нечему. Но мы это уже обсуждали, когда рассматривали циангидрины. Ай, позорище какое, я забыл, оказывается. Хорошо, тогда вкратце здесь. Итак, к альдегидной группе присоединяется слабый нуклеофил, цианид-ион. При этом обратимо образуется анионный тетраэдрический аддукт, как обычно это и бывает. Этот аддукт является основанием – это ведь алкоксид-ион типа этилата, но менее основный потому что рядом неплохой индуктивный акцептор, циано-группа. Поскольку основность меньше, запротонировать его не получится ни спиртом, ни даже водой.
Бензальдегид вобще неразрывно связан с миндалём, недаром его самого в начале 19 века называли не бензальдегидом, а маслом горького миндаля. Почему – обсудим отдельно и потом, это занятная история. Чтобы получить циангидрин бензальдегида нужно обязательно поставить эквивалент протонов, чтобы запротонировать отрицательный кислород. Поэтому реакцию делают в присутствии слабой кислоты, например, уксусной, но так, чтобы оставалось небольшое количество свободного цианида, иначе присоединяться будет нечему. Но мы это уже обсуждали, когда рассматривали циангидрины. Ай, позорище какое, я забыл, оказывается. Хорошо, тогда вкратце здесь. Итак, к альдегидной группе присоединяется слабый нуклеофил, цианид-ион. При этом обратимо образуется анионный тетраэдрический аддукт, как обычно это и бывает. Этот аддукт является основанием – это ведь алкоксид-ион типа этилата, но менее основный потому что рядом неплохой индуктивный акцептор, циано-группа. Поскольку основность меньше, запротонировать его не получится ни спиртом, ни даже водой. И реакция была бы обратимой, и, как мы сейчас увидим, пошла бы совсем в другую сторону, если бы мы не добавили почти эквивалент какой-нибудь слабой кислоты, но всё же более сильной, чем вода. Карбоновая любая пойдёт, например, уксусная. Тогда протонирование станет практически необратимым и мы выведем циангидрин из равновесия.
И реакция была бы обратимой, и, как мы сейчас увидим, пошла бы совсем в другую сторону, если бы мы не добавили почти эквивалент какой-нибудь слабой кислоты, но всё же более сильной, чем вода. Карбоновая любая пойдёт, например, уксусная. Тогда протонирование станет практически необратимым и мы выведем циангидрин из равновесия.
А теперь представим себе, что цианид мы добавили, а эквивалент слабой кислоты забыли или не догадались. Тогда произойдёт нечто очень занятное. Анионный аддукт зависнет в равновесии. И выяснится то, что в циангидрине бензальдегида есть два кислотных центра – OH и CH. И что кислотность их сравнима. Мы, к сожалению, не знаем точные величины pK для этих центров, их не удаётся померить, потому что при депротонировании начинаются другие реакции. Но можем оценить по косвенным данным, получится что для CH-кислоты pK не больше 20 – сказываются акцепторные мезомерные эффекты и фенила, и циано-группы (напишите граничные структуры сами). Это точно достаточно для обратимого депротонирования в спиртовом растворе, но, в принципе, и в водном тоже, хотя карбаниона в равновесии будет меньше. Бензоиновую конденсацию и ведут обычно в спиртовом растворе, иногда в водно-спиртовом, а в водном не получится и не только из-за недостаточной основности, но и из-за нерастворимости бензальдегида. В таком, классическом виде реакцию открыл в 1839 году хорошо нам знакомый Николай Николаевич Зинин, то самый, который первым восстановил нитробензол в анилин.
Бензоиновую конденсацию и ведут обычно в спиртовом растворе, иногда в водно-спиртовом, а в водном не получится и не только из-за недостаточной основности, но и из-за нерастворимости бензальдегида. В таком, классическом виде реакцию открыл в 1839 году хорошо нам знакомый Николай Николаевич Зинин, то самый, который первым восстановил нитробензол в анилин.
Механизм бензоиновой конденсации был предметом очень пристальных исследований, потому что этот механизм является ключом к очень большой и важной химии и биохимии. Более того, это один из самых старых механизмов в органике – его основные стадии установил ещё в 1904 году шотландский химик Артур Лэпуорс (или Лэпуорт, обычная история с неоднозначностью передачи звука th – Lapworth). В это время не было еще никаких представлений о механизмах реакций, и поэтому работа Лэпуорса с полным основанием считается классикой и семенем, из которой выросло всё то, что мы сейчас изучаем про механизмы. Когда во второй половине 20 века реакцию исследовали уже со всем арсеналом методов, от спектроскопии до кинетики, оказалось, что Лэпуорс угадал почти всё правильно, а ведь всё это делалось из общих соображений и по простым опытам.
Итак, в растворе образуется анионный аддукт, который в отсутствие кислоты находится в равновесии с циангидрином, но не превращается в него, и не выходит из равновесия. Тогда, в результате обратимых кислотно-основных равновесий с участием сопряжённых оснований из растворителя, обратимо образуется карбанион. Этот карбанион нуклеофилен. Ещё раз – в этом карбанионе нуклеофильным центром является тот углерод, который ешё недавно был электрофильным карбонильным углеродом. Узнаёте почти то же самое, что мы видели в дитиановом синтезе – Umpolung. Электрофил стал нуклеофилом. Но в растворе еще много исходного бензальдегида. И происходит обычное – нуклеофильная атака на электрофильный карбонил. Всё обратимо. Образовавшийся аддукт, ели его рассмотреть, представляет собой тоже циангидрин, но уже не альдегида, а кетона. А циангидрины кетонов совсем неустойчивы, и очень легко распадаются на кетон и цианид-ион, но только в присутствии оснований, которые переводят гидроксильную группу циангидрина в сопряжённое основание. Но в этом случае проблем с депротонированием нет – оно просто происходит внутримолекулярно от соседней группы. Циангидрин распадается и образуется бензоин. Этот распад происходит быстро и практически количественно, так, что его можно с практической точки зрения считать необратимым. Но в действительности он обратим, просто константа равновесия велика. Обратимость этой стадии делает всю бензоиновую конденсацию обратимой. Как и большиснтво других реакций на карбонильной группе – мы уже к этому должны были привыкнуть. К чему приводит обратимость бензоиновой конденсации, обсудим отдельно. Пока это не важно.
Но в этом случае проблем с депротонированием нет – оно просто происходит внутримолекулярно от соседней группы. Циангидрин распадается и образуется бензоин. Этот распад происходит быстро и практически количественно, так, что его можно с практической точки зрения считать необратимым. Но в действительности он обратим, просто константа равновесия велика. Обратимость этой стадии делает всю бензоиновую конденсацию обратимой. Как и большиснтво других реакций на карбонильной группе – мы уже к этому должны были привыкнуть. К чему приводит обратимость бензоиновой конденсации, обсудим отдельно. Пока это не важно.
Роль цианид-иона в бензоиновой конденсации. Это, безусловно, катализатор, так как возвращается в последней стадии. Такой катализ в современной химии называют нуклеофильным, подразумевая не только то, что цианид-ион нуклеофил (это ежу понятно, не стоило об этом особо напоминать), но в перевую очередь, то, что он осущетсвляет нуклеофильную активацию субстрата – увеличивает или, как в данном случае, прямо таки создаёт нуклеофильность карбаниона. Но в практическом смысле в реакциях бензоиновой конденсации цианида берут довольно много, обычно не менее половины от полной стехиометрии. Это скверно. Почти всегда берут цианид калия, если есть где взять, конечно, так как это вещество строгого учёта и просто так его достать невозможно даже в профессиональных нучных учреждениях России, в каждом таком учреждении должен быть спецотдел по работе с сильнодействующими ядовитыми веществами, где такие реактивы можно получить под роспись, обязательство полностью использовать, а излишки уничтожить или сдать обратно в отдел. Во всём остальном мире профессионалам принято доверять. Помню, как я был ошарашен, когда на 4 курсе попал на короткую стажировку в университет Этвеша Лоранда в Будапеште в Венгрии (это была тогда социалистическая страна с политическим режимом, не сильно отличающимся от советского), и прямо первую реакцию, которую мы там стали делать, был синтез какого-то нитрила, грамм на двести сразу, и руководитель на вопрос, а где мы возьмём цианид, показал на полку, где смирно стояла килограммовая банка цианида калия (или натрия, не помню уже) прямо в первом ряду.
Но в практическом смысле в реакциях бензоиновой конденсации цианида берут довольно много, обычно не менее половины от полной стехиометрии. Это скверно. Почти всегда берут цианид калия, если есть где взять, конечно, так как это вещество строгого учёта и просто так его достать невозможно даже в профессиональных нучных учреждениях России, в каждом таком учреждении должен быть спецотдел по работе с сильнодействующими ядовитыми веществами, где такие реактивы можно получить под роспись, обязательство полностью использовать, а излишки уничтожить или сдать обратно в отдел. Во всём остальном мире профессионалам принято доверять. Помню, как я был ошарашен, когда на 4 курсе попал на короткую стажировку в университет Этвеша Лоранда в Будапеште в Венгрии (это была тогда социалистическая страна с политическим режимом, не сильно отличающимся от советского), и прямо первую реакцию, которую мы там стали делать, был синтез какого-то нитрила, грамм на двести сразу, и руководитель на вопрос, а где мы возьмём цианид, показал на полку, где смирно стояла килограммовая банка цианида калия (или натрия, не помню уже) прямо в первом ряду. Предполагается, что профессиональный химик умеет обращаться с любыми реактивами, и никакой реактив не безопасен. Вообще-то, в нормальной лаборатории с совершенно любым реактивом принято обращаться со всеми мерами предосторожности. Ничего, отвесили мы тогда пару молей этой цианида, сделали реакцию, выделили продукт, остались живы, да и не могли не остаться. Если вы боитесь цианида, не занимайтесь химией, потому что обязательно отравитесь или других отравите, но не цианидом, а чем-нибудь другим, а безвредных реактивов в химии нет.
Предполагается, что профессиональный химик умеет обращаться с любыми реактивами, и никакой реактив не безопасен. Вообще-то, в нормальной лаборатории с совершенно любым реактивом принято обращаться со всеми мерами предосторожности. Ничего, отвесили мы тогда пару молей этой цианида, сделали реакцию, выделили продукт, остались живы, да и не могли не остаться. Если вы боитесь цианида, не занимайтесь химией, потому что обязательно отравитесь или других отравите, но не цианидом, а чем-нибудь другим, а безвредных реактивов в химии нет.
Почему цианида берут так много? Активация не очень эффективна, если взять меньше, по кинетическим причинам, будут низки скорости реакций, будем мало ключевого интермедиата и так далее. Поэтому берут почти стехиометрическое количество (это половина эквивалента, считая на альдегид), в редких случаях количество уменьшают где-то до одной десятой.
Как делают? Смешивают всё сразу, обычно в растворе спирта (метанола или этанола), иногда водного. И несколько часов кипятят. После разделывают реакционную смесь как обычно – разбавляют водой, экстрагируют и т.п. Посуду достаточно хорошо вымыть как обычно. Если есть сомнения, ополосните чем-нибудь окислительным, например, отбеливателем на основе хлора, цианиды очень легко и без остатка окисляются. И не устаю напоминать – посуда для работы должна быть качественной, краны в делительной воронке не должны течь, и так далее. Безусловно, если, как у нас бывает, делительная воронка течет из все шлифов в три ручья, а вы разделываете смесь с цианидом, простая операция может стать последней. Поэтому хорошая посуда в лаборатории это не блажь, а вопрос жизни и здоровья, что бы вы ни делали.
И несколько часов кипятят. После разделывают реакционную смесь как обычно – разбавляют водой, экстрагируют и т.п. Посуду достаточно хорошо вымыть как обычно. Если есть сомнения, ополосните чем-нибудь окислительным, например, отбеливателем на основе хлора, цианиды очень легко и без остатка окисляются. И не устаю напоминать – посуда для работы должна быть качественной, краны в делительной воронке не должны течь, и так далее. Безусловно, если, как у нас бывает, делительная воронка течет из все шлифов в три ручья, а вы разделываете смесь с цианидом, простая операция может стать последней. Поэтому хорошая посуда в лаборатории это не блажь, а вопрос жизни и здоровья, что бы вы ни делали.
В современных методиках в бензоиновой конденсации стал очень моден ДМСО. Вполне понятно почему – увеличивает нуклеофильность.
А какие альдегиды? А вот это проблема. В оригинале фигурирует бензальдегид и только бензальдегид. С замещёнными бензальдегидами происходит нечто трудновообразимое. Это невероятно капризная реакция, одна из очень редких, где замена метила на этил может быть фатальной. Причем не наблюдается никаких понятных тенденций. И донорные и акцепторные заместители могут и работать, и не работать, хотя в целом, по крайней мере, из простых заместителей акцепторные почти все не работают, а донорные всё же бывает, что и работают. Отчего такая странная картина? А очень просто: в механизме в каждой стадии можно увидеть влияние заместителей, и оно в разных стадиях разнонаправлено. Например, акцепторные заместители увеличивают электрофильность карбонильного углерода, но снижают нуклеофильность карбаниона. Донорные увеличивают нуклеофильность, но снижают CH-кислотность и поэтому подавляют депротонирование. А поскольку там все стадии обратимы, получается тончайший баланс кинетики и равновесия. В результате, проще перечислить те заместители, с которыми можно. Это, прежде всего, метокси-, причем годятся все три изомера. Продукт этой реакции даже имеет тривиальное название, поскольку альдегиды такие называются анисовыми, соответствующие бензоины называются анизоинами.
Это невероятно капризная реакция, одна из очень редких, где замена метила на этил может быть фатальной. Причем не наблюдается никаких понятных тенденций. И донорные и акцепторные заместители могут и работать, и не работать, хотя в целом, по крайней мере, из простых заместителей акцепторные почти все не работают, а донорные всё же бывает, что и работают. Отчего такая странная картина? А очень просто: в механизме в каждой стадии можно увидеть влияние заместителей, и оно в разных стадиях разнонаправлено. Например, акцепторные заместители увеличивают электрофильность карбонильного углерода, но снижают нуклеофильность карбаниона. Донорные увеличивают нуклеофильность, но снижают CH-кислотность и поэтому подавляют депротонирование. А поскольку там все стадии обратимы, получается тончайший баланс кинетики и равновесия. В результате, проще перечислить те заместители, с которыми можно. Это, прежде всего, метокси-, причем годятся все три изомера. Продукт этой реакции даже имеет тривиальное название, поскольку альдегиды такие называются анисовыми, соответствующие бензоины называются анизоинами. И еще один популярный альдегид дает бензоин – 3,4-метилендиоксибензальдегид, тривиально называтся пиперональ. Бензоин называется тривиально пипероином. Большинство остального не работает, или работает плохо – и метилы, и галогены, и нитро, и гидрокси, и амино в разных видах и т.п. дают низкие выходы, а иногда и вовсе другие продукты. Даже закрадывается мысль – а не работает ли бензоиновая конденсация только тогда, когда исходный альдегид имеет красивое тривиальное называние и можно дать красивое название и бензоину. Вот метилбензальдегиды называются еще толуиловыми, и как прикажете называть – толуоин? Корявенько, язык сломаешь, но, кстати, есть такое название, только не очень оно популярно, потому что вещества эти приходится получать окольными путями, а не прямой конденсацией.
И еще один популярный альдегид дает бензоин – 3,4-метилендиоксибензальдегид, тривиально называтся пиперональ. Бензоин называется тривиально пипероином. Большинство остального не работает, или работает плохо – и метилы, и галогены, и нитро, и гидрокси, и амино в разных видах и т.п. дают низкие выходы, а иногда и вовсе другие продукты. Даже закрадывается мысль – а не работает ли бензоиновая конденсация только тогда, когда исходный альдегид имеет красивое тривиальное называние и можно дать красивое название и бензоину. Вот метилбензальдегиды называются еще толуиловыми, и как прикажете называть – толуоин? Корявенько, язык сломаешь, но, кстати, есть такое название, только не очень оно популярно, потому что вещества эти приходится получать окольными путями, а не прямой конденсацией.
Залезем немного в гетероциклы, потому что еще один знаменитый и популярный бензоин, который очень легко получается конденсацией – производное фурана, называется фуроин.
А можно получить несимметричный бензоин? Как ни странно, не только можно, но в некоторых случаях и проще, чем симметричный, и даже из таких замещённых бензальдегидов, из которых обычные бензоины не получаются. Секрет именно в очень сложной зависимости стадий от эффектов заместителей. Это дает неожиданный эффект – донорные бензальдегиды (с алкилами, алкокси, даже диметиламино и т.п.) довольно легко конденсируются с бензальдегидом и умеенно акцепторными бензальдегидами (например, галогензамещенными). И всегда получается только один продукт – бензоин, у которого карбонил находится рядом с донорной фенильной группой.
Секрет именно в очень сложной зависимости стадий от эффектов заместителей. Это дает неожиданный эффект – донорные бензальдегиды (с алкилами, алкокси, даже диметиламино и т.п.) довольно легко конденсируются с бензальдегидом и умеенно акцепторными бензальдегидами (например, галогензамещенными). И всегда получается только один продукт – бензоин, у которого карбонил находится рядом с донорной фенильной группой.
Очевидную причину этого понять очень легко – гораздо выгоднее продукт, у которого акцепторная карбонильная группа сопряжена с донорным фенильным кольцом, а еще лучше – через это кольцо с мезомерным донорным заместителем. Но это только часть объяснения. Вторая часть связана с тем, что окончательный продукт реакции вовсе не обязательно тот, который образуется в собственно реакции бензоиновой конденсации. Это связано с тем, что гидроксикетоны (как и гидроксиальдегиды) очень легко изомеризуются в присутсвии оснований Бренстеда-Лоури. Это явление совсем хорошо известно в химии углеводов, но оно является общим для всех соединений этого типа. Изомеризация происходит очевидным образом через енол или енолят.
Изомеризация происходит очевидным образом через енол или енолят.
И если получить другой изомер бензоина, он перегруппируется в более устойчивый, то, укоторого карбонил рядом с донорным фенилом в присутствии щелочи или цианида. Поэтому и образуется в таких реакциях только один – более устойчивый – продукт бензоиновой конденсации.
Но из этого следует, что бензоиновая конденсация в классических условиях имеет очень узкий диапазон – бензоины, которые можно так получить, что симметричные, что несимметричные можно перечислить очень быстро.
А можно ли сделать бензоиновую конденсацию более универсальной и направленной? Можно. Есть минимум два способа, и один мы обсудим сейчас, а другой как-нибудь попозже.
Бензоиновая конденсация точно так же как альдольная, тоже может быть сделана направленной. И здесь тоже очень много вариантов. Более современные используют новые катализаторы вместо цианид-иона. Это мы пока оставим. Более старые используют тот же подход, что и направленная альдольная конденсация – мы должны заранее предпринять меры, чтобы два реагента конденсации изменились так, чтобы их роли – нуклеофила и электрофила – стали определены и зафиксированы.
Сразу определим, что альдегид, который даёт карбонильный фрагмент бензоина – нуклеофил, а тот, который даёт спиртовую часть бензоина – электрофил.
Строго говоря, мы уже умеем делать направленную бензоиновую конденсацию. Уже известный нам метод Umpolung’а с дитианами дает нам такой инструмент. Берем тот альдегид, который будет нуклеофильным реагентом, превращаем в дитиановое производное, депротонируем и присоединяем к карбонилу второго альдегида. Снимаем защиту.
Это хорошо. Можно было бы здесь и остановиться. Но можно посмотреть, нельзя ли сделать что-то, гораздо более близкое к оригинальной бензоиновой конденсации. Может быть, нам запах дитиана не нравится. Или ртуть.
Можно. Нужно просто вместо неустойчивого и имеющего кислотную гидроксильную группу циангидрина сделать нечто похожее, но с закрытой гидроксильной группой. Просто защитить её? Можно и так, но лучше сделать так, чтобы такое производное получалось в одну стадию из альдегида уже защищённым. Самый удобный вариант – силилированный циангидрин. Его можно легко получить, используя триметилсилилцианид, этот реагент готовым покупают. Смысл реакции в том, что кремний имеет очень высокое сродство к кислороду, иными словами, что связи Si-O очень прочны и легко образуются. Это делает реакцию с карбонильной группой намного более выгодной, чем присоединение HCN, и практически необратимой. Но! Просто так реакция все равно не идёт, потому что этот реагент сам по себе малополярен и ему трудно вступить в реакцию с карбонилом. Карбонил надо активировать. Как обычно, кислотой. Кислотой Льюиса, потому что протонная кислота разрушила бы образующийся аддукт. Кислоты Льюиса годятся самые разные, в самой первой работе использовали самую простую – безводный AlCl3 (Lidy, W., Sundermeyer, W. Chem.Ber. 1973, 106, 587), но это неудобно – реагент слишком агрессивный. Во второй чисто случайно нашли безводный иодистый цинк (Evans, D. A., Carroll, G. L., Truesdale, L. K. J. Org. Chem. 1974, 39, 914).
Его можно легко получить, используя триметилсилилцианид, этот реагент готовым покупают. Смысл реакции в том, что кремний имеет очень высокое сродство к кислороду, иными словами, что связи Si-O очень прочны и легко образуются. Это делает реакцию с карбонильной группой намного более выгодной, чем присоединение HCN, и практически необратимой. Но! Просто так реакция все равно не идёт, потому что этот реагент сам по себе малополярен и ему трудно вступить в реакцию с карбонилом. Карбонил надо активировать. Как обычно, кислотой. Кислотой Льюиса, потому что протонная кислота разрушила бы образующийся аддукт. Кислоты Льюиса годятся самые разные, в самой первой работе использовали самую простую – безводный AlCl3 (Lidy, W., Sundermeyer, W. Chem.Ber. 1973, 106, 587), но это неудобно – реагент слишком агрессивный. Во второй чисто случайно нашли безводный иодистый цинк (Evans, D. A., Carroll, G. L., Truesdale, L. K. J. Org. Chem. 1974, 39, 914). Это ещё откуда?? Просто под руку попался, как говорят, на полке стоял. Но это довольно удобная вещь, простая в работе, малогигроскопичная, ее можно взвешивать не торопясь. Удобнее, чем безводный хлористый цинк, который быстро расплывается на воздухе, и слегка фонит хлористым водородом, а нам это не нужно. Дорогая, конечно, но ее нужно очень мало. На мольные загрузки не более 100 мг – пустяк. Так это и осталось стандартной методикой. Можно и многие другие кислоты Льюиса использовать, но проще взять описанную методику. Реакцию ведут вообще без растворителя. При комнатной температуре или иногда нужно нагревание. Мечта, а не реакция.
Это ещё откуда?? Просто под руку попался, как говорят, на полке стоял. Но это довольно удобная вещь, простая в работе, малогигроскопичная, ее можно взвешивать не торопясь. Удобнее, чем безводный хлористый цинк, который быстро расплывается на воздухе, и слегка фонит хлористым водородом, а нам это не нужно. Дорогая, конечно, но ее нужно очень мало. На мольные загрузки не более 100 мг – пустяк. Так это и осталось стандартной методикой. Можно и многие другие кислоты Льюиса использовать, но проще взять описанную методику. Реакцию ведут вообще без растворителя. При комнатной температуре или иногда нужно нагревание. Мечта, а не реакция.
Эти соединения превращают в карбанион точно так же, как другие енолизуемые карбонильные соединения – с помощью LDA при низкой температуре. Если делать это в условиях равновесия менее сильными основаниями, получим побочные реакции и цель устроить чистую направленную реакцию не будет достигнута. Ну а дальше добавляем второй альдегид, доводим температуру до комнатной и гидролизуем раствором HCl в метаноле. Так можно получить практически любые бензоины, в том числе и с алифатическими альдегидами. Этот приём открыл Зигфрид Хюниг (известный нам по очень популярному основанию Хюнига – диизопропилэтиламину DIPEA, подробнее об этом во втором семестре) в 1979, почти сразу после появления самой концепции Umpolung, как альтернативный реагент дитиановым производным (Deuchert,K., Hertenstein,U., Hünig, S., Wehner,G. Chem. Ber. 1979, 112, 2045–2061).
Так можно получить практически любые бензоины, в том числе и с алифатическими альдегидами. Этот приём открыл Зигфрид Хюниг (известный нам по очень популярному основанию Хюнига – диизопропилэтиламину DIPEA, подробнее об этом во втором семестре) в 1979, почти сразу после появления самой концепции Umpolung, как альтернативный реагент дитиановым производным (Deuchert,K., Hertenstein,U., Hünig, S., Wehner,G. Chem. Ber. 1979, 112, 2045–2061).
Раз мы познакомились с этим новым Umpolung-реагентом, применим его для других реакций, очень похожих на соответствующие реакции дитиановых анилнов. Но имеют одно очень важное отличие. Дитиановый карбанион намного более сильное основание, а эти карбанионы относятся к делокализованным – нитрильная группа работает как мезомерный акцептор. Во втором семесте мы разберёмся с этим подробнее, а сейчас просто заметим, что такие карбанионы больше похожи на еноляты. Это дает нам выигрыш в селективности – с анионами ТМС-циангидринов можно меньше бояться элиминирования.
Во-первых, это можно алкилировать. И так получать кетоны. Циангидрины ещё иногда нужно разлагать, добавляя при гидролизе щёлочь.
И это почти то же самое, что дитиановый синтез, но без вони и ртути. Но при этом еще и более мягкий, например, он неплохо работает с вторичными алкилами (лучше взять иодпроизводное), и дает замещение, а не элиминирование. Дитиановые анионы дают намного меньшие выходы и очень много элиминирования.
И с непредельными кетонами такие анионы работают не так, как дитиановые. Дитиановые в основном дают 1,2-присоединение. А эти, делокализованные, в основном дают 1,4-присоединение. Так мы можем развести два пути Umpolung-присоединения
Восстановление с образованием новой связи углерод-углерод
- Выбираем…
- Пинаконовое сдваивание
- Пинакон-пинаколиновая перегруппировка
Отдельная группа методов связана с возможностью присоединить электрон к карбонильной группе: образующиеся радикалы сдваиваются, образуя за один присест в два раза большую молекулу, которую можно очень интересно и просто преобразовать в очень полезные соединения.
Эта реакция подробно рассмотрена на вкладке Восстановительная димеризация на странице про карбонильную группу. Здесь только повторим основное без подробностей.
Карбонильные соединения (и альдегиды, и кетоны, каждый со своей спецификой, но пока пренебрежём) восстанавливаются активными металлами в анион-радикалы, которые могут сдваиваться, образуя симметричные диолы, называемые пинаконами. Будьте здесь осторожны – диолы, то есть спирты, называются пинаконами. Для восстановления используйте магний, активированный солями ртути. Добавка TiCl4 делает эту реакцию особенно гладкой и универсальной.
Далеко не все кетоны дают пинаконы. Например, стерические препятствия не дают анион-радикалам сдваиваться. Не получите пинакон и из ненасыщенных кетонов – у них по другому устроены молекулярные орбитали. Но из более-менее простых кетонов пинаконы получаются отлично. Часто встречаются пинаконы из циклических кетонов.
Пинаконы обычно получают не просто так, а с целью использовать в очень интересной перегруппировке, с помощью которой легко получаются весьма полезные соединения. Собственно пинаконы использовать не обязательно, подойдут любые вицинальные диолы, например, полученные дигидроксилированием алкенов. Но впервые эту реакцию сделали в глубокой древности, скорее всего, при попытке получить безводный пинакон из образующегося в результате пинаконового сдваивания ацетона гидрата.
Собственно пинаконы использовать не обязательно, подойдут любые вицинальные диолы, например, полученные дигидроксилированием алкенов. Но впервые эту реакцию сделали в глубокой древности, скорее всего, при попытке получить безводный пинакон из образующегося в результате пинаконового сдваивания ацетона гидрата.
Реакцию проводят нагреванием с сильными кислотами, серной или фосфорной. И вот что происходит. Протонирование гидроксила приводит к уходу воды и образованию карбокатиона. Это третичный карбокатион, и в каком-то другом случае мы бы сказали, что это очень хорошо, и на этом всё должно остановиться, а поскольку всё, что случилось, обратимо, то пока ничего существенного не произошло. Но обычная для карбокатионов перегруппировка – перенос соседней группы со своими электронами с одновременным перемещением карбокатиона на то место, где была эта группа – всё же происходит, потому что при этом образуется ещё более стабильный катион. Мезомерный донор, гидроксил, участвует в стабилизации этого катиона, что и выражается граничными структурами. Вторая структура с плюсом, переместившимся на кислород, нам хорошо знакома – мы уже тысячу раз встречали такую структуру, когда говорили о поведении карбонильных соединений в присутствии кислот. Это уже не карбокатион, а просто протонированный кетон, и как бы ни был стабилизирован третичный карбокатион, но такая частица на много порядков стабильнее. Мы сейчас, конечно, всё сильно упрощаем, потому что в реальности там надо посмотреть и ещё на одну частицу – протонированный эпоксид. Когда-нибудь отдельно рассмотрим эту занятную систему поподробнее, потому что она имеет связь с гораздо более широким кругом превращений, но сейчас ограничимся этой схемой. Итак, образовался протонированный кетон, находящийся в равновесии с самим кетоном. После завершения реакции получаем перегруппированный кетон, который принято по историческим причинам называть пинаколином, а всю перегруппировку пинакон-пинаколиновой.
Вторая структура с плюсом, переместившимся на кислород, нам хорошо знакома – мы уже тысячу раз встречали такую структуру, когда говорили о поведении карбонильных соединений в присутствии кислот. Это уже не карбокатион, а просто протонированный кетон, и как бы ни был стабилизирован третичный карбокатион, но такая частица на много порядков стабильнее. Мы сейчас, конечно, всё сильно упрощаем, потому что в реальности там надо посмотреть и ещё на одну частицу – протонированный эпоксид. Когда-нибудь отдельно рассмотрим эту занятную систему поподробнее, потому что она имеет связь с гораздо более широким кругом превращений, но сейчас ограничимся этой схемой. Итак, образовался протонированный кетон, находящийся в равновесии с самим кетоном. После завершения реакции получаем перегруппированный кетон, который принято по историческим причинам называть пинаколином, а всю перегруппировку пинакон-пинаколиновой.
Сразу заметим, что мы не будем применять эту перегруппировку к пинаконам, образованным из несимметричных кетонов, потому что в этом случае возникает очень непростой вопрос – какая из групп будет перемещаться. Поскольку простых рецептов здесь нет, и нужно смотреть много факторов вплоть до изучения конформаций диола, мы просто ограничимся симметричными молекулами с одинаковыми группами.
Поскольку простых рецептов здесь нет, и нужно смотреть много факторов вплоть до изучения конформаций диола, мы просто ограничимся симметричными молекулами с одинаковыми группами.
Пинакон-пинаколиновую перегруппировку применяют особенно часто для получения нескольких очень полезных молекул. Проще и чаще всего – перегруппировка пинакона в самом прямом смысле этого слова в пинаколин в самом прямом смысле этого слова. Самый главный пинакон, можно сказать, Пинакон с большой буквы получается из ацетона, а самый главный пинаколин – это просто метил-трет-бутилкетон. Для нас эта реакция – самый простой способ создать трет-бутильную группу, уже сразу связанную с карбонилом. По другому сделать это было бы не очень просто. А так, видите в задаче трет-бутил где-нибудь в синтезируемой молекуле, а в исходных – ацетон – сразу, не думая, делайте пинаколин, а потому уже начинайте думать, как превратить его в конечную молекулу.
Поскольку мы ограничили себя симметричными молекулами, всё остальное, что мы сможем получить, будет очень похоже на этот случай. Нечто более интересное можно получить из пинаконов циклических кетонов. Попробуем на пинаконе циклогексанона. Третичный карбокатион перегруппируется точно так же, как и в нецикличесикх случаях, но у нас тут нет просто заместителя, который можно перетащить на соседний атом. Почему нет? – а часть кольца разве не то же самое? Перетаскиваем связь (помечена синим), рисуем сразу протонированный кетон, и превращаем его в кетон, перерисовав нормально получившееся новое кольцо. Вот какая штука забавная вышла – два кольца, одно на атом пошире другого, соединенены в одной точке, точнее, на одном атоме. Такой способ соединения колец называется спиро-соединением, такие соединения – спиро-соединениями (от греческого корня, обозначающего кручение, скручивание, этот корень сразу узнаётся в слове спираль). Из-за sp3-гибридизации атома соединения колец, кольца оказываются повёрнутыми на 90º друг относительно друга. Пинакон пинаколиновая перегруппировка позволила нам очень просто получить одно из таких соединений, а если мы учтём, что исходные пинаконы можно сделать не только из циклогексанона, но и из других циклических кетонов, то таких забавных спиро-молекул из двух неравных колец с кето-группой в более крупном кольце, можно сделать довольно много.
Нечто более интересное можно получить из пинаконов циклических кетонов. Попробуем на пинаконе циклогексанона. Третичный карбокатион перегруппируется точно так же, как и в нецикличесикх случаях, но у нас тут нет просто заместителя, который можно перетащить на соседний атом. Почему нет? – а часть кольца разве не то же самое? Перетаскиваем связь (помечена синим), рисуем сразу протонированный кетон, и превращаем его в кетон, перерисовав нормально получившееся новое кольцо. Вот какая штука забавная вышла – два кольца, одно на атом пошире другого, соединенены в одной точке, точнее, на одном атоме. Такой способ соединения колец называется спиро-соединением, такие соединения – спиро-соединениями (от греческого корня, обозначающего кручение, скручивание, этот корень сразу узнаётся в слове спираль). Из-за sp3-гибридизации атома соединения колец, кольца оказываются повёрнутыми на 90º друг относительно друга. Пинакон пинаколиновая перегруппировка позволила нам очень просто получить одно из таких соединений, а если мы учтём, что исходные пинаконы можно сделать не только из циклогексанона, но и из других циклических кетонов, то таких забавных спиро-молекул из двух неравных колец с кето-группой в более крупном кольце, можно сделать довольно много.
Реакции енолизуемых карбонильных соединений
- Выбираем…
- Алкилирование енаминов
- Ненаправленная альдольно-кротоновая конденсация
- Направленная альдольная конденсация
- Конденсация с формальдегидом — важный частный случай альдольной конденсации
- Реакция Манниха: разновидность альдольной конденсации, и тоже с формальдегидом
- Переворачиваем реакционную способность на альфа-углероде
Это важнейший раздел. Енолизуемые карбонильные соединения реагируют по α-атому углерода как нуклеофилы через нуклеофильные формы: енол, енолят, енамин, эфир енола. У каждой из этих форм есть своя область применения, и это нужно очень хорошо понимать, и применять каждую форму там, где она работает. И не применять там, где не работает, или где работает плохо. Здесь очень много важного материала, и я не смогу в обозримое время описать всё, что здесь есть. Я стараюсь, но раньше 2021 года вряд ли получится иметь здесь более-менее поное описание. Ещё раз повторю – возможно, это самая важная часть не только химии карбонильных соединений, но и всей органической химии.
Ещё раз повторю – возможно, это самая важная часть не только химии карбонильных соединений, но и всей органической химии.
Одно из двух основных применений енаминов – алкилирование, дающее после гидролиза моно-алкилпроизводные тех альдегидов и кетонов, из которых был получен енамин.
Алкилирование идёт строго по механизму SN2. С этим связаны все особенности, возможности и ограничения этой реакции. Я предупреждал, что от SN2 спасения не будет. Во всём курсе органической химии он будет преследовать вас с маниакальной наглостью и упорством. Проще один раз разобраться, как он устроен, тогда это преследование перестанет быть источником фрустрации – напротив, вы станете встречаться с ним, как с добрым приятелем, про которого известно всё.
Попробуем написать в общем виде. Енамин берём пирролидиновый или морфолиновый, причём пирролидиновый лучше. Если есть выбор уходящей группы, стараемся взять получше: иодид, тозилат, бромид. Хлорид берём, только если выбор сделан за вас, и деваться некуда, и не забываем тогда побрюзжать, что за дрянь вам подсунули, совсем не разбираются в уходящих группах.
Начинаем применять наши знания. Во-первых, скажем, что енамин – нуклеофил довольно слабый и нейтральный. Поэтому он реагирует далеко не совсеми, а только с самыми реакционноспособными субстратами для SN2. Даже не думайте ничего вторичного, или даже первичного, но разветвлённого. Даже с обычными первичными алкилами реакция идёт плохо и требует длительного нагревания, а жалкие выходы разжалобят даже самых чёрствых. Но мы можем это применять, нам плевать на такие подробности. Но всё же лучше брать что-то пошустрее – вспоминаем SN2: метил, бензил, аллил, пропаргил. Последние три могут иметь всякие заместители, желательно подальше от уходящей группы. В реальной жизни брать замещенные аллильные или пропаргильные субстраты рискованно, так как можно нарваться на перегруппировку, но в задачах это встречается, и всегда без перегруппировки.
Реакцию проводят просто при нагревании. Растворитель менять бесполезно, всякие ДМСО, ДМФА брать бесполезно – нуклеофил нейтральный, а на нейтральные нуклеофилы растворителем воздействовать нельзя. Не в смысле, что кто-то запретил, а потому что эффекта не будет. После реакции гидролизуем подкисленной водой, при этом сразу получается искомый замещенный кетон или альдегид. Пара примеров:
Не в смысле, что кто-то запретил, а потому что эффекта не будет. После реакции гидролизуем подкисленной водой, при этом сразу получается искомый замещенный кетон или альдегид. Пара примеров:
Реакция с α-галогенкарбонильными соединениями
Как мы помним из SN2, есть ещё более лучшие субстраты, чем все эти бензилы, аллилы и метил. Если у нас рядом с уходящей группой карбонил, или что-то на него похожее, то такие субстраты реагируют на 2-3 порядка быстрее метильных. И мы как раз только что наконец научились это делать – бромировать енолизуемые карбонильные соединения. Вместе с реакцией с енаминами это даёт нам возможность соединить два енолизуемых карбонильных соединения. Получаются при этом дикарбонильные соединения с карбонильными группами, разделёнными двумя атомами углерода. Это очень полезно, и нам ещё пригодится не раз. Соединим для примера ацетон и циклогексанон. Как видим, из одного карбонильного соединения (здесь, циклогексанона) мы делаем нуклеофил, из второго (здесь, ацетона) электрофил; смело соединяем их и получаем впечатляющий результат.
Ненаправленная альдольная или альдольно-кротоновая конденсация – такой способ провести эту реакцию, когда вы полагаетесь на равновесия в реакционной смеси, в которой одновременно присутствуют и карбонильная и метиленовая компоненты, а также реагенты, которые и обусловливают конденсацию. Такие реагенты в этом случае принято называть конденсирующими агентами, и они бывают или кислотами или основаниями. В современном синтезе ненаправленную конденсацию используют редко и только в тех реакциях, где результат более-менее гарантирован, во всех остальных случаях используют направленную конденсацию. Оба типа направленной конденсации возникли довольно недавно, в 1960-70-х годах, а до этого, в течение почти полного века существовала только ненаправленная конденсация. Многочисленные исследования были посвящены поиску условий, правильных конденсирующих агентов, всяких технических трюков, позволяющих в отдельных важных случаях проволить ненаправленную конденсацию более-менее селективно и с приличными выходами. Вы можете без труда найти целые книги и обзоры, посвящённые всем этим фокусам, а в некоторых случаях и сами захотите ими воспользоваться. Причина этого проста – ненаправленная конденсация проще и производительнее, и если вам в вашей научной работе понадобится какой-то конкретный альдоль или кротоновый продукт, да еще и не современный манер в количестве нескольких микрограмм, а сразу полкило – не брезгуйте старыми методиками. Иногда они чудо как хороши, да и делать их весело, это настоящая химия. Одна проблема – к каждому соединению нужен отдельный подход. Запоминать всё это невозможно.
Вы можете без труда найти целые книги и обзоры, посвящённые всем этим фокусам, а в некоторых случаях и сами захотите ими воспользоваться. Причина этого проста – ненаправленная конденсация проще и производительнее, и если вам в вашей научной работе понадобится какой-то конкретный альдоль или кротоновый продукт, да еще и не современный манер в количестве нескольких микрограмм, а сразу полкило – не брезгуйте старыми методиками. Иногда они чудо как хороши, да и делать их весело, это настоящая химия. Одна проблема – к каждому соединению нужен отдельный подход. Запоминать всё это невозможно.
Поэтому мы ограничим ненаправленную конденсацию только теми немногими вариантами, когда она даёт более-менее гарантированный результат. Ограничимся следующими:
- Карбонильная компонента – альдегид, совсем хорошо, если неенолизуемый (но не формальдегид!), но и енолизуемый тоже сойдёт хотя бы на бумаге. Метиленовая компонента – кетон, енолизуемый только с одной стороны, или с двух сторон, но тогда симметричный.
 В енолизуемых группах кетона должно быть не менее двух атомов водорода (два или три, не один!).
В енолизуемых группах кетона должно быть не менее двух атомов водорода (два или три, не один!). - Карбонильная компонента – формальдегид, метиленовая – любой енолизуемый альдегид или кетон. Этот вариант рассмотрен на отдельной вкладке.
- Карбонильная и метиленовая компонента – одно и то же енолизуемое карбонильное соединение. Этот вариант называется самоконденсацией. Точнее, межмолекулярной самоконденсацией. Хотя он кажется очень частным, так получают очень многие важные для синтеза исходные непредельные карбонильные соединения.
- Карбонильная и метиленовая компоненты – в одной молекуле дикарбонильного соединения. В этом случае возможна внутримолекулярная альдольная конденсация (тоже самоконденсация, только внутримолекулярная), если в результате может получится пяти- или шестичленный цикл. Внутримолекулярные конденсации всегда проводят ненаправленно, предварительно убедившись, что можно ожидать образования одного продукта. Мы рассмотрим этот вариант отдельно во втором семестре, когда нам понадобятся реакции циклизации.

На этой вкладке разберёмся только с первым вариантом.
Ненаправленная конденсация альдегид-кетон.
Успех этой реакции обусловливается тем, что альдегиды – намного более активные карбонильные компоненты (более сильные электрофилы), чем кетоны. Поэтому в паре с кетоном они всегда будут именно карбонильными компонентами. Если альдегид енолизуемый, обязательно побочно будет идти реакция самоконденсации альдегида. Её можно свести к минимуму, если добавлять альдегид к смеси кетона и конденсирующего агента – скорость самоконденсации самого кетона обычно невелика и ею можно пренебречь, если не мешкать в прибавлении альдегида.
Мы не будем связываться с кислотно-катализируемой конденсацией. Ограничимся конденсацией, катализируемой основанием. В качестве основания обычно применяют самую простую вещь – раствор щёлочи (KOH, NaOH) в метаноле или этаноле, в каталитическом количестве (от нескольких процентов до 10-20% от количества альдегида). Если будете это делать экспериментально, учтите, что альдегид для реакции принято брать очищенный, из новой банки, или перегнанный незадолго до работы. Альдегиды любят окисляться кислородом воздуха, в них понемногу накапливается соответствующая кислота, и если это не учесть, то щёлочь, взятая для конденсации прореагирует с этой кислотой, и катализатора конденсации может совсем не остаться. Особенно это важно, когда в методике прописано очень маленькое количество щёлочи, 1-2%. Столько кислоты в альдегиде может накопиться за неделю. И реакция самоконденсации не пойдёт.
Альдегиды любят окисляться кислородом воздуха, в них понемногу накапливается соответствующая кислота, и если это не учесть, то щёлочь, взятая для конденсации прореагирует с этой кислотой, и катализатора конденсации может совсем не остаться. Особенно это важно, когда в методике прописано очень маленькое количество щёлочи, 1-2%. Столько кислоты в альдегиде может накопиться за неделю. И реакция самоконденсации не пойдёт.
И ещё одна важная вещь. Когда мы узнаём про LDA, нам иногда кажется, что это вообще самое лучшее и самое современное основание для альдольной конденсации – лей его везде, не прогадаешь! Внимание – это ошибка!
Эту ошибку невольно поощряют некоторые неряшливо написанные учебники, бывают такие, иногда даже очень красивые и заграничные, которые просто не обращают на это внимания, типа, они выше таких мелочей – сами разбирайтесь. Разберёмся. Нет сомнения в том, что если накапать раствора LDA в смесь альдегида и кетона, пойдёт конденсация, это ведь основание, какая разница. Особенно если реакцию мы решили поставить в растворе метанола или этанола – LDA тут же превратится в алкоголят, и какие вопросы? Вопрос тут, собственно, единственный – мы серьёзно решили химией заняться, или так просто, позабавиться. Если последнее – вперёд, но без нас. Если первое, то придётся смириться с тем, что у любой профессии есть признаки компетентности, то, что отличает профессионала от любителя. Попробуем прикинуться первыми, хотя бы на время. Профессионал всегда старается докопаться до сути дела, понять, как идут реакции. И когда речь идёт об альдольной конденсации, мы не должны забывать ни на минуту, что это обратимая реакция, равновесие. Когда у нас енолят, равновесие выглядит так:
Особенно если реакцию мы решили поставить в растворе метанола или этанола – LDA тут же превратится в алкоголят, и какие вопросы? Вопрос тут, собственно, единственный – мы серьёзно решили химией заняться, или так просто, позабавиться. Если последнее – вперёд, но без нас. Если первое, то придётся смириться с тем, что у любой профессии есть признаки компетентности, то, что отличает профессионала от любителя. Попробуем прикинуться первыми, хотя бы на время. Профессионал всегда старается докопаться до сути дела, понять, как идут реакции. И когда речь идёт об альдольной конденсации, мы не должны забывать ни на минуту, что это обратимая реакция, равновесие. Когда у нас енолят, равновесие выглядит так:
Образуется не сам альдоль, а его сопряжённое основание – анион. Это равновесие обычно очень далеко от того, чтобы быть сильно сдвинутым в сторону продукта даже для пары енолят кетона – альдегид, иными словами константа равновесия хоть и больше единицы, но не очень сильно больше. Более того, ели у нас есть готовый альдоль, то в присутствии оснований мы можем получить его распад на исходные карбонильную и метиленовую компоненты. Такая реакция, обратная к альдольной конденсации, из-за чего её часто называю ретроальдольной, очень хорошо известна и имеет много любопытнейших применений и в синтезе, и даже в живой Природе. Когда-нибудь мы ей займёмся отдельно.
Такая реакция, обратная к альдольной конденсации, из-за чего её часто называю ретроальдольной, очень хорошо известна и имеет много любопытнейших применений и в синтезе, и даже в живой Природе. Когда-нибудь мы ей займёмся отдельно.
Если у нас в реакционной смеси есть слабая протонная кислота, но способная протонировать этот анион, мы получим другое равновесие.
Положение этого равновесия сильно зависит от кислотности этой кислоты. Что это может быть? Например, спирт, метанол или этанол, если мы ведём реакцию в спиртовом растворе с помощью основания – алкоголята. Но спирт слабоват как кислота в этом случае. Протонировать ему придётся точно такую же алкоксидную группу с образование спирта – альдоля. Но кислотность альдоля должна быть выше, чем кислотность простого спирта, и потому что рядом хороший индуктивный акцептор – карбонил, и потому что этот карбонил ещё и работает как акцептор водородной связи. Поэтому спирт будет слабо протонировать сопряжённое основание альдоля, и на равновесие альдольной конденсации почти не повлияет. А вот если у нас в растворе есть вода, то это другое дело – вода в протонной среде кислота вполне зачётная, и алкоксид запротонировать с существенной степени её вполне по силам. Равновесие сдвинется в сторону самого альдоля. А мы знаем, что равновесия устроены так, что ксли у нас есть два с одним общим участником, то у нас есть одно общее. В этом случае, вот такое:
А вот если у нас в растворе есть вода, то это другое дело – вода в протонной среде кислота вполне зачётная, и алкоксид запротонировать с существенной степени её вполне по силам. Равновесие сдвинется в сторону самого альдоля. А мы знаем, что равновесия устроены так, что ксли у нас есть два с одним общим участником, то у нас есть одно общее. В этом случае, вот такое:
Вот и вся игра. Получается, что в ненаправленной альдольной конденсации очень нелишне иметь в реакционной смеси не только основание, но и источник доступных протонов для того, чтобы смещать равновесие альдольной конденсации в сторону самого альдоля, а не его сопряжённого основания. И такое равновесие сдвинуто в сторону продукта в значительно более существенной степени. Собственно, в этом нет ничего нового, мы точно такую ситуацию видели, например, в равновесии образования циангидринов из карбонильного соединения и цианид-иона. Да и других примеров в химии карбонильных соединений полным полно, нужно только уметь их разглядеть в тонкостях экспериментального выполнения реакций, не уставая задавать вопросы – а это тут зачем, а это что делает, и так далее.
Итак, теперь не так сложно понять, почему использовать LDA в качестве не стехиометрического основания для получения раствора чистого енолята, а в качестве основного катализатора, довольно сомнительная идея. В этом случае у нас или вообще не будет чем протонировать сопряжённое основание альдоля, если мы реили проводить реакцию ненаправленной конденсации так же, как мы делаем направленную – в апротонном растворителе типа ТГФ, или это будет неэффективно, если мы накапаем раствор LDA в спиртовой раствор реагентов и получим просто алкоголят. И вот, оказывается, почему в самых популярных методиках ненаправленной альдольной конденсации используют спиртовой раствор обычной щёлочи, да ещё и спирт используют “из банки”, то есть такой, в котором довольно много, несколько процентов как минимум, воды. В химии очень важно во всём соблюдать меру, в том числе и в кислотности, и в основности.
Вернёмся к конденсации. Реакцию проводят в растворе в присутствии небольшого количества щёлочи, компоненты смешивают сразу, перемешивают при комнатной температуре несколько часов, нейтрализуют щёлочь расчётным количеством уксусной кислоты, и выделяют продукт обычным способом. Поскольку реакция проходит в очень мягких условиях, и продукт не соприкасается с серьёзной кислотой, есть шанс получить альдоль. Кетон берём или енолизуемый с одной стороны, или двусторонний симметричный, и с минимум двумя водородами в каждом енолизуемом положении.
Поскольку реакция проходит в очень мягких условиях, и продукт не соприкасается с серьёзной кислотой, есть шанс получить альдоль. Кетон берём или енолизуемый с одной стороны, или двусторонний симметричный, и с минимум двумя водородами в каждом енолизуемом положении.
Но эти альдоли легко дегидратируются в присутствии небольшого количества сильной кислоты, поэтому получить кротоновый продукт очень легко. Двусторонние кетоны, например, циклические легко конденсируются два раза, если в реакционной смеси есть ещё альдегид. Такие двойные альдоли особенно легко дегидратируются, так как получается сразу довольно длинная сопряжённая система.
Если хотя бы с одной стороны есть ароматическое кольцо, альдоль вы уже не получите – образование сопряжённой двойной связи настолько выгодно, что альдоль самопроизвольно превратится в кротоновый продукт, сильная кислота для этого не нужна, так как превращение альдоля в кротоновый продукт – это просто обратная реакция к 1,4-присоединению воды или гидроксида к непредельному кетону. Образование кротонового продукта окончательно смещает равновесие в сторону продукта конденсации, поэтому такие конденсации идут особенно легко. Ацетон, например, очень легко конденсируется с бензальдегидом и один и два раза, образуя очень полезные и важные соединения бензилиденацетон и дибензилиденацетон. Двойная конденсация настолько легка, что в реальности, чтобы получить бензилиденацетон приходится брать не соотношение кетон-альдегид 1:1, а довольно большой избыток ацетона, благо его не жалко, и выделению продукта он не мешает.
Образование кротонового продукта окончательно смещает равновесие в сторону продукта конденсации, поэтому такие конденсации идут особенно легко. Ацетон, например, очень легко конденсируется с бензальдегидом и один и два раза, образуя очень полезные и важные соединения бензилиденацетон и дибензилиденацетон. Двойная конденсация настолько легка, что в реальности, чтобы получить бензилиденацетон приходится брать не соотношение кетон-альдегид 1:1, а довольно большой избыток ацетона, благо его не жалко, и выделению продукта он не мешает.
Точно так же конденсируется бензальдегид и метилфенилкетон (ацетофенон). Продукт этой реакции – ярко-жёлтое кристаллическое вещество, носит тривиальное название халкон (намёк на медно-красный цвет производных этой молекулы). Его многочисленные производные с разными заместителями в фенильных кольцах тоже называются халконы, такие соединения очень распространены в растениях, и весьма интенсивно исследуются.
Направленная конденсация – такой тип альдольной реакции, в которой вы сами назначаете роли реагентам – кому быть карбонильной, и кому – метиленовой компонентами. В напрвленной конденсации мы не полагаемся ни на какие равновесные процессы, прежде всего потому что на равновесия очень трудно влиять: единственный ключ к этому, принцип Ле Шателье, всегда индивидуален и подбирается к каждой конкретной реакции, а мы хотим иметь более универсальный рецепт, работающий если не во всех, то в большинстве случаев. В направленных конденсациях специально готовят именно метиленовую компоненту, превращая её в конкретную нуклеофильную форму чисто и без примесей. Неспособность это сделать качественно и чисто часто приводит к провалу в направленной конденсации. Например, если мы не смогли на 100% превратить енолизуемый кетон в енолят, и оставили 1-2% исходного кетона (например, неверно определили количество LDA или, как мы любим, в текущей всеми кранами капельной воронке пролили часть раствора основания, эти пара процентов кетона вернут всё хозяйство в равновесный режим, и мы получим ту же кашу в результате, как если бы решили делать просто ненаправленную конденсацию.
В напрвленной конденсации мы не полагаемся ни на какие равновесные процессы, прежде всего потому что на равновесия очень трудно влиять: единственный ключ к этому, принцип Ле Шателье, всегда индивидуален и подбирается к каждой конкретной реакции, а мы хотим иметь более универсальный рецепт, работающий если не во всех, то в большинстве случаев. В направленных конденсациях специально готовят именно метиленовую компоненту, превращая её в конкретную нуклеофильную форму чисто и без примесей. Неспособность это сделать качественно и чисто часто приводит к провалу в направленной конденсации. Например, если мы не смогли на 100% превратить енолизуемый кетон в енолят, и оставили 1-2% исходного кетона (например, неверно определили количество LDA или, как мы любим, в текущей всеми кранами капельной воронке пролили часть раствора основания, эти пара процентов кетона вернут всё хозяйство в равновесный режим, и мы получим ту же кашу в результате, как если бы решили делать просто ненаправленную конденсацию.
Когда делают направленную конденсацию? В современном синтезе почти всегда, так как только направленная конденсация даёт ожидаемый продукт конденсации с высоким выходом и без побочных продуктов. Тем не менее, почти всегда это не просто всегда. Разберёмся, когда её не делают, и почему. На вопрос почему ответ простой: направленная конденсация сложна экспериментально, даже очень сложна. В условиях нашего практикума её вообще сделать не получится – нет ни нужных реагентов, ни условий, ни качественной посуды. И раз есть ряд случаев, когда отлично работает куда более простая ненаправленная, глупо вместо простой и дешёвой реакции делать сложную и дорогую. Смешить людей – не наша профессия. На отдельной вкладке мы рассмотрим, когда делают ненаправленную конденсацию, и дадим честное органическое слово никогда не делать направленную конденсацию, когда можно отлично обойтись ненаправленной.
Направленная конденсация с использованием енолята в качестве нуклеофильного производного енолизуемого карбонильного соединения (метиленовой компоненты)
В этой реакции обычно используют кинетический енолят, то есть тот енолят, который образуется при быстром отщеплении протона от енолизуемого карбонильного соединения с помощью стерически затруднённого очень сильного основания. Здесь всё очень важно – и природа основания, и условия реакции. В качестве основания почти всегда используют литиевое производное диизопропиламина, сокращённо LDA (Lithium DiisopropylAmide, русская аббревиатура ЛДА – Лития ДиизопропилАмид – тоже вполне годится). Интересно, что это первое основание, которое было применено для этой цели, и оно сразу оказалось оптимальным, и закрепилось как основное до сих пор. В сложных случаях и сложных синтезах иногда используют некоторые другие основания, но мы не будем. На очевидный вопрос, если нам так нужно стерически затруднённое основание, почему не взять ди-трет-бутиламид лития, ответ простой – неоткуда взять. Когда будем изучать химию аминов, поймём почему.
Здесь всё очень важно – и природа основания, и условия реакции. В качестве основания почти всегда используют литиевое производное диизопропиламина, сокращённо LDA (Lithium DiisopropylAmide, русская аббревиатура ЛДА – Лития ДиизопропилАмид – тоже вполне годится). Интересно, что это первое основание, которое было применено для этой цели, и оно сразу оказалось оптимальным, и закрепилось как основное до сих пор. В сложных случаях и сложных синтезах иногда используют некоторые другие основания, но мы не будем. На очевидный вопрос, если нам так нужно стерически затруднённое основание, почему не взять ди-трет-бутиламид лития, ответ простой – неоткуда взять. Когда будем изучать химию аминов, поймём почему.
LDA получают обычно прямо перед реакцией действием бутиллития на диизопропиламин. pK вторичного амина около 40, pK бутиллития точно неизвестен, но заведомо намного больше. Депротонирование амина идёт количественно и быстро. Концентрацию LDA в растворе определяют исходя из концентрации бутиллития, которую прямо перед реакцией измеряют титрованием. Как видите, уже довольно хлопотно, но без этого нельзя, так как мы должны точно знать количество LDA для изготовления кинетического енолята. Иначе ничего не выйдет. Если будет недостаток LDA, то останется непрореагировавший кетон и возобновится равновесие. Если избыток, то этот избыток LDA совсем не нужен в альдольной конденсации, он будет вызывать побочные реакции.
Концентрацию LDA в растворе определяют исходя из концентрации бутиллития, которую прямо перед реакцией измеряют титрованием. Как видите, уже довольно хлопотно, но без этого нельзя, так как мы должны точно знать количество LDA для изготовления кинетического енолята. Иначе ничего не выйдет. Если будет недостаток LDA, то останется непрореагировавший кетон и возобновится равновесие. Если избыток, то этот избыток LDA совсем не нужен в альдольной конденсации, он будет вызывать побочные реакции.
Теперь делаем кинетический енолят. Для этого к раствору рассчитанного количества LDA в ТГФ (в конце реакции должен остаться малюсенький избыток этого основания в 1-2% – это будет гарантировать от включения равновесия, и слишком невелико, чтобы потом безобразничать в самой альдольной конденсации) прикапывают раствор кетона. Всё это делают при низкой температуре (-78ºС – это просто температура одной из самых популярных охлаждающих смесей из твёрдой углекислоты (сухого льда) и ацетона) в тщательно высушенном и защищённом от влаги воздуха приборе. Защищать содержимое реакционной колбы от влаги при низкой температуре – та ещё работа, банальной хлоркальциевой трубкой тут не обойтись, – влага исключительно эффективно намораживается на любые охлаждённые до такой низкой температуры поверхности. Поэтому придётся собрать подачу чистого сухого азота или аргона, и защитить прибор булькалкой с минеральным маслом, а ещё лучше, с ртутью, и внимательно следить, чтобы булькало наружу, а не внутрь, особенно в волнительный момент самого охлаждения. Все шлифы придётся качественно смазать смазкой, не застывающей при низкой температуре, и защитить от выбивания какими-нибудь предназначенными для этого специальными фиговинами – стильными пружинками, кеками, но не резинками для денег – резинки при охлаждении становятся жёсткими и хрупкими. И посуда, и шлифы должны быть хороши – вариант нашего практикума, когда воронка или холодильник на шлифе качаются и скрипят, как мачты старинного парусника, категорически не годится. Я специально всё это пишу, чтобы вы поняли, что направленная конденсация – занятие не для ленивых и бедных.
Защищать содержимое реакционной колбы от влаги при низкой температуре – та ещё работа, банальной хлоркальциевой трубкой тут не обойтись, – влага исключительно эффективно намораживается на любые охлаждённые до такой низкой температуры поверхности. Поэтому придётся собрать подачу чистого сухого азота или аргона, и защитить прибор булькалкой с минеральным маслом, а ещё лучше, с ртутью, и внимательно следить, чтобы булькало наружу, а не внутрь, особенно в волнительный момент самого охлаждения. Все шлифы придётся качественно смазать смазкой, не застывающей при низкой температуре, и защитить от выбивания какими-нибудь предназначенными для этого специальными фиговинами – стильными пружинками, кеками, но не резинками для денег – резинки при охлаждении становятся жёсткими и хрупкими. И посуда, и шлифы должны быть хороши – вариант нашего практикума, когда воронка или холодильник на шлифе качаются и скрипят, как мачты старинного парусника, категорически не годится. Я специально всё это пишу, чтобы вы поняли, что направленная конденсация – занятие не для ленивых и бедных. В серьёзной химии лучше быть богатым и трудолюбивым, чем бедным и ленивым. Для бедных и ленивых, впрочем, есть ненаправленная конденсация, и это еще один аргумент в пользу того, чтобы её использовать, когда возможно. Богатым и трудолюбивым, кстати, тоже иногда хочется передохнуть и сэкономить.
В серьёзной химии лучше быть богатым и трудолюбивым, чем бедным и ленивым. Для бедных и ленивых, впрочем, есть ненаправленная конденсация, и это еще один аргумент в пользу того, чтобы её использовать, когда возможно. Богатым и трудолюбивым, кстати, тоже иногда хочется передохнуть и сэкономить.
И надо именно прикапывать кетон к раствору основания, а не наоборот. Это часто называют “обратным порядком прибавления” – когда основной реагент прибавляют к вспомогательному, а не наоборот. Если это делать обычным образом, прикапывая основание к кетону, в колбе сложится ситуация, когда енолят будет соседствовать с ещё непрореагировавшим кетоном. И, во-первых, сразу включится равновесие и прощай кинетический енолят. Во-вторых, начнётся самоконденсация – альдольная конденсация енолята и кетона. Образуется альдоль, и при добавлении следующих порций основания возникнет конкуренция в отщеплении протона от кетона и альдоля, что тем более включит равновесие. От самоконденсации мы немного страхуемся, проводя реакцию при низкой температуре – скорость альдольной конденсации в таких условиях очень мала. Но от включения равновесия нас это не спасёт. Выход – в обратном прибавлении, в этом случае капля раствора кетона попадает в раствор заведомого избытка основания и тут же депротонируется. Если всё сделать аккуратно и не ошибиться в концентрациях, всё получится.
Но от включения равновесия нас это не спасёт. Выход – в обратном прибавлении, в этом случае капля раствора кетона попадает в раствор заведомого избытка основания и тут же депротонируется. Если всё сделать аккуратно и не ошибиться в концентрациях, всё получится.
Если кетон симметричный, или енолизуемый с одной стороны, получится один енолят, другого нет.
Если кетон несимметричный, получится менее замещённый енолят, в основном, по стерическим причинам – протон доступнее. Не зря используется стерически затруднённое основание. Это особенно хорошо работает, когда с одной стороны метил, и даже самый простой из несимметричных кетонов, бутанон-2, даёт менее замещённый енолят с очень небольшой примесью более замещённого. Другие несимметричные кетоны тем более дают менее замещённый енолят. Причина образования этого енолята – исключение из игры равновесия кетон-енолят, и определяющую роль скорости реакции, кинетики – кинетический контроль: менее замещённый енолят образуется по стерическим причинам быстрее, чем более замещённый. Разность скоростей достаточно велика, чтобы обеспечить 98-99% менее замещённого енолята. По этой причине менее замещённый енолят называют кратко кинетическим.
Разность скоростей достаточно велика, чтобы обеспечить 98-99% менее замещённого енолята. По этой причине менее замещённый енолят называют кратко кинетическим.
Как только мы получили енолят, дальше всё просто – прикапываем карбонильную компоненту, подняв температуру до небольшой отрицательной, потом перемешиваем при комнатной, гасим смесь раствором хлорида аммония, чтобы избежать дегидратации, и получаем, как правило, именно альдоль.
В реальной жизни всё немного сложнее, но нам это не нужно, а когда у меня дойдут руки, я где-нибудь отдельно для любопытных расскажу в чём тут ещё есть проблемы и как их решают.
Возможно вы заметили, что в описании направленной конденсации с енолятами везде речь шла про кетоны. А енолизуемые альдегиды можно так же превратить в еноляты и использовать в направленной альдольной конденсации? Простой ответ – да, можно. И мы так и будем это делать в решении задач, не акцентируя внимание на различиях между альдегидами и кетонами. Но в реальной жизни различия есть и очень существенные, и мы уже не раз с этим сталкивались. В этом случае проблемы тоже есть. Альдегиды далеко не так легко дают растворы чистых енолятов при действии LDA или похожих оснований. И если поискать примеры таких синтезов, их будет гораздо меньше, чем альдольных конденсаций с енолятами кетонов. Причин этого несколько, но все они, по-видимому, связаны с более высокой реакционной способностью альдегидной группы. Во-первых, даже при всех описанных предосторожностях (низкой температуре, обратном порядке прибавления и т.п.) во время образования енолята частично проходит и альдольная самоконденсация – в случае альдегидов она настолько быстрее, что низкая температура её не блокирует, и даже в случае обратного прибавления в месте падения капли раствора альдегида некоторое время альдегид и енолят сосуществуют. Вторая причина тоже из той же серии – стерически затруднённое основание достаточно защищено от конкурентной реакции в качестве нуклеофила с кетонной карбонильной группой, но недостаточно – с альдегидной. Конкурентная атака амидного аниона по карбонилу выводит часть основания из реакции.
В этом случае проблемы тоже есть. Альдегиды далеко не так легко дают растворы чистых енолятов при действии LDA или похожих оснований. И если поискать примеры таких синтезов, их будет гораздо меньше, чем альдольных конденсаций с енолятами кетонов. Причин этого несколько, но все они, по-видимому, связаны с более высокой реакционной способностью альдегидной группы. Во-первых, даже при всех описанных предосторожностях (низкой температуре, обратном порядке прибавления и т.п.) во время образования енолята частично проходит и альдольная самоконденсация – в случае альдегидов она настолько быстрее, что низкая температура её не блокирует, и даже в случае обратного прибавления в месте падения капли раствора альдегида некоторое время альдегид и енолят сосуществуют. Вторая причина тоже из той же серии – стерически затруднённое основание достаточно защищено от конкурентной реакции в качестве нуклеофила с кетонной карбонильной группой, но недостаточно – с альдегидной. Конкурентная атака амидного аниона по карбонилу выводит часть основания из реакции. Все эти фокусы нарушают строгое соотношение реагентов, а для альдольной конденсации этого может быть достаточно для того, чтобы напрвленную альдольную реакцию сделать ненаправленной, получить в качестве побочного достаточно много продукта самоконденсации альдегида. Но, с другой стороны, у альдегидов есть и преимущества в сравнении с кетонами: они не бывают несимметричны и енолят у них один. А значит, не нужно париться по поводу конкуренции более и менее замещённого енолята. Стерическая затруднённость основания перестаёт играть такую уж важную роль, главное, чтобы основание было достаточно удалым, чтобы сдирать протон быстро и количественно. Поэтому для альдегидов иногда с успехом используют то, что для кетонов, особенно несимметричных является очень плохим выбором, например, гидрид калия. Именно калия, а не натрия или лития – большой катион снижает энергию кристаллической решётки гидрида, и делает гидрид-ион гораздо более свободным и основным. Про количественную меру основности здесь говорить не приходится, потому что все гидриды всегда действуют гетерогенно, на поверхности – они нерастворимы в органических растворителях, а константы основности всегда измеряют в растворах.
Все эти фокусы нарушают строгое соотношение реагентов, а для альдольной конденсации этого может быть достаточно для того, чтобы напрвленную альдольную реакцию сделать ненаправленной, получить в качестве побочного достаточно много продукта самоконденсации альдегида. Но, с другой стороны, у альдегидов есть и преимущества в сравнении с кетонами: они не бывают несимметричны и енолят у них один. А значит, не нужно париться по поводу конкуренции более и менее замещённого енолята. Стерическая затруднённость основания перестаёт играть такую уж важную роль, главное, чтобы основание было достаточно удалым, чтобы сдирать протон быстро и количественно. Поэтому для альдегидов иногда с успехом используют то, что для кетонов, особенно несимметричных является очень плохим выбором, например, гидрид калия. Именно калия, а не натрия или лития – большой катион снижает энергию кристаллической решётки гидрида, и делает гидрид-ион гораздо более свободным и основным. Про количественную меру основности здесь говорить не приходится, потому что все гидриды всегда действуют гетерогенно, на поверхности – они нерастворимы в органических растворителях, а константы основности всегда измеряют в растворах. Но хорошо известно, что гидрид калия – очень сильное и, главное, быстрое основание, недаром именно его применяют для ацетиленового зиппера. Вот и для генерации енолятов альдегидов гидрид калия работает быстро и точно, не давая возможности альдегиду самоконденсироваться. И, что тоже весьма удобно, можно не бояться избытка – избыток гидрида останется в виде твёрдого вещества, которое можно перед добавлением карбонильной компоненты просто убрать фильтрованием: есть такая удобная техника, которая называется передавливанием – раствор того же енолята через стальную трубочку с маленьким кусочком чего-нибудь фильтрующего на входе передавливают в другой сосуд небольшим давлением того же азота или аргона, который и так используют для создания инертной сухой атмосферы.
Но хорошо известно, что гидрид калия – очень сильное и, главное, быстрое основание, недаром именно его применяют для ацетиленового зиппера. Вот и для генерации енолятов альдегидов гидрид калия работает быстро и точно, не давая возможности альдегиду самоконденсироваться. И, что тоже весьма удобно, можно не бояться избытка – избыток гидрида останется в виде твёрдого вещества, которое можно перед добавлением карбонильной компоненты просто убрать фильтрованием: есть такая удобная техника, которая называется передавливанием – раствор того же енолята через стальную трубочку с маленьким кусочком чего-нибудь фильтрующего на входе передавливают в другой сосуд небольшим давлением того же азота или аргона, который и так используют для создания инертной сухой атмосферы.
Направленная конденсация с использованием эфира енола в качестве нуклеофильного производного
Второй вариант направленной конденсации использует кислотный катализ. В нём в качестве нуклеофильного производного енолизуемого карбонильного соединения используется эфир енола, обычно триметилсилиловый, хотя современная химия знает и десятки других вариантов. Почему используется кремниевый эфир, а не какой-нибудь более обычный, метиловый или этиловый? И потому что силиловые эфиры легче сделать, и потому что кремниевый остаток легко и почти самопроизвольно слетает прямо в ходе конденсации, а этил или метил остались бы, и получились бы весьма реакционноспособные промежуточные продукты, которые стали бы реагировать дальше.
Почему используется кремниевый эфир, а не какой-нибудь более обычный, метиловый или этиловый? И потому что силиловые эфиры легче сделать, и потому что кремниевый остаток легко и почти самопроизвольно слетает прямо в ходе конденсации, а этил или метил остались бы, и получились бы весьма реакционноспособные промежуточные продукты, которые стали бы реагировать дальше.
Этот вариант конденсации открыл японский исследователь Мукайяма (у нас его чаще называют Мукаяма, нам так благозвучнее, потому что в букве я уже есть, как теперь знают даже второклассники, а может и первоклассники, звук, соответствующий букве й, но японская фамилия Mukaiyama разбирается на слоги все же именно так – Му-кай-я-ма), и это самое важное открытие в альдольной конденсации с незапамятных времён её открытия. Первая работа Мукайямы появилась в 1973, приблизительно через сто лет после появления самой альдольной конденсации. И именно вариант Мукайямы по настоящему универсален, и позволяет сдлеть почти любую мыслимую альдольную конденсацию. Более того, в самой реакции Мукайямы заложено столько возможностей для всяческих улучшений и модификаций, что её исследование продолжается до сих пор, а найденные варианты позволяют делать реакцию в любой комбинации метиленовых и карбонильных компонент в сысочайшей селективностью, в том числе стереоселективностью и даже получать сразу оптически чистые альдоли.
Более того, в самой реакции Мукайямы заложено столько возможностей для всяческих улучшений и модификаций, что её исследование продолжается до сих пор, а найденные варианты позволяют делать реакцию в любой комбинации метиленовых и карбонильных компонент в сысочайшей селективностью, в том числе стереоселективностью и даже получать сразу оптически чистые альдоли.
Триметилсилиловые эфиры енолов
Откуда берутся силиловые эфиры енолов? Самый простой способ – силилирование енолов, существующих в равновесии у енолизуемых карбонильных соединений (это подробно рассмотрено на странице про енолиуемые карбонильные соединения). В триметилхлорсилане атом кремния обладает высокой электрофильностью, причем строго предпочитает нуклеофильный атом кислорода – в этом месте ЖМКО ак раз работает очень хорошо – жёсткий кремний предпочитает жёсткий кислород. Протон нужно куда-то девать – его убирают несильным основанием типа триэтиламина. Эту реакцию иногда (к сожалению, чаще, чем хочется) изображают через енолят, но это очевидно неверно – триэтиламин совершенно недостаточно силён как основание, чтобы создать даже мизерную концентрацию енолята. На самом деле, эта реакция скорее должна рассмативаться как кислотно-катализируемая, потому что вскоре после начала в смеси появляется слабая протонная кислота – протонированный амин, и эта кислота катализирует кето-енольное превращение, ускоряя процесс. Очень часто ещё дополнительно добавляют какую-нибудь деликатную кислоту Льюиса, например, безводные соли магния или лития, которые дополнительно дают кислотный катализ кето-енольному превращению, что совершенно нелишне, так как всё же соль аммония – слишком слабая кислота и катализатор. Силилирование енола выводит его из равновесия, и по принципу Ле Шателье, кето-енольное равновесие смещается в сторону енола, и реакция проходит количественно. На схеме, как обычно, нарисован как бы ацетон, но имеется в виду любое енолизуемое карбонильное соединение, кетон или альдегид.
На самом деле, эта реакция скорее должна рассмативаться как кислотно-катализируемая, потому что вскоре после начала в смеси появляется слабая протонная кислота – протонированный амин, и эта кислота катализирует кето-енольное превращение, ускоряя процесс. Очень часто ещё дополнительно добавляют какую-нибудь деликатную кислоту Льюиса, например, безводные соли магния или лития, которые дополнительно дают кислотный катализ кето-енольному превращению, что совершенно нелишне, так как всё же соль аммония – слишком слабая кислота и катализатор. Силилирование енола выводит его из равновесия, и по принципу Ле Шателье, кето-енольное равновесие смещается в сторону енола, и реакция проходит количественно. На схеме, как обычно, нарисован как бы ацетон, но имеется в виду любое енолизуемое карбонильное соединение, кетон или альдегид.
Если кетон енолизуемый в обе стороны и несимметричный, то продукт будет определяться равновесием, то есть стабильностью двух енолов. Как мы знаем, в этом случае будет получаться более замещённый енол. Если разница не очень большая, напрмиер, в метилэтилкетоне, то получаться будет смесь двух эфиров, но более замещённого будет всё равно сильно больше, обычно не менее 80%. Так как у таких изомерных эфиров будут заметно разные температуры кипения, нужный продукт можно дополнительно очистить аккуратной фракционной перегонкой. В общем, проблем с получением более замещённого эфира нет.
Если разница не очень большая, напрмиер, в метилэтилкетоне, то получаться будет смесь двух эфиров, но более замещённого будет всё равно сильно больше, обычно не менее 80%. Так как у таких изомерных эфиров будут заметно разные температуры кипения, нужный продукт можно дополнительно очистить аккуратной фракционной перегонкой. В общем, проблем с получением более замещённого эфира нет.
В современной химии вместо триметилсилилхлорида иногда используют гораздо более электрофильный аналог с трифторметансульфонатной (трифлатной) группой вместо хлора. Такой реагент превращает енолизуемые соединения в силиловые эфиры в очень мягких условиях и чрезвычайно быстро. Правда, это жутко дорого и применяется только для сложных и дорогих альдегидов и кетонов в микро-количествах в сложных синтезах.
Есть и другой способ – силилирование енолятов. Сначала делаем енолят, потом добавляет триметилхлорсилан. Если енолят кинетический, то мы получим менее замещённый силиловый эфир.
Таким образом, у нас есть инструменты, чтобы получать любые силиловые эфиры енолов. На самом деле, ситуация даже ещё интереснее, потому что у силиловых эфиров есть ещё и стереохимия, и про это тоже много чего известно. Но мы не будем так перенапрягаться – это более тонкие вещи, без которых мы без труда обойдёмся.
На самом деле, ситуация даже ещё интереснее, потому что у силиловых эфиров есть ещё и стереохимия, и про это тоже много чего известно. Но мы не будем так перенапрягаться – это более тонкие вещи, без которых мы без труда обойдёмся.
В качестве приятного бонуса нельзя не отметить, что в отличие от енолятов, которые нужно делать каждый раз прямо перед альдольной конденсацией, силиловые эфиры – вполне устойчивые вещества, которые можно хранить и использовать по необходимости. Самые распространённые эфиры енолов можно просто купить.
Альдольная конденсация с силиловыми эфирами – реакция Мукайямы.
Как только у нас есть необходимый силиловый эфир, всё просто. Эта реакция тоже требует аккуратности, сухих и чистых растворителей, а иногда и обычных предосторожностей, если мы её выполняем при низкой температуре. Но в остальном она гораздо проще конденсации с енолятами.
Кроме карбонильной и метиленовой компонент, нам понадобится очень простой растворитель, дихлорметан, который намного проще в обращении, чем ТГФ. И кислота Льюиса. Самая популярная,, обнаруженная ещё самим Мукайямой – хлорид титана(IV). Это довольно противная, сильно дымящая жидкость, но мы её уже применяли для пинаконового сдваивания. Она очень дешёвая, легкодоступная, и при минимальной аккуратности в работе не доставляет никаких проблем. Все реагенты смешивают, перемешивают час-другой, выливают в лёд и обычным образом достают из органического слоя продукт конденсации. Реакции с альдегидами часто настолько быстрые, что их лучше вести при низкой температуре. Реакции с кетонами чаще ведут при комнатной температуре. В реакции всегда получаются альдоли, а не продукты дегидратации.
И кислота Льюиса. Самая популярная,, обнаруженная ещё самим Мукайямой – хлорид титана(IV). Это довольно противная, сильно дымящая жидкость, но мы её уже применяли для пинаконового сдваивания. Она очень дешёвая, легкодоступная, и при минимальной аккуратности в работе не доставляет никаких проблем. Все реагенты смешивают, перемешивают час-другой, выливают в лёд и обычным образом достают из органического слоя продукт конденсации. Реакции с альдегидами часто настолько быстрые, что их лучше вести при низкой температуре. Реакции с кетонами чаще ведут при комнатной температуре. В реакции всегда получаются альдоли, а не продукты дегидратации.
Простой механизм реакции – реакция силилового эфира с комплексом карбонильного соединения с кислотой Льюиса. Роль кислоты Льюиса – просто кислотный катализ, увеличение электрофильности карбонильной компоненты за счёт координации. Альдоль образуется при гидролизе комплекса, который образуется в реакционной смеси. Более реалистические механизмы сложнее, кислота Льюиса, комплекс металла, играет в них более сложную роль, собирая в координационной сфере металла оба реагента, что даёт ещё и значительную выгоду за счёт хелатного эффекта и создаёт важные предпосылки для очень точного контроля стереохимии реакции, за что её так любят в современном органическом синтезе, помешанном на стереоселективности. Оставим это пока в стороне.
Оставим это пока в стороне.
Сила и мощь направленной альдольной реакции Макайямы в том, что мы можем получить любой альдоль, так как имеем возможности получать любой силиловый эфир. Если реакцию с участием енолятов мы в основном применяем для получения альдоля по менее замещённому положению метиленовой компоненты, конденсацию Мукайямы можно сделать и с более, и с менее замещённым эфиром енолов. В нашей програме мы, конечно, предпочтём развести эти два метода и использовать енолятный вариант для менее замещённого альдоля, а вариант Мукайямы для более замещённого альдоля. В первом приближении это верный выбор и мы на нём остановимся.
Формальдегид – наиболее реакционноспособный альдегид, и к тому же неенолизуемый. Поэтому конденсации енолизуемых альдегидов и кетонов с формальдегидом почти всегда можно проводить в равновесных условиях в присутствии оснований без необходимости предварительного получения кинетического енолята – то есть в условиях ненаправленной конденсации. Но при этом почти никогда не получается обычный альдоль один-к-одному. Что получается рассмотрим дальше, но сразу закроем более простой вопрос – что делать, если всё же простой альдоль нужен? Ответ один – делать направленную конденсацию, лучше в варианте Мукаямы: силиловый эфир енола метиленовой компоненты и формальдегид (придётся использовать газообразный, растворив его в подходящем растворителе), например:
Что получается рассмотрим дальше, но сразу закроем более простой вопрос – что делать, если всё же простой альдоль нужен? Ответ один – делать направленную конденсацию, лучше в варианте Мукаямы: силиловый эфир енола метиленовой компоненты и формальдегид (придётся использовать газообразный, растворив его в подходящем растворителе), например:
Подробнее этот вариант напрвленной альдольной конденсации рассмотрим в своём месте, а пока возьмёмся за то, как необычно и увлекательно идёт ненаправленная альдольная конденсация с формальдегидом. Итак, формальдегид всегда будет карбонильной (электрофильной) компонентой конденсации, даже если второй реагент – тоже альдегид.
Единственная проблема – формальдегид настолько реакционноспособен, что в таких условиях полностью замещает все α-водороды, сколько бы из ни было (в ацетоне, например, шесть). И никакие усилия и никакие условия не позволят вам получить продукт конденсации один-к-одному. Это явление открыл в 1891 Бернхард Толленс (мы с ним ещё встретимся в углеводах, где весьма популярен реагент Толленса и проба Толленса – это так красиво называется реакция серебряного зеркала, качественная проба на альдегидную группу), поэтому и всю конденсацию иногда называют конденсацией Толленса. Реакция идёт всегда с избытком формальдегида в присутствии известкового молока, суспензии гидроксида кальция в водном этаноле или метаноле. В этих условиях обычно происходит восстановление карбонильной группы формальдегидом по Каниццаро. Каждый из α-протонов будет замещаться на CH2OH группу, образующуюся из формальдегида. Введение такой группы часто кратко называют гидроксиметилированием. Гидроксид кальция – такое же сильное основание, как и гидроксиды натрия или калия, но реакция идёт аккуратнее и мягче, возможно, потому что ион кальция образует с образующимися полиолами хелатные комплексы, немного удерживая их от необдуманных поступков. Впрочем, и обычные щёлочи в этой реакции тоже можно использовать, но это требует более точного подбора концентрации, температуры, длительности реакции, поэтому это делают в промышленных условиях, но не любят в лаборатории.
Реакция идёт всегда с избытком формальдегида в присутствии известкового молока, суспензии гидроксида кальция в водном этаноле или метаноле. В этих условиях обычно происходит восстановление карбонильной группы формальдегидом по Каниццаро. Каждый из α-протонов будет замещаться на CH2OH группу, образующуюся из формальдегида. Введение такой группы часто кратко называют гидроксиметилированием. Гидроксид кальция – такое же сильное основание, как и гидроксиды натрия или калия, но реакция идёт аккуратнее и мягче, возможно, потому что ион кальция образует с образующимися полиолами хелатные комплексы, немного удерживая их от необдуманных поступков. Впрочем, и обычные щёлочи в этой реакции тоже можно использовать, но это требует более точного подбора концентрации, температуры, длительности реакции, поэтому это делают в промышленных условиях, но не любят в лаборатории.
Итак, в карбонильном замещении в этой реакции замещаются все протоны в енолизуемых положениях, а после формальдегид еще и восстанавливает карбонил. Самый знаменитый продукт этой реакции получается из ацетальдегида и называется пентаэритрит по очень простой причине – он отличается от хорошо известного четырёхатомного спирта эритрита, подарившего нам приставку эритро- (эритрит это эритро-бутан-1,2,3,4-тетраол, брутто-формула C4H8O4) на один единственный пятый атом углерода (C5H8O4). Толленс собственно именно это соединение и открыл вместе с реакцией. Пентаэритрит замечателен не только своей прикольной структурой (надеюсь, роскомпозор до этой страницы никогда не доберется, и никому никакая гадость не померещится), – в нём четыре совершенно одинаковые CH2OH группы, но три из них происходят из формальдегида, а один из ацетальдегида, – но и самыми разнообразными применениями в химии полимеров и не только. Тетраэфир с азотной кислотой (тетранитрат) – мощное взрывчатое вещество. Уже одно это делает конденсацию Толленса весьма интересной реакцией.
Самый знаменитый продукт этой реакции получается из ацетальдегида и называется пентаэритрит по очень простой причине – он отличается от хорошо известного четырёхатомного спирта эритрита, подарившего нам приставку эритро- (эритрит это эритро-бутан-1,2,3,4-тетраол, брутто-формула C4H8O4) на один единственный пятый атом углерода (C5H8O4). Толленс собственно именно это соединение и открыл вместе с реакцией. Пентаэритрит замечателен не только своей прикольной структурой (надеюсь, роскомпозор до этой страницы никогда не доберется, и никому никакая гадость не померещится), – в нём четыре совершенно одинаковые CH2OH группы, но три из них происходят из формальдегида, а один из ацетальдегида, – но и самыми разнообразными применениями в химии полимеров и не только. Тетраэфир с азотной кислотой (тетранитрат) – мощное взрывчатое вещество. Уже одно это делает конденсацию Толленса весьма интересной реакцией.
Человек внимательный (это под-подвид такой есть у Homo sapiens ssp. sapiens, очень-очень редкий, но в наших краях водится, я сам видел) обязательно спросит, а почему формальдегид терпеливо ждёт, пока все протоны заместятся, чтобы осуществить Каниццаро. Что такого вносят эти CH2OH группы (в старой литературе их любили называть метилольными, но новая это не рекомендует) в молекулы карбонильного соединения, что карбонильная группа легче восстанавливается. Это довольно понятно – это ведь -I-акцепторы, хотя и довольно слабые, потому что настоящий акцептор отделён от реакционного центра насыщенным атомом углерода. Акцепторы на карбониле увеличивают электрофильность карбонила, а это важно и в реакции Каниццаро тоже. Чем их больше, тем больше электрофильность, тем легче восстанавливается. Поэтому понятно, что основной продукт реакции действительно такой – все протоны в альдоль, а потом Каниццаро. Но, увы, это не настолько количественно. И увы, карбонил по дороге тоже иногда восстанавливается, и при этом получаются спирты с меньшим количеством CH2OH групп.
sapiens, очень-очень редкий, но в наших краях водится, я сам видел) обязательно спросит, а почему формальдегид терпеливо ждёт, пока все протоны заместятся, чтобы осуществить Каниццаро. Что такого вносят эти CH2OH группы (в старой литературе их любили называть метилольными, но новая это не рекомендует) в молекулы карбонильного соединения, что карбонильная группа легче восстанавливается. Это довольно понятно – это ведь -I-акцепторы, хотя и довольно слабые, потому что настоящий акцептор отделён от реакционного центра насыщенным атомом углерода. Акцепторы на карбониле увеличивают электрофильность карбонила, а это важно и в реакции Каниццаро тоже. Чем их больше, тем больше электрофильность, тем легче восстанавливается. Поэтому понятно, что основной продукт реакции действительно такой – все протоны в альдоль, а потом Каниццаро. Но, увы, это не настолько количественно. И увы, карбонил по дороге тоже иногда восстанавливается, и при этом получаются спирты с меньшим количеством CH2OH групп. Увы, это довольно серьёзная проблема. Поэтому выходы в конденсации Толленса никогда не бывают высокими, редко превышают 50%, а во многих случаях приходится довольствоваться чем-то вроде 5-10%. И зачем нам такое? Вещества интересные, любят их для разных интересных дел, а как вы по-другому это получите. Да и очень простая эта реакция, и стоит дёшево (банальные альдегиды или кетоны, извёстка, формалин, вода из ближайшей лужи) – нужно побольше продукта, месите в ведре хоть на пять килограмм. Но как раз в случае ацетона, где можно было бы напихать аж шесть метилольных групп и получить этакую насекомую молекулу с шестью ножками и одним глазом, вот была бы потеха! – получить никак не удаётся. Ацетон очень бурно реагирует с формальдегидом, но при этом получается жуткая каша из всех промежуточных продуктов неполного гидроксиметилирования с преждевременно восстановленной карбонильной группой. Делить это невозможно.
Увы, это довольно серьёзная проблема. Поэтому выходы в конденсации Толленса никогда не бывают высокими, редко превышают 50%, а во многих случаях приходится довольствоваться чем-то вроде 5-10%. И зачем нам такое? Вещества интересные, любят их для разных интересных дел, а как вы по-другому это получите. Да и очень простая эта реакция, и стоит дёшево (банальные альдегиды или кетоны, извёстка, формалин, вода из ближайшей лужи) – нужно побольше продукта, месите в ведре хоть на пять килограмм. Но как раз в случае ацетона, где можно было бы напихать аж шесть метилольных групп и получить этакую насекомую молекулу с шестью ножками и одним глазом, вот была бы потеха! – получить никак не удаётся. Ацетон очень бурно реагирует с формальдегидом, но при этом получается жуткая каша из всех промежуточных продуктов неполного гидроксиметилирования с преждевременно восстановленной карбонильной группой. Делить это невозможно.
Вот несколько примеров с другими альдегидами и кетонами. Забавного то ли паучка, то ли крабика из циклогексанона впервые получил сам Карл Манних.
А бывает, что карбонил остаётся? Да, иногда это происходит по тем или иным причинам. Например, циклопентанон сам останавливается на этой стадии. Почему – разберёмся, когда дойдём до алициклов, стереохимия так работает.
Но можно и по другому поступить. Конденсации ведь можно делать не только с основным, но и с кислотным катализом. А в условиях кислотного катализа нет Каниццаро. Но есть другая проблема – кислотный катализ понуждает карбонильную группу формальдегида образовывать циклический ацеталь с образовавшимися спиртовыми группами. Как раз получается шестичленный цикл. Тоже симпатичная штука. Её даже потом можно прогидролизовать как раз в то, что мы хотели.
Реакция Манниха присутствует в программе этого раздела как-то стеснительно, как бедная родственница. Для каких-то возвышенных целей в длинных синтезах мы её никогда не используем, так, помянем время от времени, “как кремлёвского горца”, для успокоения совести, типа, знаем мол такую, слышали, редкостная гадость, забыть бы её, проклятую, и никогда больше не вспоминать.
И напрасно. Это мощнейшая и интереснейшая реакция. В современной химии она играет огромную, просто неприлично нескромную роль. С её помощью делаются головокружительно сложные синтезы всяких природных соединений. Она просто изумительно приспособлена под все современные штучки типа органокатализа, энантиоселективности, стереодивергентности, “зелёных” фокусов и т.д. И ещё она какая-то безразмерная – никакой фантазии не хватит, чтобы понять, что ещё можно получить с её помощью. Мы, конечно, так далеко не пойдём, но знать как она устроена в общих чертах точно стоит – тогда при желании вы всегда сможете пойти дальше и разобраться в её современных приключениях.
Итак, что такое реакция Манниха. Во-первых, это не что иное как альдольная конденсация. Напомню, что альдольная конденсация – это один из самых общих типов реакций в органичской химии – это присоединение нуклеофильной формы енолизуемого карбонильного соединения (енола, енолята, эфира енола, и, в принципе, и енамина тоже) к электрофильной карбонильной группе или её аналогу, обычно, в условиях кислотного или основного катализа. Реакция Манниха – это ровно оно и есть: в ней в роли электрофильной карбонильной группы используется азотный аналог карбонила – катион иминия. В самой классической реакции Манниха, которой мы и ограничимся, каион иминия всегда получается из одного и того же карбонильного соединения, формальдегида. Вопрос – а что мешает взять что-нибудь другое? Ответ – ничего не мешает, кроме крайней сложности того, что может произойти, потому что как только мы в этой реакции что-то хоть немного усложняем, начинается игра вариантов и возможных комбинаций, такие молекулярные шахматы. И чтобы не сойти с ума раньше времени, трогать мы это не будем, а ограничимся формальдегидом.
Реакция Манниха – это ровно оно и есть: в ней в роли электрофильной карбонильной группы используется азотный аналог карбонила – катион иминия. В самой классической реакции Манниха, которой мы и ограничимся, каион иминия всегда получается из одного и того же карбонильного соединения, формальдегида. Вопрос – а что мешает взять что-нибудь другое? Ответ – ничего не мешает, кроме крайней сложности того, что может произойти, потому что как только мы в этой реакции что-то хоть немного усложняем, начинается игра вариантов и возможных комбинаций, такие молекулярные шахматы. И чтобы не сойти с ума раньше времени, трогать мы это не будем, а ограничимся формальдегидом.
Формальдегид реагирует с вторичными аминами так, как мы уже однажды писали, когда получали енамины из карбонильных соединений и вторичных аминов. Эта реакция катализируется кислотами, и приводит, как обычно, сначала к тетраэдрическому интермедиату, который теряет воду с образованием катиона иминия. Как и все такие ионы, у которых рядом с положительным углеродом сильный мезомерный донор, структура ближе к форме с двойной связью и плюсом на донорном атоме.
Иминиевый ион – аналог карбонильного соединения. Двойная связь позволяет присоединение, а положительный заряд на углероде и возможность смещения электронной плотности в сторону атома азота обусловливает присоединение именно нуклеофилов и именно к углероду. При этом, иминиевый ион более электрофилен, чем исходное карбонильное соединение, потому что второй атом на двойной связи в нём уже положителен, и значит сильнее смещает плотность к себе. По этой причине в реакции будет участвовать в первую очередь именно иминиевый ион, а нее исходное карбонильное соединение.
Реакцию Манниха почти всегда проводят в присутствии кислот, в условиях кислотного катализа. Второй участник реакции, енолизуемое карбонильное соединение, в этих условиях не может быть енолятом, но только енолом, в равновесной, обычно ничтожно малой концентрации. Реакция Манниха – одна из реакций карбонильных соединений через енольную форму – на странице про енолизуемые формы таких реакций рассмотрено много, это ещё одна. Енол – довольно слабый нуклеофил по сравнению с енамином и енолятом, но иминиевый катион вполне электрофилен и неплохо справляется с таким слабым нуклеофилом. Дальше всё очевидно. После присоединения протон переселяется с кислорода на более основный азот. Реузультат реакции Манниха – всегда протонированная форма аминокетона, а не сам аминокетон.
Енол – довольно слабый нуклеофил по сравнению с енамином и енолятом, но иминиевый катион вполне электрофилен и неплохо справляется с таким слабым нуклеофилом. Дальше всё очевидно. После присоединения протон переселяется с кислорода на более основный азот. Реузультат реакции Манниха – всегда протонированная форма аминокетона, а не сам аминокетон.
При желании после реакции протон можно снять и получить сам аминокетон. Но обычно это не делают, потому что такие аминокетоны (их по традиции называют основаниями Манниха) довольно неустойчивы по очень интересной причине – они одновременно являются продуктами 1,4-присоединения вторичного амина к енонам, а эта реакция, как мы знаем, обратима. Из-за этого основания Манниха очень часто применяют как удобный источник соответствующих енонов. Их можно хранить в виде солей, продуктов реакции Манниха, и использовать как еноны (или енали) просто в присутствии эквивалента основания. Пока на этом остановимся, но когда-нибудь продолжим – это довольно интересно.
Для нас из этого есть непосредственный вывод: если правда хотите получить основание Манниха из продукта реакции Манниха, используйте строго один эквивалент основания, и выбирайте основание послабее, что-то типа ацетата натрия.
Бромирование енолизуемых альдегидов и кетонов, дающее α-бромпроизводные, приводит к интересному результату – превращению нуклеофила в электрофил. Мы только что бурно радовались такому же трюку, только в обратном направлении – из электрофила в нуклеофил – на самом карбонильном углероде, и называли это немецким словом Umpolung. И да, и это тоже он самый, хотя это мало кто так называет, но если хотите назвать – вперёд, это будет правильно.
Бромпроизводные альдегидов и кетонов – очень реакционноспособные электрофилы в реакциях SN2-замещения. Мы уже успешно применили их в реакции с енаминами для соединения двух енолизуемых карбонильных соединений в одно дикарбонильное. А что еще можно сделать? Другие замещения. При планировании таких реакций нужно иметь в виду одну малоприятную вещь. В молекулах бромкетонов и бромальдегидов не один, а два электрофильных центра: тот, который с бромом для SN2-замещения, и карбонильный для присоединения. Об этом нужно постоянно думать, потому что это источник ошибок. Эти центры конкурируют за нуклеофилы. В некотором смысле это похоже на конкуренцию 1,2- и 1,4-присоединения в непредельных карбонильных соединениях, хотя здесь присоединение конкурирует с замещением, и закономерности ещё более нечёткие. Предсказать, кто выиграет очень сложно, хотя простые соображения помогают. Например, возьмём цианид-ион как нуклеофил. С бромкетонами идёт нормальное SN2-замещение. С условиями не суетимся – субстрат очень реакционноспособный, поэтому всяких ДМСО не нужно. А вот с бромальдегидами будет нечто иное. Альдегидный карбонил намного более электрофилен, чем кетонный, и вместо замещения идёт присоединения. А тетраэдрический аддукт превращается в эпоксид внутримолекулярным замещением брома.
В молекулах бромкетонов и бромальдегидов не один, а два электрофильных центра: тот, который с бромом для SN2-замещения, и карбонильный для присоединения. Об этом нужно постоянно думать, потому что это источник ошибок. Эти центры конкурируют за нуклеофилы. В некотором смысле это похоже на конкуренцию 1,2- и 1,4-присоединения в непредельных карбонильных соединениях, хотя здесь присоединение конкурирует с замещением, и закономерности ещё более нечёткие. Предсказать, кто выиграет очень сложно, хотя простые соображения помогают. Например, возьмём цианид-ион как нуклеофил. С бромкетонами идёт нормальное SN2-замещение. С условиями не суетимся – субстрат очень реакционноспособный, поэтому всяких ДМСО не нужно. А вот с бромальдегидами будет нечто иное. Альдегидный карбонил намного более электрофилен, чем кетонный, и вместо замещения идёт присоединения. А тетраэдрический аддукт превращается в эпоксид внутримолекулярным замещением брома.
А с более сильными нуклеофилами и кетоны будут скорее реагировать по карбонилу, и получаться будут совсем неожиданные продукты. Нам такие осложнения даром не нужны. Поэтому старайтесь избегать использования бромкетонов и бромальдегидов в реакциях с нуклеофилами, кроме тех случаев, которые рекомендованы. Пока это только енамин. Очень распространённая ошибка – брать енолят вместо енамина. Ни в коем случае! Енолят намного более сильный нуклеофил, чем енамин, и реагировать будет в основном по карбонилу в альдольной конденсации, но продукт будет сложнее чем просто альдоль по той же причине, по которой у нас получился эпоксид на схеме реакции с цианид-ионом.
Нам такие осложнения даром не нужны. Поэтому старайтесь избегать использования бромкетонов и бромальдегидов в реакциях с нуклеофилами, кроме тех случаев, которые рекомендованы. Пока это только енамин. Очень распространённая ошибка – брать енолят вместо енамина. Ни в коем случае! Енолят намного более сильный нуклеофил, чем енамин, и реагировать будет в основном по карбонилу в альдольной конденсации, но продукт будет сложнее чем просто альдоль по той же причине, по которой у нас получился эпоксид на схеме реакции с цианид-ионом.
Реакция бромкетонов и бромальдегидов с купратами
Есть распространённое мнение, что купраты отличаются от гриньяров и литийорганики гораздо большей селективностью – купраты обычно реагируют с галогенпроизводными, образуя продукт замщения галогена на органический остаток купрата. И если в молекуле есть другие функциональные группы типа карбонила, сложного эфира, нитрила, амида, они остаются нетронутыми. Это очень привлекательное свойство купратов, которое мы когда-нибудь обсудим подробнее. Такая реакция позволяла бы селективно заменять галоген на большое количество всяких полезных групп – алкилов, арилов, алкенилов, и была бы ограничена только нашей способностью запихать нужную нам группу в купрат. Мы знаем, что это не совсем просто, потому что купрат получается из литийорганики, которая несовместима с большинством функциональных групп, но в нашем распоряжении есть защитные группы, и это дает неплохой выбор. Неудивительно, что эта реакция носит громкое название реакции Кори-Хауcа, а иногда даже Кори-Познера-Хауcа-Уайтсайдса, впрочем не очень распространенное. А почему я везде пишу в условном наклонении “позволяла бы” – а не просто “позволяет”. Потому что, увы, реакция эта очень капризна и довольно часто вместо нужного продукта даёт чёрт знает что или вообще ничего не даёт. Для любопытных, я подробно разберу эту реакцию на отдельной страничке. Так или иначе, давайте считать, что она работает. Это типичный пример виртуальной химии, не первый, и не последний.
Такая реакция позволяла бы селективно заменять галоген на большое количество всяких полезных групп – алкилов, арилов, алкенилов, и была бы ограничена только нашей способностью запихать нужную нам группу в купрат. Мы знаем, что это не совсем просто, потому что купрат получается из литийорганики, которая несовместима с большинством функциональных групп, но в нашем распоряжении есть защитные группы, и это дает неплохой выбор. Неудивительно, что эта реакция носит громкое название реакции Кори-Хауcа, а иногда даже Кори-Познера-Хауcа-Уайтсайдса, впрочем не очень распространенное. А почему я везде пишу в условном наклонении “позволяла бы” – а не просто “позволяет”. Потому что, увы, реакция эта очень капризна и довольно часто вместо нужного продукта даёт чёрт знает что или вообще ничего не даёт. Для любопытных, я подробно разберу эту реакцию на отдельной страничке. Так или иначе, давайте считать, что она работает. Это типичный пример виртуальной химии, не первый, и не последний.
Итак, если у нас есть α-бромкетон, то действие купрата должно давать продукт замещения брома на органический остаток купрата. Ценность этой реакции в том, что входящий остаток R не ограничен законами SN2-замещения, хотя сама реакция, скорее всего, и идёт по SN2-механизму, но R здесь в нуклеофиле, а ограничения в основном затрагивают электрофильный реагент – галогенпроизводное. Поэтому смело используем и трет-бутил, и фенилы, и винилы. Эта реакция часто подразумевается в задачах, поэтому пользуйтесь без ограничений.
Ценность этой реакции в том, что входящий остаток R не ограничен законами SN2-замещения, хотя сама реакция, скорее всего, и идёт по SN2-механизму, но R здесь в нуклеофиле, а ограничения в основном затрагивают электрофильный реагент – галогенпроизводное. Поэтому смело используем и трет-бутил, и фенилы, и винилы. Эта реакция часто подразумевается в задачах, поэтому пользуйтесь без ограничений.
В жизни всё не так блестяще. Эту реакцию описали французы в начале 1970-х (Dubois et al, Tetrahedron Lett., 1971, 177) именно с этой заявленной целью – получать разнообразные кетоны, которые нельзя сделать через енамин. И даже действительно привели примеры с трет-бутильным купратом – и получили выходы в 4%. Четыре процента это лучше, чем совсем ничего, да вот беда – эти кетоны можно и по-другому получить. В целом по той статье получается так, что метод прилично работает только для диметилкупрата лития, то есть, прямо скажем, малость неубедительно. С бромальдегидами она совсем не работает. В последующие годы эту реакцию пытались починить, предлагая разные усовершенствования, да ничего путного не вышло, и ее совсем забросили. Более того, похоже что французы банально наврали, потому что все, кто пытался эту реакцию повторить получали совсем другие продукты, в основном просто восстановление до исходного кетона без брома. И не стыдно им, французы всё же, не последние люди в химии! Есть еще несколько индийских работ с примерами этой реакции, но это уже совсем сказки, да и найти эти статьи непросто даже с простительной целью типа поржать.
В последующие годы эту реакцию пытались починить, предлагая разные усовершенствования, да ничего путного не вышло, и ее совсем забросили. Более того, похоже что французы банально наврали, потому что все, кто пытался эту реакцию повторить получали совсем другие продукты, в основном просто восстановление до исходного кетона без брома. И не стыдно им, французы всё же, не последние люди в химии! Есть еще несколько индийских работ с примерами этой реакции, но это уже совсем сказки, да и найти эти статьи непросто даже с простительной целью типа поржать.
В общем, сильно похоже что в жизни эта реакция не дает продуктов замещения брома из α-бромзамещенных карбонильных соединений на органический остаток из купрата. Скорее всего, вместо этого происходит обмен галогена на металл, а такая металлоорганика легко перегруппировывается в енолят (это называется металлотропией по аналогии с прототропией, что просто синоним таутомерии). Ну и после гидролиза реакционной смеси естественно получается исходный кетон.
Может вы что-нибудь придумаете? Хотя вряд ли это понадобится – в современной химии на смену купратам пришли более эффективные реакции, катализируемые комплексами переходных металлов, и эта задача – запихнуть заместитель в альфа-положение енолизуемых карбонильных соединений, новая химия решает, и не одним способом.
Реакции α,β-непредельных карбонильных соединий
- Выбираем…
- Общие идеи: 1.2- и 1,4-присоединение
- Присоединение HCN
- Ацетали и тиоацетали енонов и еналей
- Реакции с енаминами
- Реакции с литийорганикой. Раздел в работе.
- Реакции с купратами. Раздел в работе.
Реакции α,β-непредельных карбонильных соединений (еналей и енонов) с нуклеофилами – мощный дополнительный инструмент синтеза. Сложность и богатство этих реакций в том, что в них монут быть вовлечены два реакционных центра, карбонильный и β-углерод, и нужно хорошо разобраться в том, как выбирать правильный метод.
Сопряжение двойной связи с карбонильной группой приводит к принципиально фундаментальному (или фундаментально принципиальному?) результату: двойная связь резко меняет свою природу, становясь из нуклеофильного реакционного центра, склонного к реакциям с электрофилами, в электрофильный реакционный центр, склонный к реакциям с нуклеофилами. И если у вас после этой фразы не поехала крыша, значит дальше пойдёт как по маслу. Если поехала, не обессудьте, никто райской жизни не обещал, здесь у нас не кафедра истории КПСС, то есть, извините, сейчас это называется политологии.
И если у вас после этой фразы не поехала крыша, значит дальше пойдёт как по маслу. Если поехала, не обессудьте, никто райской жизни не обещал, здесь у нас не кафедра истории КПСС, то есть, извините, сейчас это называется политологии.
В принципе, мы это уже обсудили в Алкенах – посмотрите вкладку про два особых типа алкенов – донорные и акцепторные олефины. Мезомерный акцептор на двойной связи делает дальний углерод этой двойной связи электрофилом. Это легко видно из граничных структур:
Некоторые могут заметить, что вторая структура сильно напоминает уже хорошо знакомый нам енолят, и не значит ли это, что первый углерод двойной связи проявляет нуклеофильные свойства. Отчасти да, следует, но это будет проявляться только в реакции с серьёзными электрофилами, которые будут направляться именно на этот атом. Поэтому такие соединения присоединяют электрофилы, например, HBr против правила Марковникова. Впрочем, электрофилы тяжело присоединяются к таким связям, и много примеров, кроме HBr вы не найдёте.
Гораздо охотнее такие карбонильные соединения присоединяют нуклеофилы. И здесь возникает большая проблема и большие возможности. У непредельных карбонильных соединений не один, а два электрофильных центра: карбонильный углерод и β-углерод. И два возможных пути реакции: типичное присоединение нуклеофила по карбонильной группе и присоединение нуклеофила к двойной связи. В обоих случаях сначала образуется аддукт, который превращается в конечный продукт после присоединения протона.
В этих двух реакциях очень легко можно усмотреть аналогию с присоединением к сопряжённому диену. Можно вспомнить про это на страничке про диены. Особенно наглядно будет, если мы присоединим реагент вида HX (Х – какой-то нуклеофил). Аналогия совершенно очевидная, особенно если у присоединения к β-углероду карбонильного соединения нарисовать сначала образующийся продукт – енол. Поэтому это так и называют:
- присоединение по карбонилу называют 1,2-присоединением.
- присоединение по двойной связи – 1,4-присоединением.
 Но еще и сопряженным присоединением. И присоединением по Михаэлю. Это всё синонимы.
Но еще и сопряженным присоединением. И присоединением по Михаэлю. Это всё синонимы.
И эти цифры не имеют никакого отношения к номенклатуре, к нумерации атомов в называниях. Поэтому не путайтесь. Например, 1,4-присоединение HBr к проп-2-еналю даёт 3-бромпропаналь.
Когда 1,2 и когда 1,4?
Разные нуклеофилы прсоединяются по разному. Во многих случаях получается один из продуктов, но довольно часто смеси. Мы не любим смеси, поэтому будем стараться выбирать те методы, которые дают чистый результат. это можно пропустить
Что определяет направление присоединения? Сразу скажем – вовсе не то, что обычно приводят в учебниках. К этой проблеме стараниями одного шустрого химика намертво прилипла совершенно идиотская концепция ЖМКО. Сразу скажу, что ЖМКО – жёсткие и мягкие кислоты и основания Льюиса – вполне основательная и полезная теория в химии координационных соединений. Там с её помощью удобно объясняют, почему разные металлы предпочитают разные лиганды. Это качественная (не в смысле “высококачественная”, а в смысле “писаная вилами на воде”) концепция без особых претензий на серьёзную предсказательную силу. В координационной химии её обычно поминают на первых страницах учебников, восхищаются ее краткостью и красотой, а после забывают и спосойно живут без неё. Но там хотя бы что-то с её помощью можно предсказать (и в лужу сесть тоже очень хорошо можно, если слишком сильно увлечься).
В координационной химии её обычно поминают на первых страницах учебников, восхищаются ее краткостью и красотой, а после забывают и спосойно живут без неё. Но там хотя бы что-то с её помощью можно предсказать (и в лужу сесть тоже очень хорошо можно, если слишком сильно увлечься).
Но к органической химии эта теория не имеет никакого отношения. Ну нет, малость перебрал, какое-то имеет. Например, когда мы для гидролиза дитианов используем катализ солями ртути. Или когда в ацилировании по Фриделю-Крафтсу объясняем, почему алюминий садится на кислород, а не на хлор. Ну и еще в паре подобных мест. Но к проблеме присоединения к ненасыщенным карбонильным соединениям не имеет никакого. И к проблеме так называемых амбидентных нуклеофилов тоже, хотя мы это и пропустили. Хотя бы потому, что в этих больших разделах нам интересны не кислоты и основания, а нуклеофилы и электрофилы. Да, между понятиями нуклеофил и основание есть параллели, и мы это хорошо знаем (кстати, и здесь нам полезнее основания не Льюиса, а Бренстеда-Лоури, а к последним жёсткость и мягкость отношения не имеют). И между кислотой и электрофилом тоже есть. Но из этих параллелей никак не получается сделать теорию жестких и мягких электрофилов и нуклеофилов (ЖМЭН?? – слышали когда-нибудь? – я нет, точнее, скажем так – о попытках создать таку теорию слышал и не раз, но о том, что их этих попыток получилось что-то путное, нет, не слышал). Вот с какого бодуна аммиак, амины, гидроксид, вода вдруг стали мягкими, если в нормальном ЖМКО они жёсткие и предпочитают жёсткие катионы металлов? И так далее в том же духе.
И между кислотой и электрофилом тоже есть. Но из этих параллелей никак не получается сделать теорию жестких и мягких электрофилов и нуклеофилов (ЖМЭН?? – слышали когда-нибудь? – я нет, точнее, скажем так – о попытках создать таку теорию слышал и не раз, но о том, что их этих попыток получилось что-то путное, нет, не слышал). Вот с какого бодуна аммиак, амины, гидроксид, вода вдруг стали мягкими, если в нормальном ЖМКО они жёсткие и предпочитают жёсткие катионы металлов? И так далее в том же духе.
Соображения сторонников этой концепции обычно выражаются простой двухходовой формулой: Этот нуклеофил даёт 1,2- (1,4-) аддукт, потому что он жёсткий (мягкий). Этот нуклеофил жёсткий (мягкий) потому что он даёт 1,2- (1,4-) аддукт. Хочется только спросить, а где у вас тут курица, а где яйцо.
В общем, если хотите, изучайте, но без меня и по другим источникам. А зачем тогда это везде рассказывают? Чтобы создать видимость простоты там, где всё довольно сложно. И я не против простоты, если картинка получается удобная и непротиворечивая. Увы, здесь это не так. И простота, которая маскирует откровенные манипуляции уж точно хуже воровства.
Увы, здесь это не так. И простота, которая маскирует откровенные манипуляции уж точно хуже воровства.
Так что же определяет результат реакции присоединения нуклеофила к сопряжённым непредельным карбонильным соединениям. Сразу скажем, что совсем простых ответов на этот вопрос нет, и не должно быть. В химии так не бывает. И нет такого правила, которое позволяет из общих соображений предсказать результат в общем случае. Можно только заметить несколько важных тенденций.
Самое важное: и 1,2- и 1,4-присоединение – обратимые реакции в большинстве случаев. Соотношение продуктов по каждому из направлений определяется точно так же, как и во всех похожих случаях, то есть, кинетическим и термодинамическим контролем.
Присоединение по карбонилу (1,2-присоединение) почти всегда быстрее, чем по 1,4. Это довольно просто понять: скорость реакции определяется электрофильностью углерода. Про электрофильность карбонильного углерода мы знаем всё, и ничего нового здесь нет. По сравнению с обычными карбонильными соединениями у этих электрофильность снижена, потому что карбонил сопряжён с двойной связью, и если карбонил по отношению к двойной связи – акцептор, то двойная связь по отношению к карбонилу – донор. Это очевидно, и приводит к относительному уменьшению положительного заряда на карбонильном углероде. Но при этом, если мы сравниваем непредельный альдегид и кетон, то альдегид по прежнему намного электрофильнее. И когда мы сравниваем электрофильность карбонильного углерода и β-углерода, мы вполне понимаем, что и та, и та обусловлена смещением электронной плотности к атому кислорода, и оба эти центра входят в одну и ту же цепь сопряжения, и более близкий в атому кислороду должен иметь больший положительный заряд. Это вполне подтверждают разные методы, например, хим. сдвиги в спектрах 13C ЯМР и всякие расчёты.
Это очевидно, и приводит к относительному уменьшению положительного заряда на карбонильном углероде. Но при этом, если мы сравниваем непредельный альдегид и кетон, то альдегид по прежнему намного электрофильнее. И когда мы сравниваем электрофильность карбонильного углерода и β-углерода, мы вполне понимаем, что и та, и та обусловлена смещением электронной плотности к атому кислорода, и оба эти центра входят в одну и ту же цепь сопряжения, и более близкий в атому кислороду должен иметь больший положительный заряд. Это вполне подтверждают разные методы, например, хим. сдвиги в спектрах 13C ЯМР и всякие расчёты.
Поэтому 1,2-продукт почти всегда образуется при кинетическом контроле, когда мы не достигаем обратимости. Это особенно верно для альдегидов и кетонов с маленькими группами. И если эта стадия вдруг необратима, как при реакции с литий-органическими соединениями или реагентами Виттига, то мы получим 1,2-продукты. То же самое происходит при гидридном восстановлении алюмогидридом лития. Или мы делаем ее необратимой, протонируя тетраэдрический аддукт, то мы тоже выводим 1,2-аддукт из равновесия. Так происходит, например, при присоединении HCN. Кстати, с точки зрения пресловутого ЖМКО это особо вопиющий случай: цианид ведь классическое мягкое основание Льюиса. И даже в SN2 замещении, где цианид – амбидентный нуклеофил (мы, к счатью, пропустили эту муть про амбидентные нуклеофилы), его считают стопроцентно мягким C-нуклеофилом те же самые люди, которые теперь будут делать вид, что ничего особенного не происходит, наблюдая как цианид присоединяется 1,2, то есть, по их мнению, по жёсткому сценарию. Еще один пример выведения аддукта из равновесия – образование ацеталей, особенно циклических.
Или мы делаем ее необратимой, протонируя тетраэдрический аддукт, то мы тоже выводим 1,2-аддукт из равновесия. Так происходит, например, при присоединении HCN. Кстати, с точки зрения пресловутого ЖМКО это особо вопиющий случай: цианид ведь классическое мягкое основание Льюиса. И даже в SN2 замещении, где цианид – амбидентный нуклеофил (мы, к счатью, пропустили эту муть про амбидентные нуклеофилы), его считают стопроцентно мягким C-нуклеофилом те же самые люди, которые теперь будут делать вид, что ничего особенного не происходит, наблюдая как цианид присоединяется 1,2, то есть, по их мнению, по жёсткому сценарию. Еще один пример выведения аддукта из равновесия – образование ацеталей, особенно циклических.
Для большинства других нуклеофилов в системе быстро достигается равновесие, и при этом почти всегда 1,4-продукт выигрывает, это продукт термодинамического контроля. Почему это так, тоже понять можно довольно легко, если мы хорошо разобрались в том, как устроены соединения с двойными связями, C=C и C=O. Тогда мы понимаем, что такие связи всегда дестабилизируют молекулу – все реакции присоединения всегда самопроизвольны и экзотермичны. Сопряжение наоборот несколько стабилизирует двойные связи, хотя и не так сильно, как иногда это пытаются представить. Но двойные связи C=C хуже чем двойные связи С=O, они больше дестабилизируют. Дальше логика проста: 1,2-присоединение выводит из сопряжения карбонил и оставляет C=C. А 1,4-присоединение выводит из сопряжения и C=C и C=O и создаёт новую сопряжённую систему енолята – это просто выгоднее энергетически, причём почти всегда. Поэтому образование 1,4-аддукта – намного более часто встречающийся результат присоединения нуклеофилов к сопряжённым непредельным карбонильным соединениям в равновесии. Можно даже сформулировать простое правило, даже два отдельных правила:
Тогда мы понимаем, что такие связи всегда дестабилизируют молекулу – все реакции присоединения всегда самопроизвольны и экзотермичны. Сопряжение наоборот несколько стабилизирует двойные связи, хотя и не так сильно, как иногда это пытаются представить. Но двойные связи C=C хуже чем двойные связи С=O, они больше дестабилизируют. Дальше логика проста: 1,2-присоединение выводит из сопряжения карбонил и оставляет C=C. А 1,4-присоединение выводит из сопряжения и C=C и C=O и создаёт новую сопряжённую систему енолята – это просто выгоднее энергетически, причём почти всегда. Поэтому образование 1,4-аддукта – намного более часто встречающийся результат присоединения нуклеофилов к сопряжённым непредельным карбонильным соединениям в равновесии. Можно даже сформулировать простое правило, даже два отдельных правила:
При присоединении нуклеофилов к сопряжённым енонам (кетонам) 1,4-присоединение происходит пости всегда кроме нескольких исключений, которые проще запомнить, чем пытаться это как-то обобщить.
При присоединении нуклеофилов к сопряжённым еналям (альдегидам) 1,2-присоединение происходит всегда, когда реакция необратима, или по природе своей, или из-за вывода аддукта из равновесия.
И последнее. 1,4-присоединение может быть основным путём реакции, если механизм реакции не является просто присодинением нуклеофила. Таковы, например, восстановление сольватированным электроном. И присоединение купратов. У этих реакций принципиально другие механизмы, и то, что мы их рассматриваем вместе с настоящими реакциями присоединения нуклеофилов – просто дань удобству.
Присоединение HCN в основном идёт как 1,2-присоединение, но только тогда, когда такое присоединение вообще может произойти. Прежде чем разбираться почему, напомню, что с обычными карбонильными соединениями присоединение HCN идёт далеко не всегда. Эта реакция обратима и требует основного катализа, потому что HCN вообще не является нуклеофилом по отношению к карбонильной группе, нуклеофилом является только цианид-ион, присоединение цианид-иона обратимо, и равновесие смещено в сторону циангидринов только у альдегидов. Протонирование аддукта выводит аддукт из равновесия, и позволяет сместить равновесие в сторону циангидринов также для более реакционноспособных кетонов типа ацетона и других метилалкилкетонов, а также циклоалканонов. Это я просто напомнил. Но это именно то, что нужно, чтобы понять, как реагируют непредельные карбонильные соединения.
Протонирование аддукта выводит аддукт из равновесия, и позволяет сместить равновесие в сторону циангидринов также для более реакционноспособных кетонов типа ацетона и других метилалкилкетонов, а также циклоалканонов. Это я просто напомнил. Но это именно то, что нужно, чтобы понять, как реагируют непредельные карбонильные соединения.
Когда мы берём непредельные карбонильные соединения, эта особенность реакции никуда не денется. Реакция по карбонильной группе (1,2-присоединение) возможно только для альдегидов (еналей) и простых енонов или циклических, или метилкетонов. И эта реакция так и идёт, поэтому для таких соединений идёт именно 1,2-присоединение, оно быстрее. Обычны способ сделать такую реакцию – цианид натрия или калия в присутствии хлорида аммония или уксусной кислоты, которые действуют как слабая кислота, протонирующая аддукт в циангидрин, и выводящая его из равновесия. В этом случае мы имеем типичный случай кинетического контроля – результат определяется более быстрой реакцией, не достигающей равновесия.
Если у енона группа покрупнее, то 1,2-присоединения мы не ожидаем, как не ожидали бы его для похожего по структуре кетона без двойной связи. В том случае мы вообще бы ничего не получили, но в этом мы имеем альтернативный реакционный центр. Мы получим 1,4-присоединение. Например:
В промежуточных случаях, когда ненасыщенный кетон не самый маленький и реакционноспособный, но и не такой большой, что 1,2-присоединение просто не идёт, мы получим смесь 1,2 – и 1,4-продуктов, и это нехорошо. Это происходит потому, что скорости 1,2-присоединения и 1,4-присоединения становятся похожи, кинетический контроль перестаёт работать, но 1,2-аддукт успевает частично выходить из равновесия – то есть и термодинамический контроль перестаёт работать. Для таких кетонов мы вообще не имеем шансов сделать 1,2-присоединение основным, и про это нужно забыть. Но вот 1,4-присоединение сделать основным можно попробовать – для этого нужно просто добиться термодинамического контроля. Почему бы просто не взять цианид-ион в остутствие слабой кислоты? Нет, это плохая идея – в этом случае в растворе начнёт накапливаться свободный енолят, который начнёт вступать во всякие побочные реакции, например, присоединяться к ещё непрореагировашему енону. Нужно как-то промылиться – это вообще в органической химии обычная ситуация: слишком реакционноспособно – плохо, много побочных; менее реакционноспособно – тоже плохо, не дождёшься пока прореагирует. Нужно как-то искусно протиснуться между крайностями – чтобы и равновесие было, и енолят образующийся как-то немного притушить, чтобы не безобразничал. Остроумный способ этого добиться придумали японские исследователи Нагата с сотрудниками. Они долго копались в условиях присоединения цианида и нашли, что на направление этой реакции сильно влияют соединения алюминия, действующие как кислоты Льюиса, координирующиеся по атому кислорода. Через несколько промежуточных вариантов они нашли очень удачный реагент, хотя выглядит он не очень очевидно. Диэтилалюминийцианид Et2AlCN смелые люди получили действием эквивалента HCN на триэтилалюминий: первый убивает с одного вздоха, второй горит на воздухе. Риск оправдался – этот реагент стал основным для 1,4-присоединения HCN к енонам, и до сих пор удерживает это положение (одномолярный раствор в толуоле можно просто купить) – ничего приятнее и эффективнее найти не удалось.
Нужно как-то промылиться – это вообще в органической химии обычная ситуация: слишком реакционноспособно – плохо, много побочных; менее реакционноспособно – тоже плохо, не дождёшься пока прореагирует. Нужно как-то искусно протиснуться между крайностями – чтобы и равновесие было, и енолят образующийся как-то немного притушить, чтобы не безобразничал. Остроумный способ этого добиться придумали японские исследователи Нагата с сотрудниками. Они долго копались в условиях присоединения цианида и нашли, что на направление этой реакции сильно влияют соединения алюминия, действующие как кислоты Льюиса, координирующиеся по атому кислорода. Через несколько промежуточных вариантов они нашли очень удачный реагент, хотя выглядит он не очень очевидно. Диэтилалюминийцианид Et2AlCN смелые люди получили действием эквивалента HCN на триэтилалюминий: первый убивает с одного вздоха, второй горит на воздухе. Риск оправдался – этот реагент стал основным для 1,4-присоединения HCN к енонам, и до сих пор удерживает это положение (одномолярный раствор в толуоле можно просто купить) – ничего приятнее и эффективнее найти не удалось.
Зачем же такое опасное производное алюминия? Почему не взять очень похожее и весьма популярное производное кремния Me3SiCN, которое и делается намного проще и безопаснее, и продаётся в чистом виде, а не в растворе? Тем более что кремний и алюминий – соседи в Периодической таблице. Соседи-то соседи, но алюминий всё же настоящий металл, и его связи с неметаллами существенно более ионные и поэтому лабильные по сравнению с чисто ковалентными и весьма прочными связями кремния. В этом случае это приводит к тому, что быстро образующийся первоначально 1,2-аддукт не выводится из равновесия, а остаётся в равновесии, и понемногу переходит в 1,4-аддукт, который как обычно стабильнее и поэтому накапливается в реакционной смеси. Когда равновесие установится, можно гасить реакцию водой и получать конечный продукт 1,4-присоединения HCN.
Этот реагент чисто и надёжно присоединяется к самым разным сопряжённым ненасыщенным кетонам (енонам), и маленьким и большим. Но с альдегидами (еналями) получается только 1,2-присоединение – у альдегидов таково положение равновесия и ничего с этим поделать нельзя. Можно ли к еналям присоединить HCN по 1,4-пути? Можно, но настолько это непросто сделать, что мы, пожалуй оставим эту задачу нерешённой. Как-нибудь обойдёмся.
Можно ли к еналям присоединить HCN по 1,4-пути? Можно, но настолько это непросто сделать, что мы, пожалуй оставим эту задачу нерешённой. Как-нибудь обойдёмся.
А уже упомянутый Me3SiCN, как уже и так, наверное, ясно, останавливается на 1,2-присоединении потому что связь O-Si намного прочнее и так просто не разрывается, и даже наоборот – хорошо известны реакции, в которых кремний переезжает с углерода на кислород. С енонами и еналями триметилсилилцианид реагирует чистенько и аккуратненько как 1,2-присоединение. И мы можем использовать аддукт дальше, как это написано на вкладке про направленную бензоиновую конденсацию – например, чтобы сделать эту реакцию и получить такие уже очень непростые аналоги бензоина.
Образование ацеталей не только очень полезно, как способ защиты карбонила, но и очень ярко показывает, как на самом деле работает выбор между 1,2 и 1,4-путями присоединения, и что всякие ЖМКО имеют к этому отношения не больше, чем к мировой революции.
Во-первых, простые ацетали мы получать не будем никогда. Обычный простой способ это сделать у обычных альдегидов и простых кетонов (напоминаю, что ацетали с простыми спиртами образуют только альдегиды и маленькие кетоны – кетоны, строго говоря, образуют кетали, но кетали часто тоже называют ацеталями; кетоны с более крупными группами, даже первичными алкилами в обычных условиях ацеталей не образуют) – нагревание с избытком спирта и кислотным катализатором. Если применить этот способ к еналю или маленькому енону, мы не получим то, что хотим, потому что у нас избыток спирта и условия равновесия, в которых мы не сможем остановиться, пока не прореагирует всё, что может прореагировать. Обычным образом сначала образуется 1,2-полуацеталь, он обратимо перейдёт в 1,4-ацеталь, который начнёт в смеси накапливаться, но имея живой карбонил, присоединит спирт и к нему. Кислотно-катализируемое превращение полуацеталя в ацеталь зафиксирует в основном именно это промежуточное соединение, в результате получится продукт присоединения нуклеофила по обоим направлениям 1,2 и 1,4, полный ацеталь продукта 1,4-присоединения.
Обычный простой способ это сделать у обычных альдегидов и простых кетонов (напоминаю, что ацетали с простыми спиртами образуют только альдегиды и маленькие кетоны – кетоны, строго говоря, образуют кетали, но кетали часто тоже называют ацеталями; кетоны с более крупными группами, даже первичными алкилами в обычных условиях ацеталей не образуют) – нагревание с избытком спирта и кислотным катализатором. Если применить этот способ к еналю или маленькому енону, мы не получим то, что хотим, потому что у нас избыток спирта и условия равновесия, в которых мы не сможем остановиться, пока не прореагирует всё, что может прореагировать. Обычным образом сначала образуется 1,2-полуацеталь, он обратимо перейдёт в 1,4-ацеталь, который начнёт в смеси накапливаться, но имея живой карбонил, присоединит спирт и к нему. Кислотно-катализируемое превращение полуацеталя в ацеталь зафиксирует в основном именно это промежуточное соединение, в результате получится продукт присоединения нуклеофила по обоим направлениям 1,2 и 1,4, полный ацеталь продукта 1,4-присоединения.
Гораздо лучше получается с циклическими ацеталями, и это хорошо, потому что от хорошей защиты карбонильной группы кто же откажется. В этом случае помогает легкость образования цикла (хелатный эффект). Быстрое образование полуацеталя с высокой вероятностью приводит к образованию циклического ацеталя, которое успешно конкурирует с обратной реакцией и обратимого превращения 1,2-аддукта в 1,4-аддукт. Тем более, что у 1,4-аддукта нет возможностей превратиться во что-нибудь циклическое, и при обратимости этого направления мы на этом продукте не останавливаемся и уходим в сторону необратимой в этих условиях реакции. Полный ацеталь, естественно, выходит их равновесия и реакция на этом заканчивается. Это очень удобно, потому что непредельные альдегиды сажают ацетальную защиту вообще без проблем в тех же условиях, что и любые другие альдегиды. С кетонами, как обычно, всё не так гладко, но мы можем считать, что маленькие еноны также неплохо защищаются ацеталем с этиленгликолем.
Образование циклических ацеталей позволяет защищать альдегидную групу, например, в продуктах кротоновой конденсации, или кетонную группу, например, в циклических енонах.
Правда, я не уверен, что такая защита нам понадобится.
Ещё более интересно, что можео истользовать и тиоацетальную защиту. Это может шокировать поклонников ЖМКО, птому что уж сернистые соединения точно мягкие, здесь двух мнений быть не должно. Но по той же причине, как и обычные ацетали, и тиоацетали тоже легко получаются, то есть реакция идёт по 1,2-пути. Необратимость образования циклического ацеталя выводит его из равновесного процесса взаимопревращения 1,2- и 1,4-аддуктов.
И это действительно полезно, потому что открывает возможность использовать дитиановый синтез для превращения в ненасыщенные кетоны ненасыщенных альдегидов, например, тех же продуктов кротоновой конденсации. Что-то типа такого:
В этом примере сборки кетона с двумя двойными связями, одной сопряженной, второй несопряжённой, мы использовали самоконденсацию простого альдегида, превращение кротонового продукта в дитиан,и замещение бывшего альдегидного протона на аллил. По такой схеме с некоторыми вариациями синтезировано довольно много интересных молекул.
Енамины очень легко реагируют с акцепторными олефинами, то есть с двойной связью, сопряжённой с -M-заместителем. После обычного гидролиза подкисленной водой получаются продукты сопряжённого присоединения к таким двойным связям.
В этой реакции мезомерный акцептор Z – обычный набор групп: карбоксил, сложный эфир (алкоксикарбонил), амид, нитрил (циан) и т.п. Всё это нам понадобится, когда дойдём до карбоновых кислот. Но мезомерные акцепторы это ещё и альдегидная и кетонная карбонильная группа. Такие реакции легко записать. Как видим, после обычного гидролиза получаем продукт с двумя карбонилами на расстоянии в 3 углеродных атома (1,5-дикетон или кетоальдегид, и теоретически даже и диальдегид, ведь енамины у альдегидов вполне бывают и мы ими пользуемся без всякого стеснения).
Дальше читают только те, кто не боится трудностей и хочет иметь более реалистическую картину. Все остальные спокойно пользуются этой реакцией, если в задачах видят необходимость получать такие дикарбонильные соединения, и не засоряют мозги всякой малосущественной фигнёй, которой в органической химии воз и десяток больших тележек в прицепе. Ошибки в этом нет, так как в изучении химии важны принципы, а не детали, а с принципиальной точки зрения всё верно – такая реакция должна идти.
Ошибки в этом нет, так как в изучении химии важны принципы, а не детали, а с принципиальной точки зрения всё верно – такая реакция должна идти.
В реальности эта реакция не даёт таких продуктов, что установил ещё сам Сторк в своей основополагающей работе, с которой и пошла вся химия енаминов. Вместо ожидаемого 1,5-дикарбонильного соединения обычно получается продукт аннелирования по Робинсону, или более сложные межмолекулярные альдоли, ну а точнее, смесь всего этого. Попробуем разобраться, в чём проблема.
Источник проблем очевиден. Аддукт енамина и енона образуется быстро, но вынужден жить в реакционной смеси и ждать, пока добрые люди погасят его водой. Но ждать ему очень тяжело. Это очередной пример молекулы, в которой содержатся группы противоположной реакционной способности – электрофильная иминиевая группа и нуклеофильный енолят. И это весьма реакционноспособные группы, если только не прикрыты хорошенько стерикой. Но это маловероятно, потому что в таком случае не пошла бы основная реакция. Поэтому эти два центра хотят и будут реагировать. И никто им не мешает делать это межмолекулярно. А почему не внутримолекулярно? Потому что тогда получился бы 4-членный цикл, а это очень невыгодно. Так дело не пойдёт.
Поэтому эти два центра хотят и будут реагировать. И никто им не мешает делать это межмолекулярно. А почему не внутримолекулярно? Потому что тогда получился бы 4-членный цикл, а это очень невыгодно. Так дело не пойдёт.
Поэтому вместо циклизации такой промежуточный продукт будет реагировать сам с собой, или с ещё непрореагировавшими енамином и еноном по своим нуклеофильным и электрофильным центрам. Получится мерзкая каша. Даже не буду это рисовать – сами попробуйте, если делать нечего.
Но если у исходного енона вторая группа (R” на схеме) на карбониле тоже енолизуемая, а так очень часто бывает, то пойдёт гораздо более чистая и полезная реакция. Дело в том, что в реальных реакционных смесях очень трудно совсем избежать примесей кислотно-основного характера, которые умеют переносить протон. И тогда енолят равновесно превратится в другой енолят. Повторю в энный раз – хотя равновесие нарисовано прямо как один енолят в другой, любые такие превращения не происходят сами собой, а требуют посредника – кислоты/основания Бренстеда-Лоури, которая забирает протон и отдаёт протон. Мы это так хорошо знаем, что уже не должны рисовать это каждый раз. Это, что называется, ежу понятно. Если мы нарисовали некоторое равновесие, которое выглядит как равновесие переноса протона (вот в этом случает протон перенёсся с одного енолизуемого положения на другое), но в схемен есть только основания (как здесь), или только кислоты, значаит, это не полное равновесие, а посредничество других равновесий с кислотами или основаниями (переносчиками протона) подразумевается.
Мы это так хорошо знаем, что уже не должны рисовать это каждый раз. Это, что называется, ежу понятно. Если мы нарисовали некоторое равновесие, которое выглядит как равновесие переноса протона (вот в этом случает протон перенёсся с одного енолизуемого положения на другое), но в схемен есть только основания (как здесь), или только кислоты, значаит, это не полное равновесие, а посредничество других равновесий с кислотами или основаниями (переносчиками протона) подразумевается.
И у этого второго енолята расстояние между электрофилом и нуклеофилом – аккурат 6 атомов, как мы любим. Идеальные условия для циклизации. Вот она. Новую связь покажем синим. Продукт – такой аминокетон, кажестя вполне нормальным конечным продуктом. Но нет. Если мы его рассмотрим получше, то обнаружим, что это продукт 1,4-присоединения вторичного амина к сопряжённому енону. А эта реакция, как мы знаем, как и почти все реакции 1,4-присоединения, обратима. И равновесие это смещено в сторону енона. Вот мы его и напишем. Это циклогексенон. Это ровно тот же результат, который получается в циклизации по Робинсону, которой мы займёмся во втором семестре, как и всеми остальными реакциями циклизации.
Это циклогексенон. Это ровно тот же результат, который получается в циклизации по Робинсону, которой мы займёмся во втором семестре, как и всеми остальными реакциями циклизации.
Получается так, что реакция енамина и енона это альтернативный способ выполнения циклизации Робинсона. Выходы никогда не бывают высокими, как минимум потому что реакция имеет довольно случайный характер – вы, наверное, заметили, что изомеризация енолята осуществляется за счёт каких-то случайных примесей, а для межмолекулярных реакций это не нужно, поэтому в каком-то смысле, здесь основной реакцией является образование каких-то ненужных продуктов конденсации, а циклизация является побочной реакцией. Но, это часто работает и это очень просто. Реакцию делают очень просто, без добавления каких-либо других реагентов, просто нагревают смесь в растворе. Потом добавляют воду, иногда с бобавлением буферных солей, например, ацетата натрия. Вот пример (J.Org.Chem., 1972, 37, 659):
Задачи на синтез активируют разобранные в разделе методы. Для решения задач используйте указанные в условиях вещества для построения скелета, и любые другие реагенты для осуществления необходимых реакций. В каждом блоке может быть несколько задач. Название блока – подсказка на основные методы, которые стоит использовать. Список пополняется, поэтому время от времени заходите и обновляйте.
Для решения задач используйте указанные в условиях вещества для построения скелета, и любые другие реагенты для осуществления необходимых реакций. В каждом блоке может быть несколько задач. Название блока – подсказка на основные методы, которые стоит использовать. Список пополняется, поэтому время от времени заходите и обновляйте.
Дитиановый синтез, реакция Виттига
- Из 1,3-дитиана, бензилхлорида, трифенилфосфина получите 1,3-дифенилпропен-1.
- Из н-бутанола, аллилбромида, метилиодида, 1,3-пропандитиола, трифенилфосфина получите 2-н-пропилпента-1,4-диен
Защита карбонила
- Из циклогексанона, окиси этилена получите 2-(2-цианоэтил)циклогексанон. Отработайте и альтернативный способ синтеза, не использующий защиту, и оцените возможность его осуществления (мешают ли друг другу функциональные группы).
Галоформная реакция, альдольная конденсация
- Из фенилуксусного альдегида и ацетона получите 4-фенилбут-2-еновую кислоту
Альдольная конденсация — выбор правильного пути
Получите эти продукты альдольной конденсации из соотвествующих карбонильных соединений, правильно выбрав метод – направленный с использованием кинетического енолята или самопроизвольный с использованием равновесного енолята. Одно из указанных соединений лишнее.
Одно из указанных соединений лишнее.
Алкилирование енаминов, пинакон
- Из ацетона, циклогексанона, морфолина получите следующий дикетон
- Из пентанола-3 и морфолина получите 4,5-диметилоктан-3,6-дион
Еноны, 1.2- и 1,4-присоединение
- Из ацетона и метилиодида получите 4,4-диметилпентан-2-он, 2,4-диметилпентан-2-ол, 5-метилгексан-3-он, динеопентилкетон (2,2,6,6-тетраметилгептан-4-он)
- Из диэтилкетона и бромбензола получите 1-фенилпентан
Енон и енамин
- Из диэтилкетона и морфолина получите 4-метилнонан-3,7-дион
- Из ацетофенона, ацетальдегида, ацетона, пиперидина получите 1-фенил-3-метилгексан-1,5-дион
Альдольная конденсация, реакции Михаэля и Виттига
- Из ацетофенона, бензальдегида, диметиламина получите 3-диметиламино-1,3-дифенилфенилпропанол-1 в виде смеси диастереоизомеров.
- Из масляного альдегида (бутаналя), винилбромида, метилиодида, трифенилфосфина получите 3-пропил-4-этилгексадиен-1,5.

Конденсации с формальдегидом, реакция Манниха
1. Сделали три эксперимента по конденсации ацетальдегида с большим избытком формальдегида в присутствии гидроксида кальция в воде.
- в первой реакции взяли дейтерированный формальдегид CD2O.
- во второй – дейтерированный ацетальдегид CD3CDO.
- в третьей – тяжёлую воду в качестве растворителя
Сколько атомов дейтерия и где будет в пентаэритрите, образовавшемся в каждой из этих реакций. В каждом эксперименте дейтерий в начале реакции только там, где сказано. Будьте внимательны – это не так просто, как может показаться на первый взгляд. Вам придётсся написать механизм превращения и аккуратно проследить за всеми участниками процесса.
примеры решений и теория. Сложение и умножение вероятностей
Тип задания: 4
Условие
Вероятность того, что аккумулятор не заряжен, равна 0,15.
Покупатель в магазине приобретает случайную упаковку, которая содержит два таких аккумулятора. Найдите вероятность того, что оба аккумулятора в этой упаковке окажутся заряжены.
Найдите вероятность того, что оба аккумулятора в этой упаковке окажутся заряжены.
Показать решение
Решение
Вероятность того, что аккумулятор заряжён, равна 1-0,15 = 0,85. Найдём вероятность события «оба аккумулятора заряжены». Обозначим через A и B события «первый аккумулятор заряжён» и «второй аккумулятор заряжён». Получили P(A) = P(B) = 0,85. Событие «оба аккумулятора заряжены» — это пересечение событий A \cap B, его вероятность равна P(A \cap B) = P(A)\cdot P(B) = 0,85\cdot 0,85 = 0,7225.
Ответ
Тип задания: 4
Тема:
Сложение и умножение вероятностей событий
Условие
Вероятность того, что ручка бракованная, равна 0,05 . Покупатель в магазине приобретает случайную упаковку, которая содержит две ручки. Найдите вероятность того, что обе ручки в этой упаковке окажутся исправными.
Показать решение
Решение
Вероятность того, что ручка исправная, равна 1-0,05 = 0,95. Найдём вероятность события «обе ручки исправны». Обозначим через A
и B
события «первая ручка исправна» и «вторая ручка исправна». Получили P(A) = P(B) = 0,95.
Событие «обе ручки исправны» — это пересечение событий A\cap B,
его вероятность равна P(A\cap B) =
P(A)\cdot P(B) =
0,95\cdot 0,95 =
0,9025.
Найдём вероятность события «обе ручки исправны». Обозначим через A
и B
события «первая ручка исправна» и «вторая ручка исправна». Получили P(A) = P(B) = 0,95.
Событие «обе ручки исправны» — это пересечение событий A\cap B,
его вероятность равна P(A\cap B) =
P(A)\cdot P(B) =
0,95\cdot 0,95 =
0,9025.
Ответ
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Тип задания: 4
Тема:
Сложение и умножение вероятностей событий
Условие
На рисунке изображён лабиринт. Жук заползает в лабиринт в точке «Вход». Развернуться и ползти в обратном направлении жук не может, поэтому на каждой развилке он выбирает один из путей, в котором еще не был. С какой вероятностью жук придет к выходу Д, если выбор дальнейшего пути является случайным.
Показать решение
Решение
Расставим на перекрёстках стрелки в направлениях, по которым может двигаться жук (см. 4=
0,0625.
4=
0,0625.
Ответ
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Тип задания: 4
Тема:
Сложение и умножение вероятностей событий
Условие
Стоянка освещается фонарём с двумя лампами. Вероятность перегорания одной лампы в течение года равна 0,4. Найдите вероятность того, что за год хотя бы одна лампа не перегорит.
Показать решение
Решение
Сначала найдём вероятность события «обе лампы перегорели в течение года», противоположного событию из условия задачи. Обозначим через A и B события «первая лампа перегорела в течение года» и «вторая лампа перегорела в течение года». По условию P(A) = P(B) = 0,4. Событие «обе лампы перегорели в течение года» — это A \cap B, его вероятность равна P(A \cap B) = P(A) \cdot P(B) = 0,4 \cdot 0,4 = 0,16 (так как события A и B независимы).
Искомая вероятность равна 1 — P(A \cap B) =
1 — 0,16 =
0,84.
Ответ
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Тип задания: 4
Тема:
Сложение и умножение вероятностей событий
Условие
В гостинице стоят два кулера. Каждый из них может быть неисправен с вероятностью 0,2 независимо от другого кулера. Определите вероятность того, что хотя бы один из этих кулеров исправен.
Показать решение
Решение
Сначала найдём вероятность события «оба кулера неисправны», противоположного событию из условия задачи. Обозначим через A и B события «первый кулер неисправен» и «второй кулер неисправен». По условию P(A) = P(B) = 0,2. Событие «оба кулера неисправны» — это A \cap B , пересечение событий A и B , его вероятность равна P(A \cap B) = P(A)\cdot P(B) = 0,2\cdot 0,2 = 0,04 (так как события A и B независимы). Искомая вероятность равна 1-P(A \cap B)=1-0,04=0,96.
Ответ
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Тип задания: 4
Тема:
Сложение и умножение вероятностей событий
Условие
На экзамене по физике студент отвечает на один вопрос из списка экзаменационных вопросов. Вероятность того, что этот вопрос на тему «Механика», равна 0,25 . Вероятность того, что этот вопрос на тему «Электричество», равна 0,3 . Вопросов, которые относились бы сразу к двум темам, нет. Найдите вероятность того, что студенту попадётся вопрос по одной из этих двух тем.
Учреждение образования «Белорусская государственная
сельскохозяйственная академия»
Кафедра высшей математики
СЛОЖЕНИЕ И УМНОЖЕНИЕ ВЕРОЯТНОСТЕЙ. ПОВТОРНЫЕ НЕЗАВИСИМЫЕ ИСПЫТАНИЯ
Лекция для студентов землеустроительного факультета
заочной формы обучения
Горки, 2012
Сложение и умножение вероятностей. Повторные
независимые испытания
Сложение вероятностей
Суммой
двух совместных событий А и В называется событие С ,
состоящее в наступлении хотя бы одного
из событий А или В . Аналогично суммой нескольких совместных
событий называется событие, состоящее
в наступлении хотя бы одного из этих
событий.
Аналогично суммой нескольких совместных
событий называется событие, состоящее
в наступлении хотя бы одного из этих
событий.
Суммой двух несовместных событий А и В называется событие С , состоящее в наступлении или события А , или события В . Аналогично суммой нескольких несовместных событий называется событие, состоящее в наступлении какого-либо одного из этих событий.
Справедлива теорема сложения вероятностей несовместных событий: вероятность суммы двух несовместных событий равна сумме вероятностей этих событий , т.е. . Эту теорему можно распространить на любое конечное число несовместных событий.
Из данной теоремы следует:
сумма вероятностей событий, образующих полную группу, равна единице;
сумма
вероятностей противоположных событий
равна единице, т.е.
.
Пример 1 . В ящике находятся 2 белых, 3 красных и 5 синих шара. Шары перемешивают и наугад извлекают один. Какова вероятность того, что шар окажется цветным?
Решение . Обозначим события:
Обозначим события:
A ={извлечён цветной шар};
B ={извлечён белый шар};
C ={извлечён красный шар};
D ={извлечён синий шар}.
Тогда A = C + D . Так как события C , D несовместны, то воспользуемся теоремой сложения вероятностей несовместных событий: .
Пример 2 . В урне находятся 4 белых шара и 6 – чёрных. Из урны наугад вынимают 3 шара. Какова вероятность того, что все они одного цвета?
Решение . Обозначим события:
A ={вынуты шары одного цвета};
B ={вынуты шары белого цвета};
C ={вынуты шары чёрного цвета}.
Так
как A = B + C и события В и С несовместны, то по теореме сложения
вероятностей несовместных событий
.
Вероятность событияВ равна
,
где
4,
.
Подставим k и n в формулу и получим
Аналогично
найдём вероятность событияС :
,
где
,
,
т. е.
е.
.
Тогда
.
Пример 3 . Из колоды в 36 карт наугад вынимают 4 карты. Найти вероятность того, что среди них окажется не менее трёх тузов.
Решение . Обозначим события:
A ={среди вынутых карт не менее трёх тузов};
B ={среди вынутых карт три туза};
C ={среди вынутых карт четыре туза}.
Так
как A = B + C ,
а события В и С несовместны, то
.
Найдём вероятности событийВ и С :
,
.
Следовательно, вероятность того, что
среди вынутых карт не менее трёх тузов,
равна
0.0022.
Умножение вероятностей
Произведением двух событий А и В называется событие С ,
состоящее в совместном наступлении
этих событий:
.
Это определение распространяется на
любое конечное число событий.
Два
события называются независимыми ,
если вероятность наступления одного
из них не зависит от того, произошло
другое событие или нет. События
,,
… ,называютсянезависимыми
в совокупности ,
если вероятность наступления каждого
из них не зависит от того, произошли или
не произошли другие события.
События
,,
… ,называютсянезависимыми
в совокупности ,
если вероятность наступления каждого
из них не зависит от того, произошли или
не произошли другие события.
Пример 4 . Два стрелка стреляют по цели. Обозначим события:
A ={первый стрелок попал в цель};
B ={второй стрелок попал в цель}.
Очевидно, что вероятность попадания в цель первым стрелком не зависит от того, попал или не попал второй стрелок, и наоборот. Следовательно, события А и В независимы.
Справедлива теорема умножения вероятностей независимых событий: вероятность произведения двух независимых событий равна произведению вероятностей этих событий : .
Эта теорема справедлива и для n независимых в совокупности событий: .
Пример
5 .
Два стрелка стреляют по одной цели.
Вероятность попадания первого стрелка
равна 0.9, а второго – 0.7. Оба стрелка
одновременно делают по одному выстрелу.
Определить вероятность того, что будут
иметь место два попадания в цель.
Решение . Обозначим события:
A
B
C ={оба стрелка попадут в цель}.
Так
как
,
а событияА и В независимы, то
,
т.е..
События А и В называются зависимыми ,
если вероятность наступления одного
из них зависит от того, произошло другое
событие или нет. Вероятность наступления
события А при условии, что событие В уже наступило, называется условной
вероятностью и обозначается
или
.
Пример 6 . В урне находятся 4 белых и 7 чёрных шаров. Из урны извлекаются шары. Обозначим события:
A ={извлечён белый шар} ;
B ={извлечён чёрный шар}.
Перед
началом извлечения шаров из урны
.
Из урны извлекли один шар и он оказался
чёрным. Тогда вероятность событияА после наступления события В будет уже другой, равной
.
Это означает, что вероятность событияА зависит от события В ,
т. е. эти события будут зависимыми.
е. эти события будут зависимыми.
Справедлива теорема умножения вероятностей зависимых событий: вероятность произведения двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило , т.е. или.
Пример 7 . В урне находятся 4 белых шара и 8 красных. Из неё наугад последовательно извлекают два шара. Найти вероятность того, что оба шара будут чёрными.
Решение . Обозначим события:
A ={первым извлечён чёрный шар};
B ={вторым извлечён чёрный шар}.
События А и В зависимы, так как
,
а
.
Тогда
.
Пример
8 .
Три стрелка стреляют по цели независимо
друг от друга. Вероятность попадания в
цель для первого стрелка равна 0.5, для
второго – 0.6 и для третьего – 0.8. Найти
вероятность того, что произойдут два
попадания в цель, если каждый стрелок
сделает по одному выстрелу.
Решение . Обозначим события:
A ={произойдут два попадания в цель};
B ={первый стрелок попадёт в цель};
C ={второй стрелок попадёт в цель};
D ={третий стрелок попадёт в цель};
={первый стрелок не попадёт в цель};
={второй стрелок не попадёт в цель};
={третий стрелок не попадёт в цель}.
По
условию примера
,
,
,
,
,
.
Так как,
то используя теорему сложения вероятностей
несовместных событий и теорему умножения
вероятностей независимых событий,
получим:
Пусть
события
образуют полную группу событий некоторого
испытания, а событииА может наступить только с одним из этих
событий. Если известны вероятности
и условные вероятностисобытияА ,
то вероятность события А вычисляется
по формуле:
или
.
Эта формула называетсяформулой
полной вероятности ,
а события
гипотезами .
Пример
9 .
На сборочный конвейер поступает 700
деталей с первого станка и 300 деталей
со второго. Первый станок даёт 0.5% брака,
а второй – 0.7%. Найти вероятность того,
что взятая деталь будет бракованной.
Первый станок даёт 0.5% брака,
а второй – 0.7%. Найти вероятность того,
что взятая деталь будет бракованной.
Решение . Обозначим события:
A ={взятая деталь будет бракованной};
={деталь изготовлена на первом станке};
={деталь изготовлена на втором станке}.
Вероятность
того, что деталь изготовлена на первом
станке, равна
.
Для второго станка
.
По условию вероятность получения
бракованной детали, изготовленной на
первом станке, равна
.
Для второго станка эта вероятность
равна
.
Тогда вероятность того, что взятая
деталь будет бракованной, вычисляется
по формуле полной вероятности
Если
известно, что в результате испытания
наступило некоторое событие А ,
то вероятность того, что это событие
наступило с гипотезой
,
равна
,
где
—
полная вероятность событияА .
Эта формула называется формулой
Байеса и позволяет вычислять вероятности
событий
после того, как стало известно, что
событиеА уже наступило.
Пример 10 . Однотипные детали к автомобилям производятся на двух заводах и поступают в магазин. Первый завод производит 80% общего количества деталей, а второй – 20%. Продукция первого завода содержит 90% стандартных деталей, а второго – 95%. Покупатель купил одну деталь и она оказалась стандартной. Найти вероятность того, что эта деталь изготовлена на втором заводе.
Решение . Обозначим события:
A ={куплена стандартная деталь};
={деталь изготовлена на первом заводе};
={деталь изготовлена на втором заводе}.
По
условию примера
,
,
и
.
Вычислим полную вероятность событияА :
0.91.
Вероятность того, что деталь изготовлена
на втором заводе, вычислим по формуле
Байеса:
.
Задания для самостоятельной работы
Вероятность
попадания в цель для первого стрелка
равна 0.8, для второго – 0.7 и для третьего
– 0.9. Стрелки произвели по одному
выстрелу. Найти вероятность того, что
имеет место не менее двух попаданий в
цель.
В ремонтную мастерскую поступило 15 тракторов. Известно, что 6 из них нуждаются в замене двигателя, а остальные – в замене отдельных узлов. Случайным образом отбираются три трактора. Найти вероятность того, что замена двигателя необходима не более, чем двум отобранным тракторам.
На железобетонном заводе изготавливают панели, 80% из которых – высшего качества. Найти вероятность того, что из трёх наугад выбранных панелей не менее двух будут высшего сорта.
Три рабочих собирают подшипники. Вероятность того, что подшипник, собранный первым рабочим, высшего качества, равна 0.7, вторым – 0.8 и третьим – 0.6. Для контроля наугад взято по одному подшипнику из собранных каждым рабочим. Найти вероятность того, что не менее двух из них будут высшего качества.
Вероятность
выигрыша по лотерейному билету первого
выпуска равна 0.2, второго – 0.3 и третьего
– 0.25. Имеются по одному билету каждого
выпуска. Найти вероятность того, что
выиграет не менее двух билетов.
Бухгалтер выполняет расчёты, пользуясь тремя справочниками. Вероятность того, что интересующие его данные находятся в первом справочнике, равна 0.6, во втором – 0.7 ив третьем – 0.8. Найти вероятность того, что интересующие бухгалтера данные содержатся не более, чем в двух справочниках.
Три автомата изготавливают детали. Первый автомат изготавливает деталь высшего качества с вероятностью 0.9, второй – с вероятностью 0.7 и третий – с вероятностью 0.6. Наугад берут по одной детали с каждого автомата. Найти вероятность того, что среди них не менее двух высшего качества.
На двух станках обрабатываются однотипные детали. Вероятность изготовления нестандартной детали для первого станка равна 0.03, в для второго – 0.02. Обработанные детали складываются в одном месте. Среди них 67% с первого станка, а остальные – со второго. Наугад взятая деталь оказалась стандартной. Найти вероятность того, что она изготовлена на первом станке.
В
мастерскую поступили две коробки
однотипных конденсаторов. В первой
коробке было 20 конденсаторов, из которых
2 неисправных. Во второй коробки 10
конденсаторов, из которых 3 неисправных.
Конденсаторы были переложены в один
ящик. Найти вероятность того, что наугад
взятый из ящика конденсатор окажется
исправным.
В первой
коробке было 20 конденсаторов, из которых
2 неисправных. Во второй коробки 10
конденсаторов, из которых 3 неисправных.
Конденсаторы были переложены в один
ящик. Найти вероятность того, что наугад
взятый из ящика конденсатор окажется
исправным.
На трёх станках изготавливают однотипные детали, которые поступают на общий конвейер. Среди всех деталей 20% с первого автомата, 30% — со второго и 505 – с третьего. Вероятность изготовления стандартной детали на первом станке равна 0.8, на втором – 0.6 и на третьем – 0.7. Взятая деталь оказалась стандартной. Найти вероятность того, эта деталь изготовлена на третьем станке.
Комплектовщик
получает для сборки 40% деталей с завода А ,
а остальные – с завода В .
Вероятность того, что деталь с завода А – высшего качества, равна 0.8, а с завода В – 0.9. Комплектовщик наугад взял одну
деталь и она оказалась не высшего
качества. Найти вероятность того, что
эта деталь с завода В .
Для участия в студенческих спортивных соревнованиях выделено 10 студентов из первой группы и 8 – из второй. Вероятность того, что студент из первой группы попадёт в сборную академии, равна 0.8, а со второй – 0.7. Наугад выбранный студент попал в сборную. Найти вероятность того, что он из первой группы.
Формула Бернулли
Испытания
называются независимыми ,
если при каждом из них событие А наступает с одной и той же вероятностью
,
не зависящей от того, появилось или не
появилось это событие в других испытаниях.
Вероятность противоположного событияв этом случае равна
.
Пример
11 .
Бросается игральный кубик n раз. Обозначим событие A ={выпадение
трёх очков}. Вероятность наступления
события А в каждом испытании равна
и не зависит от того, произошло или не
произошло это событие в других испытаниях.
Поэтому эти испытания являются
независимыми. Вероятность противоположного
события
{не
выпадение трёх очков} равна
.
Вероятность
того, что в n независимых испытаниях, в каждом из
которых вероятность наступления события А равна p ,
событие наступит ровно k раз (безразлично в какой последовательности),
вычисляется по формуле
,
где
.
Эта формула называетсяформулой
Бернулли и удобна она в том случае, если число
испытаний n
не слишком велико.
Пример 12 . Доля плодов, заражённых болезнью в скрытой форме, составляет 25%. Случайным образом отбирается 6 плодов. Найти вероятность того, что среди выбранных окажется: а) ровно 3 заражённых плода; б) не более двух заражённых плодов.
Решение . По условию примера .
а) По формуле Бернулли вероятность того, что среди шести отобранных плодов заражёнными окажутся ровно три, равна
0.132.
б) Обозначим событие A ={заражённых будет не более двух плодов}. Тогда . По формуле Бернулли:
0.297.
Следовательно,
0.178+0. 356+0.297=0.831.
356+0.297=0.831.
Теоремы Лапласа и Пуассона
По формуле Бернулли находится вероятность того, что событие А наступит k раз в n независимых испытаниях и в каждом испытании вероятность события А постоянна. При больших значениях n вычисления по формуле Бернулли становятся трудоёмкими. В этом случае для вычисления вероятности события А целесообразнее использовать другую формулу.
Локальная теорема Лапласа . Пусть вероятность p наступления события А в каждом испытании постоянна и отлична от нуля и единицы. Тогда вероятность того, что событие А наступит ровно k раз при достаточно большом числе n испытаний, вычисляется по формуле
,
где
,
а значения функции
приведены
в таблице.
Основными
свойствами функции
являются:
Функция
определена и непрерывна в интервале
.
Функция
положительна, т.е.
>0.
Функция
чётная, т. е.
е.
.
Так
как функция
чётная, то в таблице приведены её значения
только для положительных значенийх .
Пример 13 . Всхожесть семян пшеницы составляет 80%. Для опыта отбирается 100 семян. Найти вероятность того, что из отобранных семян взойдут ровно 90.
Решение .
По условию примера n =100, k =90, p =0.8, q =1-0.8=0.2.
Тогда
.
По таблице найдём значение функции
:
.
Вероятность того, что из отобранных
семян взойдут ровно 90, равна
0.0044.
При решении практических задач возникает необходимость найти вероятность наступления события А при n независимых испытаниях не менее раз и не болеераз. Такая задача решается с помощьюинтегральной теоремы Лапласа : Пусть вероятность p наступления события А в каждом из n независимых испытаний постоянна и отлична от нуля и единицы. Тогда вероятность того, что событие наступит не менее раз и не болеераз при достаточно большом числе испытаний, вычисляется по формуле
Где
,
.
Функция
называетсяфункцией
Лапласа и не выражается через элементарные
функции. Значения этой функции приведены
в специальных таблицах.
Основными
свойствами функции
являются:
.
Функция
возрастает
в интервале
.
при
.
Функция
нечётная,
т.е.
.
Пример 14 . Предприятие выпускает продукцию, из которой 13% не высшего качества. Определить вероятность того, что в непроверенной партии из 150 единиц продукции высшего качества будет не менее 125 и не более 135.
Решение .
Обозначим
.
Вычислим
,
Теорема сложения
Вероятность наступления одного из нескольких несовместных событий равна сумме вероятностей этих событий.
В случае двух несовместных событий А и В имеем:
Р(А+В) = Р(А) + Р(В) (7)
Событие, противоположное событию А обозначают . Объединение событий А и даёт событие достоверное, а поскольку события А и несовместны, то
Р(А) +Р() = 1 (8)
Вероятность события А, вычисленная в предположении, что событие В наступило, называется условной вероятностью события А и обозначается символом Р В (А).
Если события А и В независимые, то Р(В) = Р А (В).
События А, В, С, … называются независимыми в совокупности , если вероятность каждого из них не меняется в связи с наступлением или ненаступлением других событий по отдельности или в любой комбинации их и в любом числе.
Теорема умножения
Вероятность того, что произойдут события и А, и В, и С, … равна произведению их вероятностей, вычисленных в предположении, что все предшествующие каждому из них события имели место, т. е.
Р(АВ) = Р(А)Р А (В) (9)
Запись Р А (В) обозначает вероятность события В в предположении, что событие А уже имело место.
Если события А, В, С, … независимы в совокупности, то вероятность того, что произойдут все они, равна произведению их вероятностей:
Р(АВС) = Р(А)Р(В)Р(С) (10)
Пример 3.1. В мешке лежат шары: 10 белых, 15 чёрных, 20 голубых и 25 красных. Вынули один шар. Найти вероятность того, что вынутый шар окажется белым? чёрным? И ещё: белый или чёрный?
Решение.
Число всех возможных испытаний n = 10 + 15 + 20 + 25 = 70;
Вероятность Р(б) = 10/70 = 1/7, Р(ч) = 15/70 = 3/14.
Применяем теорему сложения вероятностей:
Р(б + ч) = Р(б) + Р(ч) = 1/7 + 3/14 = 5/14.
Примечание: заглавные буквы в скобках соответственно обозначают цвет каждого шара согласно условию задачи.
Пример 3.2 В первом ящике два белых и десять чёрных шаров. Во втором ящике восемь белых и четыре чёрных шара. Из каждого ящика вынули по шару. Определить вероятность того, что оба шара окажутся белыми.
Решение.
Событие А – появление белого шара из первого ящика. Событие В – появление белого шара из второго ящика. События А и В – независимые.
Вероятности Р(А) = 2/12 = 1/6, Р(В) = 8/12 = 2/3.
Применяем теорему умножения вероятностей:
Р(АВ) = Р(А)Р(В) = 2/18 = 1/9.
Вопросы для повторения
1 Что называется факториалом?
2 Перечислите основные задачи комбинаторики.
3 Что называется перестановками?
4 Что называется перемещениями?
5 Что называется сочетаниями?
6 Какие события называются достоверными?
7 Какие события называются несовместными?
8 Что называется вероятностью события?
9 Что называется условной вероятностью?
10 Сформулируйте теоремы сложения и умножения вероятностей.
11 пр .Размещением из п элементов по к (к ≤ п ) называется любое множество, состоящее из к элементов, взятых в определенном порядке из данных п элементов.
Таким образом, два размещения из п элементов по к считаются различными, если они различаются самими элементами или порядком их расположения Число размещений из п элементов по к обозначают А п к и вычисляют по формуле
А п к =
Если размещения из п элементов по п отличаются друг от друга только порядком элементов, то они представляют собой перестановки из п элементов
Пример1 . Учащиеся второго класса изучают 9 предметов. Сколькими способами можно составить расписание на один день, чтобы в нем было 4 различных предмета
Решение: Любое расписание на один день, составленное из 4 различных предметов, отличается от другого либо набором предметов, либо порядком их следования. Значит, в этом примере речь идет о размещениях из 9 элементов по 4. Имеем
Значит, в этом примере речь идет о размещениях из 9 элементов по 4. Имеем
А 9 4 = = 6 ∙ 7 ∙ 8 ∙ 9 = 3024
Расписание можно составить 3024 способами
Пример2. Сколько трехзначных чисел (без повторения цифр в записи числа) можно составить из цифр 0,1,2,3,4,5,6 ?
Решение Если среди семи цифр нет нуля, то число трехзначных чисел (без повторения цифр), которые можно составить из этих цифр, равно числу размещений
22
из 7 элементов по 3. Однако среди данных цифр есть цифра 0, с которой не может начинаться трехзначное число. Поэтом из размещений из 7 элементов по3 надо исключить те, у которых первым элементом является 0. Их число равно числу размещений их 6 элементов по 2. =
Значит искомое число трехзначных чисел равно
А 7 3 — А 6 2 = — = 5 ∙ 6 ∙ 7 — 5 ∙ 6 = 180.
3. Закрепление полученных знаний в процессе решения задач
№754 . Сколькими способами может разместиться семья из трех человек в четырехместном купе, если других пассажиров в купе нет?
Решение. Число способов равно А 4 3 = = 1∙ 2 ∙ 3 ∙ 4 = 24
Число способов равно А 4 3 = = 1∙ 2 ∙ 3 ∙ 4 = 24
№755. Из 30 участников собрания надо выбрать председателя и секретаря. Сколькими способами это можно сделать?
Решение. Т.к.любой из участников может быть как секретарем, так и председателем, то число способов их избрания равно
А 30 2 = = = 29 ∙ 30 = 870
№762 Сколько четырехзначных чисел, в которых нет одинаковых цифр, можно составить из цифр: а) 1,3,5,7,9. б) 0,2,4,6,8?
Решение а) А 5 4 = = 1∙ 2 ∙ 3 ∙ 4 ∙ 5 = 120
б)) А 5 4 — А 4 3 = 5! – 4! = 120 – 24= 96
Домашнее задание № 756, №757, № 758, №759.
6урок Тема: « Сочетания»
Цель: Дать понятие о сочетаниях, познакомить с формулой для вычисления сочетаний, научить применять эту формулу для подсчета числа сочетаний.
1 Проверка домашнего задания.
№ 756 . На станции 7 запасных путей. Сколькими способами можно расставить на них 4 поезда?
23
Решение: А 7 4 = = 4 ∙ 5 ∙ 6 ∙ 7 = 20 ∙ 42 = 840 способов
№757 Сколькими способами тренер может определить, кто из 12 спортсменок, готовых к участию в эстафете 4х100м, побежит на первом, втором, третьем и четвертом этапах?
Решение: А 12 4 = = 9 ∙ 10 ∙ 11 ∙12 = 90 ∙132 = 11 880
№ 758. В круговой диаграмме круг разбит на 5 секторов. Секторы решили закрасить разными красками, взятыми из набора, содержащего 10 красок. Сколькими способами это можно сделать?
В круговой диаграмме круг разбит на 5 секторов. Секторы решили закрасить разными красками, взятыми из набора, содержащего 10 красок. Сколькими способами это можно сделать?
Решение: А 10 5 = = 6 ∙ 7 ∙ 8 ∙ 9∙ 10 = 30 240
№759. Сколькими способами 6 студентов, сдающих экзамен, могут занять места в аудитории, в которой 20 одноместных столов?
Решение: А 20 6 = = 15∙ 16 ∙17∙ 18∙19 ∙20 = 27 907 200
Организовать проверку домашнего задания можно разными способами: устно проверить решение домашних упражнений, решения некоторых из них записать на доске, а пока идет запись решений провести опрос уч-ся по вопросам:
1. Что означает запись п!
2.Что называется перестановкой из п элементов?
3.По какой формуле считают число перестановок?
4. Что называют размещением из п элементов по к?
5. п элементов по к?
2 Объяснение нового материала
Пусть имеются 5 гвоздик разного цвета. Обозначим их буквами а, в, с, д, е. Требуется составить букет из трех гвоздик. Выясним, какие букеты могут быть составлены.
Обозначим их буквами а, в, с, д, е. Требуется составить букет из трех гвоздик. Выясним, какие букеты могут быть составлены.
Если в букет входит гвоздика а , то можно составить такие букеты:
авс, авд, аве, асд, асе, аде.
Если в букет не входит гвоздика а, но входит гвоздика в , то можно получить такие букеты:
всд, все, вде.
Наконец, если в букет не входит ни гвоздика а, ни гвоздика в, то возможен только один вариант составления букета:
сде.
24
Мы указали все возможные способы составления букетов, в которых по – разному сочетаются три гвоздики из 5. Говорят, что мы составили все возможные сочетания из 5 элементов по 3, мы нашли, что С 5 3 = 10.
Выведем формулу числа сочетаний из п элементов по к, где к ≤ п.
Выясним сначала, как С 5 3 выражается через А 5 3 и Р 3 . Мы нашли, что их 5 элементов можно составить следующие сочетания по 3 элемента:
Мы нашли, что их 5 элементов можно составить следующие сочетания по 3 элемента:
авс, авд, аве, асд, асе, аде, всд, все, вде, сде.
В каждом сочетании выполним все перестановки. Число перестановок из 3 элементов равно Р 3 . В результате получим все возможные комбинации из 5 элементов по 3, которые различаится либо самими элементами, либо порядком элементов, т.е. все размещения из 5 элементов по 3. Всего мы получим А 5 3 размещений.
Значит , С 5 3 ∙ Р 3 = А 5 3 , отсюда С 5 3 = А 5 3: Р 3
Рассуждая в общем случае получим С п к = А п к: Р к,
Пользуясь тем, что А п к = , где к ≤ п., получим С п к = .
Это формула для вычисления числа сочетаний из п элементов по к при любом
к ≤ п.
Пример1 . Из набора, состоящего из 15 красок, надо выбрать3 краски для окрашивания шкатулки. Сколькими способами можно сделать этот выбор?
Решение: Каждый выбор трех красок отличается от другого хотя бы одной краской. Значит, здесь речь идет о сочетаниях из 15 элементов по 3
Значит, здесь речь идет о сочетаниях из 15 элементов по 3
С 15 3 = = (13∙ 14∙15) : ( 1∙ 2 ∙ 3) = 455
Приме2 В классе учатся 12 мальчиков и 10 девочек. Для уборки территории около школы требуется выделить трех мальчиков и двух девочек. Сколькими способами можно сделать этот выбор?
Решение: Выбрать 3 мальчиков из 12 можно С 12 3 , а двух девочек из 10 можно выбрать С 10 2 . Т. к. при каждом выборе мальчиков можно С 10 2 способами выбрать девочек, то сделать выбор учащихся, о котором говориться в задаче можно
С 12 3 ∙ С 10 2 = ∙ = 220 ∙ 45 = 9900
3) Закрепление нового материала, в процессе решения задач
25
Задача
У Саши в домашней библиотеке есть 8 исторических романов. Петя хочет взять у него 2 любых романа. Сколькими способами можно сделать этот выбор?
Решение: С 8 2 = = (7 ∙ 8) : ( 1∙ 2) = 56: 2 = 28
№779 а
В шахматном кружке занимаются 16 человек. Сколькими способами тренер может выбрать из них для предстоящего турнира команду из 4 человек?
Сколькими способами тренер может выбрать из них для предстоящего турнира команду из 4 человек?
Решение: С 16 4 = = (13∙ 14∙15 ∙16) : ( 1∙ 2 ∙ 3 ∙ 4) = 13 ∙ 7 ∙5∙ 4 = 91 ∙20 = 1820
№774 Бригада, занимающаяся ремонтом школы, состоит из 12 маляров и 5 плотников. Из них для ремонта спротзала надо выделить 4 маляров и 2 плотников. Сколькими способами можно это сделать?
С 12 4 ∙ С 5 2 = ∙ = 495 ∙ 10 = 4950
Домашняя работа №768, №769, № 770, № 775
7урок Тема: « Решение задач на применение формул для подсчета числа перемещений, размещений, сочетаний»
Цель: Закрепление знаний учащихся. Формирование навыков решения простейших комбинаторных задач
1 Проверка домашнего задания
№768 В классе 7 человек успешно занимаются математикой. Сколькими способами можно выбрать из них двоих для участия в математической олимпиаде?
Решение: С 7 2 = = (6∙ 7) : 2 = 21
№769 В магазине « Филателия» продается 8 различных наборов марок, посвященных спортивной тематике. Сколькими способами можно выбрать из них 3 набора?
Сколькими способами можно выбрать из них 3 набора?
Решение: С 8 3 = = (6 ∙ 7 ∙ 8) : ( 1∙ 2 ∙ 3) = 56
26
№770 Учащимся дали список из 10 книг, которые рекомендуется прочитать во время каникул. Сколькими способами ученик может выбрать из них 6 книг?
Решение: С 10 6 = = (7 ∙ 8 ∙ 9∙ 10) : ( 1∙ 2 ∙ 3 ∙ 4) = 210
№775 В библиотеке читателю предложили на выбор из новых поступлений 10 книг и 4 журнала. Сколькими способами он может выбрать из них 3 книги и 2 журнала?
Решение: С 10 3 ∙ С 4 2 = ∙ = 120 ∙ 6 = 720
Вопросы классу
1.Что называется перестановкой из п элементов?
2.По какой формуле считают число перестановок?
3. Что называют размещением из п элементов по к?
4. По какой формуле считают число размещений из п элементов по к?
5. Что называют сочетанием из п элементов по к?
6. По какой формуле считают число сочетаний из п элементов по к?
По какой формуле считают число сочетаний из п элементов по к?
Задачи для совместного решения
При решении каждой задачи вначале идет обсуждение: какая из трех изученных формул поможет получить ответ и почему
1. Сколько четырехзначных чисел можно составить из цифр 4,6,8,9, при условии, что все цифры разные?
2. Из 15 человек в группе студентов надо выбрать старосту и его заместителя. Сколькими способами это можно сделать?
3. Из 10 лучших учащихся школы два человека надо послать на слет лидеров.
Сколькими способами это можно сделать?
Замечание: В задаче №3 не имеет значения кого выбрать: любых 2 человек из 10, поэтому здесь работает формула для подсчета числа сочетаний.
В задаче №2 выбирают упорядоченную пару,т.к. в выбранной паре,если фамилии поменять местами это будет уже другой выбор, поэтому здесь работает формула для подсчета числа размещений
Ответы к задачам для совместного решения:
№1 24 числа. №2 210 способов. №3 45 способов
№2 210 способов. №3 45 способов
Задачи для совместного обсуждения и самостоятельных вычислений
№1Встретились 6 друзей и каждый пожал руку каждому своему другу. Сколько было рукопожатий?
27
№2 Сколькими способами можно составить расписание для учащихся 1класса на один день, если у них 7 предметов, и в этот день должно быть 4 урока?
(Число размещений из 7 по 4)
№3 В семье 6 человек, а за столом в кухне 6 стульев. Было решено каждый вечер перед ужином рассаживаться на эти 6 стульев по- новому. Сколько дней члены семьи смогут делать это без повторений.
№4 К хозяину дома пришли гости А,В,С,Д. За круглым столом – пять разных стульев. Сколько существует способов рассаживания?
(В гости пришли 4 человека + хозяин = 5 человек рассаживаются на 5 стульях, надо посчитать число перестановок)
5. В книжке раскраске нарисованы непересекающиеся треугольник, квадрат и круг. Каждую фигуру надо раскрасить в один из цветов радуги, разные фигуры в разные цвета. 835 Сколько четных четырехзначных чисел, в которых цифры не повторяются, можно записать с помощью цифр а) 1,2,3,7 . б) 1,2,3,4.
835 Сколько четных четырехзначных чисел, в которых цифры не повторяются, можно записать с помощью цифр а) 1,2,3,7 . б) 1,2,3,4.
28
а) Наши числа должны оканчиваться четной цифрой, такая цйфра в условии одна это цифра 2 , поставим ее на последнее место, а оставшиеся 3 цифры будем переставлять, число таких перестановок равно 3! = 6 .Значит можно составить 6 четных чисел
б) рассуждаем как в примере а) поставив на последнее место цифру 2 получим 6 четных чисел, поставив на последнее место цифру 4 получим еще 6 четных чисел,
значит всего 12 четных чисел
№841 Сколькими способами из класса, где учатся 24 учащихся можно выбрать: а) двух дежурных; б) старосту и его помощника?
а) т.к. дежурными могут быть любые 2 человека из 24 , то количество пар равно
С 24 2 = = 23 ∙ 24:2 = 276
б) здесь выдирают упорядоченную пару элементов из 24 элементов, количество таких пар равно А 24 2 = = 23 ∙ 24 = 552
1 вариант решает задания № 1,2,3,4,5.
2 вариант решает задания №6,7,8,9,10.
Решение простейших комбинаторных задач
(по материалам к.р. в апреле 2010 года)
1 . Сколькими способами можно расставить на полке пять книг разных авторов?
2. Сколькими способами можно составить полдник из напитка и пирожка, если в меню указаны: чай, кофе, какао и пирожки с яблоком или с вишней?
3. В среду по расписанию в 9 «А» классе должно быть 5 уроков: химия, физика, алгебра, биология и ОБЖ. Сколькими способами можно составить расписание на этот день?
4. Имеются 2 белых лошади и 4 гнедых. Сколькими способами можно
составить пару из лошадей разной масти?
5. Каким числом способов можно разложить 5 различных монет в 5 разных карманов?
29
6. В шкафу на полке лежат 3 шапки различных фасонов и 4 шарфа разных цветов. Сколькими способами можно составить набор из одной шапки и одного шарфа?
7. 8 .Имеются 4 утки и 3 гуся. Сколькими способами можно из них выбрать две разных птицы?
8 .Имеются 4 утки и 3 гуся. Сколькими способами можно из них выбрать две разных птицы?
9. Сколькими способами можно разложить 5 разных писем по 5 разным
конвертам, если в каждый конверт кладется только одно письмо?
10. В коробке хранятся 5 красных и 4 зелёных шара. Сколькими способами можно составить пару из шаров разного цвета?
Ответы для заданий самостоятельной работы
Заголовок выглядит страшновато, но в действительности всё очень просто. На данном уроке мы познакомимся с теоремами сложения и умножения вероятностей событий, а также разберём типовые задачи, которые наряду с задачей на классическое определение вероятности обязательно встретятся или, что вероятнее, уже встретились на вашем пути. Для эффективного изучения материалов этой статьи необходимо знать и понимать базовые термины теории вероятностей и уметь выполнять простейшие арифметические действия. Как видите, требуется совсем немного, и поэтому жирный плюс в активе практически гарантирован. Но с другой стороны, вновь предостерегаю от поверхностного отношения к практическим примерам – тонкостей тоже хватает. В добрый путь:
Но с другой стороны, вновь предостерегаю от поверхностного отношения к практическим примерам – тонкостей тоже хватает. В добрый путь:
Теорема сложения вероятностей несовместных событий : вероятность появления одного из двух несовместных событий или (без разницы какого) , равна сумме вероятностей этих событий:
Аналогичный факт справедлив и для бОльшего количества несовместных событий, например, для трёх несовместных событий и :
Теорема-мечта =) Однако, и такая мечта подлежит доказательству, которое можно найти, например, в учебном пособии В.Е. Гмурмана.
Знакомимся с новыми, до сих пор не встречавшимися понятиями:
Зависимые и независимые событияНачнём с независимых событий. События являются независимыми , если вероятность наступления любого из них не зависит от появления/непоявления остальных событий рассматриваемого множества (во всех возможных комбинациях). …Да чего тут вымучивать общие фразы:
Теорема умножения вероятностей независимых событий : вероятность совместного появления независимых событий и равна произведению вероятностей этих событий:
Вернёмся к простейшему примеру 1-го урока, в котором подбрасываются две монеты и следующим событиям:
– на 1-й монете выпадет орёл;
– на 2-й монете выпадет орёл.
Найдём вероятность события (на 1-й монете появится орёл и на 2-й монете появится орёл – вспоминаем, как читается произведение событий !) . Вероятность выпадения орла на одной монете никак не зависит от результата броска другой монеты, следовательно, события и независимы.
Аналогично:
– вероятность того, что на 1-й монете выпадет решка и на 2-й решка;
– вероятность того, что на 1-й монете появится орёл и на 2-й решка;
– вероятность того, что на 1-й монете появится решка и на 2-й орёл.
Заметьте, что события образуют полную группу и сумма их вероятностей равна единице: .
Теорема умножения очевидным образом распространяется и на бОльшее количество независимых событий, так, например, если события независимы, то вероятность их совместного наступления равна: . Потренируемся на конкретных примерах:
Задача 3
В каждом из трех ящиков имеется по 10 деталей. В первом ящике 8 стандартных деталей, во втором – 7, в третьем – 9. Из каждого ящика наудачу извлекают по одной детали. Найти вероятность того, что все детали окажутся стандартными.
Из каждого ящика наудачу извлекают по одной детали. Найти вероятность того, что все детали окажутся стандартными.
Решение : вероятность извлечения стандартной или нестандартной детали из любого ящика не зависит от того, какие детали будут извлечены из других ящиков, поэтому в задаче речь идёт о независимых событиях. Рассмотрим следующие независимые события:
– из 1-го ящика извлечена стандартная деталь;
– из 2-го ящика извлечена стандартная деталь;
– из 3-го ящика извлечена стандартная деталь.
По классическому определению:
– соответствующие вероятности.
Интересующее нас событие (из 1-го ящика будет извлечена стандартная деталь и из 2-го стандартная и из 3-го стандартная) выражается произведением .
По теореме умножения вероятностей независимых событий:
– вероятность того, что из трёх ящиков будет извлечено по одной стандартной детали.
Ответ : 0,504
После бодрящих упражнений с ящиками нас поджидают не менее интересные урны:
Задача 4
В трех урнах имеется по 6 белых и по 4 черных шара. Из каждой урны извлекают наудачу по одному шару. Найти вероятность того, что: а) все три шара будут белыми; б) все три шара будут одного цвета.
Из каждой урны извлекают наудачу по одному шару. Найти вероятность того, что: а) все три шара будут белыми; б) все три шара будут одного цвета.
Опираясь на полученную информацию, догадайтесь, как разобраться с пунктом «бэ» 😉 Примерный образец решения оформлен в академичном стиле с подробной росписью всех событий.
Зависимые события . Событие называют зависимым , если его вероятность зависит от одного или бОльшего количества событий, которые уже произошли. За примерами далеко ходить не надо – достаточно до ближайшего магазина:
– завтра в 19.00 в продаже будет свежий хлеб.
Вероятность этого события зависит от множества других событий: завезут ли завтра свежий хлеб, раскупят ли его до 7 вечера или нет и т.д. В зависимости от различных обстоятельств данное событие может быть как достоверным , так и невозможным . Таким образом, событие является зависимым .
Хлеба… и, как требовали римляне, зрелищ:
– на экзамене студенту достанется простой билет.
Если идти не самым первым, то событие будет зависимым, поскольку его вероятность будет зависеть от того, какие билеты уже вытянули однокурсники.
Как определить зависимость/независимость событий?Иногда об этом прямо сказано в условии задачи, но чаще всего приходится проводить самостоятельный анализ. Какого-то однозначного ориентира тут нет, и факт зависимости либо независимости событий вытекает из естественных логических рассуждений.
Чтобы не валить всё в одну кучу, задачам на зависимые события я выделю следующий урок, а пока мы рассмотрим наиболее распространённую на практике связку теорем:
Задачи на теоремы сложения вероятностей несовместныхи умножения вероятностей независимых событий
Этот тандем, по моей субъективной оценке, работает примерно в 80% задач по рассматриваемой теме. Хит хитов и самая настоящая классика теории вероятностей:
Задача 5
Два стрелка сделали по одному выстрелу в мишень. Вероятность попадания для первого стрелка равна 0,8, для второго – 0,6. Найти вероятность того, что:
Вероятность попадания для первого стрелка равна 0,8, для второго – 0,6. Найти вероятность того, что:
а) только один стрелок попадёт в мишень;
б) хотя бы один из стрелков попадёт в мишень.
Решение : вероятность попадания/промаха одного стрелка, очевидно, не зависит от результативности другого стрелка.
Рассмотрим события:
– 1-й стрелок попадёт в мишень;
– 2-й стрелок попадёт в мишень.
По условию: .
Найдём вероятности противоположных событий – того, что соответствующие стрелки промахнутся:
а) Рассмотрим событие: – только один стрелок попадёт в мишень. Данное событие состоит в двух несовместных исходах:
1-й стрелок попадёт и 2-й промахнётся
или
1-й промахнётся и 2-й попадёт.
На языке алгебры событий этот факт запишется следующей формулой:
Сначала используем теорему сложения вероятностей несовместных событий, затем – теорему умножения вероятностей независимых событий:
– вероятность того, что будет только одно попадание.
б) Рассмотрим событие: – хотя бы один из стрелков попадёт в мишень.
Прежде всего, ВДУМАЕМСЯ – что значит условие «ХОТЯ БЫ ОДИН»? В данном случае это означает, что попадёт или 1-й стрелок (2-й промахнётся) или 2-й (1-й промахнётся) или оба стрелка сразу – итого 3 несовместных исхода.
Способ первый : учитывая готовую вероятность предыдущего пункта, событие удобно представить в виде суммы следующих несовместных событий:
попадёт кто-то один (событие , состоящее в свою очередь из 2 несовместных исходов) или
попадут оба стрелка – обозначим данное событие буквой .
Таким образом:
По теореме умножения вероятностей независимых событий:
– вероятность того, что 1-й стрелок попадёт и 2-й стрелок попадёт.
По теореме сложения вероятностей несовместных событий:
– вероятность хотя бы одного попадания по мишени.
Способ второй : рассмотрим противоположное событие: – оба стрелка промахнутся.
По теореме умножения вероятностей независимых событий:
В результате:
Особое внимание обратите на второй способ – в общем случае он более рационален.
Кроме того, существует альтернативный, третий путь решения, основанный на умолчанной выше теореме сложения совместных событий.
! Если вы знакомитесь с материалом впервые, то во избежание путаницы, следующий абзац лучше пропустить.
Способ третий : события совместны, а значит, их сумма выражает событие «хотя бы один стрелок попадёт в мишень» (см. алгебру событий ). По теореме сложения вероятностей совместных событий и теореме умножения вероятностей независимых событий:
Выполним проверку: события и (0, 1 и 2 попадания соответственно) образуют полную группу, поэтому сумма их вероятностей должна равняться единице:
, что и требовалось проверить.
Ответ :
При основательном изучении теории вероятностей вам встретятся десятки задач милитаристского содержания, и, что характерно, после этого никого не захочется пристрелить – задачи почти подарочные. А почему бы не упростить ещё и шаблон? Cократим запись:
Решение : по условию: , – вероятность попадания соответствующих стрелков. Тогда вероятности их промаха:
Тогда вероятности их промаха:
а) По теоремам сложения вероятностей несовместных и умножения вероятностей независимых событий:
– вероятность того, что только один стрелок попадёт в мишень.
б) По теореме умножения вероятностей независимых событий:
– вероятность того, что оба стрелка промахнутся.
Тогда: – вероятность того, что хотя бы один из стрелков попадёт в мишень.
Ответ :
На практике можно пользоваться любым вариантом оформления. Конечно же, намного чаще идут коротким путём, но не нужно забывать и 1-й способ – он хоть и длиннее, но зато содержательнее – в нём понятнее, что, почему и зачем складывается и умножается. В ряде случаев уместен гибридный стиль, когда прописными буквами удобно обозначить лишь некоторые события.
Похожие задачи для самостоятельного решения:
Задача 6
Для сигнализации о возгорании установлены два независимо работающих датчика. Вероятности того, что при возгорании датчик сработает, для первого и второго датчиков соответственно равны 0,5 и 0,7. Найти вероятность того, что при пожаре:
Найти вероятность того, что при пожаре:
а) оба датчика откажут;
б) оба датчика сработают.
в) Пользуясь теоремой сложения вероятностей событий, образующих полную группу , найти вероятность того, что при пожаре сработает только один датчик. Проверить результат прямым вычислением этой вероятности (с помощью теорем сложения и умножения) .
Здесь независимость работы устройств непосредственно прописана в условии, что, кстати, является важным уточнением. Образец решения оформлен в академичном стиле.
Как быть, если в похожей задаче даны одинаковые вероятности, например, 0,9 и 0,9? Решать нужно точно так же! (что, собственно, уже продемонстрировано в примере с двумя монетами)
Задача 7
Вероятность поражения цели первым стрелком при одном выстреле равна 0,8. Вероятность того, что цель не поражена после выполнения первым и вторым стрелками по одному выстрелу равна 0,08. Какова вероятность поражения цели вторым стрелком при одном выстреле?
А это небольшая головоломка, которая оформлена коротким способом. Условие можно переформулировать более лаконично, но переделывать оригинал не буду – на практике приходится вникать и в более витиеватые измышления.
Условие можно переформулировать более лаконично, но переделывать оригинал не буду – на практике приходится вникать и в более витиеватые измышления.
Знакомьтесь – он самый, который настрогал для вас немереное количество деталей =):
Задача 8
Рабочий обслуживает три станка. Вероятность того, что в течение смены первый станок потребует настройки, равна 0,3, второй – 0,75, третий – 0,4. Найти вероятность того, что в течение смены:
а) все станки потребуют настройки;
б) только один станок потребует настройки;
в) хотя бы один станок потребует настройки.
Решение : коль скоро в условии ничего не сказано о едином технологическом процессе, то работу каждого станка следует считать не зависимой от работы других станков.
По аналогии с Задачей №5, здесь можно ввести в рассмотрение события , состоящие в том, что соответствующие станки потребуют настройки в течение смены, записать вероятности , найти вероятности противоположных событий и т.д. Но с тремя объектами так оформлять задачу уже не очень хочется – получится долго и нудно. Поэтому здесь заметно выгоднее использовать «быстрый» стиль:
Поэтому здесь заметно выгоднее использовать «быстрый» стиль:
По условию: – вероятности того, что в течение смены соответствующие станки потребуют настойки. Тогда вероятности того, что они не потребуют внимания:
Один из читателей обнаружил тут прикольную опечатку, даже исправлять не буду =)
а) По теореме умножения вероятностей независимых событий:
– вероятность того, что в течение смены все три станка потребуют настройки.
б) Событие «В течение смены только один станок потребует настройки» состоит в трёх несовместных исходах:
1) 1-й станок потребует внимания и 2-й станок не потребует и 3-й станок не потребует
или :
2) 1-й станок не потребует внимания и 2-й станок потребует и 3-й станок не потребует
или :
3) 1-й станок не потребует внимания и 2-й станок не потребует и 3-й станок потребует .
По теоремам сложения вероятностей несовместных и умножения вероятностей независимых событий:
– вероятность того, что в течение смены только один станок потребует настройки.
Думаю, сейчас вам должно быть понятно, откуда взялось выражение
в) Вычислим вероятность того, что станки не потребуют настройки, и затем – вероятность противоположного события:
– того, что хотя бы один станок потребует настройки.
Ответ :
Пункт «вэ» можно решить и через сумму , где – вероятность того, что в течение смены только два станка потребуют настройки. Это событие в свою очередь включает в себя 3 несовместных исхода, которые расписываются по аналогии с пунктом «бэ». Постарайтесь самостоятельно найти вероятность , чтобы проверить всю задачу с помощью равенства .
Задача 9
Из трех орудий произвели залп по цели. Вероятность попадания при одном выстреле только из первого орудия равна 0,7, из второго – 0,6, из третьего – 0,8. Найти вероятность того, что: 1) хотя бы один снаряд попадет в цель; 2) только два снаряда попадут в цель; 3) цель будет поражена не менее двух раз.
Решение и ответ в конце урока.
И снова о совпадениях: в том случае, если по условию два или даже все значения исходных вероятностей совпадают (например, 0,7; 0,7 и 0,7), то следует придерживаться точно такого же алгоритма решения.
В заключение статьи разберём ещё одну распространённую головоломку:
Задача 10
Стрелок попадает в цель с одной и той же вероятностью при каждом выстреле. Какова эта вероятность, если вероятность хотя бы одного попадания при трех выстрелах равна 0,973.
Решение : обозначим через – вероятность попадания в мишень при каждом выстреле.
и через – вероятность промаха при каждом выстреле.
И таки распишем события:
– при 3 выстрелах стрелок попадёт в мишень хотя бы один раз;
– стрелок 3 раза промахнётся.
По условию , тогда вероятность противоположного события:
С другой стороны, по теореме умножения вероятностей независимых событий:
Таким образом:
– вероятность промаха при каждом выстреле.
В результате:
– вероятность попадания при каждом выстреле.
Ответ : 0,7
Просто и изящно.
В рассмотренной задаче можно поставить дополнительные вопросы о вероятности только одного попадания, только двух попаданий и вероятности трёх попаданий по мишени. Схема решения будет точно такой же, как и в двух предыдущих примерах:
Схема решения будет точно такой же, как и в двух предыдущих примерах:
Однако принципиальное содержательное отличие состоит в том, что здесь имеют место повторные независимые испытания , которые выполняются последовательно, независимо друг от друга и с одинаковой вероятностью исходов.
Непосредственный подсчет случаев, благоприятствующих данному событию, может оказаться затруднительным. Поэтому для определения вероятности события бывает выгодно представить данное событие в виде комбинации некоторых других, более простых событий. При этом, однако, надо знать правила, которым подчиняются вероятности при комбинации событий. Именно к этим правилам и относятся упомянутые в названии параграфа теоремы.
Первая из них относится к подсчету вероятности того, что осуществится хотя бы одно из нескольких событий.
Теорема сложения.
Пусть А и В — два несовместных события. Тогда вероятность того, что осуществится хотя бы одно из этих двух событий, равна сумме их вероятностей:
Доказательство. Пусть — полная группа попарно несовместных событий. Если то среди этих элементарных событий имеется ровно событий, благоприятствующих А, и ровно событий, благоприятствующих В. Так как события А и В несовместны, то никакое из событий не может благоприятствовать обоим этим событиям. Событию (А или В), состоящему в том, что наступает хотя бы одно из этих двух событий, благоприятствует, очевидно, как каждое из событий благоприятствующих А, так и каждое из событий
Пусть — полная группа попарно несовместных событий. Если то среди этих элементарных событий имеется ровно событий, благоприятствующих А, и ровно событий, благоприятствующих В. Так как события А и В несовместны, то никакое из событий не может благоприятствовать обоим этим событиям. Событию (А или В), состоящему в том, что наступает хотя бы одно из этих двух событий, благоприятствует, очевидно, как каждое из событий благоприятствующих А, так и каждое из событий
Благоприятствующих В. Поэтому общее число событий, благоприятствующих событию (А или В), равно сумме откуда следует:
что и требовалось доказать
Нетрудно видеть, что теорема сложения, сформулированная выше для случая двух событий, легко переносится на случай любого конечного числа их. Именно если попарно несовместные события, то
Для случая трех событий, например, можно написать
Важным следствием теоремы сложения является утверждение: если события попарно несовместны и единственно возможны, то
Действительно, событие или или или по предположению достоверно и его вероятность, как было указано в § 1, равна единице. В частности, если означают два взаимно противоположных события, то
В частности, если означают два взаимно противоположных события, то
Проиллюстрируем теорему сложения примерами.
Пример 1. При стрельбе по мишени вероятность сделать отличный выстрел равна 0,3, а вероятность сделать выстрел на оценку «хорошо» равна 0,4. Какова вероятность получить за сделанный выстрел оценку не ниже «хорошо»?
Решение. Если событие А означает получение оценки «отлично», а событие В — получение оценки «хорошо», то
Пример 2. В урне, содержащей шаров белого, красного и черного цвета, находятся белых шаров и I красных. Какова вероятность вынуть шар не черного цвета?
Решение. Если событие А состоит в появлении белого, а событие В — красного шара, то появление шара не черного цвета
означает появление либо белого, либо красного шара. Так как по определению вероятности
то по теореме сложения вероятность появления шара не черного цвета равна;
Эту задачу можно решить и так. Пусть событие С состоит в появлении черного шара. Число черных шаров равно так что Р (С) Появление шара не черного цвета является противоположным событием С, поэтому на основании указанного выше следствия из теоремы сложения имеем:
Число черных шаров равно так что Р (С) Появление шара не черного цвета является противоположным событием С, поэтому на основании указанного выше следствия из теоремы сложения имеем:
как и раньше.
Пример 3. В денежно-вещевой лотерее на серию в 1000 билетов приходится 120 денежных и 80 вещевых выигрышей. Какова вероятность какого-либо выигрыша на один лотерейный билет?
Решение. Если обозначить через А событие, состоящее в выпадении денежного выигрыша и через В — вещевого, то из определения вероятности следует
Интересующее нас событие представляет (А или В), поэтому из теоремы сложения вытекает
Таким образом, вероятность какого-либо выигрыша равна 0,2.
Прежде чем перейти к следующей теореме, необходимо ознакомиться с новым важным понятием — понятием условной вероятности. Для этой цели мы начнем с рассмотрения следующего примера.
Пусть на складе имеется 400 электрических лампочек, изготовленных на двух различных заводах, причем на первом изготовлено 75% всех лампочек, а на втором — 25%. Допустим, что среди лампочек, изготовленных первым заводом, 83% удовлетворяют условиям определенного стандарта, а для продукции второго завода этот процент равен 63. Определим вероятность того, что случайно взятая со склада лампочка окажется удовлетворяющей условиям стандарта.
Допустим, что среди лампочек, изготовленных первым заводом, 83% удовлетворяют условиям определенного стандарта, а для продукции второго завода этот процент равен 63. Определим вероятность того, что случайно взятая со склада лампочка окажется удовлетворяющей условиям стандарта.
Заметим, что общее число имеющихся стандартных лампочек состоит из лампочек, изготовленных первым
заводом, и 63 лампочек, изготовленных вторым заводом, то есть равно 312. Так как выбор любой лампочки следует считать равновозможным, то мы имеем 312 благоприятствующих случаев из 400, так что
где событие В состоит в том, что выбранная нами лампочка стандартна.
При этом подсчете не делалось никаких предположений о том, к продукции какого завода принадлежит выбранная нами лампочка. Если же какие-либо предположения такого рода сделать, то очевидно, что интересующая нас вероятность может измениться. Так, например, если известно, что выбранная лампочка изготовлена на первом заводе (событие А), то вероятность того, что она стандартна, будет уже не 0,78, а 0,83.
Такого рода вероятность, то есть вероятность события В при условии, что имеет место событие А, называют условной вероятностью события В при условии наступления события А и обозначают
Если мы в предыдущем примере обозначим через А событие, состоящее в том, что выбранная лампочка изготовлена на первом заводе, то мы можем написать
Теперь мы можем сформулировать важную теорему, относящуюся к подсчету вероятности совмещения событий.
Теорема умножения.
Вероятность совмещения событий А и В равна произведению вероятности одного из событий на условную вероятность другого в предположении, что первое имело место:
При этом под совмещением событий А и В понимается наступление каждого из них, то есть наступление как события А, так и события В.
Доказательство. Рассмотрим полную группу из равновозможных попарно несовместных событий каждое из которых может быть благоприятствующим или неблагоприятствующим как для события А, так и для события В.
Разобьем все эти события на четыре различные группы следующим образом. К первой группе отнесем те из событий которые благоприятствуют и событию А, и событию В; ко второй и третьей группам отнесем такие события которые благоприятствуют одному из двух интересующих нас событий и не благоприятствуют другому, например ко второй группе — те, которые благоприятствуют А, но не благоприятствуют В, а к третьей — те, которые благоприятствуют В, но не благоприятствуют А; наконец, к
К первой группе отнесем те из событий которые благоприятствуют и событию А, и событию В; ко второй и третьей группам отнесем такие события которые благоприятствуют одному из двух интересующих нас событий и не благоприятствуют другому, например ко второй группе — те, которые благоприятствуют А, но не благоприятствуют В, а к третьей — те, которые благоприятствуют В, но не благоприятствуют А; наконец, к
четвертой группе отнесем те из событий которые не благоприятствуют ни А, ни В.
Так как нумерация событий не играет роли, то можно предположить, что это разбиение на четыре группы выглядит так:
I группа:
II группа:
III группа:
IV группа:
Таким образом, среди равновозможных и попарно несовместных событий имеется событий, благоприятствующих и событию А, и событию В, I событий, благоприятствующих событию А, но не благоприятствующих событию событий, благоприятствующих В, но не благоприятствующих А, и, наконец, событий, не благоприятствующих ни А, ни В.
Заметим, между прочим, что какая-либо из рассмотренных нами четырех групп (и даже не одна) может не содержать ни одного события. В этом случае соответствующее число, означающее количество событий в такой группе, будет равно нулю.
Произведенная нами разбивка на группы позволяет сразу написать
ибо совмещению событий А и В благоприятствуют события первой группы и только они. Общее число событий, благоприятствующих А, равно общему числу событий в первой и второй группах, а благоприятствующих В — общему числу событий в первой и третьей группах.
Подсчитаем теперь вероятность то есть вероятность события В при условии, что событие А имело место. Теперь события, входящие в третью и четвертую группы, отпадают, так как их появление противоречило бы наступлению события А, и число возможных случаев оказывается равным уже не . Из них событию В благоприятствуют лишь события первой группы, так что мы получаем:
Для доказательства теоремы достаточно теперь написать очевидное тождество:
и заменить в нем все три дроби вычисленными выше вероятностями. Мы придем к утверждавшемуся в теореме равенству:
Мы придем к утверждавшемуся в теореме равенству:
Ясно, что написанное нами выше тождество имеет смысл лишь при что справедливо всегда, если только А не есть невозможное событие.
Так как события А и В равноправны, то, поменяв их местами, получим другую форму теоремы умножения:
Впрочем, это равенство можно получить тем же путем, что и предыдущее, если заметить, что воспользоваться тождеством
Сравнивая правые части двух выражений для вероятности Р(А и В), получим полезное равенство:
Рассмотрим теперь примеры, иллюстрирующие теорему умножения.
Пример 4. В продукции некоторого предприятия признаются годными (событие А) 96% изделий. К первому сорту (событие В) оказываются принадлежащими 75 изделий из каждой сотни годных. Определить вероятность того, что произвольно взятое изделие будет годным и принадлежит к первому сорту.
Решение. Искомая вероятность есть вероятность совмещения событий А и В. По условию имеем: . Поэтому теорема умножения дает
Пример 5. Вероятность попадания в цель при отдельном выстреле (событие А) равна 0,2. Какова вероятность поразить цель, если 2% взрывателей дают отказы (т. е. в 2% случаев выстрела не
Вероятность попадания в цель при отдельном выстреле (событие А) равна 0,2. Какова вероятность поразить цель, если 2% взрывателей дают отказы (т. е. в 2% случаев выстрела не
Решение. Пусть событие В состоит в том, что выстрел произойдет, а В означает противоположное событие. Тогда по условию и согласно следствию из теоремы сложения . Далее, по условию .
Поражение цели означает совмещение событий А и В (выстрел произойдет и даст попадание), поэтому по теореме умножения
Важный частный случай теоремы умножения можно получить, если воспользоваться понятием независимости событий.
Два события называются независимыми, если вероятность одного из них не изменяется в результате того, наступило или не наступило другое.
Примерами независимых событий являются выпадение различного числа очков при повторном бросании игральной кости или той или иной стороны монет при повторном бросании монеты, так как очевидно, что вероятность выпадения герба при втором бросании равна независимо от того, выпал или не выпал герб в первом.
Аналогично, вероятность вынуть во второй раз белый шар из урны с белыми и черными шарами, если вынутый первым шар предварительно возвращен, не зависит от того, белый или черный шар был вынут в первый раз. Поэтому результаты первого и второго вынимания независимы между собой. Наоборот, если шар, вынутый первым, не возвращается в урну, то результат второго вынимания зависит от первого, ибо состав шаров, находящихся в урне после первого вынимания, меняется в зависимости от его исхода. Здесь мы имеем пример зависимых событий.
Пользуясь обозначениями, принятыми для условных вероятностей, можно записать условие независимости событий А и В в виде
Воспользовавшись этими равенствами, мы можем привести теорему умножения для независимых событий к следующей форме.
Если события А и В независимы, то вероятность их совмещения равна произведению вероятностей этих событий:
Действительно, достаточно в первоначальном выражении теоремы умножения положить , что вытекает из независимости событий, и мы получим требуемое равенство.
Рассмотрим теперь несколько событий: Будем называть их независимыми в совокупности, если вероятность появления любого из них не зависит от того, произошли ли какие-либо другие рассматриваемые события или нет
В случае событий, независимых в совокупности, теорема умножения может быть распространена на любое конечное число их, благодаря чему ее можно сформулировать так:
Вероятность совмещения событий независимых в совокупности, равна произведению вероятностей этих событий:
Пример 6. Рабочий обслуживает три автоматических станка, к каждому из которых нужно подойти для устранения неисправности, если станок остановится. Вероятность того, что первый станок не остановится в течение часа, равна 0,9. Та же вероятность для второго станка равна 0,8 и для третьего — 0,7. Определить вероятность того, что в течение часа рабочему не потребуется подойти ни к одному из обслуживаемых им станков.
Пример 7. Вероятность сбить самолет винтовочным выстрелом Какова вероятность уничтожения неприятельского самолета при одновременной стрельбе из 250 винтовок?
Решение. Вероятность того, что при одиночном выстреле самолет не будет сбит, по теореме сложения равна Тогда можно подсчитать с помощью теоремы умножения вероятность того, что самолет не будет сбит при 250 выстрелах, как вероятность совмещения событий. Она равна После этого мы можем снова воспользоваться теоремой сложения и найти вероятность того, что самолет будетсбит, как вероятность противоположного события
Вероятность того, что при одиночном выстреле самолет не будет сбит, по теореме сложения равна Тогда можно подсчитать с помощью теоремы умножения вероятность того, что самолет не будет сбит при 250 выстрелах, как вероятность совмещения событий. Она равна После этого мы можем снова воспользоваться теоремой сложения и найти вероятность того, что самолет будетсбит, как вероятность противоположного события
Отсюда видно, что, хотя вероятность сбить самолет одиночным винтовочным выстрелом ничтожно мала, тем не менее при стрельбе из 250 винтовок вероятность сбить самолет оказывается уже весьма ощутимой. Она существенно возрастает, если число винтовок увеличить. Так, при стрельбе из 500 винтовок вероятность сбить самолет, как легко подсчитать, равна при стрельбе из 1000 винтовок — даже .
Доказанная выше теорема умножения позволяет несколько расширить теорему сложения, распространив ее на случай совместимых событий. Ясно, что если события А и В совместимы, то вероятность наступления хотя бы одного из них не равна сумме их вероятностей. Например, если событие А означает выпадение четного
Например, если событие А означает выпадение четного
числа очков при бросании игральной кости, а событие В — выпадение числа очков, кратного трем, то событию (А или В) благоприятствует выпадение 2, 3, 4 и 6 очков, то есть
С другой стороны, то есть . Таким образом, в этом случае
Отсюда видно, что в случае совместимых событий теорема сложения вероятностей должна быть изменена. Как мы сейчас увидим, ее можно сформулировать таким образом, чтобы она была справедлива и для совместимых, и для несовместных событий, так что ранее рассмотренная теорема сложения окажется частным случаем новой.
Событий, которые А не благоприятствуют.
Все элементарные события, которые благоприятствуют событию (А или В), должны благоприятствовать либо только А, либо только В, либо и А и В. Таким образом, общее число таких событий равно
а вероятность
что и требовалось доказать.
Применяя формулу (9) к рассмотренному выше примеру выпадения числа очков при бросании игральной кости, получим:
что совпадает с результатом непосредственного подсчета.
Очевидно, что формула (1) является частным случаем (9). Действительно, если события А и В несовместны, то и вероятность совмещения
Примере. В электрическую цепь включены последовательно два предохранителя. Вероятность выхода из строя первого предохранителя равна 0,6, а второго 0,2. Определим вероятность прекращения питания в результате выхода из строя хотя бы одного из этих предохранителей.
Решение. Так как события А и В, состоящие в выходе из строя первого и второго из предохранителей, совместимы, то искомая вероятность определится по формуле (9):
Упражнения
Сколько существует четырехзначных чисел? – Reviews Wiki
ЧЕТЫРЕ-ЗНАЧНЫЕ ЧИСЛА – это числа, которые состоят из четырех цифр, т.е. имеют разряды единиц, десятков, сотен и тысяч. На самом деле, чтобы найти количество чисел между любыми двумя заданными числами, мы используем одну и ту же формулу. Следовательно, всего 9000 четырехзначных чисел .
Аналогично, сколько комбинаций из 4 цифр может состоять из 10 чисел? 10 вариантов для первого циферблата, и для каждого из этих 10 вариантов для второго циферблата, и для каждого из этих 10 вариантов для третьего, и для каждого из этих 10 вариантов для четвертого. Итак, 10 х 10 х 10 х 10 = 9.0003 10 000 комбинаций , все возможные числа от 0000 до 9999.
Итак, 10 х 10 х 10 х 10 = 9.0003 10 000 комбинаций , все возможные числа от 0000 до 9999.
Какие четыре цифры самые большие и самые маленькие? Наибольшее и наименьшее четырехзначные числа 1000 и 9999 соответственно.
Какое четырехзначное число лучше? Наибольшее четырехзначное число
Итак, 9999 — это наибольшее четырехзначное число в системе счисления. Отсюда доказано, что 9999 — самое большое четырехзначное число.
Во-вторых Сколько существует четырехзначных чисел с различными цифрами? Следовательно, согласно основному принципу подсчета, количество четырехзначных чисел равно 9..9. 8,7 = 4536 . Следовательно, существует 4536 четырехзначных чисел с различными цифрами.
Какой самый сложный 4-значный пароль?
Почти 11% из 3,4 миллионов паролей имеют код 1234. Это 374 000! Он встречался чаще, чем самые низкие 4200 кодов вместе взятые. Второй по популярности четырехзначный PIN-код — 1111, почти 6% (204 000).
…
Вот что они нашли.
| Ранг | PIN-код | Частота |
|---|---|---|
| #1 | 1234 | 10.713% |
| #2 | 1111 | 6.016% |
| #3 | 0000 | 1.881% |
| #4 | 1212 | 1.197% |
тогда Сколько существует комбинаций из 4 буквенно-цифровых символов? Это 1 679 616 возможных комбинаций .
Сколько времени потребуется, чтобы угадать 4-значный PIN-код? Потребовалось бы до 112 часов для перебора 4-значного PIN-кода, потому что каждый ввод PIN-кода занимает 40 секунд.
Какое самое большое четырехзначное число, если использовать разные цифры?
Наибольшее четырехзначное число, использующее только одну цифру, равно 9 999 (9 999 также является наибольшим четырехзначным числом). Наибольшее четырехзначное число, состоящее из двух разных цифр, равно 9998. Наибольшее четырехзначное число, состоящее из всех цифр, равно 9 876 .
Наибольшее четырехзначное число, состоящее из всех цифр, равно 9 876 .
В чем разница между наибольшим четырехзначным числом? Самое большое четырехзначное число 9,999. Разница между этими числами составит = 1 00 000 – 9 999 = 90 001 .
Какое наибольшее четырехзначное число является полным квадратом?
Следовательно, мы можем сказать, что квадрат 99 — это число, которое дает наибольшее четырехзначное число. И, следовательно, 9801 — это наибольшее четырехзначное число, являющееся полным квадратом.
Какой самый сложный 4-значный PIN-код? Почти 11% из 3,4 миллиона паролей — это 1234. Это 374 000! Он встречался чаще, чем самые низкие 4200 кодов вместе взятые. Второй по популярности четырехзначный PIN-код — 1111, почти 6% (204 000).
…
Вот что нашли.
| Rank | PIN | Freq |
|---|---|---|
| #1 | 1234 | 10.713% |
| #2 | 1111 | 6. 016% 016% |
| #3 | 0000 | 1.881 % |
| #4 | 1212 | 1,197% |
Что такое жесткий четырехзначный код?
Если компьютер случайным образом угадывает числа, то каждая отдельная комбинация вряд ли будет угадана. Если он угадывает, основываясь на естественной склонности людей к шаблонам, сложнее всего угадать « 8068» . По какой-то причине, когда проводилось исследование, в то время это была наименее используемая комбинация из 4 цифр.
Какой четырехзначный код самый безопасный?
Самый безопасный 4-значный PIN-код — « 8068 » — по крайней мере, так было, пока исследователи из Data Genetics не сообщили всем на этой неделе. Исследователи изучили набор из 3,4 миллиона четырехзначных личных идентификационных номеров и обнаружили, что «8068» встречается только 25 раз.
Сколько четырехзначных чисел можно составить, используя ровно 3 разные цифры? Следовательно, искомое количество способов равно 3888 .
Сколько существует четырехзначных чисел с различными цифрами, сумма цифр каждого из которых равна натуральному нечетному числу 1880 2160 2090 2376? Но ответ 576 ..
Что такое надежный 4-значный PIN-код?
Самый безопасный 4-значный PIN-код — ‘8068 ’ — по крайней мере, так было, пока исследователи из Data Genetics не рассказали всем на этой неделе. Исследователи изучили набор из 3,4 миллиона четырехзначных личных идентификационных номеров и обнаружили, что «8068» встречается только 25 раз. … Исследование также показало, что многие PIN-коды основаны на визуальных подсказках.
Какое хорошее четырехзначное число? Исследователи компании Data Genetics, занимающейся анализом данных, обнаружили, что три самые популярные комбинации — « 1234 », «1111» и «0000» — составляют почти 20 процентов всех четырехзначных паролей.
Какое четырехзначное число самое случайное?
Если компьютер случайным образом угадывает числа, то каждая отдельная комбинация вряд ли будет угадана. Если он угадывает, основываясь на естественной склонности людей к шаблонам, труднее всего угадать «9».0003 8068” . По какой-то причине, когда проводилось исследование, в то время это была наименее используемая комбинация из 4 цифр.
Если он угадывает, основываясь на естественной склонности людей к шаблонам, труднее всего угадать «9».0003 8068” . По какой-то причине, когда проводилось исследование, в то время это была наименее используемая комбинация из 4 цифр.
Сколько существует комбинаций 4-х цветов? Первым выбором может быть любой из четырех цветов. Для каждого из этих 4 первых вариантов есть 3 вторых варианта. Следовательно, имеется 4 x 3 = 12 возможностей .
…
| Номер | Первый | Второй |
|---|---|---|
| 2 | красный | green |
| 3 | red | brown |
| x | yellow | red |
| 4 | yellow | green |
What are 4 characters in a password?
В паролях можно использовать символы четырех типов:
- строчные буквы (a, b, c)
- прописные буквы (A, B, C)
- цифры (1, 2 3)
- «специальные символы», включая знаки препинания (.
 ; !) и другие символы (# * &) 4-значные числа — Математические игры — SplashLearn
; !) и другие символы (# * &) 4-значные числа — Математические игры — SplashLearnГлавная > Игры > Математические игры > Построить 4-значные числа
Сделайте первый шаг к построению своего математического замка, потренировавшись в построении четырехзначных чисел.
Играть в игру
Отнести к классу
ПРЕДМЕТЫ И ТЕМЫ
Узнайте больше об игре «Собери четырехзначные числа»
Пришельцы застряли на острове далеко от дома. Но вы можете помочь им. Все, что вам нужно сделать, это настроить цифры на их ракетном корабле, и они улетят! Приходите помочь маленьким инопланетянам добраться до их дома. Игра дает учащимся возможность применить понятия разрядности для составления числа. В этой игре учащиеся научатся составлять четырехзначные числа.
Узнайте об удивительных играх на чтение и запись чисел
Просмотреть все 93 Игры
Чувство чисел
Спойте песенку с числами от 1 до 3
Попросите малыша спеть песенку с числами от 1 до 3, чтобы играть в эту игру.

Pre-K
K
ПОДРОБНЕЕ
Чувство числа
Считай вместе со звездами от 1 до 3
Сияй в мире математики, считая вместе со звездами от 1 до 3.
Pre-K
K
ПОСМОТРЕТЬ ДЕТАЛИ
Number Sense
Числовая последовательность от 1 до 3
Окунитесь в безумие математической мультивселенной, практикуя числовую последовательность от 1 до 3.
Pre-K
K
ПОДРОБНЕЕ
Чувство чисел
Считай и называй числа от 1 до 3
Дети должны считать и называть числа от 1 до 3, чтобы тренировать чувство числа.
Pre-K
K
ПОДРОБНЕЕ
Чувство числа
Прыгай и считай от 1 до 3
Используй свои навыки восприятия чисел, чтобы прыгать и считать от 1 до 3.
Чувство числа
Считай и сопоставляй числа от 1 до 3
Примени свои знания о смысле чисел, чтобы считать и сопоставлять числа от 1 до 3.

Чувство числа
Сопоставьте карточки с числами от 1 до 3
Добавьте больше стрелок в математический колчан вашего ребенка, сопоставляя карточки с числами от 1 до 3.
Pre-K
K
СМОТРЕТЬ ПОДРОБНОСТИ
Number Sense
Распознавание чисел от 1 до 3
Наслаждайтесь чудом математической мультивселенной, определяя числа от 1 до 3.
Pre-K
K
ПОДРОБНЕЕ
Number Sense
Идентификационные номера карт до 3
Попросите вашего малыша определить карточки с числами до 3, чтобы играть в эту игру.
Pre-K
K
ПОДРОБНЕЕ
Number Sense
Sing the Number Song от 1 до 5
Погрузитесь в мир чисел, напевая числовую песню от 1 до 5.
Pre-K
K
СМОТРЕТЬ ПОДРОБНОСТИ
Чувство числа
Считай вместе со звездами от 1 до 5
Считай вместе со звездами от 1 до 5 в этой игре на чувство числа.

Pre-K
K
ПОДРОБНЕЕ
Чувство числа
Спойте песенку с числом от 2 до 5
Дети должны спеть песенку с числом от 2 до 5, чтобы попрактиковаться в числах.
Pre-K
K
ПОДРОБНЕЕ
Чувство чисел
Числовая последовательность от 1 до 5
Попросите вашего малыша попрактиковаться в числовой последовательности от 1 до 5, чтобы играть в эту игру.
Пре-К
К
ПОСМОТРЕТЬ ПОДРОБНОСТИ
Number Sense
Считай и называй числа от 1 до 5
Наслаждайся чудом математики, изучая, как считать и называть числа от 1 до 5.
Pre-K
K
ПОДРОБНЕЕ
Чувство числа
Прыгай и считай от 1 до 5
Пусть твой ребенок увидит мир сквозь математические оттенки с нашей игрой «Прыгай и считай от 1 до 5»!
Пре-К
K
ПОДРОБНЕЕ
Откройте для себя веселые игры на Place Value
Посмотреть все 122 игры
Number Sense
Соедините числовые звезды от 1 до 5
Насладитесь чудом математики, соединив числовые звезды от 1 до 5.

Pre-K
K
ПОДРОБНЕЕ
Чувство чисел
Давайте составим песенку с числами от 1 до 5
Сияй в мире математики, выучив песенку с числами от 1 до 5.
Pre-K
K
ПОДРОБНЕЕ
Чувство чисел
Давайте составим песенку о числах от 2 до 5
Упражнение с цифрами от 2 до 5!
Pre-K
K
ПОДРОБНЕЕ
Чувство числа
Найди номер один
Отточи свои навыки счета, отслеживая номер один.
Pre-K
K
ПОДРОБНЕЕ
Чувство числа
Найди число два
Отточи свои навыки счета, наведя число два.
Pre-K
K
ПОДРОБНЕЕ
Чувство числа
Найди число три
Отточи свои навыки счета, наведя число три.

Pre-K
K
ПОДРОБНЕЕ
Чувство числа
Найди цифру четыре
Отточи свои навыки счета, нарисовав цифру четыре.
Pre-K
K
ПОДРОБНЕЕ
Чувство числа
Найди число пять
Отточи свои навыки счета, наведя число пять.
Pre-K
K
ПОДРОБНЕЕ
Number Sense
Счет и сопоставление чисел до 5
Откройте для себя мудрость математики, научившись считать и сопоставлять числа до 5.
Pre-K
K
СМОТРЕТЬ ПОДРОБНОСТИ
Чувство чисел
Сопоставление карточек с числами от 1 до 5
Откройте для себя мудрость математики, научившись сопоставлять карточки с числами от 1 до 5.
Pre-K
K
ПОДРОБНЕЕ
Number Sense
Распознавание чисел от 1 до 5
Наслаждайтесь чудом математики, определяя числа от 1 до 5.

Pre-K
K
СМОТРЕТЬ ПОДРОБНОСТИ
Чувство чисел
Определить карточки с числами до 5
Дети должны распознавать карточки с числами до 5, чтобы практиковать чувство числа.
Pre-K
K
ПОДРОБНЕЕ
Чувство чисел
Угадай спрятанные числа от 1 до 5
Попросите малыша угадать спрятанные числа от 1 до 5, чтобы сыграть в эту игру.
Pre-K
K
ПОДРОБНЕЕ
Чувство чисел
Пойте песенку о числах от 1 до 8
Дети должны спеть песенку с числами от 1 до 8, чтобы попрактиковаться в числах.
Pre-K
K
ПОДРОБНЕЕ
Number Sense
Считай по звездочкам от 1 до 8
Помогите ребенку взлететь, считая по звездочкам от 1 до 8.
Найдите увлекательные игры на Number Sense
Просмотреть все 387 игр
Чувство числа
Пойте числовую песню от 1 до 10
Окунитесь в безумие математической мультивселенной, узнав, как петь числовое представление от 1 до 10.
 911
911Pre-K
K
СМОТРЕТЬ ПОДРОБНОСТИ
Чувство чисел
Счет по звездочкам от 1 до 10
Используйте свое чувство числа, чтобы считать по звездочкам от 1 до 10.
Pre-K
K
ПОДРОБНЕЕ
Чувство чисел
Песнь чисел от 2 до 10
Раскройте мудрость математики, научившись петь песню чисел от 2 до 10.
Pre-K
K
ПОДРОБНЕЕ
Чувство чисел
Прыжки и счет от 1 до 8
Примените свои знания в области чисел, чтобы подпрыгивать и считать от 1 до 8.
Чувство числа
Считай и называй числа от 6 до 10
Стань ярким в мире математики, научившись считать и называть числа от 6 до 10.
Pre-K
K
ПОДРОБНЕЕ
Number Sense
Числовая последовательность от 1 до 10
Наслаждайтесь чудом математической мультивселенной, практикуя числовую последовательность от 1 до 10.

Pre-K
K
ПОДРОБНЕЕ
Чувство числа
Счет на 1 с
Примените свои знания о смысле чисел, чтобы считать на 1 с.
Pre-K
K
ПОДРОБНЕЕ
Number Sense
Соедините числовые звездочки от 1 до 8
Попросите вашего малыша соединить числовые звездочки от 1 до 8.
Pre-K
K
ПОДРОБНЕЕ
Чувство чисел
Давайте составим песенку с цифрами от 1 до 8
Пусть ваш ребенок увидит мир сквозь цветные математические тени с песенкой о цифрах от 1 до 8!
Pre-K
K
ПОДРОБНЕЕ
Number Sense
Соедините числовые звезды от 1 до 10
Используйте свои навыки восприятия чисел, чтобы соединить числовые звезды от 1 до 10.
Pre-K
K
ПОДРОБНЕЕ
Чувство чисел
Давайте составим песенку с числами от 1 до 10
В этой игре вы сможете сыграть песенку с числами от 1 до 10.

Пре-К
К
ПОСМОТРЕТЬ ПОДРОБНОСТИ
Number Sense
Давайте составим числовую песенку от 2 до 8
Пересмотри числа с числовой песенкой от 2 до 8.
Pre-K
K
СМОТРЕТЬ ДЕТАЛИ
Чувство числа
Пропустить счет на 1 с
Попросите вашего малыша пропустить счет на 1, чтобы играть в эту игру.
Pre-K
K
ПОДРОБНЕЕ
Чувство числа
Давайте составим песенку о числах от 2 до 10
Наслаждайтесь чудом математики с песенкой о числах от 2 до 10.
Pre-K
K
ПОДРОБНЕЕ
Чувство чисел
Обратный отсчет и завершение последовательности
Практикуйте сверхсилу восприятия чисел, научившись считать в обратном порядке и завершать последовательность.

Pre-K
K
ПОДРОБНЕЕ
Связанные рабочие листы
Просмотреть все 305 рабочих листов
Чувство числа
Завершить счет
Будьте на пути к тому, чтобы стать математиком, практикуясь в счете.
ПОДРОБНЕЕ
Чувство чисел
Угадай пропущенное число
Раскройте секреты математического волшебства, угадав пропущенное число.
ПОДРОБНЕЕ
Number Sense
Счет с помощью картинок
Проверьте свои навыки, потренировавшись считать по картинкам.
ПОДРОБНЕЕ
Чувство чисел
Считай и сопоставляй предметы
Преврати математику в увлекательное занятие, считая и сопоставляя предметы.
ПОДРОБНЕЕ
Чувство числа
Определить больше или меньше
Распечатайте этот рабочий лист, чтобы потренироваться определять «больше» или «меньше», как математическую легенду!
ПОДРОБНЕЕ
Чувство числа
Счет с помощью предметов
Превратите математику в увлекательное занятие, считая с помощью предметов.

ПОДРОБНЕЕ
Чувство числа
Счет предметов до 10
Научитесь чувствовать число со скоростью молнии, считая предметы до 10.
ПОДРОБНЕЕ
Чувство числа
Счет с использованием предметов
Учащиеся должны считать с помощью предметов, чтобы улучшить свои математические навыки.
ПОСМОТРЕТЬ ПОДРОБНОСТИ
Чувство числа
Сколько объектов
Разбавьте время занятий математикой, определив, сколько объектов.
ПОДРОБНЕЕ
Чувство числа
Счет в группе
Используйте этот рабочий лист для распечатки, чтобы считать в группе, чтобы укрепить свои математические навыки.
ПОДРОБНЕЕ
Чувство числа
Считай и сравнивай
Используйте этот рабочий лист для печати, чтобы считать и сравнивать, чтобы укрепить свои математические навыки.

ПОСМОТРЕТЬ ПОДРОБНОСТИ
Чувство чисел
Создание групп объектов
Изучайте чувство чисел со скоростью молнии, создавая группы объектов.
ПОДРОБНЕЕ
Чувство чисел
Группы животных
Сосредоточьтесь на основных математических навыках с помощью этого забавного рабочего листа, работая с группами животных.
ПОДРОБНЕЕ
Чувство числа
Группа яблок
Сосредоточьтесь на основных математических навыках с помощью этого веселого рабочего листа, потренировавшись с группой яблок.
ПОДРОБНЕЕ
Чувство чисел
Определить лишние предметы
В этом рабочем листе учащиеся получат возможность идентифицировать лишние предметы.
ПОДРОБНЕЕ
Универсальное решение для всех потребностей обучения в классе.

Дайте вашему ребенку страсть и уверенность, чтобы безбоязненно учиться чему-либо самостоятельно
Родители, зарегистрируйтесь бесплатно
Учителя, используйте бесплатно
4413+
4417+
ПОХОЖИЕ ТЕМЫЗагадочный номер 6174 | plus.maths.org
Март 2006 г.
Каждый может разгадать тайну
Число 6174 — действительно загадочное число. На первый взгляд это может показаться не столь очевидным. Но, как мы скоро увидим, любой, кто умеет вычитать, может раскрыть тайну, которая делает 6174 таким особенным.
Операция Капрекара
В 1949 году математик Д. Р. Капрекар из Девлали, Индия, разработал процесс, теперь известный как операция Капрекара . Сначала выберите четырехзначное число, в котором цифры не одинаковы (это не 1111, 2222,…). Затем переставьте цифры, чтобы получить наибольшее и наименьшее числа, которые могут состоять из этих цифр.
 Наконец, вычтите
наименьшее число из наибольшего, чтобы получить новое число, и продолжайте повторять операцию для каждого нового числа.
Наконец, вычтите
наименьшее число из наибольшего, чтобы получить новое число, и продолжайте повторять операцию для каждого нового числа.Это простая операция, но Капрекар обнаружил, что она приводит к удивительному результату. Давайте попробуем, начиная с числа 2005, цифры прошлого года. Максимальное число, которое мы можем составить из этих цифр, — 5200, а минимальное — 0025 или 25 (если одна или несколько цифр равны нулю, вставьте их в левую часть минимального числа). Вычитания:
5200 — 0025 = 5175
7551 — 1557 = 5994
9954 — 4599 = 5355
5553 — 3555 = 1998
9981 — 1899 = 8082
8820 — 0288 = 8532
8532 —
8820 — 0288 = 8532
8532 —
8820 — 0288 = 8532
8532 — 8082
8820 — 0288 = 8532
853. 8532 — 2352 —
8820 — 0288.Когда мы достигаем 6174, операция повторяется, каждый раз возвращая 6174. Мы называем число 6174 ядром этой операции. Итак, 6174 — это ядро для работы Kaprekar, но так ли оно особенное, как 6174? Что ж, мало того, что 6174 является единственным ядром для этой операции, у него в рукаве есть еще один сюрприз.
 Давайте попробуем еще раз, начиная с другого числа, скажем, 1789..
Давайте попробуем еще раз, начиная с другого числа, скажем, 1789..9871 — 1789 = 8082
8820 — 0288 = 8532
8532 — 2358 = 6174Мы снова достигли 6174!
Очень загадочное число…
Когда мы начали с 2005, процесс достиг 6174 за семь шагов, а для 1789 за три шага. Фактически, вы достигаете 6174 для всех четырехзначных чисел, у которых не все цифры одинаковы. Это чудесно, не так ли? Операция Капрекара настолько проста, но дает такой интересный результат. И это станет еще более интригующим, если мы подумаем о причине, по которой все четырехзначные числа достигают это загадочное число 6174.
Только 6174?
Цифры любого четырехзначного числа можно расположить в максимальное число, расположив цифры в порядке убывания, и в минимальное число, расположив их в возрастающем порядке. Итак, для четырех цифр a,b,c,d , где
9 ≥ а ≥ б ≥ в ≥ г ≥ 0
и a, b, c, d не все одинаковые цифры, максимальное число abcd и минимальное dcba .

Мы можем вычислить результат операции Капрекара, используя стандартный метод вычитания, примененный к каждому столбцу этой задачи:
и б в д — д в б и А Б С Д что дает отношения
D = 10 + d — а (так как а > d) С = 10 + с — 1 — b = 9 + с — b (так как b > с — 1) B = b — 1 — c (так как b > c) А = а — г для тех номеров, где a>b>c>d .
Число будет повторяться при операции Капрекара, если полученное число ABCD можно записать, используя начальные четыре цифры a,b,c и d . Таким образом, мы можем найти ядра операции Капрекара, рассматривая все возможные комбинации { a, b, c, d } и проверяя, удовлетворяют ли они приведенным выше соотношениям.
 Каждый из 4-х! = 24 комбинации дают систему из четырех
одновременных уравнений с четырьмя неизвестными, поэтому мы должны решить эту систему для a, b, c и d .
Каждый из 4-х! = 24 комбинации дают систему из четырех
одновременных уравнений с четырьмя неизвестными, поэтому мы должны решить эту систему для a, b, c и d .Оказывается, что только одна из этих комбинаций имеет целочисленные решения, удовлетворяющие 9 ≥ a ≥ b ≥ c ≥ d ≥ 0 . Эта комбинация равна ABCD = bdac , а решение уравнений равно a =7, б =6, в =4 и г =1. Это ABCD = 6174. Не существует действительных решений одновременных уравнений, полученных из некоторых цифр в {a,b,c,d} быть равным. Поэтому число 6174 — единственное число, не изменённое операцией Капрекара — наше таинственное число уникально.
Для трехзначных чисел происходит то же самое. Например, применение операции Капрекара к трехзначному числу 753 дает следующее:
753 — 357 = 396
963 — 369 = 594
954 — 459 = 495
954 — 459 = 495Число 495 является уникальным ядром для операции над трехзначными числами, и все трехзначные числа достигают 495 с помощью операции.
 Почему бы вам не проверить это самостоятельно?
Почему бы вам не проверить это самостоятельно?Как быстро до 6174?
Это было примерно в 1975 году, когда я впервые услышал о числе 6174 от друга, и тогда я был очень впечатлен. Я думал, что будет легко доказать, почему это явление произошло, но я не мог найти причину этого. Я использовал компьютер, чтобы проверить, все ли четырехзначные числа достигли ядра 6174 за ограниченное количество шагов. Программа, в которой было около 50 операторов на языке Visual Базовый, проверено все 8991 четырехзначное число от 1000 до 9999, где цифры не были одинаковыми.
В таблице ниже показаны результаты: каждое четырехзначное число, в котором не все цифры равны, достигает 6174 в процессе Капрекара и не более чем за семь шагов. Если вы не достигли 6174 после семикратного использования операции Капрекара, значит, вы допустили ошибку в своих расчетах и должны попробовать еще раз!
Итерация Частота 0 1 1 356 2 519 3 2124 4 1124 5 1379 6 1508 7 1980 Куда до 6174?
Моя компьютерная программа проверила все 8991 число, но в своей статье Малкольм Лайнс объясняет, что при исследовании операции Капрекара достаточно проверить только 30 из всех возможных четырехзначных чисел.

Как и раньше, предположим, что четырехзначное число равно abcd , где
9 ≥ а ≥ б ≥ в ≥ г ≥ 0 .
Вычислим первое вычитание в процессе. Максимальное число — 1000a+100b+10c+d , а минимальное число — 1000d+100c+10b+a . Итак, вычитание:
1000а + 100b + 10с + d — (1000d + 100с + 10b + а)
= 1000(а-г) + 100(б-в) + 10(в-б) + (д-а)
= 999(а-г). ) + 90(б-в)Возможные значения (a-d) от 1 до 9, а (b-c) от 0 до 9. Перебрав все возможности, мы можем увидеть все возможные результаты первого вычитания в процесс. Они показаны в таблице 1.
Таблица 1: Числа после первого вычитания в процессе Капрекара
Нас интересуют только числа, в которых не все цифры равны и
а ≥ б ≥ в ≥ г ,
поэтому нам нужно рассматривать только те, где (а-г) ≥ (б-в) . Таким образом, мы можем игнорировать серую область в таблице 1, которая содержит те числа, где
(а-г) < (б-в) .

Теперь расположим цифры чисел в таблице в порядке убывания, чтобы получить максимальное число, готовое ко второму вычитанию:
Таблица 2: Максимальное число, готовое ко второму вычитанию
Мы можем игнорировать дубликаты в таблице 2 (серые области), и осталось всего 30 чисел, чтобы пройти остальную часть процесса. На следующем рисунке показаны маршруты, по которым эти числа достигают 6174.
Как эти 30 чисел достигают 6174
Из этого рисунка видно, как все четырехзначные числа достигают 6174 и достигают его не более чем за семь шагов. Даже в этом случае я все еще думаю, что это очень таинственно. Я предполагаю, что Капрекар, который открыл это число, был чрезвычайно умен или имел много времени, чтобы подумать об этом!
Двухзначные, пятизначные, шестизначные и далее…
Мы видели, что четырех- и трехзначные числа достигают уникального ядра, но как насчет других чисел? Оказывается, ответы на них не так впечатляют. Давайте попробуем это для двузначного числа, скажем, 28:
82 — 28 = 54
54 — 45 = 9
90 — 09 = 81
81 — 18 = 63
63 — 36 = 27
72 — 27 = 45
54 — 45 = 9Не нужно много времени, чтобы проверить, что все двузначные числа попадут в цикл 9→81→63→27→45→9.
 В отличие от трех- и четырехзначных чисел, для двузначных чисел нет уникального ядра.
В отличие от трех- и четырехзначных чисел, для двузначных чисел нет уникального ядра.А как насчет пяти цифр? Есть ли ядро для пятизначных чисел, таких как 6174 и 495? Чтобы ответить на этот вопрос, нам нужно использовать тот же процесс, что и раньше: проверить 120 комбинаций из {a,b,c,d,e} вместо ABCDE такой, что
9 ≥ а ≥ б ≥ в ≥ г ≥ д ≥ 0
и
abcde-edcba = ABCDE .
К счастью, расчеты уже были выполнены на компьютере, и известно, что ядра для работы Капрекара с пятизначными числами нет. Но все пятизначные числа достигают одного из следующих трех циклов:
71973→83952→74943→62964→71973
75933→63954→61974→82962→75933
59994→53955→59994Как отмечает Малкольм Лайнс в своей статье, проверка того, что происходит для шести и более цифр, займет много времени, и эта работа становится крайне скучной! Чтобы избавить вас от этой участи, в следующей таблице показаны ядра для двухзначных и десятизначных чисел (подробнее см.
 Развлекательная математика). Оказывается, операция Капрекара переводит каждое число в уникальное ядро только для трех- и четырехзначных чисел.
Развлекательная математика). Оказывается, операция Капрекара переводит каждое число в уникальное ядро только для трех- и четырехзначных чисел.Цифры Ядро 2 Нет 3 495 4 6174 5 Нет 6 549945, 631764 7 Нет 8 63317664, 97508421 9 554999445, 864197532 10 6333176664, 9753086421, 9975084201 Красиво, но особенно?
Мы видели, что все трехзначные числа достигают 495, а все четырехзначные числа достигают 6174 при операции Капрекара. Но я не объяснил, почему все такие числа достигают уникального ядра. Является ли это явление случайным или существует какая-то более глубокая математическая причина, почему это происходит? Каким бы красивым и таинственным ни был результат, он может быть случайным.

Давайте остановимся и рассмотрим красивую головоломку Юкио Ямамото из Японии.
Если перемножить два пятизначных числа, получится 123456789. Сможете ли вы угадать два пятизначных числа?
Это очень красивая головоломка и можно подумать, что за ней должна скрываться большая математическая теория. Но на самом деле красота эта второстепенна, есть и другие очень похожие, но не такие красивые экземпляры. Например:
(Мы можем дать вам подсказку, которая поможет вам решить эти головоломки, и вот ответы.)
Если бы я показал вам головоломку Ямамото, вы бы вдохновились решить ее, потому что она такая красивая, но если я показал вам вторую загадку, которая может вас совсем не заинтересовать. Я думаю, что задача Капрекара похожа на головоломку Ямамото с угадыванием чисел. Нас тянет к обоим, потому что они такие красивые. И поскольку они так прекрасны, мы чувствуем, что в них должно быть что-то большее, хотя на самом деле их красота может просто случайно.
 Такие недоразумения привели к развитию математики и естественных наук в прошлом.
Такие недоразумения привели к развитию математики и естественных наук в прошлом.Достаточно ли знать, что все четырехзначные числа достигают 6174 с помощью операции Капрекара, но не знать, почему? До сих пор никто не мог сказать, что все числа, попадающие в уникальное ядро для трех- и четырехзначных чисел, являются случайным явлением. Это свойство кажется настолько удивительным, что заставляет нас ожидать, что за ним скрывается большая теорема теории чисел. Если мы сможем ответить на этот вопрос, мы может найти это просто красивое недоразумение, но мы надеемся, что нет.
Примечание от редакции: многие читатели заметили, что многократное сложение цифр любого из ядер операции Капрекара всегда равно 9. Узнайте почему в этом продолжении статьи.
Ссылки
- Капрекар, Д. Р., «Другой пасьянс», Scripta Mathematica , том 15, стр. 244-245 (1949)
- Гарднер, Мартин, «Волшебные числа Доктора Матрицы», японская версия, Токио: Кинокуния (1978)
- Lines, Малкольм Э.
 , Число для ваших мыслей: факты и предположения о числах … , Бристоль: Hilger (1986)
, Число для ваших мыслей: факты и предположения о числах … , Бристоль: Hilger (1986) - Нишияма, Ютака, Алгоритм Кураши-но, Киото: Наканисия (1993)
Об авторе
Ютака Нишияма — профессор Экономического университета Осаки, Япония. После изучения математики в Университете Киото он проработал 14 лет в IBM Japan. Он интересуется математикой, которая встречается в повседневной жизни, и написал семь книг на эту тему. Самый последний, названный «Тайна пяти в природе», исследует, среди прочего, почему многие цветы имеют пять лепестков. Профессор Нишияма в настоящее время находится с визитом в Кембриджском университете.
Игра в угадывание четырехзначных чисел · GitHub
»’Создать случайным образом 4-значное число. Попросите пользователя угадать четырехзначное число. За каждую цифру, которую пользователь правильно угадывает в правильном месте, он получает «корову». 
За каждую цифру, правильно угаданную пользователем в неправильном месте, стоит «бык». Каждый раз, когда пользователь делает предположение, сообщайте ему, сколько у него «коров» и «быков». Как только пользователь угадает правильное число, игра окончена.»’ случайный импорт #Компьютер выбирает случайное число, и мы превращаем это число в строку, которая нам понадобится позже. число = случайный.randint(1000,10000) число_строка = строка (число) Оператор #Print, предоставляющий игроку инструкции по игре. 
print «Я выбрал четырехзначное число. Ваша задача — угадать его. За каждую правильную цифру на правильном месте в угаданном числе вы получаете «корову». За каждую правильную цифру на неправильном месте вы получить «быка». #Подскажите игроку сделать первое предположение. предположение = str(raw_input(«Давай: Угадай четырехзначное число:»)) #Инициализируйте число догадок равным 1. В конце мы предоставим игроку общее количество догадок, которое потребовалось для получения правильного ответа. догадок = 1 #Основной цикл, благодаря которому игра работает.  Продолжается, пока предположение игрока не совпадает с числом компьютера.
Продолжается, пока предположение игрока не совпадает с числом компьютера.в то время как предположение != num_string: список1 = список(num_string) список2 = список(угадать) коров = [] быков = [] «»»Первый цикл для проверки «коров», ниже. Обратите внимание на строки ‘should_restart’ для сброса цикла после того, как корова будет найдена. Это необходимо для того, чтобы «диапазон» оператора работал после удаления совпадающих элементов из их исходных списков (что изменяет «диапазон»). 
Удаление совпадающих элементов из исходных списков может быть (?) самым простым способом заставить игру работать, чтобы предотвратить двойной подсчет.»»» должен_перезапустить = Истина , а должен_перезапустить: должен_перезапустить = Ложь для i в диапазоне (len (list1)): , если список1[i] == список2[i]: коров.добавление(список1[i]) список1[i] список2[i] должен_перезапустить = Истина перерыв «»»Второй цикл для проверки «быков», ниже. 
Еще раз обратите внимание на строки ‘should_restart’ для сброса цикла после обнаружения быка.»»» должен_перезапустить = Истина , а должен_перезапустить: должен_перезапустить = Ложь для i в диапазоне (len (list1)): , если список1[i] в списке2: быки.append(list1[i]) list2.remove(list1[i]) список1[i] должен_перезапустить = Истина перерыв print «У вас есть %d коров и %d быков» % (len(коровы), len(быки)) предположение = str(raw_input(«Угадай другое четырехзначное число:»)) догадок += 1 print «Да! Это ответ.  Вы угадали за %d догадок.» % (догадки)
Вы угадали за %d догадок.» % (догадки)Насколько безопасны четырех- и шестизначные мобильные телефоны
изображение: Филипп Маркерт из Института ИТ-безопасности имени Хорста Гёртца (слева) и Максимилиан Голла из Института безопасности и конфиденциальности Макса Планка в Бохуме совместно работали над исследованием. посмотреть еще
Кредит: RUB, Marquard
Немецко-американская группа исследователей ИТ-безопасности исследовала, как пользователи выбирают PIN-код для своих мобильных телефонов и как их можно убедить использовать более безопасную комбинацию цифр. Они обнаружили, что шестизначные PIN-коды на самом деле обеспечивают немногим большую безопасность, чем четырехзначные. Они также показали, что черный список, используемый Apple для предотвращения особенно частых PIN-кодов, можно оптимизировать, и что было бы еще более целесообразно реализовать его на устройствах Android.

Филипп Маркерт, Даниэль Бейли и профессор Маркус Дюрмут из Института ИТ-безопасности имени Хорста Герца в Рурском университете Бохума провели исследование совместно с доктором Максимилианом Голлой из Института безопасности и конфиденциальности Макса Планка в Бохуме и профессором Адамом Авивом из Университет Джорджа Вашингтона в США. Исследователи представят результаты на симпозиуме IEEE по безопасности и конфиденциальности в Сан-Франциско в мае 2020 года. Препринт статьи можно найти в Интернете: https://arxiv.org/abs/2003.04868.
Обширное исследование пользователей
В ходе исследования исследователи попросили пользователей устройств Apple и Android установить четырех- или шестизначный PIN-код, а затем проанализировали, насколько легко их было угадать. При этом они предположили, что злоумышленник не знал жертву и ему было все равно, чей мобильный телефон разблокирован. Соответственно, лучшей стратегией атаки будет сначала попробовать наиболее вероятные PIN-коды.

Некоторые участники исследования могли выбрать свой PIN-код наугад. Другие могли выбирать только те PIN-коды, которые не были включены в черный список. Если они пытались использовать один из PIN-кодов из черного списка, они получали предупреждение о том, что эту комбинацию цифр легко угадать.
В ходе эксперимента эксперты по ИТ-безопасности использовали различные черные списки, в том числе настоящий список от Apple, который они получили, проверив на компьютере все возможные комбинации PIN-кодов на iPhone. Более того, они также создали свои собственные более или менее полные черные списки.
Шестизначные PIN-коды не более безопасны, чем четырехзначные
Выяснилось, что шестизначные PIN-коды не обеспечивают большей безопасности, чем четырехзначные. «С математической точки зрения, конечно, огромная разница», — говорит Филипп Маркерт. С помощью четырехзначного PIN-кода можно создать 10 000 различных комбинаций, а с помощью шестизначного PIN-кода можно создать миллион комбинаций.
 «Однако пользователи предпочитают определенные комбинации; некоторые PIN-коды используются чаще, например, 123456 и 654321», — объясняет Филипп Маркерт. Это означает, что пользователи не используют весь потенциал шестизначных кодов. «Похоже, что в настоящее время пользователи интуитивно не понимают, что делает шестизначный PIN-код безопасным», — полагает Маркус Дюрмут.
«Однако пользователи предпочитают определенные комбинации; некоторые PIN-коды используются чаще, например, 123456 и 654321», — объясняет Филипп Маркерт. Это означает, что пользователи не используют весь потенциал шестизначных кодов. «Похоже, что в настоящее время пользователи интуитивно не понимают, что делает шестизначный PIN-код безопасным», — полагает Маркус Дюрмут.Предусмотрительно выбранный четырехзначный PIN-код достаточно надежен, главным образом потому, что производители ограничивают количество попыток ввода PIN-кода. Apple полностью блокирует устройство после десяти неверных вводов. На Android-смартфоне нельзя вводить разные коды один за другим в быстрой последовательности. «За 11 часов можно проверить 100 комбинаций чисел», — отмечает Филипп Маркерт.
Черные списки могут быть полезны
Исследователи обнаружили 274 комбинации цифр в черном списке Apple для четырехзначных PIN-кодов. «Поскольку у пользователей есть только десять попыток угадать PIN-код на iPhone, черный список не делает его более безопасным», — заключает Максимилиан Голла.
 По мнению исследователей, черный список будет иметь больше смысла на устройствах Android, поскольку там злоумышленники могут опробовать больше PIN-кодов.
По мнению исследователей, черный список будет иметь больше смысла на устройствах Android, поскольку там злоумышленники могут опробовать больше PIN-кодов.Исследование показало, что идеальный черный список для четырехзначных PIN-кодов должен содержать около 1000 записей и немного отличаться от списка, используемого в настоящее время Apple. Согласно исследованию, наиболее распространенными четырехзначными PIN-кодами являются 1234, 0000, 2580 (цифры располагаются вертикально друг под другом на цифровой клавиатуре), 1111 и 5555.
На iPhone пользователи могут игнорировать предупреждение о том, что они ввели часто используемый PIN-код. Таким образом, устройство не всегда предотвращает выбор записей из черного списка. В целях своего исследования эксперты по ИТ-безопасности также более внимательно изучили этот аспект. Некоторым участникам тестирования, которые ввели ПИН-код из черного списка, после предупреждения было позволено выбрать, вводить ли новый ПИН-код или нет. Остальным пришлось установить новый PIN-код, которого не было в списке.
 В среднем PIN-коды обеих групп было одинаково трудно угадать.
В среднем PIN-коды обеих групп было одинаково трудно угадать.Более безопасны, чем замки с графическим ключом
Еще один результат исследования показал, что четырех- и шестизначные PIN-коды менее безопасны, чем пароли, но более безопасны, чем замки с графическим ключом.
Самые популярные PIN-коды
Согласно исследованию, десять самых популярных четырехзначных PIN-кодов: самые популярные шестизначные PIN-коды: 123456, 654321, 111111, 000000, 123123, 666666, 121212, 112233, 789.456, 159753
###
Отказ от ответственности: AAAS и EurekAlert! не несут ответственности за достоверность новостных сообщений, размещенных на EurekAlert! содействующими учреждениями или для использования любой информации через систему EurekAlert.
Personal Security_v2 — Hudson Reporter
Автор: Carl Mazzanti, президент eMazzanti Technologies в Хобокене
Продолжается рост утечек данных для малых предприятий, и владельцам необходимо защитить свои деловые и личные учетные записи от хакеров.
 Эта угроза усугубляется тем, что киберпреступники часто используют LinkedIn и другие профили в социальных сетях в качестве входа в компанию, где они могут получить незаконный доступ к мегабайтам конфиденциальных данных.
Эта угроза усугубляется тем, что киберпреступники часто используют LinkedIn и другие профили в социальных сетях в качестве входа в компанию, где они могут получить незаконный доступ к мегабайтам конфиденциальных данных.— Реклама —
Несколько лет назад Марк Цукерберг усвоил этот урок на собственном горьком опыте. Сообщаемый взлом LinkedIn привел к раскрытию дополнительных учетных записей, принадлежащих генеральному директору Facebook (Meta). Несмотря на его предполагаемую сообразительность — он является магнатом социальных сетей №1 в мире — Цукерберг, как сообщается, совершил несколько фатальных ошибок, в том числе использовал легко взламываемый пароль (дадада) для нескольких учетных записей.
Опасные ярлыки
Элементарные запреты включают использование общих слов и одного и того же пароля для более чем одной учетной записи. Но другие распространенные ошибки часто совершают знающие пользователи, которые не хотят запоминать длинные коды входа.
 Например, АНБ, ФБР и другие спецслужбы отметили, что Главный центр специальных технологий ГРУ при Главном разведывательном управлении Генерального штаба России выпустил вредоносное ПО, нацеленное на американцев и других пользователей. Таким образом, повторение паролей еще более опасно сейчас, когда хакеры стали более изощренными.
Например, АНБ, ФБР и другие спецслужбы отметили, что Главный центр специальных технологий ГРУ при Главном разведывательном управлении Генерального штаба России выпустил вредоносное ПО, нацеленное на американцев и других пользователей. Таким образом, повторение паролей еще более опасно сейчас, когда хакеры стали более изощренными.Хорошая новость заключается в том, что защитить учетные записи несложно. Одной из простых мер является многофакторная аутентификация (MFA), для которой требуется как минимум два независимых фактора для входа в аккаунт. Одним фактором может быть пароль, а вторым может быть одноразовый пароль, отправленный на телефон пользователя. Таким образом, учетная запись будет в безопасности, даже если один фактор будет украден.
Другим решением является увеличение длины исходного пароля или PIN-кода (персонального идентификационного номера). 7777 — один из самых распространенных — и поэтому легко угадываемых PIN-кодов. Тем не менее, многие устройства теперь поддерживают PIN-коды, длина которых превышает четыре цифры, и простое добавление еще нескольких цифр дает большую разницу из-за задействованной математики.
 Например, четырехзначный ПИН-код имеет только 10 000 уникальных комбинаций, а шестизначный ПИН-код — 1 000 000.
Например, четырехзначный ПИН-код имеет только 10 000 уникальных комбинаций, а шестизначный ПИН-код — 1 000 000.Некоторые устройства поддерживают буквенно-цифровые PIN-коды или пароли, что еще больше усложняет задачу для хакеров. Пользователи могут упростить процесс, используя слова или фразы, которые значимы для них, но малоизвестны другим; поэтому следует избегать легко взламываемых комбинаций, таких как дни рождения, годовщины, личные номера телефонов и адреса.
Как и числовые PIN-коды, более длинные пароли лучше. Рассмотрим пароль из восьми символов, например betashow — злоумышленник, имеющий доступ к сложным программным инструментам, может мгновенно взломать этот пароль. Но если добавить четыре символа, возможно, сделать его бета-шоу лучше , хакеру потребуется около двух недель (может быть, меньше), чтобы угадать этот 12-символьный пароль. Однако при добавлении еще восьми символов, таких как betashowbest shipping , злоумышленнику потребуется около 21 веков , чтобы взломать этот 20-буквенный пароль.
 Это большая отдача от небольших усилий.
Это большая отдача от небольших усилий.Креативные парольные фразы — более длинные пароли, состоящие из нескольких случайных слов — также могут замедлить работу хакеров. Есть простые способы сделать пароль длиннее, например, «самые быстрые тропические лыжи», «прогулка по апельсинам» или «BrieflyMoreDiamond». Конечно, эти специфические фразы не следует использовать, так как они теперь появились в широко распространенной публикации. Хотя пароли труднее взломать, их несложно запомнить, поскольку пользователь может создавать в уме картинки в качестве напоминания, например «синий нос на фиолетовой кирпичной стене».
Комбинации могут быть созданы из различных ситуаций. Например, когда у вас есть шумный коллега, эта ситуация может привести к фразе-паролю, например: «Я слышу Билла через весь офис!» Можно использовать слова или фразы, которые оживляют личную память, но слов, связанных друг с другом, таких как кодовая фраза «нежный океанский бриз», следует избегать, поскольку их легко угадать.
 Вместо этого более сильной, но запоминающейся фразой может быть «ноутбук черничный автомобиль».
Вместо этого более сильной, но запоминающейся фразой может быть «ноутбук черничный автомобиль».Изложите некоторые правила
Создание паролей и кодовых фраз – это только часть решения, поскольку при их создании также важно знать и соблюдать политику организации. Например, компании может потребоваться учетная запись с минимальным количеством символов, сочетание буквенных и цифровых символов или специальных символов. Эти требования безопасности могут немного усложнить задачу для пользователя, но они также усложнят ее для хакеров.
Со всеми этими требованиями некоторые люди могут опасаться, что не смогут запомнить уникальный пароль для каждого устройства: ноутбука, настольного компьютера, iPad, мобильного устройства, бизнес-ноутбука и т. д. Но есть решение: использование менеджера паролей – программного приложения, которое безопасно хранит учетные данные в Интернете и управляет ими. Он стоит за мастер-паролем, поэтому нужно помнить только один пароль, а менеджер автоматически генерирует новые пароли каждый раз, когда пользователь входит в устройство.

Менеджер паролей похож на защищенное хранилище: когда все имена пользователей и пароли учетных записей находятся в хранилище, главный пароль — единственный, который необходимо сохранить в памяти. Ввод этого мастер-пароля разблокирует хранилище паролей, и оттуда пользователь может получить любой пароль, который ему нужен.
Однако безопасность разработки пароля или парольной фразы будет нарушена, если пользователь запишет их. Тайник может показаться хорошим, но опыт показывает, что есть большая вероятность, что кто-то найдет пароль, мастер-пароль или PIN-код. Точно так же пароли, PIN-коды и другая информация для входа не должны храниться на самом устройстве, даже если оно зашифровано. А пользователь, который отправляет себе ПИН-код или пароль по электронной почте или в текстовом сообщении, навлекает на себя неприятности.
Еще одна рекомендация — никогда не сообщать пароль или PIN-код, потому что никогда нельзя быть уверенным, что кто-то другой сохранит их учетные данные в безопасности.



 Занятия данного факультатива должны содействовать развитию у детей математического образа мышления: краткости речи, умелому использованию символики, правильному применению математической терминологии и т.д.
Занятия данного факультатива должны содействовать развитию у детей математического образа мышления: краткости речи, умелому использованию символики, правильному применению математической терминологии и т.д.


 Сравнение предметов по размеру и форме. Пространственные представления, взаимное расположение предметов. Уяснение формальной сущности логических умозаключений при решении задач с неполными данными, лишними, нереальными данными.
Сравнение предметов по размеру и форме. Пространственные представления, взаимное расположение предметов. Уяснение формальной сущности логических умозаключений при решении задач с неполными данными, лишними, нереальными данными. Игроматика. (4часа).
Игроматика. (4часа). Числа. Арифметические действия. (4часа).
Числа. Арифметические действия. (4часа).

 (4часа).
(4часа). 3 – 4 классы. – Волгоград: Учитель, 2008.
3 – 4 классы. – Волгоград: Учитель, 2008.



 Но в реальной жизни часто придерживаются более компромиссных подходов. Во-первых, цис- и транс-изомеры часто неплохо делятся, потому что у них очень разные свойства. Транс-изомеры, например, часто более легко кристаллизуются потому что у них более симметричные молекулы, которые легче пакуются в хорошие кристаллы. Да и обычная колоночная хроматография тоже вполне неплохо делит большинство цис- и транс-изомеров. Поэтому, если для Виттига есть исходные, а это часто именно так и есть, потому что это очень простые исходные, иной раз проще замесить Виттига, и потратить немного времени на разделение изомеров. Особенно это касается получение диарилэтиленов (стильбенов) и диарилбутадиенов – это очень легко делается по Виттигу, потому что исходные бензилгалогениды и бензальдегиды или коричные альдегиды весьма легкодоступны, а сама реакция Виттига идет чрезвычайно легко и с очень высокими выходами. Не стоит забывать, что из-за мезомерного эффекта такие Виттиги можно считать стабилизированными, хоть и не в такой степени, как те, что мы рассмотрели выше – а любая дополнительная стабилизация увеличивает относительный выход транс-изомера.
Но в реальной жизни часто придерживаются более компромиссных подходов. Во-первых, цис- и транс-изомеры часто неплохо делятся, потому что у них очень разные свойства. Транс-изомеры, например, часто более легко кристаллизуются потому что у них более симметричные молекулы, которые легче пакуются в хорошие кристаллы. Да и обычная колоночная хроматография тоже вполне неплохо делит большинство цис- и транс-изомеров. Поэтому, если для Виттига есть исходные, а это часто именно так и есть, потому что это очень простые исходные, иной раз проще замесить Виттига, и потратить немного времени на разделение изомеров. Особенно это касается получение диарилэтиленов (стильбенов) и диарилбутадиенов – это очень легко делается по Виттигу, потому что исходные бензилгалогениды и бензальдегиды или коричные альдегиды весьма легкодоступны, а сама реакция Виттига идет чрезвычайно легко и с очень высокими выходами. Не стоит забывать, что из-за мезомерного эффекта такие Виттиги можно считать стабилизированными, хоть и не в такой степени, как те, что мы рассмотрели выше – а любая дополнительная стабилизация увеличивает относительный выход транс-изомера. Стабилизация проявляется ещё и в том, что для образования таких илидов не всегда нужны такие сильные основания как були, очень часто используют что-то попроще и подешевле, например, трет-бутилат или даже другие алкоголяты, или даже межфазная щёлочь – кислотность соответствующих фосфониевых солей повышена и они легче депротонируются. Многие такие реакции вообще можно вести, не получая заранее илид, а добавляя основание в смесь альдегида и фосфониевой соли, это тем более возможно потосу что бензальдегиды неенолизуемы и очень стойки к действию сильных оснований. В этих реакциях обычно образуется смесь с преобладанием транс-изомера, из которой часто этот транс-изомер просто выкристаллизовывается или прямо в реакции, или во время выделения продуктов. Про цис-изомер даже часто вообще забывают, он остается в маточнике. Поэтому в литературе полно примеров, когда такими Виттигами как будто получаются чистые транс-изомеры – авторам нужно было именно это, оно вывалилось, выход не фонтан, но, в общем, плевать на то, что остался невыделенным еще и цис-изомер, утащивший в канализацию хорошую долю выхода.
Стабилизация проявляется ещё и в том, что для образования таких илидов не всегда нужны такие сильные основания как були, очень часто используют что-то попроще и подешевле, например, трет-бутилат или даже другие алкоголяты, или даже межфазная щёлочь – кислотность соответствующих фосфониевых солей повышена и они легче депротонируются. Многие такие реакции вообще можно вести, не получая заранее илид, а добавляя основание в смесь альдегида и фосфониевой соли, это тем более возможно потосу что бензальдегиды неенолизуемы и очень стойки к действию сильных оснований. В этих реакциях обычно образуется смесь с преобладанием транс-изомера, из которой часто этот транс-изомер просто выкристаллизовывается или прямо в реакции, или во время выделения продуктов. Про цис-изомер даже часто вообще забывают, он остается в маточнике. Поэтому в литературе полно примеров, когда такими Виттигами как будто получаются чистые транс-изомеры – авторам нужно было именно это, оно вывалилось, выход не фонтан, но, в общем, плевать на то, что остался невыделенным еще и цис-изомер, утащивший в канализацию хорошую долю выхода. С точки зрения хорошего органика так делать нехорошо, но, что поделать, людям часто нужны соединения для какой-то серьёзной работы, хочется их получить хоть с каким выходом и не париться.
С точки зрения хорошего органика так делать нехорошо, но, что поделать, людям часто нужны соединения для какой-то серьёзной работы, хочется их получить хоть с каким выходом и не париться.