Неравенства Бернулли в математике с примерами решения
Оглавление:
Неравенства БернуллиБернулли Якоб (1654-1705) — швейцарский учёный, профессор Базель-ского университета (Швейцария). Известен своими работами по дифференциальной геометрии, вариационному исчислению и математической физике.
Теорема 1 (неравенство Бернулли с натуральным показателем). При любом действительном x (x > — 1) и при любом натуральном n справедливо неравенство
Доказательство. Воспользуемся для доказательства методом полной математической индукции (по параметру n ).
1) При n=1 имеем: — верно.
2) Предположим, что неравенство выполняется при некотором произвольном n = k , т.е. и докажем, что тогда оно выполняется и при n = k + 1, т. е. . В самом деле,
е. . В самом деле,
3) В силу произвольности k отсюда следует, что данное неравенство выполнено сразу при всех натуральных n . Заметим, что неравенство Бернулли обращается в равенство только при x = 0 или n = 1.
Сформулируем без доказательства неравенство Бернулли в случае, когда показатель степени в неравенстве не является натуральным.
Теорема 2 (неравенство Бернулли с произвольным показателем). Пусть . Тогда справедливы неравенства
причём неравенства обращаются в равенства только при x = 0.
Пример №135.Найти наибольшее значение функции
Решение:
Дважды воспользуемся на области определения функции неравенством Бернулли:
Складывая эти неравенства, получаем неравенство
причём равенство достигается при x = 0 (в каждом из двух неравенств). Поэтому f(о) = 2 — наибольшее значение функции.
Поэтому f(о) = 2 — наибольшее значение функции.
Ответ:
Рассмотрим, наконец, обобщённое неравенство Бернулли для нескольких действительных чисел.
Теорема 3 (неравенство Бернулли для n чисел). Пусть— числа одного знака, Тогда
Доказательство (методом математической индукции).
1) При n = 1 неравенство, очевидно, выполняется.
2) Предположим, что неравенство верно при некотором n = k
и докажем, что тогда оно выполняется и при n = k + 1, т.е.
Действительно,
3) В силу произвольности k отсюда заключаем, что данное неравенство выполняется при любом натуральном n . Неравенство обращается в равенство, только если n = 1 или
В частности, при получаем
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Предмет математика
Эти страницы возможно вам будут полезны:
Помогите решить / разобраться (М)
Сообщения без ответов | Активные темы | Избранное
Правила форума
Посмотреть правила форума
| CMTV |
| ||
26/08/16 |
| ||
| |||
| Shadow |
| ||
26/08/11 |
| ||
| |||
| nnosipov |
| |||
20/12/10 |
| |||
| ||||
| novichok2018 |
| |||
16/04/18 |
| |||
| ||||
| CMTV |
| ||
26/08/16 |
| ||
| |||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 5 ] |
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
| Найти: |
 $$
$$$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.

 01.2020, 11:56
01.2020, 11:56  То есть, получаем противоречие.
То есть, получаем противоречие. 01.2020, 13:45
01.2020, 13:45  01.2020, 18:32
01.2020, 18:32 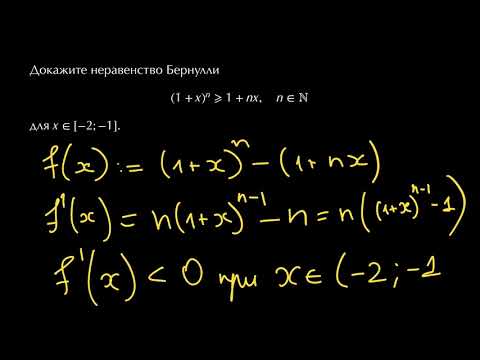 65-81) эти результаты повторены более подробно, а также рассмотрены несколько десятков обобщений неравенства Бернулли. Кстати там замечено, что обычно пропускается, что это неравенство в обычной формулировке справедливо и при .
65-81) эти результаты повторены более подробно, а также рассмотрены несколько десятков обобщений неравенства Бернулли. Кстати там замечено, что обычно пропускается, что это неравенство в обычной формулировке справедливо и при . 
