как самому вычислить арктангенс угла зная его тангенс, без таблицы и калькулятора? — Спрашивалка
как самому вычислить арктангенс угла зная его тангенс, без таблицы и калькулятора? — СпрашивалкаСЛ
Светлана Лаврова
Учусь дома по видео урокам одной интернет школы. Но тут незадача: учитель объясняет урок и говорит «Мы знаем что тангенс угла равен 0.8 чтобы узнать скольким градусам равен угол которому этот тангенс принадлежит нужно сделать «Shift tan» и получится что угол равен 38.6 градусов» И всё! Урок кончается и я так и не понял что за «Shift tan» и как он это решил.
Очень прошу помочь если кто знает что это такое объясните пожалуйста понятным я зыком (Т. К. я с лингвистическими наклонностями ребёнок, и собираюсь поступать в лингвистический университет, я плохо понимаю математику. Но сдавать математику всё равно надо, чтоб школу закончить)
- угол
- таблица
- калькулятор
- тангенс
Анастасия Кислова
У меня на калькуляторе, чтобы включить обратные функции надо нажать кнопку Shift.
Если хочу посчитать арктангенс, то потом жму кнопку tan
А без калькулятора и таблиц можно попробовать разложить в ряд
Ольга Рослова
Чтобы с такой точностью определить угол с гуманитарным наклоном — нужно очень постараться (и думаю без таблиц и калькулятора не получиться) .
тангенс угла = отношение отношение противоположного катета к прилягаемом = 0.8 (один катет больше от другого в 0.8 раз)
Имея эти данные можно найти размер гипотенузы (теорема Пифагора) и соответсвенно остальные углы.
Но для точного определения угола — калькулятор, таблицы…
ДШ
Денис Шкватов
Он объяснял как пользоваться калькулятором.
Странно, ты этого не понял. Не мог же калькулятор из неоткуда взяться! Неужели ни в начальных уроках ни на протяжении этого никто ничего о калькуляторе не говорил? Может, язык, сперва, подтянуть нужно, что бы понять, о чём речь идёт, а потом уже математику учить ?
И, кстати, вне СНГ калькуляторы прям с детского сада — нормальное явление (и в учебниках и на экзаменах — везде !), так что подавляющее большинство видеоуроков иностранного происхождения будут идти с использованием оного прибора.
Похожие вопросы
Какие функции есть на калькуляторах? Что делает кнопка М+? Как вычислить арктангенс, арксинус и т. п. на калькуляторе?
Нахождение угла по известному тангенсу. Как найти угол, если тангенс равен -0,5780
как на телефонном калькуляторе вычислить косинус, синус, тангенс?
как найти арктангенс? я знаю что тангенс считается как синус делить на косинус, а арктангенс?
как найти синус, косинус и тангенс угла?
Пожалуйста, помогите найти тангенс угла
Тангенс угла между двумя катетами
СРОЧНО!! ! Найдите тангенс угла АОВ
Помогите найти тангенс угла
Как, зная тангенс угла, найти значение угла?
Арктангенс числа a. Функция y = arctg x, её свойства и график. Как найти арктангенс числа
12+
3 дня назад
Математика от Баканчиковой74 подписки
Тригонометрия 8-11 класс. Что такое арктангенс числа? Как найти арктангенс любого числа? Как построить график функции y = arctg x? Какие свойства есть у функции y = arctg x? Сегодня мы ответим на эти вопросы.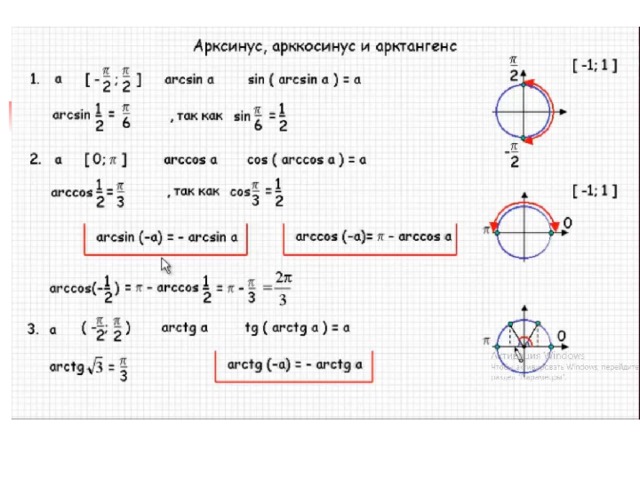
Если Вы не видели наши предыдущие уроки по теме: «Функция y=arcsin x, её график и свойства», «Функция y=arccos x, её график и свойства» и «Обратная функция, её свойства и график», то обязательно посмотрите их, тогда этот урок будет Вам очень понятен. Мы покажем Вам, как получается график функции y = arctg x, и почему область значений функции y = arctg x ограничена интервалом (-π/2; π/2). Дадим Вам определение арктангенса числа а. Отметим две характерные ошибки, которые допускают ученики при вычислении арктангенса. На примере 5 упражнений покажем Вам нюансы вычисления арктангенса числа. Подробный план урока и ссылки на предыдущие уроки Вы можете найти в описании под видео.
00:00 Начало видео.
00:29 Что нужно вспомнить?
01:04 График функции y = arctg x.
07:05 Что такое арктангенс числа а?
08:29 Как найти арктангенс любого числа?
11:10 Характерные ошибки при вычислении арктангенса.
12:23 На следующем уроке …
Если Вы впервые на нашем канале или не смотрели наши предыдущие уроки, то рекомендуем Вам посмотреть следующие видео:
Арккосинус числа a.
Arctan Функции Excel: Используйте ATAN и ATAN2 для вычисления арктангенса
В Excel есть две функции для вычисления арктангенса или арктангенса.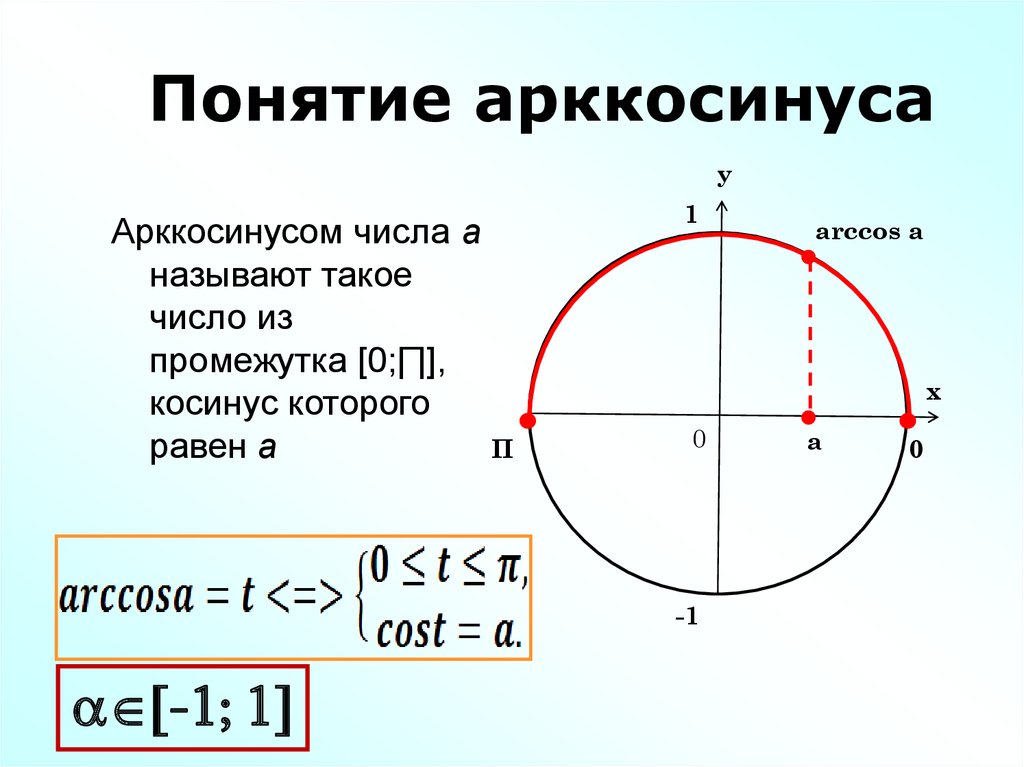
Эти две функции — ATAN и ATAN2 («атан» — сокращение от арктангенса), и каждая из них имеет специфическое применение в зависимости от желаемых результатов, которые вы хотите получить, и доступных входных данных. В общем, я бы рекомендовал использовать ATAN, если:
- Вас интересует только первый квадрант единичного круга
- Вы не знаете значения x и y
Однако используйте функцию ATAN2, если:
- Вы хотите вернуть углы во всех четырех квадрантах единичной окружности
- Вы знаете значения x и y
Использование ATAN для расчета арктангенса в Excel
Функция ATAN возвращает результат между -π/2 и π/2 радиан (или от -90 до 90 градусов), или, другими словами, в первом и четвертом квадрантах.
Синтаксис:
ATAN(число)
У ATAN есть только один аргумент: число, из которого вы хотите вычислить арктангенс. А поскольку имеется только один аргумент, Excel не может определить, в каком квадранте должно находиться решение.
Чтобы продемонстрировать это, я настроил единичный круг в электронной таблице, показанной ниже, создав серию углов от 0 до 360 градусов и вычислив значения x и y с помощью функций COS и SIN. , соответственно:
Далее я вычислил арктангенс y относительно x с помощью ATAN, а так как Excel работает с углами в радианах, я преобразовал результат в градусы с помощью функции ГРАДУСЫ. Формула выглядела так:
=ГРАДУСЫ(ATAN(y/x))
Здесь следует отметить несколько вещей:
- Абсолютные значения углов никогда не превышают 90 градусов, и
- Значения во втором (II) квадранте столбца C теперь находятся в четвертом квадранте столбца F.
- Значения в третьем (III) квадранте столбца C теперь находятся в первом квадранте столбца F.
Нанесение результатов на единичный круг выглядит следующим образом:
Как видите, Excel ограничил результаты первым и четвертым квадрантами.
Почему это случилось?
Поскольку у функции ATAN есть только один аргумент, Excel вычисляет значение y/x до того, как вычислит функцию ATAN.
Таким образом, он не может определить, является ли ввод в ATAN отрицательным, потому что значение x или значение y отрицательно. Следовательно, он не может сказать, должен ли результат быть во втором квадранте или в четвертом квадранте, поэтому по умолчанию он просто указывает на четвертый квадрант.
Аналогичным образом, когда входное значение положительное, исходный квадрант может быть либо первым (и x, и y положительными), либо третьим (и x, и y отрицательными).
Мы могли бы использовать сложную вложенную функцию ЕСЛИ, чтобы получить результаты обратно во все четыре квадранта, но, к счастью, в Excel есть еще одна функция под названием ATAN2, которая поможет нам.
Использование ATAN2 для вычисления арктангенса в Excel
Функцию ATAN2 также можно использовать для вычисления арктангенса в Excel. Эта функция возвращает результат в диапазоне от -π до π радиан (или от -180 до 180 градусов) с использованием всех четырех квадрантов.
Синтаксис:
ATAN2(x_num,y_num)
Есть два аргумента:
- Значение x «x_num»
- Y-значение «y_num»
Вводя в функцию два значения, Excel может определить, к какому квадранту относится значение.
- Квадрант 1, если оба значения x и y положительны
- Квадрант 2, если x отрицательный, а y положительный
- Квадрант 3, если и x, и y отрицательные
- Квадрант 4, если x положительный, а y отрицательный
Итак, если мы используем формулу
=ГРАДУСЫ(ATAN2(x_num,y_num))
Мы получаем следующие результаты: возвращая значения во всех четырех квадрантах. Однако, если мы предпочитаем получать результаты в виде углов от 0 до 360 градусов, а не от -180 до 180, мы можем использовать простую функцию ЕСЛИ, чтобы добавить 360, если результат меньше 0.
= ЕСЛИ(результат<0,результат+360,результат)
Подведение итогов
Надеюсь, теперь вы понимаете ограничения ATAN и когда лучше использовать ATAN2 для вычисления арктангенса или арктангенса в Excel.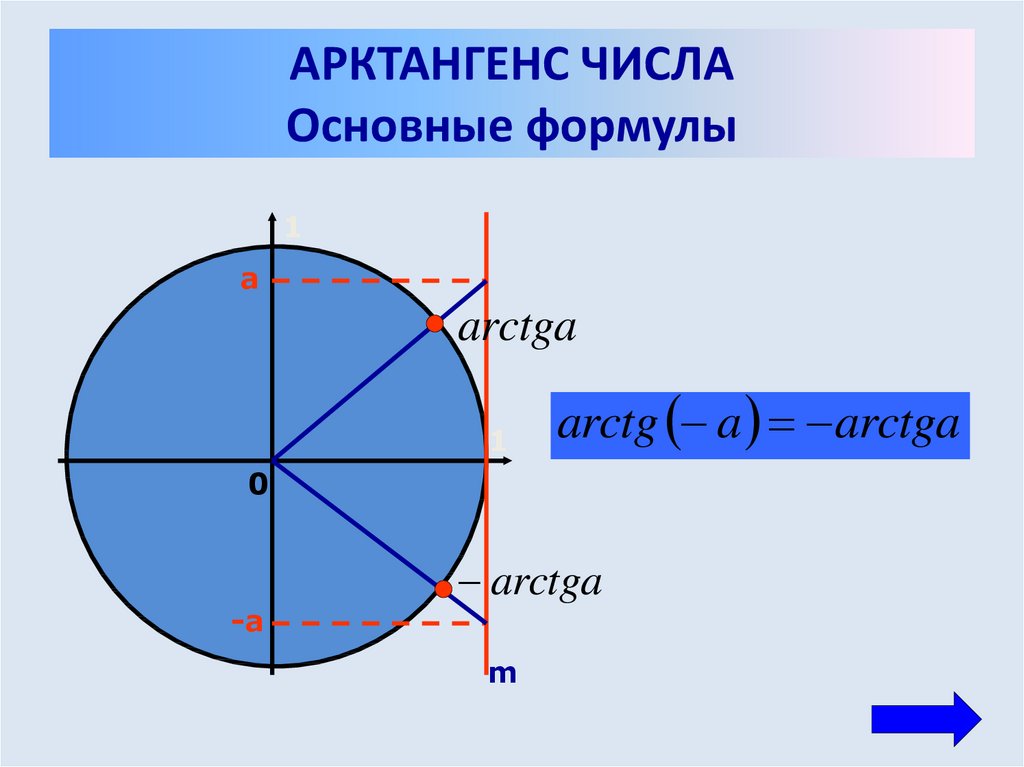
В общем, используйте ATAN, если:
- Вы работаете только в первом квадранте
- Вы не знаете значения x или y
Используйте функцию ATAN2, если:
- Вам нужны углы во всех четырех квадрантах
- Значения x и y известны 9{\circ}$. Но я не понимаю, вручную, как я могу получить степени.
Это со страницы Википедии:
$8/20 = 0,4$
0,4$ — это отношение подъема к пробегу, но я не знаю, что они сделали после этого.
Как это получилось до $21,8$ градусов (или $0,38$ радиан)?
- тригонометрия
$\endgroup$
7
$\begingroup$ 97}{7}+….. $$ Здесь следует отметить, что эта серия продолжается без конца. Это просто означает, что мы не можем найти точное значение $\arctan$ любого угла в радианах. Следовательно, мы приближаемся.
