Дроби меньше больше: Сравнение дробей

Сравнение дробей

Продолжаем изучать дроби. Сегодня мы поговорим об их сравнении. Тема интересная и полезная. Она позволит новичку почувствовать себя учёным в белом халате.

Суть сравнения дробей заключается в том, чтобы узнать какая из двух дробей больше или меньше.

Чтобы ответить на вопрос какая из двух дробей больше или меньше, пользуются операциями отношения, такими как больше (>) или меньше (<).

Ученые-математики уже позаботились о готовых правилах, позволяющие сразу ответить на вопрос какая дробь больше, а какая меньше. Эти правила можно смело применять.

Мы рассмотрим все эти правила и попробуем разобраться, почему происходит именно так.

Сравнение дробей с одинаковыми знаменателями

Дроби, которые нужно сравнить, попадаются разные. Самый удачный случай это когда у дробей одинаковые знаменатели, но разные числители. В этом случае применяют следующее правило:

Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше. И соответственно меньше будет та дробь, у которой числитель меньше.

Например, сравним дроби  и  и ответим какая из этих дробей больше. Здесь одинаковые знаменатели, но разные числители. У дроби  числитель больше, чем у дроби  . Значит дробь   больше, чем . Так и отвечаем. Отвечать нужно с помощью значка больше ( > )

Этот пример можно легко понять, если вспомнить про пиццы, которые разделены на четыре части. пиццы больше, чем пиццы:

Каждый согласится с тем, что первая пицца больше, чем вторая.

---

Сравнение дробей с одинаковыми числителями

Следующий случай это когда числители дробей одинаковые, но знаменатели разные. Для таких случаев предусмотрено следующее правило:

Из двух дробей с одинаковыми числителями больше та дробь, у которой знаменатель меньше. И соответственно меньше та дробь, у которой знаменатель больше.

Например, сравним дроби и . У этих дробей одинаковые числители. У дроби знаменатель меньше, чем у дроби . Значит дробь больше, чем дробь . Так и отвечаем:

Этот пример можно легко понять, если вспомнить про пиццы, которые разделены на три и четыре части. пиццы больше, чем пиццы:

 

Каждый согласится с тем, что первая пицца больше, чем вторая.

---

Сравнение дробей с разными числителями и разными знаменателями

Нередко случается так, что приходиться сравнивать дроби с разными числителями и разными знаменателями. Например, сравнить дроби  и .

Чтобы ответить на вопрос, какая из этих дробей больше или меньше, нужно привести их к одинаковому (общему) знаменателю. Затем можно будет легко определить какая дробь больше или меньше.

Приведём дроби  и  к одинаковому (общему) знаменателю. Найдём наименьшее общее кратное (НОК) знаменателей обеих дробей. НОК знаменателей дробей  и  это число 6.

Теперь находим дополнительные множители для каждой дроби. Разделим НОК на знаменатель первой дроби . НОК это число 6, а знаменатель первой дроби это число 2. Делим 6 на 2, получаем дополнительный множитель 3. Записываем его над первой дробью:

Теперь найдём второй дополнительный множитель. Разделим НОК на знаменатель второй дроби . НОК это число 6, а знаменатель второй дроби это число 3. Делим 6 на 3, получаем дополнительный множитель 2. Записываем его над второй дробью:

Умножим дроби на свои дополнительные множители:

Мы пришли к тому что дроби, у которых были разные знаменатели, превратились в дроби, у которых одинаковые знаменатели. А как сравнивать такие дроби мы уже знаем. Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше:

Правило правилом, а мы попробуем разобраться почему больше, чем . Для этого выделим целую часть в неправильной дроби . В дроби ничего выделять не нужно, поскольку эта дробь уже правильная.

После выделения целой части в дроби , получим следующее выражение:

Теперь можно легко понять, почему больше, чем .  Давайте нарисуем эти дроби в виде пицц:

2 целые пиццы и пиццы, больше чем пиццы.

---

Вычитание смешанных чисел. Сложные случаи.

Вычитая смешанные числа иногда можно обнаружить, что всё идёт не так гладко как хотелось бы.

При вычитании чисел уменьшаемое должно быть больше вычитаемого. Только в этом случае будет получен нормальный ответ.

Например, 10 − 8 = 2

10 — уменьшаемое

8 — вычитаемое

2 — разность

Уменьшаемое 10 больше вычитаемого 8, поэтому мы получили нормальный ответ 2.

А теперь посмотрим, что будет если уменьшаемое окажется меньше вычитаемого. Пример 5 − 7 = −2

5 — уменьшаемое

7 — вычитаемое

−2 — разность

В этом случае мы выходим за пределы привычных для нас чисел и попадаем в мир отрицательных чисел, где нам ходить пока рано, а то и опасно. Чтобы работать с отрицательными числами, нужна соответствующая математическая подготовка, которую мы ещё не получили.

Если при решении примеров на вычитание вы обнаружите, что уменьшаемое меньше вычитаемого, то можете пока пропустить такой пример. Работать с отрицательными числами допустимо только после их изучения.

С дробями ситуация та же самая. Уменьшаемое должно быть больше вычитаемого. Только в этом случае можно будет получить нормальный ответ. А чтобы понять больше ли уменьшаемая дробь, чем вычитаемая, нужно уметь сравнить эти дроби.

Например, решим пример .

Это пример на вычитание. Чтобы решить его, нужно проверить больше ли уменьшаемая дробь, чем вычитаемая. больше чем 

поэтому смело можем вернуться к примеру и решить его:

Теперь решим такой пример 

Проверяем больше ли уменьшаемая дробь, чем вычитаемая. Обнаруживаем, что она меньше:

В этом случае разумнее остановиться и не продолжать дальнейшее вычисление. Вернёмся к этому примеру, когда изучим отрицательные числа.

Смешанные числа перед вычитанием тоже желательно проверять. Например, найдём значение выражения .

Сначала проверим больше ли уменьшаемое смешанное число, чем вычитаемое. Для этого переведём смешанные числа в неправильные дроби:

Получили дроби с разными числителями и разными знаменателями. Чтобы сравнить такие дроби, нужно привести их к одинаковому (общему) знаменателю. Не будем подробно расписывать как это сделать. Если испытываете затруднения на этом моменте, обязательно изучите действия с дробями.

После приведения дробей к одинаковому знаменателю, получаем следующее выражение:

Теперь нужно сравнить дроби и . Это дроби с одинаковыми знаменателями. Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше.

У дроби числитель больше, чем у дроби  . Значит дробь больше, чем дробь .

А это значит что уменьшаемое больше, чем вычитаемое

А значит мы можем вернуться к нашему примеру и смело решить его:

---

Пример 3. Найти значение выражения

Проверим больше ли уменьшаемое, чем вычитаемое.

Переведём смешанные числа в неправильные дроби:

Получили дроби с разными числителями и разными знаменателями. Приведем данные дроби к одинаковому (общему) знаменателю:

Теперь сравним дроби   и . У дроби числитель меньше, чем у дроби , значит дробь меньше, чем дробь

А это значит, что и уменьшаемое меньше, чем вычитаемое

А это гарантировано приведёт нас в мир отрицательных чисел. Поэтому разумнее остановиться на этом месте и не продолжать вычисление. Продолжим его после изучения отрицательных чисел.

---

Пример 4. Найти значение выражения

Проверим больше ли уменьшаемое, чем вычитаемое.

Переведём смешанные числа в неправильные дроби:

Получили дроби с разными числителями и разными знаменателями. Приведем их к одинаковому (общему) знаменателю:

Теперь нужно сравнить дроби    и  . У дроби  числитель больше, чем у дроби . Значит дробь  больше, чем дробь .

А это значит, что уменьшаемое больше, чем вычитаемое

Поэтому мы смело можем продолжить вычисление нашего примера:

Сначала мы получили ответ . Эту дробь мы сократили на 2 и получили дробь , но такой ответ нас тоже не устроил и мы выделили целую часть в этом ответе. В итоге получили ответ .

---

Задания для самостоятельного решения

Задание 1. Сравнить дроби:

Решение:

Показать решение

Задание 2. Сравнить дроби:

Решение:

Показать решение

Задание 3. Сравнить дроби:

Решение:

Показать решение

Задание 4. Сравнить дроби:

Решение:

Показать решение

---

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Опубликовано Автор

§ Сравнение дробей. Сравнение дробей с разными знаменателями

Дроби. Числитель и знаменатель Сокращение дробей Сравнение дробей Смешанные числа. Выделить целую часть Сложение дробей. Общий знаменатель Вычитание дробей Умножение дробей Деление дробей Нахождение дроби от числа Нахождение целого по известной дроби

Также как и натуральные числа обыкновенные дроби можно сравнивать.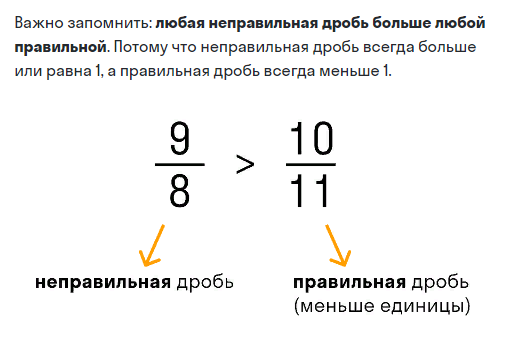

Рассмотрим две неравные дроби на числовой оси. Меньшая дробь будет располагаться левее, а большая — правее.

Равные дроби соответствует одной и той же точке на числовой оси.

На рисунке хорошо видно, что

<

. Но необязательно пользоваться числовой осью, чтобы сравнивать дроби.

Сравнение дробей с одинаковыми знаменателями

Запомните!

Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше.

Пример. Сравним

и

.

В обеих дробях одинаковый знаменатель равный 5.

В первой дроби числитель равен 1 и он меньше числителя второй дроби, который равен 4.

Поэтому первая дробь

меньше второй

.

Сравнение дробей с одинаковыми числителями

Запомните!

Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше.

Пример. Сравним

и

. Ответ:

Правило выше легче понять, если представить, что у вас в руках куски торта. В первом случае торт разделили на 2 части (знаменатель дроби равен 2), и у вас в руках половина торта, а во втором — торт поделили на 8 частей, и у вас в руках маленькая часть торта.

Сравнение дробей с разными знаменателями

Запомните!

Чтобы сравнить дроби с разными знаменателями, нужно привести дроби к общему знаменателю.

После приведения дробей к общему знаменателю, дроби сравниваются по правилу сравнения дробей с одинаковыми знаменателями.

Пример. Сравним

и

.

• Приводим дроби к общему знаменателю.
• Сравниваем дроби с одинаковыми знаменателями.

Запомните!

Любая неправильная дробь больше любой правильной.

Это объясняется тем, что неправильная дробь всегда больше или равна 1, а правильная дробь всегда меньше 1.

Дроби. Числитель и знаменатель Сокращение дробей Сравнение дробей Смешанные числа. Выделить целую часть Сложение дробей. Общий знаменатель Вычитание дробей Умножение дробей Деление дробей Нахождение дроби от числа Нахождение целого по известной дроби

Калькулятор сравнения дробей

Базовый калькулятор

Сравнение дробей

Сравнение целых чисел, десятичных дробей, дробей, смешанных чисел или процентов

Операнд 1
а также Операнд 2

Ответ:

1 3/4 < 1,875

---

с показателем работы

---

Использование приведенных входов:

1 3/4

1.

875

Переписывание этих вводов AS DECIMAL:

1 3/

1.875 1.875 1.875 1.875.

1,75

1,875

Сравнение десятичных значений, которые мы имеем:

1 3/4

1,875

1,75

<

1,75

<

0002 1,875

Следовательно, сравнение показывает:

1 3/4 < 1,875

Поделитесь этой ссылкой для ответа: help
Вставьте эту ссылку в электронное письмо, текст или социальные сети.

Получить виджет для этого калькулятора

© Calculator Soup

Поделитесь этим калькулятором и страницей

Калькулятор Используйте

Сравните дроби, чтобы найти, какая дробь больше, а какая меньше. Вы также можете использовать этот калькулятор для сравнения смешанных чисел, сравнения десятичных дробей, сравнения целых чисел и сравнения неправильных дробей.

Как сравнивать дроби

Чтобы сравнить дроби с разными знаменателями, преобразуйте их в эквивалентные дроби с одинаковым знаменателем.

1. Если у вас есть смешанные числа, преобразуйте их в неправильные дроби
2. Найдите наименьший общий знаменатель (LCD) дробей
3. Преобразуйте каждую дробь в ее эквивалент с ЖК-дисплеем в знаменателе
4. Сравните дроби: если знаменатели совпадают, вы можете сравнить числители. Дробь с большим числителем и есть большая дробь.

Пример:

Сравните 5/6 и 3/8.

Найдите ЖК-дисплей: числа, кратные 6, равны 6, 12, 18, 24, 30 и т. д. Кратные 8 равны 8, 16, 24, 32 и т. д. Наименьшее общее кратное равно 24, поэтому мы используем его как наименьший общий знаменатель.

Преобразуйте каждую дробь в эквивалентную дробь с помощью ЖК-дисплея.
Для 5/6 умножьте числитель и знаменатель на 4, чтобы получить LCD = 24 в знаменателе.

\( \dfrac{5}{6} \times \dfrac{4}{4} = \dfrac{20}{24} \)

Для 3/8 умножьте числитель и знаменатель на 3, чтобы получить LCD = 24 в знаменателе.

\( \dfrac{3}{8} \times \dfrac{3}{3} = \dfrac{9}{24} \)

Сравните дроби. Поскольку знаменатели похожи, вы можете сравнить числители. 20 больше 9, поэтому:

Так как   

\( \dfrac{20}{24} > \dfrac{9}{24} \)

  мы заключаем   

\( \dfrac{5}{6} > \dfrac{3}{8} \)

Дополнительную справку по дробям см. Калькулятор фракций, Упрощение калькулятор дробей и Калькулятор смешанных чисел.

Ссылки: Помощь с дробями Нахождение наименьшего общего знаменателя.

 

Подписаться на CalculatorSoup:

Сравнение дробей.

Методы, объяснение и примеры

Сравнение дробей означает определение большей и меньшей дроби между любыми двумя или более дробями. Поскольку дроби состоят из двух частей — числителя и знаменателя, их сравнивают по определенному набору правил. Давайте узнаем больше о сравнении дробей на этой странице.

1.	Как сравнивать дроби?
2.	Сравнение дробей с одинаковыми знаменателями
3.	Сравнение дробей с разными знаменателями
4.	Десятичный метод сравнения дробей
5.	Сравнение дробей с помощью визуализации
6.	Сравнение дробей с помощью перекрестного умножения
7.	Часто задаваемые вопросы о сравнении дробей

Как сравнивать дроби?

Сравнение дробей включает набор правил, связанных с числителем и знаменателем. При сравнении любых двух дробей мы узнаем большую и меньшую дробь. Нам нужно сравнивать дроби в нашей повседневной жизни. Например, когда нам нужно сравнить соотношение ингредиентов при соблюдении рецепта или сравнить результаты экзаменов и т. д. Итак, давайте рассмотрим различные методы сравнения дробей, чтобы лучше понять концепцию.

Что такое дробь?

Прежде чем исследовать концепцию сравнения дробей, давайте вспомним дроби. Дробь является частью целого и состоит из двух частей — числителя и знаменателя. Числитель — это число в верхней части дробной черты, а знаменатель расположен под дробной чертой.

Теперь давайте поговорим подробнее о сравнении дробей.

Сравнение дробей с одинаковыми знаменателями

При сравнении дробей с одинаковыми знаменателями становится легче определить большую или меньшую дробь. Проверив, совпадают ли знаменатели, мы можем просто найти дробь с большим числителем. Если и числители, и знаменатели равны, дроби также равны. Например, сравним 6/17 и 16/17

• Шаг 1: Обратите внимание на знаменатели данных дробей: 6/17 и 16/17. Знаменатели одинаковы.
• Шаг 2: Теперь сравните числители. Мы видим, что 16 > 6,
• Шаг 3: Дробь с большим числителем является большей дробью. Следовательно, 6/17 < 16/17.

Сравнение дробей с разными знаменателями

Для сравнения дробей с разными знаменателями нам нужно преобразовать их в одинаковые знаменатели, для чего мы должны найти наименьшее общее кратное (НОК) знаменателей. Когда знаменатели сделаны одинаковыми, мы можем легко сравнивать дроби. Например, сравним 1/2 и 2/5.

• Шаг 1: Обратите внимание на знаменатели данных дробей: 1/2 и 2/5. Они разные. Итак, найдем НОК 2 и 5. НОК(2, 5) = 10,
.
• Шаг 2: Теперь переведем их так, чтобы знаменатели стали одинаковыми. Умножим первую дробь на 5/5, то есть 1/2 × 5/5 = 5/10.
• Шаг 3: Теперь умножим вторую дробь на 2/2, то есть 2/5 × 2/2 = 4/10.
• Шаг 4: Сравните дроби: 5/10 и 4/10. Поскольку знаменатели одинаковы, мы сравним числители и увидим, что 5 > 4 .
• Шаг 5: Дробь с большим числителем является большей дробью, то есть 5/10 > 4/10. Следовательно, 1/2 > 2/5

Следует отметить, что если знаменатели разные, а числители одинаковые, то мы можем легко сравнивать дроби, глядя на их знаменатели. Дробь с меньшим знаменателем имеет большее значение, а дробь с большим знаменателем имеет меньшее значение. Например, 2/3 > 2/6.

Десятичный метод сравнения дробей

В этом методе мы сравниваем десятичные значения дробей. Для этого числитель делится на знаменатель и дробь преобразуется в десятичную. Затем сравниваются десятичные значения. Например, давайте сравним 4/5 и 6/8.

• Шаг 1: Напишите 4/5 и 6/8 десятичными знаками. 4/5 = 0,8 и 6/8 = 0,75.
• Шаг 2: Сравните десятичные значения. 0,8 > 0,75
• Шаг 3: Дробь с большим десятичным значением будет большей дробью. Следовательно, 4/5 > 6/8

Сравнение дробей с помощью визуализации

Мы можем использовать различные графические методы и модели для визуализации более крупных фракций. Обратите внимание на приведенный ниже рисунок, на котором показаны модели A и B, представляющие две дроби. Мы можем легко определить, что 4/8 < 4/6, потому что 4/6 покрывает большую заштрихованную область, чем 4/8. Обратите внимание, что меньшая часть занимает меньшую площадь того же целого. Здесь следует принять во внимание, что размер моделей A и B должен быть точно таким же, чтобы сравнение было достоверным. Затем каждая модель делится на равные части, соответствующие их соответствующим знаменателям.

Сравнение дробей с помощью перекрестного умножения

Для сравнения дробей методом перекрестного умножения мы умножаем числитель одной дроби на знаменатель другой дроби. Давайте разберемся в этом с помощью примера. Сравните 1/2 и 3/4. Обратите внимание на приведенный ниже рисунок, который лучше объясняет это.

• Шаг 1: Когда мы умножаем данные дроби крестом для их сравнения, мы должны иметь в виду, что если мы умножаем числитель первой дроби на знаменатель второй дроби, мы должны записать произведение следующим к первой дроби. Здесь 1 × 4 = 4, и мы будем писать 4 рядом с первой дробью. (Напишите произведение рядом с выбранным числителем)
• Шаг 2: Точно так же, когда мы умножаем числитель второй дроби на знаменатель первой дроби, мы должны писать произведение рядом со второй дробью. Здесь 3 × 2 = 6, и мы будем писать 6 возле второй дроби.
• Шаг 3: Теперь сравним произведения 4 и 6. Поскольку 4 < 6, можно легко сравнить соответствующие дроби, то есть 1/2 < 3/4. Следовательно, 1/2 < 3/4

☛ Похожие темы

• Типы дробей
• Калькулятор сравнения дробей
• Умножение дробей
• Деление дробей
• Десятичные числа и дроби

 

Примеры сравнения дробей

1. Пример 1: Почему 5/11 > 4/11? Вы можете объяснить?

   Решение:

   Сравнение дробей упрощается, если знаменатели совпадают. 5/11 и 4/11 имеют одинаковые знаменатели; следовательно, мы можем просто сравнивать дроби, наблюдая за числителями. Дробь с большим числителем и будет большей дробью. 5 > 4. Следовательно, 5/11 > 4/11.

2. Пример 2: Райана попросили доказать, что данные дроби: 4/6 и 6/9 равны. Можете ли вы доказать это, используя метод LCM?

   Решение:

   Мы можем сделать знаменатели одинаковыми, найдя НОК знаменателей данных дробей. НОК 6 и 9 равно 18. Итак, мы умножим 4/6 на 3/3, (4/6) × (3/3) = 12/18 и 6/9 на 2/2, (6/ 9) × (2/2) = 12/18, что преобразует их в одинаковые дроби с одинаковыми знаменателями. Новые дроби с теми же знаменателями будут 12/18 и 12/18. Следовательно, обе дроби равны: 4/6 = 6/9.. Следовательно, 4/6 = 6/9.

3. Пример 3: Сравните дроби 5/8 и 7/12.

   Решение: Для сравнения дробей с разными знаменателями нам нужно найти НОК знаменателей. НОК 8 и 12 равно 24. Итак, давайте умножим 5/8 на 3/3, то есть 5/8 × 3/3 = 15/24. Теперь умножим 7/12 на 2/2, то есть 14/24. Теперь, когда у нас есть похожие дроби 15/24 и 14/24, мы можем легко их сравнить. Так как 15 > 14, 5/8 > 7/12. Следовательно, 5/8 > 7/12.

перейти к слайдуперейти к слайдуперейти к слайду

Хотите построить прочную основу в математике?

Выйдите за рамки запоминания формул и поймите «почему», стоящее за ними. Испытайте Cuemath и приступайте к работе.

Записаться на бесплатный пробный урок

Практические вопросы по сравнению дробей

 

перейти к слайдуперейти к слайдуперейти к слайду

Часто задаваемые вопросы о сравнении дробей

Что означает сравнение дробей?

Сравнение дробей означает сравнение заданных дробей, чтобы определить, является ли одна дробь меньше, больше или равна другой дроби. Как и целые числа, мы можем сравнивать дроби, используя одни и те же символы: <,> и =. Существуют различные методы и правила сравнения дробей в зависимости от числителя и знаменателя, а также от вида дробей.

Каково правило сравнения дробей с одинаковым знаменателем?

Когда знаменатели данного набора дробей одинаковы, дробь с меньшим числителем является меньшей дробью, а дробь с большим числителем — большей дробью. При равенстве числителей дроби считаются равными. Например, если нам нужно сравнить 2/5 и 4/5, нам просто нужно проверить и сравнить числители. Поскольку 2 < 4, можно сказать, что 2/5 < 4/5.

По какому правилу сравнивать дроби с одинаковым числителем?

Если дроби имеют одинаковый числитель, то дробь с меньшим знаменателем больше. Например, сравним дроби с одним и тем же числителем. Даны дроби 1/2 и 1/6. Теперь из них дробь с меньшим знаменателем равна 1/2. Таким образом, 1/2 является большей из данных дробей.

Что такое эквивалентные дроби?

Дроби, имеющие разные числители и знаменатели, но равные по своим значениям, называются эквивалентными дробями. Например, 5/10 и 6/12 являются эквивалентными дробями, поскольку обе они в упрощенном виде равны 1/2.

Какой самый простой способ сравнения дробей?

Самый простой и быстрый способ сравнения дробей — преобразовать их в десятичные числа. Дробь с большим десятичным значением является большей дробью.

Зачем нужно сравнивать дроби?

Сравнение дробей является важным компонентом, который помогает учащимся развивать свое числовое представление о размере дроби. Это помогает им понять, что стратегии, которые они используют для сравнения целых чисел, не обязательно применимы при сравнении дробей. Например, 1/4 больше 1/8, хотя целое число 8 больше 4.

Как сравнивать дроби с разными знаменателями?

Чтобы сравнивать дроби с разными знаменателями, нам нужно найти наименьшее общее кратное (НОК) знаменателей и преобразовать данные дроби в подобные дроби, сделав их знаменатели одинаковыми, и тогда числители можно будет легко сравнить. Например, давайте сравним 7/12 и 9/16.