Дробно-рациональные неравенства — алгоритмы и примеры решения
Наибольшую трудность в алгебре 7 класса вызывают дробно-рациональные неравенства. Их решение выполняется по определенной методике. Чтобы ею воспользоваться, необходимы некоторые базовые знания, без которых применить алгоритм будет невозможно. С этой целью специалисты разработали пошаговую инструкцию, позволяющую за короткий промежуток времени освоить материал на профессиональном уровне.
Содержание
- Общие сведения
- Неравенства и их классификация
- Понятие многочлена
- Формулы сокращенного произведения
- Метод интервалов
- Способы решения уравнений
- Обыкновенные дроби
- Методика вычислений
Общие сведения
Дробно-рациональные неравенства — тождества, состоящие из числителя и знаменателя, которые представлены многочленами произвольной степени. Для их решения потребуются следующие знания:
Специалисты рекомендуют последовательно изучать каждый из пунктов, даже при условии, что тема является знакомой. Необходимо с самого начала пройти все необходимые темы, заполнив ими «пробелы». Начинать следует с общих понятий о неравенствах.
Неравенства и их классификация
Неравенство — это математическое выражение, состоящее из левой и правой частей, разделенных между собой символами логических операций, а именно: больше (>), меньше (<), больше или равно (>=) и меньше или равно (<=). Данные тождества классифицируются на 2 группы:
К первой группе относятся выражения, которые не содержат знаменателя с переменной.
Если она присутствует, то оно относится ко второй. Примером является выражение вида: (t-4)/(t+4) > 0. Однако «(t-4)/4 > 0» относится к первой группе.
Неравенства также классифицируются по степеням. Их можно разделить на 4 вида:
Линейные имеют степень при переменной, равной единице, квадратные — двойке, кубические — тройке, а высшие формы — от четверки и выше. Кроме того, при решении неравенств нужно знать специальные обозначения и положения:
Кроме того, неравенства можно разделить на строгие и нестрогие. Вторые отличаются от первых только добавлением знака равенства.
Примером простейшего строгого неравенства является выражение «t-4<0». Его решение записывается таким образом: t ∈ (-inf;4). Чтобы переделать его в нестрогое, нужно поменять знак «<» на «<=», т. е. t-4<=0. Его решением будет такой интервал: t ∈ (-inf;4].
Очень часто неравенства представляются в виде многочленов. Каждый ученик должен иметь общее представление об этом математическом объекте.
Понятие многочлена
Многочленом называется выражение, состоящее из нескольких математических операций и переменных. Примером тождества является 4t 2 +5t+2 — квадратичный трехчлен. Он состоит из трех компонентов: 4t 2 , 5t и 2. Многочлены классифицируются по степеням и количеству частей.
Кроме того, они бывают и простыми (линейными). Примером одного из них является выражение вида «3t+4».
3 = t 3 — 3t 2 * v + 3tv 2 + v 3 .
Разность кубов: t 3 — v 3 = (t — v)(t 2 + tv + v 2 ).
Очень часто сокращенное умножение применяется при решении дробно-рациональных неравенств методом интервалов. Кроме того, их рекомендуется использовать при нахождении корней уравнений различных типов.
Метод интервалов
Метод интервалов основан на задании диапазона, на котором неравенство является истинным. Для нахождения решения нужно найти корни уравнения, а затем отметить их на числовой прямой. Однако это схематический способ. Его можно понять и при помощи логических отождествлений.
Для примера нужно решить строгое неравенство «3-t > 0». Необходимо обратить внимание на само математическое выражение. В нем следует заменить знак «>» на «=», а затем найти корень уравнения, т. е. t=3. После этого нужно отметить на числовой прямой точку «3». По условию (если перенести переменную в одну сторону, а известную — в другую) t<3.
Решение записывается в виде принадлежности переменной t такому интервалу, а именно: (-inf;3). Это означает, что неизвестная величина «t» может принимать значения от «минус бесконечности» до трех не включительно, поскольку тройка превращает неравенство в ложное тождество, т. е. 3−3<0 (нуль не может быть больше 0).
Однако не все неравенства имеют такой простой вид. Существуют и более сложные выражения. Чтобы уметь решать рациональные неравенства, необходимо разобрать уравнения, а также способы нахождения их корней.
Способы решения уравнений
Для решения уравнения необходимо выполнить операцию идентификации на основании классификации. Равенства с переменными можно разделить на 4 распространенных вида, а именно:
Первые являются наиболее простыми соотношениями.
Они имеют вид: Qt+C=0, где t — неизвестная величина. Решать их нужно по такому алгоритму:
Следует отметить, что корни тождеств, представленных в виде квадратичной функции «Qt 2 + Pt + C = 0», находятся по теореме Виета или через промежуточную величину. Последняя называется дискриминантом и обозначается литерой «D». Алгоритм решения уравнений выглядит таким образом:
Записать выражение: Qt 2 + Pt + C = 0.
Сократить его на Q при условии, что коэффициенты не будут дробными величинами: t 2 + P’t + C’ = 0.
2 + P (t2) + C = 0.Существуют неполные квадратные уравнения, т. е. у них может отсутствовать константа «С» или Pt. В этом случае их решение сводится к математическим преобразованиям с вынесением общего множителя за скобки.
Тождества с неизвестными в третьей и высших степенях решаются посредством понижения показателей до двойки или единицы. При этом можно применять замену, формулы сокращенного произведения, вынесение общего множителя и т. д.
Кроме того, уравнения любого типа могут объединяться в системы, т. е. иметь общие корни. Все переменные в них взаимосвязаны. На основании такой особенности можно выражать одну неизвестную через другую.
Для проверки результатов решения можно воспользоваться специальными сервисами. Они называются онлайн-калькуляторами.
Обыкновенные дроби
Обыкновенная дробь — число, состоящее из двух частей: числителя и знаменателя. Дробные выражения делятся на два вида: правильные и неправильные.
У первых величина числителя меньше, чем значение знаменателя. У вторых — все наоборот.
Дроби обыкновенного вида обладают определенными свойствами. К ним относятся:
Последнее утверждение доказывается очень просто. Для этого необходимо взять произвольное дробное выражение «2/5». Далее возвести в квадрат обе его части, т. е. 4/25. Затем необходимо сравнить величины, конвертировав их в десятичные дроби, т. е. 2/5=0,4 и 4/25=0,16.
Из результатов вычислений видно, что величины отличаются между собой. На основании этого можно сделать вывод о правдивости четвертого утверждения.
2>0.
Величина «t» может принимать любые значения, кроме двойки, которая превращает неравенство в ложное. Такой широкий диапазон связан со свойствами выражения, возведенного во вторую степень (отрицательное и положительное число в квадрате является положительным).
Таким образом, решение дробно-рациональных выражений в виде неравенств выполняется по определенной методике. Однако для ее применения нужно «обновить» знания в области таких направлений: метод интервалов, работа с обыкновенными дробями и вычисления корней уравнений.
Предыдущая
МатематикаИррациональность дроби — как правильно избавиться от знака корня в знаменателе?
Следующая
МатематикаДеление с остатком — алгоритмы и примеры решения для 5 класса
Как перевернуть дробь в неравенстве
Дробные неравенства и их решение
(знак может быть ) называется дробно-линейным неравенством.
Решать дробно-линейные неравенства можно методом интервалов. Для этого находим нули числителя и знаменателя и отмечаем их на числовой оси. Нуль знаменателя всегда отмечаем выколотой точкой (не включается в решение). На каждом из полученных интервалов проверяем знак дроби, выбираем нужный интервал и записываем решением.
Примеры решения дробных неравенств
Отметим их на числовой прямой
Решением неравенства будет промежуток
Найдем нули числителя и знаменателя
и отметим их на числовой оси
Выбираем те интервалы, на которых дробь меньше либо равна нулю, т.е .
Как перевернуть дробь в неравенстве
Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.
What can I do to prevent this in the future?
If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.
If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.
Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.
Cloudflare Ray ID: 71a9fbb11ac992a8 • Your IP : 82.102.23.104 • Performance & security by Cloudflare
Дробно рациональные неравенства
Дробно рациональное неравенство – это неравенство, в котором есть дробь, в знаменателе которой стоит переменная, т.е. неравенство одного из следующих видов:
f ( x ) g ( x ) < 0 f ( x ) g ( x ) ≤ 0 f ( x ) g ( x ) > 0 f ( x ) g ( x ) ≥ 0
Дробно рациональное неравенство не обязательно сразу выглядит так. Иногда, для приведения его к такому виду, приходится потрудиться (перенести слагаемые в левую часть, привести к общему знаменателю).
Примеры дробно рациональных неравенств:
x − 1 x + 3 < 0 3 ( x + 8 ) ≤ 5 x 2 − 1 x > 0 x + 20 x ≥ x + 3
Как же решать эти дробно рациональные неравенства? Да всё при помощи того же всемогущего метода интервалов.
Алгоритм решения дробно рациональных неравенств:
- Привести неравенство к одному из следующих видов (в зависимости от знака в исходном неравенстве):
f ( x ) g ( x ) < 0 f ( x ) g ( x ) ≤ 0 f ( x ) g ( x ) > 0 f ( x ) g ( x ) ≥ 0
- Приравнять числитель дроби к нулю f ( x ) = 0. Найти нули числителя .
- Приравнять знаменатель дроби к нулю g ( x ) = 0. Найти нули знаменателя .
В этом пункте алгоритма мы будем делать всё то, что нам запрещали делать все 9 лет обучения в школе – приравнивать знаменатель дроби к нулю. Чтобы как-то оправдать свои буйные действия, полученные точки при нанесении на ось x будем всегда рисовать выколотыми, вне зависимости от того, какой знак неравенства.
- Нанести нули числителя и нули знаменателя на ось x .
Вне зависимости от знака неравенства
при нанесении на ось x нули знаменателя всегда выколотые .
Если знак неравенства строгий ,
при нанесении на ось x нули числителя выколотые .
Если знак неравенства нестрогий ,
при нанесении на ось x нули числителя жирные.
- Расставить знаки на интервалах.
- Выбрать подходящие интервалы и записать ответ.
Примеры решения дробно рациональных неравенств:
№1. Решить неравенство x − 1 x + 3 > 0.
Решение:
Будем решать данное неравенство в соответствии с алгоритмом.
- Первый шаг алгоритма уже выполнен. Неравенство приведено к виду f ( x ) g ( x ) > 0.
- Приравниваем числитель к нулю f ( x ) = 0.
x = 1 – это ноль числителя . Поскольку знак неравенства строгий, ноль числителя при нанесени на ось x будет выколотым. Запомним это.
- Приравниваем знаменатель к нулю g ( x ) = 0.
x = − 3 – это ноль знаменателя . При нанесении на ось x точка будет всегда выколотой (вне зависимости от знака неравенства).
- Наносим нули числителя и нули знаменателя на ось x .
При нанесении нулей числителя обращаем внимание на знак неравенства. В данном случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя выколоты всегда.
- Расставляем знаки на интервалах.
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2 . Подставляем эту точку в исходное выражение f ( x ) g ( x ) : x − 1 x + 3 = 2 − 1 2 + 3 = 1 5 > 0,
Это значит, что знак на интервале, в котором лежит точка 2 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
- Выбираем подходящие интервалы и записываем ответ.
Поскольку знак неравенства > , выбираем в ответ интервалы со знаком +.
В ответ пойдут два интервала. Точки -3 и 1 будут в круглых скобках, так как обе они выколотые.
Ответ: x ∈ ( − ∞ ; − 3 ) ∪ ( 1 ; + ∞ )
№2. Решить неравенство 3 ( x + 8 ) ≤ 5.
Решение:
Будем решать данное неравенство в соответствии с алгоритмом.
- Привести неравенство к виду f ( x ) g ( x ) ≤ 0.
3 ( x + 8 ) − 5 \ x + 8 ≤ 0
3 x + 8 − 5 ( x + 8 ) x + 8 ≤ 0
3 − 5 ( x + 8 ) x + 8 ≤ 0
3 − 5 x − 40 x + 8 ≤ 0
− 5 x − 37 x + 8 ≤ 0
- Приравнять числитель к нулю f ( x ) = 0.
x = − 37 5 = − 37 5 = − 7,4
x = − 7,4 – ноль числителя . Поскольку знак неравенства нестрогий, при нанесении этой точки на ось x точка будет жирной.
- Приравнять знаменатель к нулю g ( x ) = 0.
x = − 8 – это ноль знаменателя . При нанесении на ось x , точка будет всегда выколотой (вне зависимости от знака неравенства).
- Наносим нули числителя и нули знаменателя на ось x .
При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства нестрогий, значит нули числителя будут жирными. Ну а нули знаменателя выколоты всегда.
- Расставляем знаки на интервалах.
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 0 . Подставляем эту точку в исходное выражение f ( x ) g ( x ) :
− 5 x − 37 x + 8 = − 5 ⋅ 0 − 37 0 + 8 = − 37 8 < 0
Это значит, что знак на интервале, в котором лежит точка 0 будет -.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
- Выбираем подходящие интервалы и записываем ответ.
Поскольку знак неравенства ≤ , выбираем в ответ интервалы со знаком -.
В ответ пойдут два интервала. Точка -8 будет в круглой скобке, так как она выколотая, точка -7,4 будет в квадратных скобках, так как она жирная.
Ответ: x ∈ ( − ∞ ; − 8 ) ∪ [ − 7,4 ; + ∞ )
№3. Решить неравенство x 2 − 1 x > 0.
Решение:
Будем решать данное неравенство в соответствии с алгоритмом.
- Первый шаг алгоритма уже выполнен. Неравенство приведено к виду f ( x ) g ( x ) > 0.
- Приравнять числитель к нулю f ( x ) = 0.
( x − 1 ) ( x + 1 ) = 0 ⇒ [ x − 1 = 0 x + 1 = 0 [ x = 1 x = − 1
x 1 = 1, x 2 = − 1 – нули числителя . Поскольку знак неравенства строгий, при нанесении этих точек на ось x точки будут выколотыми.
- Приравнять знаменатель к нулю g ( x ) = 0.
x = 0 – это ноль знаменателя . При нанесении на ось x , точка будет всегда выколотой (вне зависимости от знака неравенства).
- Наносим нули числителя и нули знаменателя на ось x .
При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства строгий, значит нули числителя будут выколотыми.
Ну а нули знаменателя и так выколоты всегда.
- Расставляем знаки на интервалах.
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2 . Подставляем эту точку в исходное выражение f ( x ) g ( x ) :
x 2 − 1 x = 2 2 − 1 2 = 4 − 1 2 = 3 2 > 0, Это значит, что знак на интервале, в котором лежит точка 2, будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
- Выбираем подходящие интервалы и записываем ответ.
Поскольку знак неравенства > , выбираем в ответ интервалы со знаком +.
В ответ пойдут два интервала. Все точки будут в круглых скобках, так как они выколотые.
Ответ: x ∈ ( − 1 ; 0 ) ∪ ( 1 ; + ∞ )
Если вас интересуют более сложные неравенства (с корнем чётной степени кратности, например), посмотрите видео «Метод интервалов: сложные случаи».
Спасибо за просмотр этого урока! Если у вас остались вопросы, напишите их в комментариях.
Презентация по алгебре 9 класс Квадратные и дробные неравенства доклад, проект
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экономика
Презентация на тему Презентация по алгебре 9 класс Квадратные и дробные неравенства, предмет презентации: Алгебра.
Этот материал в формате pptx (PowerPoint) содержит 18 слайдов, для просмотра воспользуйтесь проигрывателем. Презентацию на заданную тему можно скачать внизу страницы, поделившись ссылкой в социальных сетях! Презентации взяты из открытого доступа или загружены их авторами, администрация сайта не отвечает за достоверность информации в них, все права принадлежат авторам презентаций и могут быть удалены по их требованию.
«Решение квадратных и дробно-рациональных неравенств методом интервалов»
урок алгебры в 9 классе
Устный счет
1. Угадайте корень уравнения:
а) 2х+3у=13; б) х² =64; в) х³= — 8; г) х⁵ =32
Устный счет
2.Является ли число (-1) корнем уравнения: х²-4х-5=0
3.
Брат младше сестры на 3 года, а вместе им 21год. Сколько лет брату и сестре?
а) х+3х=21; б) х+ (х+3)=21;
в) х+(х-3)=21;
г)х:3+х=21
Устный счет
Имеют единственный корень
6х=42 4х-5=4х 0,3x=0 7x=2
Не имеют корней
-3,4x=0
0х=5
Имеют множество корней
5х+2=(5х-4)+6
2x=-0,06
4.
Назовите те уравнения, которые:
Решите неравенство:
4х+2
ответ:(- ∞;-0,5)
5. Решить методом интервалов
(2х-6)(32-х)≥0
План применения метода интервалов
Проверь своё решение
.
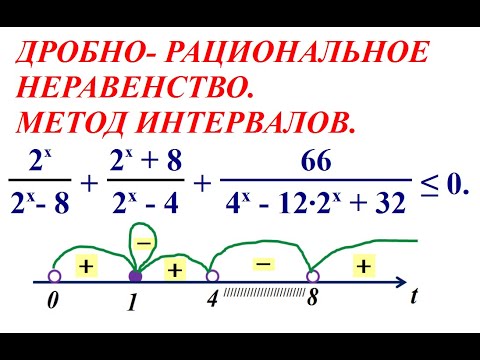Решим методом интервалов неравенства:
32
3
Ответ:
+
+
–
(2х-6)(х-32)≥0
2х-6=0 х-32=0
2х=6 х=32
х=3
№1. Определите нули левой части неравенства:
№3. Найдите наибольшее целое отрицательное (положительное) значение х, удовлетворяющее неравенству:
Вариант 1.
Вариант 2.
Самостоятельная работа
Желаю удачи!
на «4»
на «5»
2(х-5)(2х+1) >0.
4(х+6)(6х-3)
(2х-5)(х+3)≥0
(5х-2)(х+4)
х2 + 2х – 3 > 0.
х2 – 5х + 4
№2. Решите неравенство:
Проверь своё решение
№1. определите нули левой части неравенства:
Вариант 1.
Вариант 2.
Проверь своё решение
№2.
Решите методом интервалов неравенства:
Вариант 1.
Вариант 2.
а)
а)
2,5
0,4
-3
-4
Ответ:
+
+
–
+
+
–
Ответ:
Оценка самостоятельной работы
За каждый верно выполненный пример – поставьте 1 балл.
1 балл – удовлетворительно, «3».
2 балла – хорошо, «4».
3 балла – отлично, «5».
0 баллов – плохо, «2».
Решение рациональных неравенств
Итак:
Решите неравенство
№390 (в, г),
№ 481 (а, в),
№646(а),
№394(а).
Работа с учебником
решите неравенство методом интервалов
Найти область определения функции
> 0
Дополнительно для сильных учеников:
Решите неравенство методом интервалов
Повторить §15 (глава II),
№389 (б), № 376 (а), №383, №389 (а).
Домашнее задание.
3. Что вам более всего удалось, какие моменты были выполнены наиболее успешно?
Рефлексия.
1.Что вы ожидали от работы на данном уроке? Сравните свои предварительные цели и реально достигнутые результаты.
2. Какие чувства и ощущения возникали у вас в ходе работы?
Скачать презентацию
Это сайт презентаций, где можно хранить и обмениваться своими презентациями, докладами, проектами, шаблонами в формате PowerPoint с другими пользователями. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами.
Для правообладателей
Обратная связь
Email: Нажмите что бы посмотреть
ORCCA Линейные уравнения и неравенства с дробями
В этом разделе мы научимся решать линейные уравнения и неравенства с дробями.
Подраздел 3.3.1 Введение
До сих пор на последнем шаге решения для переменной мы разделили каждую часть уравнения на константу, например:
\begin{align*} 2x\ампер=10\\ \divideunder{2x}{2} \amp= \divideunder{10}{2}\\ х\ампер=5 \end{align*}
Если у нас есть коэффициент, который является дробью, мы
\begin{align*} \frac{1}{2}x\amp=10\\ \divideunder{\frac{1}{2}x}{\frac{1}{2}} \amp= \divideunder{10}{\frac{1}{2}}\\ х\amp=10\cdot \frac{2}{1}=20 \конец{выравнивание*}
Что, если бы наше уравнение или неравенство были более сложными, например, \(\frac{1}{4}x+\frac{2}{3}=\frac{1}{6}\text{?}\) Мы пришлось бы сначала выполнить много арифметических операций с дробями, чтобы затем разделить каждую сторону на коэффициент \(x\text{.
}\). Альтернативный подход состоит в том, чтобы вместо этого умножить с каждой стороны уравнения на выбранную константу, исключающую знаменатель. В уравнении \(\frac{1}{2}x=10\text{,}\) мы могли бы просто умножить каждую часть уравнения на \(2\text{,}\), что исключило бы знаменатель \ (2\текст{:}\)
\начать{выровнять*} \frac{1}{2}x\amp=10\\ \multiplyleft{2}\left(\frac{1}{2}x\right)\amp=\multiplyleft{2}10\\ х\ампер=20 \конец{выравнивание*}
Для более сложных уравнений мы умножим каждую часть уравнения на наименьший общий знаменатель (НОД) всех дробей, содержащихся в уравнении.
Подраздел 3.3.2 Исключение знаменателей
Пример 3.3.1.
Дешон посадил у себя во дворе деревце высотой \(4\) фута. Дерево будет расти на \(\frac{2}{3}\) фута каждый год. Через сколько лет его дерево вырастет \(10\) футов в высоту?
Поскольку дерево растет на \(\frac{2}{3}\) фута каждый год, мы можем использовать таблицу, чтобы написать формулу, моделирующую рост дерева:
| Прошло лет | Высота дерева (футы) |
| \(0\) | \(4\) |
| \(1\) | \(4+\фракция{2}{3}\) |
| \(2\) | |
| \(\вдоц\) | \(\вдоц\) |
| \(у\) | \(4+\фракция{2}{3}у\) |
Исходя из этого, мы определили, что через \(y\) лет с момента посадки дерева высота дерева будет \(4+\frac{2}{3}y\) футов.
Чтобы найти, когда дерево Дешона будет \(10\) футов в высоту, мы напишем и решим это уравнение:
\begin{выравнивание*} 4+\frac{2}{3}y\amp=10\\ \multiplyleft{3}\left(4+\frac{2}{3}y\right)\amp=\multiplyleft{3}10\\ 3\cdot4+3\cdot\frac{2}{3}y\amp=30\\ 12+2г\ампер=30\\ 2г\ампер=18\\ у\ампер=9 \end{align*}
Теперь проверим решение \(9\) в уравнении \(4+\frac{2}{3}y=10\text{:}\)
\begin{align *} 4+\frac{2}{3}y\amp=10\\ 4+\frac{2}{3}(\substitute{9})\amp\stackrel{?}{=}10\\ 4+6\amp\stackrel{\checkmark}{=}10 \конец{выравнивание*}
Таким образом, дереву Дешона потребуется \(9\) лет, чтобы достичь \(10\) футов в высоту.Давайте рассмотрим еще несколько примеров.
Пример 3.3.2.
Найдите \(x\) в \(\frac{1}{4}x+\frac{2}{3}=\frac{1}{6}\text{.}\)
Объяснение
Чтобы решить это уравнение, нам сначала нужно определить LCD всех дробей в уравнении. С левой стороны у нас есть \(\frac{1}{4}\) и \(\frac{2}{3}\text{.
}\) С правой стороны у нас есть \(\frac{1}{ 6}\text{.}\) ЖК-дисплей \(3, 4\text{,}\) и \(6\) равен \(12\text{,}\), поэтому мы умножим каждую часть уравнения на \(12\), чтобы исключить все знаменателей:
\begin{align*} \frac{1}{4}x+\frac{2}{3}\amp=\frac{1}{6}\\ \multiplyleft{12}\left(\frac{1}{4}x+\frac{2}{3}\right)\amp=\multiplyleft{12}\frac{1}{6}\\ 12\cdot\left(\frac{1}{4}x\right)+12\cdot\left(\frac{2}{3}\right)\amp=12\cdot\frac{1}{6} \\ 3x+8\усилитель=2\\ 3x\ампер=-6\\ \divideunder{3x}{3}\amp=\divideunder{-6}{3}\\ х\ампер=-2 \end{align*}
Проверка решения \(-2\text{:}\)
\begin{align*} \frac{1}{4}x+\frac{2}{3}\amp=\frac{1}{6}\\ \frac{1}{4}(\substitute{-2})+\frac{2}{3}\amp\stackrel{?}{=}\frac{1}{6}\\ -\frac{2}{4}+\frac{2}{3}\amp\stackrel{?}{=}\frac{1}{6}\\ -\frac{6}{12}+\frac{8}{12}\amp\stackrel{?}{=}\frac{1}{6}\\ \frac{2}{12}\amp\stackrel{\checkmark}{=}\frac{1}{6} \end{выравнивание*}
Следовательно, решение равно \(-2\), а набор решений равен \(\{-2\}\text{.
}\)
Пример 3.3.3.
Найдите \(z\) в \(-\frac{2}{5}z-\frac{3}{2}=-\frac{1}{2}z+\frac{4}{5}\ текст{.}\)
Объяснение
Первое, что нам нужно сделать, это определить LCD всех знаменателей в этом уравнении. Поскольку знаменатели равны \(2\) и \(5\text{,}\), ЖК-дисплей равен \(10\text{.}\). Итак, в качестве нашего первого шага мы умножим каждую часть уравнения на \( 10\), чтобы исключить все знаменатели:
\begin{выравнивание*} -\frac{2}{5}z-\frac{3}{2}\amp=-\frac{1}{2}z+\frac{4}{5}\\ \multiplyleft{10}\left(-\frac{2}{5}z-\frac{3}{2}\right)\amp=\multiplyleft{10}\left(-\frac{1}{2} z+\frac{4}{5}\right)\\ 10\left(-\frac{2}{5}z\right)-10\left(\frac{3}{2}\right)\amp=10\left(-\frac{1}{2}z \вправо)+10\влево(\фракция{4}{5}\вправо)\\ -4z-15\amp=-5z+8\\ z-15\ампер=8\\ г\ампер=23 \end{align*}
Проверка решения \(23\text{:}\)
\begin{align*} -\frac{2}{5}z-\frac{3}{2}\amp=-\frac{1}{2}z+\frac{4}{5}\\ -\frac{2}{5}(\substitute{23})-\frac{3}{2}\amp\stackrel{?}{=}-\frac{1}{2}(\substitute{23} )+\фракция{4}{5}\\ -\frac{46}{5}-\frac{3}{2}\amp\stackrel{?}{=}-\frac{23}{2}+\frac{4}{5}\\ -\frac{46}{5}\cdot\frac{2}{2}-\frac{3}{2}\cdot\frac{5}{5}\amp\stackrel{?}{=}-\ frac{23}{2}\cdot\frac{5}{5}+\frac{4}{5}\cdot\frac{2}{2}\\ -\ гидроразрыв{92}{10}-\frac{15}{10}\amp\stackrel{?}{=}-\frac{115}{10}+\frac{8}{10}\\ -\frac{107}{10}\amp\stackrel{\checkmark}{=}-\frac{107}{10} \end{align*}
Таким образом, решение равно \(23\), поэтому множество решений равно \(\{23\}\text{.
}\)
Пример 3.3.4.
Найдите \(a\) в уравнении \(\frac{2}{3}(a+1)+5=\frac{1}{3}\text{.}\)
Объяснение
\begin{align*} \frac{2}{3}(a+1)+5\amp=\frac{1}{3}\\ \multiplyleft{3}\left(\frac{2}{3}(a+1)+5\right)\amp=\multiplyleft{3}\frac{1}{3}\\ 3\cdot\frac{2}{3}(a+1)+3\cdot5\amp=1\\ 2(а+1)+15\амп=1\\ 2а+2+15\амп=1\\ 2а+17\амп=1\\ 2а\ампер=-16\\ а\ампер=-8 \end{выравнивание*}
Проверяем решение \(-8\) в уравнении \(\frac{2}{3}(a+1)+5=\frac{1}{3}\text{,}\) мы находим, что :
\begin{выравнивание*} \frac{2}{3}(a+1)+5\amp=\frac{1}{3}\\ \frac{2}{3}(\substitute{-8}+1)+5\amp\stackrel{?}{=}\frac{1}{3}\\ \frac{2}{3}(-7)+5\amp\stackrel{?}{=}\frac{1}{3}\\ -\frac{14}{3}+\frac{15}{3}\amp\stackrel{\checkmark}{=}\frac{1}{3} \end{align*}
Следовательно, решение равно \(-8\), а набор решений равен \(\{-8\}\text{.}\)
Пример 3.3.5.
Найдите \(b\) в уравнении \(\frac{2b+1}{3}=\frac{2}{5}\text{.}\)
Объяснение
\begin{align*} \frac{2b+1}{3}\amp=\frac{2}{5}\\ \multiplyleft{15}\frac{2b+1}{3}\amp=\multiplyleft{15}\frac{2}{5}\\ 5(2b+1)\amp=6\\ 10b+5\amp=6\\ 10б\ампер=1\\ b\amp=\frac{1}{10} \end{align*}
Проверка решения \(\frac{1}{10}\text{:}\)
\begin{align*} \frac{2b+1}{3}\amp=\frac{2}{5}\\ \frac{2\left(\substitute{\frac{1}{10}}\right)+1}{3}\amp\stackrel{?}{=}\frac{2}{5}\\ \frac{\frac{1}{5}+1}{3}\amp\stackrel{?}{=}\frac{2}{5}\\ \ frac {\ frac {1} {5} + \ frac {5} {5} {3} \ amp \ stackrel {?} {=} \ frac {2} {5} \\ \ frac {\ frac {6} {5} {3} \ amp \ stackrel {?} {=} \ frac {2} {5} \\ \frac{6}{5}\cdot \frac{1}{3}\amp\stackrel{\checkmark}{=}\frac{2}{5} \end{выравнивание*}
Решение: \(\frac{1}{10}\), а набор решений: \(\left\{\frac{1}{10}\right\}\text{.
}\)
Пример 3.3.7.
В научной лаборатории в 9:00 утра в контейнере было \(21\) унций воды. Вода испарялась со скоростью \(3\) унций каждые \(5\) минут. Когда останется \(8\) унций воды?
Объяснение
Поскольку контейнер теряет \(3\) унций воды каждые \(5\) минут, он теряет \(\frac{3}{5}\) унций каждую минуту. Через \(м\) минут с 9:00 утра контейнер потеряет \(\frac{3}{5}m\) унций воды. Поскольку вначале в контейнере было \(21\) унций воды, количество воды в контейнере можно смоделировать как \(21-\frac{3}{5}м\) (в унциях).
Чтобы определить, когда останется \(8\) унций воды, запишем и решим это уравнение:
\begin{align*} 21-\frac{3}{5}m\amp=8\\ \multiplyleft{5}\left(21-\frac{3}{5}x\right)\amp=\multiplyleft{5}8\\ 5\cdot21-5\cdot\frac{3}{5}x\amp=40\\ 105-3м\ампер=40\\ 105–3 м\вычитание вправо{105}\amp=40\вычитание вправо{105}\\ -3м\ампер=-65\\ \divideunder{-3m}{-3}\amp=\divideunder{-65}{-3}\\ m\amp=\frac{65}{3} \end{выравнивание*}
Проверка решения \(\frac{65}{3}\text{:}\)
\begin{align*} 21-\frac{3}{5}m\amp=8\\ 21-\frac{3}{5}\left(\substitute{\frac{65}{3}}\right)\amp\stackrel{?}{=}8\\ 21-13\amp\stackrel{\checkmark}{=}8 \end{align*}
Следовательно, решение равно \(\frac{65}{3}\text{.
}\) В качестве смешанного числа это \(21\frac{2}{3}\text {.}\) В контексте это означает, что \(21\) минут и \(40\) секунд после 9:00 в 9:21:40 в контейнере будет \(8\) унций воды. оставил.
КПП 3.3.8.
Подраздел 3.3.3 Решение неравенств с дробями
Мы также можем решать линейные неравенства с дробями, умножая каждую часть неравенства на НЛД всех дробей в неравенстве.
Помните, что с линейными неравенствами все работает точно так же, как и с решением линейных уравнений, за исключением того, что знак неравенства меняет направление всякий раз, когда мы умножаем каждую часть неравенства на отрицательное число.
Давайте рассмотрим несколько примеров, чтобы увидеть, как решить линейное неравенство, сначала очистив дроби.
Пример 3.3.9.
Найдите \(x\) в неравенстве \(\frac{3}{4}x-2\gt\frac{4}{5}x\text{.}\) Запишите набор решений в обоих множествах- нотация построителя и нотация интервала.
Объяснение
\begin{align*} \frac{3}{4}x-2\amp\gt\frac{4}{5}x\\ \multiplyleft{20}\left(\frac{3}{4}x-2\right)\amp\gt\multiplyleft{20}\frac{4}{5}x\\ 20\cdot\frac{3}{4}x-20\cdot2\amp\gt16x\\ 15x-40\ампер\gt16x\\ 15x-40\subtractright{15x}\amp\gt16x\subtractright{15x}\\ -40\ампер\гт х\\ х\усилитель\лт-40 \end{выравнивание*}
Набор решений в нотации построителя наборов имеет вид \(\{x\mid x\lt-40\}\text{.
}\) Обратите внимание, что это эквивалентно записи \(\{x\mid-40\gt x \}\text{,}\), но это легче понять, если мы сначала напишем \(x\) в неравенстве.
Набор решений в интервальной нотации: \((-\infty,-40)\text{.}\)
Пример 3.3.10.
Найдите \(y\) в неравенстве \(\frac{4}{7}-\frac{4}{3}y\le\frac{2}{3}\text{.}\) Запишите набор решений как в нотации построителя наборов, так и в нотации интервала.
Объяснение
\begin{align*} \frac{4}{7}-\frac{4}{3}y\amp\le\frac{2}{3}\\ \multiplyleft{21}\left(\frac{4}{7}-\frac{4}{3}y\right)\amp\le\multiplyleft{21}\left(\frac{2}{3}\ Правильно)\\ 21\влево(\frac{4}{7}\вправо)-21\влево(\frac{4}{3}y\вправо)\amp\le21\влево(\frac{2}{3}\вправо) \\ 12-28лет\ампер\ле14\\ -28г\ампер\ле2\\ \divideunder{-28y}{-28}\amp\ge\divideunder{2}{-28}\\ y\amp\ge-\frac{1}{14} \end{align*}
Обратите внимание, что когда мы разделили каждую часть неравенства на \(-28\text{,}\), символ неравенства изменил направление.
Набор решений в нотации построителя наборов: \(\left\{y\mid y\ge-\frac{1}{14}\right\}\text{.}\)
Набор решений в интервале обозначение \(\left[-\frac{1}{14},\infty\right)\text{.}\)
Пример 3.3.11.
В определенном классе оценка учащегося рассчитывается по среднему баллу за 3 теста. Эйдан набрал \(78\%\) и \(54\%\) в первых двух тестах. Если он хочет получить хотя бы оценку C \((70\%)\text{,}\), какой самый низкий балл ему нужно получить на третьем экзамене?
Объяснение
Предположим, Эйдан наберет \(x\%\) на третьем тесте. Чтобы его средний балл за тест был больше или равен \(70\%\text{,}\), запишем и решим это неравенство:
\begin{align*} \frac{78+54+x}{3}\amp\ge70\\ \frac{132+x}{3}\amp\ge70\\ \multiplyleft{3}\frac{132+x}{3}\amp\ge\multiplyleft{3}70\\ 132+х\усилитель\ge210\\ х\amp\ge78 \end{align*}
Чтобы получить хотя бы оценку C, Эйдан должен набрать не менее \(78\%\) в третьем тесте.
Упражнения 3.
3.4 УпражненияОбзор и прогрев
1.
Умножить: \(\displaystyle{8\cdot \frac{2}{3} }\)
2.
Умножить: \(\displaystyle{3\cdot \frac{3}{8} }\)
3.
Умножить: \(\displaystyle{4\cdot\left( -{\frac{5}{2}} \right)}\)
4.
Умножить: \(\displaystyle{28\cdot\left( -{\frac{6}{7}} \right)}\)
5.
Выполните следующие умножения.
\(14 \cdot \frac{5}{7}\)
\(21 \cdot \frac{5}{7}\)
\(28 \cdot \frac{5}{7}\)
6.
Выполните следующие умножения.
\(27 \cdot \frac{5}{9}\)
\(36 \cdot \frac{5}{9}\)
\(45 \cdot \frac{5}{9}\)
Решение линейных уравнений с дробями
7.
Решите уравнение.
\(\displaystyle{{\frac{q}{7}+120}={3q}}\)
8.
Решите уравнение.
\(\displaystyle{{\frac{y}{4}+57}={5y}}\)
9.
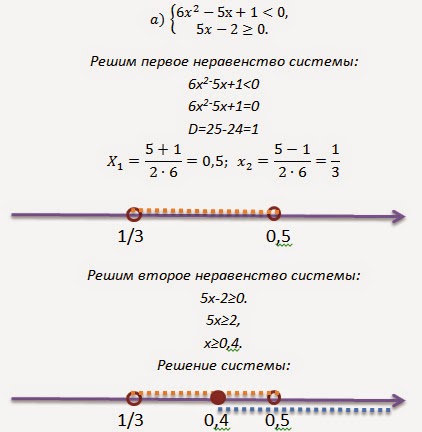
Решите уравнение.
\(\displaystyle{{\frac{t}{10}+8}={13}}\)
10.
Решите уравнение.
\(\displaystyle{{\frac{a}{7}+5}={7}}\)
11.
Решите уравнение.
\(\displaystyle{ {3-\frac{c}{7}} = {1} }\)
12.
Решите уравнение.
\(\displaystyle{ {9-\frac{A}{2}} = {3} }\)
13.
Решите уравнение.
\(\displaystyle{{-42} = {6-\frac{8C}{5}} }\)
14.
Решите уравнение.
\(\displaystyle{ {-22} = {2-\frac{4m}{9}} }\)
15.
Решите уравнение.
\(\displaystyle{{5p} = {\frac{3p}{10}+282}}\)
16.
Решите уравнение.
\(\displaystyle{{5q} = {\frac{7q}{6}+115}}\)
17.
Решите уравнение.
\(\displaystyle{{64} = {{\frac{10}{3}}y+2y}}\)
18.
Решите уравнение.
\(\displaystyle{{195} = {{\frac{4}{7}}r+5r}}\)
19.
Решите уравнение.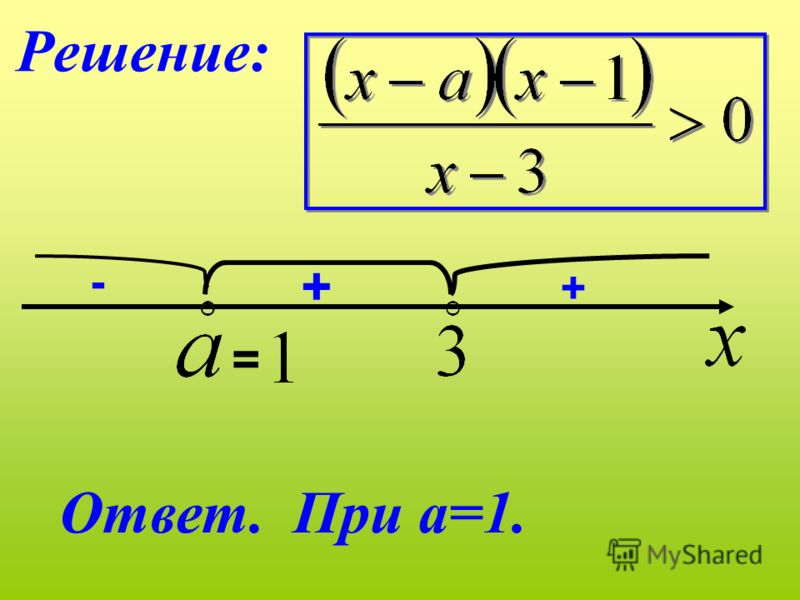
\(\displaystyle{{74-{\frac{7}{6}}a} = {5a}}\)
20.
Решите уравнение.
\(\displaystyle{{65-{\frac{5}{2}}c} = {4c}}\)
21.
Решите уравнение.
\(\displaystyle{ {5A} = {{\frac{4}{9}}}A+8} }\)
22.
Решите уравнение.
\(\displaystyle{{3C} = {{\frac{2}{3}}C+4}}\)
23.
Решите уравнение.
\(\displaystyle{{{\frac{7}{2}}-9m}={8}}\)
24.
Решите уравнение.
\(\displaystyle{{{\frac{3}{8}}-7p}={8}}\)
25.
Решите уравнение.
\(\displaystyle{{{\frac{5}{4}}-{\frac{1}{4}}q}={3}}\)
26.
Решите уравнение.
\(\displaystyle{{{\frac{9}{2}}-{\frac{1}{2}}y}={1}}\)
27.
Решите уравнение.
\(\displaystyle{{\frac{4r}{7}-8}={-{\frac{40}{7}}}}\)
28.
Решите уравнение.
\(\displaystyle{{\frac{6a}{5}-6}={-{\frac{6}{5}}}}\)
29.
Решите уравнение.
\(\displaystyle{{{\frac{2}{9}}+{\frac{8}{9}}c}={7c}}\)
30.
Решите уравнение.
\(\displaystyle{{{\frac{6}{7}}+{\frac{10}{7}}A}={7A}}\)
31.
Решите уравнение.
\(\ displaystyle { {\ frac {3C} {7} — {\ frac {32} {7}}} = {- {\ frac {5} {7}} C}} \)
32.
Решите уравнение.
\(\ displaystyle { {\ frac {5m} {11} — {\ frac {21} {11}}} = {- {\ frac {2} {11}} m}} \)
33.
Решите уравнение.
\(\ displaystyle { {\ frac {6p} {7} + {\ frac {7} {2}}} = {p}} \)
34.
Решите уравнение.
\(\ displaystyle { {\ frac {2q} {3} + {\ frac {5} {8}}} = {q}} \)
35.
Решите уравнение.
\(\ displaystyle { {\ frac {4y} {7} -111} = {- {\ frac {3} {4}} y}} \)
36.
Решите уравнение.
\(\displaystyle{{\frac{2r}{5}-19}={-{\frac{3}{2}}r}}\)
37.
Решите уравнение.
\(\displaystyle{ {-{\frac{5}{8}}a+39}={\frac{3a}{16}}}\)
38.
Решите уравнение.
\(\displaystyle{{-{\frac{7}{10}}b+51}={\frac{3b}{20}}}\)
39.
Решите уравнение.
\(\displaystyle{{\frac{5A}{6}-8A}={{\frac{5}{12}}}}\)
40.
Решите уравнение.
\(\displaystyle{{\frac{7C}{2}-8C}={{\frac{3}{4}}}}\)
41.
Решите уравнение.
\(\displaystyle{{\frac{7m}{6}+{\frac{8}{9}}}={{\frac{3}{4}}m}}\)
42.
Решите уравнение.
\(\ displaystyle { {\ frac {7p} {4} + {\ frac {4} {7}}} = {{\ frac {3} {8}} p}} \)
43.
Решите уравнение.
\(\displaystyle{{{\frac{3}{2}}q}={{\frac{4}{7}}+\frac{5q}{3}}}\)
44.
Решите уравнение.
\(\displaystyle{{{\frac{5}{6}}y}={{\frac{5}{7}}+\frac{3y}{5}}}\)
45.
Решите уравнение.
\(\displaystyle{{{\frac{7}{6}}}={\frac{r}{24}}}\)
46.
Решите уравнение.
\(\displaystyle{{{\frac{3}{2}}}={\frac{a}{8}}}\)
47.
Решите уравнение.
\(\displaystyle{{-\frac{b}{14}}={{\frac{8}{7}}}}\)
48.
Решите уравнение.
\(\displaystyle{{-\frac{A}{30}}={{\frac{2}{5}}}}\)
49.
Решите уравнение.
\(\displaystyle{{-\frac{C}{10}}={-{\frac{5}{2}}}}\)
50.
Решите уравнение.
\(\displaystyle{{-\frac{m}{24}}={-{\frac{9}{8}}}}\)
51.
Решите уравнение.
\(\displaystyle{{-{\frac{3}{4}}}={\frac{7p}{5}}}\)
52.
Решите уравнение.
\(\displaystyle{ {-{\frac{7}{10}}}={\frac{5q}{9}}}\)
53.
Решите уравнение.
\(\displaystyle{{{\frac{3}{8}}}={\frac{y+6}{24}}}\)
54.
Решите уравнение.
\(\displaystyle{{{\frac{7}{4}}}={\frac{r+3}{12}}}\)
55.
Решите уравнение.
\(\displaystyle{ \frac{9}{10} = \frac{a-4}{9} }\)
56.
Решите уравнение.
\(\displaystyle{ \frac{5}{6} = \frac{b-4}{7} }\)
57.
Решите уравнение.
\(\ displaystyle { {\ frac {A-8} {2}} = {\ frac {A + 5} {4}}} \)
58.
Решите уравнение.
\(\ displaystyle { {\ frac {B-2} {6}} = {\ frac {B + 2} {8}}} \)
59.
Решите уравнение.
\(\ displaystyle { {\ frac {m + 7} {4} — \ frac {m-9{8}}={{\frac{9}{4}}} }\)
60.
Решите уравнение.
\(\displaystyle{{\frac{p+1}{2}-\frac{p-6}{4}}={{\frac{3}{4}}}}\)
61.
Решите уравнение.
\(\ displaystyle { {\ frac {q} {7} -2} = {\ frac {q} {9}}} \)
62.
Решите уравнение.
\(\ displaystyle { {\ frac {y} {5} -1} = {\ frac {y} {10}}} \)
63.
Решите уравнение.
\(\displaystyle{{\frac{r}{2}-3}={\frac{r}{5}+6}}\)
64.
Решите уравнение.
\(\ displaystyle { {\ frac {a} {6} -2} = {\ frac {a} {9} +1}} \)
65.
Решите уравнение.
\(\displaystyle{{{\frac{5}{2}}b+{\frac{7}{4}}}={{\frac{1}{2}}b+{\frac{5}{2} }}} }\)
66.
Решите уравнение.
\(\displaystyle{{1A+3}={5A+{\frac{3}{2}}}}\)
67.
Решите уравнение.
\(\ displaystyle { {\ frac {7B+6} {4} — \ frac {4-B} {8}} = {{\ frac {1} {9}}}} }\)
68.
Решите уравнение.
\(\displaystyle{{\frac{5m+6}{2}-\frac{1-m}{4}}={{\frac{1}{5}}}}\)
69.
Решите уравнение.
\(\displaystyle{{11}={\frac{p}{3}+\frac{p}{8}}}\)
70.
Решите уравнение.
\(\displaystyle{{27}={\frac{q}{7}+\frac{q}{2}}}\)
71.
Решите уравнение.
\(\ displaystyle { {{\ frac {5} {9}}y — {\ frac {6} {7}}} = {- {\ frac {7} {2}} y + {\ frac {1} {2}}} }\)
72.
Решите уравнение.
\(\displaystyle{{-{\frac{1}{2}}r-1}={-r-{\frac{7}{5}}}}\)
73.
Решите уравнение.
\(\ displaystyle { {-{\ frac {7} {8}} a — {\ frac {10} {9}}} = {{\ frac {7} {2}} a — {\ frac {5 {2}}} }\)
74.
Решите уравнение.
\(\displaystyle{{-{\frac{5}{9}}b+{\frac{5}{7}}}={{\frac{5}{3}}b-1}}\)
75.
Решите уравнение.
\(\displaystyle{ {-\frac{A}{2}+8}={4} }\)
\(\displaystyle{{\frac{-q}{2}+8}={4}}\)
\(\displaystyle{{\frac{t}{-2}+8}={4}}\)
\(\displaystyle \displaystyle{ {\frac{-c}{-2}+8}={4}}\)
76.
Решите уравнение.
\(\displaystyle{{-\frac{B}{2}+2}={-4}}\)
\(\displaystyle{{\frac{-C}{2}+2}={-4}}\)
\(\displaystyle{{\frac{r}{-2}+2}={-4}}\)
\(\displaystyle \displaystyle{ {\frac{-x}{-2}+2}={-4}}\)
Приложения
77.
Линдси бежит по прямой. У нее была фора в \(10\) метрах от стартовой линии, и она пробегала \(2\) метра каждые \(7\) секунд. Через сколько секунд Линдсей окажется в \(18\) метрах от линии старта?
Линдси будет в \(18\) метрах от линии старта секунд с момента начала бега.
78.
Эмбер бежит по прямой. Она стартовала в месте \(30\) метров от линии старта и бежала к линии старта со скоростью \(2\) метров каждые \(3\) секунды. Через сколько секунд Эмбер окажется в \(26\) метрах от линии старта?
Эмбер будет в \(26\) метрах от стартовой линии секунд с тех пор, как начала бежать.
79.
В копилке Джозефа было всего \({\$10.00}\), и он решил начать откладывать больше. Он сохраняет \({\$5.00}\) каждые \(8\) дней. Через сколько дней у него будет \({\$25.00}\) в копилке?
Джозеф будет откладывать \({\$25.00}\) в свою копилку спустя несколько дней.
80.
Росс накопил в своей копилке \({\$50.00}\) и решил начать их тратить. Он тратит \({\$3.00}\) каждые \(4\) дней. Через сколько дней у него останется \({\$44.00}\) в копилке?
Через несколько дней в копилке Росса останется \({\$44.00}\).
Решение неравенств с дробями
Для каждой задачи, приведенной ниже, решите неравенство и, в дополнение к написанию построителя наборов и обозначений интервалов для каждого набора решений, нарисуйте график каждого набора решений на числовой прямой.
81.
\({\frac{x}{3}+84}\geq{5x}\)
;
82.
\({\frac{x}{4}+28}\geq{2x}\)
;
83.
\({{\frac{3}{4}}-5y} \lt{3}\)
;
84.
\({{\frac{5}{4}}-2y} \lt{6}\)
;
85.
\({-{\frac{3}{4}}t} > {{\frac{4}{5}}t-93}\)
;
86.
\({-{\frac{5}{6}}t} > {{\frac{2}{7}}t-47}\)
;
87.
\(\)
;
88.
\(\)
;
89.
\({-\frac{z}{4}} \lt {-\frac{3}{2}}\)
;
90.
\({-\frac{z}{8}} \lt {-\frac{9}{2}}\)
;
91.
\({\ frac {x} {7}-12} \leq {\ frac {x} {3}} \)
;
92.
\({\ frac {x} {7}-4} \leq {\ frac {x} {5}} \)
;
93.
\({\frac{y-8}{6}} \geq {\frac{y+8}{4}}\)
;
94.
\({\frac{y-4}{6}} \geq {\frac{y+3}{4}}\)
;
95.
\({{\frac{17}{12}}} \lt {\frac{x+1}{6}-\frac{x-7}{12}}\)
;
96.
\({{\frac{17}{12}}} \lt {\frac{x+7}{6}-\frac{x-1}{12}}\)
;
Приложения
97.
Ваша оценка в классе определяется средним баллом по трем тестам. Вы набрали \(75\) и \(86\) в первых двух тестах. Чтобы заработать не менее \(80\) за этот курс, сколько вам нужно набрать на третьем тесте? Пусть \(x\) будет баллом, который вы заработаете на третьем тесте.
Напишите неравенство, представляющее эту ситуацию.
Решите это неравенство. Каков минимум, который вы должны заработать на третьем тесте, чтобы получить \(80\) за курс?
Вы не можете набрать больше \(100\) в третьем тесте. Используйте обозначение интервала для представления диапазона баллов, которые вы можете заработать на третьем тесте, чтобы заработать не менее \(80\) за этот курс.
98.
Ваша оценка в классе определяется средним баллом по трем тестам. Вы набрали \(70\) и \(90\) на первых двух тестах.
Чтобы заработать не менее \(83\) за этот курс, сколько вам нужно набрать на третьем тесте? Пусть \(x\) будет баллом, который вы заработаете на третьем тесте.
Напишите неравенство, представляющее эту ситуацию.
Решите это неравенство. Каков минимум, который вы должны заработать на третьем тесте, чтобы получить \(83\) за курс?
Вы не можете набрать больше \(100\) в третьем тесте. Используйте обозначение интервала для представления диапазона баллов, которые вы можете заработать на третьем тесте, чтобы заработать не менее \(83\) за этот курс.
Видео с вопросами: Поиск решения набора линейных неравенств с действительными числами
Стенограмма видео
Найдите набор решений
неравенство пять 𝑥 минус один больше 10 меньше, чем минус два 𝑥 плюс пять, что равно
меньше 𝑥 плюс три больше двух в действительных числах. Дайте свой ответ в интервале
обозначение.
Это относительно сложный вопрос. Имеем двустороннее неравенство, у нас есть некоторые дроби, и у нас также есть наша переменная 𝑥, появляющаяся в каждой части это неравенство. Давайте сначала рассмотрим, как мы могли бы решить эту проблему, рассматривая две части неравенства отдельно. Итак, у нас есть односторонний неравенство пять 𝑥 минус один больше 10 меньше, чем минус два 𝑥 плюс пять и другое одностороннее неравенство минус два 𝑥 плюс пять меньше, чем 𝑥 плюс три более двух.
С помощью нашего первого неравенства мы
начните с умножения каждой стороны на 10, чтобы исключить дроби. И теперь у нас пять 𝑥 минус один
меньше, чем минус 20 𝑥 плюс 50. Затем мы можем добавить по одному к каждой стороне
это неравенство. Теперь у нас все еще есть термины 𝑥
появляющиеся с каждой стороны. Итак, далее мы хотим сгруппировать все
𝑥 на той же стороне.
А если мы добавим по 20𝑥 с каждой стороны,
у нас будет положительное число 𝑥 в левой части нашего неравенства. Добавляя 20𝑥 к каждой стороне
Таким образом, неравенство дает 25𝑥 меньше 51. Наконец, разделив обе части нашего
неравенство на 25 дает 𝑥 меньше 51 на 25. И мы сохраним этот ответ в
дробная форма.
Итак, мы решили первую часть, и теперь давайте рассмотрим, как мы можем решить вторую часть. Во-первых, мы можем умножить обе части на два, чтобы исключить дроби, что дает минус четыре 𝑥 плюс 10 меньше, чем 𝑥 плюс три. Затем мы можем вычесть три из каждая сторона дает отрицательные четыре 𝑥 плюс семь меньше, чем 𝑥, а затем добавьте четыре 𝑥 к каждая сторона неравенства дает семь меньше пяти 𝑥. Наконец, мы делим на пять, что дает семь больше пяти меньше 𝑥 или 𝑥 больше семи больше пяти.
Итак, мы решили две части задачи.
наше неравенство отдельно. Но на самом деле мы можем объединить эти
ответы. Мы можем выразить это как
двустороннее неравенство, 𝑥 больше семи на пять и меньше 51 на
25. Однако вопрос задавал нам
дайте нашему ответу интервальную запись. Тогда мы можем записать это как
интервал с конечными точками семь на пять и 51 на 25. И поскольку каждое из неравенств
строгие неравенства, означающие, что ни одна из конечных точек не включена в интервал,
это означает, что наш интервал будет открытым с обоих концов. Итак, у нас есть ответ на
проблема. Множество решений этого неравенства
открытый интервал от семи на пять до 51 на 25.
Теперь, несмотря на шаги, связанные с
решение наших двух отдельных неравенств здесь было другим, на самом деле это возможно
решить это неравенство, сохранив все вместе, хотя это не всегда будет
дело.
В качестве знаменателей, участвующих в
дроби равны 10 и 2, а так как 2 — это коэффициент 10, мы можем исключить каждую из
знаменатели, умножая каждую часть нашего неравенства на 10. Что приводит нас к пяти 𝑥 минус один
меньше, чем минус 20 𝑥 плюс 50, что меньше пяти 𝑥 плюс 15. В этой последней части коэффициент
два в числителе сократились с множителем два в знаменателе. Но у нас все еще есть коэффициент пять
умножить 𝑥 плюс три на.
Теперь мы можем вычесть 50 из каждого
часть неравенства, дающая пять 𝑥 минус 51, меньше, чем минус 20 𝑥, то есть
меньше пяти 𝑥 минус 35. Но на данном этапе мы замечаем, что
у нас все еще есть 𝑥 членов, участвующих в каждой части нашего неравенства. Нам нужно сгруппировать их все вместе
в центре. И в данном случае, поскольку
количество 𝑥 в крайнем левом углу неравенства, то есть пять 𝑥, такое же, как и
количество 𝑥 в крайней правой части нашего неравенства, мы можем сделать это, вычитая
по пять 𝑥 с каждой части.
Однако, если бы число 𝑥 не
было одинаковым по обе стороны неравенства, мы не смогли бы сделать
это. И нам нужно было бы использовать наши
первый метод.
Теперь у нас есть минус 51 меньше
минус 25𝑥, что меньше минус 35. Наконец, мы можем разделить каждую часть
наше неравенство минус 25. Но мы должны быть очень осторожны здесь
потому что мы должны помнить, что когда мы умножаем или делим неравенство на
отрицательное число, мы должны изменить направление знака неравенства. Так что каждый из наших меньше, чем знаки должны
становятся больше, чем знаки. Таким образом, у нас есть минус 51 над
отрицательный 25 больше, чем 𝑥, что больше, чем отрицательный 35 над отрицательным
25. В каждой из наших фракций
отрицательные значения в числителях и знаменателях сокращаются. И дробь 35 на 25 может быть
упрощено до семи вместо пяти.
Записываем наше неравенство другое наоборот, чтобы наименьшее число было слева, у нас семь больше пяти меньше 𝑥 меньше 51 больше 25, что совпадает с найденным нами решением используя наш предыдущий метод. Таким образом, мы можем преобразовать наш ответ в интервальная запись точно таким же образом.
Решение рациональных неравенств — Minute Math
В этом разделе рассматриваются следующие темы:
- Решение рациональных неравенств
- Решение неравенства с рациональными функциями
Мы научились решать линейные неравенства после того, как научились решать линейные уравнения. Техники были почти такими же, за одним важным исключением. Когда мы умножаем или делим на отрицательное число, знак неравенства меняется на противоположный.
Только что научившись решать рациональные уравнения, мы теперь готовы решать рациональные неравенства.
A рациональное неравенство 9{2}}≤\frac{3}{x}$ являются рациональными неравенствами, поскольку каждое из них содержит рациональное выражение.
Когда мы решим рациональное неравенство, мы будем использовать многие методы, которые мы использовали при решении линейных неравенств. Мы особенно должны помнить, что когда мы умножаем или делим на отрицательное число, знак неравенства должен измениться.
Еще одно отличие состоит в том, что мы должны тщательно рассмотреть, какое значение может сделать рациональное выражение неопределенным и поэтому должно быть исключено.
Когда мы решаем уравнение и в результате получаем $x=3$, мы знаем, что существует одно решение, равное $3$.
Когда мы решаем неравенство и получаем $x>3$, мы знаем, что решений много. Мы наносим результат на график, чтобы лучше показать все решения, и начинаем с $3$. Три становится критической точкой , а затем мы решаем, заштриховывать ли ее слева или справа от нее. Числа справа от $3$ больше, чем $3$, поэтому мы затеняем вправо.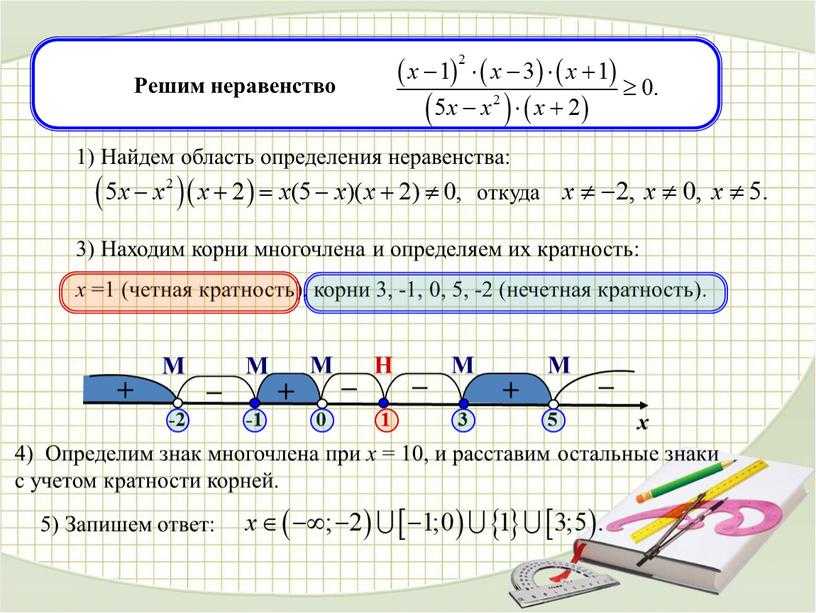
Чтобы решить рациональное неравенство, мы сначала должны написать неравенство только с одним частным слева и $0$ справа.
Затем мы определяем критические точки, чтобы использовать их для разделения числовой прямой на интервалы. Критическая точка — это число, которое делает рациональное выражение равным нулю или неопределенным.
Затем мы оценим множители числителя и знаменателя и найдем частное в каждом интервале. Это позволит определить интервал или интервалы, содержащие все решения рационального неравенства.
Мы записываем решение в интервальной нотации, стараясь определить, включены ли конечные точки.
Пример 1Решите и запишите решение в интервальной записи: $\frac{x-1}{x+3}≥0$.
РешениеШаг 1. Запишите неравенство в виде единицы слева и нуля справа.
Наше неравенство имеет такую форму. $\frac{x−1}{x+3}≥0$
Шаг 2. Определить критические точки — точки, в которых рациональное выражение будет равно нулю или неопределенно.
Рациональное выражение будет равно нулю, если числитель равен нулю. Поскольку $x−1=0$ при $x=1$, тогда $1$ является критической точкой.
Рациональное выражение будет неопределенным, если знаменатель равен нулю. Поскольку $x+3=0$ при $x=−3$, тогда $-3$ является критической точкой.
Критические точки: $1$ и $−3$.
Шаг 3. Используйте критические точки, чтобы разделить числовую прямую на интервалы.
Числовая строка делится на три интервала:
| $(-∞, -3)$ | $(-3, 1)$ | $(1, ∞)$ |
Чтобы найти знак каждого фактора в интервале, мы выбираем любую точку в этом интервале и используем ее в качестве контрольной точки. Любая точка интервала даст выражению тот же знак, поэтому мы можем выбрать любую точку интервала
Интервал $(-∞, -3)$
-∞, -3)$.
Проверить $x=-4$ в выражении в числителе и знаменателе.
| числитель | $x-1$ | знаменатель | $x+3$ |
| $\textcolor{red}{-4}-1$ | $\textcolor{red}{-4}+3$ | ||
| $-5$ | $-1$ | ||
| Отрицательное | Отрицательное |
Над числовой чертой отметьте множитель $x-1$ отрицательным и отметьте множитель $x+3 отрицательным.
Поскольку отрицательное число, деленное на отрицательное, является положительным, пометьте положительное частное в интервале $(-∞, -3)$.
Интервал $(-3, 1)$
Число $0$ находится в интервале $(-3, 1)$. Тест $x=0$.
| The Numerator | $ x-1 $ | The Denimanator | $ x+3 $ | ||||
| $ \ TextColor {Red} {0} -1 $ | $ \ TextColor {Red}}}} -1 $ | $ \ TextColor {Red}}}} -1 $ | $ \ \ red}}}}} -1 $ | $ \ \ \ {0} -1 $ | $ \ \ {0} -1 $ | $ \. } {0}+3 $ | |
| $ -1 $ | $ 3 $ | ||||||
| Отрицательный | Положительный |
выше. и отметим множитель $x+3$ положительным.
Поскольку отрицательное число, деленное на положительное, равно отрицательному, частное в интервале $(-3, 1)$ помечается как отрицательное.
Интервал $(1, ∞)$
Число $2$ находится в интервале $(1, ∞)$. Тест $x=2$.
| the numerator | $x-1$ | the denominator | $x+3$ |
| $\textcolor{red}{2}-1$ | $\textcolor{red {2}+3$ | ||
| $1$ | $5$ | ||
| Положительный | Положительный |
Над числовой строкой отметьте множитель $x-1$ положительным и отметьте $x+3$ положительным.
Поскольку положительное число, деленное на положительное, является положительным, отметим положительное частное в интервале $(1, ∞)$.
Шаг 5. Определите интервалы, на которых неравенство верно. Запишите решение в интервальной записи.
Мы хотим, чтобы частное было больше или равно нулю, поэтому числа в интервалах $(-∞, -3)$ и $(1,∞)$ являются решениями.
А как насчет критических точек?
Критическая точка $x=-3$ делает знаменатель $0$, поэтому ее нужно исключить из решения и отметить скобкой.
Критическая точка $x=1$ делает все рациональное выражение $0$. Неравенство требует, чтобы рациональное выражение было больше или равно $0$. Итак, $1$ является частью решения, и мы будем отмечать его скобкой.
Вспомним, что когда у нас есть решение, состоящее из более чем одного интервала, мы используем символ объединения $\cup$, чтобы соединить два интервала. Решением в интервальной записи является $(-∞, -3) \cup [1,∞)$.
Мы суммируем шаги для удобства.
- Запишите неравенство в виде одного частного слева и нуля справа.
- Определите критические точки — точки, в которых рациональное выражение будет равно нулю или неопределенно.
- Используйте критические точки, чтобы разделить числовую прямую на интервалы.
- Проверка значения в каждом интервале. Над числовой прямой показывают знак каждого множителя числителя и знаменателя в каждом интервале. Ниже числовой строки укажите знак частного.
- Определите интервалы, на которых неравенство верно. Запишите решение в интервальной записи.
Следующий пример требует, чтобы мы сначала привели рациональное неравенство в правильную форму.
Пример 2Решите и запишите решение в интервальной записи: $\frac{4x}{x-6}<1$.
Решение| $\frac{4x}{x-6}<1$ | |
Вычтите 1$, чтобы получить ноль справа. | $\frac{4x}{x-6}-1<0$ |
| Перепишите $1$ как дробь с помощью ЖК-дисплея. | $\frac{4x}{x-6}-\frac{x-6}{x-6}<0$ |
| Вычтите числители и поместите разницу над общим знаменателем. | $\frac{4x-(x-6)}{x-6}<0$ |
| Упростить. | $\frac{3x+6}{x-6}<0$ |
| Разложите числитель, чтобы показать все множители. | $\frac{3(x+2)}{x-6}<0$ |
| Найдите критические точки. | |
| Частное будет равно нулю, когда числитель равен нулю. Частное не определено, когда знаменатель равен нулю. | $x+2=0 \ \ \ x-6=0$ $x=-2 \ \ \ \ x=6$ |
Используйте критические точки, чтобы разделить числовую прямую на интервалы.
Проверка значения в каждом интервале.
Над числовой линией покажите знак каждого множителя рационального выражения в каждом интервале.
Под числовой чертой покажите знак частного.
Определите интервалы, на которых неравенство верно.
Мы хотим, чтобы частное было отрицательным, поэтому решение включает точки между $-2$ и $6$. Поскольку неравенство строго меньше, конечные точки не учитываются.
Запишем решение в виде интервала $(-2, 6)$.
В следующем примере числитель всегда положителен, поэтому знак рационального выражения зависит от знака знаменателя.
Пример 3 9{2}-2x-15}>0$Частное равно $0$, когда числитель равен $0$.
$x=-3 \ \ \ \ x=5$
Используйте критические точки, чтобы разделить числовую прямую на интервалы. 9{2}=0 \ \ x-6=0 \ \ x+1-0$
$x=0 \ \ \ x=6 \ \ \ x=-1$
Используйте критические точки для деления числовую прямую на интервалы.
Над числовой линией покажите знак каждого фактора в каждом интервале. Под числовой линией укажите знак каждого частного.
Поскольку $0$ исключено, решением являются два интервала $(-1, 0)$ и $(0, 6)$. Решение в интервальной записи: $(-1, 0) \cup (0, 6)$.
7.6.2 Решение неравенства с рациональными функциямиПри работе с рациональными функциями иногда полезно знать, когда функция больше или меньше определенного значения. Это приводит к рациональному неравенству.
Пример 5 Для заданной функции $R(x)=\frac{x+3}{x-5}$ найдите значения $x$, при которых функция меньше или равна $0$.
| $R(x)≤0$ | |
| Подставим рациональное выражение вместо $R(x)$. | $\frac{x+3}{x-5}≤0, x≠5$ |
| Найдите критические точки. | $x+3=0 \ \ \ x-5=0$ $x=-3 \ \ \ \ \ x=5$ |
Используйте критические точки, чтобы разделить числовую прямую на интервалы.
Тестовые значения в каждом интервале. Над числовой линией покажите знак каждого фактора в каждом интервале. Под числовой прямой покажите знак частного.
Запишите решение в виде интервала: $[3,5)$
Поскольку $5$ исключено, мы не включаем его в интервал.
Пример 6Функция $C(x)=10x+3000$ представляет затраты на производство $x$ количества изделий. Найдите:
- функцию средней стоимости, $c(x)$
- сколько изделий нужно произвести, чтобы средняя стоимость была меньше $\$40$.
Часть 1
| $C(x)=10x+3000$ | |
| Чтобы найти функцию средней стоимости, разделите функцию стоимости на $x$. | $c(x)=\frac{C(x)}{x}$ $c(x)=\frac{10x+3000}{x}$ |
| Функция средней стоимости $c (x)=\frac{10x+3000}{x}$ |
Часть 2
| Мы хотим, чтобы функция $c(x)$ была меньше $40$. | $c(x)<40$ |
| Подставьте рациональное выражение вместо $c(x)$. | $\frac{10x+3000}{x}<40, x≠0$ |
| Вычтите 40$, чтобы получить 0$ справа. | $\frac{10x+3000}{x}-40<0$ |
| Перепишите левую часть как одно частное, найдя ЖКД. | $\frac{10x+3000}{x}-40(\frac{x}{x})<0$ |
| Упростить. | $\frac{10x+3000}{x}-\frac{40x}{x}<0$ $\frac{10x+3000-40x}{x}<0$ $\frac{-30x+ 3000}{x}<0$ |
| Разложите числитель на множители, чтобы показать все множители. | $\frac{-30(x-100)}{x}<0$ |
Найдите критические точки. |