Математика для блондинок: Икс плюс икс равно
Просматривая комментарии, приходишь к неутешительному выводу: некоторые математики не в состоянии объяснить своим ученикам самых элементарных вещей. Как и что можно делать с иксами? С этим мы попытаемся разобраться. А для любителей быстрых ответов скажу сразу: икс плюс икс равно два икс. Это типа сапог плюс сапог — два сапога пара. Если к одному иксу прибавить другой икс получится чудненькая парочка иксов.
| Икс плюс икс равно два икс |
Первая проблема, с которой сталкиваются обучаемые математике — это отсутствие чисел возле букв. В грамматике буквы просто читают. В математике с буквами что-то нужно делать, типа складывать или умножать. Но ведь до этого складывать и умножать учили только числа.
Вторая проблема — что можно делать с буквами, а что нельзя? Четкий ответ на этот вопрос вы вряд ли найдете у математиков.
Начнем по порядку. Почему математики не всегда пишут числа возле букв? Врать не буду, я не путин, но версия появления букв в математике у меня есть. Как любят говорить политики, «так исторически сложилось». Если изменить математические правила и всегда писать количество букв перед самой буквой, тогда проблем будет гораздо меньше. Но вы представляете, что означает «изменить математические правила»? Это всё равно, что Библию изменить.
| Буквы с числами |
Как видите, с циферками всё гораздо понятнее: если к одному иксу прибавить ещё один икс, то у нас получится два икса. Никто из математиков вам этого не скажет, но вспомните детский садик. Там вас учили отрывать числа от их содержания и тупо выполнять действия с числами: один плюс один равно два. Когда вы начинаете выполнять математические действия с буквами, вам нужно прилепить содержание к числам.
Математики, как черт ладана, боятся детского садика. Никогда никто о нем не вспоминает. И есть чего бояться. Давайте вернемся в детский садик и посмотрим, что получается.
| Сложение в детском садике |
Зайчик плюс зайчик равно два зайчика, икс плюс икс равно два икса. То, что вы делаете в детском садике со зверушками, на уроках алгебры можно делать с буквами — ашками, бешками, иксами, игреками… Чуть-чуть усложним задачу и добавим циферок в каждый из примеров.
| Пример сложения |
Зайчик плюс три зайчика равно четыре зайчика, икс плюс три икса равно четыре икса. Буквы в математике можно складывать и вычитать точно так же, как вы складывали и вычитали зверушек или счетные палочки в детском садике. Рассмотрим более сложные примеры.
Буквы в математике можно складывать и вычитать точно так же, как вы складывали и вычитали зверушек или счетные палочки в детском садике. Рассмотрим более сложные примеры.
| Пример с иксами |
То, что здесь проделано с иксами, можно сделать с любыми зверушками из детского садика или с любыми буквами из алгебры. По своим математическим свойствам детсадовские зверушки ничем не отличаются от алгебраических букв. Наш пример решен двумя способами — без скобок и со скобками. Получается, что когда в детском садике нас учат отрывать числа от содержания, мы практически учимся выполнять математические действия с числами в скобках. В начале мы отрываем числа от названий зверушек, выполняем математические действия с числами и в конце решения прикрепляем название зверушки к результату.
Названия зверушек в детском садике выполняют роль единиц измерения чисел. В алгебре буквы выполняют ту же самую роль. Когда в одном примере встречаются разные зверушки, мы по их названиям выполняем сложение или вычитание: зайчики с зайчиками, уточки с уточками. Когда в одном алгебраическом примере встречаются разные буквы, поступать нужно точно так же — ашки с ашками, бешки с бешками, иксы с иксами, игреки с игреками.
В алгебре буквы выполняют ту же самую роль. Когда в одном примере встречаются разные зверушки, мы по их названиям выполняем сложение или вычитание: зайчики с зайчиками, уточки с уточками. Когда в одном алгебраическом примере встречаются разные буквы, поступать нужно точно так же — ашки с ашками, бешки с бешками, иксы с иксами, игреки с игреками.
| Пример с двумя буквами |
Теперь наступает самый интересный момент — умножение в детском садике. Такое математикам может присниться только в самом страшном сне. Смотрите сами. Берем сложение в детском садике и заменяем его умножением.
| Умножение в детском садике |
Зайчик, умноженный на зайчика, равен зайчику в квадрате. Бред получился. Вот почему в детском садике умножение никогда не изучают. Икс, умноженный на икс, равен иксу в квадрате. Вроде как и ничего страшного, к иксу без шапочки добавляется шапочка со степенью. А вот метр, умноженный на метр, равняется метру квадратному. Длина, умноженная на ширину, дает площадь. Здесь совсем всё понятно.
Как видим, не все единицы измерения имеют одинаковые математические свойства. Сегодня ни один математик вам ничего толком не объяснит — не изучают в математике единицы измерения. Мы с вами рассмотрим математические свойства единиц измерения немного позже. Здесь нужен уровень чуть выше, чем в детском садике или на первых уроках алгебры. Собственно, высшую математику специально для того и придумали, чтобы математики могли с умным видом вам объяснять, почему они не понимают самых элементарных вещей.
Когда математики вам рассказывают, что умножение можно заменить сложением — не верьте им, они врут, как путин. Только умножение числа на число можно представить в виде сложения. Во всех остальных остальных случаях, когда речь идет о единицах измерения, сложение и умножение — это совершенно разные вещи. Получается, что математика без единиц измерения — это детская игра в числа для взрослых дядек и тёток.
Но продолжим дальше. Как быть, если в одном примере единицы измерения или буквы разные? Единицы измерения перемножаются между собой, а буквы… То же правило, что и при сложении: ашки с ашками, бешки с бешками, иксы с иксами… Только теперь не складываются, а перемножаются. Числа перемножаете отдельно с числами.
| Умножение двух букв |
Да, зайко-уточка — это, конечно, жесть. Но… Таковы законы математики. Надеюсь, со сложением и умножением иксов мы разобрались.
Теперь второй вопрос — что можно делать с иксами? Да что угодно, хоть ногами пинайте, но только не нарушайте равенство. Как это? А вот так — икс плюс икс равно…
| Икс плюс икс |
Вариантов преобразования равенства может быть бесконечное множество. Математики, без особой нужды, такими штучками не балуются. Но и относиться к иксам, как к святыне — тоже не правильно. Буквы в математике — это самые обычные рабочие инструменты, которыми нужно грамотно пользоваться.
Что ещё можно отметить? Если раньше, в примерах с числами, учителя вам писали, какие действия нужно выполнять, ну, там, типа, сложение или умножение, то в алгебраических выражениях с буквами вы уже сами, как Боги, определяете, что делать можно, а что нельзя.
Коль мы уже затронули тему умножения и получили зайко-уточку, то уместно будет дать ответ на самый популярный детский вопрос.
Использование режимов камеры на iPhone, iPad и iPod touch
Узнайте, как использовать режимы «Портрет», «Панорама», «Замедленно» и другие режимы камеры на вашем устройстве.
Выбор подходящего режима для съемки
Различные режимы камеры, доступные непосредственно на iPhone, iPad и iPod touch, помогут вам добиваться идеального результата при фото- и видеосъемке. Чтобы переключаться между режимами, смахивайте вправо или влево. Доступны следующие режимы: «Фото», «Видео», «Таймлапс», «Замедленно», «Квадрат», «Портрет» и «Панорама».
Сначала убедитесь, что у вас установлена последняя версия iOS или iPadOS.
Режим «Фото»
«Фото» — это стандартный режим, который вы увидите, открыв приложение «Камера». В этом режиме вы можете делать обычные фотографии и снимки Live Photos.
Ваша камера автоматически сфокусируется и установит экспозицию в зависимости от того, на что вы ее наведете. Вы можете коснуться другой области в видоискателе, чтобы изменить фокус и экспозицию. Затем, если необходимо оставить фокус и экспозицию в той же точке, нажмите на экран и удерживайте нажатие, пока не появится надпись «Фиксация экспозиции/фокуса».
Затем, если необходимо оставить фокус и экспозицию в той же точке, нажмите на экран и удерживайте нажатие, пока не появится надпись «Фиксация экспозиции/фокуса».
На iPhone XS, iPhone XR и более поздних моделях можно использовать функцию QuickTake, чтобы легко снимать видео в режиме фотосъемки. На других моделях iPhone можно нажать и удерживать кнопку спуска затвора, чтобы выполнить серийную съемку. Чтобы остановить съемку, просто отпустите кнопку спуска затвора.
Режим «Портрет»
Режим «Портрет» создает эффект глубины поля, благодаря которому объект съемки остается резким на размытом фоне. Вы можете использовать режим «Портрет» на следующих моделях iPhone: iPhone 13, iPhone 13 mini, iPhone 13 Pro, iPhone 13 Pro Max, iPhone 12, iPhone 12 mini, iPhone 12 Pro, iPhone 12 Pro Max, iPhone SE (2-го поколения), iPhone 11, iPhone 11 Pro, iPhone 11 Pro Max, iPhone XR, iPhone XS, iPhone XS Max, iPhone X, iPhone 8 Plus и iPhone 7 Plus. На iPhone X или более поздних моделей также можно делать селфи в режиме «Портрет». Кроме того, вы можете использовать режим «Портрет» с фронтальной камерой на моделях iPad Pro 11 дюймов (все поколения) и iPad Pro 12,9 дюйма (3-го поколения и более поздние).
Кроме того, вы можете использовать режим «Портрет» с фронтальной камерой на моделях iPad Pro 11 дюймов (все поколения) и iPad Pro 12,9 дюйма (3-го поколения и более поздние).
Чтобы использовать режим «Портрет», откройте приложение «Камера» и перейдите в режим «Портрет». Если приложение посоветует отойти дальше от объекта съемки, сделайте это. Когда поле «Эффект глубины» станет желтым, сделайте снимок.
Теперь изображения, полученные в режиме «Портрет» на iPhone X и более поздней модели, а также iPhone 8 Plus, можно сделать еще более завораживающими благодаря эффектам освещения студийного качества. После съемки нажмите «Править» и выберите один из эффектов: «Студийный свет», «Контурный свет», «Сценический свет» или «Сценический свет — моно». На iPhone 13, iPhone 13 mini, iPhone 13 Pro, iPhone 13 Pro Max, iPhone 12, iPhone 12 mini, iPhone 12 Pro, iPhone 12 Pro Max, iPhone SE (2-го поколения), iPhone XR, iPhone XS и iPhone XS Max можно создать красивый классический вид с помощью эффекта «Светлая тональность — Ч/Б».
Камера iPhone XR на задней панели не поддерживает эффекты «Сценический свет», «Сценический свет — Ч/Б» и «Светлая тональность — Ч/Б».
Режим «Квадрат»
В режиме «Квадрат» область кадра на экране камеры ограничивается квадратом — такой размер фотографии оптимален для большинства социальных сетей. Таким образом, сделанный снимок можно тут же опубликовать в любимой социальной сети.
На iPhone 13, iPhone 13 mini, iPhone 13 Pro, iPhone 13 Pro Max, iPhone 12, iPhone 12 mini, iPhone 12 Pro, iPhone 12 Pro Max, iPhone SE (2-го поколения), iPhone 11 или iPhone 11 Pro нажмите стрелку , чтобы получить доступ к режиму «Квадрат» и другим вариантам.
Режим «Панорама»
Используйте режим «Панорама», чтобы получить широкоугольный снимок ландшафта, медленно перемещая свое устройство. В режиме «Панорама» в центре экрана отображается направляющая линия, которая помогает сделать фотографию. Если нужно снять панораму в направлении слева направо, убедитесь, что стрелка указывает вправо. А если справа налево — нажмите стрелку для смены направления.
А если справа налево — нажмите стрелку для смены направления.
Нажмите кнопку затвора и медленно перемещайте камеру по прямой линии от одной стороны снимка к другой. Старайтесь двигать камеру так, чтобы стрелка постоянно находилась на желтой направляющей линии.
Видео
Если выбрать любой режим видеосъемки, кнопка затвора меняет свой цвет с белого на красный. Нажмите кнопку спуска, чтобы начать съемку, а затем нажмите ее еще раз, чтобы завершить.
Хотите изменить длину видео? Нажмите «Править» или кнопку редактирования и перемещайте ползунок, чтобы изменить время начала и завершения видео. Нажмите кнопку «Готово», чтобы сохранить изменения.
Если у вас модель iPhone 13, вы можете добавить глубину резкости в свои видеоролики, воспользовавшись режимом «Киноэффект». Чтобы ускорить или замедлить свой видеоролик на всех устройствах, попробуйте режимы «Замедленно» и «Таймлапс».
Режим «Киноэффект»
Режим «Киноэффект» в камере iPhone 13 позволяет записывать видео в кинематографическом формате с малой глубиной резкости и добавлять функцию плавного перемещения фокуса.
Режим «Киноэффект» поддерживается на моделях iPhone 13, iPhone 13 mini, iPhone 13 Pro и iPhone 13 Pro Max. Узнайте больше об использовании режима «Киноэффект» на iPhone.
Режим «Замедленно»
Продлевайте любимые моменты, просматривая видео с эффектом замедленного воспроизведения. В этом режиме видео записывается как обычно, но при воспроизведении применяется эффект замедленного воспроизведения. Можно редактировать видео, чтобы действие режима замедленной съемки запускалось и останавливалось в указанное вами время.
Режим «Таймлапс»
Снимки делаются через выбранные временные интервалы, и в результате получается ускоренное видео, которое можно тут же опубликовать. Если перейти в режим «Таймлапс» и нажать кнопку затвора, камера будет делать снимки с заданной периодичностью, пока вы не нажмете эту кнопку еще раз.
Дополнительная информация
Дата публикации:
Видео с вопросами: Составление и решение квадратных уравнений
Стенограмма видео
Определите положительное число, квадрат которого вдвое превышает его значение на 15.
Теперь может возникнуть соблазн попытаться подойти к этому вопросу методом проб и ошибок. Но будет более эффективно, если мы сможем использовать алгебраический метод. Мы можем ввести букву 𝑥 для обозначения этого положительного числа. Затем нам говорят, что квадрат этого числа, который будет 𝑥 в квадрате, вдвое превышает его значение, то есть это вдвое больше исходного числа, на 15. Мы можем выразить это уравнением. Квадрат 𝑥, 𝑥 в квадрате, равен 15 более чем в два раза больше 𝑥. Это два 𝑥 плюс 15. Теперь у нас есть квадратное уравнение относительно 𝑥, потому что наибольшая степень 𝑥, которая появляется, равна двум. Здесь у нас есть 𝑥 в квадрате.
Наш первый шаг в решении любого квадратного уравнения — собрать все члены на одной стороне. Мы можем сделать это, вычитая два 𝑥 и 15 из каждой части уравнения, чтобы получить 𝑥 в квадрате минус два 𝑥 минус 15 равно нулю. Мы решили сгруппировать члены в левой части уравнения, потому что тогда у нас есть положительный коэффициент 𝑥 в квадрате, что часто делает вещи немного проще.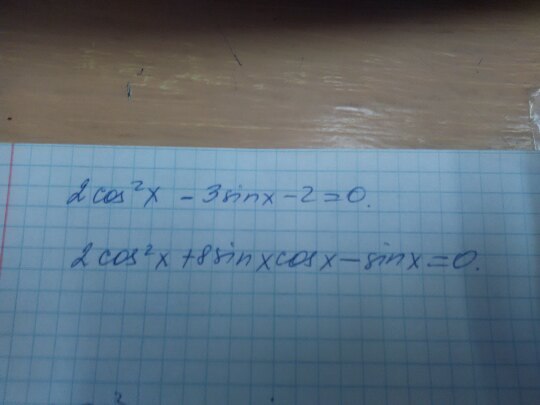 Тогда есть ряд методов, которые мы можем знать для решения квадратных уравнений. Они факторизуют, используя квадратичную формулу или завершая квадрат. Если квадратное уравнение можно решить с помощью факторизации, то это обычно самый простой метод. Итак, мы начнем с проверки, можно ли разложить этот квадрат на множители.
Тогда есть ряд методов, которые мы можем знать для решения квадратных уравнений. Они факторизуют, используя квадратичную формулу или завершая квадрат. Если квадратное уравнение можно решить с помощью факторизации, то это обычно самый простой метод. Итак, мы начнем с проверки, можно ли разложить этот квадрат на множители.
Коэффициент при квадрате 𝑥 в этом уравнении равен единице. Так что это один из самых простых квадратичных коэффициентов. Мы хотим найти два линейных выражения, которые при умножении дают 𝑥 в квадрате минус два 𝑥 минус 15. Первый член в каждом из этих выражений должен быть 𝑥, потому что 𝑥, умноженное на 𝑥, дает 𝑥 в квадрате. Чтобы завершить скобки, мы ищем два числа с определенным набором свойств. Во-первых, их сумма должна быть коэффициентом 𝑥, равным двум. Во-вторых, их произведение должно быть постоянным членом уравнения, то есть отрицательным 15,9.0005
Мы можем найти эти два числа, перечислив пары множителей числа 15. Это один и 15, три и пять. Но мы хотели, чтобы произведение было отрицательным, равным 15, а это значит, что нам нужно, чтобы одно из чисел было положительным, а другое — отрицательным.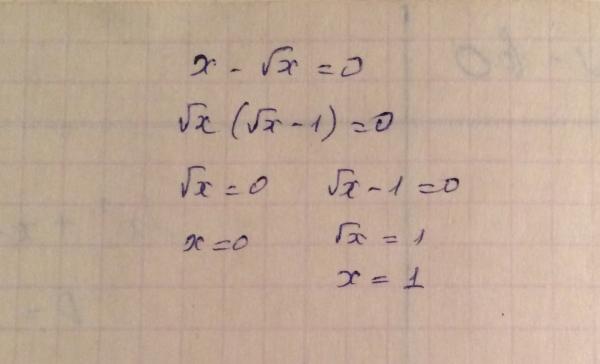 Если мы возьмем вторую пару множителей и оставим три положительными, но сделаем пять отрицательными, то три, умноженные на отрицательные пять, действительно дадут произведение минус 15, а три плюс минус пять дают сумму минус два. Это два числа, которые нам нужны, чтобы закрыть скобки. Итак, квадратичные множители как 𝑥 плюс три, умноженные на 𝑥 минус пять.
Если мы возьмем вторую пару множителей и оставим три положительными, но сделаем пять отрицательными, то три, умноженные на отрицательные пять, действительно дадут произведение минус 15, а три плюс минус пять дают сумму минус два. Это два числа, которые нам нужны, чтобы закрыть скобки. Итак, квадратичные множители как 𝑥 плюс три, умноженные на 𝑥 минус пять.
Мы можем, конечно, проверить это, перераспределив скобки, возможно, используя метод FOIL. Умножая первые члены вместе, 𝑥, умноженное на 𝑥, дает 𝑥 в квадрате. Умножая внешние члены, 𝑥, умноженное на минус пять, дает минус пять 𝑥. Умножая внутренние члены, три умножить на 𝑥 равно трем 𝑥. И, наконец, умножение последних слагаемых вместе, умножение трех на минус пять, дает минус 15. Собирая одинаковые слагаемые в центре нашего разложения, мы получаем 𝑥 в квадрате минус два 𝑥 минус 15, что и является квадратичным числом, которое мы пытались разложить на множители. Итак, у нас есть 𝑥 плюс три, умноженное на 𝑥 минус пять равно нулю.
Затем мы вспоминаем, что если произведение двух чисел или двух выражений равно нулю, по крайней мере один из этих отдельных множителей должен сам равняться нулю. Таким образом, либо 𝑥 плюс три равно нулю, либо 𝑥 минус пять равно нулю. Каждое из этих линейных уравнений можно решить за один шаг. Мы решаем первое уравнение, вычитая по три с каждой стороны, чтобы получить 𝑥 равно отрицательному трем. И чтобы решить второе уравнение, мы добавляем пять к каждой стороне, чтобы получить 𝑥 равно пяти. Итак, у нас есть два решения нашего квадратного уравнения. Либо 𝑥 равно минус трем, либо 𝑥 равно пяти.
Оглядываясь назад на вопрос, мы использовали 𝑥 для представления положительного числа. Таким образом, хотя отрицательное число три является допустимым решением этого квадратного уравнения, это не возможное значение для 𝑥. Тогда наш ответ — пять, но давайте проверим это. Пять в квадрате равно 25. Дважды пять равно 10. И если мы прибавим 15, мы действительно получим 25. Таким образом, квадрат пяти действительно превышает свое значение в два раза на 15. Тогда наш ответ — пять.
Тогда наш ответ — пять.
Математическая сцена — Уравнения III — Урок 1
Математическая сцена — Уравнения III — Урок 1 — Квадратные уравнения2008 Расмус Эф и Джанн Сак Птурссон | Уравнения III |
Урок 1
Квадратичный уравнения
Теперь мы рассмотрим, как решать квадратные уравнения (второй степени уравнения). Это тот же процесс, что и нахождение графика квадратичного уравнения. функция, такая как
f(x) = ax 2 + bx + c пересекает ось x
Сначала мы будем рассмотрим уравнения, в которых коэффициенты b или c равны нулю (b = 0 или c = 0).
Пример 1
| а) 2x 2 − 8 = 0 2x 2 = 8 х 2 = 4 х = 2 | Первый
переместите постоянный член над знаком равенства, затем разделите обе части
уравнение на 2. |
| б) 2x 2 + 8 = 0 2x 2 = -8 х 2 = -4 нет решения | В этом Например, мы не можем извлечь квадратный корень из-за знака минус. |
Пример 2
| а) 2x 2х(х — 4) = 0 2x = 0 каждый x — 4 = 0 х = 0 каждый х = 4 | Разложить на множители, вынеся за скобки 2x. Один из двух факторов должен быть ноль, чтобы умножение было равно нулю. |
| б) 2x 2 + 8x = 0 2х(х + 4) = 0 2x = 0 шт.  x + 4 = 0 x + 4 = 0 х = 0 каждый х = −4 | Опять мы имеют два решения. Квадратные уравнения, где c=0 , всегда имеют два решения. |
Мы
иметь более сложную задачу, если ни один из коэффициентов
а, b и с равны нулю.
Легче всего решать уравнения, соответствующие шаблону
.p 2 2pq + p 2 = (p q) 2
Пример 3
| а) x 2 + 2х + 1 = 0 (х + 1) 2 = 0 (х + 1) = 0 х = −1 | Это точно вписывается в приведенную выше схему. |
| б) 2x 2 − 8x + 8 = 0 2(х 2 −4x + 4) = 0 2(x 2) 2 = 0 (х — 2) = 0 х = 2 | Если мы
возьмите 2 за скобки, это тоже соответствует шаблону. |
Иногда мы можем факторизовать уравнение путем проверки (угадывания факторов), затем найти значение x, которое делает каждый фактор равным нулю.
Пример 4
Решить уравнение x 2 − 5x + 6 = 0
х 2 — 5х + 6 = 0
(х — 2) (х — 3) = 0
х = 2 или х = 3
Пример 5
| Решите уравнение x 2 − 4x − 5 = 0. х 2 — 4х — 5 = 0 x 2 − 4x + 2 2 − 2 2 − 5 = 0 (х 2 — 4х + 4) — 9 = 0 | Здесь мы завершаем квадрат, добавляя (и затем вычитая) половину коэффициент b в квадрате. Затем мы можем использовать правило p 2 2pq + q 2 = (p q) 2 |
| (х — 2) 2 — 9 = 0 | Результат имеет вид (x + r) 2 + s |
х — 2 = 3 х = 2 3 х = 5 или х = -1 | который был
введен в 3-м. |
Пример 6
Решить уравнение 3x 2 − 24x + 21 = 0
3(x 2 − 8x) + 21 = 0
3(x 2 − 8x + 4 2 ) − 3∙4 2 + 21 = 0
3(x − 4) 2 − 48 + 21 = 0
3(x − 4) 2 = 27
(x − 4) 2 = 9
х — 4 = 3
х = 4 + 3 = 7 или х = 4 — 3 = 1
Пример 7
Сейчас мы идем найти формулу, с помощью которой можно решить любое уравнение второй степени форма ax 2 + bx + c = 0
Возьми вне скобок.. Добавить половину коэффициент при х в квадрате. Вычесть одно и то же число, не забывая умножить на а. | |
Напишите первый три члена уравнения в виде скобки в квадрате Переместить два других
слагаемые над знаком равенства и найти общий знаменатель. |
Теперь возьмем квадрат корень обеих частей уравнения, помня + и -. Окончательно найти x путем перемещения термина внутри скобки через знак равенства. |
Алгебра в это доказательство довольно сложное, но как только мы нашли формулу, у нас нет повторить процесс, и мы можем использовать его для решения любого квадратичного уравнение.
Это формула, которую мы можем использовать для решения уравнения ax 2 + bx + c = 0
Эта формула одна из самых известных и наиболее полезных формул в математике.
Пример 8
Теперь мы будем использовать эта формула для решения уравнения 2x 2 — 10x + 8 = 0
| коэффициенты: | а = 2 |
| б = -10 | |
| с = 8 |
Поместите эти числа для a,b и c в формулу
Пример 9
Решить уравнение x 2 − 3x + 6 = 0
коэффициенты: a = 1, b = −3 и c = 6,
Положить их в
формула.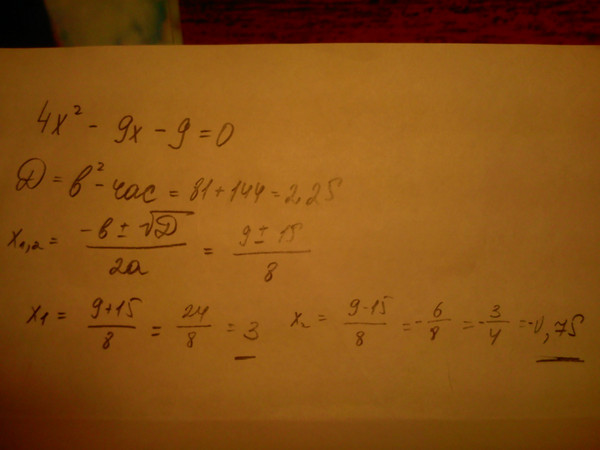
В этом примере число под квадратным корнем отрицательно, поэтому уравнение не имеет решения.
| Пример 10 |
Мы можем решить квадратные уравнения с помощью графического калькулятора.
Вот как решить уравнение 2x 2 − 10x + 8 = 0 с помощью графического калькулятор.
Первый выбор ЭКВА в меню.
Получаем:
Теперь выберите Многочлен с F2 .
Решаем квадратное уравнение, выбрав 2 (нажмите F1). Мы также можем решить третью степень уравнений, выбрав 3. Это экран, который мы видим:
Ставим в значения а = 2, б = −10 и c = 8, нажимая exe между каждым значением.
Следующее показывает последовательность действий:
Наконец выберите SOLV нажав F1. Решения 4 и 1 появляются на следующем экране:
Пример 11
Давайте посмотрим, как
калькулятор имеет дело с уравнением, которое не имеет решения.

 Наконец, возьмите квадратный корень из обеих сторон
уравнение с учетом + и -.
Наконец, возьмите квадратный корень из обеих сторон
уравнение с учетом + и -.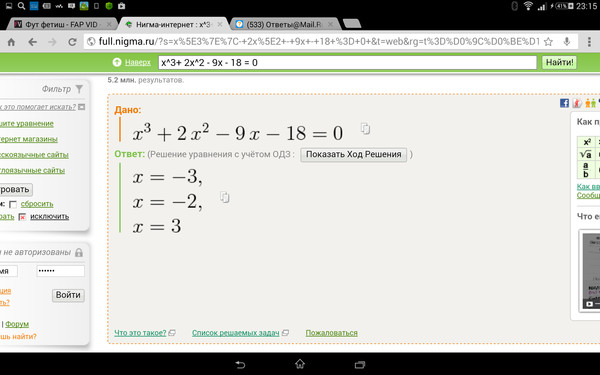
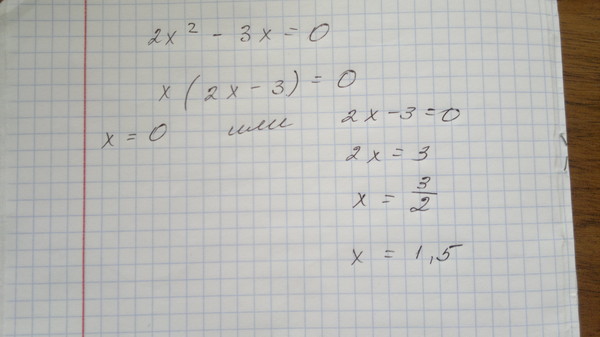 урок функций 1
урок функций 1