Пошаговое решение :
Шаг 1 :
Попытка разложить на множители путем разделения среднего члена
1.1 Разложение на множители x 2 +x-22
4 Первый член равен
4 , x 2 его коэффициент равен 1 .
Средний член равен +x , его коэффициент равен 1 .
Последний член, «константа», равен -22 Шаг-1: Умножьте коэффициент первого члена на константу 1 • -22 = -22 равен коэффициенту среднего члена, который равен 1 .
-22 + 1 = -21 -11 + 2 = -9 -2 + 11 = -1 + 22 = + 22 = + 22 = + 22 = + 22 = + 22 = + 22 = + 22 = + 22 0033 21
Наблюдение: Невозможно найти два таких фактора!!
Заключение: Трехчлен нельзя разложить на множители
Уравнение в конце шага 1 :
x 2 + x - 22 = 0
Шаг 2 :
Парабола, поиск вершины :
2. 1 Найдите вершину y = x 2 +x-22
1 Найдите вершину y = x 2 +x-22
Параболы имеют наивысшую или низшую точку, называемую вершиной. Наша парабола раскрывается и, соответственно, имеет низшую точку (абсолютный минимум). Мы знаем это еще до того, как начертили «у», потому что коэффициент первого члена, 1 , положителен (больше нуля).
Каждая парабола имеет вертикальную линию симметрии, проходящую через ее вершину. Из-за этой симметрии линия симметрии, например, будет проходить через середину двух точек пересечения x (корней или решений) параболы. То есть, если парабола действительно имеет два действительных решения.
Параболы могут моделировать многие реальные жизненные ситуации, такие как высота над землей объекта, брошенного вверх через некоторый период времени. Вершина параболы может предоставить нам такую информацию, как максимальная высота, на которую может подняться объект, брошенный вверх. По этой причине мы хотим иметь возможность найти координаты вершины.
Для любой параболы, Ax 2 +Bx+C, x координата вершины определяется как -B/(2A) . В нашем случае координата х равна -0,5000
В нашем случае координата х равна -0,5000
. Подставляя в формулу параболы -0,5000 для х, мы можем вычислить координату у: 22,250
Парабола, графическая вершина и точки пересечения X:
Корневой график для: y = x 2 +x-22
Ось симметрии (пунктирная) {x}={-0,50}
Вершина в {x,y } = {-0,50,-22,25}
x -Отсечения (корни):
Корень 1 при {x,y} = {-5,22, 0,00}
Корень 2 при {x,y} = {4,22, 0,00}
Решите квадратное уравнение, заполнив квадрат
2.2 Решение x 2 +x-22 = 0 путем заполнения квадрата.
Прибавьте 22 к обеим частям уравнения:
x 2 +x = 22
Теперь немного хитрости: возьмите коэффициент при x , равный 1, разделите на два, получив 1/2, и, наконец, возведите его в квадрат. что дает 1/4
Добавьте 1/4 к обеим частям уравнения:
В правой части имеем :
22 + 1/4 или, (22/1)+(1/4)
Общий знаменатель двух дробей равен 4 Складываем (88/4)+(1/4) дает 89/4
Таким образом, прибавив к обеим сторонам, мы наконец получим :
x 2 +x+(1/4) = 89/4
Добавление 1/4 завершило левую часть в правильный квадрат:
x 2 +x+(1/4) =
(x+(1/2)) • (x+(1/2)) =
(x+(1/2)) 2
Вещи, равные одному и тому же также равны между собой. С
С
x 2 +x+(1/4) = 89/4 и
x 2 +x+(1/4) = (x+(1/2)) 2
тогда по закону транзитивности ,
(x+(1/2)) 2 = 89/4
Мы будем называть это уравнение уравнением #2.2.1
Принцип квадратного корня гласит, что когда две вещи равны, их квадратные корни равны.
Обратите внимание, что квадратный корень из
(x+(1/2)) 2 равен
(x+(1/2)) 2/2 =
(x+(1/2)) 1 =
x+(1/2)
Теперь, применяя принцип квадратного корня к уравнению #2.2.1 получаем:
x+(1/2) = √ 89/4
Вычтем 1/2 с обеих сторон, чтобы получить:
x = -1/2 + √ 89/4
Поскольку квадратный корень имеет два значения, одно положительное, а другое отрицательное 4
Обратите внимание, что √ 89/4 можно записать как
√ 89 / √ 4 что равно √ 89/ 2
Решение квадратного уравнения с помощью квадратной формулы
2. 3 Решение x 2 +x-22 = 0 с помощью квадратной формулы .
3 Решение x 2 +x-22 = 0 с помощью квадратной формулы .
Согласно квадратичной формуле, x, решение для AX 2 +BX +C = 0, где A, B и C являются числами, часто называемыми коэффициентами, определяются как:
-B a √ B 2 -4AC
x = ————————
2A
В нашем случае A = 1
B = 1
C = -22
Соответственно, B 2 -4AC =
1-(-88) =
89
Применение квадратичной формулы:
-1 ± √ 89
x = —————
2
√ 89, округление до 4 десятичных цифр, составляет 9,4340
, так что теперь мы смотрим на:
x = (-1 ± 9.434 ) / 2
Два решения были найдены:
- x =(-1-√89)/2=-5,217
- x =(-1+√89)/2= 4,217
В этом видео мы рассмотрим
некоторые примеры квадратных уравнений и использовать факторизацию или факторизацию, чтобы найти
их корни. Мы также поговорим о некоторых
различные обозначения, которые вы можете использовать, чтобы представить свои ответы. Мы рассмотрели факторинг различных
типы квадратичных уравнений более подробно описаны в других видеороликах, поэтому мы просто кратко повторим
процесс здесь.
Мы рассмотрели факторинг различных
типы квадратичных уравнений более подробно описаны в других видеороликах, поэтому мы просто кратко повторим
процесс здесь.
Но сначала помните, что
квадратичное выражение имеет квадратный член, линейный член и постоянный член. Так это плюс или минус
число, умноженное на 𝑥 в квадрате, положительное или отрицательное число, умноженное на 𝑥, и число, умноженное на 𝑥.
положительная или отрицательная константа на конце. Также помните, что коэффициент
𝑥 или постоянный член в конце, поэтому 𝑏 или значение 𝑐 здесь может либо
быть нулевым, или они оба могут быть нулевыми в этом отношении. Но 𝑎-значение здесь не может быть
ноль, иначе оно не было бы квадратичным.
Так, например, если 𝑎 было единицей, 𝑏
было минус пять, а 𝑐 было шесть, у нас было бы квадратное выражение 𝑥 в квадрате
минус пять 𝑥 плюс шесть. А также помните, что у него нет
быть 𝑥; это может быть любая буква. Корнями квадратного являются
𝑥-значения, которые генерируют ваш нулевой результат, когда вы подставляете их в
выражение. Так, например, вопрос типа:
Найдите корни квадратного уравнения 𝑦 равно 𝑥 в квадрате минус пять 𝑥 плюс шесть
означает решить 𝑥 в квадрате минус пять 𝑥 плюс шесть равно нулю. Другими словами, найти значения
𝑥, которые соответствуют этому уравнению.
А также помните, что у него нет
быть 𝑥; это может быть любая буква. Корнями квадратного являются
𝑥-значения, которые генерируют ваш нулевой результат, когда вы подставляете их в
выражение. Так, например, вопрос типа:
Найдите корни квадратного уравнения 𝑦 равно 𝑥 в квадрате минус пять 𝑥 плюс шесть
означает решить 𝑥 в квадрате минус пять 𝑥 плюс шесть равно нулю. Другими словами, найти значения
𝑥, которые соответствуют этому уравнению.
В этом случае не беспокойтесь
на данный момент, как мы их нашли, но есть два возможных ответа. Когда 𝑥 равно двум, мы кладем
это число, и мы получаем нулевой ответ, так что это работает. А когда 𝑥 равно трем, мы
подставьте это число вместо 𝑥, и мы получим нулевой ответ, так что это тоже работает.
Теперь мы можем представить наш ответ в
два пути. Мы можем либо представить его в виде списка,
так что 𝑥 равно двум или 𝑥 равно трем; или мы можем представить это как решение
набор, так что два и три в записи набора. И с квадратиками вы, вероятно,
столкнуться с этой идеей действительных чисел, поэтому наш набор решений из набора
вещественные числа. Итак, возвращаясь к тому, что наш
как выглядят квадратичные графы, если граф пересекает ось 𝑥 в двух местах, то мы
получил два решения. Если он коснется оси 𝑥 за один раз
место, то у нас есть одно решение. И если это не пробивает
𝑥-ось вообще, то у нас нет реальных решений. Если мы используем мнимые или сложные
числа, то мы можем придумать некоторые решения, но мы не будем углубляться в это.
прямо сейчас.
И с квадратиками вы, вероятно,
столкнуться с этой идеей действительных чисел, поэтому наш набор решений из набора
вещественные числа. Итак, возвращаясь к тому, что наш
как выглядят квадратичные графы, если граф пересекает ось 𝑥 в двух местах, то мы
получил два решения. Если он коснется оси 𝑥 за один раз
место, то у нас есть одно решение. И если это не пробивает
𝑥-ось вообще, то у нас нет реальных решений. Если мы используем мнимые или сложные
числа, то мы можем придумать некоторые решения, но мы не будем углубляться в это.
прямо сейчас.
Хорошо. Давайте посмотрим на некоторые примеры. Итак, номер один: найдите решение
множество 𝑥 в квадрате плюс десять 𝑥 равно нулю. Это могло бы также означать: «Найди
корни 𝑦 равны 𝑥 в квадрате плюс десять 𝑥.
Теперь это уравнение, которое
легко факторизуется или факторизуется. У нас тут 𝑥 и 𝑥, так что 𝑥
будет нашим общим термином, который мы можем вынести. Таким образом, мы можем выразить это как 𝑥 lot-
умножить на 𝑥 плюс десять равно нулю. Теперь, когда 𝑥 прямо напротив
скобка означает, что это 𝑥 раз 𝑥 плюс десять, так что у нас есть что-то раз
что-то равно нулю. Теперь единственный способ получить
нулевой ответ, когда вы умножаете две вещи вместе, если одна из них
нуль. Значит, либо 𝑥 равно нулю, либо
𝑥 плюс десять равно нулю. И если я вычту десять из каждого
часть этого уравнения, у меня осталось 𝑥 равно минус десять. Так что, если бы я просто писал их как
list, я бы сказал, что мой ответ 𝑥 равен нулю или 𝑥 равен минус десяти. Но вопрос задал
набор решений. Таким образом, используя обозначение набора, два
значения, которые может принимать 𝑥, равны нулю и отрицательным десяткам; так что это будет мой ответ.
У нас тут 𝑥 и 𝑥, так что 𝑥
будет нашим общим термином, который мы можем вынести. Таким образом, мы можем выразить это как 𝑥 lot-
умножить на 𝑥 плюс десять равно нулю. Теперь, когда 𝑥 прямо напротив
скобка означает, что это 𝑥 раз 𝑥 плюс десять, так что у нас есть что-то раз
что-то равно нулю. Теперь единственный способ получить
нулевой ответ, когда вы умножаете две вещи вместе, если одна из них
нуль. Значит, либо 𝑥 равно нулю, либо
𝑥 плюс десять равно нулю. И если я вычту десять из каждого
часть этого уравнения, у меня осталось 𝑥 равно минус десять. Так что, если бы я просто писал их как
list, я бы сказал, что мой ответ 𝑥 равен нулю или 𝑥 равен минус десяти. Но вопрос задал
набор решений. Таким образом, используя обозначение набора, два
значения, которые может принимать 𝑥, равны нулю и отрицательным десяткам; так что это будет мой ответ.
Номер два: Найдите набор решений
из 𝑥 плюс семь все в квадрате равно нулю.
Теперь 𝑥 плюс семь, все в квадрате означает
𝑥 плюс семь раз 𝑥 плюс семь. Итак, у нас есть что-то раз
что-то равно нулю. Опять что-то раз что-то
равен нулю, единственный способ, которым мы можем это получить, — это если одна из этих вещей равна нулю
сам. Таким образом, либо 𝑥 плюс семь равно
ноль, что сделало бы 𝑥 равным отрицательной семерке или тому же самому. Итак, у нас есть повторяющиеся корни. Это одна из тех ситуаций
где, если мы нарисуем график этой функции 𝑦 равно 𝑥 плюс семь в квадрате, это
выглядело бы примерно так. Он коснется оси 𝑥 за один раз.
поместите в минус семь, и на самом деле это пересечет ось 𝑦 в сорок девять. Таким образом, наш набор решений получил только
один пункт в нем, минус семь.
Тогда переходим к третьему. Найдите набор решений 𝑥 в квадрате
плюс два 𝑥 минус тридцать пять равно нулю в ℝ, наборе действительных чисел.
Найдите набор решений 𝑥 в квадрате
плюс два 𝑥 минус тридцать пять равно нулю в ℝ, наборе действительных чисел.
Так что просто стоит помнить, что
просто 𝑥 в квадрате означает один 𝑥 в квадрате. И когда у нас есть один 𝑥 в квадрате,
существует определенный набор правил, которым мы можем следовать, когда делаем
факторинг. Так что помните, если у нас есть 𝑥 плюс
число умножить на 𝑥 плюс еще одно число, и мы умножаем их почленно, мы получили
𝑥 раз 𝑥, что дает нам 𝑥 в квадрате, и у нас есть 𝑥 раз 𝑏, так что это положительно
𝑏𝑥 и 𝑎 умножить на 𝑥, что положительно 𝑎𝑥, и 𝑎 умножить на 𝑏, что положительно
𝑎𝑏.
Теперь, глядя на это, у нас есть 𝑏𝑥
и 𝑎𝑥, так что здесь не учитывается 𝑥; у нас есть 𝑎 плюс 𝑏𝑥. Таким образом, при преобразовании между этими двумя
различные формы нашего выражения, у нас есть, в конце у нас есть 𝑎 раз 𝑏 так
это число умножить на это число. И здесь, как кратное 𝑥,
у нас есть 𝑎 плюс 𝑏. Поэтому я собираюсь добавить 𝑎 к 𝑏. Так что это должно помочь нам сделать нашу
факторинг запоминая тот-то формат.
И здесь, как кратное 𝑥,
у нас есть 𝑎 плюс 𝑏. Поэтому я собираюсь добавить 𝑎 к 𝑏. Так что это должно помочь нам сделать нашу
факторинг запоминая тот-то формат.
Итак, я ищу 𝑥 плюс или минус
что-то раз 𝑥 плюс или минус что-то еще. И если я умножу эти два числа
вместе, я получу минус тридцать пять, а если их сложить, то
получить положительные два. Итак, прежде всего, я просто собираюсь
выпишите все множители числа тридцать пять.
Поэтому всегда начинайте с одного и
число, поэтому один раз тридцать пять, два не является фактором, три не является, четыре не является, пять
— это множитель, пять умножить на семь, шесть — не множитель, и теперь мы дошли до семи. Мы уже встретили семь в
наш список, чтобы мы знали, что у нас есть все факторы, которые нам нужны; один раз
тридцать пять или пять раз по семь. Ну, они являются факторами
тридцать пять.
Теперь, чтобы получить минус тридцать пять,
один должен быть положительным, а другой должен быть отрицательным. Так что просто имейте это в виду, один из
эти будут положительными, другие — отрицательными. Теперь, когда я добавляю эти два фактора
вместе, они должны дать мне положительные два. Теперь для одного и тридцати пяти,
разница тридцать четыре. Так что неважно, какой из
те положительные, а какие отрицательные. Когда я складываю их вместе, я никогда не
собираюсь получить положительный ответ два. Но с пятью и семью, их
разница в два. Так что я должен тщательно подумать, какой
один должен быть положительным, который должен быть отрицательным. И когда я складываю их вместе,
результат положительный. Таким образом, большее число должно быть
положительным, а меньшее число должно быть отрицательным. Итак, 𝑥 минус пять раз 𝑥 плюс
семь равно нулю. Теперь давайте просто проверим, что мы получаем
то же самое выражение, когда мы умножаем их. 𝑥 раз 𝑥 равно 𝑥 в квадрате, 𝑥 раз
семь семь 𝑥, минус пять раз 𝑥 минус пять 𝑥 и минус пять раз
плюс семь минус тридцать пять. И упрощая это, семь 𝑥
отнять пять 𝑥 будет два 𝑥. Это оставляет нам 𝑥 в квадрате плюс
два 𝑥 минус тридцать пять. Это то, что мы искали
изначально, поэтому мы-мы рассчитали это правильно.
Теперь давайте просто проверим, что мы получаем
то же самое выражение, когда мы умножаем их. 𝑥 раз 𝑥 равно 𝑥 в квадрате, 𝑥 раз
семь семь 𝑥, минус пять раз 𝑥 минус пять 𝑥 и минус пять раз
плюс семь минус тридцать пять. И упрощая это, семь 𝑥
отнять пять 𝑥 будет два 𝑥. Это оставляет нам 𝑥 в квадрате плюс
два 𝑥 минус тридцать пять. Это то, что мы искали
изначально, поэтому мы-мы рассчитали это правильно.
Итак, мы оказываемся в
ситуация, когда у нас есть что-то, умноженное на что-то, равное нулю. И если что-то раз что-то
равно нулю, одна из этих вещей должна быть равна нулю. Так что либо 𝑥 минус пять равно нулю,
что означало бы, что 𝑥 будет пять; или 𝑥 плюс семь будет ноль, в котором
случай 𝑥 будет равен отрицательной семерке. Итак, наш набор решений состоит из
минус семь и пять.
Номер четыре: Найдите набор решений
из четырех 𝑥 в квадрате минус двадцать пять равно нулю в наборе действительных чисел.
Итак, вот квадратное число, имеющее
𝑏 значение ноль. И на самом деле, это очень особенное
случай, потому что четыре 𝑥 в квадрате можно записать как два 𝑥 все в квадрате, а двадцать пять
можно записать как пять в квадрате. Итак, у нас есть разница в два
𝑥- из двух квадратов; два 𝑥 все в квадрате минус пять в квадрате. Теперь давайте на секунду
помните разницу техники двух квадратов. Если бы у меня было две скобки здесь 𝑥
минус 𝑎 умножить на 𝑥 плюс 𝑎, 𝑥 умножить на 𝑥 𝑥 в квадрате, 𝑥 умножить на положительное 𝑎
положительный 𝑎𝑥, отрицательный 𝑎 раз 𝑥 отрицательный 𝑎𝑥 и отрицательный 𝑎 раз положительный
𝑎 отрицательное 𝑎 в квадрате. Таким образом, умножая эти
скобки, у меня есть 𝑥 в квадрате плюс 𝑎𝑥 забрать 𝑎𝑥. Итак, эти два термина, если я начну
с 𝑎𝑥 и я уберу 𝑎𝑥, это даст мне ноль; так что это отменит
вне.
А то у меня минус 𝑎
в квадрате. Так что у меня есть 𝑥 в квадрате на вынос 𝑎
в квадрате; разница в два квадрата. Так что я воспользуюсь этим результатом 𝑥
минус 𝑎 раз 𝑥 плюс 𝑎 дает мне 𝑥 в квадрате минус 𝑎 в квадрате, чтобы помочь мне
фактор это выражение здесь. Что-то в квадрате минус
что-то еще в квадрате дает мне что-то минус что-то еще, умноженное на
что-то плюс что-то еще. Так что буду делать по той же схеме
здесь. Итак, это то, что мы учитываем и
помните из нашего исходного уравнения, что оно равно нулю. Итак, у нас есть что-то раз
что-то равно нулю. Таким образом, либо два 𝑥 минус пять
равно нулю, что, когда я переставляю и решаю это уравнение, я получаю 𝑥 равно
пять больше двух; или два 𝑥 плюс пять равно нулю, которые я могу переставить и решить
получить 𝑥 равно минус пять больше двух. Итак, вот два моих ответа: 𝑥 is
пять больше двух или минус пять больше двух. И используя установленную нотацию, подобную этой
заданный в вопросе, мой набор решений действительных чисел отрицателен пять на два
или- и пять больше двух.
Итак, вот два моих ответа: 𝑥 is
пять больше двух или минус пять больше двух. И используя установленную нотацию, подобную этой
заданный в вопросе, мой набор решений действительных чисел отрицателен пять на два
или- и пять больше двух.
Наконец, номер пять. Найдите набор решений из шести 𝑥
квадрат плюс одиннадцать 𝑥 минус десять равно нулю в наборе действительных чисел.
Итак, здесь мы должны разложить на множители
квадратное выражение, в котором нет ни одного 𝑥 в квадрате; у него больше одного 𝑥
там в квадрате. Таким образом, мы должны учитывать это
квадратичный, приравняем его к нулю и посмотрим, какие два решения мы получим. Теперь это немного сложнее, чем
эти моники. Таким образом, слово моник означает, когда
коэффициент старшего степенного члена равен единице. Так, например, один 𝑥 в квадрате плюс
два 𝑥 плюс пять. Как мы уже говорили, эти моники были
легче разложить на множители, чем эти немоники. Итак, давайте просто рассмотрим метод
затем факторизации этих немонических квадратичных уравнений.
Как мы уже говорили, эти моники были
легче разложить на множители, чем эти немоники. Итак, давайте просто рассмотрим метод
затем факторизации этих немонических квадратичных уравнений.
Итак, прежде всего я сделаю
коэффициент 𝑥 в квадрате, шесть, умноженный на постоянный член, минус десять. И шесть раз минус десять
минус шестьдесят. Тогда что я собираюсь сделать, это написать
все факторы — ну я просто сделаю шестьдесят, а потом разберемся с минусом
подпишись потом. Итак, один раз шестьдесят шестьдесят, два
умножить на тридцать шестьдесят, трижды на двадцать, четырежды на пятнадцать, пять раз на двенадцать,
шесть раз десять, семь не множитель, восемь не множитель, ни девять, ни десять,
мы уже встретили десять; так что у нас есть все наши факторы шестьдесят.
Итак, у меня есть шесть пар множителей
шестьдесят. Но то, что мне нужно знать сейчас, это
какую пару из них, если я их сложу, я получу положительно одиннадцать; коэффициент
члена 𝑥. Теперь помните, потому что они собираются
умножьте вместе, чтобы получить минус шестьдесят, один из них должен быть положительным, один из
они должны быть отрицательными. Поэтому, когда я складываю их вместе, я
собираюсь получить разницу двух. Итак, я ищу два фактора, которые
имеют разницу в одиннадцать. Так что, очевидно, один и шестьдесят не
будет разница в одиннадцать, два и тридцать не будет разницы в
одиннадцать, а не три и двадцать, четыре и
Теперь помните, потому что они собираются
умножьте вместе, чтобы получить минус шестьдесят, один из них должен быть положительным, один из
они должны быть отрицательными. Поэтому, когда я складываю их вместе, я
собираюсь получить разницу двух. Итак, я ищу два фактора, которые
имеют разницу в одиннадцать. Так что, очевидно, один и шестьдесят не
будет разница в одиннадцать, два и тридцать не будет разницы в
одиннадцать, а не три и двадцать, четыре и пять [пятнадцать], у них есть
разница в одиннадцать. Так что мне нужно решить, какой из них
должен быть положительным, а какой — отрицательным. Я пытаюсь генерировать позитив
одиннадцать, так что самый большой из них должен быть положительным, а самый маленький должен быть
быть отрицательным. Итак, минус четыре плюс пятнадцать дает
me neg- дает мне положительное одиннадцать.
Итак, я сейчас переформулирую это
средний член плюс одиннадцать 𝑥 как комбинация отрицательных четырех 𝑥 и положительных пятнадцати
𝑥. Теперь неважно, как
вокруг я пишу что, плюс пятнадцать 𝑥 убери четыре 𝑥, или минус четыре 𝑥 прибавь
пятнадцать 𝑥; поэтому я решил сделать это таким образом. Но в основном пятнадцать 𝑥 убери
четыре 𝑥 дает мне одиннадцать 𝑥, как мы получили в строке выше; так что эти две строки
полностью эквивалентны. Таким образом, повторно выразив эту середину
срок, 𝑥, теперь я буду рассматривать это как две отдельные половины, шесть 𝑥 в квадрате плюс
пятнадцать 𝑥 и отрицательные четыре 𝑥 убирают десять 𝑥. И я буду учитывать первый
половина. Итак, шесть и пятнадцать получили
наибольший общий делитель трех, а 𝑥 в квадрате и 𝑥 имеют наибольший общий делитель
коэффициент 𝑥. Так что это будет три 𝑥 раза
две 𝑥. Потому что три 𝑥 раз два 𝑥 дает
мне шесть 𝑥 в квадрате, на что мне нужно умножить три 𝑥, чтобы получить пятнадцать 𝑥; это
всего пять.
Потому что три 𝑥 раз два 𝑥 дает
мне шесть 𝑥 в квадрате, на что мне нужно умножить три 𝑥, чтобы получить пятнадцать 𝑥; это
всего пять.
Итак, я только что учел первый
половина этого выражения здесь. Теперь это дело в скобках, два 𝑥
плюс пять, я хочу, чтобы это было общим фактором. Так что я просто напишу это
здесь снова скобка, два 𝑥 плюс пять. И мне нужно решить, что я делаю
нужно умножить это на, чтобы получить это выражение здесь, минус четыре 𝑥
убери десятку. Итак, две 𝑥, что мне нужно
умножьте два 𝑥 на, чтобы получить минус четыре 𝑥. Ну, это должно быть отрицательным
два, минус два лота два 𝑥 минус четыре 𝑥. Итак, давайте сейчас проверим, что
отрицательное два раза положительное пять, что дает нам отрицательную десятку. Да, это другой термин, который
мы ищем.
Так что эти две строки тоже
эквивалентно, мы просто переписали его немного по-другому. Вместо шести 𝑥 в квадрате плюс
пятнадцать 𝑥, у нас есть три 𝑥 много два 𝑥 плюс пять и вместо минус четыре
𝑥 отнимите десять 𝑥, у нас получится минус два умножить на два 𝑥 плюс пять. Теперь у меня есть что-то раз два 𝑥
плюс пять убери что-нибудь умножить на два 𝑥 плюс пять. Два 𝑥 плюс пять — обычное дело
фактор к этим двум терминам. Так что я возьму это как анно-
как фактор. Сейчас в первом триместре у меня было два 𝑥
плюс пять раз три 𝑥. А во втором семестре у меня было два
𝑥 плюс пять раз минус два. Итак, я факторизовал свой квадратичный
выражение до двух 𝑥 плюс пять раз три 𝑥 минус два. И если мы быстро проверим это
два 𝑥 умножить на три 𝑥 будет шесть 𝑥 в квадрате, два 𝑥 умножить на минус два будет минус четыре
𝑥, положительное пять раз три 𝑥 равно пятнадцати 𝑥, а положительное пять раз отрицательное два
минус десять.
Вместо шести 𝑥 в квадрате плюс
пятнадцать 𝑥, у нас есть три 𝑥 много два 𝑥 плюс пять и вместо минус четыре
𝑥 отнимите десять 𝑥, у нас получится минус два умножить на два 𝑥 плюс пять. Теперь у меня есть что-то раз два 𝑥
плюс пять убери что-нибудь умножить на два 𝑥 плюс пять. Два 𝑥 плюс пять — обычное дело
фактор к этим двум терминам. Так что я возьму это как анно-
как фактор. Сейчас в первом триместре у меня было два 𝑥
плюс пять раз три 𝑥. А во втором семестре у меня было два
𝑥 плюс пять раз минус два. Итак, я факторизовал свой квадратичный
выражение до двух 𝑥 плюс пять раз три 𝑥 минус два. И если мы быстро проверим это
два 𝑥 умножить на три 𝑥 будет шесть 𝑥 в квадрате, два 𝑥 умножить на минус два будет минус четыре
𝑥, положительное пять раз три 𝑥 равно пятнадцати 𝑥, а положительное пять раз отрицательное два
минус десять. И, как мы уже говорили, минус четыре
𝑥 плюс пятнадцать 𝑥 будет плюс одиннадцать 𝑥. Так что да, это выражение, которое мы
мы ищем. Итак, похоже, мы разложили на множители
это правильно.
И, как мы уже говорили, минус четыре
𝑥 плюс пятнадцать 𝑥 будет плюс одиннадцать 𝑥. Так что да, это выражение, которое мы
мы ищем. Итак, похоже, мы разложили на множители
это правильно.
Делая факторинг, мы получили
что-то, умноженное на что-то, равно нулю. Так что один из них будет
нуль. Итак, либо два 𝑥 плюс пять равно нулю,
другими словами, 𝑥 равно минус пяти больше двух; или три 𝑥 минус два равно нулю,
другими словами 𝑥 равно двум третям. Итак, наш набор решений отрицателен.
пять на два или две трети. И помните, если бы мы писали
это как список, мы бы написали 𝑥 минус пять больше двух, или 𝑥 равно
две трети.
Подводя итог, корни
𝑥-значения, которые заменяют, чтобы придать выражению нулевое значение. Квадратичных может быть две, или одна, или
нет настоящих корней. Затем нужно выбрать метод
факторинг.
Наблюдение: Невозможно найти два таких фактора!!
Заключение: Трехчлен нельзя разложить на множители
 1 Найдите вершину y = x 2 +x-22
1 Найдите вершину y = x 2 +x-22 В нашем случае координата х равна -0,5000
В нашем случае координата х равна -0,5000 Ось симметрии (пунктирная) {x}={-0,50}
Вершина в {x,y } = {-0,50,-22,25}
x -Отсечения (корни):
Корень 1 при {x,y} = {-5,22, 0,00}
Корень 2 при {x,y} = {4,22, 0,00}
x 2 +x = 22
В правой части имеем :
22 + 1/4 или, (22/1)+(1/4)
Общий знаменатель двух дробей равен 4 Складываем (88/4)+(1/4) дает 89/4
Таким образом, прибавив к обеим сторонам, мы наконец получим :
x 2 +x+(1/4) = 89/4
x 2 +x+(1/4) =
(x+(1/2)) • (x+(1/2)) =
(x+(1/2)) 2
Вещи, равные одному и тому же также равны между собой.
 С
С x 2 +x+(1/4) = 89/4 и
x 2 +x+(1/4) = (x+(1/2)) 2
тогда по закону транзитивности ,
(x+(1/2)) 2 = 89/4
(x+(1/2)) 2 равен
(x+(1/2)) 2/2 =
(x+(1/2)) 1 =
x+(1/2)
x+(1/2) = √ 89/4
x = -1/2 + √ 89/4
√ 89 / √ 4 что равно √ 89/ 2
 3 Решение x 2 +x-22 = 0 с помощью квадратной формулы .
3 Решение x 2 +x-22 = 0 с помощью квадратной формулы .-B a √ B 2 -4AC
x = ————————
2A
B = 1
C = -22
1-(-88) =
89
x = —————
2
, так что теперь мы смотрим на:
x = (-1 ± 9.434 ) / 2
 Мы рассмотрели факторинг различных
типы квадратичных уравнений более подробно описаны в других видеороликах, поэтому мы просто кратко повторим
процесс здесь.
Мы рассмотрели факторинг различных
типы квадратичных уравнений более подробно описаны в других видеороликах, поэтому мы просто кратко повторим
процесс здесь. А также помните, что у него нет
быть 𝑥; это может быть любая буква. Корнями квадратного являются
𝑥-значения, которые генерируют ваш нулевой результат, когда вы подставляете их в
выражение. Так, например, вопрос типа:
Найдите корни квадратного уравнения 𝑦 равно 𝑥 в квадрате минус пять 𝑥 плюс шесть
означает решить 𝑥 в квадрате минус пять 𝑥 плюс шесть равно нулю. Другими словами, найти значения
𝑥, которые соответствуют этому уравнению.
А также помните, что у него нет
быть 𝑥; это может быть любая буква. Корнями квадратного являются
𝑥-значения, которые генерируют ваш нулевой результат, когда вы подставляете их в
выражение. Так, например, вопрос типа:
Найдите корни квадратного уравнения 𝑦 равно 𝑥 в квадрате минус пять 𝑥 плюс шесть
означает решить 𝑥 в квадрате минус пять 𝑥 плюс шесть равно нулю. Другими словами, найти значения
𝑥, которые соответствуют этому уравнению. И с квадратиками вы, вероятно,
столкнуться с этой идеей действительных чисел, поэтому наш набор решений из набора
вещественные числа. Итак, возвращаясь к тому, что наш
как выглядят квадратичные графы, если граф пересекает ось 𝑥 в двух местах, то мы
получил два решения. Если он коснется оси 𝑥 за один раз
место, то у нас есть одно решение. И если это не пробивает
𝑥-ось вообще, то у нас нет реальных решений. Если мы используем мнимые или сложные
числа, то мы можем придумать некоторые решения, но мы не будем углубляться в это.
прямо сейчас.
И с квадратиками вы, вероятно,
столкнуться с этой идеей действительных чисел, поэтому наш набор решений из набора
вещественные числа. Итак, возвращаясь к тому, что наш
как выглядят квадратичные графы, если граф пересекает ось 𝑥 в двух местах, то мы
получил два решения. Если он коснется оси 𝑥 за один раз
место, то у нас есть одно решение. И если это не пробивает
𝑥-ось вообще, то у нас нет реальных решений. Если мы используем мнимые или сложные
числа, то мы можем придумать некоторые решения, но мы не будем углубляться в это.
прямо сейчас.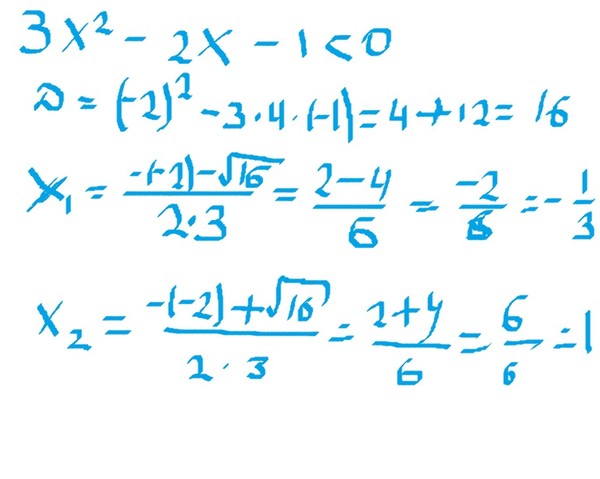 У нас тут 𝑥 и 𝑥, так что 𝑥
будет нашим общим термином, который мы можем вынести. Таким образом, мы можем выразить это как 𝑥 lot-
умножить на 𝑥 плюс десять равно нулю. Теперь, когда 𝑥 прямо напротив
скобка означает, что это 𝑥 раз 𝑥 плюс десять, так что у нас есть что-то раз
что-то равно нулю. Теперь единственный способ получить
нулевой ответ, когда вы умножаете две вещи вместе, если одна из них
нуль. Значит, либо 𝑥 равно нулю, либо
𝑥 плюс десять равно нулю. И если я вычту десять из каждого
часть этого уравнения, у меня осталось 𝑥 равно минус десять. Так что, если бы я просто писал их как
list, я бы сказал, что мой ответ 𝑥 равен нулю или 𝑥 равен минус десяти. Но вопрос задал
набор решений. Таким образом, используя обозначение набора, два
значения, которые может принимать 𝑥, равны нулю и отрицательным десяткам; так что это будет мой ответ.
У нас тут 𝑥 и 𝑥, так что 𝑥
будет нашим общим термином, который мы можем вынести. Таким образом, мы можем выразить это как 𝑥 lot-
умножить на 𝑥 плюс десять равно нулю. Теперь, когда 𝑥 прямо напротив
скобка означает, что это 𝑥 раз 𝑥 плюс десять, так что у нас есть что-то раз
что-то равно нулю. Теперь единственный способ получить
нулевой ответ, когда вы умножаете две вещи вместе, если одна из них
нуль. Значит, либо 𝑥 равно нулю, либо
𝑥 плюс десять равно нулю. И если я вычту десять из каждого
часть этого уравнения, у меня осталось 𝑥 равно минус десять. Так что, если бы я просто писал их как
list, я бы сказал, что мой ответ 𝑥 равен нулю или 𝑥 равен минус десяти. Но вопрос задал
набор решений. Таким образом, используя обозначение набора, два
значения, которые может принимать 𝑥, равны нулю и отрицательным десяткам; так что это будет мой ответ.
 Найдите набор решений 𝑥 в квадрате
плюс два 𝑥 минус тридцать пять равно нулю в ℝ, наборе действительных чисел.
Найдите набор решений 𝑥 в квадрате
плюс два 𝑥 минус тридцать пять равно нулю в ℝ, наборе действительных чисел. И здесь, как кратное 𝑥,
у нас есть 𝑎 плюс 𝑏. Поэтому я собираюсь добавить 𝑎 к 𝑏. Так что это должно помочь нам сделать нашу
факторинг запоминая тот-то формат.
И здесь, как кратное 𝑥,
у нас есть 𝑎 плюс 𝑏. Поэтому я собираюсь добавить 𝑎 к 𝑏. Так что это должно помочь нам сделать нашу
факторинг запоминая тот-то формат.
 Теперь давайте просто проверим, что мы получаем
то же самое выражение, когда мы умножаем их. 𝑥 раз 𝑥 равно 𝑥 в квадрате, 𝑥 раз
семь семь 𝑥, минус пять раз 𝑥 минус пять 𝑥 и минус пять раз
плюс семь минус тридцать пять. И упрощая это, семь 𝑥
отнять пять 𝑥 будет два 𝑥. Это оставляет нам 𝑥 в квадрате плюс
два 𝑥 минус тридцать пять. Это то, что мы искали
изначально, поэтому мы-мы рассчитали это правильно.
Теперь давайте просто проверим, что мы получаем
то же самое выражение, когда мы умножаем их. 𝑥 раз 𝑥 равно 𝑥 в квадрате, 𝑥 раз
семь семь 𝑥, минус пять раз 𝑥 минус пять 𝑥 и минус пять раз
плюс семь минус тридцать пять. И упрощая это, семь 𝑥
отнять пять 𝑥 будет два 𝑥. Это оставляет нам 𝑥 в квадрате плюс
два 𝑥 минус тридцать пять. Это то, что мы искали
изначально, поэтому мы-мы рассчитали это правильно.

 Итак, вот два моих ответа: 𝑥 is
пять больше двух или минус пять больше двух. И используя установленную нотацию, подобную этой
заданный в вопросе, мой набор решений действительных чисел отрицателен пять на два
или- и пять больше двух.
Итак, вот два моих ответа: 𝑥 is
пять больше двух или минус пять больше двух. И используя установленную нотацию, подобную этой
заданный в вопросе, мой набор решений действительных чисел отрицателен пять на два
или- и пять больше двух.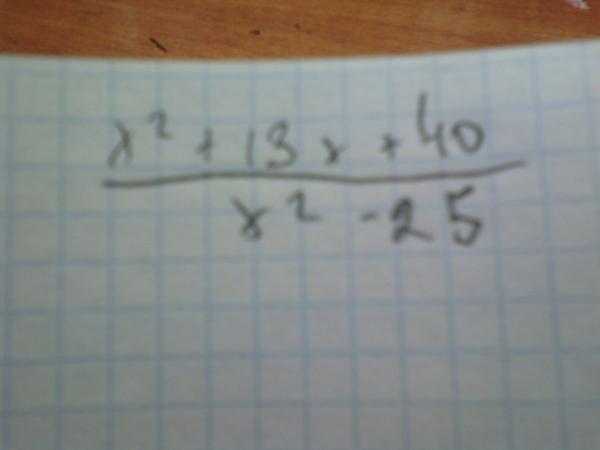 Как мы уже говорили, эти моники были
легче разложить на множители, чем эти немоники. Итак, давайте просто рассмотрим метод
затем факторизации этих немонических квадратичных уравнений.
Как мы уже говорили, эти моники были
легче разложить на множители, чем эти немоники. Итак, давайте просто рассмотрим метод
затем факторизации этих немонических квадратичных уравнений. Теперь помните, потому что они собираются
умножьте вместе, чтобы получить минус шестьдесят, один из них должен быть положительным, один из
они должны быть отрицательными. Поэтому, когда я складываю их вместе, я
собираюсь получить разницу двух. Итак, я ищу два фактора, которые
имеют разницу в одиннадцать. Так что, очевидно, один и шестьдесят не
будет разница в одиннадцать, два и тридцать не будет разницы в
одиннадцать, а не три и двадцать, четыре и
Теперь помните, потому что они собираются
умножьте вместе, чтобы получить минус шестьдесят, один из них должен быть положительным, один из
они должны быть отрицательными. Поэтому, когда я складываю их вместе, я
собираюсь получить разницу двух. Итак, я ищу два фактора, которые
имеют разницу в одиннадцать. Так что, очевидно, один и шестьдесят не
будет разница в одиннадцать, два и тридцать не будет разницы в
одиннадцать, а не три и двадцать, четыре и 
 Потому что три 𝑥 раз два 𝑥 дает
мне шесть 𝑥 в квадрате, на что мне нужно умножить три 𝑥, чтобы получить пятнадцать 𝑥; это
всего пять.
Потому что три 𝑥 раз два 𝑥 дает
мне шесть 𝑥 в квадрате, на что мне нужно умножить три 𝑥, чтобы получить пятнадцать 𝑥; это
всего пять. Вместо шести 𝑥 в квадрате плюс
пятнадцать 𝑥, у нас есть три 𝑥 много два 𝑥 плюс пять и вместо минус четыре
𝑥 отнимите десять 𝑥, у нас получится минус два умножить на два 𝑥 плюс пять. Теперь у меня есть что-то раз два 𝑥
плюс пять убери что-нибудь умножить на два 𝑥 плюс пять. Два 𝑥 плюс пять — обычное дело
фактор к этим двум терминам. Так что я возьму это как анно-
как фактор. Сейчас в первом триместре у меня было два 𝑥
плюс пять раз три 𝑥. А во втором семестре у меня было два
𝑥 плюс пять раз минус два. Итак, я факторизовал свой квадратичный
выражение до двух 𝑥 плюс пять раз три 𝑥 минус два. И если мы быстро проверим это
два 𝑥 умножить на три 𝑥 будет шесть 𝑥 в квадрате, два 𝑥 умножить на минус два будет минус четыре
𝑥, положительное пять раз три 𝑥 равно пятнадцати 𝑥, а положительное пять раз отрицательное два
минус десять.
Вместо шести 𝑥 в квадрате плюс
пятнадцать 𝑥, у нас есть три 𝑥 много два 𝑥 плюс пять и вместо минус четыре
𝑥 отнимите десять 𝑥, у нас получится минус два умножить на два 𝑥 плюс пять. Теперь у меня есть что-то раз два 𝑥
плюс пять убери что-нибудь умножить на два 𝑥 плюс пять. Два 𝑥 плюс пять — обычное дело
фактор к этим двум терминам. Так что я возьму это как анно-
как фактор. Сейчас в первом триместре у меня было два 𝑥
плюс пять раз три 𝑥. А во втором семестре у меня было два
𝑥 плюс пять раз минус два. Итак, я факторизовал свой квадратичный
выражение до двух 𝑥 плюс пять раз три 𝑥 минус два. И если мы быстро проверим это
два 𝑥 умножить на три 𝑥 будет шесть 𝑥 в квадрате, два 𝑥 умножить на минус два будет минус четыре
𝑥, положительное пять раз три 𝑥 равно пятнадцати 𝑥, а положительное пять раз отрицательное два
минус десять. И, как мы уже говорили, минус четыре
𝑥 плюс пятнадцать 𝑥 будет плюс одиннадцать 𝑥. Так что да, это выражение, которое мы
мы ищем. Итак, похоже, мы разложили на множители
это правильно.
И, как мы уже говорили, минус четыре
𝑥 плюс пятнадцать 𝑥 будет плюс одиннадцать 𝑥. Так что да, это выражение, которое мы
мы ищем. Итак, похоже, мы разложили на множители
это правильно.
