|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов… Процедура выполнения команд. Рабочий цикл процессора: Функционирование процессора в основном состоит из повторяющихся рабочих циклов, каждый из которых соответствует… История развития методов оптимизации: теорема Куна-Таккера, метод Лагранжа, роль выпуклости в оптимизации… Интересное: Наиболее распространенные виды рака: Раковая опухоль — это самостоятельное новообразование, которое может возникнуть и от повышенного давления… Как мы говорим и как мы слушаем: общение можно сравнить с огромным зонтиком, под которым скрыто все. Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 3 из 9Следующая ⇒ Данный факт является очевидным, но необходимо рассмотреть более полезные утверждения, касающиеся такой системы объектов, как две параллельные прямые и секущая (прямая, пересекающая две параллельные прямые) (см. Рис. 5. Две параллельные прямые и секущая Если известно, что , как на Рис. 5, то у указанных углов существуют специальные названия: и – накрест лежащие, и – односторонние, и – соответственные, и , и – вертикальные. Для соотношений между этими углами можно сформулировать ряд признаков параллельности двух прямых: 1. – накрест лежащие углы равны тогда и только тогда, когда прямые параллельны. 2. – соответственные углы равны тогда и только тогда, когда прямые параллельны. 3. – сумма односторонних углов равна тогда и только тогда, когда прямые параллельны. Примечательно то, что указанные признаки параллельности можно применять и в обратном направлении и получать соотношения между углами при пересечении двух параллельных прямых секущей. Знание этих фактов может помочь не только при решении геометрических задач, а при доказательстве важнейших теорем о треугольнике, которые мы сейчас и рассмотрим. Теорема о сумме углов треугольника Сумма внутренних углов в любом треугольнике равна (см. Рис. 6). Рис. 6. Теорема о сумме углов треугольника или, в обозначениях латинских букв, . Доказательство. Проведем прямую . как накрест лежащие, как накрест лежащие. как развернутый угол. Доказано.
Рис. 7. Теорема о внешнем угле треугольника Теорема о внешнем угле треугольника Любой внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним. . Доказательство. Сумма углов треугольника . С другой стороны, находится с использованием смежного к нему угла : . Используя равенство, полученное выше, имеем: . Доказано. В качестве примера докажем еще один важный факт, который можно назвать еще одним признаком равенства треугольников. Пример (признак равенства треугольников по двум сторонам и большему углу) Рис. Признак равенства треугольников по двум сторонам и большему углу Два треугольника равны, если две стороны и наибольший угол одного треугольника равны соответственно двум сторонам и наибольшему углу другого треугольника. . Доказательство. Если наибольшим углом окажется угол , то признак доказан, т.к. он сводится к первому признаку равенства треугольником. Поэтому на Рис. 8 изображен общий случай, когда наибольшим является угол, не лежащий между указанными сторонами, например, это угол . Кстати, наибольший угол не обязательно должен быть тупым, на рисунке так изображено только для наглядности. Для доказательства равенства треугольников вспомним, что фигуры равны, если их можно совместить. Мысленно наложим один треугольник поверх второго так, чтобы совпали точки и . Ввиду равенства сторон и угла несложно представить, что точки и тоже совпадут. Получим, что у двух сравниваемых треугольников уже совпали две вершины, но не факт, что совпадет третья ( и ), это и осталось доказать. Докажем этот факт от противного: изобразим исходный треугольник поверх другого треугольника (в скобках указаны совпавшие вершины) и представим, что вершины и не совпали, как это указано на Рис. 9. Рис. 9 Нам необходимо доказать, что ситуация несовпадения точек и невозможна. Рассмотрим получившейся в результате наложения треугольник . В нем стороны по условию, следовательно, он равнобедренный, следовательно, . А , если назвать вершины, как в исходном треугольнике. Но угол является внешним для треугольника , следовательно, . Получили такие соотношения: , что противоречит условию задачи. Следовательно, точки и совпадают, и . Доказано. В рамках урока мы повторили признаки равенства треугольников и две важнейшие теоремы о треугольниках. На следующем уроке мы вспомним свойства такого частного вида треугольников, как прямоугольный треугольник.
Домашнее задание 1. 2. Равнобедренные треугольники и имеют общее основание . Докажите, что прямая – серединный перпендикуляр отрезка . 3. В треугольнике , биссектрисы внешних углов при вершинах и пересекаются в точке . Найдите угол . 4. В треугольнике , . На стороне отметили точку так, что . Найдите углы треугольника
Урок 4: Повторение. Прямоугольные треугольники. Данный урок посвящен прямоугольным треугольникам и их свойствам. Прямые углы, а значит, и прямоугольные треугольники, встречаются в жизни человека практически на каждом углу (в прямом и переносном смысле). Поэтому изучение их свойств может пригодиться не только при дальнейшем изучении курса геометрии, но и в простых жизненных ситуациях. В 7 классе были изучены самые простые свойства прямоугольных треугольников. Поскольку в 8 классе изучению более сложных свойств будет уделено достаточно большое внимание, необходимо вспомнить то, что нам уже известно про прямоугольные треугольники. ⇐ Предыдущая123456789Следующая ⇒ Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого… Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни… Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)… Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим… |
Теорема о соответственных углах / Параллельные прямые / Справочник по геометрии 7-9 класс
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Параллельные прямые
- Теорема о соответственных углах
Теорема
Если две параллельные прямые пересечены секущей, то соответственные углы равны. |
Дано: , — секущая, 1 и 2 — соответственные (Рис.1).
Доказать: 1 = 2.
Доказательство:
По условию , значит накрест лежащие углы 1 и 3 равны, т.е. 1 = 3 (по теореме о накрест лежащих углах). При этом 2 = 3 как вертикальные углы.
Из равенств 1 = 3 и 2 = 3 следует, что 1 = 2. Что и требовалось доказать.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Параллельные прямые
Признаки параллельности двух прямых
Практические способы построения параллельных прямых
Аксиомы геометрии
Аксиома параллельных прямых
Теорема о накрест лежащих углах
Теорема об односторонних углах
Теорема об углах с соответственно параллельными сторонами
Теорема об углах с соответственно перпендикулярными сторонами
Параллельные прямые
Правило встречается в следующих упражнениях:
7 класс
Задание 427, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 447, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 554, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 587, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 588, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 590, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 18, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 848, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 853, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1286, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
мягкий вопрос — Хороший способ описать «сходящиеся параллельные линии»?
Прежде всего, «две прямые являются ограничивающими параллелями» имеет смысл только тогда, когда они обе проходят через точку не на третьей прямой.
Геодезическая не является секущей с бесконечностью других геодезических, проходящих через точку вне данной геодезической, эти геодезические ультрапараллельны данной геодезической.
Геодезическая имеет (как минимум и не более) две геодезические, являющиеся ее предельными параллелями (горизонтальными параллелями) и проходящие через точку, не принадлежащую данной геодезической.
Вы сделали два утверждения о том, что легко понять и что является правдой:
- Идеальные точки существуют : рассмотрим модель диска Пуанкаре, идеальные точки находятся на диске так, что $|z| = 1$. Их гиперболическое расстояние от любой другой точки равно бесконечности.
Возьмем, например, точку A на геодезической и другую точку B на той же геодезической. Вы можете сделать расстояние от А до В сколь угодно большим, и когда это расстояние станет достаточно большим (бесконечность), вы в конце концов достигнете Идеальной Точки.
Таким образом, каждая геодезическая, проходящая через A и B, также может быть выражена как геодезическая между двумя идеальными точками.
Геодезическая, проходящая через точку, не принадлежащую второй геодезической, и с которой Идеальная точка является общей, называется предельной параллелью (оропараллелью).
Для каждой геодезической, имеющей две идеальные точки, легко понять, почему существует по крайней мере и не более двух хоропараллелей геодезической, проходящих через точку, не принадлежащую данной геодезической.
- Линии не двигаются, но точки могут : убедитесь, что линии не двигаются. Но если вы возьмете произвольную точку на геодезической, вы сможете переместить ее только двумя способами: вперед или назад. И поскольку вы можете оценить расстояние между двумя точками, вы можете узнать, являются ли две геодезические асимптотическими или нет.
«Движение в одном направлении» в гиперболической геометрии бессмысленно, потому что нет понятия коллинеарности.
Но геодезическая ЯВЛЯЕТСЯ направлением и имеет два направления.
Имея две геодезические, мы можем узнать, являются ли они асимптотическими, проверив их сходимость четырьмя способами.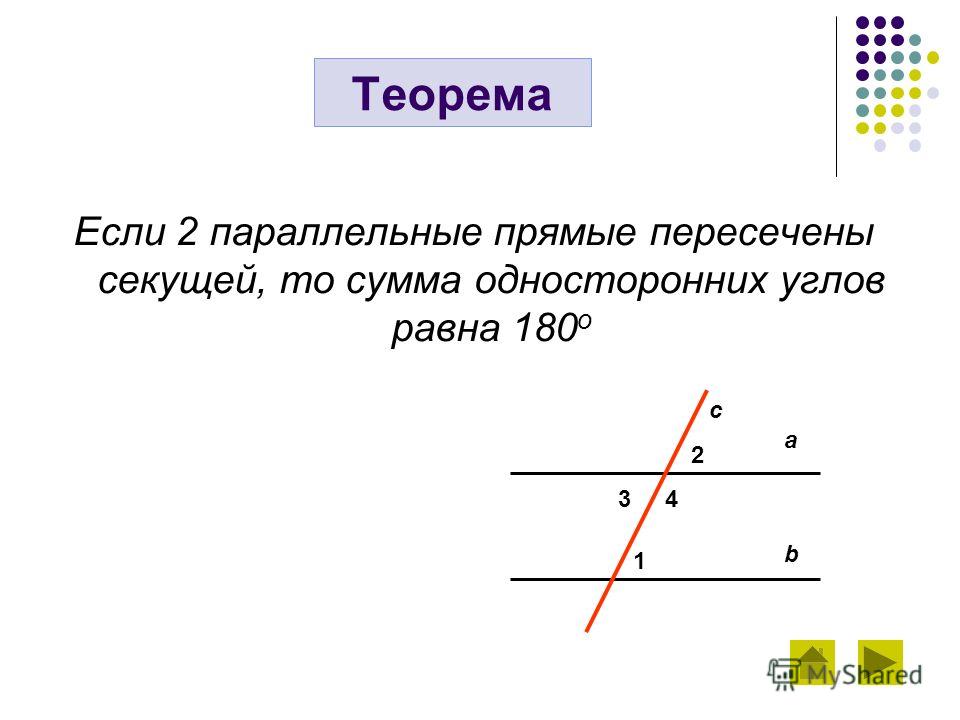
Имея точку $P$ на геодезической $G$, вы можете переместить ее вперед или назад. Рассмотрим точку $P_1$, лежащую на $G$, гиперболическое расстояние между $P$ и $P_1$ равно 1, и путь лежит вперед. Рассмотрим точку $P_{-1}$, лежащую на $G$, гиперболическое расстояние между $P$ и $P_1$ равно 1, а путь в обратном направлении. Теперь рассмотрим точку $Q$ на геодезической $L$, где $Q_1$ и $Q_{-1}$ построены так же, как $P_1$ и $P_{-1}$.
- $dist(P_n, Q_n) = F_n$
- $dist(P_n, Q_{-n}) = F_{-n}$
- $расстояние(P_{-n}, Q_n) = B_n$
- $dist(P_{-n}, Q_{-n}) = B_{-n}$
Есть три случая:
G и L являются несекансными , существует n, например, когда n увеличивается, все расстояния также увеличиваются.
G и L равны секансу , существует n, например, когда n увеличивается, все расстояния также увеличиваются.
G и L достигают одной и той же идеальной точки , существует n, например, когда n становится больше, одно из четырех расстояний сойдется к 0,
геометрия — Две касательные окружности и параллельные линии
Задавать вопрос
спросил
Изменено 3 года, 10 месяцев назад
Просмотрено 2к раз
$\begingroup$
У меня проблемы с решением следующей задачи:
Рассмотрим две окружности, которые имеют только одну общую точку $A$, т. е. касаются друг друга. Теперь рассмотрим две прямые, проходящие через A, такие, что прямые пересекаются с окружностями в следующих точках $B,C,D,E$. Я хочу доказать, что прямые $DE$ и $BC$ являются параллельными прямыми ($D,E$ — точки на одной окружности, а $B,C$ — на другой).
е. касаются друг друга. Теперь рассмотрим две прямые, проходящие через A, такие, что прямые пересекаются с окружностями в следующих точках $B,C,D,E$. Я хочу доказать, что прямые $DE$ и $BC$ являются параллельными прямыми ($D,E$ — точки на одной окружности, а $B,C$ — на другой).
Я пытался использовать такие теоремы, как теорема о вписанном угле, но пока безуспешно. Кто-нибудь знает, как решить эту проблему?
Если возможно, я хочу использовать только геометрические аргументы, а не аналитические аргументы. Есть ли у этого результата какое-нибудь название?
С наилучшими пожеланиями
- геометрия
$\endgroup$
1
$\begingroup$
Подсказка:
Пусть $M,N$ две точки общей касательной на противоположных сторонах относительно $A$, чем $\угол DAM = \угол DEA$, так как они опираются на одну и ту же дугу $DA$ ( $\ угол DAM$ является «предельным» углом, являющимся касательной к стороне $AM$, но, если вам не нравится понятие «предельного» угла, вы можете доказать то же утверждение как следствие касательной теорема о секущих).

 ..
.. Рис. 5).
Рис. 5).
 8.
8.

