18. Замена переменных в двойном интеграле
Пусть функции осуществляют взаимно однозначное непрерывно дифференцируемое отображение области P плоскости на область S плоскости . Тогда существует обратное непрерывно дифференцируемое отображение , области S на область P, если якобиан преобразования
=.
Величины U и V можно рассматривать как прямоугольные координаты для точек области P и в то же время как Криволинейные координаты точек области S. Точки плоскости Oxy, для которых одна из координат U и V сохраняет постоянное значение, образуют Координатную линию. Всего будет два семейства таких линий.
Теорема 14.3. Пусть есть дифференцируемое преобразование области P из плоскости на область S Из плоскости . Тогда справедливо равенство
(2.5)
Замечание. Равенство (2.5) сохраняет справедливость, когда условие взаимно однозначного соответствия между областями S и
Переход в двойном интеграле к полярным координатам
Формулы
(2.6)
Преобразуют полярные координаты точки в декартовы координаты этой точки и переводят область (или область ) на всю плоскость Oxy.
Обратное преобразование декартовых координат в полярные осуществляется по формулам:
Фиксируя в последних формулах И, получим координатные линии из разных семейств: окружность с центром в точке И луч, исходящий из точки .
Якобиан преобразования
И формула (2.5) принимает вид:
(2.7)
Рекомендация. К полярным координатам целесообразно переходить, когда в подынтегральное выражение или в уравнения границы области интегрирования входит комбинация .
В некоторых случаях при вычислении двойного интеграла удобно перейти от декартовых координат к Эллиптическим полярным Координатам по формулам
, (2.8)
— постоянные, . Тогда
, (2.9)
Пример 6. Записать в полярной системе координат область S , заданную в декартовой системе координат неравенством (круг радиуса R с центром в точке ).
Ñ Перейдем от декартовых координат X, Y к полярным по формулам , . Подставим X и Y в исходное неравенство, получим: или . На координату j дополнительных ограничений не накладывается, поэтому (или ).
В полярной системе координат круг записывается неравенствами: . #
Пример 7. Записать в полярной системе координат область S — часть круга, ограниченную линиями , , (), — постоянные, .
Ñ Изобразим область S (рис. 14.9). Запишем заданные линии в полярных координатах, которые связаны с декартовыми формулами , : 1)Þ ;
2) Þ, ;
3)Þ.
Область переходит в область
.
В полярной системе координат заданная область определяется системой неравенств: . #
|
Пример 8. Вычислить двойной интеграл , S — множество точек, удовлетворяющих неравенству .
Ñ Границей области является линия или — окружность радиуса 2 с центром в точке (Рис. 14.10).
Рис. 14.10
Наличие в уравнении границы комбинации наводит на мысль, что для вычисления двойного интеграла удобно перейти к полярным координатам по формулам , , . Уравнение границы переходит в уравнение или . Отсюда r=0 (соответствует полюсу O) и — уравнение окружности. Так как всегда (по смыслу r), то из следует , отсюда получаем (этот же результат можно усмотреть из рисунка). Итак, в полярных координатах область интегрирования есть . Тогда по формуле (2.7)
. #
Пример 9. Вычислить , где .
Ñ Область D ограничена линиями: – эллипс с полуосями A и B, – эллипс с полуосями и , Y=0 – прямая (ось Ox), – прямая (рис. 14.11).
Рис.14.11
Анализ границы области указывает на целесообразность перехода к Эллиптическим полярным координатам по формулам (2.8), (2.
9): , . Уравнения границы области в координатах будут: 1), 2) , 3) ,
4) . Итак, область интегрирования в координатах есть
. Тогда
. #
Задачи для самостоятельного решения
Перейти в двойном интеграле к полярным координатам и расставить пределы интегрирования в порядке: внешнее – по j, внутреннее — по r:
27. D – область, ограниченная окружностями , и прямыми , .
28. D — область, являющаяся общей частью двух кругов и .
29. D
30. D — внутренняя часть правой петли лемнискаты Бернулли .
31. D:.
32. D: .Указание. Перейти к эллиптическим полярным координатам.
33. D — область, ограниченная линией . Указание. Перейти к эллиптическим полярным координатам.
34. . 35. . 36. .
С помощью перехода к полярным координатам вычислить интегралы:
37.
. 38. .
39. . 40. , D — часть кольца ,
, . 41. .
Вычислить, перейдя к эллиптическим полярным координатам, интегралы:
42. .
43. — область, ограниченная линией .
| < Предыдущая | Следующая > |
|---|
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. |
⇐ ПредыдущаяСтр 3 из 7Следующая ⇒ Важнейшимчастным случаем криволинейных координат являются полярные координаты (r,φ). Они связаны с прямоугольными координатами формулами: , . Якобиан преобразования в этом случае , а формула перехода к полярным координатам в двойном интеграле имеет вид: (4) Переходить к полярным координатам удобно в тех случаях, когда область интегрирования есть круг, кольцо или их часть, а так же в случае, когда подынтегральная функция имеет вид . В полярных координатах выражение . Границей круга является окружность и ее уравнение в полярных координатах принимает вид: r=R. Тогда область D — круг в полярной системе координат на плоскости Оrφ переходит в прямоугольную область Ω, которая задается неравенствами : (рис.17а,б). Интегрирование в полярных координатах проводится по координатным линиям  Линии r=const представляют из себя окружности с центром в начале координат. По окружностям происходит изменение координаты φ. Линии φ=const – это семейства лучей, выходящих из начала координат, по которым происходит изменение координаты r. Координатная сетка в полярных координатах изображена на рис.18.
Рис.17а Рис.17б Рис.18
Пусть область D расположена между лучами φ=α и φ=β, где α< β, и ограничена линиями и , где и любой луч, выходящий из полюса φ=const ( ) пересекает ее границу не более чем в двух точках (простая область относительно r) (рис.19).Тогда двойной интеграл сводится к повторному по формуле:
Рис.19 Рис.20 (5) Пусть область D расположена между окружностями r=а и r=b, где а< b и ограничена линиями и , где и любая окружность радиуса r=const ( ) пересекает границу области не более чем в двух точках (правильная относительно φ) (рис. 6)
Пример 1. Вычислить двойной интеграл , где область D ограничена окружностью . Решение: Как уже говорилось выше, если интегрирование ведется по кругу, то уравнение его границы в полярных координатах имеет вид r=1, а на плоскости Оrφ область Ω является прямоугольником . Осталось записать в полярных координатах подынтегральную функцию: . Вычисляем интеграл Пример 2. Вычислить , если область D ограничена окружностью , лежащей в первой четверти, и прямыми y=x и . Решение: Область D изображена на рис.21. Переведем ее границы в полярные координаты: уравнение окружности имеет вид r=a , а отрезки прямых y=x являются лучами и . Проводя лучи φ=const , определяем, что координата r изменяется от 0 до а. Тогда по формуле (5) получаем: Рис. Пример 3. В двойном интеграле перейти к полярным координатам и расставить пределы интеграции в том и другом порядке, если область D ограничена кривой . Решение: Чтобы построить область D, приведем уравнение кривой к каноническому виду, для чего выделяем полный квадрат по переменной х: , . Получаем уравнение окружности с центром на оси Ох в точке х=а, у=0, радиуса а, при этом окружность касается оси Оу (рис.22а,б).
Рис.22а Рис.22б
Переведем границу области D в полярные координаты, для этого удобнее воспользоваться уравнением окружности в виде : или . Область D находится между лучами и и проводя лучи при , определяем, что координата r изменяется от 0 в начале координат до значения радиуса на окружности, т. Чтобы расставить пределы интегрирования в другом порядке, определим границы изменения координаты r. Для этого проведем координатные линии r=const, пересекающие область D, и определим окружности, которые касаются нашей области. Очевидно, что это будут линии r=0 и r=2а, так что r изменяется в пределах от 0 до а (рис.22б). Для нахождения границ изменения переменной φ уравнение окружности разрешим относительно φ: или . Для нижней ветви окружности берется знак «-», а для верхней ветви – знак «+». Теперь по координатным линиям r=const, которые пересекают область D, определяем границы изменения φ: от значения на нижней ветви окружности до значения на верхней ветви окружности. В результате по формуле (6) получаем:
Пример 4. В двойном интеграле перейти к полярным координатам и расставить пределы интеграции в том и другом порядке, если область D ограничена линиями Решение: Кривая является уравнением окружности с центром в точке (0,1): . .
Рис.23а Рис.23б
Проведем линии r=const и определяем, что область заключена между координатными линиями r=1 и r=2, а координатная линия проходит через точки (±1,1), в которых пересекаются границы области — окружность и прямая (рис.23б). Поэтому D необходимо разбить на две простые области относительно φ: и и пределы интегрирования в двойном интеграле расставляются так:
Замечание: В некоторых случаях, если область интегрирования в двойном интеграле ограничена окружностью , удобнее делать замену . Пример 5. Вычислить интеграл , где область D – лежащая в первой четверти часть эллиптического кольца . Замечание: В случае, когда область интегрирования в двойном интеграле является эллипс или его часть, то вводят обобщенные полярные или эллиптические координаты . При этом J=abr (проверить самостоятельно), а выражение преобразуется в выражение . Решение: Перейдем к эллиптическим координатам, при этом границы эллиптического кольца принимают вид r=1 и r=2, а вся область расположена между лучами φ=0 и .
⇐ Предыдущая1234567Следующая ⇒ Читайте также: Формы дистанционного обучения Передача мяча двумя руками снизу Значение правильной осанки для жизнедеятельности человека Основные ошибки при выполнении передач мяча на месте |
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 9865; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. |
20). В этом случае двойной интеграл сводится к повторному по формуле:
21
е. до значения (рис.22а). Тогда по формуле (5) расставляем пределы интегрирования:
При выбирается верхняя половина круга – это и будет область D . Переведем границы области в полярные координаты, при этом уравнение окружности имеет вид . Если из него выразить φ, получаем для правой ветки окружности и — для левой. Прямая y=1 в полярных координатах имеет уравнение или и для отрезков прямых, лежащих в первой и во второй четверти соответственно. Нанесем координатные линии φ=const, откуда определяем, что область D расположена между лучами и , а радиус изменяется от значения на отрезке прямой y=1 до значения на дуге окружности (рис.23а). Тогда получаем:
При такой замене осуществляется параллельный перенос системы координат в центр окружности, а якобиан преобразования при этом не изменяется, т.е. J=r (предлагается убедиться в этом самостоятельно). В частности, если в примере 4 ввести замену , то уравнение окружности преобразуется к виду r=1, а область интегрирования Ω в координатах Оrφ становится прямоугольной: .
Поэтому интеграл вычисляем следующим образом:
Обратная связь — 161.97.168.212 (0.011 с.)Двойной интеграл в полярной системе координат — Студопедия
Поделись
Замена переменных интегрирования х и у в двойном интеграле, часто существенно упрощает его вычисление.
Пусть с помощью функций:
(2.5.1)
осуществляют переход от старых координат x, y к новым u, υ.
Эти функции должны быть непрерывными вместе со своими частными производными и однозначно решаться относительно u и υ. При этих условиях область D будет однозначно отображаться в область D* .
При переходе от декартовых к криволинейным координатам элемент площади dxdy преобразуется в элемент площади dudυ при этом они связаны соотношением:
(2.5.2)
где – функциональный определитель Якоби, или Якобиан, он равен:
Таким образом, в общем случае замену переменных интегрирования в двойном интеграле осуществляют по формуле:
(2.
5.3)
Из выражения (2.5.3) следует, что для того чтобы в двойном интеграле перейти к новым переменным интегрирования, нужно: переменные x и y заменить функциями (2.5.1), вместо элемента площади ds = dxdy подставить выражение dudυ и область D заменить ее отображением D*. Затем, вычисление двойного интеграла (2.5.3) сводят к последовательному вычислению двух линейных интегралов по новым переменным u и υ.
Перейдем в двойном интеграле от декартовых к полярным координатам по формуле (2.5.3), при этом за u примем полярный радиус r, а за υ – угол φ:
Функции x(r,φ) и y(r, φ) известны, они равны:
Найдем определитель Якоби:
Тогда
(2.5.4)
и двойной интеграл в полярной системе координат примет вид:
(2.5.5)
Чтобы вычислить полученный интеграл (2.5.5), следует перейти к двукратному интегрированию по новым переменным r и φ, а для этого нужно найти пределы их изменения в области D*.
Построение области D* в полярных координатах не обязательно. Если построена область D в декартовой системе координат, то пределы изменения полярного радиуса r и угла φ в новой системе отсчета легко определить по области D.
Например, пусть область D ограничена замкнутой кривой, а полюс лежит внутри кривой (рис. 2.5.1).
В этом случае нужно найти полярное уравнение ограничивающей линии r = r(φ).
Тогда угол φ внутри области будет изменяться от 0 до 2π, а полярный радиус r – от 0 до своих значений на кривой r = r(φ), т.е.:
Если область D в декартовой системе отсчета есть полукруг радиуса R с центром в начале координат, расположенный в верхней полуплоскости (рис. 2.5.2), то значения полярного радиуса r и угла φ внутри D заключены в пределах 0 ≤ r ≤ R, 0 ≤ φ ≤ π,
следовательно:
И наконец может быть еще такой случай.
Полюс лежит за пределами области D (Рис. 2.5.3), которая ограничена двумя линиями:
r1 = r1(φ) и r2 = r2(φ),
тогда
Приведем несколько примеров.
Пример 1. Вычислить двойной интеграл где область D есть первая четверть круга .
Решение. Построим область D в декартовой системе координат (рис. 2.5.4). В двойном интеграле перейдем к полярным координатам по формуле (2.5.5):
Полярный угол φ в области D изменяется от 0 до , а полярный радиус r – от 0 до R, следовательно:
Пример 2. Вычислить двойной интеграл где область D верхняя часть круга .
Решение. Перейдем к полярным координатам в двойном интеграле
Значения переменных φ и r заключены в пределах 0 ≤ φ ≤ π, 0 ≤ r ≤ 1, поэтому
Каждый из линейных интегралов в правой части равенства можно вычислить отдельно, так как пределы постоянны:
Находя первообразные и подставляя пределы окончательно получим:
Пример 3. Вычислить двойной интеграл
где D есть часть кольца, определяемая неравенствами:
Решение. Построим область D (рис. 2.5.5). Вычисление данного интеграла в декартовой системе координат довольно громоздко, поэтому лучше преобразовать двойной интеграл к полярным координатам:
В области D полярный радиус r изменяется от 1 до 3, а полярный угол φ от до . Переходя к двукратному интегрированию по φ и r, получим: .
Примечание. Уравнения окружностей x2 + y2 = 1 и x2 + y2 = 9 в полярной системе представляют собой координатные линии вида r = 1 и r = 3 соответственно. В этом легко убедиться, если в данные уравнения вместо переменных x и y подставить их выражения через полярные координаты:
x = r·cosφ, y = r·sinφ, в самом деле
r = 3
Уравнения прямых и , проходящих через начало координат, в полярной системе также переходят в координатные линии и .
В частности, .
Пример 4. Вычислить двойной интеграл
где область интегрирования задана неравенством
Решение. Преобразуем уравнение , выделив полный квадрат по переменной x:
Следовательно, границей области D является окружность радиуса центр которой смещен вправо по оси Ох на величину (рис. 2.5.6).
В данном случае также удобно перейти к полярным координатам:
Полярный угол φ будет изменяться от до . Чтобы определить пределы для второй переменной r, найдем уравнение окружности в полярной системе:
Полярный радиус r внутри области D изменяется от 0 до своих значений на линии r = Rcosφ (Рис. 2.5.6), т.е. пределы во внутреннем интеграле зависят от φ. Поэтому интегрируем сначала по r:
В последнем выражении вынесем за знак интеграла R3 и учтем, что тогда :
Вычисляя последние интегралы по переменной φ, окончательно получим:
Из приведенных примеров следует, что когда область интегрирования представляет собой круг, кольцо или часть круга и кольца с центром в начале координат, то при переходе к полярной системе, пределы у новых переменных φ и r становятся постоянными, а это значительно упрощает вычисления двойных интегралов.
Задачи для самостоятельного решения. Перейти к полярным координатам в двойном интеграле ,
Расставить пределы для переменных r и j.
1.
2.
3.
4. Перейти к полярным координатам в интеграле ,
расставить пределы, если область D ограничена линиями:
; ;
5. . Перейти к полярным координатам, расставить пределы, если
6. Вычислить ; D – первая четверть круга .
Практическое занятие 2.6. Тройной интеграл в цилиндрической и сферической системах координат
В общем случае замену переменных интегрирования в тройном интеграле осуществляют так же, как и в двойном.
Пусть функции:
(2.6.1)
непрерывны вместе со своими частными производными и однозначно разрешаются относительно u, υ, ω. Тогда, с помощью этих функций область W в декартовой системе координат однозначно отображается в область W* в криволинейной системе координат.
При этом элементы dV и dV* в старой и новой системах будут связаны соотношением:
или
(2.6.2)
где
В результате тройной интеграл преобразуется по формуле:
(2.6.3),
а его вычисление сводят к трехкратному интегрированию по переменным u, υ, ω. Примерами криволинейных систем в пространстве могут служить цилиндрическая и сферическая системы координат. Перейдем к их рассмотрению.
Тройной интеграл в цилиндрических координатах
Положение точки в пространстве в цилиндрической системе координат однозначно задают тремя числами φ, r, z.
Цилиндрические координаты точки получают путем добавления к ее полярным координатам аппликаты z (рис. 2.6.1). Цилиндрические и декартовые координаты точки связаны между собой соотношениями:
(2.6.4)
Перейдем в тройном интеграле от декартовых к цилиндрическим координатам. Элемент объема dV преобразуется по формуле
Найдем определитель Якоби:
следовательно:
(2.
6.5)
Далее, нужно перейти к трем линейным интегралам по переменным r,φ,z. Пределы изменения новых переменных расставляют по виду области W. Так же как и в двойном интеграле строить область W* не обязательно. Покажем это на примере.
Пример 1. Вычислить тройной интеграл где область W задана неравенствами:
Решение. Область, по которой нужно вычислить тройной интеграл, заключена внутри цилиндра , а сверху отрезана конусом (рис. 2.6.2).
Цилиндрическая поверхность и конус пересекаются по линии на высоте z=1. Перейдем в тройном интеграле к цилиндрическим координатам по формуле (2.6.5):
Найдем пределы изменения r,φ,z. Проекция W на плоскость xОy – есть круг, ограниченный окружностью уравнение которой в полярной системе является координатной линией r = 1. Следовательно, значения переменных r и φ заключены в пределах:
Для определения границ изменения переменной z, проведем прямые, параллельные оси Oz.
Эти прямые будут входить в область W на плоскости
z = 0 и выходить из нее на конической поверхности Найдем уравнение этой поверхности в цилиндрической системе
Таким образом, переменная z в области W изменяется от 0 до своих значений на конусе z = r. Переходя к трехкратному интегрированию по переменным r, φ и z, получим:
В данном примере проекцией W на плоскость xOy был круг с центром в начале координат, поэтому при переходе к цилиндрическим координатам пределы у переменных r и φ были постоянными. Это упростило вычисление тройного интеграла.
Пример 2. Вычислить тройной интеграл , где область W задана неравенствами
Решение. Область ограничена двумя поверхностями: снизу – конусом сверху – параболоидом вращения (рис. 2.6.3).
Их линией пересечения является окружность. Найдем ее уравнение из условия . Для этого в уравнении параболоида заменим выражение на :
Корни полученного квадратного уравнения раны
Подставляя z = 2 в любое из уравнений, либо конуса, либо параболоида вращения, найдем уравнение их линии пересечения:
Так как область W проектируется на плоскость xOy в круг с радиусом R = 2, и центром в начале координат, в тройном интеграле перейдем к цилиндрическим координатам:
Внутри области W полярный угол φ изменяется от 0 до 2π, а полярный радиус r – от 0 до 2.
Значения переменной z заключены между двумя поверхностями и
Найдем их уравнения в цилиндрической системе отсчета
Расставляя пределы изменения для переменных φ, r и z и переходя к трехкратному интегрированию, получим
Двойные интегралы в полярных координатах – определение, формула и примеры
Двойные интегралы в полярных координатах очень помогают, когда мы хотим вычислить повторные интегралы, особенно двойные интегралы, выражений, которые включают круговые области. Умение работать с полярными координатами в целом важно, если мы хотим исследовать широкий круг тем в математике и прикладных науках. Вот почему мы должны знать, как интегрировать выражения, переводя их в полярные координаты.
Двойные интегралы в полярных координатах важны, когда мы хотим вычислить сложные выражения, которые выиграют от преобразования полярных координат.
Знание того, как работать с двойными интегралами, включающими полярные координаты, позволяет нам преобразовывать выражения и интегрировать их, используя более простые методы.
В этой статье мы покажем вам такие области, как диски, кольца и их комбинации, которые выигрывают от использования двойных интегралов в полярных координатах вместо декартовых координат. Мы также покажем вам, как вычислять двойные интегралы, если они у нас есть в полярных координатах. К этому моменту вы должны быть знакомы с полярными координатами и интегральными свойствами, но не волнуйтесь, мы связали важные ресурсы на случай, если вам понадобится освежить знания!
Как преобразовать двойной интеграл в полярные координаты? Мы можем преобразовать двойной интеграл в полярные координаты, переписав $\int \int_R f(x, y) \phantom{x}dA$ как $\int \int_{R} f(r \cos \theta, r \ sin \theta) \phantom{x}r \phantom{x}dr d\theta$. Этот метод важен, когда мы хотим интегрировать выражения, представляющие области, включающие круги, такие как показанные ниже.
Во-первых, давайте быстро вспомним, как мы преобразовываем декартовы координаты в полярные координаты и выражения. Этот навык необходим, если мы хотим понять более подробный процесс преобразования двойных интегралов в полярные координаты. Когда нам дана декартова координата $(x,y)$, мы можем преобразовать ее в полярную координату $(r, \theta)$: 9{-1} \left(\dfrac{y}{x}\right) \end{aligned}
Мы также можем использовать эти уравнения для преобразования выражений из одной формы в другую. Вот несколько эквивалентных уравнений, показывающих как их полярную, так и декартову формы.
Полярная форма | Cartesian Form |
\ BEGIN {Aligned} R \ COS \ Theta & = 4 \ END {Aligned {Aligned} r \ Cos \ Theta & = 4 \ end {aligned} 9005 | 3938 | 9003. }x &= 4\конец{выровнено} 92 &= 2\end{align}
Попробуйте преобразовать эти примеры из декартовой формы обратно в полярную, чтобы перепроверить свои знания о полярных координатах.
2 \end{align} 9{r_2 (\theta)} f(r\cos \theta, r\sin \theta) \phantom{x} rdr d\theta\end{aligned}
После преобразования двойного интеграла из декартовой формы в его полярной форме, вычислите двойной интеграл в его полярной форме. Одной из самых сложных частей преобразования двойных интегралов в полярные координаты является нахождение пределов интегрирования двойного интеграла в полярной форме. Вот почему мы подготовили специальный раздел для процесса нахождения пределов двойных интегралов в полярной форме.
Как найти пределы двойных интегралов в полярных координатах?Как мы уже упоминали, мы можем использовать полярные формы $x$ и $y$, чтобы найти пределы двойных интегралов в полярных координатах.
\begin{aligned}x &= r \cos \theta\\ y &= r \sin \theta\end{aligned}
Используя эти полярные формы, мы можем найти значения $r$ и $\ тета$. Мы также можем переписать пределы интегрирования в полярных координатах, сначала нарисовав область, представляющую функцию, которую мы представляем.
9{r_2 (\тета) = 3}$.
Бывают случаи, когда найти выражение для функции в полярной форме не так просто. Приведенный выше график является примером более сложных областей, и мы можем оценить их двойной интеграл, установив пределы интегрирования, как показано ниже.
Предположим, что $f(x, y)$ является непрерывной функцией, заданной над областью $R$, которая ограничена в следующих пределах в полярных координатах: \begin{aligned} r_1( \theta) &< r < r_2(\theta) \\ \theta_1 &< \theta < \theta_2 \end{aligned}, где $r_1(\theta)$ и $r_2(\theta$ — функции радиусов в в терминах $\theta. Мы можем записать двойной интеграл его области как: 9{r_2 (\theta)} f(r\cos \theta, r\sin \theta) \phantom{x}rdrd\theta\end{aligned} |
Как видно из общего вида, мы просто оцените дифференциал $r$, используя пределы интегрирования в терминах $\theta$ для радиусов. Процесс будет аналогичен интегрированию двойных интегралов с областями неправильной формы.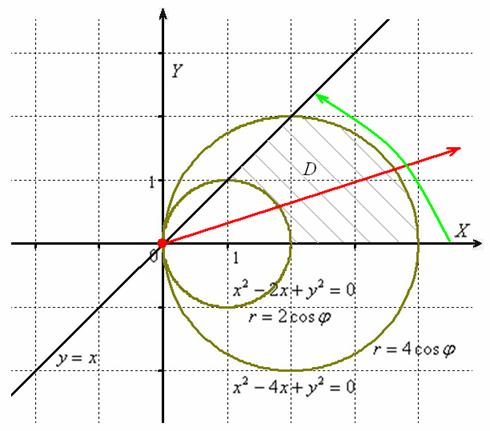
2 &= 4\\r&= 2\end{выровнено}
\begin{align}x &=0\\ r \cos \theta &=0 \\\theta &= \dfrac{\pi}{2}\\\\x &= 2\\r\ cos\theta&= 2\\2\cos\theta&= 2\\\cos \theta &= 1\\\theta &= 0\end{aligned}
Из полукруглой области мы можем видим, что значение $\theta$ находится в диапазоне от $\theta = 0$ до $\theta = \pi$. Это также показывает, что сначала набросок области с использованием пределов из $y$ сделает процесс нахождения двойных интегралов ‘ пределы в полярных координатах намного проще. Следовательно, имеем $0 \leq \theta \leq \pi$ и $0 \leq r \leq 2$. 93 \sin \theta \phantom{x}r dr d\theta\end{aligned}
Мы можем видеть, что пределы $x$ лежат в пределах от $0$ до $1$, а пределы $y$ равны от $0$ до $x$. В декартовой форме мы видим, что область интегрирования ограничена: $R = \{(x, y) | 0 \leq x \leq 1, 0 \leq y \leq x\}$.
Теперь преобразуем пределы интегрирования, приравняв пределы $x$ к $r \cos\theta$ и $y$ к $r\sin\theta$.
Это поможет нам понять график, показанный справа.
\begin{выровнено}\boldsymbol{y = r \sin \theta}\end{выровнено} | \begin{выровнено}\boldsymbol{x = r \cos \theta}\end{ выровнено} |
\begin{выровнено}y &=0\\ r \sin\theta &=0 \\\theta &= 0\\\\y&= x\\r\sin \theta &= r \ cos \ theta \\\ tan \ theta & = 1 \\\ theta & = \ dfrac {\ pi} {4} \ end {align} | \ begin {align} x & = 0 \\ r \cos \theta &=0 \\\theta &= \dfrac{\pi}{2}\\\\x &= 1\\r\cos\theta&= 1\\r &= \dfrac{1}{ \cos\theta}\end{выровнено} |
Эти выражения для $r$ и $\theta$ представляют пределы интегрирования нашего двойного интеграла в двойные интегралы.
\begin{align}R &= \left\{(r, \theta)| 0 \leq \theta \leq \dfrac{\pi}{4}, 0 \leq r \leq \dfrac{1}{\cos \theta}\right\} \end{aligned}
Теперь, когда у нас есть выражения для $f(x,y) \phantom{x}dA$ и пределы интегрирования в полярной форме, нам пора переписать наш двойной интеграл в полярной форме.
3 \ грех \ тета \ фантом {x} dr d\theta\end{выровнено} 93\sin \theta \phantom{x} dr d\theta$ и вычислить его вместо этого. Фактически мы показали, что значение двойного интеграла равно $\dfrac{2\sqrt{2} – 1}{3}$ или приблизительно равно $0,152$.
Эти примеры демонстрируют важность преобразования двойных интегралов в полярные координаты, особенно при работе с областями, включающими диски, кольца и окружности. Мы подготовили для вас больше примеров, чтобы к концу следующего раздела вы уже были уверены в двойных интегралах в полярных координатах!
Пример 1
Вычислить интеграл $\int \int_R 6x \phantom{x}dA$ по области, ограниченной следующими пределами: $\{1 \leq r \leq 4, 0 \ leq\theta\leq\pi\}$.
Решение
Из пределов интегрирования видно, что наша область образована двумя окружностями, образованными двумя радиусами: $1$ единиц и $4$ единиц. Поскольку $0 \leq \theta \leq \pi$, мы ожидаем, что область будет представлять собой полукруг, лежащий над осью $x$.
Решение
Мы видим, что вычисление этого интеграла в декартовой форме почти невозможно, поэтому переписывание его в полярной форме является таким важным шагом. От верхнего предела $y$ область, с которой мы работаем, представляет собой полукруг, расположенный ниже оси $x$.
Мы также можем перепроверить пределы значений интегрирования с помощью уравнения, приравнивающего каждую пару значений к $x = r\cos\theta$ и $y = r\sin\theta$, как показано ниже. 9*$ определяется $0 \le r \le 6$ и $0 \le \theta \ле 2\пи$.
К сожалению, это не так просто. Нам нужно учитывать один
большее последствие изменения переменных, то есть то, как меняется
область изменения переменных. Вы помните, что $dA$ означает площадь
части области $\dlr$. В прямоугольных координатах мы
заменил $dA$ на $dx\,dy$ (или $dy\,dx$).
Нам нужно определить, во что превращается $dA$, когда мы меняем переменные.
Как вы увидите, в полярных координатах $dA$ делает вместо становится $dr \,
д\тета$.
*$ до максимального размера. 9*$.
Итак, нам нужно оценить площадь каждого «изогнутого прямоугольника» в $\dlr$,
которую мы будем обозначать через $\Delta A$.
Мы можем вычислить площадь «изогнутого прямоугольника»
аппроксимируя его параллелограммом со сторонами $\pdiff{\cvarf}{r} \Delta r$
и $\pdiff{\cvarf}{\theta}\Delta\theta$.
Площадь параллелограмма – это величина
перекрестного произведения
$\слева\| \pdiff{\cvarf}{r} \times \pdiff{\cvarf}{\theta}\right\| \Дельта г\Дельта\тета$
двух векторов, охватывающих параллелограмм.
Кроме того, поскольку мы находимся в двух измерениях, мы записываем площадь проще с помощью определителя $2\times 2$.
После некоторого
упрощение, площадь
«извилистый прямоугольник» сводится к выражению
\начать{выравнивать*}
\Дельта А \приблизительно | \det \jacm{\cvarf}(r,\theta)|\Delta r\Delta\theta,
\конец{выравнивание*}
где $\jacm{\cvarf}$ —
производная матрица
карты $\cvarf$. Точно так же, как производную матрицу $\jacm{\cvarf}$ иногда называют «матрицей Якоби», ее определитель $\det \jacm{\cvarf}$ иногда называют «якобианским определителем».
Обратите внимание, что $D$ в $\jacm{\cvarf}(r,\theta)$ не совпадает с $D$ в качестве области интегрирования $\dlr$. Потому что нам нужно взять абсолютное значение определителя, мы обычно используем обозначение «det» для обозначения определителя во избежание путаницы (см. обсуждение в конце страницы о матрицах и определителях).
Для $\cvarf$, заданного уравнением \eqref{polartrans}, можно рассчитать что $| \det \jacm{\cvarf}(r,\theta)| = r$ так, что площадь каждого «извилистого прямоугольника» есть $r \Delta r \Delta \theta$. Это согласен с изображением выше, так как «извилистые прямоугольники» были больше, когда $r$ был больше. 9*$.
Иногда мы можем записать определитель производной матрицы как
$$\det \jacm{\cvarf}(\cvarfv,\cvarsv)=\pdiff{(x,y)}{(\cvarfv,\cvarsv)}$$
так что коэффициент расширения площади равен
$$| \det \jacm{\cvarf}(\cvarfv,\cvarsv)|=
\left|\pdiff{(x,y)}{(\cvarfv,\cvarsv)}\right|.$$
Это просто разные обозначения для одного и того же объекта, но они означают, что мы берем производную переменных $(x,y)$ по переменным $(\cvarfv,\cvarsv)$.
{\textstyle *}}
g(\cvarf(\cvarfv,\cvarsv)) \left|\pdiff{(x,y)}{(\cvarfv,\cvarsv)}\right|
д\cvarfv\,d\cvarsv.
\конец{выравнивание*}
Очевидно, мы пропустили довольно много деталей на этой вводной странице. в попытке просто дать общую картину. В частности, у нас есть замалчивали, как мы получили выражение для расширения площади фактор. Вы можете прочитать, как мы получить это формула.
Вы можете изучить некоторые
примеры изменения переменных, включая более подробную информацию о примере с диском.
Чтобы получить больше интуиции о том, как изменение переменных трансформирует регионы, вы можете прочитать иллюстрированный пример конкретной функции изменения переменной.
93$ что
параметризует
поверхность.
мы можем повторить
расчет
для коэффициента расширения площади практически без изменений
чтобы получить коэффициент расширения площади для
площадь поверхности
или поверхность
интегралы.
Единственная разница, возникающая в результате пребывания в трех измерениях, заключается в том,
что вы не можете изменить перекрестный продукт
для площади параллелограмма к
Определитель $2 \times 2$.
Следовательно, коэффициент расширения площади для параметризованных поверхностей представляет собой векторное произведение
$\слева\| \pdiff{\dlsp}{\spfv} \times \pdiff{\dlsp}{\spsv} \right\|$.
Двойная интеграция APEX с полярными координатами
Мы использовали повторные интегралы для вычисления двойных интегралов, которые дают объем со знаком под поверхностью, \(z=f(x,y)\text{,}\) над областью \(R\) \(xy \)-самолет. Подынтегральное выражение просто \(f(x,y)\text{,}\), а границы интегралов определяются областью \(R\text{.}\)
Некоторые области \(R\) легко описать с помощью прямоугольных координат, то есть с помощью уравнений вида \(y=f(x)\text{,}\) \(x=a\text{,}\ ) и т. д. Однако с некоторыми областями проще работать, если представить их границы полярными уравнениями вида \(r=f(\theta)\text{,}\) \(\theta = \alpha\text{,} \) и т. д.
Рисунок 15.3.1. Введение двойного интеграла в полярных координатах Основная форма двойного интеграла: \(\iint_R f(x,y)\, dA\text{.
}\) Мы интерпретируем этот интеграл следующим образом: по области \(R\ text{,}\) суммирует множество произведений высот (заданных \(f(x_i,y_i)\)) и площадей (заданных \(\Delta A_i\)). То есть \(dA\) представляет собой «небольшую площадь». В прямоугольных координатах мы можем описать небольшой прямоугольник как имеющий площадь \(dx\, dy\) или \(dy\, dx\) — площадь прямоугольника равна просто длине × ширине — небольшое изменение в \(x\ ) умножить на небольшое изменение \(y\text{.}\). Таким образом, мы заменим \(dA\) в двойном интеграле на \(dx\, dy\) или \(dy\, dx\text{.}\ )
Теперь рассмотрим представление области \(R\) с полярными координатами. Рассмотрим рисунок 15.3.2.(a). Пусть \(R\) — область в первом квадранте, ограниченная кривой. Мы можем аппроксимировать эту область, используя естественную форму полярных координат: части секторов кругов. На рисунке одна такая область заштрихована, она снова показана на рисунке 15.
2\Delta \theta\text{.}\) Площадь заштрихованная область — разность этих площадей: 92\big)\big(\Delta\theta\big) = \frac{r_2+r_1}{2}\big(r_2-r_1\big)\Delta\theta\text{.}
\end{уравнение*}
Обратите внимание, что \((r_2+r_1)/2\) — это просто среднее значение двух радиусов.
Для аппроксимации области \(R\text{,}\) мы используем множество таких подобластей; при этом разница \(r_2-r_1\) между радиусами уменьшается до 0, а изменение угла \(\Delta \theta\) также уменьшается до 0. Мы представляем эти бесконечно малые изменения радиуса и угла как \(dr\) и \(d\theta\text{,}\) соответственно. Наконец, поскольку \(dr\) мало, \(r_2\приблизительно r_1\text{,}\) и, следовательно, \((r_2+r_1)/2\приблизительно r_1\text{.}\) Таким образом, когда \( dr\) и \(d\theta\) малы,
\begin{уравнение*} \Delta A_i \приблизительно r_i\, dr\, d\theta\text{.} \end{уравнение*}
Принимая предел, при котором количество подрегионов стремится к бесконечности, а \(r_2-r_1\) и \(\Delta\theta\) стремятся к 0, мы получаем
\begin{уравнение*}
dA = r\, dr\, d\theta\text{.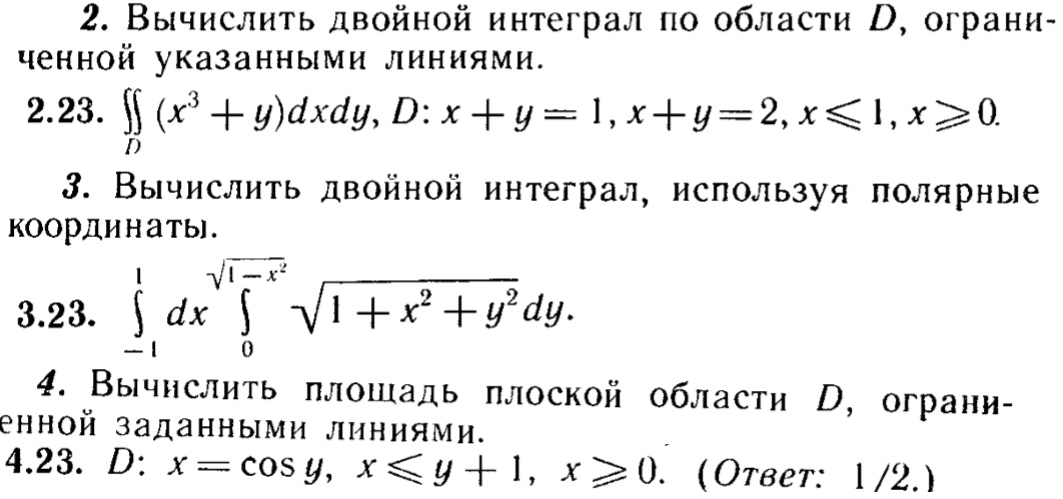
}
\end{уравнение*}
Итак, чтобы вычислить \(\iint_Rf(x,y)\, dA\text{,}\) замените \(dA\) на \(r\, dr\, d\theta\text{.}\) Преобразуйте функции \(f(x,y)\) в функцию с полярными координатами с заменами \(x=r\cos(\theta)\text{,}\) \(y=r\sin(\theta)\ text{.}\) Наконец, найдите границы \(g_1(\theta)\leq r\leq g_2(\theta)\) и \(\alpha\leq\theta\leq\beta\), которые описывают \(R\ text{.}\) Это ключевой принцип этого раздела, поэтому мы повторяем его здесь как ключевую идею. 92=1\text{.}\) Нам нужно найти полярные границы для этой области. Это может помочь просмотреть раздел 9.4; границы для этого диска равны \(0\leq r\leq 1\) и \(0\leq \theta\leq 2\pi\text{.}\)
Мы заменяем \(f(x,y)\) с \(f(r\cos(\theta) ,r\sin(\theta))\text{.}\) Это означает, что мы делаем следующие замены:
\begin{equation*} 4-x-2y \Rightarrow 4-r\cos(\theta) -2r\sin(\theta)\text{.} \end{equation*}
Наконец, мы заменяем \(dA\) в двойном интеграле на \(r\, dr\, d\theta\text{.}\) Это дает окончательный повторный интеграл, который мы оцениваем : 92=4\текст{.
2+1}\text{.}
\end{уравнение*} 93\text{;}\) мы обосновали эту формулу нашим расчетом.
Пример 15.3.13. Нахождение объема твердого тела.
Скульптор хочет сделать бронзовую отливку твердого тела, показанного на рисунке 15.3.14, где основание твердого тела имеет границу в полярных координатах \(r=\cos(3\theta)\text{,}\ ), а вершина определяется плоскостью \(z=1-x+0.1y\text{.}\) Найдите объем твердого тела.
Рисунок 15.3.14. Визуализация твердого тела, использованного в примере 15.3.13Решение.
С самого начала мы должны признать, что знание того, как решать эту задачу, вероятно, важнее, чем знание того, как вычислять интегралы. Итерированный интеграл не является «сложным» для вычисления, хотя он длинный и требует большого количества алгебраических вычислений. Как только правильный повторный интеграл определен, можно использовать легкодоступную технологию, чтобы помочь вычислить окончательный ответ.
3 \ text {.}
\end{уравнение*} 93\текст{.}\)
Мы использовали повторные интегралы для нахождения площадей плоских областей и объемов под поверхностями. Точно так же, как один интеграл может использоваться для вычисления гораздо большего, чем просто «площадь под кривой», повторные интегралы могут использоваться для вычисления гораздо большего, чем мы до сих пор видели. В следующих двух разделах показаны два среди многих приложений повторных интегралов.
Упражнения Упражнения
Термины и концепции
1.
При вычислении \(\iint_R f(x,y)\, dA\) с использованием полярных координат \(f(x,y)\) заменяется на , а \(dA\) заменяется на .
2.
Зачем кому-то интересоваться вычислением двойного интеграла с полярными координатами?
Проблемы
Группа упражнений.
Дана функция \(f(x,y)\) и описана область \(R\) плоскости \(xy\). Настройте и оцените \(\iint_Rf(x,y)\, dA\), используя полярные координаты.