Дифференциальное и интегральное исчисления для втузов, т.2
Дифференциальное и интегральное исчисления для втузов, т.2
ОглавлениеПРЕДИСЛОВИЕ К ДЕВЯТОМУ ИЗДАНИЮГЛАВА XIII. § 18. Некоторые типы дифференциальных уравнений второго порядка, приводимых к уравнениям первого порядка. Задача о второй космической скорости § 19. Графический метод интегрирования дифференциального уравнения второго порядка § 20. Линейные однородные уравнения. Определения и общие свойства § 21. Линейные однородные уравнения второго порядка с постоянными коэффициентами § 22. Линейные однородные уравнения n-го порядка с постоянными коэффициентами § 23. Неоднородные линейные уравнения второго порядка § 24. Неоднородные линейные уравнения второго порядка с постоянными коэффициентами § 25. Неоднородные линейные уравнения высших порядков § 26. Дифференциальное уравнение механических колебаний § 27. Свободные колебания. Векторное и комплексное изображение гармонических колебаний § 28. Вынужденные колебания § 29. Системы обыкновенных дифференциальных уравнений § 30. Системы линейных дифференциальных уравнений с постоянными коэффициентами § 31.  Понятие о теории устойчивости Ляпунова. Поведение траектории дифференциального уравнения в окрестности особой точки§ 32. Приближенное решение дифференциальных уравнений первого порядка методом Эйлера § 33. Разностный метод приближенного решения дифференциальных уравнений, основанный на применении формулы Тейлора.. Метод Адамса § 34. Приближенный метод интегрирования систем дифференциальных уравнений первого порядка Упражнения к главе XIII ГЛАВА XIV. КРАТНЫЕ ИНТЕГРАЛЫ § 2. Вычисление двойного интеграла § 3. Вычисление двойного интеграла (продолжение) § 4. Вычисление площадей и объемов с помощью двойных интегралов § 5. Двойной интеграл в полярных координатах § 6. Замена переменных в двойном интеграле (общий случай) § 9. Момент инерции площади плоской фигуры § 10. Координаты центра масс площади плоской фигуры § 11. Тройной интеграл § 12. Вычисление тройного интеграла § 13. Замена переменных в тройном интеграле § 14. 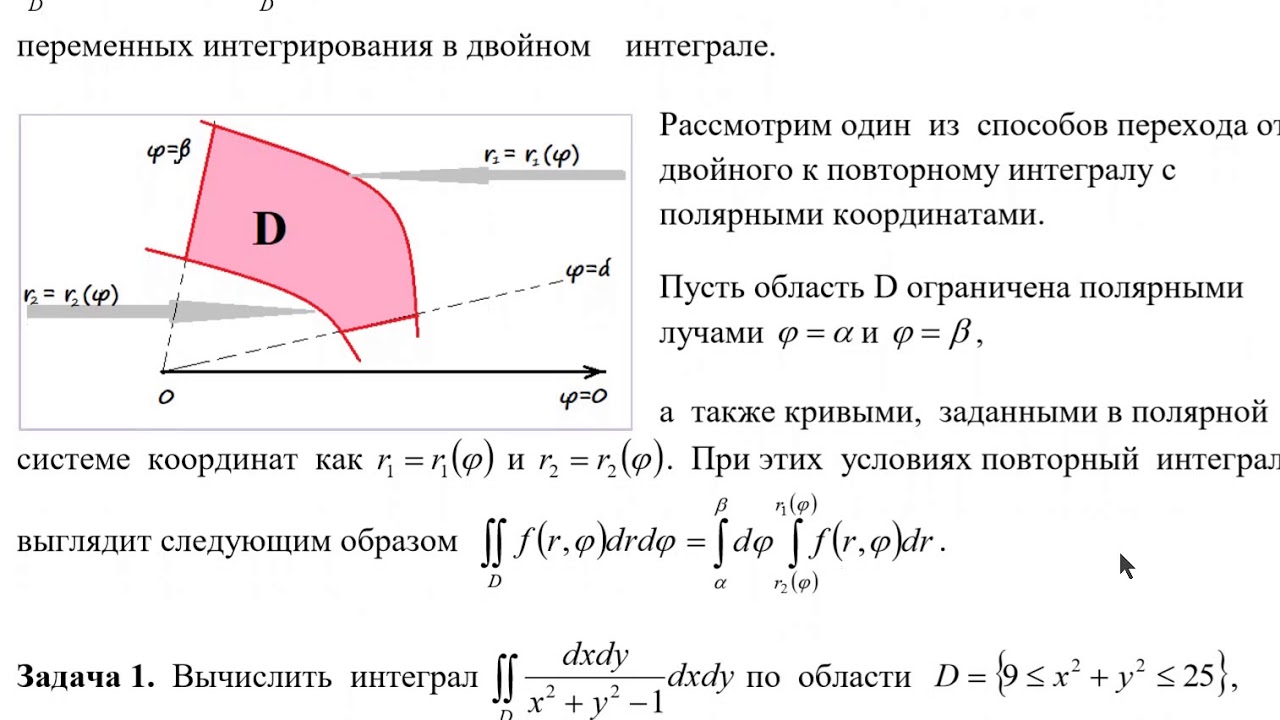 Момент инерции и координаты центра масс тела§ 15. Вычисление интегралов, зависящих от параметра Упражнения к главе XIV ГЛАВА XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЫ ПО ПОВЕРХНОСТИ § 2. Вычисление криволинейного интеграла § 3. Формула Грина § 4. Условия независимости криволинейного интеграла от пути интегрирования § 5. Поверхностный интеграл § 6. Вычисление поверхностного интеграла § 7. Формула Стокса § 9. Оператор Гамильтона. Некоторые его применения Упражнения к главе XV ГЛАВА XVI. РЯДЫ § 1. Ряд. Сумма ряда § 2. Необходимый признак сходимости ряда § 3. Сравнение рядов с положительными членами § 4. Признак Даламбера § 5. Признак Коши § 6. Интегральный признак сходимости ряда § 7. Знакочередующиеся ряды. Теорема Лейбница § 8. Знакопеременные ряды. Абсолютная и условная сходимость § 9. Функциональные ряды § 10. Мажорируемые ряды § 11. Непрерывность суммы ряда § 12. Интегрирование и дифференцирование рядов § 13.  Степенные ряды. Интервал сходимости§ 14. Дифференцирование степенных рядов § 15. Ряды по степеням x-a § 16. Ряды Тейлора и Маклорена § 17. Примеры разложения функций в ряды § 18. Формула Эйлера § 19. Биномиальный ряд § 20. Разложение функции ln(1+x) в степенной ряд. Вычисление логарифмов § 21. Вычисление определенных интегралов с помощью рядов § 22. Интегрирование дифференциальных уравнений с помощью рядов § 23. Уравнение Бесселя § 25. Степенные ряды с комплексной переменной § 26. Решение дифференциального уравнения первого порядка методом последовательных приближений (метод итераций) § 27. Доказательство существования решения дифференциального уравнения. Оценка погрешности при приближенном решении § 28. Теорема единственности решения дифференциального уравнения Упражнения к главе XVI ГЛАВА XVII. РЯДЫ ФУРЬЕ § 2. Примеры разложения функций в ряды Фурье § 3. Одно, замечание о разложении периодической функции в ряд Фурье § 4.  Ряды Фурье для четных и нечетных функций§ 5. Ряд Фурье для функции с периодом 2l § 6. О разложении непериодической функции в ряд Фурье § 7. Приближение в среднем заданной функции с помощью тригонометрического многочлена § 8. Интеграл Дирихле § 9. Сходимость ряда Фурье в данной точке § 10. Некоторые достаточные условия сходимости ряда Фурье § 11. Практический гармонический анализ § 12. Ряд Фурье в комплексной форме § 13. Интеграл Фурье § 14. Интеграл Фурье в комплексной форме § 15. Ряд Фурье по ортогональной системе функций § 16. Понятие о линейном функциональном пространстве. Аналогия между разложением функций в ряд Фурье и разложением векторов Упражнения к главе XVII ГЛАВА XVIII. УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ § 1. Основные типы уравнений математической физики § 2. Вывод уравнения колебаний струны. Формулировка краевой задачи. Вывод уравнений электрических колебаний в проводах § 3. Решение уравнения колебаний струны методом разделения переменных (методом Фурье) § 4.  Уравнение распространения тепла в стержне. Формулировка краевой задачи§ 5. Распространение тепла в пространстве § 7. Распространение тепла в неограниченном стержне § 8. Задачи, приводящие к исследованию решений уравнения Лапласа. Формулировка краевых задач § 9. Уравнение Лапласа в цилиндрических координатах. Решение задачи Дирихле для кольца с постоянными значениями искомой функции на внутренней и внешней окружностях § 10. Решение задачи Дирихле для круга § 11. Решение задачи Дирихле методом конечных разностей Упражнения к главе XVIII ГЛАВА XIX. ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ И НЕКОТОРЫЕ ЕГО ПРИЛОЖЕНИЯ § 1. Начальная функция и ее изображение § 2. Изображение функций … § 3. Изображение функции с измененным масштабом независимой переменной. Изображение функций sin at, cos at § 4. Свойство линейности изображения § 5. Теорема смещения § 6. Изображение функций … § 7. 
Дифференцирование изображения§ 8. Изображение производных § 9. Таблица некоторых изображений § 10. Вспомогательное уравнение для данного дифференциального уравнения § 11. Теорема разложения § 12. Примеры решения дифференциальных уравнений и систем дифференциальных уравнений операционным методом § 13. Теорема свертывания § 14. Дифференциальные уравнения механических колебаний. Дифференциальные уравнения теории электрических цепей § 15. Решение дифференциального уравнения колебаний § 16. Исследование свободных колебаний § 17. Исследование механических и электрических колебаний в случае периодической внешней силы § 18. Решение уравнения колебаний в случае резонанса § 19. Теорема запаздывания § 20. Дельта-функция и ее изображение Упражнения к главе XIX ГЛАВА XX. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ § 1. Случайное событие. Относительная частота случайного события. Вероятность события. Предмет теории вероятностей  Классическое определение вероятности и непосредственный подсчет вероятностей§ 3. Сложение вероятностей. Противоположные случайные события § 4. Умножение вероятностей независимых событий § 5. Зависимые события. Условная вероятность. Полная вероятность § 6. Вероятность гипотез. Формула Байеса § 7. Дискретная случайная величина. Закон распределения дискретной случайной величины § 8. Относительная частота и вероятность относительной частоты при повторных испытаниях § 9. Математическое ожидание дискретной случайной величины § 10. Дисперсия. Среднеквадратичное отклонение. Понятие о моментах § 11. Функции от случайных величин § 12. Непрерывная случайная величина. Плотность распределения непрерывной случайной величины. Вероятность попадания случайной величины в заданный интервал § 13. Функция распределения, или интегральный закон распределения. Закон равномерного распределения вероятностей § 14. Числовые характеристики непрерывной случайной величины § 15.  Нормальный закон распределения. Математическое ожидание нормального распределения§ 16. Дисперсия и среднеквадратичное отклонение случайной величины, подчиненной нормальному закону распределения § 17. Вероятность попадания значения случайной величины в заданный интервал. Функция Лапласа. Интегральная функция распределения для нормального закона § 18. Вероятное (срединное) отклонение или срединная ошибка § 19. Выражение нормального закона распределения через срединное отклонение. Приведенная функция Лапласа § 20. Правило трех сигм. Шкала вероятностей распределения ошибок § 21. Среднеарифметическая ошибка § 22. Мера точности. Соотношение между характеристиками распределения ошибок § 24. Нормальный закон распределения на плоскости § 25. Вероятность попадания двумерной случайной величины в прямоугольник со сторонами, параллельными главным осям рассеивания, при нормальном законе распределения § 26. Вероятность попадания двумерной случайной величины в эллипс рассеивания § 27.  Задачи математической статистики. Статистический материал§ 28. Статистический ряд. Гистограмма § 29. Определение подходящего значения измеряемой величины § 30. Определение параметров закона распределения. Теорема Ляпунова. Теорема Лапласа Упражнения к главе XX ГЛАВА XXI. МАТРИЦЫ. МАТРИЧНАЯ ЗАПИСЬ СИСТЕМ И РЕШЕНИЙ СИСТЕМ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ § 1. Линейные преобразования. Матрица § 2. Общие определения, связанные с понятием матрицы § 3. Обратное преобразование § 4. Действия над матрицами. Сложение матриц § 5. Преобразование вектора в другой вектор с помощью матрицы § 6. Обратная матрица § 7. Нахождение матрицы, обратной данной § 8. Матричная запись системы линейных уравнений § 9. Решение системы линейных уравнений матричным методом § 10. Ортогональные отображения. Ортогональные матрицы § 11. Собственный вектор линейного преобразования § 12. Матрица линейного преобразования, при котором базисные векторы являются собственными векторами § 13.  Преобразование матрицы линейного преобразования при переходе от одного базиса к другому§ 14. Квадратичные формы и их преобразования § 15. Ранг матрицы. Существование решений системы линейных уравнений § 16. Дифференцирование и интегрирование матриц § 17. Матричная запись системы дифференциальных уравнений и решений системы дифференциальных уравнений с постоянными коэффициентами § 18. Матричная запись линейного уравнения n-го порядка § 19. Решение систем линейных дифференциальных уравнений с переменными коэффициентами методом последовательных приближений с использованием матричной записи Упражнения к главе XXI ПРИЛОЖЕНИЯ |
Вычисление двойного интеграла в полярной системе координат
Пусть
существует ф-ция f(x,y)
интегр на области Д, можно прямолинейные
координаты x,
y
с помощью формул преобразования перейти
к криволинейным: x
= x(u,v),
y=y(u,v),
где эти ф-ции непрерывные вместе с
частными производными первого порядка,
устанавливают взаимно однозначное и в
обе стороны непрерывное соответствие
между точками плоской области Д и области
Д’ и определитель преобразования, наз.
Якобианом не обращается в 0:
если
это выполняется можно пользоваться
ф-лой:
Двойной интеграл в полярных координатах
Переход к полярным координатам частный случай замены переменных.
Луч, проходящий из произв точки О имеет на плоскости полярные координаты A(r, ) где r = |ОA| расстояние от О до А полярный радиус. = угол между векторами ОА и ОР – полярный угол отсчитываемой от полярной оси против часовой стрелки. всегда 0<=r<=+, 0<= <=2 .
Зависимость между прямоугольными и полярными координатами: x = rcos , y = rsin .
Якобиан преобразования будет равен:
И формула при переходе примет вид:
-
Вычисление объема с помощью двойного интеграла
Если f (x,y) > 0 в области интегрирования R, то объем цилиндрического тела с основанием R, ограниченного сверху поверхностью z = f (x,y), выражается формулой
В случае, когда R является областью типа I, ограниченной линиями , объем тела равен
Для области R типа II, ограниченной графиками функций , объем соответственно равен
Если в области R выполняется неравенство , то объем цилиндрического тела между поверхностями z1 = f (x,y) и z2 = g (x,y) с основанием R равен
-
Вычисление площади поверхности с помощью двойного интеграла
Предположим,
что поверхность задана функцией z
= f (x,y),
имеющей область определения R.
Тогда площадь такой поверхности над
областью z определяется
формулой
при условии, что частные производные и непрерывны всюду в области R.
-
Тройной интеграл и его свойства
Пусть на некоторой ограниченной замкнутой области V трехмерного пространства задана ограниченная ф-ция f (x,y,z). Разобьем область V на n произвольных частичных областей, не имеющих общих внутренних точек, с объемами V1… Vn В каждой частичной области возбмем произв. точку М с кооорд Mi(i,i,i) составим сумму: f(i,i,i)Vi, кот наз интегральной суммой для ф-ции f(x,y,z). Обозначим за максимальный диаметр частичной области. Если интегральная сумма при 0 имеет конечный предел, то сей предел и называется тройным интегралом от ф-ции f(x,y,z) по области V И обозначается:
Св-ва такие же как у двойного интеграла.
-
Вычисление тройного интеграла в декартовой системе координат
Вычисление
тройного интеграла в декартовых
координатах.
Пусть
является
цилиндрическим телом, проекция которого
на плоскость
есть
область
и
которое ограничено снизу поверхностью
,
а сверху v поверхностью
,
где
—
непрерывные функции в . Тогда
,
то есть интегрированием по z тройной
интеграл сводится к двойному интегралу
по области
.
Для областей более сложной формы
вычисление двойных и тройных интегралов
производится разбиением областей на
конечное число простых областей с уже
рассмотренными свойствами.
Что, если вместо этого мы хотим проинтегрировать \(f(x,y)\) по полярному прямоугольнику \(R\)?
Мы можем записать \(f(x,y)\) в полярных координатах как \(f(r\cos\theta, r\sin\theta)\)
с помощью соотношений \(x=r\cos\theta\), \(y=r\sin\theta\).
\beta f(r\cos\theta, r\sin\theta)\, r\, d\theta\, dr.\] 9\Пи \\
&= \left(\frac{\pi}{4}+0\right)-\left(\frac{\pi}{8}-1\right) \\
&= \frac{\pi}{8}+1.
\конец{выровнено}\]
Визуализация примера
Следующая анимация показывает полярные суммы Римана, аппроксимирующие этот двойной интеграл по мере увеличения числа подразделений.
Обратите внимание, что полярные прямоугольники ближе к началу координат намного уже.
чем те, что дальше, поэтому, если бы у нас было две коробки в
полярная сумма Римана с той же высотой, та, что ближе к началу координат
внесет меньший вклад в результат, чем тот, что дальше.
Это неверно для обычных, неполярных сумм Римана, которые мы рассматривали;
в этих суммах все подпрямоугольники имеют одинаковую площадь
\(\Delta A = \Delta x \Delta y\), поэтому два прямоугольника одинаковой высоты
имеют одинаковый объем и, следовательно, всегда вносят одинаковый вклад в сумму Римана.
Однако в полярных суммах Римана площадь полярного подпрямоугольника
равно \(\Delta A = r\Delta r\Delta\theta\),
который также зависит от \(r\), расстояния от начала координат.
Таким образом, полярные подпрямоугольники ближе к началу координат (с малым \(r\))
вносят меньший вклад в результат, чем полярные подпрямоугольники
дальше от начала координат (с большим \(r\)).
Мы видим это графически в узких прямоугольниках возле начала координат,
и символически в дополнительном множителе \(r\), который появляется
при записи двойного интеграла в виде повторного интеграла в полярных координатах.
Дополнительные вопросы
- Повторите этот пример, используя другой порядок интегралов, сначала интегрируя по \(\theta\), затем по \(r\).
- Как изменится наш ответ, если наш регион интеграции вместо этого был сектор единичного диска в первом квадранте? А третий квадрант? Четвертый квадрант? Попробуйте ответить на эти вопросы, не переделывая весь расчет; вместо этого подумайте, какие части расчета изменятся и как. 92\) по всему единичному диску?
-
В поле «Двойные интегралы в полярных координатах»
мы определили угловой диапазон как \(\alpha\le\theta\le\beta\),
с \(0\le \beta-\alpha\le 2\pi\).
Что может пойти не так с нашими полярными прямоугольниками, если мы допустим \(\beta-\alpha > 2\pi\)?
- В поле «Двойные интегралы в полярных координатах» мы определили радиальный диапазон как \(0\le a\le r\le b\). Что может пойти не так с нашими полярными прямоугольниками, если мы допустим \(a
Использование демоверсии Mathematica
Все изображения на этой странице были сгенерированы по блокноту Mathematica 15_4Двойные интегралы в полярных координатах.nb.
Этот блокнот создает изображения и анимацию, подобные тем, что на этой странице. полярных сумм Римана для любого подынтегрального выражения \(f(r,\theta)\) и любого полярного прямоугольника.
В качестве упражнения используйте тетрадь, чтобы дать четкие графические ответы. к вопросам 2 и 3 выше.
Тогда можете ли вы придумать подынтегральную функцию \(f(r,\theta)\) и границы так, чтобы блокнот выводит суммы Римана, аппроксимирующие площадь единичного круга, или объем единичной сферы? Как насчет конуса радиуса 1 и высоты 1?
Двойные интегралы в полярных координатах – интерактивные трехмерные графики для многомерного исчисления
Перейти к содержимому
Единицы
Концепция
Теперь рассмотрим понятие двойных интегралов в полярных координатах .
Вместо использования декартовой (или прямоугольной) системы координат , которую мы использовали до сих пор для вычисления одинарных и двойных интегралов, мы будем использовать полярную систему координат. Полярная система координат — это двумерная система координат, в которой каждая точка на плоскости определяется с помощью расстояния от опорной точки и угла от опорного направления. Прямоугольная система координат лучше всего подходит для графиков и областей, которые естественным образом рассматриваются на прямоугольной сетке. Полярная система координат является альтернативой, которая предлагает хорошие возможности для функций и областей, имеющих более круговые характеристики.
В то время как точка [латекс]P[/латекс] в прямоугольных координатах описывается упорядоченной парой [латекс](х,у)[/латекс], она также может быть описана в полярных координатах с помощью [латекс](r, \ theta)[/latex], где r — расстояние от [latex]P[/latex] до начала координат, а [latex]\theta[/latex] — угол, образованный отрезком прямой и положительным [latex]x[ /латекс]x-ось.
Мы можем преобразовать точку из прямоугольных координат в полярные, используя следующие уравнения:2}[/латекс] и [латекс]\тан(\тета) = \фрак{у}{х}[/латекс],
или преобразовать точку из полярных координат в прямоугольные, используя следующие уравнения:
[латекс]x = r \cos\theta[/latex] и [латекс]y = r \sin\theta[/latex].
Двойной интеграл [latex]\iint_D f(x,y)\,dA[/latex] в прямоугольных координатах может быть преобразован в двойной интеграл в полярных координатах как [latex]\iint_D f(r \cos\theta, r \sin\theta)\,r\,dr d\theta[/latex].
Сюжет
Теперь вы должны изучить график ниже, чтобы понять полярные координаты [1] . Выполните следующие шаги, чтобы применить изменения к графику и наблюдать за эффектами:
- Измените границы двойного интеграла в полярных координатах для границ [latex]r[/latex] и [latex]\theta[/latex]. Ограниченная область будет показана на графике, а [латекс]t[/латекс] на графике представляет [латекс]\тета[/латекс].
