Вычисление двойных интегралов с помощью повторного интегрирования
Пусть функция определена в области
,
где и — непрерывные функции на отрезке .
Область, в которой всякая прямая параллельная оси , проходящая через внутреннюю точку области, пересекает ее границы в двух точках, называется правильной относительно оси (рис.3).
Аналогично определяется о бласть правильная относительно оси :
где функции и — непрерывные функции на отрезке (рис.4).
Выражения вида
,
называются повторными интегралами от функции по
области .
Теорема. Двойной интеграл от непрерывной функции по правильной области равен повторному интегралу от этой функции по области .
= .
Если область правильная относительно оси , то двойной интеграл вычисляется как повторный вида
=
В
случае, когда область
не является правильной, ее разбивают
на части, каждая из которых является
правильной.
Частный случай. Если область интегрирования есть прямоугольник, ограниченный прямыми то формула преобразования двойного интеграла в повторный имеет вид
.
Если кроме того, в подынтегральной функции переменные разделены, то есть , то двойной интеграл превращается в произведение двух определенных интегралов:
.
Пример. Найти , где — область, ограниченная линиями (рис.5).
Решение. =
=
Пример. Найти , где — квадрат (рис.6).
Решение. =
=
Представление двойного интеграла в виде повторного
=
называют расстановкой пределов интегрирования в определенном порядке. Задача расстановки пределов интегрирования допускает несколько вариантов.
1. Задан двойной интеграл по области . Расставить пределы интегрирования в том и другом порядке.
Пример. Область лежит в правой полуплоскости (т.е. и ограничена
кривыми: (рис.7). В двойном интеграле
расставить пределы интегрирования в
одном и другом порядке.
Решение. Запишем неравенства, которым должны удовлетворять координаты точек области :
или
Расставим пределы интегрирования
= =
2. Задан двойной интеграл по области . Расставить пределы интегрирования в каком-либо порядке.
В этом случае выбирают порядок интегрирования, при котором интеграл имеет наиболее простое представление. Выбор может определяться как видом области интегрирования, так и свойствами подынтегральной функции. Например, расстановка пределов в одном порядке требует разбиения множества на меньшее число составляющих, чем расстановка в другом порядке.
Пример. Расставить пределы интегрирования в интеграле , где — область ограниченная линиями: ,
, (рис.8).
Решение.
Для расстановки пределов интегрирования
в порядке можно не разбивать
на составляющие области, а для другого
порядка расстановки пределов такое
разбиение необходимо. Исходя из этого
выбираем порядок
.
Решая систему получаем координаты точек пересечения:
.
Следовательно, и
=
.
3.Задан повторный интеграл . Поменять порядок интегрирования.
Для решения такой задачи сначала делают переход от заданного повторного интеграла к двойному, то есть восстанавливают по данным пределам область интегрирования : = . Условия на координаты точек ( множества получаем исходя из заданного повторного интеграла . В полученном двойном интеграле проведем расстановку пределов интегрирования в требуемом порядке. Таким образом, считая область правильной относительно обеих осей и , получаем цепочку равенств
= = .
Пример. Изменить порядок интегрирования в повторном интеграле .
Решение. Запишем условие на координаты точек из множества , по которому берется
интеграл:
(рис.9).
Область правильная как относительно оси , так и относительно оси . Так как при интегрировании в порядке верхняя граница области задается двумя различными функциями, представим множество в виде , где
Итак,
=
.
Двойной интеграл в полярной системе координат
Выведем формулу перехода от декартовых координат к полярным в двойном интеграле.
Пусть
— непрерывная функция на ограниченной
замкнутой области
.
Так как при определении двойного
интеграла предел последовательности
интегральных сумм не зависел от способа
разбиения области
на
части
,
то разобьем область
на
концентрическими окружностями и лучами (рис.
10). Тогда площадь
с точностью до бесконечно малых более высокого порядка малости чем . Таким образом, двумерный элемент площади в полярных координатах запишется в виде
.
Пусть теперь область правильная относительно , то есть любой луч, исходящий из полюса и проходящий через внутреннюю точку области пересекает границу области только в двух точках. В этом случае область можно задать множеством (рис.11). Тогда повторный интеграл по области представим в виде
Е сли любая окружность с центром в начале координат, проходящая через внутреннюю точку области пересекает линию границы в двух точках, то есть область есть множество:
, (рис.12), то повторный интеграл примет вид
=
В случае, когда полюс лежит внутри области и любой луч пересекает границу не более чем в одной точке (рис.13), для вычисления удобно использовать формулу
Пример. Вычислить двойной интеграл в
полярной
системе координат по области
,
ограниченной линиями
,
расположенной в I
квадранте (рис.
Решение.
Пример. Вычислить двойной интеграл в полярной системе координат по области , ограниченной окружностью (рис.15).
Решение. Перейдем к полярным координатам c полюсом в точке
: Угол изменяется от до Подставляя полярные
координаты в уравнение окружности, получим , откуда или — уравнение окружности в полярных координатах. Двойной интеграл по области сводится повторному
=
Замена переменных в двойном интеграле.
Рассмотрим двойной интеграл вида . Замена переменных в двойном интеграле состоит в переходе от
переменных и к новым переменным и по формулам
, . При этом каждая точка области соответствует некоторой точке области , а каждая точка области переходит в некоторую точку области Функции называют также отображением области плоскости на область плоскости . Пусть отображение удовлетворяет следующим условиям:
1.
Отображение взаимно однозначно, то есть
различным точкам области
соответствуют различные точки области
.
2.Функции имеют в области непрерывные частные производные первого порядка.
3. Якобиан отображения отличен от нуля во всех точках области .
Тогда справедливо равенство
=
Эта формула называется формулой замены переменных в
двойном интеграле.
Замечание. При переходе к полярной системе координат якобиан перехода имеет вид
Приложения двойных интегралов.
Двойные
интегралы применяются для вычисления
площадей плоских фигур и поверхностей,
объемов пространственных тел, механических
величин связанных с непрерывным
распределением массы в плоской области,
а также для решения многих других задач.
Двойной интеграл. Порядок интегрирования в двойном интеграле. Решение задач и контрольных работ по высшей математике онлайн
Краткая теория
Двойным интегралом от непрерывной функции , распространенным на ограниченную замкнутую область плоскости , называется предел соответствующей двумерной интегральной суммы:
где
и сумма распространена на те значения и , для которых точки принадлежат области .
Различают два основных вида области интегрирования.
1) Область интегрирования ограничена слева и справа прямыми и ( )
а сверху и снизу непрерывными кривыми и , каждая из которых пересекается с вертикалью только в одной точке.
В области
переменная
меняется от
до
,
а переменная
при постоянном
меняется от
до
.
Вычисление интеграла может быть произведено путем сведения к повторному интегралу по формуле:
где при вычислении
величину полагают постоянной.
2) Область интегрирования снизу и сверху ограничена прямыми и ( ), а слева и справа непрерывными кривыми и , каждая из которых пересекается с горизонталью только в одно точке.
Аналогично предыдущему имеем:
где при вычислении интеграла
величина считается постоянной.
Если область интегрирования не принадлежит ни к одному из разобранных выше видов, то ее стараются разбить на части, каждая из которых относится к одному из этих двух видов.
Площадь плоской области равна:
Примеры решения задач
Задача 1
Изменить
порядок интегрирования.
Изобразить область интегрирования.
Решение
Область интегрирования представляет собой область, ограниченную линиями:
и
Повторный интеграл с внешним интегрированием по :
Задача 2
Расставить пределы интегрирования в двойном интеграле
в том и в другом порядке, если область задана указанными линиями и вычислить площадь этой области с помощью двойного интеграла.
Решение
Сделаем чертеж:
Интеграл с внешним интегрированием по :
Интеграл с внешним интегрированием по :
Искомая площадь:
Ответ:
Задача 3
Вычислить двойной интеграл:
По области , ограниченной линиями:
Решение
Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:
ВКонтакте
WhatsApp
Telegram
Я буду работать с вами, над вашей проблемой, пока она не решится.
Указанная область имеет следующий вид:
Получаем:
Ответ:
Задача 4
Вычислить двойной интеграл по области , ограниченной указанными линиями, переходя, где это необходимо, к полярным координатам.
где
Решение
Сделаем чертеж области :
Искомый двойной интеграл:
Ответ:
Двойное интегрирование по общим областям
Все ресурсы исчисления 3
6 Диагностические тесты 373 практических теста Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 Следующая →
Исчисление 3 Помощь » Множественная интеграция » Двойные интегралы » Двойное интегрирование по общим областям
Вычислите следующий интеграл.
Возможные ответы:
Правильный ответ:
Объяснение:
Давайте сначала разберемся с внутренним интегралом.
Теперь вычислим это выражение во внешнем интеграле.
5
Сообщить об ошибке
Правильный ответ:
Объяснение:
Поскольку нет вложенных термов, содержащих как и , мы можем переписать интеграл как
Это позволяет нам вычислить двойной интеграл и произведение двух независимых одинарных интегралов. Из правил интегрирования из исчисления с одной переменной мы должны прийти к результату
.
Отчет о ошибке
Оцените следующий интеграл по указанному региону:
, где r — область, определяемая Условиями:
Возможные ответы:
Правильный ответ:
Правильный ответ: 9000 9000
Объяснение:
Сообщить об ошибке
Оценка:
Возможные ответы:
Правильный ответ:
Объяснение:
Поскольку члены x и y в подынтегральном выражении независимы друг от друга, мы можем переместить их в соответствующие интегралы:
Мы использовали следующие правила интегрирования:
,
Сообщить об ошибке
Оцените следующий интеграл.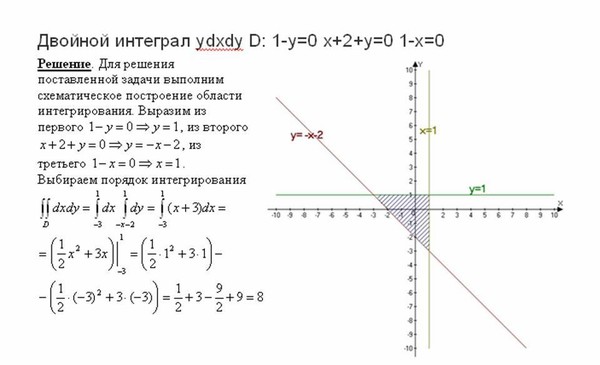
Возможные ответы:
Правильный ответ:
Объяснение:
Сначала вы должны вычислить интеграл по y (из-за обозначения ).
Используя правила интегрирования, мы получаем
.
При вычислении от y=2 до y=3 получаем
.
Интегрируя это по x, мы получаем , а оценивая от x=0 до x=1, вы получаете .
Сообщить об ошибке
Вычислите следующий интеграл:
Возможные ответы:
Правильный ответ:
Объяснение:
Во-первых, вы должны вычислить интеграл по y и найти решение в допустимых пределах.
При этом вы получаете и оцениваете y от 0 до 2.
Это дает вам
.
На этот раз вычисление интеграла по x дает
.
Вычисление x от 1 до 2 дает
.
Сообщить об ошибке
Вычисление двойного интеграла.
Возможные ответы:
Правильный ответ:
Объяснение:
При решении двойных интегралов сначала вычисляется внутренний интеграл.
Сообщить об ошибке
Вычислить двойной интеграл.
Возможные ответы:
Правильный ответ:
Объяснение:
При решении двойных интегралов сначала вычисляется внутренний интеграл.
Отчет о ошибке
Оцените двойной интеграл
Возможные ответы:
Правильно:
595959595 .
Ответ:
. Объяснение:
При решении двойных интегралов сначала вычисляется внутренний интеграл.
Отчет о ошибке
Оцените интеграл
Возможные ответы:
Правильный ответ:
9005669 . Правильный ответ:
900566669 . Объяснение:
Сначала вы должны вычислить интеграл по x. Это дает вам оценку от до . Это становится . Решение этого интеграла относительно y дает вам . Вычисляя от до , вы получаете .
Сообщить об ошибке
← Назад 1 2 3 Далее →
Уведомление об авторских правах
Все ресурсы исчисления 3
6 Диагностические тесты 373 практических теста Вопрос дня Карточки Learn by Concept
Глава 14, МНОЖЕСТВЕННЫЕ ИНТЕГРАЛЫ Видеорешения, Ранние трансцендентальные исчисления
Раздел 1
Двойные интегралы
Выберите Раздел 14.
1: Двойные интегралы 14.2: Двойные интегралы по непрямоугольным областям 14.3: Двойные интегралы в полярных координатах 14.4: Площадь поверхности; Параметрические поверхности 14.5: Тройные интегралы 14.6: Тройные интегралы в цилиндрических и сферических координатах 14.7: Замена переменных в кратных интегралах; Якобианы 14.8: центры тяжести с использованием кратных интегралов 9{2}} д А ; R=\{(x, y): 0 \leq x \leq 1,2 \leq y \leq 3\}
$$
Танишк Гупта
Учитель нумерейд
02:01
Задача 16
Вычислить двойной интеграл по прямоугольной области R.
$$
\begin{array}{l}{\iint_{R}(x \sin y-y \sin x) d A} \\ {R=\{(x , y): 0 \leq x \leq \pi / 2,0 \leq y \leq \pi / 3\}}\end{array}
$$
Tanishq Gupta
Numerade Educator 9{*}\right)$ быть центром $k$-го прямоугольника и аппроксимировать двойной интеграл от $f$ по $R$ полученной суммой Римана.
(б) Сравните результат в части (а) с точным значением интеграла.
Заходите скорее!
02:03
Задача 19
Каждый повторный интеграл представляет объем твердого тела. Сделайте набросок твердого тела. Используйте геометрию, чтобы найти объем твердого тела, а затем оцените повторный интеграл. 9{4} f(x, y) d x d y
$$
Tanishq Gupta
Numerade Educator
02:02
Задача 26
Определите, является ли утверждение истинным или ложным. Поясните свой ответ.
Предположим, что для некоторой области $R$ в плоскости $x y$
$$
\iint_{R} f(x, y) d A=0
$$
Если $R$ разбит на две области $R_ {1}$ и $R_{2},$ тогда
$$
\iint_{R_{1}} f(x, y) d A=-\iint_{R_{2}} f(x, y) d А 9{y}+1} \tan x d x d y
$$
при проверке. Объясните свои рассуждения.
Танишк Гупта
Педагог-счетчик
01:58
Задача 29
Используйте двойной интеграл, чтобы найти объем.
Объем под плоскостью $z=2 x+y$ и над прямоугольником $R=\{(x, y): 3 \leq x \leq 5,1 \leq y \leq 2\}$
Tanishq Гупта
Учитель нумерейд
02:01
9{2}$ и плоскости $x=0, x=2, y=3, y=0,$ и $z=0$Tanishq Gupta
Numerade Educator
01:14
Задача 32
Используйте двойной интеграл, чтобы найти объем.
Объем в первом октанте, ограниченный координатными плоскостями, плоскостью $y=4,$ и плоскостью $(x/3)+(z/5)=1$
Tanishq Gupta
Numerade Educator
02:13
Задача 33 9{2} \pi x d A ; R=\left[0, \frac{1}{2}\right] \times[0, \pi]
$$
Танишк Гупта
Учитель нумерадов
02:31
Задача 34
(a) Нарисуйте тело в первом октанте, заключенное
плоскостями $x=0, z=0, x=5, z-y=0,$ и $z=-2 y+6 .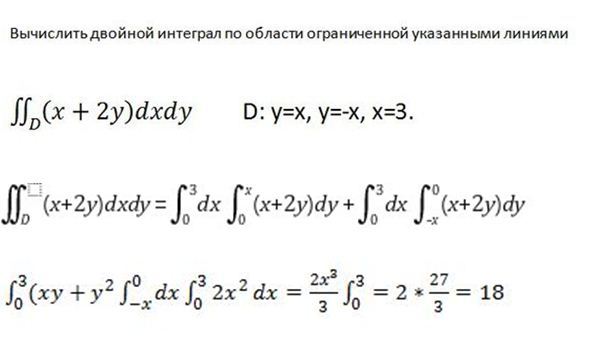
$
(b ) Найдите объем твердого тела, разбив его на две части.
Танишк Гупта
Педагог-счетчик
02:25
Задача 35
Среднее значение или среднее значение непрерывной функции $f(x, y)$ по прямоугольнику $R=[a, b] \times[c, d]$ определяется как
$$
f_{\mathrm{ ave}}=\frac{1}{A(R)} \iint_{R} f(x, y) d A
$$
, где $A(R)=(b-a)(d-c)$ — площадь прямоугольник $R$ (ср. с определением 5.8.1). Используйте это определение в этих упражнениях.
Найти среднее значение $f(x, y)=y \sin x y$ по прямоугольнику $[0,1] \times[0, \pi / 2].$
Карсон Меррилл
Преподаватель нумерадов
02:44
Задача 36
Среднее значение или среднее значение непрерывной функции $f(x, y)$ по прямоугольнику $R=[a, b] \times[c, d]$ определяется как
$$
f_{\mathrm{ ave}}=\frac{1}{A(R)} \iint_{R} f(x, y) d A
$$
, где $A(R)=(b-a)(d-c)$ — площадь прямоугольник $R$ (ср.
с определением 5.8.1). Используйте это определение в этих упражнениях. 9{1 / 2}$ над прямоугольником $[0,1] \times[0,3].$
Танишк Гупта
Педагог-счетчик
01:38
Задача 37
Среднее значение или среднее значение непрерывной функции $f(x, y)$ по прямоугольнику $R=[a, b] \times[c, d]$ определяется как
$$
f_{\mathrm{ ave}}=\frac{1}{A(R)} \iint_{R} f(x, y) d A
$$
, где $A(R)=(b-a)(d-c)$ — площадь прямоугольник $R$ (ср. с определением 5.8.1). Используйте это определение в этих упражнениях. 9{2}$
, где $x$ и $y$ указаны в метрах. Найти среднюю температуру
прямоугольной части пластины, для которой $0 \leq x \leq 1$ и $0 \leq y \leq 2$
Tanishq Gupta
Numerade Educator
01:35
Задача 38
Покажите, что если $f(x, y)$ постоянна на прямоугольнике $R=[a, b] \times[c, d],$, скажем $f(x, y)=k,$, то $f_{ \text {ave}}=k$ свыше $R .