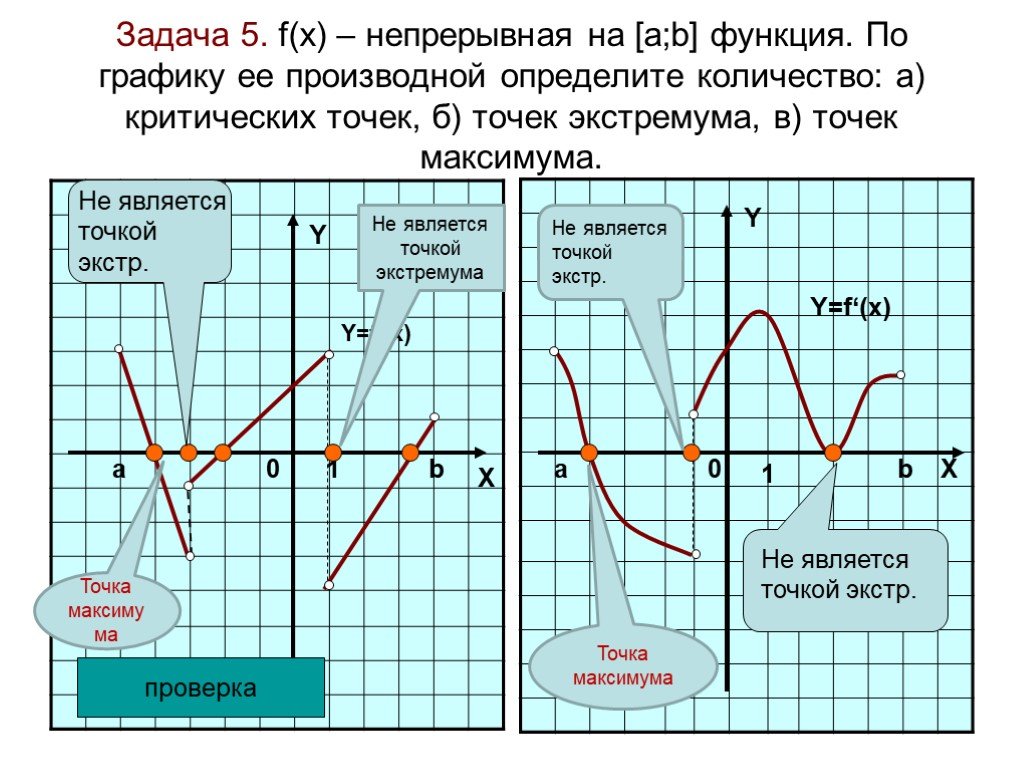
Использование графика производной для исследования функции | Методическая разработка по алгебре (11 класс) по теме:
Тест 7
Исследование функции по графику ее производной
В1. Функции у=f(x) задана на отрезке [a;b]. у
На рисунке изображен график ее производной
у=f ´(x). Исследуйте на экстремумы 1 b
функцию у=f(x). В ответе укажите количество a 0 1 х
точек минимума.
В2. Функции у=f(x) задана на отрезке [a;b].
На рисунке изображен график ее производной у
у=f ´(x). Исследуйте функцию у=f(x) на
монотонность и в ответе укажите длину 1
промежутка убывания.
а 0 1 b х
В3. Функции у=f(x) определена на промежутке у
(-7; 8). На рисунке изображен график ее
производной у=f ´(x). Найдите промежутки -7 1 8
невозрастания функции у=f(x). В ответе 0 1 х
укажите наибольшую из длин этих промежутков.
В4. Функции у=f(x) определена на промежутке у
(а; b). Ее производной является функция у=f ´(x),
а на рисунке изображен график функции a 1 b
у=f ´(x)+2. Укажите число точек максимума 0 1 x
функции у=f(x) на промежутке (а; b).
В5. Функции у=f(x) определена на промежутке
(а; b). На рисунке изображен график ее у
производной. Укажите число точек максимума
функции у = f(x) — х на промежутке (а; b). a 1 b
0 1 х
В6. Функции у=f(x) определена на промежутке
(а; b). На рисунке изображен график ее у
производной. Укажите число точек минимума
функции у = f(x) — 3х на промежутке (а; b). 1
a 0 1 b х
В7. Функция определена
на промежутке (– 3; 7).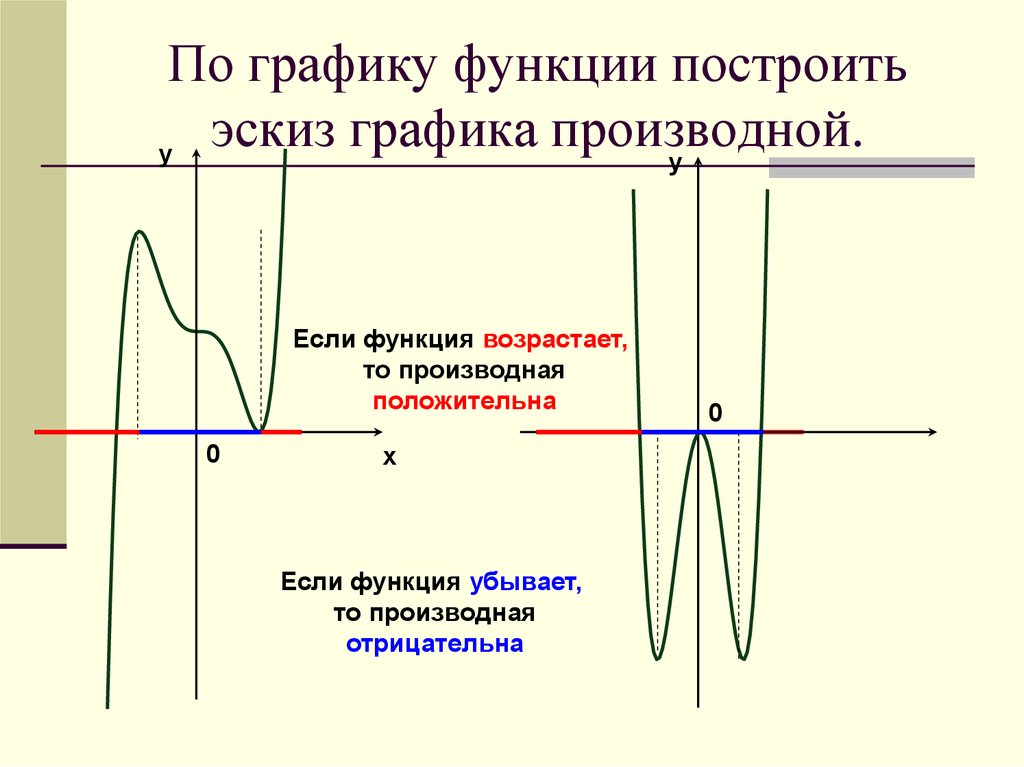
На рисунке
изображен график ее производной.
Найдите точку , в которой функция
принимает наибольшее значение.
В8. На рисунке изображен график производной у =f ´(x).
Найдите точку максимума функции у =f(x).
В9. На рисунке изображен график производной у =f ´(x).
Найдите точку минимума функции у =f(x).
Построить график функции, провести ее полное исследование
Построить график функции, провести ее полное исследование
Часто при сдаче тестов по математике попадаются задания, в которых необходимо исследовать квадратичную функцию.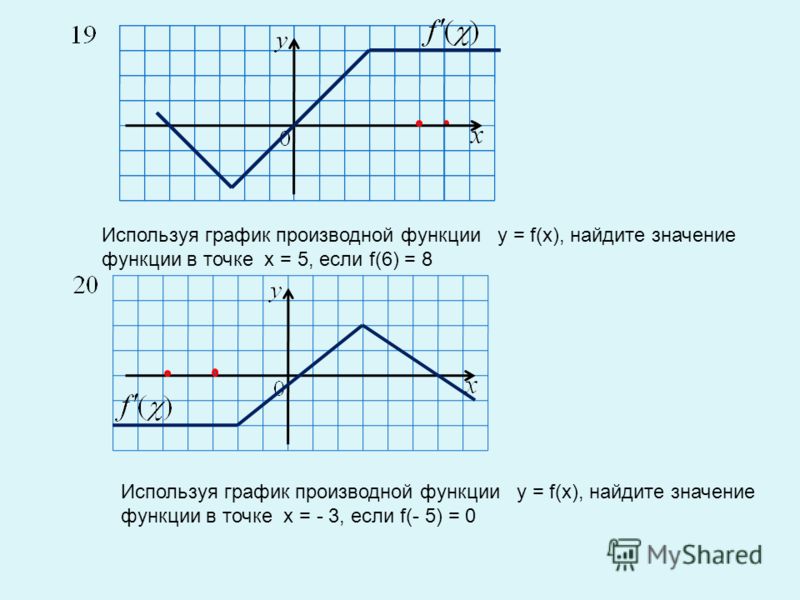
Вот типичный пример .
Исследуем функцию, заданную формулой:
Область определения: множество всех действительных чисел
Первая производная:
Используем правило о том, что производная суммы равна сумме производных.
На тестах по математике помним, что производная константы равна нулю.
Воспользуемся правилом производной степени .
Производная произведения константы и функции равна произведению константы на производную функции.
Вторая производная:
При сдаче тестов по математике вспоминает правило о том, что вторая производная — это производная от первой производной.
Производная суммы равна сумме производных.
Производная произведения константы и функции равна произведению константы на производную функции.
Производная константы равна нулю.
Когда вы решаете тесты по математике, в который нужно построить график функции, то необходимо найти точки пересечения с осью x:
Нет
Для нахождения точек пересечения с осью абсцисс приравняем функцию к нулю.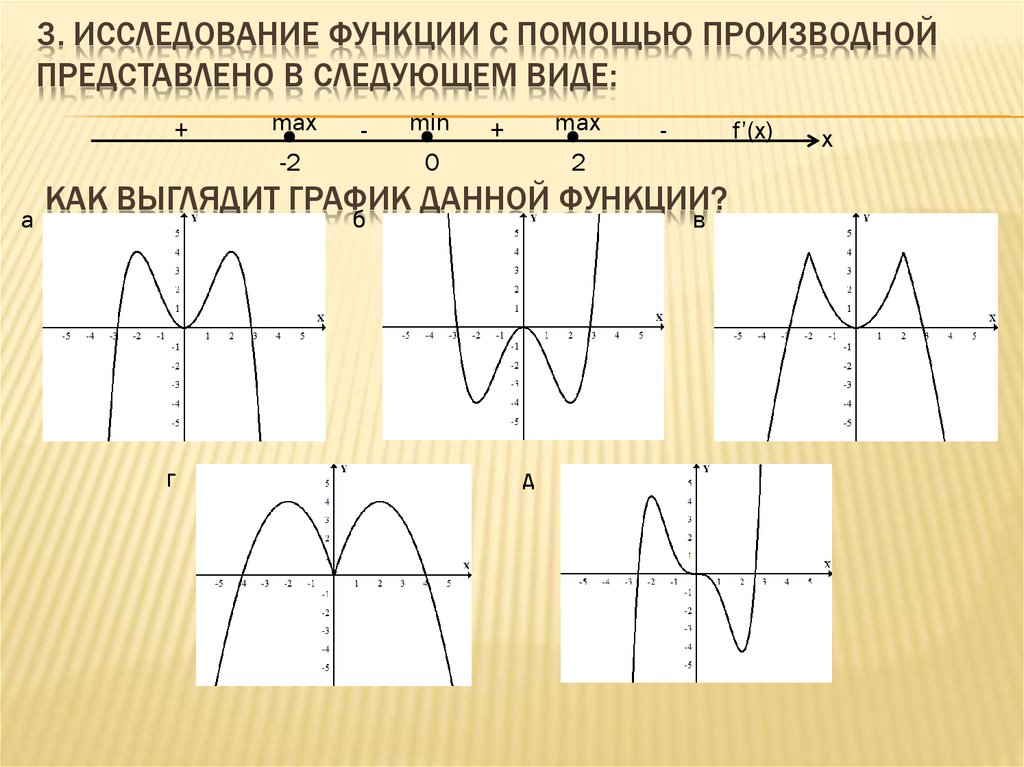
Ответ: нет решений.
Точки разрыва: нет
Симметрия относительно оси ординат: нет
Функция f(x) называется четной, если f(-x)f(x).
Раскрываем скобки.
Выносим знак минус из произведения.
Производим сокращение.
Приводим подобные члены.
Симметрия относительно начала координат: нет
Функция f(x) называется нечетной, если f(-x)-f(x).
Раскрываем скобки.
Выносим знак минус из произведения.
Производим сокращение.
Приводим подобные члены.
На тестах по математике надо указать тестовые интервалы:
Относительные экстремумы:
Проходя через точку минимума, производная функции меняет знак с (-) на (+).
Относительный минимум
(-2, 17)
Данные таблицы нанесем на координатную плоскость.
| PHP |
| Алгебраические преобразования, уравнения, неравенства |
| Другое |
| Логарифмические, показательные уравнения , неравенства |
| Начала анализа |
| Планиметрия |
| Прогрессии |
| Стереометрия |
| Текстовые задачи |
| Тригонометрия |
| Числа и выражения |
Как оценить производную по графику
Обновлено 08 декабря 2020 г.
Ли Джонсон
Скорость изменения проявляется повсюду в науке, и особенно в физике, через такие величины, как скорость и ускорение. Производные математически описывают скорость изменения одной величины по отношению к другой, но иногда их вычисление может быть сложным, и вам может быть представлен график, а не функция в форме уравнения.
Если вам представлен график кривой и вам нужно найти производную от него, вы, возможно, не сможете быть столь же точными, как с уравнением, но вы можете легко сделать надежную оценку.
TL;DR (слишком длинный; не читал)
Выберите точку на графике, чтобы найти значение производной.
Проведите прямую, касательную к кривой графика в этой точке.
Возьмите наклон этой линии, чтобы найти значение производной в выбранной вами точке на графике.
Помимо абстрактной настройки дифференцирования уравнения, вы можете немного запутаться в том, что такое производная на самом деле. В алгебре производная функции — это уравнение, которое сообщает вам значение «наклона» функции в любой точке. Другими словами, он говорит вам, насколько изменится одна величина при небольшом изменении другой. На графике градиент или наклон линии говорит вам, насколько зависимая переменная (помещенная на y -оси) изменяется с независимой переменной (по x -оси).
Для прямолинейных графиков вы определяете (постоянную) скорость изменения, вычисляя наклон графика. С отношениями, описываемыми кривыми, не так просто иметь дело, но принцип, что производная просто означает наклон (в этой конкретной точке), остается верным.
Для отношений, описываемых кривыми, производная принимает разные значения в каждой точке кривой. Чтобы оценить производную графика, вам нужно выбрать точку, в которой будет браться производная. Например, если у вас есть график, показывающий пройденное расстояние в зависимости от времени, на прямолинейном графике наклон покажет вам постоянную скорость. Для скоростей, которые меняются со временем, график будет представлять собой кривую, но прямая линия, которая касается кривой только в одной точке (линия, касательная к кривой), представляет скорость изменения в этой конкретной точке.
Выберите точку, в которой вам нужно знать производную. Используя пример зависимости пройденного расстояния от времени, выберите время, в которое вы хотите узнать скорость движения.
Если вам нужно узнать скорость в нескольких разных точках, вы можете запустить этот процесс для каждой отдельной точки. Если вы хотите узнать скорость через 15 секунд после начала движения, выберите точку на кривой через 15 секунд по оси x .
Нарисуйте линию, касательную к кривой в интересующей вас точке. Не торопитесь, потому что это самая важная и самая сложная часть процесса. Ваша оценка будет лучше, если вы проведете более точную касательную. Держите линейку до точки на кривой и отрегулируйте ее ориентацию, чтобы линия, которую вы рисуете, была только коснитесь кривой в интересующей вас точке.
Нарисуйте линию, насколько позволяет график. Убедитесь, что вы можете легко прочитать два значения для координат x и y , одно рядом с началом вашей строки, а другое ближе к концу. Вам не обязательно рисовать длинную линию (технически подходит любая прямая линия), но наклон более длинных линий, как правило, легче измерить.
Найдите два места на вашей линии и запишите цифру x и y координаты для них.
Например, представьте свою касательную в виде двух примечательных точек x = 1, y = 3 и x = 10, y = 30, которые вы можете назвать точкой 1. и точка 2. Используя символы x 1 и y 1 для обозначения координат первой точки и для представления координат второй точки, наклон м определяется как:
м = \frac{y_2 — y_1}{x_2 — x_1}
Это говорит вам о производной кривой в точке, где линия касается кривой. В примере x 1 = 1, x 2 = 10, y 1 = 3 и y 2 = 30, SO:
\begin{align} m &= \frac{30 — 3}{10 — 1} \\ \,\\ &= \frac{27}{9} \\ \,\\ &=9 \end{ выровнено}
В примере этим результатом будет скорость в выбранной точке. Итак, если 9Ось 0017 x измерялась в секундах, а ось y измерялась в метрах, результат будет означать, что рассматриваемое транспортное средство двигалось со скоростью 3 метра в секунду.
Независимо от конкретной величины, которую вы вычисляете, процесс оценки производной одинаков.
Функции Afin и производная | |
| Простейшими функциями являются линейные функции. Нас интересует изучение производной простых функций с помощью интуитивного и визуального подхода. Начнем с линейной функции. ПОНЯТИЕ ПРОИЗВОДНОЙ ФУНКЦИИ Производную функции в точке можно определить как мгновенную скорость изменения или как наклон касательной к точке. график функции в этой точке. Мы можем сказать, что этот наклон тангенса функции в точке есть наклон функция. Наклон функции, вообще говоря, будет зависеть от x. Тогда, начиная с функции, мы можем получить новую функцию, производную от исходной функции. Процесс нахождения производной функции называется дифференцированием. Значение производной функции для любого значения x представляет собой наклон исходной функции в точке x. Как нарисовать производную заданной функции (в нашем случае линейной)? Общая процедура проста: мы начинаем рисовать касательную к функции в заданной точке. В нашем случае это очень просто, потому что касательная к прямой — это одна и та же линия: Затем проводим параллельную прямую касательной, проходящей через значение x-1, и получаем прямоугольный треугольник. Длина вертикальной стороны — наклон касательной. Затем мы можем нарисовать производную линейной функции, что очень просто, потому что это постоянная функция. Значение этого постоянная функция представляет собой наклон исходной линейной функции. Например, линейная функция с положительным наклоном: Другой пример, линейная функция с отрицательным наклоном: Когда функция является постоянной функцией, ее график представляет собой горизонтальную линию (наклон равен 0). Тогда производная постоянной функции есть постоянная функция 0. Одна простая и интересная идея заключается в том, что когда мы переводим вверх и вниз график функции (мы добавляем или вычитаем число из исходной функции),
производная не меняется. Причина очень интуитивна, и мы можем поиграть с интерактивным приложением, чтобы увидеть это свойство. |
Их формулы представляют собой полиномы первой или нулевой степени (это
случай, когда функция является постоянной функцией). Их графики представляют собой прямые линии.
