НОУ ИНТУИТ | Лекция | Двойственный симплекс – метод. Исследование моделей задач линейного программирования на чувствительность
< Лекция 5 || Лекция 6: 123 || Лекция 7 >
Аннотация: В данной лекции широко рассматривается такой метод решения двойственной задачи линейного программирования, как двойственный симплекс – метод. Также рассматриваются его основные свойства и характеристики, проводится сравнительный анализ с обычным симплекс – методом. Кроме того, проводится исследование моделей задач на чувствительность с использованием экономической интерпретации обычной задачи линейного программирования.
Ключевые слова: симплекс-метод, двойственный симплекс-метод, оптимальный план, двойственная задача, сопряженный базис, базисное решение, псевдоплан прямой задачи, оптимальное решение прямой задачи, метод полного исключения, разложение вектора, симплекс-таблица, симплекс, метод искусственных переменных, оптимальные значения двойственных переменных, базисными векторами
1.
 Двойственный симплекс – метод
Двойственный симплекс – методИспользование идей двойственности в сочетании с общей идеей симплекс-метода позволило разработать еще один метод решения задач ЛП — двойственный симплекс-метод. Впервые этот метод был предложен Лемке в 1954г. Решение задачи ЛП двойственным симплекс-методом сводится к отысканию оптимального плана прямой задачи последовательным переходом от одного базиса к другому.
Задача ЛП в канонической форме имеет вид:
| ( 1.1) |
при условиях
(
1. 2) 2) |
или .
Предположим, что и ранг матрицы А равен m.
Двойственная задача к задаче (1.1), (1.2) записывается так:
| ( 1.3) |
при условиях
| ( 1.4) |
Назовем сопряженным базисом, или базисом двойственной задачи такую систему из m линейно-независимых векторов матрицы ограничений прямой задачи , для которой базисное решение y соответствующей системы линейных уравнений вида
(
1. 5) 5) |
удовлетворяет всем ограничением (1.4).
Разложим вектор b по сопряженному базису
| ( 1.6) |
Решив систему (1.6), получим некоторое ее базисное решение , которое называется псевдопланом прямой задачи, так как для него может выполняться условие неотрицательности переменных xi0.
Таким образом, псевдоплан прямой задачи есть базисное решение относительно сопряженного базиса.
Как известно, оценки для небазисных векторов определяется в соответствии с
(
1. 7) 7) |
Псевдоплан можно найти и независимо от двойственной задачи. Пусть — произвольная система линейно-независимых векторов прямой задачи.
Выразим все небазисные векторы {Aj} через базисные:
| ( 1.8) |
| ( 1.9) |
Обозначим решение (1.9) через х0. Тогда можно дать дополнительное определение псевдоплана: n — мерный вектор X, для которого xi = xi0при , и xj=0 при , является псевдопланом тогда и только тогда, когда все
.
Доказательство. Векторы , линейно независимы.
Поэтому можно вычислить такой y={y1,y2,…,ym}, для которого
| ( 1.10) |
Тогда
С учетом (1.4) получим
| ( 1.11) |
что и требовалось доказать.
Рассмотрим некоторый сопряженный
базис и соответствующий ему псевдоплан.
Справедлив следующий признак оптимальности: если среди базисных компонентов псевдоплана Х нет отрицательных, то псевдоплан Х={xi0} оказывается оптимальным решением прямой задачи.
Доказательство. Имеет место такая цепочка равенств:
Равенство (1) следует из (1.2), равенство (2) получено переменой порядка суммирования, равенство (3) следует из (1.10).
Так как
| ( 1.12) |
то
(
1.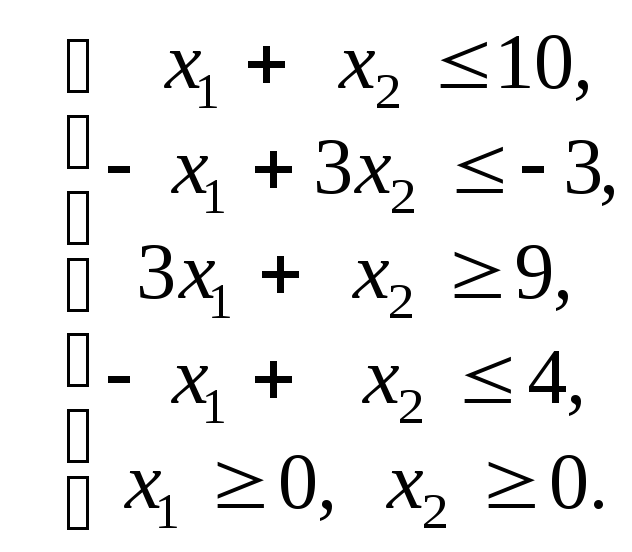 13) 13) |
Таким образом, , что и является признаком оптимальности планов х и у, если .
Этот признак является необходимым и достаточным условием оптимальности в случае невыродженности базисного решения y двойственной задачи .
- базисные компоненты для всех ;
- среди хi имеются отрицательные, причем для некоторого i: хi0<0, а все ;
- псевдоплан содержит отрицательные компоненты хi0<0,
но для каждой из них среди элементов {хij}, j=1,.
 ..,n,
имеются отрицательные. В первом случае, как следует из достаточного признака
оптимальности, псевдоплан х — оптимальное решение. Во втором случае
задача не разрешима. В третьем случае можно перейти к некоторому новому сопряженному
базису и, следовательно, к новому псевдоплану с меньшим значением L.
..,n,
имеются отрицательные. В первом случае, как следует из достаточного признака
оптимальности, псевдоплан х — оптимальное решение. Во втором случае
задача не разрешима. В третьем случае можно перейти к некоторому новому сопряженному
базису и, следовательно, к новому псевдоплану с меньшим значением L.
Дальше >>
< Лекция 5 || Лекция 6: 123 || Лекция 7 >
Двойственный симплекс метод онлайн
С помощю этого онлайн калькулятора можно решить задачу линейного программирования (ЛП) двойственным симплекс методом. Для решения задачи ЛП, введите данные задачи в ячейки нажмите на кнопку «Вычислить». Теоретическую часть смотрите ниже.
Очистить все ячейки?
Введите имя файла
Двойственный симплекс метод − теория, примеры и решения
- Содержание
- 1. Обоснование алгоритма двойственного симплекс метода
- 2. Алгоритм двойственного симплекс метода
1.
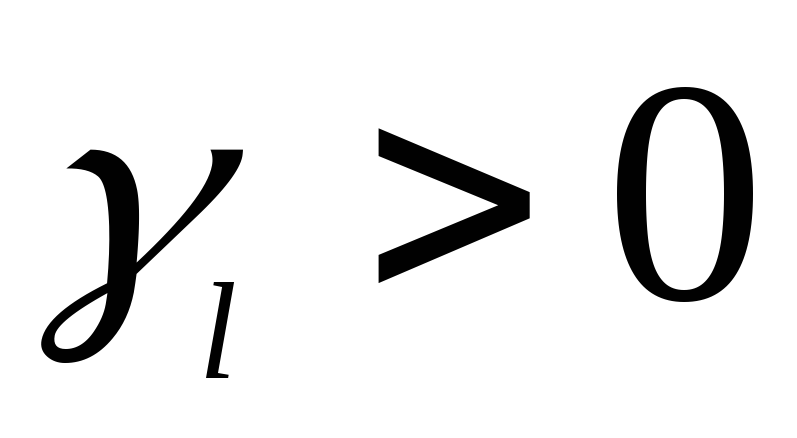 Обоснование алгоритма двойственного симплекс метода
Обоснование алгоритма двойственного симплекс методаДвойственный симплекс метод, как и симплекс метод используется для решения задачи линейного программирования (ЛП) в канонической форме (см. статью Формы записи задачи линейного программирования). При этом в системе уравнений должны быть m единичных линейно независимых векторов столбцов, где m количество уравнений. При решениии задачи ЛП обычным симплекс методом свободные члены ограничений предполагались неотрицательными, а при решении задачи ЛП двойственным симплекс методом, свободные члены могут быть любыми числами.
Рассмотрим следующую задачу линейного программирования:
Предполагая, что первые m векторы столбцы уравнений (1b) единичные линейно независимые векторы столбцы, запишем задачу ЛП:
Запишем задачу ЛП (2a)-(2c) в матричной форме:
где , , , , ,
Пусть среди координат вектора B имеются отрицательные числа. Очевидно, что является решением системы линейных уравнений (2b), но не является планом задачи ЛП (2a)−(2b), так как среди его компонент имеются отрицательные числа.
Для целевой функции (2a), учитывая (2b), сделаем следующие преобразования
где
ΔF − вектор-строка длины n-m.
Сделаем следующее обозначение:
или
где 0m− нулевой вектор-строка длины m, Δ − вектор-строка длины n.
Для того, чтобы двойственный симплекс метод работал, нужно, чтобы выполнялось сдедующее условие:
Определение 1. Решение системы линейных уравнений (2b) называется псевдопланом задачи (2a)-(2c), если Δ ≥ 0.
Заметим, что при Δ ≥ 0, CB является допустимым планом двойственной к (3) задачи ЛП:
Действительно. CB удовлетворяет системе линейных неравенств (9) и первые m неравенства в (9) удовлетворяются как равенства (поскольку первые m координат вектор-строки Δ нулевые). Другими словами CB является вершиной выпуклого многогранного множества (9). Целевая функция в этой точке равна:
Из вершины \(\small C_B \) нужно передвигатся по одной из m ребер так, чтобы новая точка осталось в допустимой области (9) и целевая функция (8) уменьшалась. Параметрическое равнение прямой, по которой нужно передвигаться имеет следующий вид:
Параметрическое равнение прямой, по которой нужно передвигаться имеет следующий вид:
где t − параметр, \( \small e_p \)− направляющий вектор прямой, \( \small e_p \)− один из единичных векторов-строк единичной матрицы:
где E − матрица порядка m×m
Подставим (10) в (8):
Посмотрев правую часть равенства (12) видим, что для того, чтобы целевая функция \( \small YB \) уменьшилась нужно, чтобы \( \small B_p \lt 0,\;t \gt 0.\) То есть выбираем строку p, в котором свободный член отрицательное число.
Подставим (10) в (9):
где \( \small A_p \)− p-я строка матрицы A.
Решим (13) относительно t:
где \( \small a_{pj} \) −\( \small j \)-ый элемент вектора строки \( \small A_p \).
Из (14) и (15) находим нижнюю и верхнюю границы параметра :
Нас интересует верхняя граница параметра t так как нам нужно максимально уменьшить целевую функцию (8). При этом новый план остается в допустимой области задачи (8)- (9), т. е. удовлетворяется условие (7). Обозначим через q индекс j, при котором достигается минимум в (17). Строка с номером q входит в базис задачи (8)-(9) или, что то же самое столбец q входит в базис в задаче (2a)-(2c). Для столбца q делается шаг Жордана-Гаусса, учитывая, что ведущим элементом является \( \small a_{pq} \).
е. удовлетворяется условие (7). Обозначим через q индекс j, при котором достигается минимум в (17). Строка с номером q входит в базис задачи (8)-(9) или, что то же самое столбец q входит в базис в задаче (2a)-(2c). Для столбца q делается шаг Жордана-Гаусса, учитывая, что ведущим элементом является \( \small a_{pq} \).
Подставляя найденный \( \small t_{верх} \) в (10) находим новый план двойственной задачи (8)-(9). Отметим, что если при всех , то параметр t не имеет ограничение сверху и может быть увеличен бесконечно. Тогда целевая функция задачи (8)-(9) будет неограничен снизу и задача не будет иметь решение. Соответственно, в этом случае, допустимая область исходной задачи пуста.
Мы доказали следующие две теоремы:
Теорема 1. Если в псевдоплане есть хотя бы одно отрицательное число \(\small b_i \lt 0 \) такое, что все \(\small a_{ij}\ge 0 \;\;(j=\overline{1,n})\), то задача (2a)-(2c) вообще не имеет решения.
Теорема 2. Если в псевдоплане имеются отрицательные числа \(\small b_i \lt 0 \) такие, что для любого из них существуют числа \(\small a_{ij}\lt 0 \;\;(j=\overline{1,n})\), то можно перейти к новому псевдоплану, при котором значение целевой функции задачи (8)-(9) не увеличится.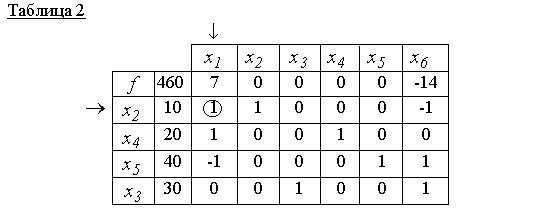
Вышеизложенные соображения и теоремы дают основание для построения алгоритма двойственного симплекс метода.
2. Алгоритм двойственного симплекс метода
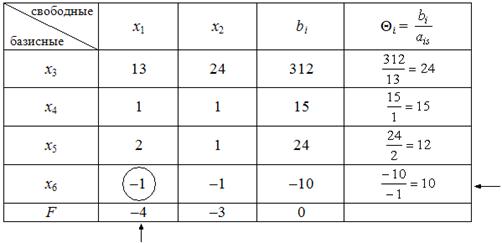
Пусть псевдоплан задачи ЛП (2a)-(2c). На основе исходных данных составляют симплекс-таблицу:
Пусть в этой таблице некоторые элементы вектора-столбца B отрицательные числа. Если таких чисел нет, то в симплекс таблице, в столбце «Базис» записаны индексы оптимального плана, а в столбце B − соответственные координаты плана (отметим, что целевая (последняя) строка таблицы неотрицательна, т.е. должна выполняться условие (7)). Если в столбце B есть отрицательные числа, то переходим от одной симплекс таблицы к другой пока все отрицательные числа вектора B не станут неотрицательными. При этом преобразования с таблицей должны выпоняться так, чтобы все элементы последней строки таблицы оставались неотрицательными т.е. выполнялось условие (7).
После составления симплекс таблицы проверяют, имеются ли отрицательные числа в столбце B. Если таких нет, то найден оптимальный план, а если такие есть, выбирается самый большой по модулю отрицательный элемент (например элемент с индексом p). Тогда из базиса выходит переменная \(\small x_{p} \). Чтобы определить, какой вектор следует ввести в базис, вычисляем
Если таких нет, то найден оптимальный план, а если такие есть, выбирается самый большой по модулю отрицательный элемент (например элемент с индексом p). Тогда из базиса выходит переменная \(\small x_{p} \). Чтобы определить, какой вектор следует ввести в базис, вычисляем
Пусть минимальное значение принимается при j=q. Тогда в базис входит переменная \(\small x_{q} \). Далее производится шаг Жордана-Гаусса для столбца q, учитывая, что ведущим элементом является \(\small a_{pq} \). Итерационный процесс заканчивается тогда, когда в столбце B больше нет отрицательных чисел. В этом случае получен оптимальный план. Если на каком-то этапе итерационного процесса в столбце B стоит отрицательное число, а среди остальных элементов этой строки нет отрицательных чисел, то задача не имеет решения.
Таким образом алгоритм решения задачи ЛП двойственным симплекс методом содержит следующие шаги:
1. Находят псевдоплан задачи.
2. Проверяют псевдоплан на оптимальность. Если псевдоплан не содержит отрицательных чисел, то найдено оптимальное решение. В противном случае либо устанавливают неразрешимость задачи, либо переходят к другому псевдоплану.
Если псевдоплан не содержит отрицательных чисел, то найдено оптимальное решение. В противном случае либо устанавливают неразрешимость задачи, либо переходят к другому псевдоплану.
3. Находят наибольшую по абсолютной величине отрицательный элемент столбца B. Фиксируют индекс этой строки p. Находят наименьшую по абсолютной величине отношения элементов целевой (последней) строки к элементам разрешающей строки p. Пусть минимальное значение принимается при j=q.
4. Делают шаг Жордана-Гаусса для столбца q, учитывая, что разрешающим (ведущим) элементом является \( a_{pq} \). Находят новый псевдоплан и переходят к шагу 2.
Для просмотра примеров решения, введите данные на онлайн калькулятор выше и нажмите на кнопку «Вычислить». Калькулятор представит решение задачи ЛП двойственным симплекс методом подробно, по шагам. Для решения задачи линейного программирования обычным симплекс методом используйте калькулятор Симплекс метод онлайн.
[PDF] Двойной симплекс | Semantic Scholar
- DOI:10.
 1002/9780470400531.eorms0269
1002/9780470400531.eorms0269 - Идентификатор корпуса: 17438010
@inproceedings{Banciu2011DualS,
title={Двойной симплекс},
автор={Михай Банчиу},
год = {2011}
} - Mihai Banciu
- Опубликовано в 2011 г.
- Математика
Алгоритм двойного симплекса является привлекательной альтернативой в качестве метода решения задач линейного программирования. Поскольку добавление новых ограничений к проблеме обычно нарушает первичную выполнимость, но не двойную выполнимость, двойной симплекс может быть развернут для быстрой повторной оптимизации без необходимости поиска новых первичных основных допустимых решений. Это особенно полезно в целочисленном программировании, где использование методов секущей плоскости требует введения новых ограничений в различных…
Просмотр через Publisher
columbia.eduПравило ценообразования с положительным преимуществом для двойного симплекса
- J.
 Omer, Mehdi Towhidi, F. Soumis
Omer, Mehdi Towhidi, F. Soumis Математика
Comput. Опер. Рез.
- 2015
Инициализация простого для простой: обзор методов и тенденций
- Mengyu Huang, Yuxting Zhong, Ling Shi
Компьютерная наука
- 2021
. Этот опрос. в основном и двойном симплексе, соответственно, и предлагает несколько потенциальных будущих направлений того, как улучшить существующие методы инициализации с помощью передовых технологий обучения.
Интеллектуальное программирование для классификации ортогональных массивов
- D. Bulutoglu, K. J. Ryan
Математика
- 2015
Классифицирующие ортогонные массивы-это хорошо известный класс. отрицательные целые решения класса систем ограничений. Решено…
Нахождение группы симметрии ЛП с ограничениями-равенствами и ее применение к классификации ортогональных массивов
- Эндрю Дж.
 Гейер, Д. Булутоглу, К. Дж. Райан
Гейер, Д. Булутоглу, К. Дж. Райан Математика
Дискрет. Оптим.
- 2019
Использование декомпозиции Бендера для оптимального управления мощностью и маршрутизации в сотовых системах D2D с несколькими сегментами
В этом документе основное внимание уделяется поиску эффективных методов решения упрощенной версии основной подзадачи, которая отвечает за получение нижних границ для оптимальную целевую функцию и предлагает эталонную непересекающуюся схему, которая выполняет маршрутизацию и управление мощностью отдельно.
Оптимальное управление помехами, управление питанием и маршрутизация в сотовых системах D2D с несколькими сегментами
Разработан эффективный метод решения упрощенной версии основной подзадачи, который отвечает за формирование нижних границ оптимального значения целевой функции и эталонного подзадачи. -предложена оптимальная непересекающаяся схема для той же задачи, выполняющая маршрутизацию и управление мощностью отдельно.
Оптимальная политика кэширования контента с учетом выбора режима и предпочтений пользователя в режиме Overlay D2D Communications
В этой работе предлагается оптимальная политика кэширования контента для кэширования ценного контента с учетом как выбора режима, так и пользовательских предпочтений соседей, а также используется метод двойного симплекса для решения проблемы максимальной вероятности разгрузки D2D.
ПОКАЗАНЫ 1-10 ИЗ 29 ССЫЛОК
СОРТИРОВАТЬ ПОРелевантности Наиболее влиятельные документыНедавность
Обобщенный двухфазный симплексный алгоритм
- I. Maros
Информатика 90.18 Дж. Опер. Рез.
- 2003
Прогресс в двойном симплекс-методе для крупномасштабных задач ЛП: практические алгоритмы двойной фазы 1
Резюме Алгоритм двойного симплекса стал сильным соперником в решении крупномасштабных задач LP. Одной из ключевых проблем любого двойного симплексного алгоритма является получение двойного допустимого базиса в качестве отправной точки…
Прогресс в двойном симплексном алгоритме для решения крупномасштабных задач ЛП: методы быстрой и стабильной реализации
Математические алгоритмы, вычислительные методы и Представлены детали реализации, которые являются ключевыми факторами для двойного симплексного кода, чтобы сократить разрыв в производительности между исследовательскими кодами с открытым исходным кодом и коммерческими LP-системами.
Симплексные алгоритмы наибольшего фронта для линейного программирования
- Джон Дж. Х. Форрест, Д. Гольдфарб
Информатика
Матем. Программа.
- 1992
Мы представляем несколько новых симплекс-алгоритмов с наикрутым фронтом для решения задач линейного программирования, включая варианты как прямого, так и двойного симплекс-метода. Эти алгоритмы различаются в зависимости от…
Новый полиномиальный алгоритм линейного программирования
- Н. Кармаркар
Математика, информатика
STOC ’84
- 1984
Доказано, что для заданного многогранника P и строго внутренней точки a εP существует проективное преобразование пространства, которое отображает a toP′, a′, обладающий следующим свойством: отношение радиуса наименьшей сферы с центром a′, содержащей P′, к радиусу наибольшей сферы с центром a′, содержащейся в P′, равно O(n).
Двойственный метод решения задачи линейного программирования
- К.
 Э. Лемке
Э. Лемке Бизнес, Математика
- 1954
Многие задачи логистики могут быть сформулированы как задачи линейного программирования. Например, одной из таких задач является так называемая транспортная задача, связанная с получением…
Линейное программирование и сетевые потоки
- М. Базараа, Дж. Дж. Джарвис, Х. Шерали
Информатика
- 1977
Линейное программирование
Функция ∑n i=1 cixi известна как целевая функция, а m неравенств известны как ограничения; матрица коэффициентов линейной программы представляет собой матрицу A размером m × n, элементами которой являются aji.
Линейное программирование и расширения
- Ричард Дж. Коппинс, Неса Л’аббе Ву
Бизнес, математика
- 1981
Формулировка навыков для решения математических задач линейной модели, применение детерминированных программ и обширный анализ чувствительности, чтобы ответить на вопросы «что, если».
НАСКОЛЬКО ХОРОШ АЛГОРИТМ СИМПЛЕКС
- В. Клее, Г. Минти
Информатика
- 1970
линейные программы не являются «хорошим алгоритмом» в смысле Дж. Эдмондса.
Методы первичного и двойного симплекса
Моя статья о линейном программировании является обязательным условием. Для второй части (двойственного симплекса и вырождения) моя статья о двойственности в линейном программировании является обязательным условием.
Линейные программы имеют удивительную структуру. Симплексные методы используют эту удивительную структуру для быстрого поиска оптимума. Благодаря этому теперь можно решать задачи с миллионами переменных, а значит, решать чрезвычайно сложные промышленные задачи. Вот почему симплексные методы стали ключевыми в нашем мире сегодня.
Почему вы используете множественное число, когда говорите о симплексных методах?
Правильно спрашиваешь. На самом деле существует только один симплекс-метод, введенный американским математиком Джорджем Данцигом сразу после Второй мировой войны. Однако были введены варианты, в основном метод двойного симплекса, который я представлю позже в этой статье. Сначала рассмотрим симплексный метод.
Однако были введены варианты, в основном метод двойного симплекса, который я представлю позже в этой статье. Сначала рассмотрим симплексный метод.
Рассмотрим проблему умного грабителя, которую я описал в своей статье по линейному программированию, то есть мы можем украсть купюры или золото, но общий объем украденного ограничен, как и общий вес украденного. Вот рисунок допустимой области.
Симплекс-метод
Напомним, что в линейной программе обязательно есть крайняя точка, являющаяся оптимумом.
Итак, мы могли бы просто перечислить все крайние точки и выбрать лучшую…
Есть две проблемы с перечислением всех крайних точек. Во-первых, их может быть очень много, особенно при рассмотрении задач с миллионами переменных и сотнями тысяч ограничений. Во-вторых, найти крайнюю точку может быть довольно сложно, так как это требует решения системы со всеми ограничениями, которые могут не привести к допустимому решению. Короче говоря, перечисление всех крайних точек — плохая идея.
Что делает симплекс-метод, так это движется от экстремальных точек к строго лучшим экстремальным точкам до тех пор, пока не будет найдена оптимальная экстремальная точка. Эта простая идея считается одним из главных прорывов 20-го века в вычислительной технике, по крайней мере, согласно журналу Computing in Science and Engineering !
Визуально это не кажется слишком сложным, но как вычисляются крайние точки?
Любая крайняя точка является пересечением достаточного количества граней многогранника. Сколько лиц? Столько, сколько размерность допустимого множества. Давайте позвоним n это измерение. Будьте осторожны, если вы читаете другие статьи о линейном программировании, и могут относиться к чему-то другому, например, к количеству переменных.
Теперь заметим, что грани многогранника являются ограничениями. Таким образом, экстремальной точкой является пересечение n ограничений. В нашем случае допустимое множество имеет размерность 2, поэтому любая крайняя точка является пересечением как минимум двух ограничений.
О, я понял. Мы можем описать каждую крайнюю точку набором из n ограничения находятся на пересечении, верно?
Почти. Определим базу ограничений как набор n ограничений.
База ограничений — это концепция, которую я придумал, и поэтому она не является обычной. Линейные программисты обычно говорят о «базе», то есть наборе переменных, не соответствующих ограничениям n . Очевидно, мы можем одинаково говорить о базе или базе ограничений, но я предпочитаю использовать базу ограничений, которая более наглядна.
Может показаться, что базы ограничений могут эквивалентно описывать экстремальные точки. К сожалению, связь между базами ограничений и крайними точками не так проста по двум причинам. Во-первых, база ограничений не обязательно описывает крайнюю точку. Во-первых, два ограничения могут полностью совпадать или быть параллельными, а пересечение и ограничений может быть пустым или бесконечным. Это редкость и с этим можно справиться. Но, что более важно и чаще, пересечение может быть точкой за пределами допустимого множества (как, например, пересечение красного и желтого ограничений в нашем примере). Такие базы ограничений называются недопустимыми базами ограничений.
Но, что более важно и чаще, пересечение может быть точкой за пределами допустимого множества (как, например, пересечение красного и желтого ограничений в нашем примере). Такие базы ограничений называются недопустимыми базами ограничений.
Еще одна вещь, которая может случиться, это то, что крайняя точка может быть описана несколькими базами ограничений. На самом деле возможно, что более n ограничений пересекаются в крайней точке. В этом случае любая база ограничений, описывающая эту вырожденную точку, называется вырожденной базой ограничений.
Тем не менее, несмотря на эти значения по умолчанию, мы используем базы ограничений для описания экстремальных точек. Теперь я повторю то, что сказал ранее о симплексном методе, но прямо сейчас буду использовать базы ограничений. В любой крайней точке симплекс-метод ищет следующую допустимую базу ограничений для посещения, которая строго лучше, чем текущая база ограничений. Для этого он ищет возможное направление, в котором он может двигаться, чтобы достичь следующей крайней точки через ребро многогранника. Это направление описывается ограничением, которое оно выведет из базы ограничений. База ограничений без одного ограничения дает линию, по которой следует следовать, ограниченную нашей текущей крайней точкой. По мере того, как мы идем вдоль линии, мы в конце концов достигаем нового ограничения, которое войдет в базу ограничений. Это определяет новую возможную крайнюю точку.
Это направление описывается ограничением, которое оно выведет из базы ограничений. База ограничений без одного ограничения дает линию, по которой следует следовать, ограниченную нашей текущей крайней точкой. По мере того, как мы идем вдоль линии, мы в конце концов достигаем нового ограничения, которое войдет в базу ограничений. Это определяет новую возможную крайнюю точку.
Опять же, люди обычно используют основания для описания симплекса. Эквивалентно то, что мы здесь делаем, — это берем переменную в базу, так как в конечном итоге мы находим переменную, которая выходит из базы. Я нахожу это описание трудным для понимания, поэтому я его не использовал.
Есть еще кое-что особенно интересное в этом методе. Хотя вычисление экстремальной точки с учетом ее базы ограничений может быть затруднено для больших размерностей (для этого требуется обращение матрицы n x n ), переход от одной крайней точки к соседней крайней точке можно осуществить очень быстро. Это одна из причин, почему симплекс-метод очень эффективен.
Но как узнать, улучшит ли направление целевую функцию?
Он узнает, глядя на снижение стоимости, связанной с направлением. Приведенная стоимость показывает, насколько целевая функция улучшится на один шаг в заданном направлении. Его можно вычислить, выполняя простые операции над постоянными параметрами линейной программы или рассматривая двойственные переменные. Я не буду вдаваться в вычисления приведенных затрат, так как было бы гораздо интереснее, если бы я рассказал об этих двойных переменных. Узнайте больше, прочитав мою статью о двойственности в линейном программировании.
На следующем рисунке показано, что будет делать симплекс-метод в нашем случае:
Вот способ визуализации симплекс-метода. Представьте, что вы держите в руках многогранник. Это ваш допустимый набор. Добавьте трубы на каждом краю. Эти трубы соединяют крайние точки многогранника. Теперь выберите наклон многогранника. Этот наклон представляет собой целевую функцию: горизонтальная плоскость должна быть набором уровня, а вертикальная должна быть градиентом (не обращайте внимания на это слово, если вы не знаете, что оно означает). Теперь симплекс выбирает первую крайнюю точку и вводит в нее каплю воды. Тогда симплекс будет выбирать путь капли воды (при условии, что она никогда не делится) до достижения нижней точки многогранника, которая и будет оптимальной точкой.
Теперь симплекс выбирает первую крайнюю точку и вводит в нее каплю воды. Тогда симплекс будет выбирать путь капли воды (при условии, что она никогда не делится) до достижения нижней точки многогранника, которая и будет оптимальной точкой.
Вы говорили о начальной крайней точке. Как мы можем выбрать его?
Как вы понимаете, выбор хорошей начальной точки крайне важен для скорости алгоритма. Лучше иметь один, близкий к оптимальному. Однако это трудная проблема. На самом деле, найти даже одну крайнюю точку сложно. Обычно мы вводим другую программу для решения этой проблемы: минимизация недопустимости решений. В этой программе под названием Фаза I возможно любое решение, и что особенно замечательно, программа является линейной программой… поэтому ее можно решить симплексным методом!
Симплексный метод стал известен и широко использовался, поскольку он позволял решать задачи с миллионами переменных и сотнями тысяч ограничений за разумное время. Однако в случаях вырождения возникают проблемы: возможно, что направление приведенной стоимости указывает за пределы многогранника (и это действительно очень часто происходит при использовании генерации столбцов).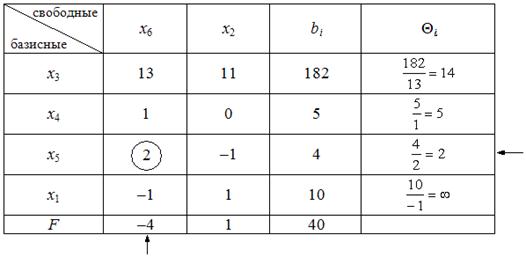 Трудно предугадать, будет ли направление указывать на многогранник или нет, и проверка всех направлений может занять довольно много времени.
Трудно предугадать, будет ли направление указывать на многогранник или нет, и проверка всех направлений может занять довольно много времени.
Кроме того, производительность симплексного метода ставится под сомнение из-за появления методов внутренних точек. Короче говоря, методы внутренних точек штрафуют точки на границе допустимого множества и медленно уменьшают эти штрафы, чтобы сходиться к оптимальной точке. Методы внутренних точек заслуживают отдельной статьи. Если вы их знаете, пожалуйста, напишите о них!
Почему вы написали о симплексном методе, если существует лучший метод?
Потому что исследования по симплекс-методам до сих пор очень продуктивны, и многие их варианты являются современными для решения конкретных задач. Давайте упомянем генерацию столбцов для планирования смен, маршрутизации транспортных средств или кластеризации. Этот метод особенно развит в компаниях и университетах Монреаля. Он используется с разложением Данцига-Вольфа. Короче говоря, идея состоит в том, чтобы рассматривать только те векторы, которые могут улучшить целевую функцию.
Стохастическое программирование позволяет очень эффективно решать программы с вероятностями благодаря L-образному методу, полученному из разложения Бендера. L-образный метод можно понимать как метод, который добавляет только релевантные ограничения, обнаруживая те, которые не выполняются, если они не удалены.
И последнее, но не менее важное: целочисленное линейное программирование очень эффективно при использовании симплекс-метода! Целочисленное линейное программирование позволяет моделировать очень и очень большой диапазон полей, которые включают, например, бинарные переменные. Примерами таких полей являются проблемы с назначением, цепочкой поставок и местоположением. Узнайте больше из моей статьи на эту тему!
Все эти методы соответствуют точным методам (что означает, что они находят действительный оптимум). Они могут быть слишком длинными. Вот почему было разработано множество приближенных методов, называемых эвристиками, для нахождения точки, близкой к оптимуму. Эти эвристики могут отличаться от симплексных.
Эти эвристики могут отличаться от симплексных.
Очевидно, что об этих вариантах и их применении можно многое сказать. Если вы можете объяснить, пожалуйста, напишите статью. Пожалуйста, сделайте его более полным и/или более понятным, чем страницы википедии! Кроме того, я мог забыть некоторые ключевые варианты симплексных методов. Пожалуйста, укажите их.
Почему в этих случаях симплексный метод лучше?
Главным образом потому, что когда мы немного модифицируем линейную программу, повторная оптимизация с использованием симплекс-метода может быть выполнена очень быстро, так как мы можем начать с крайней точки, которая будет близка к одной из новых крайних оптимальных точек. Для сравнения, метод внутренних точек не может использовать информацию из разрешения предыдущей линейной программы для решения слегка измененной линейной программы. Эта повторная оптимизация, вероятно, потребует использования двойного симплекса, который я сейчас представлю.
Я уверен, что если вы работаете над методами внутренних точек, вам есть что сказать! Пожалуйста, сделай!
Двойной симплекс
Моя статья о двойственности в линейном программировании является предпосылкой для следующего. Это хорошо помогает нам определить другой способ решения линейных программ, известный как двойной симплекс. Чтобы было о чем поговорить, предположим, что оптимальное решение — воровать только купюры. Это дает нам следующие первично-двойственные пространства.
Это хорошо помогает нам определить другой способ решения линейных программ, известный как двойной симплекс. Чтобы было о чем поговорить, предположим, что оптимальное решение — воровать только купюры. Это дает нам следующие первично-двойственные пространства.
Как видно из графиков, простые и двойные основания могут быть связаны. Оптимальные первично-двойственные решения — голубые точки. Давайте посмотрим на возможный путь симплексного алгоритма в простом и двойственном пространствах.
Можете ли вы объяснить, что происходит в двойном пространстве?
Черная точка — исходный базовый раствор. Напомним, что симплекс-метод завершится, когда мы достигнем двойственной допустимой базы. В основной черной точке основные приведенные затраты положительны как при выходе из желтых, так и зеленых основных ограничений. Это соответствует наличию двух нарушенных двойных желтых и зеленых ограничений. Нам нужно выбрать одну из основных базовых переменных с положительной приведенной стоимостью, что соответствует выбору одного из двух нарушенных двойных ограничений. В нашем случае мы выбрали зеленое ограничение.
В нашем случае мы выбрали зеленое ограничение.
Теперь, когда мы выбрали первичное зеленое ограничение для выхода (и, что эквивалентно, двойное зеленое ограничение для достижения), нам нужно решить, где остановиться. В основном пространстве мы должны следовать желтому ограничению, пока не достигнем базы. Эквивалентно мы выбираем другую допустимую базу с желтым ограничением. Это соответствует основной оранжевой точке, а не белой точке. Чему это соответствует в дуале? Включив зеленое ограничение в базу двойных ограничений, мы можем либо потерять двойное красное ограничение, либо двойное синее ограничение (одно из ограничений, которое уже было в базе двойных ограничений). Тот, который мы должны выбрать, чтобы он соответствовал основному основанию, — это тот, у которого наихудшее лучшее двойное значение (поскольку у нас есть проблема двойной минимизации, это наименьшее высшее двойное значение). В итоге нам нужно выбрать оранжевую точку.
Как следует интерпретировать этот выбор наихудшего лучшего двойного значения?
Мы должны выбрать наихудшее лучшее двойное значение, потому что нам нужно сохранить положительное двойное приведенное значение (если двойная программа является программой минимизации), чтобы, когда мы достигнем возможного двойного основания, мы наверняка были бы в оптимуме .
Каждый поворот в двойном пространстве должен выполняться так же, как мы только что сделали. Из двойной оранжевой точки только двойное желтое ограничение недействительно, поэтому мы должны ввести его в базу двойного ограничения, что приводит к выбору наихудшего двойного значения между желтой и розовой точками. Розовая точка имеет худшее двойное значение, поэтому мы поворачиваемся к ней.
Тогда из двойной розовой точки не выполняется только синее ограничение, поэтому мы перенесем его в базу двойного ограничения. Затем нам нужно выбрать между голубыми и белыми точками, но, поскольку белая точка имеет худшее двойственное значение, мы не можем пойти туда. Итак, мы перейдем к голубой точке. Голубая точка достижима, поэтому это двойной оптимум.
Это отличный способ понять симплекс. Но полезно ли это?
Ну, это полезно для нашего понимания первичного симплекса. Но это не все. Двойной симплекс очень полезен, если наша начальная точка недопустима, и в этом случае первичный симплекс бесполезен (и нам действительно нужно решить подзадачу, называемую фазой I, чтобы найти допустимую первичную точку).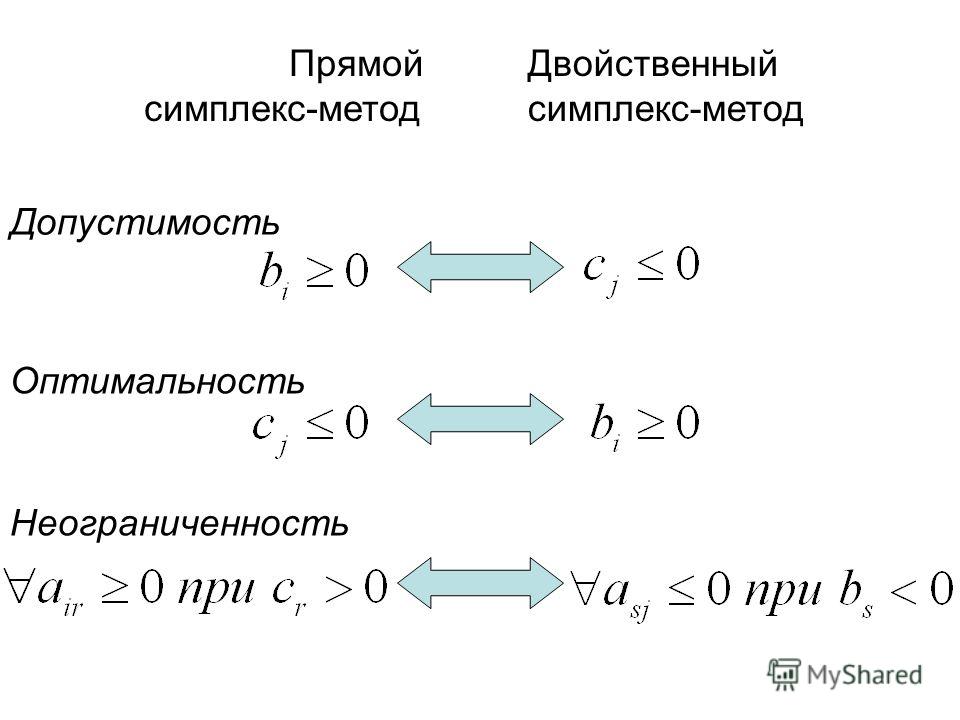 Тем не менее, наличие начальной невыполнимой точки очень часто происходит в случае целочисленного программирования или стохастического программирования с использованием декомпозиции Бендера. В обоих случаях мы фактически добавляем к исходной линейной программе новые ограничения, которые делают нашу текущую базу недопустимой. Поэтому мы можем применить двойной симплекс для повторной оптимизации. Более того, двойной симплекс будет работать очень быстро, так как начальная база, которая обычно является оптимальной без новых ограничений, скорее всего, будет близка к новому оптимуму.
Тем не менее, наличие начальной невыполнимой точки очень часто происходит в случае целочисленного программирования или стохастического программирования с использованием декомпозиции Бендера. В обоих случаях мы фактически добавляем к исходной линейной программе новые ограничения, которые делают нашу текущую базу недопустимой. Поэтому мы можем применить двойной симплекс для повторной оптимизации. Более того, двойной симплекс будет работать очень быстро, так как начальная база, которая обычно является оптимальной без новых ограничений, скорее всего, будет близка к новому оптимуму.
Двойной симплекс на самом деле является причиной того, что варианты симплекс-метода работают лучше, чем метод внутренней точки, на нескольких важных классах задач.
Я действительно не знаю, что было сделано с методами внутренних точек для повторной оптимизации. Если вы знаете, пожалуйста, сообщите нам.
Вырождение
Как и в случае простого симплекса, двойственный симплекс хорошо работает в случае невырождения. Однако, если первичный симплекс достигает вырожденной точки, ему может быть очень трудно выбраться из нее из-за множества оснований, которые могут представлять вырожденную точку.
Однако, если первичный симплекс достигает вырожденной точки, ему может быть очень трудно выбраться из нее из-за множества оснований, которые могут представлять вырожденную точку.
Чему это соответствует с двойной точки зрения?
Давайте нарисуем это, чтобы найти ответ.
Как и в моей статье о двойственности, мы переместили основное синее ограничение, чтобы создать основное вырожденное решение. В результате основная зеленая точка на самом деле представляет собой слияние основных оранжевых, белых и розовых точек. Тем не менее, перемещение основного ограничения не влияет на двойные ограничения. Однако это изменяет двойную целевую функцию, поэтому кривые уровня искривляются.
Поскольку оранжевая, белая и розовая первичная основа соответствуют одной и той же точке, они имеют одинаковое объективное значение, что означает, что двойные оранжевые, белые и розовые точки находятся на одной кривой двойного уровня. Вырожденная первичная точка на самом деле может быть связана с двойственным многогранником, определяемым выпуклой оболочкой трех двойных точек. Эта концепция двойственного многогранника очень важна для генерации столбцов.
Эта концепция двойственного многогранника очень важна для генерации столбцов.
В нашем случае все остается просто, потому что вырождения не так много, а размерность очень мала. Таким образом, путь, который мы использовали ранее, все еще действителен и фактически выбран. Более того, двойной многогранник, связанный с вырожденной точкой, очень прост, так как это линия с тремя основаниями. Однако в случае большего вырождения и более высокой размерности двойственный многогранник может быть огромным, и двойственный симплекс будет путешествовать по всему двойственному многограннику. Нам может понадобиться очень много времени, чтобы покинуть этот двойственный многогранник.
Важно отметить, что первичная вырожденная точка опоры (то есть модификация базы, которая не изменяет соответствующее решение) соответствует фактической двойной опоре, которая не улучшает целевое значение. В случаях более высокой размерности и более высокого вырождения количество таких поворотов может быть экспоненциальным.

 ..,n,
имеются отрицательные. В первом случае, как следует из достаточного признака
оптимальности, псевдоплан х — оптимальное решение. Во втором случае
задача не разрешима. В третьем случае можно перейти к некоторому новому сопряженному
базису и, следовательно, к новому псевдоплану с меньшим значением L.
..,n,
имеются отрицательные. В первом случае, как следует из достаточного признака
оптимальности, псевдоплан х — оптимальное решение. Во втором случае
задача не разрешима. В третьем случае можно перейти к некоторому новому сопряженному
базису и, следовательно, к новому псевдоплану с меньшим значением L. 1002/9780470400531.eorms0269
1002/9780470400531.eorms0269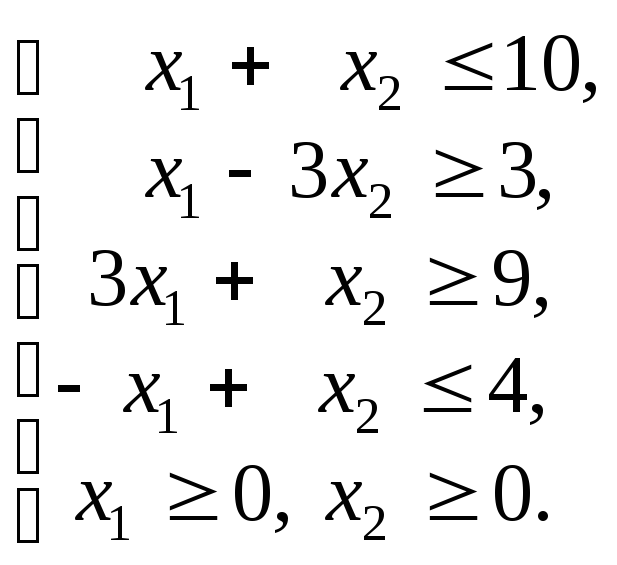 Omer, Mehdi Towhidi, F. Soumis
Omer, Mehdi Towhidi, F. Soumis Гейер, Д. Булутоглу, К. Дж. Райан
Гейер, Д. Булутоглу, К. Дж. Райан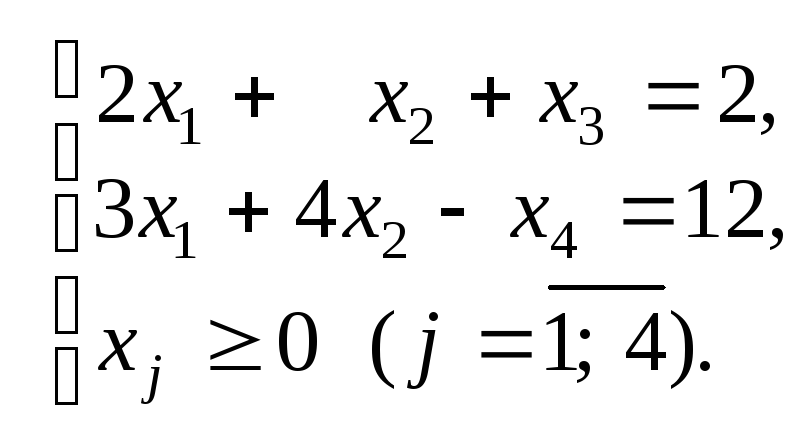 Э. Лемке
Э. Лемке