Вершина геометрия: Вершина (геометрия)

Вершина (геометрия)

Вершина — точка, в которой две кривые, две прямые либо два ребра сходятся. Из этого определения следует, что точка, в которой сходятся два луча, образуя угол, является вершиной, а также ею являются угловые точки многоугольников и многогранников.

Определение

Вершина угла

Вершина угла — это точка, откуда берут начало два луча; где сходятся два отрезка; где две прямые пересекаются; где любая комбинация лучей, отрезков и прямых, образующих две (прямолинейные) «стороны», которые сходятся в одной точке.

Вершина многоугольника многогранника

Вершина — это угловая точка многоугольника или многогранника (любой размерности), иначе говоря его 0-мерная граней.

В многоугольнике вершина называется «выпуклой», если внутренний угол многоугольника меньше π радиан (180° — два прямых угла). В противном случае вершина называется «вогнутой».

Более обще, вершина многогранника является выпуклой, если пересечение многогранника с достаточно малой сферой, имеющей вершину в качестве центра, представляет собой выпуклую фигуру; в противном же случае вершина является вогнутой.

Вершины многогранника связаны с вершинами графа, поскольку многогранника является графом, вершины которого соответствуют вершинам многогранника, а следовательно, граф многогранника можно рассматривать как одномерный симплициальный комплекс, вершинами которого служат вершины графа. Однако, в теории графов вершины могут иметь менее двух инцидентных рёбер, что обычно не разрешается для вершин геометрических. Также имеется связь между геометрическими вершинами и вершинами кривой, точками экстремумов её кривизны — вершины многоугольника в некотором смысле являются точками бесконечной кривизны, и, если многоугольник приблизить гладкой кривой, точки экстремальной кривизны будут лежать вблизи вершин многоугольника. Однако, приближение многоугольника с помощью гладкой кривой даёт дополнительные вершины в точках минимальной кривизны.

Вершины плоских мозаик

Вершина плоской мозаики (замощения) — это точка, где встречаются три и более плиток мозаики, но не только: плитки замощения также являются многоугольниками, а вершины мозаики являются вершинами этих плиток. Более обще, замощение можно рассматривать как вид топологического CW-комплекса. Вершины других видов комплексов, таких как симплициальные, — это грани нулевой размерности.

Основная вершина

Вершина x i {displaystyle x_{i}} простого многоугольника P {displaystyle P} является основной вершиной, если диагональ [ x i − 1 , x i + 1 ] {displaystyle [x_{i-1},x_{i+1}]} пересекает границы P {displaystyle P} только в точках x i − 1 {displaystyle x_{i-1}} и x i + 1 {displaystyle x_{i+1}} . Существует два типа основных вершин: «уши» и «рты» (см. ниже).

«Уши»

Основная вершина x i {displaystyle x_{i}} простого многоугольника P {displaystyle P} называется «ухом», если диагональ [ x i − 1 , x i + 1 ] {displaystyle [x_{i-1},x_{i+1}]} лежит полностью в P {displaystyle P} . (см. также выпуклый многоугольник)

«Рты»

Основная вершина x i {displaystyle x_{i}} простого многоугольника P {displaystyle P} называется «ртом», если диагональ [ x i − 1 , x i + 1 ] {displaystyle [x_{i-1},x_{i+1}]} лежит вне P {displaystyle P} .

Число вершин многогранника

Любая поверхность трёхмерного выпуклого многогранника имеет эйлерову характеристику:

V − E + F = 2 , {displaystyle V-E+F=2,}

где V {displaystyle V} — число вершин, E {displaystyle E} — число рёбер, а F {displaystyle F} — число граней. Это равенство известно как уравнение Эйлера. К примеру, куб имеет 12 рёбер и 6 граней, а потому — 8 вершин: 8 − 12 + 6 = 2 {displaystyle 8-12+6=2} .

Вершины в компьютерной графике

В компьютерной графике объекты часто представляются как триангулированные многогранники, в которых вершинам объекта сопоставляются не только три пространственные координаты, но и другая необходимая для правильного построения изображения объекта графическая информация, такая как цвет, отражательная способность, текстура, нормали вершин. Эти свойства используются при построении изображения с помощью вершинного шейдера, части обработчика вершин.

Работа с вершинами представлений—Справка | Документация

Доступно с лицензией Standard или Advanced.

• Вершины представления
• Кривые Безье и их вершины
• Контрольные точки представлений

Вершины определяют форму и местоположение линейных и полигональных представлений пространственных объектов. Вы можете настроить форму представлений линейных и полигональных объектов, перемещая, добавляя и удаляя вершины. Вы можете сгладить форму представлений объектов, конвертировав вершины в вершины Безье. Вы можете контролировать стадии некоторых геометрических эффектов и стилей размещения маркеров, конвертируя вершины в контрольные точки представления.

Вершины представления

Вершины можно выбрать, используя инструментЧастичный выбор (Direct Select) или инструмент Частичный выбор лассо (Lasso Direct Select) на панели инструментов Представления (Representation) во время сеанса редактирования. Появится маленький квадратик рядом с инструментом Частичный выбор (Direct Select) указатель (), когда курсор находится над геометрией доступных для выбора представлений объекта. С инструментом Частичный выбор (Direct select) щелкните на одной из вершин или растяните прямоугольник над несколькими вершинами, чтобы выбрать их вместе. Вы также можете растянуть произвольную форму вокруг вершин с помощью инструментаЧастичный выбор лассо (Lasso Direct Select) . Вершины могут быть одновременно выбраны из нескольких объектов. Если вы щелкните на линейном участке между двумя вершинами с помощью инструментаЧастичный выбор (Direct Select) обе вершины будут выделены.

При выборе объекта целиком с помощью инструмента Выбрать (Select) автоматически выберутся все вершины. Если вы переключитесь на инструмент Частичный выбор (Direct Select) после выбора объектов с помощью инструментаВыбрать (Select) , все вершины будут выбраны, и пропадет ограничивающий прямоугольник выборки исчезнет. Вы можете отменить выбор вершин, удерживая клавишу SHIFT и нажимая на них при активном инструменте Частичный выбор (Direct Select) .

Выбранные вершины выделяются заливкой, невыбранные отображаются «пустыми» значками. Только выбранные вершины будут перемещены, когда вы перетаскиваете курсор при активном инструменте Частичный выбор (Direct Select) .

Как перемещать вершины представления

1. Выберите одно или несколько представлений, используя инструмент Частичный выбор (Direct Select) или инструмент Частичный выбор лассо (Lasso Direct Select) на панели инструментов Представления (Representation). Выбранные вершины будут отображены в виде квадратиков с заливкой.
2. Наведите указатель на выбранную вершину при активном инструменте Частичный выбор (Direct Select) . Курсор примет форму стрелки с четырьмя направлениями .
3. Щелкните и переместите курсор, чтобы переместить выбранные узлы на новое место.

Как вставлять вершины представлений

1. В сеансе редактирования выберите одно или несколько представлений с помощью любого из инструментов выборки представлений.
2. Щелкните на инструменте Вставить вершину (Add Vertex) на панели инструментов Представления (Representation).
3. Щелкните в любом месте подсвеченной геометрии представления пространственного объекта, чтобы добавить новую вершину.

Как удалять вершины представления

1. В сеансе редактирования выберите одно или несколько представлений с помощью любого из инструментов выборки представлений.
2. Щелкните на инструменте Удалить вершину (Delete Vertex) из инструмента Вставить вершину (Add Vertex) в палитре панели инструментов Представления (Representation).
3. Щелкните на вершине, чтобы удалить ее.

Подсказка:

• Для определения линии необходимо как минимум две вершины, поэтому вы не сможете удалить вершины на линии, состоящей всего из двух вершин. Для определения полигона необходимо как минимум три вершины, соответственно, удалить вершину в полигоне, состоящем всего из трех вершин, будет невозможно.

Кривые Безье и их вершины

Параметрические кривые представляют собой сглаженные линии связи между двумя вершинами. Форма кривой определяется положением обеих вершин и положением двух дополнительных точек на концах направляющей Безье, которая выходит из каждой вершины.

Примеры кривой Безье

Существующему сегменту линии можно добавить возможности кривой Безье, конвертировав его конечные вершины в вершины Безье с помощью инструмента Вставить Безье (Insert Bezier) . Формы кривых Безье можно изменить, перемещая вершины и направляющие Безье с помощью инструмента Частичный выбор (Direct Select) . Свойства Безье из сегмента линии можно удалить, нажав на вершины с инструментом Удалить Безье (Delete Bezier) , после чего они вновь станут обычными вершинами.

Конвертирование вершины представления в вершину Безье

1. В сеансе редактирования выберите одно или несколько представлений с помощью любого из инструментов выборки представлений.
2. Щелкните на инструменте Вставить Безье (Insert Bezier) из инструмента Вставить вершину (Add Vertex) в палитре панели инструментов Представления (Representation).
3. Щелкните и перетащите существующую вершину, чтобы разнести направляющие Безье от вершины в нужном направлении. Теперь эта вершина является вершиной Безье. Она может быть в дальнейшем отредактирована с помощью направляющих с активным инструментом Частичный выбор (Direct Select) .

Добавление вершины Безье

1. В сеансе редактирования выберите одно или несколько представлений с помощью любого из инструментов выборки представлений.
2. Использование инструмента Вставить Безье (Insert Bezier) из инструмента Вставить вершину (Add Vertex) на панели инструментов Представления (Representation) щелкните и перетащите подсвеченное представление объекта, чтобы разнести направляющие кривой Безье на необходимое расстояние под нужным углом.

Удаление вершины Безье

1. В сеансе редактирования выберите одно или несколько представлений с помощью любого из инструментов выборки представлений.
2. Использование инструмента Удалить Безье (Delete Bezier) из инструмента Вставить вершину (Add Vertex) на панели инструментов Представления (Representation) выберите любую вершину, чтобы удалить ее свойства Безье. На его месте появится стандартная вершина представления, а геометрия будет обновлена в соответствии с изменениями.

Редактирование кривой Безье

1. всеансе редактирования выберите вершины, используя инструмент Частичный выбор (Direct Select) или инструмент Частичный выбор лассо (Lasso Direct Select) на панели инструментов Представления (Representation). Направляющие вершин Безье появятся, когда вы их выберете.
2. Используя инструмент Частичный выбор (Direct select) , наведите курсор на конечную точку направляющей Безье и удерживайте, пока курсор не примет форму четырехнаправленной стрелки .
3. Щелкните и переместите указатель, чтобы изменить длину и угол направляющей Безье.

Контрольные точки представлений

Контрольные точки представления являются специальными вершинами, которые определяют последовательность геометрических эффектов и стилей размещения маркеров и, таким образом, управляют тем, как символы представлений применяются к линейным и полигональным пространственным объектам.

Геометрические эффекты, основанные на распределении, могут управляться контрольными точками . Контрольные точки определяют специальные участки на геометрии объекта, где узор должен быть применен определенным образом. Например, геометрический эффект пунктира может быть определен таким образом, что центр штриха пунктира будет попадать на каждую контрольную точку. Так, если вы поместите контрольные точки в острых углах, вы можете быть уверены, что если линия изменит свое направление, никакой неоднозначности не появится. Нарушения в порядке расположения элементов узора распределяются равномерно вдоль объекта, то есть визуальное воздействие на изменения определенного узора минимально.

Без контрольных точекС контрольными точками

Вместе с тем, контрольные точки используются для определения местоположения ограничителей в ключевых местах в стилях размещения маркеров. Например, стиль размещения маркеров может быть использован для размещения символов опор вдоль линии электропередачи. Очевидно, что опоры используются для поддержки линии, где она меняет свое направление, и условные обозначения должны это отразить. Контрольные точки, помещенные в стратегически важные области, такие как места изменения направления, могут принудительно разместить символ маркера (например, опор) вдоль условного обозначения.

Без контрольных точекС контрольными точками

Контрольные точки не могут существовать отдельно от вершин, потому что, по сути, они являются вершинами с специальными свойствами. Вы можете добавить поведение контрольной точки к существующей вершине вручную, используя инструмент Вставить контрольную точку (Insert Control Point) или удалите ее с помощью инструмента Удалить контрольную точку (Delete Control Point) . Вы можете добавить новую вершину с поведением контрольной точки, щелкнув на участке геометрии с активным инструментом Вставить контрольные точки (Insert Control Point). Контрольные точки, добавленные вручную, отличаются от стандартных вершин, показанных квадратиками, формой символа отображения в виде ромба.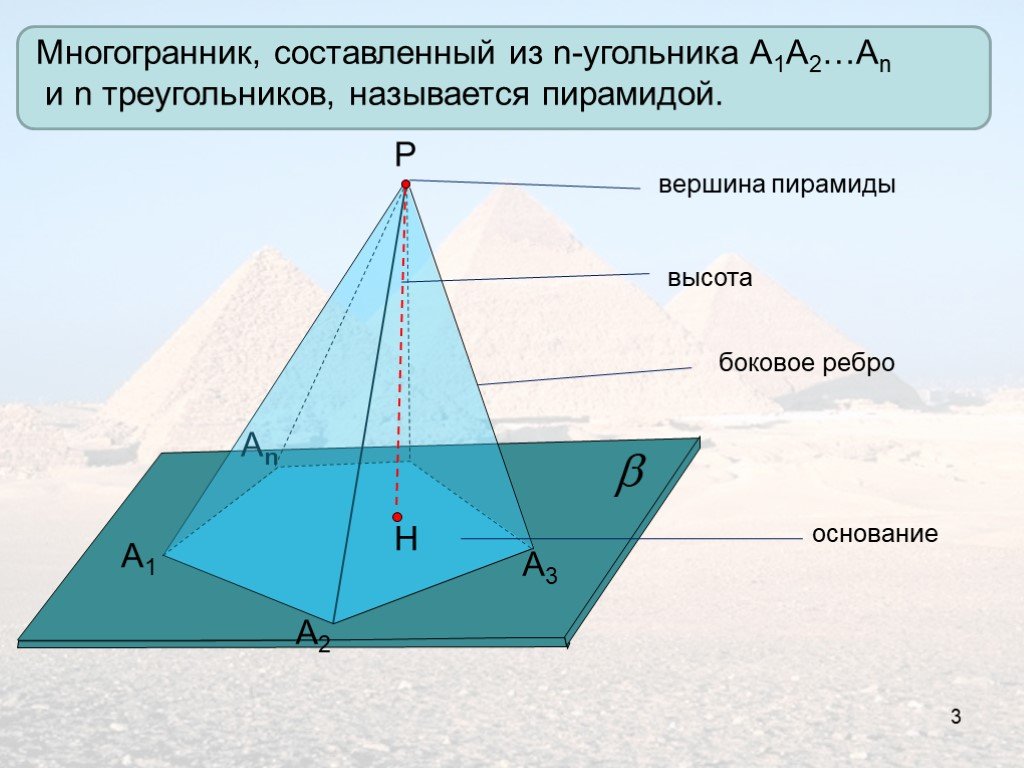 Их можно вручную удалить с помощью инструмента Удалить контрольные точки (Delete Control Point).

Подсказка:

Вы можете автоматически добавить контрольную точку к изменениям направления геометрии, основываясь на определенном угле с помощью геометрического эффекта Добавить контрольные точки (Add Control Points) или с использованием инструмента геообработки Установить контрольные точки представления по углу (Set Representation Control Point By Angle). Инструмент Установить контрольные точки представления в пересечениях (Set Representation Control Point At Intersect) создает контрольную точку представления в вершинах, общих для нескольких линейных или полигональных объектов.

Конвертирование вершины в контрольную точку

1. В сеансе редактирования выберите одно или несколько представлений с помощью любого из инструментов выборки представлений.
2. Использование инструмента Вставить контрольные точки (Insert Control Point) из инструмента Вставить вершину (Add Vertex) на панели инструментов Представления (Representation), щелкните вершину. Вершина превращается в контрольную точку представления и отображается с помощью ромба, вместо стандартного квадрата.

Добавление контрольных точек представления

1. В сеансе редактирования выберите одно или несколько представлений с помощью любого из инструментов выборки представлений.
2. Использование инструмента Вставить контрольные точки (Insert Control Point) из инструмента Вставить вершину (Add Vertex) на панели инструментов Представления (Representation) щелкните выбранное представление объекта для добавления контрольной точки.

Удаление контрольной точки представления

1. В сеансе редактирования выберите одно или несколько представлений с помощью любого из инструментов выборки представлений.
2. Использование инструмента Удалить контрольные точки (Delete Control Point) из инструмента Вставить вершину (Add Vertex) на панели инструментов Представления (Representation) выберите любую вершину, чтобы удалить поведение контрольной точки. На ее месте появится стандартная вершина, а условные обозначения представления обновятся в соответствии с изменениями.

Связанные разделы

Что такое Вертекс? Значение, определение, примеры, свойства, факты

Вершина — это точка на многоугольнике, где встречаются стороны или ребра объекта или где встречаются два луча или отрезка линии. Множественное число вершины — вершины.

История
Вершина является частью евклидовой геометрии, впервые опубликованной в книге о геометрии в конце 19 века. Понятие вершины лежит в основе объяснения многих передовых понятий геометрии.

Сегмент линии является частью линии. Луч — это отрезок, который мы можем продолжать бесконечно. Когда встречаются два отрезка или луча, они образуют угол. По определению, когда две линии встречаются, образуя угол, образуется вершина. Итак, мы можем сказать, что встреча двух отрезков или лучей образует вершину.

На приведенном выше рисунке показаны два сегмента луча, сходящиеся в одной точке и образующие вершину.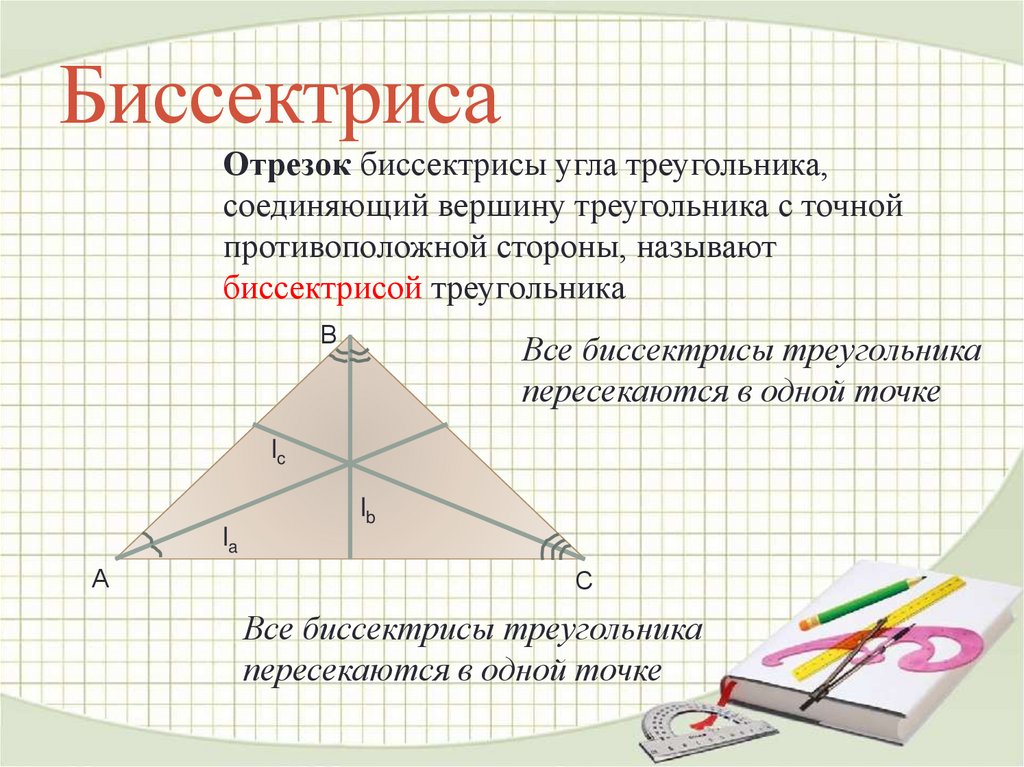

Двухмерная или двухмерная фигура — это фигура или форма, которую мы можем представить в двух измерениях или на бумаге. Некоторые двумерные формы включают круг, квадрат, прямоугольник и треугольник. Вершина 2D-фигуры — это точка пересечения двух сторон фигуры. Две стороны формы или фигуры встречаются, образуя угол, и таким образом формируется вершина.

На двухмерных рисунках выше буква V представляет вершины каждой фигуры. Квадрат и прямоугольник имеют по четыре вершины. У треугольника три вершины, а у окружности нет ни одной вершины.

Трехмерная или трехмерная фигура — это фигура или объект, представленный в трехмерном пространстве. Трехмерная фигура или твердое тело имеют все три атрибута, включая длину, ширину и высоту. Вершина трехмерной фигуры — это точка пересечения двух сторон фигуры. Несколько сторон и ребер могут пересекаться в одной точке трехмерной фигуры. Каждая такая точка пересечения образует вершину. Некоторые трехмерные формы включают кубы, прямоугольные параллелепипеды, пирамиды, сферы и цилиндры.

Приведенные выше фигуры представляют собой куб и октаэдр. У куба восемь вершин, а у октаэдра шесть вершин. Красные точки представляют собой вершины этих 3D-объектов.

Геометрия является важнейшей частью математики, которая составляет большую часть учебного плана для учащихся. Углубленное изучение геометрии возможно только при правильном понимании основ геометрии. Вершина — это одна из предварительных тем, составляющих основу геометрии. Помогите своим детям узнать о вершинах с помощью подробных материалов курса от SplashLearn. Увлекательные игры и интерактивные рабочие листы от SplashLearn обеспечивают достаточную практику для юных учащихся, чтобы освоить концепцию. Так что извлеките максимальную пользу из онлайн-обучения с эффективными ресурсами от SplashLearn!

1 Сколько вершин у окружности? 1 2 3 Правильный ответ: 0 Окружность не имеет вершин, так как в окружности нет ни углов, ни ребер. Правильный вариант д. 2 Сколько вершин у пятиугольника? 2 3 4 5 Правильный ответ: 5 Пятиугольник имеет пять вершин. Правильный вариант д. 3 Сколько вершин у квадрата? 2 4 6 8 Правильный ответ: 4 Квадрат имеет четыре вершины. Правильный вариант б.

Сколько вершин у конуса?

Конус имеет одну вершину. На конусе есть только одна точка, где его поверхности сходятся и образуют угол. Следовательно, в конусе образуется только одна вершина.

Сколько вершин у куба?

Куб имеет восемь вершин. Куб — это трехмерный объект с шестью гранями, двенадцатью ребрами и восемью вершинами.

Какие объекты не имеют вершины?

Любой объект без прямых ребер или углов, образованных ребрами, не имеет вершины. Примерами объектов без вершины являются круги, цилиндры и сферы.

Сколько вершин у тетраэдра?

Тетраэдр имеет четыре вершины. Он также имеет шесть ребер и четыре треугольных грани.

Вершины и диагонали — Концепция

Форма множественного числа вершины, вершины обычно являются пересечениями или углами на рисунках. В угле вершина — это место, где встречаются две линии, лучи или сегменты. Диагональ – это отрезок, концы которого являются вершинами. В многоугольнике вершина — это место, где встречаются два ребра или стороны. В многограннике вершина — это место, где сходятся три ребра.

вершина равнобедренный треугольник многоугольник диагональ конус пирамида призма

Слово, которое используется в Geometry — Vertex. Если у вас есть только один, это Vertex, если у вас есть более одного, если вы хотите сделать его множественным, это вершины. Таким образом, одна вершина, две вершины и еще одна вершина появляются во множестве разных областей.
Например, если мы говорим об углах; вершина является конечной точкой двух лучей. Итак, здесь точка b будет нашей вершиной, где лучи ba и лучи bc начинают формировать стороны этого угла.

А треугольники? Если у вас есть равнобедренный треугольник, у вас есть две стороны, которые, я думаю, я мог бы обозначить так, чтобы сторона была здесь, а сторона здесь, и этот угол, образованный двумя сторонами, называется вашим углом при вершине, поэтому я буду называть его своим углом при вершине. Таким образом, вершина также может относиться к равнобедренным треугольникам.
А как насчет других типов многоугольников? Ну, точка, где встречаются две стороны, которую я написал здесь синим цветом, так что вот эта точка, где пересекаются две стороны. Итак, у нас есть пять вершин-вершин в этом многоугольнике. Диагональ связана с вершиной, потому что диагональ — это отрезок, соединяющий любые две непоследовательные вершины. Что ж, последовательные вершины, если я посмотрю на эту вершину, ее последовательные вершины — это одна справа и одна слева от нее. Таким образом, диагональ из этой вершины соединила бы эти две непоследовательные вершины. Я также могу нарисовать одну в одной другой непоследовательной вершине. Вот как диагональ связана с вершиной.
Если мы говорим о трех измерениях, мы можем посмотреть на конус или пирамиду, и эта точка прямо здесь в конусе и точка в пирамиде также известна как вершина. Таким образом, вершина может применяться к трехмерным телам.
А куб? В кубе или прямоугольной призме любого типа есть точка, в которой пересекаются три или более ребер. Таким образом, ребра — это эти отрезки линии, где пересекаются две плоскости, поэтому вершина может быть прямо здесь, вот здесь, у вас будет этот куб, если я нарисую в остальной части его скрытые стороны и скрытые ребра, которые у вас будут.