Натуральный логарифм, функция ln x
Приведены основные свойства натурального логарифма, график, область определения, множество значений, основные формулы, производная, интеграл, разложение в степенной ряд и представление функции ln x посредством комплексных чисел.
Определение
- Натуральный логарифм
- – это функция y = ln x, обратная к экспоненте, x = e y, и являющаяся логарифмом по основанию числа е: ln x = loge x.
Натуральный логарифм широко используется в математике, поскольку его производная имеет наиболее простой вид: (ln x)′ = 1/x.
Исходя из определения, основанием натурального логарифма является число е:
е ≅ 2,718281828459045…;
.
График натурального логарифма ln x
График функции y = ln x.
График натурального логарифма (функции y = ln x) получается из графика экспоненты зеркальным отражением относительно прямой y = x.
Натуральный логарифм определен при положительных значениях переменной x. Он монотонно возрастает на своей области определения.
При x → 0 пределом натурального логарифма является минус бесконечность ( – ∞ ).
При x → + ∞ пределом натурального логарифма является плюс бесконечность ( + ∞ ). При больших x логарифм возрастает довольно медленно. Любая степенная функция xa с положительным показателем степени a растет быстрее логарифма.
Свойства натурального логарифма
Область определения, множество значений, экстремумы, возрастание, убывание
Натуральный логарифм является монотонно возрастающей функцией, поэтому экстремумов не имеет. Основные свойства натурального логарифма представлены в таблице.
| Область определения | 0 < x + ∞ |
| Область значений | – ∞ < y < + ∞ |
| Монотонность | монотонно возрастает |
| Нули, y = 0 | x = 1 |
| Точки пересечения с осью ординат, x = 0 | нет |
| + ∞ | |
| – ∞ |
Значения ln x
ln 1 = 0
Основные формулы натуральных логарифмов
Формулы, вытекающие из определения обратной функции:
Основное свойство логарифмов и его следствия
Формула замены основания
Любой логарифм можно выразить через натуральные логарифмы с помощью формулы замены основания:
Доказательства этих формул представлены в разделе «Логарифм».
Обратная функция
Обратной для натурального логарифма является экспонента.
Если , то
Если , то .
Производная ln x
Производная натурального логарифма:
.
Производная натурального логарифма от модуля x:
.
Производная n-го порядка:
.
Вывод формул > > >
Интеграл
Интеграл вычисляется интегрированием по частям:
.
Итак,
Выражения через комплексные числа
Рассмотрим функцию комплексной переменной z:
.
Выразим комплексную переменную z через модуль r и аргумент φ:
.
Используя свойства логарифма, имеем:
.
Или
.
Аргумент φ определен не однозначно. Если положить
, где n – целое,
то будет одним и тем же числом при различных n.
Поэтому натуральный логарифм, как функция от комплексного переменного, является не однозначной функцией.
Разложение в степенной ряд
При имеет место разложение:
Использованная литература:
И.
Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92 |
Производные экспоненциальной и логарифмической функций
Подход
к
C A L C U L U S
Содержание | Главная
14
Производная от ln x
Производная e с функциональным показателем
Производная от ln u ( x )
Общее силовое правило
В СИСТЕМЕ НАТУРАЛЬНЫХ ЛОГАРИФМОВ основанием является число, называемое е; это система, которую мы используем во всей теоретической работе.
(В следующем уроке мы увидим, что e приблизительно равно 2 . 718.) Система натуральных логарифмов отличается от системы десятичных логарифмов, в основе которой лежит 10 и которая используется в большинстве практических работ.
Мы обозначаем логарифмическую функцию с основанием e как «ln x ».
ln x = log e x .
y = ln x подразумевает e y = x .
Другими словами, эта логарифмическая функция —
у = пер х
— имеет обратную экспоненциальную функцию,
у = е х .
Вот обратные соотношения:
ln e x = x и e ln x = x .
А логарифм самого основания всегда 1:
лн е = 1.
(Тема 20 предварительного исчисления.)
Функция y = ln x является непрерывным и определяется для всех положительных значений x .
Оно будет подчиняться обычным законам логарифмов:
1 . ln ab = ln a + ln b .
| 2 . номер | а б |
3 . ln a n = n ln a .
(Тема 20 предварительного исчисления.)
Как и все правила алгебры, они подчиняются правилу симметрии.
Например,
н лн а = лн а н .
Производная от ln x
Теперь мы применим определение производной, чтобы доказать:
| д дх | л х | = | 1 х |
Предел в доказательстве будет иметь тот же вид.
Позже мы будем называть переменную x , а не v . А на следующем уроке, при замене переменной с на на , следует знакомое определение.
Вот коэффициент разности:
| по 2-му закону; | |||
| = | при умножении на x / x ; | |
| = | в соответствии с 3-м законом. | |
Теперь мы принимаем предел, поскольку ч приближается к 0.
| = |
| Ограничение не распространяется на | 1 х | , потому что ч это переменная |
| приближается к 0. | 1 х | – постоянный коэффициент. |
Теперь мы определим этот предел как основание натуральных логарифмов, число, которое мы будем называть e. (Этот предел указан выше, с v = ; когда 0, 0.)
Следовательно,
| = | ||
| = | ||
| = | ||
Что мы и хотели доказать.
Увидеть, что этот предел —
— то есть e существует, поскольку x приближается к 0, вот график
y имеет определенное значение, так как x приближается к 0. И в следующем уроке мы увидим, что это приблизительно 2,718.
Производная от e x
Сейчас мы докажем:
| д дх | е х | = e x |
«Производная от e x по отношению к x
равно e x .
С у = е x является обратным y = ln x , мы можем получить его производную следующим образом:
| у | = | е х | ||
| подразумевает | п у | = | ln e x | = x . |
Следовательно, взяв производную от обеих сторон относительно x и применив цепное правило к ln y :
| = | 1. | ||
| у’ | = | и . | |
| То есть | |||
| = | е х . | ||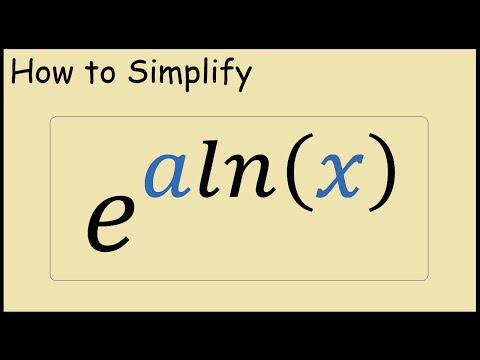
e x является собственной производной.
Что это значит? Это подразумевает значение экспоненциального роста. Ибо мы говорим, что количество растет «экспоненциально», когда оно растет в 9 раз.0919 скорость , что пропорционально его размеру. Чем он больше в любой момент времени, тем быстрее он растет в это время. Типичным примером является население. Чем больше будет индивидуумов, тем больше будет рождений и, следовательно, тем больше скорость изменения населения — число рождений в каждом году.
Все экспоненциальные функции имеют вид a x , где a — основание. Следовательно, сказать, что скорость роста пропорциональна его размеру, значит сказать, что производная a x пропорционально a x .
| д дх | а х | = тыс. лет назад x | , |
, где k — константа пропорциональности. (Урок 39алгебры.) Когда мы вычислим эту производную ниже, мы увидим, что эта константа становится ln
| д дх | а х | = ln а · а x | . |
В системе натуральных логарифмов, в которой e — это основание, у нас есть самая простая возможная константа, а именно 1.
| д дх | е х | = e x . |
Производная от e с функциональным показателем
Когда y = e u ( x ) , то по цепному правилу:
То есть
«Производная от e с функциональным показателем
равно e с этим показателем, в
раз превышающим производную от этого показателя».
Пример 1. Вычислить производную e 2 x + 3 .
| Решение . |
Задача 1. Вычислить производную e x 2 .
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы снова закрыть ответ, нажмите «Обновить» («Reload»).
Сначала решай проблему сам!
e x 2 · 2 x = 2 x e x 2
Задача 2. Вычислите производную от следующего.
а) e sin x . e sin x cos x
б) e −x . e − x (−1) = −e − x
c) x 2 e x . x 2 e x + 2 x e x
Согласно правилу произведения.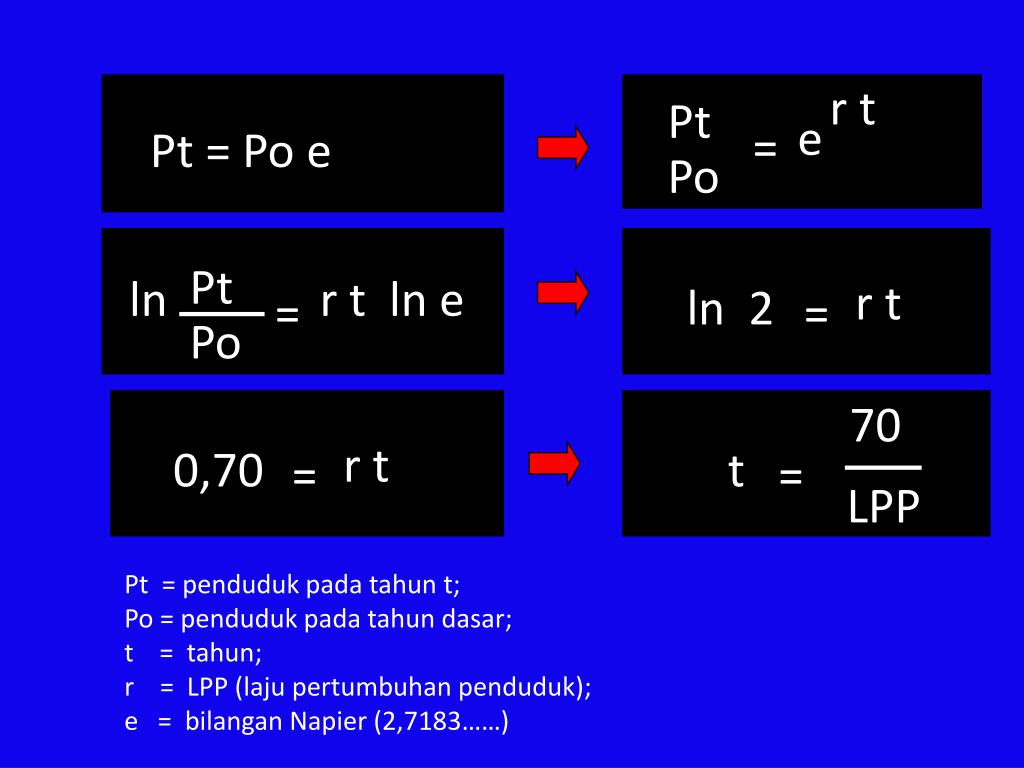
| г) | Согласно частному правилу: |
Производная от ln u ( x )
Когда y = ln u ( x ), то по цепному правилу:
То есть
| Пример 2. |
| Пример 3. | д дх | ln sin x | = | 1 sin x | · cos x | = | cos x sin x | = детская кроватка x . |
Пример 4. Найдите производную от ln x 2 .
Раствор . Мы можем применить законы логарифмов:
| д дх | л x 2 | = | д дх | 2 ln x , 3-й закон, | |||
| = | 2 | д дх | л х | ||||
| = | 2 х | . | |||||
| Пример 5. Найти производную от ln | . x 3 x − 4 | . |
Решение . По 2-му закону:
| д дх | в | x 3 x − 4 | = | д дх | [ln x — ln (3 x — 4)] |
| = | |||||
| = | |||||
| = | |||||
Задача 3. Дифференцируйте следующее.
а) в x 3 .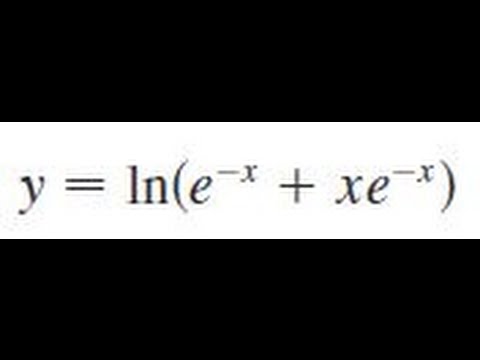 | д дх | ln x 3 = | д дх | 3 дюйма x | = | 3 х |
| b) (ln x ) 3 . | 3 (пер. x ) 2 · | 1 х | = | 3(ln x ) 2 x |
| c) ln (3 x 2 − 4 x ). | 1 3 x 2 − 4 x | · (6 х — 4) | = | 6 x − 4 3 x 2 − 4 x |
| d) ln (3 x − 4) 2 . | 1 (3 x − 4) 2 | · 2(3 x − 4) · 3 | = | 6(3 x — 4) (3 x — 4) 2 | = | 6 3 x − 4 |
e) ln cos x . | 1 cos x | (−sin x ) | = | − | sin x cos x | = | −загар x |
| Задача 4. Вычислить производную от ln | . 2 х | . |
| д дх | п | 2 х | = | д дх | (ln 2 — ln x ) = 0 — | 1 х | = − | 1 х |
Задача 5. Производная от log a x .
По правилу перехода с базы e на другую базу a :
Тема 20 предварительного исчисления.
Вычислите предел этой производной
а) когда x больше 1 и становится больше.
Эта производная приближается к 0, то есть становится меньше.
б) когда x меньше 1 и становится меньше.
Эта производная становится больше.
Общее силовое правило
Теперь мы можем доказать, что производная от f ( x ) = x n , где n — любой рациональный показатель, выглядит следующим образом:
| д дх | x нет | = n x n −1 |
Пусть
| у | = | x n . | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Затем | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| п г | = | n ln x (3-й закон). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Поэтому, взяв производную по x : | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| = | нет x | |||
| так что | ||||
| у’ | = | нет x | · г | |
| = | нет x | · x н | ||
| = | n x n −1 . | |||
Именно это мы и хотели доказать.
(Если n равно 0, то x 0 = 1, константа; ее производная равна 0.
Если n иррационально, потребуется рациональное приближение.)
| Задача 6. Вычислить производную от |
Производная от a x
Докажем:
| д дх | а х | = ln a · a x |
«Производная экспоненциальной функции с основанием a
равно натуральному логарифму по основанию
. экспоненциальная функция умножается на«.
Пусть
| у | = | и х . | ||
| Тогда после натурального логарифма обеих частей: | ||||
| ln y | = | x ln a . (3-й закон) | ||
| Следовательно, | ||||
| = | ||||
| Но по правилу цепочки: | ||||
| = | ||||
| Следовательно, | ||||
| = | в и . | |||
| = | по | |||
| у’ | = | ln a · y | ||
| То есть | ||||
| = | ln a · a x . | |||