Егэ решение показательных неравенств: Задание 14. Неравенства — профильный ЕГЭ по математике

Задание 14. Неравенства — профильный ЕГЭ по математике

Задание 14 Профильного ЕГЭ по математике можно считать границей между «неплохо сдал ЕГЭ» и «поступил в вуз с профильной математикой». Здесь не обойтись без отличного знания алгебры. Потому что встретиться вам может любое неравенство: показательное, логарифмическое, комбинированное (например, логарифмы и тригонометрия). И еще бывают неравенства с модулем и иррациональные неравенства. Некоторые из них мы разберем в этой статье.

Хотите получить на Профильном ЕГЭ не менее 70 баллов? Учитесь решать неравенства!

Темы для повторения:

^New 

Решаем задачи из сборника И. В. Ященко, 2021

Квадратичные неравенства

Метод интервалов 

Уравнения и неравенства с модулем 

Иррациональные неравенства

Показательные неравенства

Логарифмические неравенства

Метод замены множителя (рационализации)

Решение неравенств: основные ошибки и полезные лайфхаки

Решаем задачи из сборника И. В. Ященко, 2020. Вариант 8, задача 15

Решаем задачи из сборника И. В. Ященко, 2020. Вариант 32, задача 15

Решаем задачи из сборника И. В. Ященко, 2020. Вариант 36, задача 15

Логарифмические неравенства повышенной сложности

Разберем неравенства разных типов из вариантов ЕГЭ по математике.

Дробно-рациональные неравенства 

1. Решите неравенство:

Сделаем замену

Тогда , а

Получим:

Решим неравенство относительно t методом интервалов:

Получим:

Вернемся к переменной x:

Ответ:

Показательные неравенства

2. Решите неравенство

Сделаем замену Получим:

Умножим неравенство на

Дискриминант квадратного уравнения

Значит, корни этого уравнения:

Разложим квадратный трехчлен на множители.

. Вернемся к переменной x.

Внимание. Сначала решаем неравенство относительно переменной t. Только после этого возвращаемся к переменной x. Запомнили?

Ответ:

Следующая задача — с секретом. Да, такие тоже встречаются в вариантах ЕГЭ.

3. Решите неравенство

Сделаем замену Получим:

Вернемся к переменной

Первое неравенство решим легко: С неравенством тоже все просто. Но что делать с неравенством ? Ведь Представляете, как трудно будет выразить х?

Оценим Для этого рассмотрим функцию

Сначала оценим показатель степени. Пусть Это парабола с ветвями вниз, и наибольшее значение этой функции достигается в вершине параболы, при х = 1. При этом

Мы получили, что

Тогда , и это значит, что Значение не достигается ни при каких х.

Но если и , то

Мы получили:

Ответ:

Логарифмические неравенства

4. Решите неравенство

Запишем решение как цепочку равносильных переходов. Лучше всего оформлять решение неравенства именно так.

Ответ:

Следующее неравенство — комбинированное. И логарифмы, и тригонометрия!

5. Решите неравенство

ОДЗ:

Замена

Ответ:

А вот и метод замены множителя (рационализации). Смотрите, как он применяется. А на ЕГЭ не забудьте доказать формулы, по которым мы заменяем логарифмический множитель на алгебраический.

6. Решите неравенство:

Мы объединили в систему и область допустимых значений, и само неравенство. Применим формулу логарифма частного, учитывая, что . Используем также условия

Обратите внимание, как мы применили формулу для логарифма степени. Строго говоря,

Поскольку

Согласно методу замены множителя, выражение заменим на

Получим систему:

Решить ее легко.

Ответ: .

Разберем какое-нибудь нестандартное неравенство. Такое, что не решается обычными способами.

7. Решите неравенство:

ОДЗ:

Привести обе части к одному основанию не получается. Ищем другой способ.

Заметим, что при x = 9 оба слагаемых равны 2 и их сумма равна 4.

Функции и — монотонно возрастающие, следовательно, их сумма также является монотонно возрастающей функцией и каждое свое значение принимает только один раз.

Поскольку при x=9 значение монотонно возрастающей функции равно 4, при значения этой функции меньше 4. Конечно, при этом , то есть x принадлежит ОДЗ.

Ответ:

Поиск материала «Задание 15 из ЕГЭ по математике, Неравенство» для чтения, скачивания и покупки

Ниже показаны результаты поиска поисковой системы Яндекс. В результатах могут быть показаны как эта книга, так и похожие на нее по названию или автору.

Search results:

1. ЕГЭ Профиль №15. Рациональные неравенства — math200. ru

   15 заданием профильного ЕГЭ по математике является неравенство. Одним из видов неравенств которое может оказаться в 15 задание является рациональное неравенство. Прежде чем решать рациональные неравенства, следует научиться решать рациональные уравнения. Как правило, рациональное неравенство решается методом интервалов, который не требует каких-то специальных навыков, но при этом решение оказывается достаточно объемным и требует внимательности. Также не следует забывать про метод замен.

   math200.ru

2. ЕГЭ Профиль №15. Логарифмические неравенства — math200.ru

   15 заданием профильного ЕГЭ по математике является неравенство. Самым часто встречаемым неравенством, которое предлагают на реальных экзаменах в 15 задание, является логарифмическое неравенство. При решении логарифмических неравенств, в большинстве случаев (но не всегда) необходимо полностью находить область допустимых неравенств. Большая часть логарифмических неравенств, предлагаемых на реальных экзаменах, решается с помощью замен, методом интервалов или разложением на множители.

   math200.ru

3. Купить эту книгу

4. Канцтовары

   Канцтовары: бумага, ручки, карандаши, тетради. Ранцы, рюкзаки, сумки. И многое другое.

   my-shop.ru

6. ЕГЭ Профиль №15. Показательные неравенства — math200.ru

   Одним, из наиболее часто встречаемых неравенств, которое может оказаться в 15 задание, является показательное неравенство. Большая часть показательных неравенств предлагаемых на реальных экзаменах решается с помощью замен, методом интервалов или разложением на множители. Прежде чем решать показательные неравенства необходимо знать свойства показательной функции и уметь решать показательные уравнения (см. задание 13 профильного ЕГЭ «Показательные уравнения»).

   math200.ru

7. Задание 15 ЕГЭ по математике

   В пособии разобраны все прототипы неравенств (№15) за все годы проведения ЕГЭ. Все решения являются авторскими. Автор разрешает свободное использование пособия в любых учебных целях. Пожелания учащимся. Неравенство №15 на экзамене верно решают около 20% учеников. Автор надеется, что это пособие поможет вам войти в их число. Обсуждайте решения с одноклассниками, задавайте вопросы учителям, репетиторам и на сайтах самоподготовки. Ведь активность в учебе – залог успеха!

   prooge.ru

8. 00-book-c3.dvi

   В тех случаях, когда вариант ЕГЭ по математике содержит систему двух неравенств с одной переменной, за её верное решение обычно да-ётся три первичных балла: по баллу за правильное решение каждого из неравенств системы и третий балл — за правильно найденное решение всей системы. Однако существуют системы неравенств, для которых нельзя решить одно из неравенств системы (или даже нельзя найти множество решений ни одного из неравенств системы), а множество решений всей системы найти, тем не менее, удаётся.

   kaluginaee. lien.ru

9. ЕГЭ–2022, математика: задания
   , ответы, решения. Обучающая…

   Тысячи заданий с решениями для подготовки к ЕГЭ—2022 по всем предметам.

   Аналоги к заданию № 508210: 508353 508545 511505 Все. Классификатор алгебры: Неравенства рациональные относительно показательной функции. Кодификатор ФИПИ/Решу ЕГЭ: 2.2.3 Показательные неравенства.

   ege.sdamgia.ru

10. ЕГЭ–2022, математика: задания, ответы, решения. Обучающая…

    Задача допускает решение без замены переменной: тождественными преобразованиями данное неравенство приводится к откуда также получается ответ. Приведем решение Наиля Мусина для нахождения нулей числителя. Выполним преобразования

    Здравствуйте, я заметил ошибку в ответе после замены.z правильно подобран от (3;6] и от (9;15]. Далее, возвращаемся из замены подставляя x корень из 3. Получается, что 3<xкореньиз3_>6 и 9<xкореньиз3_<15.

    Далее, я задумался и нашел очевидную ошибку.

    ege.sdamgia.ru

11. ЕГЭ–2022, математика: задания, ответы, решения. Обучающая…

    Тысячи заданий с решениями для подготовки к ЕГЭ—2022 по всем предметам.

    Образовательный портал для подготовки к экзаменам. Математика профильного уровня.

    Марианна 18.10.2017 15:18. просьба, проверить данный ответ,комментарий был по делу, а Вы

    Кодификатор ФИПИ/Решу ЕГЭ: 2.2.4 Логарифмические неравенства, 2.2.9 Метод интервалов.

    ege.sdamgia.ru

12. МАТЕМАТИКА ЕГЭ 201 9 | ЕГЭ 2013. Решите систему неравенств

    Разработчиками КИМов 2012-2013 го-да были предложены задания С3, в кото-рых необходимо было решить систему неравенств (либо систему показательных и логарифмических неравенств, либо систему, содержащую рациональное не-равенство и показательное или логариф-мическое неравенство).

    При проверке задачи С3 в ЕГЭ 2012-2013 гг. выставление баллов производи-лось в соответствии со следующими кри-териями. экзамена в 2010 году, 3,7% – в 2011 и 2,4% – в 2012 году.

    down.ctege.info

13. ЕГЭ Профиль №15. Иррациональные неравенства — math200.ru

    Иррациональные неравенства в формате pdf. Нашли ошибку в заданиях? Оставьте, пожалуйста, отзыв.

    math200.ru

14. Задание 14. Неравенства — профильный ЕГЭ по математике

    Задание 14 Профильного ЕГЭ по математике можно считать границей между «неплохо сдал ЕГЭ» и «поступил в вуз с профильной математикой». Здесь не обойтись без отличного знания алгебры. Потому что встретиться вам может любое неравенство: показательное, логарифмическое, комбинированное (например, логарифмы и тригонометрия). И еще бывают неравенства с модулем и иррациональные неравенства.

    Некоторые из них мы разберем в этой статье.

    ege-study.ru

15. Логарифмические неравенства в ЕГЭ по математике.

    Разбор решения логарифмических неравенств — от самых простых (тренировочных) до самых сложных, которые могут попасться во второй части ЕГЭ по математике. Использование метода рационализации, свойств логарифмической функции.

    Главная » Профильный ЕГЭ по математике » Задания 15. Логарифмические неравенства, метод рационализации.

    mat-ege.ru

16. ЕГЭ–2022, математика: задания, ответы, решения. Обучающая…
    Тысячи заданий с решениями для подготовки к ЕГЭ—2022 по всем предметам.

    Аналоги к заданию № 508210: 508353 508545 511505 Все. Классификатор алгебры: Неравенства рациональные относительно показательной функции. Кодификатор ФИПИ/Решу ЕГЭ: 2.2.3 Показательные неравенства.

    math-ege.sdamgia.ru

17. ЕГЭ по математике 2011 | Критерии проверки задания 15

    Зеленоград. 30 ноября 2017. Рекомендации по подготовке к выполнению задания №15. (неравенства) ЕГЭ профильного уровня. Прокофьев Александр Александрович, Зав.каф. «Высшей математики – 1», НИУ МИЭТ, учитель математики ГБОУ г. Москвы «Школа №1298».

    С чего следует начинать? 1. Научить решению простейших рациональных неравенств. 2. Полезно решать «обратные» задачи: составлять неравенства по. ответу, заданному в виде системы неравенств или картинки.

    alexlarin.net

18. Задача 15 ЕГЭ математика профиль, сортировка по темам

    Тема 1: Реальные задачи ЕГЭ последних лет Тема 2: Вклады Тема 3: Кредиты Тема 4: Оптимальный выбор.

    Задачи из любой темы вполне реально встретить на настоящем экзамене ЕГЭ. Внутри каждой темы задачи мы постарались расположить по возрастанию сложности. Тема 1: Реальные задачи ЕГЭ последних лет.

    www.mathm.ru

19. Неравенства. №15 | 4ЕГЭ

    → Иррациональные неравенства: irr.pdf → Неравенства с модулем: s-modulem.pdf → Показательные неравенства: pokazatelnyie-neravenstva-1.pdf → Логарифмические неравенства: log.pdf → Рациональные неравенства: ratsionalnyie-neravenstva.pdf.

    Макет новой системы высшего образования, которая должна будет сменить Болонскую, будет представлен к концу года в виде федерального государственного образовательного стандарта, сообщили ТАСС в пресс-службе Минобрнауки.

    4ege.ru

20. ЕГЭ–2022, математика: задания, ответы, решения. Обучающая…

    Найдем ограничения на Обратим внимание на то, что левая часть неравенства имеет смысл при одном условии: оба выражения и обязаны быть положительными. А это значит, что каждое из выражений: и должны иметь одинаковый знак: либо оба положительны, либо оба отрицательны. Такое условие будет выполнено, если будет верным неравенство. Оценим Очевидно, что т. е. для любого. Следовательно, при любом значении Отсюда вывод: выражение также обязано быть отрицательным.

    ege.sdamgia.ru

21. ЕГЭ–2022, математика: задания, ответы, решения. Обучающая…

    Каталог заданий Показательные неравенства. Сортировка Основная Сначала простые Сначала сложные По популярности Сначала новые Сначала старые. Пройти тестирование по 10 заданиям Пройти тестирование по всем заданиям Вернуться к каталогу заданий.

    Аналоги к заданию № 508210 : 508353 508545 511505 Все. Классификатор алгебры: Неравенства рациональные относительно показательной функции. Методы алгебры: Выделение полного квадрата. Кодификатор ФИПИ/Решу ЕГЭ: 2.2.3 Показательные неравенства.

    math-ege. sdamgia.ru

22. ЕГЭ Профиль №15. Неравенства с модулями — math200.ru

    Неравенства с модулямиadmin2018-11-26T23:18:16+03:00. Скачать ЕГЭ Профиль №15. Неравенства с модулями в формате pdf. Нашли ошибку в заданиях? Оставьте, пожалуйста, отзыв.

    math200.ru

23. Показательные уравнения и неравенства на ЕГЭ по математике

    Здесь приведены показательные уравнения и неравенства, которые предлагались на ЕГЭ по матема-тике (профильный уровень, сложная часть), а также на диагностических, контрольных и трени-ровочных работах МИОО начиная с 2009 года.

    29. (Санкт-Петербург, пробный ЕГЭ, 2017 ) а) Решите уравнение 4x − 2x+3 + 15 = 0. √. б) Определите, какие из его корней принадлежат отрезку 2; 10 .

    mathus.ru

24. Путеводитель по неравенствам (задачи №15 ЕГЭ по математике)

    Подготовка к ЕГЭ и ГИА по математике. Видеоуроки, справочные материалы, обучающие тесты.

    !!! Смотрите также подборку задач С3 (с ответами) для подготовки к ЕГЭ !!! Список всех неравенств (С3), разобранных на сайте

    egemaximum.ru

25. Задачник и справочник по 15 заданию ЕГЭ по математике.

    TG 4ЕГЭ. Решаем неравенства. Математика.

    Результаты ГИА 2022 и планируемые изменения КИМ ЕГЭ 2023. Математика. Видеоуроки ЕГЭ по математике | Сегодня, 20:19.

    4ege.ru

26. ЕГЭ — 2019. №15 Профильный уровень. Логарифмические…

    Уважаемые коллеги!Актуальной задачей на сегодняшний день является качественная подготовка учащихся к единому государственному экзамену (ЕГЭ) по математике, а также абитуриентов к вступител… Решение логарифмических неравенств и систем неравенств.

    Программа дистанционного курса «Показательные и логарифмические неравенства в заданиях ЕГЭ с развернутым ответом» предназначена для занятий в 11 классе для высокомотивиро. .. Решение уравнений и неравенств в плане подготовки к ЕГЭ (профильный уровень).

    nsportal.ru

27. Решение рациональных неравенств (задание № 15 из ЕГЭ)

    Подписи к слайдам: Слайд 1. Решение рациональных неравенств (задание 15 ЕГЭ).

    Математический диктант по теме «Решение рациональных неравенств» составлен в 2 вариантах и состоит из 4 заданий. Данная работа оценит знания и умения обучающихся решать простейшие рациональн…

    nsportal.ru

28. Неравенства. Задания ЕГЭ по математике (профильный уровень)

    Примеры и решения заданий по теме неравенства. Задания C3 из ЕГЭ по математике (профильный уровень).

    1. Заметим, что x=0 решением системы не является, так как второе неравенство системы при x=0 не является верным (6 \leqslant 0). Пусть x>0. Вычитая из первого неравенства второе, получаем.

    academyege.ru

29. Презентация для задания №15 ЕГЭ по математике профильный…

    Решение логарифмических. неравенств. Задание № 15 ЕГЭ (профильный. уровень). Попкова Е.В., учитель математики МОУ «СОШ №63» г. Магнитогорска. ПЛАН ВЕБИНАРА. 1 Обзор задания № 15 за последние три года. 2 Решение логарифмических неравенств реальных вариантов ЕГЭ и демоверсий. 3 Специальные методы решения логарифмических неравенств.

    100ballnik.com

30. Задание №15 профильного ЕГЭ: решение уравнений и неравенств.

    Другие пособия от автора: → Решение задач ОММО → Решение задач по математике из открытого банка ФИПИ → Подготовка к олимпиадам по математике → Экономическая задача (17) → Тригонометрические уравнения (13).

    Шкала ЕГЭ Видеоуроки Пробники Демоверсии ЕГЭ 2023 ОГЭ 2023 Итоговое сочинение 2022-2023 Все темы сочинений 2014-2022 Олимпиады 2022-2023.

    4ege.ru

31. Задача 15 ЕГЭ-2021 Решение неравенств

    Решив неравенство с помощью метода интервалов, получим: Сделаем обратную замену: t=. а так как функция монтонно возрастает на R, то. Ответ: 3. Решите неравенство: Решение: 1) Найдем ОДЗ.

    Можно не только читать, но и смотреть новые объяснения и разборы на нашем YouTube канале! Пожалуйста, подпишитесь на канал и нажмите колокольчик, чтобы не пропустить новые видео. Задавайте свои вопросы в комментариях и оставляйте задачи, которые вы хотите, чтобы мы разобрали.

    ege-study.ru

32. Показательные неравенства. Задания ЕГЭ по математике…

    Примеры и решения заданий по теме показательные неравенства. Задания C3 из ЕГЭ по математике (профильный уровень).

    Информационный портал для подготовки к ЕГЭ. Онлайн тесты по официальным примерам из курса ЕГЭ за 2018 — 2019 гг.

    academyege.ru

33. Неравенства С3 (№15). Подготовка к ЕГЭ по математике

    Подготовка к ЕГЭ и ГИА по математике. Видеоуроки, справочные материалы, обучающие тесты.

    Главная › 14 (С3) Неравенства › Неравенства С3 (№15). Подготовка к ЕГЭ по математике.

    Неравенства с модулем. Скачать (PDF, 376KB).

    Задание №17 Т/Р №104 А. Ларина. С3 из ЕГЭ 2013 от 3 июня.

    egemaximum.ru

34. Проект «Подготовка к ЕГЭ» Решение неравенств (задание15)

    Решение неравенств (зад15) вызывает трудности у обучающихся. Данный проект позволит выпускникам самостоятельно ознакомиться с методами решения неравенств. Особенно полезен метод замены множителей.

    Выполнила проект Зарьянцева ВП. учитель математики высшей категории МОУ «СОШ84» г. Саратова.

    intolimp.org

35. ЕГЭ Неравенства — задание № 15 — Решите неравенство

    Досрочный вариант ЕГЭ по математике 2017 профильный уровень задание №15. Решите неравенство.

    При 1<x<2 получаем log 15 x>log 25 x, log 9 (2-x)<log 15 (2-x),поэтому левая часть неравенства отрицательна и не превосходит log 25 9. Таким образом, решение исходного неравенства (0;1) и (1;2).

    onlyege.ru

На данной странице Вы можете найти лучшие результаты поиска для чтения, скачивания и покупки на интернет сайтах материалов, документов, бумажных и электронных книг и файлов похожих на материал «Задание 15 из ЕГЭ по математике, Неравенство»

Для формирования результатов поиска документов использован сервис Яндекс.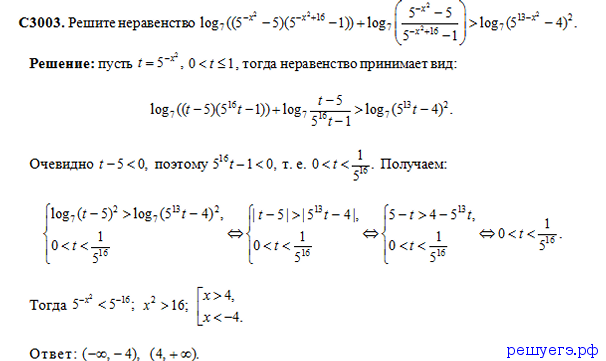 XML.

Нашлось 14 млн ответов. Показаны первые 32 результата(ов).

Дата генерации страницы: пятница, 21 октября 2022 г., 10:22:24 GMT

логарифмических неравенств профиля ege. Все о логарифмических неравенствах. Примеры разбора

Это эквивалентно этой системе:

Рассмотрим еще примеры решения простейших логарифмических неравенств, показанные на картинке ниже:

Решение примеров

Упражнение. Попробуем решить это неравенство:

Решение области допустимых значений.

Теперь попробуем умножить его правую часть на:

Посмотрим, что у нас получится:

Теперь перейдем к сублогарифмическим преобразованиям. Поскольку основание логарифма равно 0

3x — 8 > 16;
3x > 24;
х > 8.

А отсюда следует, что полученный нами интервал целиком принадлежит ОДЗ и является решением такого неравенства.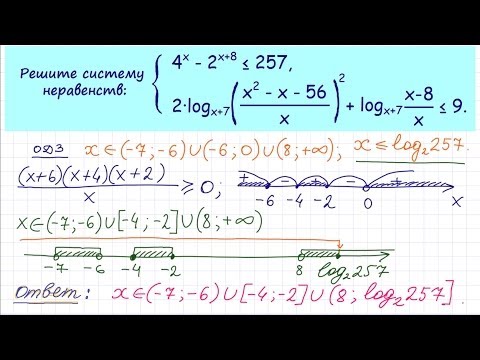

Вот ответ, который мы получили:

Что нужно для решения логарифмических неравенств?

Теперь попробуем проанализировать, что нам нужно для успешного решения логарифмических неравенств?

Во-первых, сосредоточьте все свое внимание и постарайтесь не делать ошибок при выполнении преобразований, которые даны в этом неравенстве. Также следует помнить, что при решении таких неравенств необходимо не допускать расширения и сужения неравенства ОДЗ, которые могут привести к потере или приобретению посторонних решений.

Во-вторых, при решении логарифмических неравенств нужно научиться логически мыслить и понимать разницу между такими понятиями, как система неравенств и совокупность неравенств, чтобы без труда подбирать решения неравенства, руководствуясь при этом его ДХС.

В-третьих, чтобы успешно решать такие неравенства, каждый из вас должен в совершенстве знать все свойства элементарных функций и четко понимать их смысл. К таким функциям относятся не только логарифмические, но и рациональные, степенные, тригонометрические и т. д., словом, все те, что вы изучали во время школьной алгебры.

Как видите, изучив тему логарифмических неравенств, в решении этих неравенств нет ничего сложного, при условии, что вы внимательны и настойчивы в достижении поставленных целей. Чтобы не было проблем с решением неравенств, нужно как можно больше тренироваться, решая различные задачи и при этом запоминать основные способы решения таких неравенств и их системы. При неудачных решениях логарифмических неравенств следует тщательно проанализировать свои ошибки, чтобы в дальнейшем не возвращаться к ним снова.

Домашнее задание

Для лучшего усвоения темы и закрепления пройденного материала решите следующие неравенства:

Как вы думаете, до экзамена еще есть время, и вы успеете подготовиться? Возможно, это так. Но в любом случае, чем раньше студент приступит к обучению, тем успешнее он сдаст экзамены. Сегодня мы решили посвятить статью логарифмическим неравенствам. Это одно из заданий, которое означает возможность получить дополнительный балл.

Вы уже знаете, что такое логарифм (log)? Мы очень на это надеемся. Но даже если у вас нет ответа на этот вопрос, это не проблема. Очень легко понять, что такое логарифм.

Почему именно 4? Нужно возвести число 3 в такую ​​степень, чтобы получилось 81. Когда вы поймете принцип, можно переходить к более сложным вычислениям.

Вы прошли через неравенство несколько лет назад. И с тех пор вы постоянно встречаете их в математике. Если у вас возникли проблемы с решением неравенств, загляните в соответствующий раздел.
Теперь, когда мы познакомились с понятиями по отдельности, перейдем к их рассмотрению в целом.

Простейшее логарифмическое неравенство.

Простейшие логарифмические неравенства этим примером не ограничиваются, есть еще три, только с другими знаками. Зачем это нужно? Чтобы лучше понять, как решить неравенство с логарифмами. Теперь приведем более применимый пример, пока достаточно простой, сложные логарифмические неравенства оставим на потом.

Как это решить? Все начинается с ОДЗ. Вы должны знать больше об этом, если хотите всегда легко решать любое неравенство.

Что такое ОДЗ? DPV для логарифмических неравенств

Аббревиатура обозначает диапазон допустимых значений. В заданиях к ЕГЭ часто всплывает эта формулировка. DPV пригодится вам не только в случае логарифмических неравенств.

Посмотрите еще раз на приведенный выше пример. Будем рассматривать ОДЗ на его основе, чтобы вы поняли принцип, а решение логарифмических неравенств не вызывало вопросов. Из определения логарифма следует, что 2x+4 должно быть больше нуля. В нашем случае это означает следующее.

Это число должно быть положительным по определению. Решите представленное выше неравенство. Это можно сделать даже устно, здесь понятно, что Х не может быть меньше 2. Решением неравенства будет определение диапазона допустимых значений.
Теперь перейдем к решению простейшего логарифмического неравенства.

Отбрасываем сами логарифмы из обеих частей неравенства. Что остается нам в результате? простое неравенство.

Это легко решить. X должен быть больше -0,5. Теперь объединяем два полученных значения в систему. Таким образом,

Это будет область допустимых значений рассматриваемого логарифмического неравенства.

Зачем вообще нужна ОДЗ? Это возможность отсеять неверные и невозможные ответы. Если ответ не находится в диапазоне допустимых значений, то ответ просто не имеет смысла. Это стоит запомнить надолго, так как на экзамене часто возникает необходимость искать ОДЗ, и касается это не только логарифмических неравенств.

Алгоритм решения логарифмического неравенства

Решение состоит из нескольких шагов. Во-первых, необходимо найти диапазон допустимых значений. В ОДЗ будет два значения, это мы рассматривали выше. Следующим шагом является решение самого неравенства. Методы решения следующие:

• метод замены множителя;
• разложение;
• метод рационализации.

В зависимости от ситуации следует использовать один из вышеперечисленных методов. Перейдем непосредственно к решению. Мы раскроем самый популярный метод, который подходит для решения задач ЕГЭ практически во всех случаях. Далее рассмотрим метод декомпозиции. Это может помочь, если вы столкнетесь с особенно «хитрым» неравенством. Итак, алгоритм решения логарифмического неравенства.

Примеры решений :

Мы не зря взяли именно такое неравенство! Обратите внимание на базу. Помните: если оно больше единицы, знак остается прежним при нахождении диапазона допустимых значений; в противном случае необходимо изменить знак неравенства.

В итоге получаем неравенство:

Теперь приведем левую часть к виду уравнения равному нулю. Вместо знака «меньше» ставим «равно», решаем уравнение. Таким образом, мы найдем ОДЗ. Надеемся, что у вас не возникнет проблем с решением такого простого уравнения. Ответы -4 и -2. Это не все. Вам нужно отобразить эти точки на графике, расставив «+» и «-». Что для этого нужно сделать? Подставьте числа из интервалов в выражение. Где значения положительные, там ставим «+».

Ответ : x не может быть больше -4 и меньше -2.

Мы нашли диапазон допустимых значений только для левой части, теперь нам нужно найти диапазон допустимых значений для правой стороны. Это ничуть не легче. Ответ: -2. Пересекаем обе полученные области.

И только теперь начинаем решать само неравенство.

Максимально упростим, чтобы было легче решать.

В решении снова используем интервальный метод. Опустим расчеты, с ним все и так понятно из предыдущего примера. Отвечать.

Но этот способ годится, если логарифмическое неравенство имеет те же основания.

Решение логарифмических уравнений и неравенств с разными основаниями предполагает первоначальное приведение к одному основанию. Затем используйте описанный выше метод. Но есть и более сложный случай. Рассмотрим один из самых сложных типов логарифмических неравенств.

Логарифмические неравенства с переменным основанием

Как решать неравенства с такими характеристиками? Да и такие можно найти на ЕГЭ. Решение неравенств следующим образом также благотворно скажется на вашем учебном процессе. Давайте рассмотрим вопрос подробно. Отложим теорию и сразу перейдем к практике. Для решения логарифмических неравенств достаточно один раз ознакомиться с примером.

Для решения логарифмического неравенства представленной формы необходимо привести правую часть к логарифму с тем же основанием. Принцип напоминает эквивалентные переходы. В результате неравенство будет выглядеть так.

Собственно, осталось составить систему неравенств без логарифмов. Используя метод рационализации, перейдем к эквивалентной системе неравенств. Само правило вы поймете, когда будете подставлять подходящие значения и следить за их изменениями. Система будет иметь следующие неравенства.

Используя метод рационализации при решении неравенств, нужно помнить следующее: из основания нужно вычесть единицу, x по определению логарифма вычитается из обеих частей неравенства (правой из левой), два выражения перемножаются и устанавливаются под исходным знаком относительно нуля.

Дальнейшее решение осуществляется интервальным методом, здесь все просто. Вам важно понимать различия в методах решения, тогда все начнет получаться легко.

В логарифмических неравенствах много нюансов. Простейшие из них достаточно легко решить. Как сделать так, чтобы каждую из них решить без проблем? Вы уже получили все ответы в этой статье. Теперь вам предстоит долгая практика. Постоянно практикуйтесь в решении различных задач в рамках экзамена, и вы сможете получить наивысший балл. Удачи в вашем нелегком деле!

Неравенство называется логарифмическим, если оно содержит логарифмическую функцию.

Методы решения логарифмических неравенств ничем не отличаются кроме двух вещей.

Во-первых, при переходе от логарифмического неравенства к неравенству сублогарифмических функций следует следовать знаку полученного неравенства . Он подчиняется следующему правилу.

Если основание логарифмической функции больше $1$, то при переходе от логарифмического неравенства к неравенству сублогарифмических функций знак неравенства сохраняется, а если меньше $1$, то он меняется на обратный.

Во-вторых, решение любого неравенства есть интервал, а значит, в конце решения неравенства сублогарифмических функций необходимо составить систему двух неравенств: первое неравенство этой системы будет неравенство сублогарифмических функций, а вторым будет интервал области определения логарифмических функций, входящих в логарифмическое неравенство.

Практика.

Решим неравенства: 9(3),$

$x \in )

Ege решение задачи 13 представляет собой логарифмическое уравнение. Какие типичные ошибки допускают экзаменаторы?

домашний

Что нужно знать о показательных и логарифмических уравнениях для решения задач ЕГЭ по математике?

Умение решать показательные и логарифмические уравнения очень важно для успешной сдачи ЕГЭ по математике на профильном уровне. Важно по двум причинам :

Во первых , задание №13 варианта КИМ ЕГЭ, пусть и нечасто, но все же иногда это просто такое уравнение, которое нужно не только решить, но и (по аналогии с заданием по тригонометрии) выбрать корни из уравнение, удовлетворяющее любому условию.

Итак, один из вариантов на 2017 год включал следующую задачу:

а) Решите уравнение 8 x – 7 . 4 х – 2 х +4 + 112 = 0.

б) Укажите корни этого уравнения, принадлежащие отрезку.

Ответ: а) 2; log 2 7 и б) log 2 7.

В другой версии была такая задача:

а) Решите уравнение 6log 8 2 x – 5 log 8 x + 1 = 0

б) Найдите все корни этого уравнения, принадлежащие отрезку.

Ответ: а) 2 и 2√ 2 ; б) 2.

Было еще такое:

а) Решите уравнение 2log 3 2 (2cos x ) – 5log 3 (2cos x ) + 2 = 0.

б) Найдите все корни этого уравнения, принадлежащие интервалу [π; 5π/2].

Ответ: а) (π/6 + 2πk; -π/6 + 2πk, k∊Z) и б) 11π/6; 13π/6.

Во-вторых , изучение методов решения показательных и логарифмических уравнений хорошо, так как основные методы решения как уравнений, так и неравенств фактически используют одни и те же математические идеи.

Основные методы решения показательных и логарифмических уравнений легко запомнить, их всего пять: приведение к простейшему уравнению, использование эквивалентных переходов, введение новых неизвестных, логарифмирование и факторизация. Отдельно стоит метод использования свойств экспоненциальных, логарифмических и других функций при решении задач: иногда ключом к решению уравнения является область определения, область значений, неотрицательность, ограниченность, четность включаемых функций в этом.

Как правило, в задаче № 13 встречаются уравнения, требующие применения пяти основных методов, перечисленных выше. Каждый из этих методов имеет свои особенности, которые необходимо знать, так как именно их незнание приводит к ошибкам в решении задач.

Какие типичные ошибки допускают экзаменаторы?

Часто при решении уравнений, содержащих показательно-степенную функцию, студенты забывают рассмотреть один из случаев, когда выполняется равенство. Как известно, уравнения такого вида эквивалентны совокупности двух систем условий (см. ниже), речь идет о случае, когда а( х ) = 1

Эта ошибка связана с тем, что при решении уравнения испытуемый формально использует определение показательной функции (y= x , a>0, a ≠ 1): при a ≤ 0 экспоненциальная функция на самом деле не определена,

Но при a = 1 определено, но не экспоненциально, так как единица в любой действительной степени тождественно равна самой себе. Это означает, что если в рассматриваемом уравнении при а ( х ) = 1 имеет место истинное числовое равенство, то соответствующие значения переменной будут корнями уравнения.

Еще одной ошибкой является применение свойств логарифмов без учета диапазона допустимых значений. Например, известное свойство «логарифм произведения равен сумме логарифмов» оказывается имеющим обобщение:
log a( f ( x ) g ( x )) = log a │ f ( x )│ + log a │g( x )│, at f ( x ) g

( x ) > 9 a > 0, a ≠ 1

Действительно, для определения выражения в левой части этого равенства достаточно, чтобы произведение функций f и г был положительным, но сами функции могут быть одновременно и больше, и меньше нуля, поэтому при применении этого свойства необходимо использовать понятие модуля.

И таких примеров много. Поэтому для эффективного освоения методов решения показательных и логарифмических уравнений лучше всего использовать сервисы, которые смогут рассказать о таких «подводных камнях» на примерах решения соответствующих экзаменационных задач.

Регулярно практикуйтесь в решении проблем

Для начала обучения на портале 1С:Репетитор достаточно.
Вы можете:

Все курсы состоят из методически правильной последовательности теории и практики, необходимой для успешного решения задач. Это теория в виде текстов, слайдов и видео, задания с решениями, интерактивные тренажеры, модели и тесты.

Есть вопросы? Позвоните нам по телефону 8 800 551-50-78 или напишите в онлайн-чат.

Вот ключевые фразы, чтобы поисковые роботы лучше находили наши советы:
Как решить задание 13 ЕГЭ, задания на логарифмы, Ким ЕГЭ 2017, подготовка к ЕГЭ профиль математика, профиль Математика, решение уравнений и логарифмы, решение задач на показательные уравнения ЕГЭ, вычисление свойств логарифмов, показательно-степенная функция, задания по математике профильного уровня, применение свойств логарифмов, решение задач на корни, задания ЕГЭ 2017 с использованием показательных уравнений , подготовка к ЕГЭ для выпускников 11 классов 2018 года поступающих в технический вуз.

В задании 13 профильного уровня ЕГЭ по математике необходимо решить уравнение, но повышенного уровня сложности, так как задания прежнего уровня С начинаются с задания 13, и это задание можно назвать С1 . Перейдем к рассмотрению примеров типовых задач.

Разбор типовых вариантов заданий №13 ЕГЭ по математике на профильном уровне

Первый вариант задания (демонстрационная версия 2018 г.)

а) Решить уравнение cos2x = 1-cos(p/2-x)

б) Найдите все корни этого уравнения, принадлежащие интервалу [-5p/2;-p].

Алгоритм решения:

1. т
2. Делаем обратную замену и решаем простейшие тригонометрические уравнения.

1. Строим числовую прямую.
2. Укореняем его.
3. Отметьте концы сегмента.
4. Выбираем те значения, которые лежат внутри интервала.
5. Записываем ответ.

Решение:

1. Преобразовать правую часть равенства по формуле приведения cos( π/ 2− x )=sin x . Имеем:

cos2x = 1 — sin x .

Преобразуем левую часть уравнения, используя формулу двойного аргумента косинуса, используя синус:

cos(2x)=1−2sin 2 x

Получим следующее уравнение: −sin x

Теперь в уравнении 9 есть только одна тригонометрическая функция sin0243 х .

2. Вводим замену: t = sin х . We solve the resulting quadratic equation:

1−2 t 2 =1− t,

−2 t 2 + t =0,

t (−2 t + 1)=0,

t = 0 или -2t + 1 = 0 ,

t 1 = 0 t 2 = 1/2.

3. Делаем обратную замену:

sin x = 0 или sin x = ½

Решаем следующие уравнения:

sin x =0↔ x = πn, nЄZ

sin( x =-1-14 )=1/2↔4 ∙( π/6) + πn, nЄZ .

Таким образом, мы получаем два семейства решений.

1. В предыдущем пункте были получены два семейства, каждое из которых имеет бесконечно много решений. Необходимо выяснить, какие из них находятся в заданном интервале. Для этого строим числовую прямую.

2. Наносим на него корни обоих семейств, помечая их зеленым (первое) и синим (второе).

3. Отметьте концы зазора красным цветом.

4. В указанном интервале есть три корня, которые являются тремя корнями: −2 π ;−11 π/ 6 и -7 π/ 6.

а) πн, нЄЗ; (-1)n ∙( π/6) + πn, nЄZ

б) −2 π ;−11 π 6;−7 π 6

Второй вариант задачи (от Ященко №1)

Алгоритм решения:

1. Заменяем эту функцию переменной t и решаем полученное квадратное уравнение.
2. Делаем обратную замену и решаем простейшие показательные, затем тригонометрические уравнения.

1. Строим координатную плоскость и окружность единичного радиуса на ней.
2. Отмечаем точки, являющиеся концами отрезка.
3. Выбираем те значения, которые лежат внутри отрезка.
4. Записываем ответ.

Решение:

1. Введем замену t = 4 cos x. тогда уравнение примет вид:

Решаем квадратное уравнение по формулам дискриминанта и корней:

D = b 2 — c = 81 — 4 ∙ 4 ∙ 2 = 49,

t 1 = (9 — 7) / 8 = ¼, t 2 = (9 + 7) / 8 = 2.