Разбор и анализ сложности одной из новых задач ЕГЭ-2022
В статье автор разбирает решение одной из новых задач по теории вероятностей, введённой в ЕГЭ-2022. Рассматриваются как классический вариант решения, не приводящий к решению, так и альтернативные, которые оказываются наиболее оптимальными. Приводятся аргументы, критикующие повышенную сложность данной задачи относительно стандартов школьной программы.
Ключевые слова: ЕГЭ, теория вероятностей, числа Каталана, задача о пьянице, бесконечная сумма.
В 2022 году, в первой части профильного ЕГЭ по математике будет впервые присутствовать 2 задачи на теорию вероятностей. Первая задача (номер 2) не изменится, а вторая (номер 10), по нашему мнению, будет в разы сложнее. Это задача требует более глубокого анализа, и включает несколько шагов, для получения верного ответа. Пример данных задач, был опубликован на официальном сайте «Открытый банк задач ЕГЭ по математике».
Несмотря на то, что это первая часть экзамена (размышление над задачами которой, подразумевает порядка 5 минут времени), здесь встречаются задачи, которые могут быть сложнее всей содержательной части ЕГЭ. Рассмотрим пример одной из таких задач.
«Первый член бесконечной последовательности целых чисел равен 0. Каждый последующий член данной последовательности с вероятностью на единицу больше предыдущего, и с вероятностью меньше предыдущего. Найдите вероятность того, что среди членов этой последовательности можно найти число » [1].
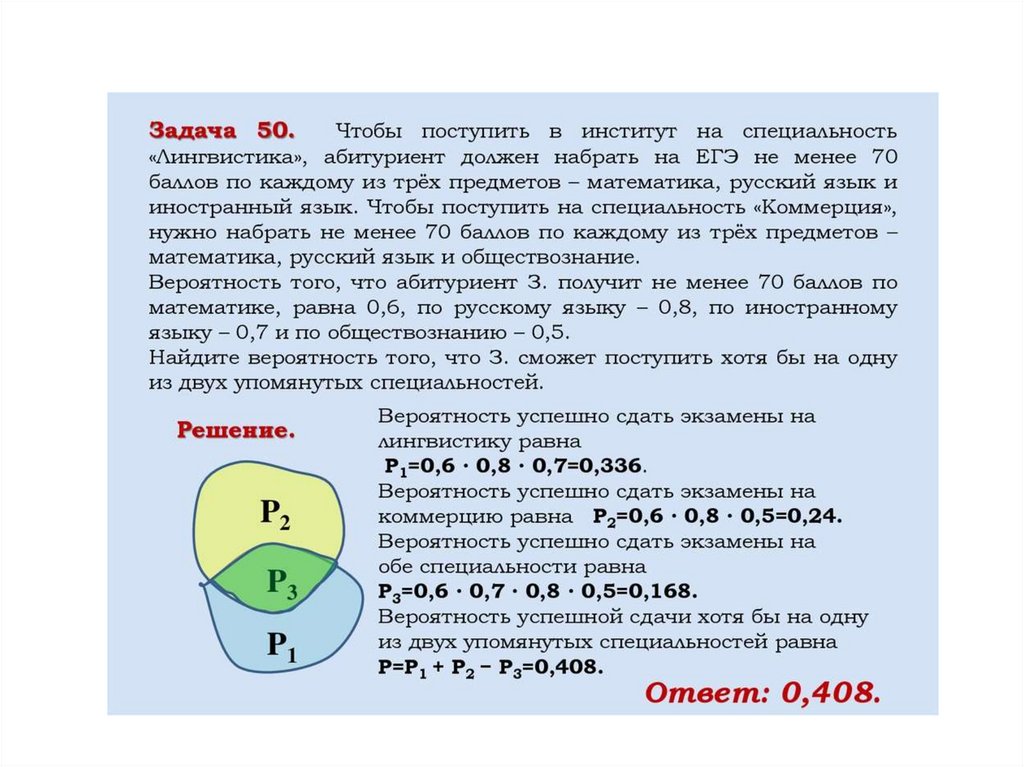
Есть множество вариантов попадания в . Рассмотрим некоторые из них (рис.1):
Рис. 1. Математическая модель задачи
- Возможно, попасть в с первого хода. Тогда вероятность равна
- , тогда вероятность равна:
- или . Здесь, вероятность равна: .
Но что делать дальше? Ведь этим можно заниматься бесконечно! Начнём с классического способа, заключающегося в нахождении бесконечной суммы ряда (что не входит в школьную программу, за одним исключением — суммы бесконечно-убывающей геометрической прогрессии).
Итак, посчитаем сумму вероятностей попадания в .
- Вероятность попасть из в =
- Можно из попасть в , а затем спуститься в . Вероятность будет равна
- Попасть в можно также с вероятностью:
Так можно считать до бесконечности. Получаем следующее выражение:
Нахождение способов подняться до , а потом спустить до уже вызывает проблемы. В связи с этим просто посчитать сумму ряда, по крайней мере со знаниями школьной программы не видится возможным. Соответственно, классический способ решения на этом заканчивается и не даёт никакого решения.
Приходится искать альтернативные методы решения, и такие, как оказалось, есть. Первый — заключается в привлечении расширенных знаний по комбинаторике, а второй с широким кругозором знаний различных математических головоломок. Начнём с первого.
Очевидно, что нам мешает старший коэффициент, выражающий количество способов подняться до
-го числа и опуститься до
. Обозначим количество этих способов коэффициентом
.
Обозначим количество этих способов коэффициентом
.
Тогда, например, количество способов подняться до 4 и опуститься до будет обозначено, как .
Перепишем наше выражение, полученное суммированием:
Теперь, используем знания комбинаторики [2, 3]. Оказывается, что у наших коэффициентов есть название — числа Каталана.
Числа Каталана это количество правильных скобочных последовательностей длины , то есть таких последовательностей из левых и правых скобок, в которых количество открывающихся скобок равно количеству закрывающихся. То есть ((())) или (())().
Теперь, для решения нашей задачи, требуется воспользоваться производящей функцией. Данное понятие выходит далеко за рамки школьной программы, а также программы некоторых высших учебных заведений. Благо в данном контексте, глубокое понимание данного термина не требуется, однако его привлечение вызывает множество вопросов.
Стоит отметить, что данную функцию можно вывести, как показано, например в [4]. Но, по нашему мнению, процесс вывода достаточно трудоемкий, и точно не имеет место быть на экзамене, когда на счету каждая минута. Итак, воспользуемся производящей функцией для чисел Каталана [4]:
Но, по нашему мнению, процесс вывода достаточно трудоемкий, и точно не имеет место быть на экзамене, когда на счету каждая минута. Итак, воспользуемся производящей функцией для чисел Каталана [4]:
Теперь, с помощью данной функции, мы можем найти сумму ряда без значительных проблем.
Ответ получен, однако сколько времени для его получения бы затратил среднестатистический школьник? Отметим, также, что данный способ решения избавляет от следующей проблемы.
Если поменять вероятности и местами, т. е. мы будем удаляться от с меньшей вероятностью, то мы получим в ответе 1.
Когда мы будем рассматривать следующий способ, мы заметим, что у нас будет два ответа и выбор из них — проблема.
Итак, рассмотрим второй способ решения, за счёт широкого кругозора. В книге Мостеллера [5] была приведена следующая задача «На краю утеса» (рис. 2):
Есть пьяница, стоящий на обрыве. С вероятностью
он каждую секунду делает шаг вправо или влево.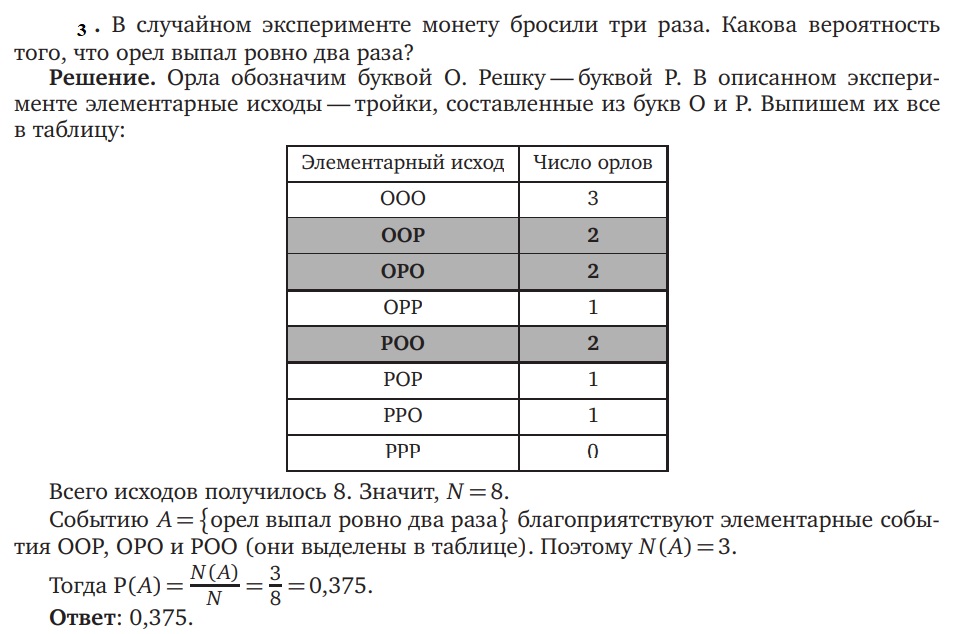 Какая вероятность того, что когда-нибудь он упадет?
Какая вероятность того, что когда-нибудь он упадет?
Рис. 2. Вырезка из книги
Опустим полное решение, описанное в данной книге, и приведём её урезанный вариант.
Вероятность того, что он упадет из точки 0 — . Из точки 1 — , а из точки 2 — (рис. 3). Что же должно произойти, чтобы человек свалился?
- Гуляя, человек должен оказаться в точке 0
- А после этого, он должен упасть
Рис. 3. Иллюстрация к задаче
Какова вероятность того, что человек из единицы попадет в ноль? Заметим, что мы можем мысленно сдвинуть обрыв, получая тем сам аналогичную задачу (отметим, что это возможно благодаря тому, что ряд бесконечный, и сдвиг или удаление/добавление ограниченного количества элементов не меняет предел). Соответственно, вероятность упасть из позиции 1 есть вероятность того, что мы когда-нибудь сместимся на шаг назад, т. е.
. Это вероятность того, что человек сместится влево. Получаем, что
,
и т. д. Значит, нам осталось лишь найти
.
Получаем, что
,
и т. д. Значит, нам осталось лишь найти
.
Находясь в точке 0, человек может сразу пойти влево, или же сделать шаг вправо, а потом когда-нибудь влево. Тогда мы получаем равенство, зная, что .
Теперь, решим полученное равенство, пользуясь тем, что :
Это означает, что как бы далеко от обрыва не стоял человек, рано или поздно он упадет. Заметим, что, данное рассуждение достаточно сложно провести, не зная его заранее. Также стоит отметить, что в данной задаче вероятности и были равны. Посмотрим, что будет в нашем случае.
Вернемся к исходной задаче (рис. 1). Какова вероятность попасть в ? Можно сразу из точки попасть в , а можно сначала попасть в , потом в , а потом в :
Вероятность попасть из единицы в минус единицу, по аналогии с данной задачей, будет равна
Выполнив замену, получаем равенство:
Итак, мы получаем два ответа, причём правильным из них оказывается 0,25.
Насколько нам известно, ответ будет зависеть от следующего частного . В случае, если его значение больше 1, в ответе всегда получится 1 (что автоматически решает задачу, еще на стадии её задания, и моментально выписывается ответ, целесообразность чего мы не понимаем), если же значение меньше 1, как в нашем случае ( ), то мы получаем ответ.
Отметим, что данный вывод достаточно очевиден, если понимать основы случайных процессов (также не изучающщихся в школьной программе). В случае если частное больше 1, подразумевается, что вероятность спуститься ниже выше, а следовательно, в среднем, на каждый шаг вверх, приходится шагов вниз. В таком случае, очевидно, что мы всегда достигнем значения , сколь долго мы бы не удалялись от него.
В обратном случае ситуация противоположная, и шанс опуститься до снижается в зависимости от уменьшения значения .
На фоне этого, возникает максимально оптимальный вариант решения данной задачи — алгоритмический.
Рассмотрим частное , ответом будет следующее значение:
Отметим, что данный способ полностью обесценивает какие-либо рассуждения данной задачи, и позволяет, даже не читать задачу, а просто записать ответ, что очевидно, не соответствует уровню итогового экзамена, проверяющего знания.
Также, в заключении отметим, что большинство элементов, рассмотренных в данной статье отсутствуют в подавляющем числе школьных учебников, что напрямую увеличивает нагрузку как на педагогов, за счёт поиска и подготовки данного материала, а также сложность грамотной передачи знаний в головы учащихся, а также увеличивает нагрузку на учащихся в плане восприятия новой для них информации, и форсированного расширения кругозора знаний.
Использование же, последнего приведённого способа помимо обесценивания задачи, приводит также к банальной зубрежке формулы, что для изучения математики грозит резким снижением качества образования.
Литература:
- Открытый банк математических задач ЕГЭ.
 Профильный уровень. https://prof.mathege.ru/
Профильный уровень. https://prof.mathege.ru/ - Спивак А. Числа Каталана. // Квант. 2004. — № 3. — с. 2–10.
- Гарднер М. Числа Каталана. // Квант. 1978. — № 7. — с. 20–26.
- Числа Каталана. https://internat.msu.ru/media/uploads/2015/12/CHisla-Katalana_jk.pdf
- Мостеллер, Ф. Пятьдесят занимательных вероятностных задач с решениями / Ф. Мостеллер. — М.: Наука, 1971. — 103 с.
4 задание ЕГЭ по математике профильного уровня 2023: теория и практика
Русский язык Математика (профиль) Математика (база) Обществознание История Биология Физика Химия Английский язык Информатика Литература
Задание 1 Задание 2 Задание 3 Задание 4 Задание 5 Задание 6 Задание 7 Задание 8 Задание 9 Задание 10 Задание 11 Задание 12 Задание 13 Задание 14 Задание 15 Задание 16 Задание 17 Задание 18
За это задание ты можешь получить 1 балл. На решение дается около 5 минут. Уровень сложности: повышенный.
На решение дается около 5 минут. Уровень сложности: повышенный.
Средний процент выполнения: 86.9%
Ответом к заданию 4 по математике (профильной) может быть целое число или конечная десятичная дробь.
Разбор сложных заданий в тг-канале
Посмотреть
Задачи для практики
Задача 1
Чтобы поступить в институт на специальность «Комплексное использование и охрана водных ресурсов», абитуриент должен набрать на ЕГЭ не менее $70$ баллов по каждому из трёх предметов — математике, русскому языку и физике. Чтобы поступить на специальность «Безопасность жизнедеятельности в техносфере», нужно набрать не менее $70$ баллов по каждому из трёх предметов — математике, русскому языку и химии. Вероятность того, что абитуриент Э. получит не менее $70$ баллов по математике, равна $0{,}5$, по русскому языку — $0{,}7$, по физике — $0{,}6$ и по химии — $0{,}3$. Найдите вероятность того, что Э. сможет поступить хотя бы на одну из двух упомянутых специальностей.
сможет поступить хотя бы на одну из двух упомянутых специальностей.
Решение
Чтобы поступить хотя бы на одну специальность, абитуриенту Э. надо набрать не менее 70 баллов по математике, русскому языку и хотя бы по одному из предметов химия и физика.
Найдём вероятность того, что абитуриент Э. наберёт не менее 70 баллов хотя бы по одному из предметов химия и физика. Сначала отыщем вероятность противоположного события, то есть вероятность того, что абитуриент Э. по обоим этим предметам не наберёт 70 баллов. Результаты экзаменов не зависят друг от друга, вероятность не набрать 70 баллов по физике равна 1 — 0.6 = 0.4, а вероятность не набрать 70 баллов по химия равна 1 — 0.3 = 0.7. Отсюда вероятность того, что абитуриент Э. по обоим этим предметам не наберёт 70 баллов, равна 0. 4 · 0.7 = 0.28. Следовательно, вероятность того, что абитуриент Э. наберёт не менее 70 баллов хотя бы по одному из предметов химия и физика, равна 1 — 0.28 = 0.72.
4 · 0.7 = 0.28. Следовательно, вероятность того, что абитуриент Э. наберёт не менее 70 баллов хотя бы по одному из предметов химия и физика, равна 1 — 0.28 = 0.72.
Таким образом, вероятность того, что абитуриент Э. наберёт не менее 70 баллов по математике, русскому языку и хотя бы по одному из предметов химия и физика, равна 0.5 · 0.7 · 0.72 = 0.252.
Ответ: 0.252
Показать решение
Полный курс
Задача 2
Биатлонист Алексей Антонов пять раз стреляет по мишеням. Вероятность попадания при одном выстреле равна $0{,}7$. Найдите вероятность того, что биатлонист Алексей Антонов один раз попал по мишени, а четыре — промахнулся. Результат округлите до сотых.
Решение
Вероятность промахнуться при одном выстреле равна $1 — 0.7 = 0.3$. Обозначим события.
1. $A_1$ — «Алексей попал по мишени при первом выстреле».
2. $A_2$ — «Алексей попал по мишени при втором выстреле».
3. $A_3$ — «Алексей попал по мишени при третьем выстреле».
4. $A_4$ — «Алексей попал по мишени при четвёртом выстреле».
5. $A_5$ — «Алексей попал по мишени при пятом выстреле».
События ${A_1}↖{-}, {A_2}↖{-}, {A_3}↖{-}, {A_4}↖{-}$ и ${A_5}↖{-}$ — означают, что Алексей промахнулся при соответствующем выстреле.
Событие «Алексей Антонов первый раз попал по мишени, а последние четыре промахнулся» означает одновременное наступление (пересечение) независимых событий ${A_1}, {A_2}↖{-}, {A_3}↖{-}, {A_4}↖{-}$ и ${A_5}↖{-}$.
$P (A_1 ∩ {A_2}↖{-} ∩ {A_3}↖{-} ∩ {A_4}↖{-} ∩ {A_5}↖{-}) = P (A_1) · P ({A_2}↖{-}) · P ({A_3}↖{-}) · P ({A_4}↖{-}) · P ({A_5}↖{-}) = 0.7 · 0.3 · 0.3 · 0.3 · 0.3 = 0.00567$.
По условию Алексей мог попасть единожды, но это попадание могло прийтись на любой из пяти выстрелов, не обязательно на первый.
Тогда, аналогично, $P ({A_1}↖{-} ∩ A_2 ∩ {A_3}↖{-} ∩ {A_4}↖{-} ∩ {A_5}↖{-}) = P ({A_1}↖{-}∩ {A_2}↖{-} ∩ A_3 ∩ {A_4}↖{-} ∩ {A_5}↖{-}) =$
$= P ({A_1}↖{-} ∩ {A_2}↖{-} ∩ {A_3}↖{-} ∩ A_4 ∩ {A_5}↖{-}) = P ({A_1}↖{-} ∩ {A_2}↖{-} ∩ {A_3}↖{-} ∩ {A_4}↖{-} ∩ A_5) =$
$= P (A_1 ∩ {A_2}↖{-} ∩ {A_3}↖{-} ∩ {A_4}↖{-} ∩ {A_5}↖{-}) = (0. 4 · 0.7 = 0.00567$.
4 · 0.7 = 0.00567$.
Следовательно, искомая вероятность равна $0.00567 · 5 = 0.02835 ≈0.03$.
Ответ: 0.03
Показать решение
Полный курс
Задача 3
Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы $4$ очка в двух играх. Если команда выигрывает, она получает $3$ очка, в случае ничьей — $1$ очко, если проигрывает — $0$ очков. Найдите вероятность того, что команде «Ветерок» удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны $0{,}3$.
Решение
Вероятность ничьей в каждой игре равна 1 — 0.3 — 0.3 = 0.4 (из единицы вычитаем вероятность выигрыша и вероятность проигрыша). «Ветерок» выйдет в следующий круг в одном из трёх следующих случаев.
1. «Ветерок» выиграет обе игры. Вероятность этого равна 0.3 · 0.3 = 0.09.
2. «Ветерок» выиграет первую игру и сыграет вничью вторую. Вероятность этого равна 0.3 · 0.4 = 0.12.
Вероятность этого равна 0.3 · 0.4 = 0.12.
3. «Ветерок» сыграет вничью первую игру и выиграет вторую. Вероятность этого равна 0.4 · 0.3 = 0.12.
Искомая вероятность равна 0.09 + 0.12 + 0.12 = 0.33.
Ответ: 0.33
Показать решение
Полный курс
Задача 4
Помещение торгового дома «Светлый» освещается фонарём с двумя лампами. Вероятность перегорания одной лампы в течение года равна $0{,}6$. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
Решение
Найдём вероятность события «перегорели обе лампы», а затем искомую вероятность.
Вероятность события «перегорела первая лампа» равна вероятности события «перегорела вторая лампа» и равна 0.6. Эти два события независимы, значит, вероятность того, что они наступили оба, равна произведению их вероятностей, то есть равна 0.6 · 0.6 = 0.36. Это вероятность события «перегорели обе лампы».
События «перегорели обе лампы» и «хотя бы одна лампа не перегорела» противоположны, следовательно, сумма их вероятностей равна 1. Значит, вероятность события «хотя бы одна лампа не перегорела» равна 1 — 0.36 = 0.64.
Ответ: 0.64
Показать решение
Полный курс
Задача 5
В ларьке на улице Счастья стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью $0{,}1$ независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.
Решение
Найдём вероятность события «оба автомата неисправны», а затем искомую вероятность.
Вероятность события «неисправен первый автомат» равна вероятности события «неcисправен второй автомат» и равна 0,1. Эти два события независимы, значит, вероятность того, что они наступят оба, равна произведению их вероятностей, то есть равна 0.1 · 0.1 = 0.01. Таким образом, мы нашли вероятность события «оба автомата неисправны».
События «оба автомата неисправны» и «хотя бы один автомат исправен» противоположны, следовательно, сумма их вероятностей равна 1. Значит, вероятность события «хотя бы один автомат исправен» равна 1 — 0.01 = 0.99.
Ответ: 0.99
Показать решение
Полный курс
Задача 6
Если шахматист А. играет белыми фигурами, то он выигрывает у шахматиста Б. с вероятностью $0{,}72$. Если А. играет чёрными, то А. выигрывает у Б. с вероятностью $0{,}6$. Шахматисты А. и Б. играют две партии, причём во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.
Решение
По условию вероятность события «шахматист А. выиграет белыми» равна $0{,}72$, вероятность события «шахматист А. выиграет чёрными» равна $0{,}6$. Эти события независимы. Значит, вероятность того, что оба этих события наступят (А. выиграет оба раза) равна произведению вероятностей, то есть равна $0{,}72⋅ 0{,}6=0{,}432$.
Ответ: 0.432
Показать решение
Полный курс
Задача 7
На железнодорожном вокзале $3$ кассира. Каждый из них занят с клиентом с вероятностью $0{,}2$ независимо от других кассиров. Найдите вероятность того, что в случайный момент времени все три кассира заняты одновременно.
Решение
События «первый кассир занят», «второй кассир занят» и «третий кассир занят» по условию независимы. Тогда вероятность их одновременного наступления (вероятность пересечения событий) равна произведению вероятностей этих событий, то есть равна 0.2 · 0.2 · 0.2 = 0.008.
Ответ: 0.008
Показать решение
Полный курс
Задача 8
В магазине сантехники три продавца. Каждый из них занят с клиентом с вероятностью $0{,}7$ независимо от других продавцов. Найдите вероятность того, что в случайный момент времени все три продавца заняты одновременно.
Решение
События «первый продавец занят», «второй продавец занят» и «третий продавец занят» по условию независимы.
Тогда вероятность их одновременного наступления (вероятность пересечения событий) равна произведению вероятностей этих событий
То есть равна $0.7 · 0.7 · 0.7 = 0.343$
Ответ: 0.343
Показать решение
Полный курс
Задача 9
Вероятность того, что новый электрический чайник прослужит больше года, равна $0{,}93$. Вероятность того, что он прослужит больше двух лет, равна $0{,}84$. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
Решение
Заметим, что из событий «чайник прослужит меньше года», «чайник прослужит от 1 до 2 лет» и «чайник прослужит больше двух лет» произойдёт обязательно ровно одно, то есть, говоря математическим языком, они попарно несовместны, а их объединение — достоверное событие. Следовательно, сумма вероятностей этих событий равна 1.
При этом события «чайник прослужит меньше года» и «чайник прослужит больше года» противоположны, поэтому вероятность события «чайник прослужит меньше года» равна 1 — 0.93 = 0.07. Заполним таблицу.
| Событие | Прослужит меньше года | Прослужит от 1 до 2 лет | Прослужит больше двух лет |
| Вероятность | 0.07 | ? | 0.84 |
Отсюда искомая вероятность равна 1 — 0.07 — 0.84 = 0.09.
Ответ: 0.09
Показать решение
Полный курс
Задача 10
На экзамене по биологии студент отвечает на один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос по теме «Млекопитающие», равна $0{,}36$. Вероятность того, что это вопрос по теме «Бактерии», равна $0{,}18$. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене студенту достанется вопрос по одной из этих двух тем.
Решение
Из условия следует, что события A = «достанется вопрос по теме Млекопитающие» и B = «достанется вопрос по теме Бактерии» несовместны. Действительно, нет билетов, относящихся к обоим этим темам одновременно. Событие «достанется вопрос по одной из этих двух тем» — это объединение событий A и B (A $∪$ B). По формуле вероятности объединения несовместных событий получим, что искомая вероятность равна P(A $∪$ B) = P(A) + P(B) = 0.36 + 0.18 = 0.54.
Ответ: 0.54
Показать решение
Полный курс
Задача 11
В торговом центре два одинаковых автомата продают лимонад. Вероятность того, что к концу дня в автомате закончится лимонад, равна $0{,}2$. Вероятность того, что лимонад закончится в обоих автоматах, равна $0{,}09$. Найдите вероятность того, что к концу дня лимонад останется в обоих автоматах.
Решение
По условию вероятность события A =«лимонад закончится в первом автомате» равна вероятности события B =«лимонад закончится во втором автомате» и равна $0. 2$. Эти два события зависимые.
2$. Эти два события зависимые.
В этом случае воспользуемся формулой $P (A + B) = P (A) + P (B) — P (A B)$.
$P (A + B) = 0.2 + 0.2 — 0.09 = 0.31$. Событие $A + B$ — это событие «лимонад закончилась хотя бы в одном автомате». Указанное событие противоположно искомому. Отсюда вероятность события «лимонад останется в обоих автоматах» равна $1 — 0.31 = 0.69$.
Ответ: 0.69
Показать решение
Полный курс
Задача 12
Предприниматель закупает для продажи на рынке куриные яйца в двух хозяйствах. $50%$ яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — $40%$ яиц высшей категории. При продаже яиц на рынке оказалось, что всего получилось $42%$ яиц высшей категории. Найдите вероятность того, что яйцо, купленное у предпринимателя, окажется из второго хозяйства.
Решение
Ответ: 0.8
Показать решение
Полный курс
Задача 13
Робин Гуд подошел к столу, на котором лежали 3 его старых лука и 2 новых. Он решил сбить стрелой яблоко с дерева. Робин попадает в цель из своего старого лука с вероятностью $0{,}8$, а из нового — с вероятностью $0{,}3$. Робин случайным образом выбирает один лук. Найдите вероятность того, что Робин промахнётся при стрельбе.
Он решил сбить стрелой яблоко с дерева. Робин попадает в цель из своего старого лука с вероятностью $0{,}8$, а из нового — с вероятностью $0{,}3$. Робин случайным образом выбирает один лук. Найдите вероятность того, что Робин промахнётся при стрельбе.
Решение
Ответ: 0.4
Показать решение
Полный курс
Показать еще
Для доступа к решениям необходимо включить уведомления от группы Турбо в вк — это займет буквально 10 секунд. Никакого спама, только самое важное и полезное для тебя. Ты всегда можешь запретить уведомления.
Включить уведомления
Готовим к ЕГЭ на 85+ баллов и побеждаем лень
Каждый месяц 12 онлайн-занятий в дружелюбной атмосфере + 16 домашних работ с жесткими сроками.
Не готовишься — вылетаешь.
 Подробнее о курсе
Подробнее о курсеИнформация для заказа учебников и учебных пособий
Распространители учебников и учебных пособий
Общество актуариев предоставляет эту информацию своим кандидатам для удобства. Ни одна из этих услуг не спонсируется и не поддерживается Обществом. Нет необходимости использовать какие-либо из этих услуг, но многие кандидаты предпочитают ими пользоваться.
Обратите внимание, что экзаменационная комиссия ожидает, что кандидаты прочитают материалы, указанные в Syllabus и использовать другие материалы в качестве дополнения к первоисточникам, а не их замены.
ACTEX Learning — все экзамены и модули
- Учебные пособия — экзамены P, FM, FAM, ALTAM, ASTAM, SRM, PA, VEE, многие экзамены уровня FSA, а также EA-1, EA-2F- EA- 2л.
- GOAL — Управляемое актуарное онлайн-обучение — P, FM, FAM, ALTAM, ASTAM и SRM.
- Обучающие видео — P, FM, FAM, ALTAM, ASTAM, SRM, PA ATPA
- Учебные курсы – P, FM, FAM, SRM
- Онлайн-курсы – P.
 FM, ATPA и VEE.
FM, ATPA и VEE. - Учебники — для многих экзаменов — как обязательные, так и рекомендуемые
- Гарантия прохождения — P, FM, IFM, LTAM, STAM, SRM, PA и VEE.
- тел.: +1-800-282-2839 (в США и Канаде)
- тел.: +1-860-379-5470 Электронная почта
- : [email protected]
Книжный магазин актуариев – Все экзамены и модули – США и Канада
- Полный спектр услуг, полный охват всех ваших актуарных учебных потребностей.
- тел.: +1-800-582-9672
- тел.: +1-603-430-1252
- электронная почта: [email protected]
ASM (актуарные учебные материалы) – экзамены P, FM, FAM, ALTAM, ASTAM, SRM и EA–1, EA–2 F и EA–2 L
- Эксклюзивно продается ACTEX Learning и The Actuarial Bookstore.
- Учебные пособия — Exam P, FM, FAM, ALTAM, ASTAM, SRM и EA-1, EA-2F, EA-2L.
- GOAL — Управляемое актуарное онлайн-обучение — P, FM, FAM, ALTAM, ASTAM, SRM.

- Обучающие видео — P, FM, FAM, ALTAM, ASTAM, SRM.
- Видеорешения — FAM
- Учебные курсы – P, FM, FAM, SRM
- Гарантия прохождения — P, FM, FAM, ALTAM, ASTAM, SRM.
- электронная почта: [email protected]
Коучинг актуариев-экзамен P, FM, FAM, ALTAM, ASTAM, SRM, PA, VEE
- Адаптация (онлайн-практические тесты): P, FM, FAM, SRM, ASTAM и ALTAM.
- Руководства: P, FM, FAM, ALTAM, ASTAM и SRM
- видеоуроков: P, FM FAM, ALTAM, ASTAM, SRM, PA (включая пробные экзамены) и VEE
- Таблицы формул и другие продукты также доступны.
- Доступна скидка для студентов, обратитесь в службу поддержки по адресу [email protected].
Экзамены Edge Actuarial – Пенсионные экзамены DA, FR и RPIRM
- Только в The Actuarial Bookstore и ACTEX
- +1-800-582-9672 (только в США и Канаде)
- +1-603-430-1252 (за пределами США)
- электронная почта: sales@actuarialbookstore.
 com
com
Книжный магазин FIA – учебники для всех экзаменов; Учебные пособия для экзаменов ASA, FSA Exams, GH, RET, ERM, QFI, ILA Tracks
- 200 Dey St., Suite 247
- Харрисон, Нью-Джерси 07029
- электронная почта: [email protected]
Актуарные учебные пособия Говарда Малера – экзамены ASTAM, CAS S, CAS 5 и CAS 8
- электронная почта: [email protected]
Бесконечный актуарий – экзамены P, FM, ALTAM, ASTAM, SRM, FAM, GHDP, GHRM и GHVR, LFM, LAM и LPM, EA–1, EA–2F, EA–2 L, ERM, QFIQF, QFI IRM, QFIPM
- Семинары онлайн и онлайн
- 3590-B US Hwy 31 South Ste #227
- Пелхам, штат Алабама 35124
- тел.: +1-888-842-1006
- Ф: +1-888-544-6164 Электронная почта
- : [email protected]
PAK Study Manual – Exams ERM, CFE, SDM, QFIQF, QFIPM, IRM, LPM, LFM, LAM, GHVR, GHDP, GHRM и RPIRM
- электронная почта: services@pakstudymanual.
 com
com
XP Актуарные экзамены SDM
- электронная почта: [email protected]
Экзамен SOA P (вероятность) Примеры задач
- Список продуктов
- Партнерство
- Обучение
- Цены
- Войти
- Помощь и обратная связь
Практические вопросы SOA Exam P
Получите доступ к более чем 500 практическим задачам в стиле экзамена
Зарегистрироваться бесплатно
У нас в AnalystPrep есть все, что вам нужно для оттачивания вашего вероятностного ума. Наши проблемы с вероятностной практикой отражают сложность и стиль живого экзамена P от Общества актуариев. Все наши вопросы с несколькими вариантами ответов (от A до E – как и на самом экзамене) регулярно обновляются с учетом последних обзоров нашей команды ученых и актуариев.
Помимо получения актуальных учебных материалов, вы также получаете доступ к нашим настраиваемым викторинам и показателям производительности, разработанным специально для того, чтобы помочь вам улучшить свои слабые стороны. Кроме того, наши учебные записи и круглосуточная поддержка гарантированно помогут вам подготовиться к актуарному экзамену P.
Кроме того, наши учебные записи и круглосуточная поддержка гарантированно помогут вам подготовиться к актуарному экзамену P.
3,5 Миллион
Вопросы, на которые ответили наши пользователи
50 Тысяч
Довольных клиентов
# 1 Рейтинг
Подготовительная платформа в соответствии с отзывами на веб-сайтах
Как подразделяется банк вопросов
?Банк вопросов AnalystPrep для экзамена P был специально разработан на основе программы, разработанной Обществом актуариев. Таким образом, он подразделяется на три темы:
- Общая вероятность (10-17%)
- Одномерные случайные величины (40-47%)
- Многомерные случайные величины (40-47%)
Тем не менее, каждая тема также подразделяется на каждую из целей обучения, указанных в SOA syallbus. Например, одна цель обучения может звучать так:
Рассчитать дисперсию, стандартное отклонение для условного и предельного распределения вероятностей.
После того, как вы попрактикуетесь с несколькими нашими практическими вопросами из данной учебной цели, вы можете перейти к следующему. При этом вы убедитесь, что ни одна важная концепция не осталась позади.
Однако банк вопросов и ответов не означает, что вы будете пересматривать и практиковаться в одиночку. Наша команда опытных инструкторов всегда готова дополнить предлагаемые решения дополнительными советами и рекомендациями.
Вопрос 93
Общая вероятность (условные вероятности)
60 % страхователей страховщика — мужчины и 40 % — женщины. Вероятность того, что у мужчины будет претензия, в два раза выше, чем у женщины. Учитывая, что у случайно выбранного страхователя есть претензия, какова вероятность того, что это мужчина?
A) 25%
B) 40%
C) 50%
D) 60%
E) 75%
Подтвердить
Правильный ответ: E)
\( P\left( Male|Claim\right) ={ P\left( Male\quad and\quad Claim \right) }/{ P\left( Claim\right) }={ . 60\ast 2x }/{ \left( .60\ast 2x+.40\ast x \right) }={ 1.2x }/{ 1.6x }=\bf .75\quad or\quad 75\ %\)
60\ast 2x }/{ \left( .60\ast 2x+.40\ast x \right) }={ 1.2x }/{ 1.6x }=\bf .75\quad or\quad 75\ %\)
Более 500 практических вопросов
Вопрос 121
Общая вероятность (теорема Байеса)
Тест на болезнь сердца дает ложноположительный результат в 5% случаев. 25% населения имеют болезни сердца и 20% имеют положительный результат теста. При отрицательном результате теста какова вероятность того, что у пациента нет болезни сердца?
A) 67%
B) 70%
C) 55%
D) 87%
E) 93%
Подтвердить
Правильный ответ: E)
Пусть событие \(H\) — болезнь сердца, а событие \(+\) — положительный тест.
\(P\left( H’ \right) =P\left( H’|+ \right) \ast P\left( + \right) +P\left( H’|- \right) \ast \left ( 1-P\влево( + \вправо) \вправо) \)
\(.75 = .05 \ast .20 + x \ast \влево(1-.20\вправо) \)
\(.75 = .01 + .80x\)
\({.74}/{.80} = x\)
\(x = .925 \quad or \quad \bf 93\%\)
Попробуйте бесплатно
Вопрос 306
Одномерные случайные величины (кумулятивные функции распределения)
Вы думаете о получении кредита на свой первый дом, но обнаруживаете, что процентная ставка является переменной величиной и обычно находится в интервале (0,09{ln(v)-ln(100,000)}\\
& = 11,11ln(v) — 11,11ln(100,000) — 1\\
& = 11,11\bigg[ln\bigg(\frac{v}{100,000} -0. 09\bigg)\bigg]
09\bigg)\bigg]
\end{align*}
Практика, чтобы пройти
Вопрос 155
Одномерные случайные величины (вычисление ожидаемого значения, моды, медианы, процентиля и высших моментов)
Учитывая следующую функцию плотности вероятности:
$$ f\left( x \right) =\begin{cases} .15 & x=1 \\ .25 & x=2 \\ .35 & x=3 \\ C & x=4 \end{cases} $$ 9{th}\) процентиль равен \(\bf X=2\).
Отслеживайте эффективность по темам
Вопрос 261
Одномерные случайные величины (сумма независимых случайных величин – распределение Пуассона)
Учитывая, что время (в днях) до момента подачи иска в страховую компанию является экспоненциальной случайной величиной с \(\lambda =.05\), а время до выплаты иска после его подачи является экспоненциальной случайной величиной с \(\lambda=.10\) и не зависит от времени до подачи иска, найти \(SD\влево(X+Y\вправо)\). 9{ x=1 }=\bf .17 \\ \end{align*}
Обобщенные примечания по каждой цели обучения
Вопрос 336
Многомерные случайные величины (совместные функции вероятности)
Пусть X представляет возраст застрахованного автомобиля, попавшего в аварию.

 Профильный уровень. https://prof.mathege.ru/
Профильный уровень. https://prof.mathege.ru/
 com
com com
com