Эксцентриситет формула: Как найти эксцентриситет 🚩 длина окружности эллипса формула 🚩 Математика

Как рассчитать эксцентриситет орбиты Земли

содержание

Как рассчитать эксцентриситет орбиты?

⁠) дает угол проекции идеального круга на эллипс с эксцентриситетом e. Например, чтобы визуализировать эксцентриситет планеты Меркурий (e = 0.2056), нужно просто вычислить арксинус, чтобы найти угол проекции 11.86 градуса.

Что такое эксцентриситет Земли?

Эксцентриситет орбиты Земли можно получить из отношения максимального расстояния к минимальному расстоянию между Землей и Солнцем. Простой способ сделать вывод об эксцентриситете земной орбиты — посмотреть на изменение видимого диаметра Солнца.

Как рассчитать орбиту планеты?

Эти расчеты основаны на трех законах Кеплера и на данных Кеплера, наборе из шести параметров, позволяющих определить орбиту объекта вокруг любого другого небесного тела. Среди этих параметров у нас есть длина эллипса по его самой широкой оси — главной оси.

Что такое эксцентриситет орбит?

Эксцентриситет орбиты — это отношение расстояния между двумя фокусами эллипса и большой полуосью — чем ближе к нулю, тем более круговой орбита планеты.

Как рассчитать орбиту?

Эти расчеты основаны на трех законах Кеплера и на данных Кеплера, наборе из шести параметров, позволяющих определить орбиту объекта вокруг любого другого небесного тела. Среди этих параметров у нас есть длина эллипса по его самой широкой оси — главной оси.

Что такое орбита L2?

Л2. Точка L2 расположена на внешней части орбиты Земли вдоль линии, соединяющей Землю и Солнце. Спутник WMAP установлен в этой точке с 2001 года, а также планируется установка космического телескопа Джеймса Уэбба, который дополнит космический телескоп Хаббла.

Как рассчитать эксцентриситет?

2) поскольку эксцентриситет e эллипса определяется как e = c/a , в крайнем случае членов b = a кривая будет не эллипсом, а окружностью с нулевым эксцентриситетом, поскольку b = a приводит к c = 0 и, следовательно, e = c/a = 0/a = 0.

Каково значение эксцентриситета?

Эксцентриситет говорит нам, насколько сглажен эллипс, чем выше значение эксцентриситета, тем ближе к окружности будет эллипс. Поскольку большая ось всегда длиннее фокусного расстояния, то, следовательно, с < а, поэтому это деление всегда представляет собой число от 0 до 1.

Насколько больше эксцентриситет?

эксцентриситет эллипса

Еще одним важным соотношением является эксцентриситет, чем больше эксцентриситет, тем более плоским будет эллипс, эксцентриситет является отношением длины с и длины а: Так как а > с, то.

Как рассчитать радиус орбиты?

Средний радиус орбиты, используемый при расчете третьего закона Кеплера, определяется как среднее значение между максимальным и минимальным радиусом. Показанные на рисунке положения, характеризующие наибольшее и наименьшее расстояние Земли от Солнца, называются соответственно афелием и перигелием.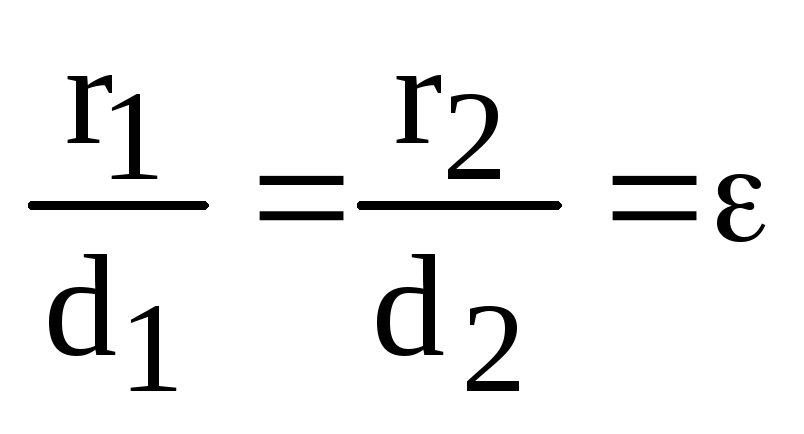

Какова формула третьего закона Кеплера?

Куб среднего радиуса орбиты планеты (т.е. R3) прямо пропорционален квадрату периода обращения (т.е. Т2) небесного тела вокруг Солнца.

Формула третьего закона Кеплера.

Планета	Период (земные годы)	Средний радиус (AU)
Нетуно	164,800	30,060

Как высоко покинуть орбиту Земли?

Данные подтвердили теории других ученых, установивших высоту 118 километров как последнюю границу Земли. Выше этой высоты космическое пространство можно считать начинающимся.

Какова величина эксцентриситета коники?

Неподвижная точка F называется фокусом, неподвижная линия d — направляющей, а постоянное отношение «е» — эксцентриситетом коники. – Если e = 1, коника является параболой.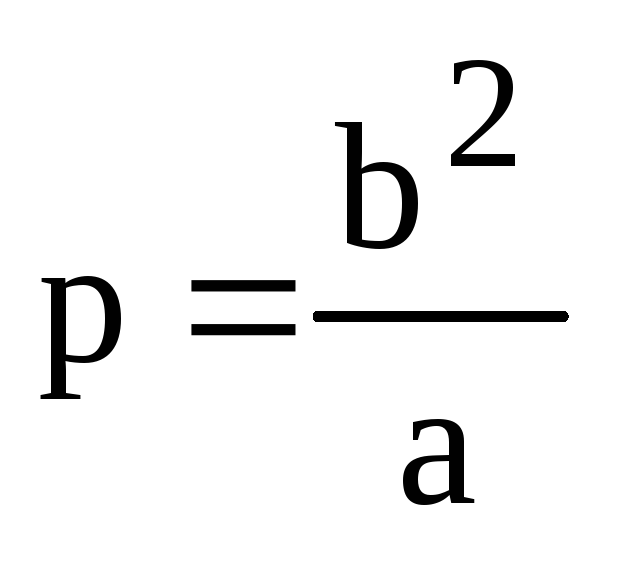 – Если e < 1, коника является эллипсом. — Если e > 1, то коника является гиперболой.

Как называется наклон Земли?

В настоящее время наклон оси Земли составляет 23°26’21”, однако это значение не является фиксированным. Наклон планеты колеблется между 22° и 25° в цикле, для завершения которого требуется 41.000 XNUMX лет.

Какая из планет имеет наибольший и наименьший эксцентриситеты?

Гиперболическая орбита имеет эксцентриситет больше 1. Нептун, Венера и Земля — планеты с наименьшим эксцентриситетом орбит в нашей Солнечной системе. Плутон и Меркурий — планеты с самыми эксцентричными орбитами в нашей Солнечной системе.

Какова скорость обращения вокруг Земли?

Средняя орбитальная скорость Земли составляет 29,78 км/с, максимальная — 30,29 км/с, минимальная — 29,29 км/с.

Какова орбитальная скорость Земли?

Когда Земля находится ближе всего к Солнцу (R = 147. 100.000 30,2 108.720,7 км), мы находим для ее скорости за счет поступательного движения 152.100.000 км/с (109.040 XNUMX км/ч). Когда Земля находится дальше всего от Солнца (R = XNUMX XNUMX XNUMX км), полученная скорость составляет примерно XNUMX XNUMX км/ч.

Как рассчитать орбитальную скорость Земли вокруг Солнца?

Если мы разделим это значение на время, за которое Земля совершает полный оборот вокруг Солнца (т. е. на год), что соответствует 365 дням * 24 часам * 60 минутам * 60 секундам, мы вскоре получим значение, близкое к 30 км/с. . Таким образом, Земля вращается вокруг Солнца с линейной скоростью, близкой к 30 км/с.

Сколько существует типов орбит?

Существует три типа орбит, на которых обычно располагается спутник: низкая околоземная орбита (НОО), средняя околоземная орбита (СОО) и геостационарная орбита (ГЕО).

Точки Лагранжа — это места между орбитами двух тел в пространстве, где их гравитационные поля компенсируют друг друга. Они очень удобны для размещения телескопов, как в случае с James Webb и SOHO.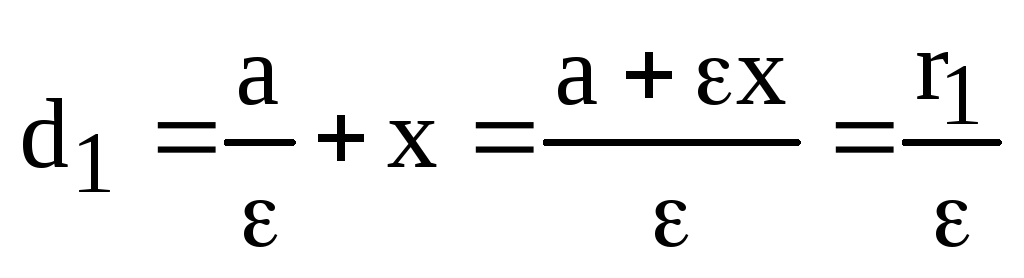 Но кроме того, они помогли решить одну из величайших задач в физике.

В микроэкономике функция Лагранжа (или просто лагранжиан) — это функция, используемая для решения задач условной оптимизации как в механике, так и в других областях, не обязательно в физике.

Что такое эксцентриситет окружности?

Окружность на самом деле представляет собой идеальный эллипс, эксцентриситет которого равен нулю.

Что такое равносторонняя гипербола?

Мы говорим, что гипербола равносторонняя, если длина фокальной оси равна длине нефокальной оси, то есть а = b. Таким образом, прямоугольник основания равносторонней гиперболы на самом деле является квадратом.

Что такое начальный эксцентриситет?

Начальный эксцентриситет (ei): это отношение между изгибающим моментом и нормальной силой, полученное в результате анализа конструкции.

Как вычислить эксцентриситет гиперболы?

1 – Определить эксцентриситет гиперболы уравнения 25x² — 16лет² – 400 = 0. РЕШЕНИЕ: Имеем: 25x² — 16лет² = 400. Обратите внимание, что уравнение гиперболы не в редуцированной форме. Разделим обе части на 400.

Что такое эксцентриситет коники?

В математике эксцентриситет — это параметр, связанный с любой коникой, который измеряет ее отклонение от окружности.

Как рассчитать эксцентриситет сваи?

Mx и My — моменты, обусловленные эксцентриситетом свай; Мх = Р*Еу; Мой = Р*Ех; Ex и Ey — разность координат между центром приложения нагрузки (центром колонны) и центром реакции сваи.

Что говорит нам первый закон Кеплера?

Первый закон Кеплера, называемый законом эллиптических орбит, гласит следующее: в фиксированной системе отсчета на Солнце орбиты планет представляют собой эллипсы, а Солнце занимает один из фокусов. В таблице ниже показаны эксцентриситеты орбит восьми планет Солнечной системы.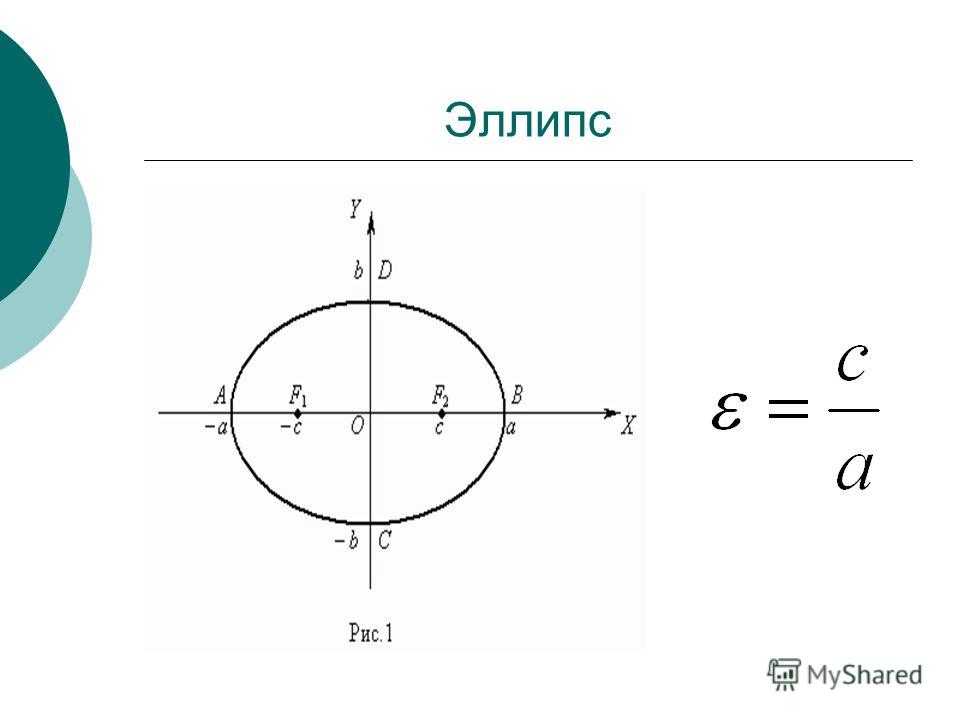

Как уменьшить уравнение эллипса?

Учитывая эллипс в декартовой плоскости, мы определяем его редуцированное уравнение, которое представляет собой уравнение вида (xh)²/a²+(yk)²/b²=1.

Каков радиус орбиты Земли?

Радиус орбиты Земли составляет 1,496.10 11 м, а радиус орбиты Ура.

По какой формуле вычисляется радиус?

Радиус составляет ровно половину диаметра. Итак, формула r = D/2. Эта формула идентична методу, используемому для вычисления радиуса круга по его диаметру.

Какова формула второго закона Кеплера?

Согласно этому закону области, выделенные как A₁ и A₂ равны и охватываются отрезком, соединяющим планету с Солнцем, через одинаковые промежутки времени. Следовательно, интервал времени Δt₁, затрачиваемое на сканирование области 1, должно быть равно интервалу времени Δt₂, затраченный на зачистку зоны 2.

Как там рассчитывается постоянная Кеплера?

Таблица 1: Расчет постоянной Кеплера для орбит вокруг Солнца.

Ошибка относительно K = 1 год²UA^–3 на Землю.

Закон периодов.

Планета	Юпитер
Период (лет)	11,85654
Среднее расстояние до Солнца (а.е.)	5,203
постоянная Кеплера	0,9981
Относительная ошибка (%)	0,2

О чем говорит четвертый закон Кеплера?

«Скорость планеты в любой момент времени обратно пропорциональна расстоянию от Солнца». Под орбитальной скоростью понимается скорость, касательная к траектории, описываемой планетой вокруг Солнца.

Сколько км до схода с орбиты?

Чтобы спутник всегда оставался над определенной точкой на поверхности Земли без необходимости вертикального и горизонтального движения, он должен всегда вращаться на фиксированном расстоянии 35 786 км над уровнем моря в плоскости земного экватора.

Сколько км оставаться на орбите?

Согласно второму закону Ньютона, чтобы объект на орбите оставался в фиксированном положении по отношению к земной поверхности, он должен находиться на фиксированном расстоянии 35. 786 XNUMX км от уровня моря и под экватором.

Какова скорость ухода с орбиты?

Это скорость, необходимая телу для обращения вокруг Земли: около 7,9 км/с (или 28.440 11,2 км/ч). Однако, чтобы навсегда покинуть Землю, ракете нужна стартовая скорость (XNUMX км/с) — больше, чем у спутников.

Как рассчитать конику?

Сумма расстояний d₁ издание₂ обозначается через 2a, т. е. 2a = d₁ + д₂ а расстояние между фокусами называется 2с, где 2а > 2с. Наибольшее расстояние между двумя точками, принадлежащими эллипсу, называется большой осью и его значение равно 2а. Наименьшее расстояние называется малой осью и обозначается 2b.

Как определить конику?

В обоих случаях пересечение конуса K с плоскостью π определяет конику. В случае, когда V ∈ π, коника вырождена и может быть прямой, парой прямых или точкой. В случае, когда V /∈ π, коника гладкая и может быть эллипсом, гиперболой или параболой.

Чему равен эксцентриситет уравнения эллипса?

Это измерение показывает, насколько эллипс «сплющен» или ближе к окружности. Поскольку у нас всегда будет a>c, мы можем заключить, что эксцентриситет эллипса всегда будет числом от 0 до 1.

Как вычислить эксцентриситет эллипса?

2) поскольку эксцентриситет e эллипса определяется как e = c/a , в крайнем случае членов b = a кривая будет не эллипсом, а окружностью с нулевым эксцентриситетом, поскольку b = a приводит к c = 0 и, следовательно, e = c/a = 0/a = 0.

Какова величина эксцентриситета коники?

Неподвижная точка F называется фокусом, неподвижная линия d — направляющей, а постоянное отношение «е» — эксцентриситетом коники. – Если e = 1, коника является параболой. – Если e < 1, коника является эллипсом. — Если e > 1, то коника является гиперболой.

Как рассчитать эксцентриситет конуса?

В этом случае c > a, а значит, эксцентриситет гиперболы есть действительное число больше единицы, то есть e > 1. a = b, мы будем иметь равностороннюю гиперболу, эксцентриситет которой будет равен e = … 2, результат, полученный путем подстановки a = b в приведенной выше формуле.

Эксцентриситет коник.

конический	e
гипербола	и > 1

05.2. Эксцентриситет и директрисы конических сечений

Эксцентриситет и директрисы конических сечений

Изучение кривых второго порядка окажется неполным, если обойти вниманием некоторые их замечательные свойства, используемые в разнообразных приложениях.

Для эллипса, отличного от окружности, а также для гиперболы и параболы обнаруживается универсальное свойство: существует прямая, называемая директрисой (в зависимости от типа кривой их может быть одна или две), для которой отношение расстояния от точек этих кривых до фокуса к расстоянию до отвечающей этому фокусу директрисы есть величина постоянная.

Как известно, в частном случае это свойство справедливо для параболы согласно ее определению. Покажем также справедливость данного свойства для эллипса и гиперболы. Введем предварительно в рассмотрение параметр, характеризующий форму эллипса и гиперболы.

Эксцентриситетом эллипса (гиперболы) будем называть величину

(5.8)

Где с – половина фокусного расстояния эллипса (гиперболы), а – длина большей полуоси эллипса (длина действительной полуоси гиперболы).

Учитывая, что половина фокусного расстояния с и длины полуосей связаны известными соотношениями:

Для эллипса

Для гиперболы

Получим формулы вычисления эксцентриситета этих кривых по параметрам канонических уравнений:

для эллипса (5.9)

для гиперболы (5.10)

Очевидно, что эксцентриситет эллипса меньше единицы, а эксцентриситет гиперболы – больше единицы. Если длины полуосей эллипса близки друг к другу, то его эксцентриситет неограниченно приближается к нулю, а эллипс – к окружности.

Эксцентриситет эллипса характеризует его «сплюснутость»: чем он ближе к единице, тем более эллипс «вытянут» вдоль оси абсцисс. На рис. 5.12 показано семейство эллипсов, у которых при постоянной длине большой полуоси а малая полуось меняется.

Рис. 5.12. Влияние величины эксцентриситета
на форму эллипса.

Как по заданным длинам полуосей а и b с помощью циркуля и линейки найти фокусы гиперболы? Изобразите семейство гипербол, у которых мнимая ось постоянна, а действительная полуось а меняется.

Эксцентриситет гиперболы также характеризует «сплюснутость» кривой. Ветви гиперболы расположены между асимптотами

и

Если действительная ось гиперболы совпадает с осью Ох (рис. 5.13), то величина угла между асимптотами будет уменьшаться с уменьшением b при постоянном a, и чем меньше отношение для гиперболы, тем меньше ее эксцентриситет е. На рис. 5.13 показано семейство гипербол, у которых при постоянной длине действительной полуоси a малая полуось b меняется.

Рис. 5.13. Влияние величины эксцентриситета
на форму гиперболы.

При определении параболы мы уже столкнулись с описанием этого геометрического места точек с помощью вспомогательной прямой, называемой директрисой. Такая прямая полезна также при изучении свойств эллипса и гиперболы. Более того, сами понятия эллипса и гиперболы могут быть введены через описание их свойств по отношению к директрисам и фокусам.

Будем называть директрисами эллипса, у которого большая полуось расположена вдоль оси Ох, прямые

.

Эти прямые расположены (рис.5.14) вне эллипса (так как ) на одинаковом расстоянии от его центра перпендикулярно оси Ох.

Рис. 5.14. Директрисы эллипса.

Точки эллипса обладают интересным свойством, которое мы сформулируем в виде теоремы.

ТЕОРЕМА 1. Для любой точки эллипса отношение ее расстояния до фокуса к расстоянию до
Соответствующей директрисы равно эксцентриситету.

Доказательство.

Пусть d1 и d2 – расстояния от произвольной точки эллипса до директрис и соответственно (рис. 5.15). Расстояние от этой точки до фокуса будет , а до фокуса =, где, как известно, и  – фокальные радиусы. Теорема утверждает:

Ранее уже получено: . Учитывая, что , будем иметь:

.

Так как директрисы перпендикулярны главной оси эллипса, то расстояния d1 и d2 находятся как длины отрезков, параллельных оси Ох:

Рис. 5.15. Расстояния от точки эллипса до фокуса
и соответствующей директрисы.

Тогда:

Что и требовалось доказать.

Директрисы для гиперболы вводятся так же, как и для эллипса.

Будем называть директрисами гиперболы, у которой действительная ось расположена на оси Ох, прямые

Эти прямые располагаются (рис. 5.16) между ветвями гиперболы (так как ) на расстоянии от ее центра перпендикулярно оси Ох.

Рис. 5.16. Директрисы гиперболы.

Докажем теорему, отражающую свойства директрис гиперболы.

ТЕОРЕМА 2. Для любой точки М(Х,У) гиперболы отношение ее расстояния до фокуса к расстоянию до соответствующей директрисы равно эксцентриситету е.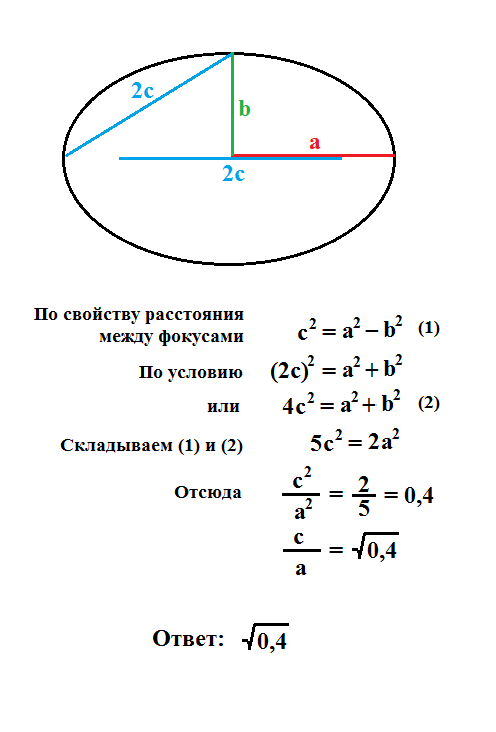

Доказательство:

Для доказательства теоремы следует выделить четыре случая:

1. Точка располагается на левой ветви гиперболы, при этом рассматриваются фокус и директриса .

2. Точка находится на левой ветви гиперболы, при этом берутся фокус и директриса .

3. Точка принадлежит правой части гиперболы, при этом рассматриваются фокус и директриса .

4. Точка взята на правой ветви гиперболы, при этом используются фокус и директриса .

Рассуждения во всех этих случаях аналогичны. Выделим один из них, например, четвертый (рис. 5.17).

Рис. 5.17. Свойства директрис и фокусов гиперболы.

Для этого случая

Тогда

Такой же результат мы получим в трех других случаях, что и доказывает теорему.

Сформулируем без доказательства теорему, которая позволяет по-новому определить эллипс и гиперболу.

ТЕОРЕМА 3. Геометрическое место точек М, для которых отношение е модуля радиус-вектора к расстоянию d точек М до заданной прямой есть величина постоянная, является эллипсом при и гиперболой при .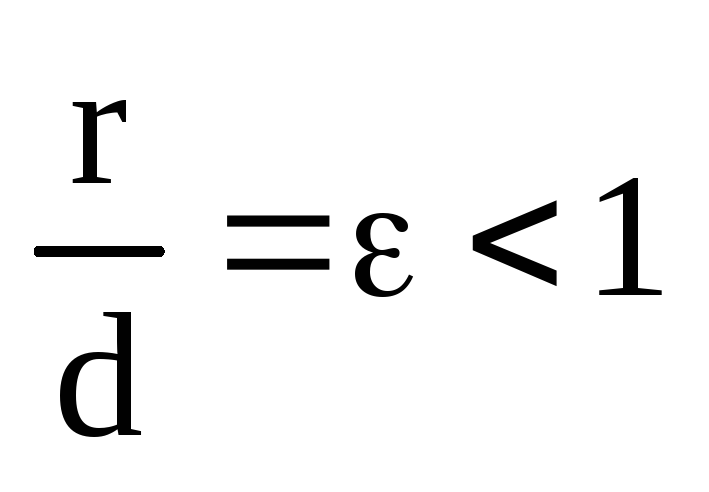

Точка F называется фокусом кривой, радиус-вектор  –фокальным радиус–вектором, а упомянутая прямая – директрисой.

Таким образом, есть векторное уравнение эллипса при , либо гиперболы, если , а для оно определяет параболу.

Постройте семейство кривых при фиксированном е и различных d.

Полученный результат означает, что задание параметров e и d однозначно определяет эллипс, гиперболу, параболу.

Эллипс, гипербола и парабола, как уже отмечалось, могут быть получены путем конических сечений. Обоснование этому дает следующая теорема, которую мы приводим также без доказательства.

ТЕОРЕМА 4. Для всякой линии, будь то эллипс (включая окружность), гипербола или парабола, может быть найден такой круговой конус и такая плоскость, что пересечением конуса с этой плоскостью будет являться именно данная кривая.

Связь между этими линиями имеет и алгебраическое обоснование: все они задаются уравнениями второй степени. Можно доказать, что в любой прямоугольной системе координат уравнения таких кривых имеют вид

Где A, B,C, D,E и F – числа, причем

Каков геометрический смысл этого условия?

Справедливо и обратное утверждение: любое алгебраическое уравнение второй степени

Каким будет геометрический образ этого уравнения, когда левая его часть раскладывается на множители?

Определяет эллипс, гиперболу или параболу, если только левая часть уравнения не раскладывается на множители.

Вот почему для эллипса, гиперболы и параболы используется обобщающее название: кривые второго порядка.

< Предыдущая		Следующая >

Эксцентриситет — значение, определение | Формула эксцентриситета

Эксцентриситет любой криволинейной формы характеризует ее форму, независимо от ее размера. Четыре кривые, которые образуются при пересечении плоскости с конусом с двумя вершинами, — это окружность, эллипс, парабола и гипербола. Их особенности классифицируются на основе их форм, которые определяются интересным фактором, называемым эксцентриситетом. Окружности имеют нулевой эксцентриситет, а параболы имеют единичный эксцентриситет. Эллипсы и гиперболы имеют различные эксцентриситеты. Остановимся подробнее на расчете эксцентриситетов конических сечений.

1.	Что такое эксцентриситет?
2.	Формула эксцентриситета
3.	Эксцентриситет эллипса
4.	Эксцентриситет окружности
5.	Эксцентриситет параболы
6.	Эксцентриситет гиперболы
7.	Часто задаваемые вопросы об эксцентриситете

Что такое эксцентриситет?

Эксцентриситет конических сечений определяется как отношение расстояния от любой точки конического сечения до фокуса к перпендикулярному расстоянию от этой точки до ближайшей директрисы. Для любого конического сечения эксцентриситет конического сечения – это расстояние от любой точки кривой до ее фокуса ÷ расстояние от той же точки до ее направляющей = константа. Это постоянное значение известно как эксцентриситет, который обозначается e. Эксцентриситет изогнутой формы определяет, насколько она круглая. Кривизны уменьшаются по мере увеличения эксцентриситета.

Если эксцентриситеты большие, кривые меньше. Таким образом, мы заключаем, что кривизна этих конических сечений уменьшается по мере увеличения их эксцентриситета.

• Эксцентриситет окружности = 0
• Эксцентриситет эллипса = от 0 до 1
• Эксцентриситет параболы = 1
• Эксцентриситет гиперболы > 1
• Эксцентриситет линии = бесконечность

Формула эксцентриситета

Планеты вращаются вокруг Земли по эллиптической орбите. Эксцентриситет земной орбиты (e = 0,0167) меньше, чем у Марса (e = 0,0935). Чем больше значение эксцентриситета отдаляется от нуля, тем меньше форма похожа на круг. В то время как эллипс и гипербола имеют два фокуса и две директрисы, парабола имеет один фокус и одну директрису. Их формулы эксцентриситета даны в терминах их большой полуоси (a) и малой полуоси (b) в случае эллипса и a = полупоперечная ось и b = полусопряженная ось в случае гиперболы. Формула эксцентриситета дается

Эксцентриситет = Расстояние до фокуса/ Расстояние до директрисы.

e = c/a

где,

• e = эксцентриситет
• c = расстояние от любой точки конического сечения до ее фокуса
• а = расстояние от любой точки конического сечения до его направляющей

Эксцентриситет эллипса

Эллипс – это множество всех точек на плоскости, где сумма расстояний от двух фиксированных точек (фокусов) на плоскости постоянна. 2}\) 92}}{b}\)

Где a = большая полуось

• b = малая полуось и
• c = расстояние от центра эллипса до любого фокуса. Эксцентриситет эллипса равен 0 ≤ e< 1,

Эксцентриситет окружности

Множество всех точек плоскости, равноудаленных от фиксированной точки (центра) плоскости, называется окружностью. Окружность – это эллипс, у которого оба фокуса совпадают с его центром. Поскольку фокусы находятся в одной точке, для круга расстояние от центра до фокуса равно нулю. Этот эксцентриситет придает кругу круглую форму. Таким образом, эксцентриситет любой окружности равен 0,9.0003

Эксцентриситет параболы

Парабола — это множество всех точек на плоскости, которые равноудалены от фиксированной линии, называемой направляющей, и неподвижной точки, называемой фокусом. Геометрическое место движущейся точки P образует параболу, которая возникает, когда эксцентриситет e = 1. Это придает U-образную форму кривой параболы. 2}}{a}\). Расстояние между двумя фокусами = 2аэ. 92}\) в случае эллипса.

☛ Также проверьте:

• Локус
• Уравнение окружности

Часто задаваемые вопросы об эксцентриситете

Что такое эксцентриситет?

Эксцентриситет — это математическая константа, заданная для конического сечения. Это отношение расстояний от любой точки конического сечения до его фокуса до той же точки до соответствующей ему директрисы. Эксцентриситет конического сечения говорит о том, насколько кривая отклоняется от круговой.

Что такое Формула эксцентриситета?

Эксцентриситет конического сечения – это расстояние любой точки до ее фокуса/расстояние той же точки до ее директрисы. Формула эксцентриситета: e = c/a, где c = √(a ² +b ² ) и

c = расстояние от любой точки конического сечения до его фокуса

a = расстояние от любой точки на коническом сечении до его направляющей

Что такое эксцентриситет эллипса?

Эксцентриситет эллипса находится в диапазоне от 0 до 1.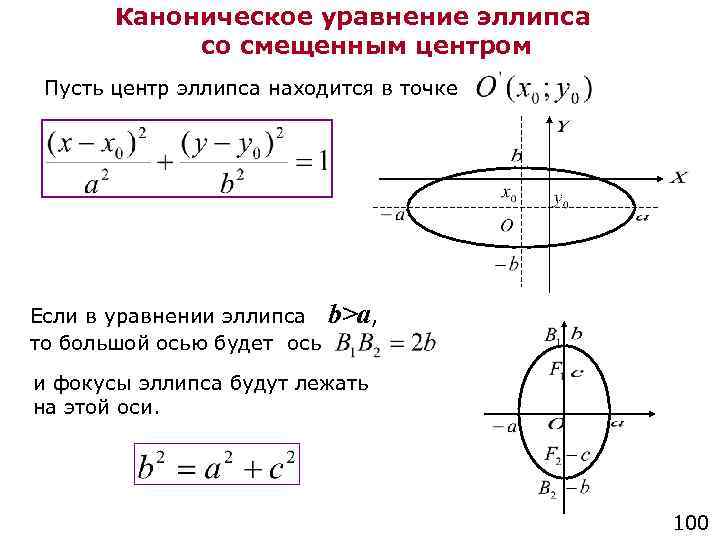 Эксцентриситет эллипса представляет собой отношение расстояний от центра эллипса до одного из фокусов и до одной из вершин эллипса. Если эксцентриситет достигает 0, он становится кругом, а если он достигает 1, он становится параболой.

Что такое эксцентриситет окружности?

Эксцентриситет окружности всегда равен единице.

Что такое эксцентриситет параболы?

Эксцентриситет параболы всегда равен единице. Расстояние между любой точкой и ее фокусом и перпендикулярное расстояние между той же точкой и директрисой равны. Таким образом, с = а. Следовательно, эксцентриситет e = c/a дает единицу.

Почему эксцентриситет окружности равен нулю?

Эксцентриситет окружности всегда равен нулю, поскольку фокусы окружности совпадают в центре.

Что происходит, когда эксцентриситет равен 1?

Если кривая эксцентриситета равна 1, это означает, что кривая является параболой.

Как найти эксцентриситет конуса?

Эксцентриситет находится путем нахождения отношения расстояния между любой точкой на коническом сечении до ее фокуса к расстоянию по перпендикуляру от этой точки до ее директрисы.

Какое максимальное значение может иметь эксцентриситет?

Эксцентриситет гиперболы всегда больше 1. Когда эксцентриситет достигает бесконечности, это уже не кривая, а прямая линия.

Каким может быть минимальное значение эксцентриситета?

Минимальное значение эксцентриситета равно 0, как у окружности.

Конические сечения — Общее уравнение коники и эксцентриситет

Если мы поместим чихуахуа и немецкого дога рядом, они, очевидно, будут выглядеть немного по-разному. В то же время у нас нет проблем с тем, чтобы назвать их обоих собаками. То же самое и с коническими сечениями. Все они выглядят по-разному, но мы все равно распознаем их как один и тот же тип вещей.

Все различные конические сечения на самом деле имеют даже больше общего, чем мы видели до сих пор. Мы относились к ним так, как будто все они имеют разные уравнения, но на самом деле существует только одно уравнение для всех коник. Если вы нам не верите, проверьте это: общее уравнение коники .

AX ² + BXY + CY ² + DX + EY + F = 0 0003 2 2 2

.0214 и F — константы. Они не слишком похожи ни на одно из уравнений, с которыми мы работали. Но внешность может быть обманчивой.

Первое, что мы скажем, это то, что B всегда было 0 для каждой коники, которую мы рассматривали до сих пор, и так и останется. х и х , перемноженные вместе, — рецепт головной боли. Если вы задавались вопросом, почему все наши коники каким-то образом загадочным образом параллельны осям x или y , B = 0 вот почему. B — это то, что вращает конику вокруг, так что мы вообще не заморачивались с этим.

Давайте посмотрим на другие переменные, особенно на A и C . Предположим, что один из них, допустим A , равнялся 0. Тогда мы имели бы:

Cy ² + Dx + Ey + F = 3 0 9000 Ranging, мы могли бы записать это как:

Dx + F = — Cy ² + Ey

Это всего лишь небольшое завершение квадрата, а не параболы; один терм x , равный некоторому терму y ² . Мы могли бы сделать что-то подобное и найти все конические сечения, но мы не собираемся. Мы просто продолжим и подведем итоги для вас. B считается равным 0 для всех из них.

• Если либо А = 0, либо С = 0, но не оба, то мы имеем параболу.
• Если A = C и оба они не равны 0, то у нас есть круг.
• Если A ≠ C и AC > 0, то у нас есть эллипс.
• Если A ≠ C и AC < 0, то мы имеем гиперболу.

Видите ли, нам действительно нужны только A и C , константы, присоединенные к x ² и y ² . Но что с проверкой, если AC больше или меньше 0? Это знак, глупышка. Если A и C оба положительны или оба отрицательны, то AC положительна и коника будет эллипсом. Если один из них отрицательный, то AC отрицательный и мы имеем гиперболу.

Итак, все коники имеют больше общего, чем просто название. Хорошо знать. Но теперь у нас есть сюрприз; у нас есть другой способ определить коники и отличить их друг от друга. Разве это не заставляет просто хотеть встать и танцевать? Наверное, нет, но разве тебе нужен повод, чтобы танцевать? Вероятно. Тогда мы просто пойдем дальше.

Они не странные, они просто эксцентричные

Казалось бы, что мы определили все возможные способы определения конического сечения, но мы добавили еще один. Эксцентриситет представляет собой отношение двух различных частей коники.

f — расстояние от центра до очага/фокусов. Мы уже много раз видели этого парня. Однако мы назвали его p , когда работали с параболами. a — это расстояние от центра до вершины/вершин или длина большой полуоси в эллипсе. Названия или их точное значение менялись от одного типа коники к другому, но мы уже знакомы со всеми ними.

Это тоже хорошо, потому что мы можем использовать эксцентриситет для определения коник. Проверьте это:

• Если e = 0, у нас есть круг. Фокус и центр находятся прямо друг над другом на расстоянии 0.
• Если e больше 0, но меньше 1, у нас есть эллипс. Мы уже упоминали, что фокусы находятся внутри эллипса, поэтому f < a .
• Если e = 1, то у нас есть парабола. Параболы не имеют центра, но мы знаем, что p — это расстояние от вершины как до фокуса, так и до директрисы, поэтому мы можем видеть, откуда берется этот результат.
• Если e больше 1, то мы имеем гиперболу. Фокус находится дальше от центра, чем вершина, так что это работает.

  No related posts.