Онлайн решить транспортную задачу: Транспортная задача онлайн

Онлайн-калькулятор:Метод дифференциальных рент

Назначение. Онлайн-калькулятор предназначен для решения транспортной задачи методом дифференциальных рент (см. пример решения). Для этого выберите размерность матрицы тарифов (количество поставщиков и количество магазинов).

• Шаг №1
• Шаг №2
• Видеоинструкция
• Оформление Word

Количество столбцов (магазины) 2345678910
Количество строк (поставщики) 2345678910

Если при определении оптимального плана ТЗ методом потенциалов сначала находился какой-нибудь опорный план, а затем он последовательно улучшался, то при нахождении решения ТЗ методом дифференциальных рент сначала распределяют между пунктами назначения часть груза (так называемое оптимальное распределение) и на последующих итерациях постепенно уменьшают общую величину нераспределенных поставок. Первоначальный вариант распределения груза определяют следующим образом.

В каждом из столбцов таблицы данных находят минимальный тариф. Найденные числа заключают в кружки, а клетки, в которых стоят указанные числа, заполняют. В них записывают максимально возможные числа. В результате получают некоторое распределение поставок груза в пункты назначения. Это распределение в общем случае не удовлетворяет ограничениям исходной транспортной задачи. Поэтому в результате последующих шагов следует постепенно сокращать нераспределенные поставки груза так, чтобы при этом общая стоимость перевозок оставалась минимальной. Для этого сначала определяют избыточные и недостаточные строки.

Строки, соответствующие поставщикам, запасы которых полностью распределены, а потребности пунктов назначения, связанных с данными потребителями запланированными поставками, не удовлетворены, считаются недостаточными. Эти строки иногда называют также отрицательными. Строки, запасы которых исчерпаны не полностью, считаются избыточными. Иногда их называют также положительными.

После того, как определены избыточные и недостаточные строки, для каждого из столбцов находят разности между числом в кружке и ближайшим к нему тарифом, записанным в избыточной строке. Если число в кружке находится в положительной строке, то разность не определяют. Среди полученных чисел находят наименьшее. Это число называется промежуточной рентой. После определения промежуточной ренты переходят к новой таблице. Эта таблица получается из предыдущей таблицы прибавлением к соответствующим тарифам, стоящим в отрицательных строках, промежуточной ренты. Остальные элементы остаются прежними. При этом все клетки новой таблицы считают свободными. После построения новой таблицы начинают заполнение ее клеток. Теперь уже число заполняемых клеток на одну больше, чем на предыдущем этапе. Эта дополнительная клетка находится в столбце, в котором была записана промежуточная рента. Все остальные клетки находятся по одной в каждом из столбцов, и в них записаны наименьшие для данного столбца числа, заключенные в кружки.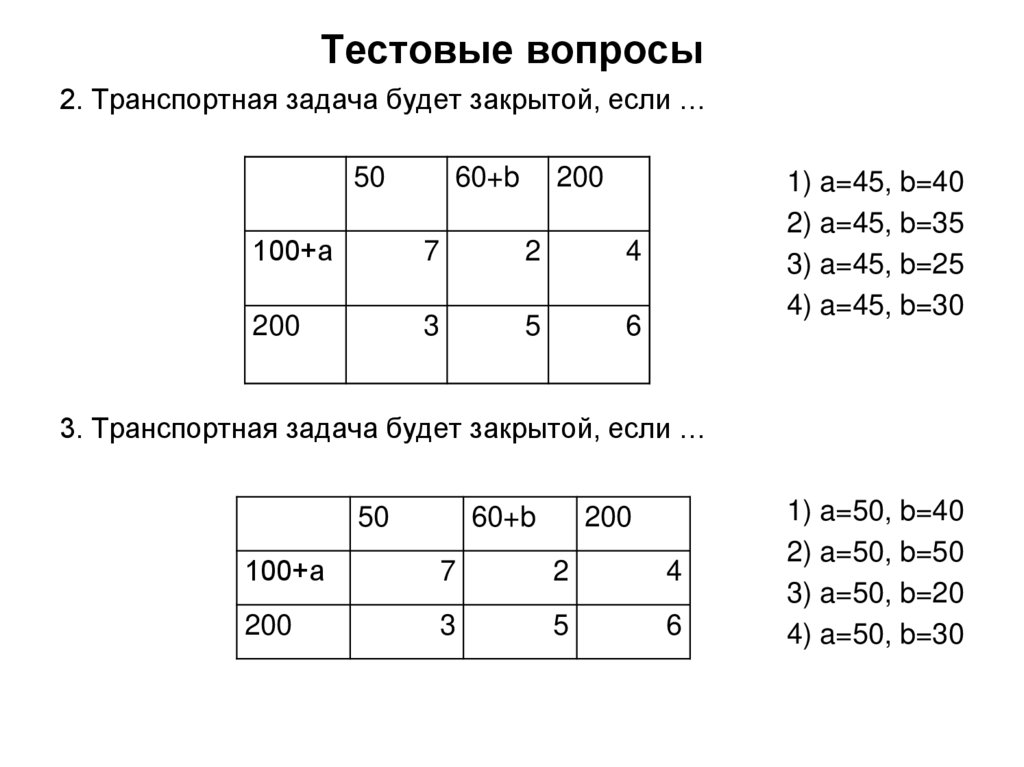

Заключены в кружки и два одинаковых числа, стоящих в столбце, в котором в предыдущей таблице была записана промежуточная рента.

Поскольку в новой таблице число заполняемых клеток больше, чем число столбцов, то при заполнении клеток следует пользоваться специальным правилом, которое состоит в следующем. Выбирают некоторый столбец (строку), в котором имеется одна клетка с помещенным в ней кружком. Эту клетку заполняют и исключают из рассмотрения данный столбец (строку). После этого берут некоторую строку (столбец), в которой имеется одна клетка с помещенным в ней кружком. Эту клетку заполняют и исключают из рассмотрения данную строку (столбец). Продолжая так, после конечного числа шагов заполняют все клетки, в которых помещены кружки с заключенными в них числами. Если к тому же удается распределить весь груз, то получают оптимальный план. Если же оптимальный план ТЗ не получен, то переходят к новой таблице. Для этого находят избыточные и недостаточные строки, промежуточную ренту и строят новую таблицу.

При этом могут возникнуть некоторые затруднения при определении знака строки, когда ее нераспределенный остаток равен нулю. В этом случае строку считают положительной при условии, что вторая заполненная клетка, стоящая в столбце, связанном с данной строкой еще одной заполненной клеткой, расположена в положительной строке.

После описанных выше итераций нераспределенный остаток становится равным нулю. В результате получается оптимальный план ТЗ.

Исследование операций

Исследование операций

Вентцель Е. С. Исследование операций. М., «Советское радио», 1972, 552 с. Излагаются основы исследования операций — науки, занимающейся количественным обоснованием решений во всех областях целенаправленной человеческой деятельности. В книге рассматриваются основные понятия и методологические принципы исследования операций, математические методы оптимизации (линейное, динамическое программирование, теория игр и статистических решений), а также методы математического моделирования операций. Большое внимание уделяется прикладной теории марковских случайных процессов (с приложениями в области теории массового обслуживания, теории надежности) и математическому описанию процессов, протекающих в сложных, многоэлементных системах (метод динамики средних). Рассматриваются методы статистического моделирования операций на ЭЦВМ и основы метода сетевого планирования. Книга содержит ряд новых материалов, разработанных автором в последние годы и нигде ранее не публиковавшихся. Изложение ведется на сравнительно элементарном уровне, вполне доступном читателю, знакомому с обычным вузовским курсом математики и с элементами теории вероятностей. Излагаемые методы иллюстрируются большим количеством примеров из разных областей практики. Книга рассчитана на широкий круг читателей — инженеров, экономистов, научных работников и хозяйственных руководителей, интересующихся применением математики к обоснованию оптимальных решений Оглавление ПРЕДИСЛОВИЕ ВВЕДЕНИЕ 1. ОСНОВНЫЕ ПОНЯТИЯ ИССЛЕДОВАНИЯ ОПЕРАЦИЙ 1. ОПЕРАЦИЯ. ЭФФЕКТИВНОСТЬ ОПЕРАЦИИ 2. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ОПЕРАЦИИ 3. ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ ИССЛЕДОВАНИЯ ОПЕРАЦИЙ. ДЕТЕРМИНИРОВАННЫЙ СЛУЧАЙ 4. ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ ИССЛЕДОВАНИЯ ОПЕРАЦИЙ. ОПТИМИЗАЦИЯ РЕШЕНИЯ В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ 5. ОЦЕНКА ОПЕРАЦИИ ПО НЕСКОЛЬКИМ ПОКАЗАТЕЛЯМ 2. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ 1. ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ 2. Задача о загрузке станков. 3. Задача о распределении ресурсов. 4. Задача о перевозках. 5. Задача о производстве сложного оборудования. 2. ОСНОВНАЯ ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ 3. ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ОСНОВНОЙ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ 4. ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ С ОГРАНИЧЕНИЯМИ-НЕРАВЕНСТВАМИ. ПЕРЕХОД ОТ НЕЕ К ОЗЛП И ОБРАТНО 5. СИМПЛЕКС-МЕТОД РЕШЕНИЯ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ 6. ТАБЛИЧНЫЙ АЛГОРИТМ ЗАМЕНЫ БАЗИСНЫХ ПЕРЕМЕННЫХ 7. ОТЫСКАНИЕ ОПОРНОГО РЕШЕНИЯ ОСНОВНОЙ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ 8. ОТЫСКАНИЕ ОПТИМАЛЬНОГО РЕШЕНИЯ ОСНОВНОЙ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ 9. ТРАНСПОРТНАЯ ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ 10. НАХОЖДЕНИЕ ОПОРНОГО ПЛАНА 11. УЛУЧШЕНИЕ ПЛАНА ПЕРЕВОЗОК. ЦИКЛ ПЕРЕСЧЕТА 12. РЕШЕНИЕ ТРАНСПОРТНОЙ ЗАДАЧИ МЕТОДОМ ПОТЕНЦИАЛОВ 13. ТРАНСПОРТНАЯ ЗАДАЧА С НЕПРАВИЛЬНЫМ БАЛАНСОМ 2. ТЗ с избытком заявок 14. РЕШЕНИЕ ТРАНСПОРТНОЙ ЗАДАЧИ ПО КРИТЕРИЮ ВРЕМЕНИ 3. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ 1. ЗАДАЧИ ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ 2. ЗАДАЧА О НАБОРЕ ВЫСОТЫ И СКОРОСТИ ЛЕТАТЕЛЬНЫМ АППАРАТОМ 3. ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ. ИНТЕРПРЕТАЦИЯ УПРАВЛЕНИЯ В ФАЗОВОМ ПРОСТРАНСТВЕ 4. ЗАДАЧИ РАСПРЕДЕЛЕНИЯ РЕСУРСОВ 5. ПРИМЕР РЕШЕНИЯ ЗАДАЧИ РАСПРЕДЕЛЕНИЯ РЕСУРСОВ 6. ДРУГИЕ ЗАДАЧИ РАСПРЕДЕЛЕНИЯ РЕСУРСОВ 1. Распределение ресурсов по неоднородным этапам 2. Задача о резервировании ресурсов 3. Задача распределения ресурсов между тремя и более отраслями 7. РАСПРЕДЕЛЕНИЕ РЕСУРСОВ СО ВЛОЖЕНИЕМ ДОХОДОВ В ПРОИЗВОДСТВО 8. РЕШЕНИЕ ЗАДАЧИ ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ С УЧЕТОМ ПРЕДЫСТОРИИ ПРОЦЕССА 9. ЗАДАЧИ ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ, НЕ СВЯЗАННЫЕ СО ВРЕМЕНЕМ 10. ЗАДАЧИ ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ С МУЛЬТИПЛИКАТИВНЫМ КРИТЕРИЕМ 11. БЕСКОНЕЧНОШАГОВЫЙ ПРОЦЕСС ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ 4. МОДЕЛИРОВАНИЕ ОПЕРАЦИЙ ПО СХЕМЕ МАРКОВСКИХ СЛУЧАЙНЫХ ПРОЦЕССОВ 1. МАРКОВСКИЙ СЛУЧАЙНЫЙ ПРОЦЕСС С ДИСКРЕТНЫМИ СОСТОЯНИЯМИ 2. СЛУЧАЙНЫЕ ПРОЦЕССЫ С ДИСКРЕТНЫМ И НЕПРЕРЫВНЫМ ВРЕМЕНЕМ. МАРКОВСКАЯ ЦЕПЬ 3. МАРКОВСКИЙ ПРОЦЕСС С ДИСКРЕТНЫМИ СОСТОЯНИЯМИ И НЕПРЕРЫВНЫМ ВРЕМЕНЕМ. УРАВНЕНИЯ КОЛМОГОРОВА ДЛЯ ВЕРОЯТНОСТЕЙ СОСТОЯНИЙ 4. ПОТОК СОБЫТИИ. ПРОСТЕЙШИЙ ПОТОК И ЕГО СВОЙСТВА 5. ПОТОКИ ПАЛЬМА. ПОТОКИ ЭРЛАНГА 6. ПУАССОНОВСКИЕ ПОТОКИ СОБЫТИЙ И НЕПРЕРЫВНЫЕ МАРКОВСКИЕ ЦЕПИ 7. ПРЕДЕЛЬНЫЕ ВЕРОЯТНОСТИ СОСТОЯНИЙ 8. ПРОЦЕСС «ГИБЕЛИ И РАЗМНОЖЕНИЯ» 9. ЦИКЛИЧЕСКИЙ ПРОЦЕСС 10. ПРИБЛИЖЕННОЕ СВЕДЕНИЕ НЕМАРКОВСКИХ ПРОЦЕССОВ К МАРКОВСКИМ. МЕТОД «ПСЕВДОСОСТОЯНИЙ» 5. ТЕОРИЯ МАССОВОГО ОБСЛУЖИВАНИЯ 1. ЗАДАЧИ ТЕОРИИ МАССОВОГО ОБСЛУЖИВАНИЯ 2. КЛАССИФИКАЦИЯ СИСТЕМ МАССОВОГО ОБСЛУЖИВАНИЯ И ИХ ОСНОВНЫЕ ХАРАКТЕРИСТИКИ 3. ОДНОКАНАЛЬНАЯ СМО С ОТКАЗАМИ 4. МНОГОКАНАЛЬНАЯ СМО С ОТКАЗАМИ 5. ОДНОКАНАЛЬНАЯ СМО С ОЖИДАНИЕМ 6. МНОГОКАНАЛЬНАЯ СМО С ОЖИДАНИЕМ 7. СМО С ОГРАНИЧЕННЫМ ВРЕМЕНЕМ ОЖИДАНИЯ 8. ЗАМКНУТЫЕ СИСТЕМЫ МАССОВОГО ОБСЛУЖИВАНИЯ 9. СИСТЕМЫ МАССОВОГО ОБСЛУЖИВАНИЯ СО «ВЗАИМОПОМОЩЬЮ» МЕЖДУ КАНАЛАМИ 1. СМО с отказами 2. СМО с очередью 10. СИСТЕМА МАССОВОГО ОБСЛУЖИВАНИЯ С ОШИБКАМИ 11. СИСТЕМЫ МАССОВОГО ОБСЛУЖИВАНИЯ С НЕ-ПУАССОНОВСКИМИ ПОТОКАМИ СОБЫТИЙ 2. Одноканальная СМО с ожиданием 6. МЕТОД ДИНАМИКИ СРЕДНИХ 1. ИДЕЯ МЕТОДА. ОБЛАСТЬ ПРИМЕНИМОСТИ 2. УЧЕТ ЗАВИСИМОСТИ ИНТЕНСИВНОСТЕЙ ПОТОКОВ СОБЫТИЙ ОТ ЧИСЛЕННОСТЕЙ СОСТОЯНИИ. ПРИНЦИП КВАЗИРЕГУЛЯРНОСТИ 3. УЧЕТ ПОПОЛНЕНИЯ ЧИСЛЕННОСТЕЙ СОСТОЯНИЙ 4. МЕТОД ДИНАМИКИ СРЕДНИХ ДЛЯ СИСТЕМЫ, СОСТОЯЩЕЙ ИЗ НЕОДНОРОДНЫХ ЭЛЕМЕНТОВ 5. ПРЕДЕЛЬНОЕ ПОВЕДЕНИЕ СРЕДНИХ ЧИСЛЕННОСТЕЙ СОСТОЯНИЙ 6. УРАВНЕНИЯ ДИНАМИКИ БОЯ (МОДЕЛЬ А) 7. УЧЕТ ПОПОЛНЕНИЯ СИЛ, УПРЕЖДАЮЩЕГО УДАРА, ТЕМПА МОБИЛИЗАЦИИ И ПРОЧИХ ФАКТОРОВ В УРАВНЕНИЯХ ДИНАМИКИ БОЯ 8. МОДЕЛЬ Б. СЛУЧАЙ ОТСУТСТВИЯ ПЕРЕНОСА ОГНЯ 9. МОДЕЛЬ В. УЧЕТ ДЕЯТЕЛЬНОСТИ РАЗВЕДКИ И СИСТЕМЫ УПРАВЛЕНИЯ БОЕМ 10. УЧЕТ ВОССТАНОВЛЕНИЯ ЕДИНИЦ В ХОДЕ БОЕВЫХ ДЕЙСТВИЙ 11. УРАВНЕНИЯ ДИНАМИКИ БОЯ ДЛЯ НЕОДНОРОДНЫХ ЕДИНИЦ. ФУНКЦИИ РАСПРЕДЕЛЕНИЯ ОГНЯ 12. УРАВНЕНИЯ СМЕШАННОГО ТИПА 13. НЕКОТОРЫЕ УТОЧНЕНИЯ МЕТОДА ДИНАМИКИ СРЕДНИХ 7. МЕТОДЫ УЧЁТА НАДЕЖНОСТИ ТЕХНИЧЕСКИХ УСТРОЙСТВ 2. НАДЕЖНОСТЬ ЭЛЕМЕНТА. ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ ВРЕМЕНИ БЕЗОТКАЗНОЙ РАБОТЫ. СРЕДНЕЕ ВРЕМЯ БЕЗОТКАЗНОЙ РАБОТЫ 3. ЭКСПОНЕНЦИАЛЬНЫЙ ЗАКОН НАДЕЖНОСТИ. 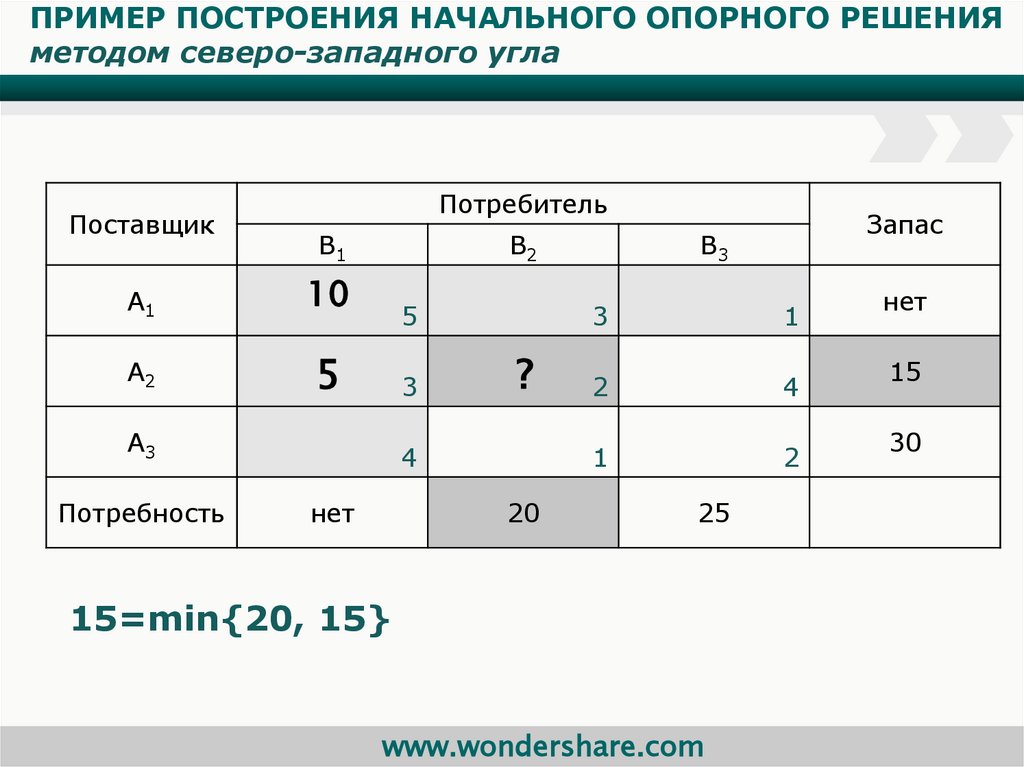ИНТЕНСИВНОСТЬ ОТКАЗОВ 4. ОПРЕДЕЛЕНИЕ НАДЕЖНОСТИ СИСТЕМЫ ПО НАДЕЖНОСТИ ЕЕ ЭЛЕМЕНТОВ. НАДЕЖНОСТЬ НЕРЕЗЕРВИРОВАННОЙ СИСТЕМЫ 5. НАДЕЖНОСТЬ РЕЗЕРВИРОВАННОЙ СИСТЕМЫ («ГОРЯЧИЙ РЕЗЕРВ») 6. НАДЕЖНОСТЬ РЕЗЕРВИРОВАННОЙ СИСТЕМЫ («ХОЛОДНЫЙ» И «ОБЛЕГЧЕННЫЙ» РЕЗЕРВ) 7. НАДЕЖНОСТЬ СИСТЕМЫ С ВОССТАНОВЛЕНИЕМ 8. УЧЕТ ЗАВИСИМОСТИ ОТКАЗОВ ПРИ ОЦЕНКЕ НАДЕЖНОСТИ ТЕХНИЧЕСКИХ УСТРОЙСТВ 8. МОДЕЛИРОВАНИЕ ОПЕРАЦИЙ МЕТОДОМ СТАТИСТИЧЕСКИХ ИСПЫТАНИЙ 2. ЕДИНИЧНЫЙ ЖРЕБИЙ 3. РОЗЫГРЫШ ЗНАЧЕНИЯ НОРМАЛЬНО РАСПРЕДЕЛЕННОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ 4. ПОЛУЧЕНИЕ СЛУЧАЙНОГО ЧИСЛА R ОТ 0 ДО 1 5. ПРИМЕРЫ МОДЕЛИРОВАНИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ МЕТОДОМ МОНТЕ-КАРЛО 6. ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК СТАЦИОНАРНОГО СЛУЧАЙНОГО ПРОЦЕССА МЕТОДОМ МОНТЕ-КАРЛО ПО ОДНОЙ РЕАЛИЗАЦИИ 7. ОЦЕНКА ТОЧНОСТИ ХАРАКТЕРИСТИК, ПОЛУЧЕННЫХ МЕТОДОМ МОНТЕ-КАРЛО. НЕОБХОДИМОЕ ЧИСЛО РЕАЛИЗАЦИЙ 9. ИГРОВЫЕ МЕТОДЫ ОБОСНОВАНИЯ РЕШЕНИЙ 1. ЗАДАЧИ ТЕОРИИ ИГР И СТАТИСТИЧЕСКИХ РЕШЕНИЙ 2. ПРЕДМЕТ ТЕОРИИ ИГР. ОСНОВНЫЕ ПОНЯТИЯ 3. ПЛАТЕЖНАЯ МАТРИЦА 4. НИЖНЯЯ И ВЕРХНЯЯ ЦЕНА ИГРЫ. ПРИНЦИП МИНИМАКСА 5. РЕШЕНИЕ ИГРЫ В СМЕШАННЫХ СТРАТЕГИЯХ 6. УПРОЩЕНИЕ ИГР 7. ИГРА 2Х2 8. ИГРЫ 2xn И mx2 9. РЕШЕНИЕ ИГР mxn 10. РЕШЕНИЕ КОНЕЧНЫХ ИГР МЕТОДОМ ИТЕРАЦИЙ 11. ФИЗИЧЕСКАЯ СМЕСЬ СТРАТЕГИЙ 12. ЭЛЕМЕНТЫ ТЕОРИИ СТАТИСТИЧЕСКИХ РЕШЕНИЙ 13. КРИТЕРИЙ, ОСНОВАННЫЙ НА ИЗВЕСТНЫХ ВЕРОЯТНОСТЯХ УСЛОВИЙ. КРИТЕРИИ ВАЛЬДА, ГУРВИЦА, СЭВИДЖА 14. ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ 10. МЕТОД СЕТЕВОГО ПЛАНИРОВАНИЯ 2. СЕТЕВОЙ ГРАФИК КОМПЛЕКСА РАБОТ. ВРЕМЕННОЙ СЕТЕВОЙ ГРАФИК 3. ФОРМАЛЬНАЯ ЗАПИСЬ (АЛГОРИТМ) ЗАДАЧИ СЕТЕВОГО ПЛАНИРОВАНИЯ 4. ОПТИМИЗАЦИЯ ПЛАНА КОМПЛЕКСА РАБОТ 5. СЕТЕВОЕ «ПЛАНИРОВАНИЕ ПРИ СЛУЧАЙНЫХ ВРЕМЕНАХ ВЫПОЛНЕНИЯ РАБОТ. ПРИМЕНЕНИЕ ЭЦВМ ПРИЛОЖЕНИЕ ЛИТЕРАТУРА

Транспортная задача 1 | решатель

Свернуть затраты на доставку товаров от фабрик к покупателям, а не более
» colspan=»6″> поставка доступна с каждого завода и удовлетворяет спрос каждого клиента.
Стоимость доставки ($ за продукт)
	Направления
	Клиент 1	Клиент 2	Клиент 3	Клиент 4	Клиент 5
Завод 1	1,75 $	2,25 $	1,50 $	2,00 $	5″> 1,50 $
Фабрика 2	2,00 $	2,50 $	2,50 $	1,50 $	1,00 $
Количество продукция отгружена
	Клиент 1	Клиент 2	Клиент 3	Клиент 4	Клиент 5	Всего	Емкость
Завод 1	0	0	0	0	0	0	60 000
Завод 2	0	0	0	0	0	0	60 000
Итого	0	0	0	0	0
Спрос	30 000	23 000	15 000	32 000	16 000
Общая стоимость доставка		$0
Проблема
» colspan=»8″> А компания хочет минимизировать стоимость доставки товара из двух разных фабрики для 5 различных клиентов.
Каждый фабрика имеет ограниченное предложение и у каждого клиента есть определенный спрос. Как должен компания распространяет
товар?
Решение
These are given the » colspan=»8″> 1) Переменные — это количество продукции, которую необходимо отправить с каждой фабрики на клиенты. Им дается
имя Products_shipped на листе Транспорт1.
2) Логический ограничение равно
	Products_shipped >= 0 с помощью параметра «Предполагать неотрицательное значение»
Два других ограничения
	Total_received >= Спрос
	Total_shipped <= вместимость
3) цель — минимизировать затраты.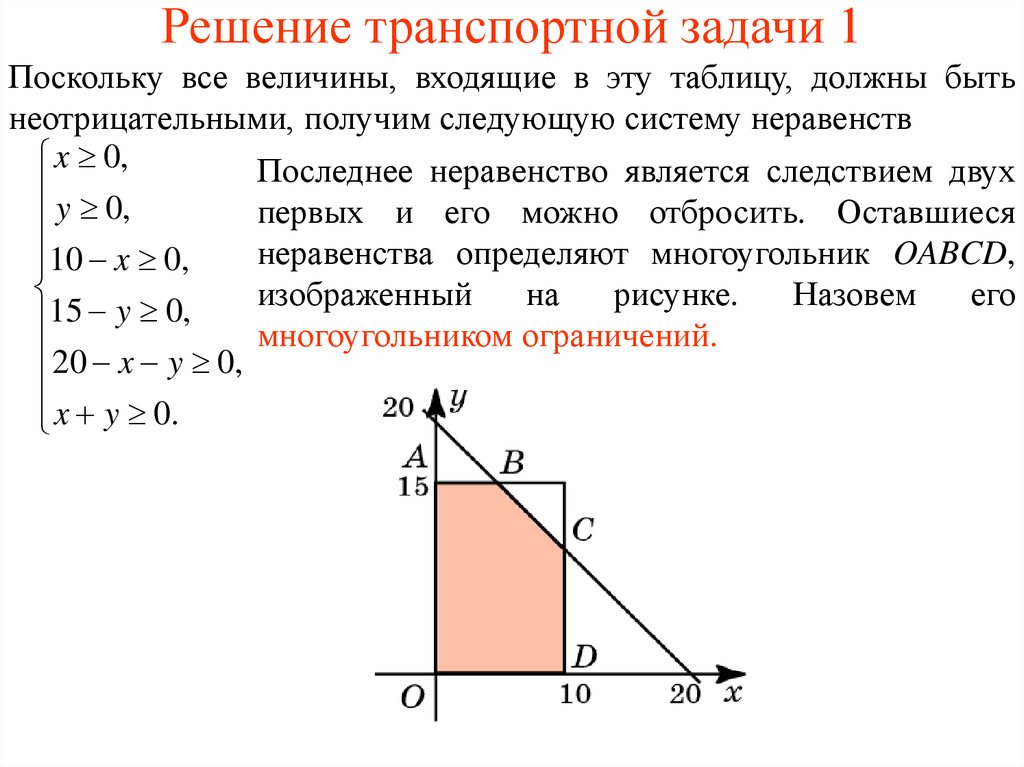 Этому дается имя Total_cost.
Примечания
Это является транспортной задачей в ее простейшей форме. Тем не менее, этот тип модели широко используется для спасения многих
тыс. долларов каждый год.
В worksheet Transport2 мы будем рассматривать 2-х уровневую перевозку, а в рабочий лист Transport3 мы расширяем это до
а многопродуктовая двухуровневая транспортная задача.

целей обучения | Интернет-ресурсы

B-1: Сформулируйте и решите транспортные задачи, используя как ручные методы, так и Excel Solver, и интерпретируйте решения.

При проектировании сети цепочки поставок расположение заводов, складов и распределительных центров является стратегическим решением, влияющим на затраты. Следовательно, компании тратят значительное количество времени и ресурсов на рассмотрение и оценку альтернатив, чтобы выбрать наиболее подходящую для них. В частности, транспортная модель может помочь компаниям свести к минимуму общие затраты на транспортировку и распределение от различных источников поставок до пунктов назначения спроса, принимая решения о расположении их заводов или источников поставок по отношению к пунктам назначения спроса и решения о количестве единиц продукции. конкретный продукт должен транспортироваться из каждого источника поставки в каждый пункт назначения спроса, чтобы удовлетворить существующий спрос на продукцию компании.

Транспортная модель является частным случаем задач линейного программирования, целью которых является минимизация общих затрат на транспортировку товаров из различных источников поставки в различные пункты назначения спроса. Модель часто классифицируют как задачу линейного программирования, поскольку связь между переменными затратами на транспортировку и количеством отгруженных единиц предполагается линейной. Существуют важные правила принятия решений, которые необходимо применять к транспортной задаче. Транспортная модель требует следующих допущений:

а. Пропускная способность в каждом пункте поставки или пункте отправления ограничена.

б. Требования к спросу в каждом пункте назначения известны.

г. Независимо от места происхождения или назначения отправляемые товары одинаковы (однородны).

д. Независимо от количества отправленных единиц, стоимость доставки за единицу остается неизменной.

эл. Между каждым пунктом отправления и пунктом назначения используемый вид транспорта не меняется, и используется только один маршрут.

Два метода, которые можно использовать для получения начального базового допустимого решения, — это правило северо-западного угла и матричный метод минимальной стоимости. Преимущество правила северо-западного угла состоит в том, что оно позволяет нам найти начальное допустимое решение транспортной задачи. Особое внимание уделяется поиску начального решения, удовлетворяющего всем ограничениям, независимо от относительных затрат на доставку этих заказов. Правило северо-западного угла дает возможные решения, но не обязательно оптимальное решение с наименьшими затратами. Целью матричного метода минимальных затрат является минимизация общих затрат, что делает этот метод более интуитивно привлекательным. Этот метод также сокращает количество вычислений и время, необходимое для нахождения оптимального решения.

Метод ступенек предназначен для поиска улучшенных решений транспортных проблем. Модель начинается с начального допустимого решения, а затем используется для определения того, является ли это начальное решение оптимальным. Термин ступенька относится к занятым ячейкам в исходном решении транспортной матрицы, которые используются для получения улучшенного решения.

Excel Solver предлагает средства для поиска оптимальных решений транспортной задачи. Процедура решения транспортных задач с помощью Excel Solver почти идентична шагам, используемым для решения задач линейного программирования (см. модуль A).

B-2: Примените транспортное моделирование к другим ситуациям.

Если транспортная проблема не сбалансирована, ее необходимо преобразовать в сбалансированную ситуацию путем добавления фиктивных источников предложения или фиктивных пунктов назначения спроса в транспортной матрице. Транспортная задача является вырожденной, если один из занятых маршрутов (ячейка) полностью исчерпывает предложение из источника и удовлетворяет требованиям спроса для пункта назначения.