Экспоненциальная функция | это… Что такое Экспоненциальная функция?
ТолкованиеПеревод
- Экспоненциальная функция
Экспонента — функция exp(x) = ex, где e — основание натуральных логарифмов.
Содержание
- 1 Определение
- 2 Свойства
- 3 Экспонента от комплексного аргумента
- 4 Вариации и обобщения
- 4.1 Матричная экспонента
- 5 Обратная функция
- 6 См. также
Определение
Экспоненциальная функция может быть определена различными эквивалентными способами. Например через ряд Тейлора:
или через предел:
Здесь x — любое вещественное или комплексное число.
Свойства
- (ex)’ = ex, в частности
- Экспонента является единственным решением дифференциального уравнения
 Кроме того через экспоненту выражаются общие решения однородных дифференциальных уравнений.
Кроме того через экспоненту выражаются общие решения однородных дифференциальных уравнений. - Экспонента определена на всей вещественной оси. Она всюду возрастает и строго больше нуля.
- Экспонента является выпуклой функцией.
- Обратная функция к ней — натуральный логарифм .
- Производная в нуле равна 1, поэтому касательная к экспоненте в этой точке проходит под углом 45°.
- Основное функциональное свойство экспоненты:
- exp(a + b) = exp(a)exp(b).
- Непрерывная функция с таким свойством либо тождественно равна 0, либо имеет вид exp(ct), где c — некоторая константа.
Экспонента от комплексного аргумента
От комплексного аргумента z = x + iy экспонента определяется следующим образом:
- ez = e x + iy = exeiy = ex(cosy + isiny) (формула Эйлера)
В частности,
- eiπ + 1 = 0
Вариации и обобщения
Аналогично экспонента может быть определена для элемента произвольной ассоциативной алгебры.
 В конкретном случае требуется также доказательство того, что указанные пределы существуют.
В конкретном случае требуется также доказательство того, что указанные пределы существуют.Матричная экспонента
Экспоненту от квадратной матрицы (или линейного оператора) можно формально определить, подставив матрицу в соответствующий ряд:
Определённый таким образом ряд сходится для любого оператора A с ограниченной нормой, поскольку мажорируется рядом для экспоненты нормы A: Следовательно, экспонента от матрицы всегда определена и сама является матрицей.
Обратная функция
Обратной функцией к экспоненциальной функции является натуральный логарифм.
Обозначается ln(x):ln(x) = loge(x)
См.
 также
также- Экспонента комплексного переменного (обобщение)
- Показательная функция
Wikimedia Foundation. 2010.
Игры ⚽ Нужно решить контрольную?
- Экспонента группы
- Экспансия Третьего рейха
Полезное
Экспоненциальная функция | это… Что такое Экспоненциальная функция?
ТолкованиеПеревод
- Экспоненциальная функция
-
Экспонента — функция exp(x) = ex, где e — основание натуральных логарифмов.
Содержание
- 1 Определение
- 2 Свойства
- 3 Экспонента от комплексного аргумента
- 4 Вариации и обобщения
- 4.1 Матричная экспонента
- 5 Обратная функция
- 6 См.
 также
также
Определение
Экспоненциальная функция может быть определена различными эквивалентными способами. Например через ряд Тейлора:
или через предел:
Здесь x — любое вещественное или комплексное число.
Свойства
- (ex)’ = ex, в частности
- Экспонента является единственным решением дифференциального уравнения y‘ = y с начальными данными
- Экспонента определена на всей вещественной оси. Она всюду возрастает и строго больше нуля.
- Экспонента является выпуклой функцией.
- Обратная функция к ней — натуральный логарифм .
- Производная в нуле равна 1, поэтому касательная к экспоненте в этой точке проходит под углом 45°.
- Основное функциональное свойство экспоненты:
- exp(a + b) = exp(a)exp(b).

- Непрерывная функция с таким свойством либо тождественно равна 0, либо имеет вид exp(ct), где c — некоторая константа.
- exp(a + b) = exp(a)exp(b).
Экспонента от комплексного аргумента
От комплексного аргумента z = x + iy экспонента определяется следующим образом:
- ez = ex + iy = exeiy = ex(cosy + isiny) (формула Эйлера)
В частности,
- eiπ + 1 = 0
Вариации и обобщения
Аналогично экспонента может быть определена для элемента произвольной ассоциативной алгебры. В конкретном случае требуется также доказательство того, что указанные пределы существуют.
Матричная экспонента
Экспоненту от квадратной матрицы (или линейного оператора) можно формально определить, подставив матрицу в соответствующий ряд:
Определённый таким образом ряд сходится для любого оператора A с ограниченной нормой, поскольку мажорируется рядом для экспоненты нормы A: Следовательно, экспонента от матрицы всегда определена и сама является матрицей.

С помощью матричной экспоненты легко задать вид решения линейного дифференциального уравнения с постоянными коэффициентами: уравнение с начальным условием x(0) = x0 имеет своим решением x(t) = exp(At)x0.
Обратная функция
Обратной функцией к экспоненциальной функции является натуральный логарифм.
Обозначается ln(x):ln(x) = loge(x)
См. также
- Экспонента комплексного переменного (обобщение)
- Показательная функция
Wikimedia Foundation. 2010.
Игры ⚽ Поможем сделать НИР
- Экспонента группы
- Экспансия Третьего рейха
Полезное
Экспоненциальная функция | математика | Британика
- Развлечения и поп-культура
- География и путешествия
- Здоровье и медицина
- Образ жизни и социальные вопросы
- Литература
- Философия и религия
- Политика, право и правительство
- Наука
- Спорт и отдых
- Технология
- Изобразительное искусство
- Всемирная история
- Этот день в истории
- Викторины
- Подкасты
- Словарь
- Биографии
- Резюме
- Популярные вопросы
- Обзор недели
- Инфографика
- Демистификация
- Списки
- #WTFact
- Товарищи
- Галереи изображений
- Прожектор
- Форум
- Один хороший факт
- Развлечения и поп-культура
- География и путешествия
- Здоровье и медицина
- Образ жизни и социальные вопросы
- Литература
- Философия и религия
- Политика, право и правительство
- Наука
- Спорт и отдых
- Технология
- Изобразительное искусство
- Всемирная история
- Britannica объясняет
В этих видеороликах Britannica объясняет различные темы и отвечает на часто задаваемые вопросы.
- Britannica Classics
Посмотрите эти ретро-видео из архивов Encyclopedia Britannica. - Demystified Videos
В Demystified у Britannica есть все ответы на ваши животрепещущие вопросы. - #WTFact Видео
В #WTFact Britannica делится некоторыми из самых странных фактов, которые мы можем найти. - На этот раз в истории
В этих видеороликах узнайте, что произошло в этом месяце (или любом другом месяце!) в истории.
- Студенческий портал
Britannica — это главный ресурс для учащихся по ключевым школьным предметам, таким как история, государственное управление, литература и т. д. - Портал COVID-19
Хотя этот глобальный кризис в области здравоохранения продолжает развиваться, может быть полезно обратиться к прошлым пандемиям, чтобы лучше понять, как реагировать сегодня. - 100 женщин
Britannica празднует столетие Девятнадцатой поправки, выделяя суфражисток и политиков, творящих историю.
- Спасение Земли
Британника представляет список дел Земли на 21 век. Узнайте об основных экологических проблемах, стоящих перед нашей планетой, и о том, что с ними можно сделать! - SpaceNext50
Britannica представляет SpaceNext50. От полёта на Луну до управления космосом — мы исследуем широкий спектр тем, которые подпитывают наше любопытство к космосу!
Содержание
- Введение
Краткие факты
- Связанный контент
Викторины
- Числа и математика
Горизонтальный и вертикальный перевод экспоненциальных функций
Результаты обучения
- Нарисуйте график экспоненциальных функций, сдвинутых по горизонтали или вертикали, и напишите соответствующее уравнение.


 Кроме того через экспоненту выражаются общие решения однородных дифференциальных уравнений.
Кроме того через экспоненту выражаются общие решения однородных дифференциальных уравнений.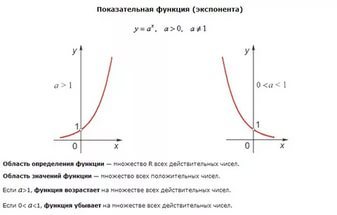 В конкретном случае требуется также доказательство того, что указанные пределы существуют.
В конкретном случае требуется также доказательство того, что указанные пределы существуют.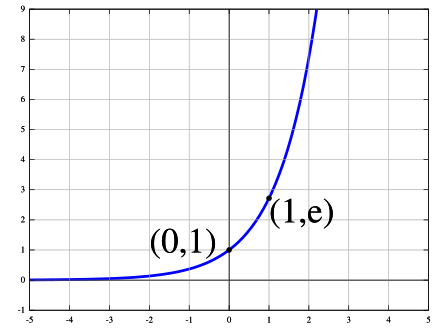 также
также также
также