Экспонента равно: Что такое экспонента или как заставить чай остывать не так быстро — T&P

Содержание

Что такое экспонента или как заставить чай остывать не так быстро — T&P

Когда снежный ком катится с горы, он постоянно увеличивается. Чем больше он становится, тем быстрее катится, чем быстрее катится, тем быстрее растет.

Математики и физики очень любят описывать мир при помощи чисел. А еще больше — при помощи функций. Функция — это правило, по которому одному числу (например, x) ставится в соответствие другое (например y). Функции бывают простые, вроде y=10x или y=x², а бывают посложнее вроде y=10*sin(7×2+3x-9). Если вместо x и y подставить определенные физические параметры и найти функцию, которая их связывает, то получится закон природы.

Еще у функций есть производная. Это — скорость изменения функции. То есть то, насколько изменится y при небольшом изменении x. Например, в случае функции y=10x производная всегда постоянная: y всегда будет расти в 10 раз быстрее, чем x. А в случае функции y=x²

производная будет меняться. Если мы увеличим x c 0 до 1, то y тоже увеличится с 0 до 1. А если увеличим x с 1 до 2, то y увеличится с 1 до 4. То есть, производная с ростом x увеличилась.

Экспонентой называется функция y=e^x, где e — хитрое математическое число, которое примерно равно 2,72. Она обладает замечательным свойством: ее производная равна ей самой. То есть, если расстояние, которое проходит снежный ком, зависит от времени как экспонента, то и его скорость выражается той же самой экспонентой. Это свойство очень помогает математикам решать разные дифференциальные уравнения. Они очень любят с ней работать и стараются разные другие функции путем сдвига, растяжения, или переворачивания графика превратить в экспоненту. Все такие функции можно назвать экспоненциальными. У экспоненциально протекающих процессов есть одно общее свойство: за одинаковый интервал времени их параметры меняются в одинаковое число раз.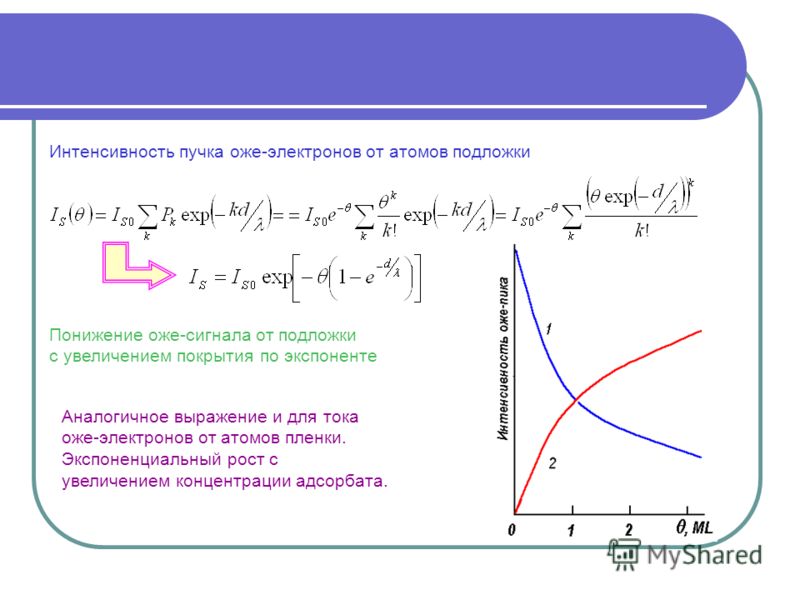

Банковский вклад каждый год увеличивается на 7%, снежный ком за минуту увеличивается в три раза, а количество урана-235 на атомных электростанциях уменьшается вдвое каждые 700 миллионов лет. Экспоненциальные функции окружают нас повсюду. Экспоненциально развиваются все явления, в которых присутствует обратная связь, когда результат влияет на скорость процесса. В случае со снежным комом обратная связь положительная: чем больше результат, тем быстрее протекает процесс. А масса и скорость снежного кома y экспоненциально возрастают со временем x. Аналогично ведут себя деньги в банке при фиксированной процентной ставке. Чем больше денег, тем больше ежегодный прирост — и тем быстрее денег хватит на домик на Мальдивах. Так же увеличивается численность животных при отсутствии внешних угроз: чем больше популяция, тем больше размножающихся особей, тем быстрее она увеличивается. А еще, когда микрофон подносишь близко к динамику, то самый тихий шорох через секунду превратится в звонкий гул.

Бывает, что обратная связь отрицательная: чем больше результат, тем медленнее идет процесс. Например, когда мы голодны, мы начинаем быстро поглощать еду, но как только чувство голода уменьшается, мы начинаем есть спокойно, потом лениво доедаем десерт. Чай остывает тоже по экспоненте: чем больше разность температур между чаем и воздухом, тем быстрее он остывает. Так что, если вам надо срочно отвлечься на 15 минут, а горячего чаю выпить хочется — налейте в него холодного молока или воды. Тогда разница температур уменьшится, и чай не остынет так быстро, как если бы он был горячим.

Чем быстрее движется струна гитары, тем быстрее она тормозится о воздух, поэтому громкость звука после дерганья за струну экспоненциально уменьшается. Еще один пример — ядерный распад. Каждое ядро может распасться в случайный момент времени, но чем ядер больше, тем больше распадов будет происходить за одну минуту. Чем быстрее ядра распадаются, тем меньше их становится, а значит и интенсивность радиации со временем падает.

Константин Катамадзе

Числа π и e

Все знают геометрический смысл числа π — это длина окружности с единичным диаметром:

А вот смысл другой важной константы, e, имеет свойство быстро забываться. То есть, не знаю, как вам, а мне каждый раз стоит усилий вспомнить, чем же так замечательно это число, равное 2,7182818284590… (значение я, однако, по памяти записал). Поэтому я решил написать заметку, чтобы больше из памяти не вылетало.

Число e по определению — предел функции y = (1 + 1 / x)^x при x → ∞:

x	y
1	(1 + 1 / 1)¹	= 2
2	(1 + 1 / 2)²	= 2,25
3	(1 + 1 / 3)³	= 2,3703703702. ..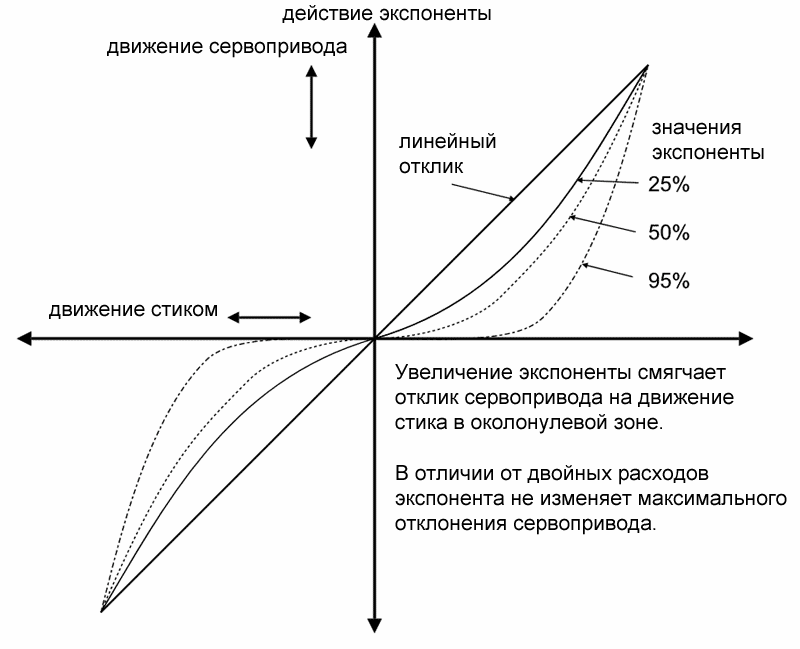
10	(1 + 1 / 10)¹⁰	= 2,5937424601…
100	(1 + 1 / 100)¹⁰⁰	= 2,7048138294…
1000	(1 + 1 / 1000)¹⁰⁰⁰	= 2,7169239322…
∞	lim_{× → ∞}	= 2,7182818284590…

Это определение, к сожалению, не наглядно. Непонятно, чем замечателен этот предел (несмотря на то, что он называется «вторым замечательным»). Подумаешь, взяли какую-то неуклюжую функцию, посчитали предел. У другой функции другой будет.

Но число e почему-то всплывает в целой куче самых разных ситуаций в математике.

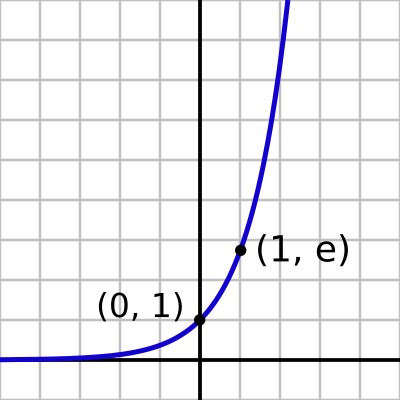
Для меня главный смысл числа e раскрывается в поведении другой, куда более интересной функции, y = k^x. Эта функция обладает уникальным свойством при k = e, которое можно показать графически так:

В точке 0 функция принимает значение e⁰ = 1. Если провести касательную в точке x = 0, то она пройдёт к оси абсцисс под углом с тангенсом 1 (в жёлтом треугольнике отношение противолежащего катета 1 к прилежащему 1 равно 1). В точке 1 функция принимает значение e¹ = e. Если провести касательную в точке x = 1, то она пройдёт под углом с тангенсом e (в зелёном треугольнике отношение противолежащего катета e к прилежащему 1 равно e). В точке 2 значение e² функции снова совпадает с тангенсом угла наклона касательной к ней. Из-за этого, заодно, сами касательные пересекают ось абсцисс ровно в точках −1, 0, 1, 2 и т. д.

Среди всех функций y = k^x (например, 2^x, 10^x, π^x и т. д.), функция e^x — единственная обладает такой красотой, что тангенс угла её наклона в каждой её точке совпадает со значением самой функции. Значит по определению значение этой функции в каждой точке совпадает со значением её производной в этой точке: (e^x)´ = e^x. Почему-то именно число e = 2,7182818284590… нужно возводить в разные степени, чтобы получилась такая картинка.

Именно в этом, на мой вкус, состоит его смысл.

Числа π и e входят в мою любимую формулу — формулу Эйлера, которая связывает 5 самых главных констант — ноль, единицу, мнимую единицу

i и, собственно, числа π и е:

e^iπ + 1 = 0

Почему число 2,7182818284590… в комплексной степени 3,1415926535…i вдруг равно минус единице? Ответ на этот вопрос выходит за рамки заметки и мог бы составить содержание небольшой книги, которая потребует некоторого начального понимания тригонометрии, пределов и рядов.

Меня всегда поражала красота этой формулы. Возможно, в математике есть и более удивительные факты, но для моего уровня (тройка в физико-математическом лицее и пятёрка за комплексный анализ в универе) это самое главное чудо.

Как определить неизвестный показатель степени

Обновлено 16 февраля 2020 г.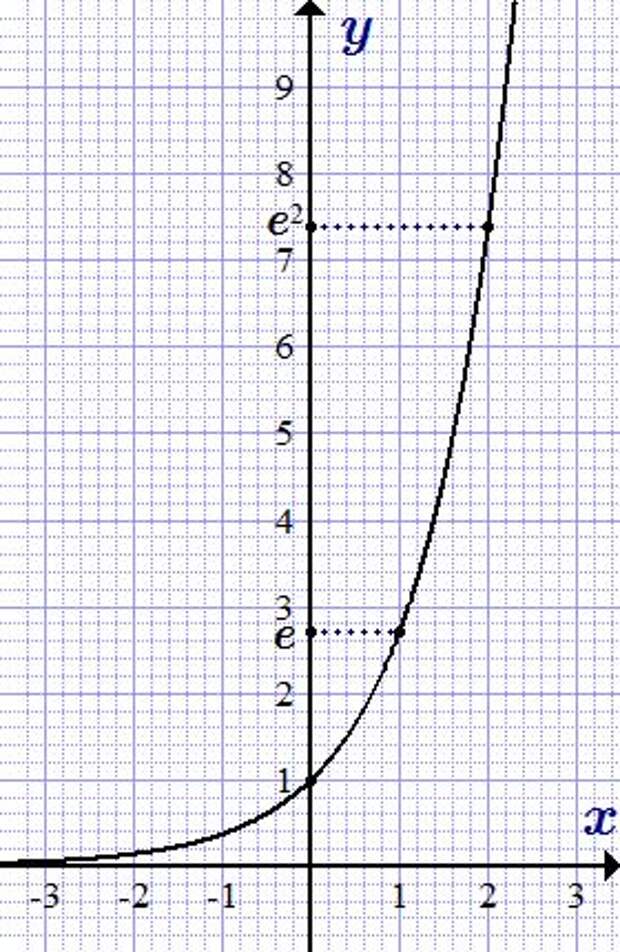

Кевин Бек

Если вы видите выражения 3 ² и 5 ³ , вы можете с размаху объявить, что они означают «три в квадрате» и «пять в кубе», и сможете найти эквивалентные числа без показателей степени , числа, представленные верхними индексами вверху справа выше. Эти числа в данном случае 9и 125.

Но что, если вместо, скажем, простой экспоненциальной функции, такой как y = x ³ , вам нужно решить уравнение вида y = 3 ^x . Здесь x, зависимая переменная, появляется как экспонента. Есть ли способ вытащить эту переменную из ее насеста, чтобы упростить математические операции с ней?

На самом деле есть, и ответ кроется в естественном дополнении показателей, которые представляют собой забавные и полезные величины, известные как логарифмов .

Что такое экспоненты?

Показатель степени , также называемый степенью , представляет собой сжатый способ выражения многократного умножения числа на самого себя. 4 ⁵ = 4 × 4 × 4 × 4 × 4 = 1024.

Любое число, возведенное в степень 1, сохраняет то же значение; любое число с показателем степени 0 равно 1. Например, 72 ¹ = 72; 72 ⁰ = 1.

Показатели степени могут быть отрицательными, что дает отношение x ⁻ⁿ = 1/(x ⁿ ) . Их также можно представить в виде дробей, например, 2 ^(5/3) . При выражении в виде дробей и числитель, и знаменатель должны быть целыми числами.

Что такое логарифмы?

Логарифмы, или «логарифмы», можно рассматривать как показатели степени, выраженные не в степени, а в чем-то другом. Это, вероятно, не очень поможет, поэтому, возможно, пример или два будут.

В выражении 10 ³ = 1000 число 10 равно основание , и оно возводится в третью степень (или степень три). Вы можете выразить это как «основание 10, возведенное в третью степень, равно 1000».

Пример логарифма: log ₁₀ (1000) = 3 . Обратите внимание, что числа и их отношения друг к другу такие же, как и в предыдущем примере, но они были перемещены. Другими словами, это означает, что «логарифмическая база 10 из 1000 равна 3».

Число справа — это степень, в которую нужно возвести основание числа 10, чтобы оно равнялось 9.0013 аргумент или ввод лога, значение в скобках (в данном случае 1000). Это значение должно быть положительным, потому что основание — которое может быть числом, отличным от 10, но предполагается равным 10, если оно опущено, например, «log 4» — также всегда положительно.

Полезные правила логарифмирования

Так как же легко работать между логарифмами и экспонентами? Несколько правил поведения журналов помогут вам начать работу с экспонентами.

log_{b}(xy) = log_{b}{x} + log_{b}y log_{b}(\dfrac{x}{y}) = log_{b}{x} \text{ − } log_{b}y log_{b}(x^A) = A⋅log_{b}(x) log_{b}(\dfrac{1}{y}) = -log_{b}(y)

Нахождение показателя степени

Имея приведенную выше информацию, вы готовы попытаться найти показатель степени в уравнении.

Пример: Если 50 = 4 ^x , чему равно x?

Если взять логарифм по основанию 10 с каждой стороны и опустить явную идентификацию основания, получится log 50 = log 4 ^x . Из приведенного выше поля вы знаете, что log 4 ^x = x log 4. Это оставляет вас с

log 50 = x log 4, или x = (log 50)/(log 4).

С помощью калькулятора или другого электронного устройства вы обнаружите, что решение равно (1,689/0,602) = 2,82 .

Решение экспоненциальных уравнений с e

Те же правила применяются, когда основанием является e , так называемый натуральный логарифм , который имеет значение около 2,7183. У вас также должна быть кнопка для этого на вашем калькуляторе. Это значение также получает собственное обозначение: log _e x пишется просто «ln x».

Функция y = e ^x i, где e не является переменной, а константой с этим значением, является единственной функцией с наклоном, равным ее собственной высоте для всех x и y.
Так же, как журнал ₁₀ 10 ^x = x, ln e ^x = x для всех x.

Пример: Решите уравнение 16 = e ^2,7x .

Как и выше, ln 16 = ln e ^2,7x = 2,7x.

ln 16 = 2,77 = 2,7x, поэтому x = 2/77/2,7 = 1,03.

алгебраическое предварительное исчисление — Что-нибудь в нулевой степени равно единице?

спросил 5 лет, 2 месяца назад 90 = 1 $$

Вы сделали то, что делают многие изучающие элементарную алгебру, и думаете, что распределение показателей степени через бином разрешено. Это допускается только в более сложном смысле, когда $x$ и $y$ являются членами коммутативного кольца характеристики $p$ — простого числа. Конечно, это делается в абстрактной алгебре, курсе, который изучают математики на младших или старших курсах колледжа.