Решение задач по дискретной математике – Страница не найдена | Алматинский филиал Санкт-Петербургского Гуманитарного университета профсоюзов

Решение практических заданий по дискретной математике

Содержание

Введение

Задание 1

Представить с помощью кругов Эйлера множественное выражение

Используя законы и свойства алгебры множеств, упростить заданное выражение

Задание 2

Заданы множества кортежей

Показать, что эти множества представляют собой соответствия между множествами N₁ и N₂ , если N₁ = N₂ =

. Дать полную характеристику этих соответствий

Задание 3

Частично упорядоченное множество М задано множеством упорядоченных пар

Построить диаграмму и определить, является ли данное множество решеткой. Если заданное множество является решеткой, то определить, является ли решетка дедекиндовой , дистрибутивной …

Задание 4

Является ли полной система булевых функций

? Если система функций полная ,то выписать все возможные базисы

Задание 5

Минимизировать булеву функцию

по методу Квайна – Мак-Класки

Задание 6

Для неориентированного графа

, у которого ,

а) вычислить числа

;

б) определить хроматическое число

…

Задание 7

Для заданной сети

:

а) найти величину минимального пути и сам путь от вершины

до вершины по алгоритму Дейкстры ;

б) используя алгоритм Форда-Фалкерсона, определить максимальный поток

( v₁ – вход , v₆ – выход сети ) и указать минимальный разрез, отделяющий v₁ от v₆ , если задана матрица весов (длин, пропускных способностей) Р…

Литература

Введение

Проблемы, связанные с понятиями бесконечности, дискретности и непрерывности, рассматривались в математике, как и в философии, древнегреческими мыслителями, начиная с 6 века до нашей эры. Под влиянием сочинений Аристотеля они широко обсуждались средневековыми учеными и философами в странах Европы и Азии. Через всю историю математики проходит идея преодоления между актуальной и потенциальной бесконечностью, с одной стороны, между дискретным характером числа и непрерывной природой геометрических величин – с другой. Впервые проблема математической бесконечности и связанных с нею понятий была широко поставлена в наиболее общем виде в теории множеств, основы которой были разработаны в последней четверти 19 века Георгом Кантором.

Цель контрольной работы – ознакомится с основными понятиями и методами решения по дискретной математике, уметь применить полученные знания при решении практического задания.

Задание 1

Представить с помощью кругов Эйлера множественное выражение

.

Используя законы и свойства алгебры множеств, упростить заданное выражение.

Решение:

Используя круги Эйлера и, учитывая, что операция пересечения выполняется раньше операции объединения, получим следующие рисунки:

Объединяя заштрихованные области, получим искомое множество:

Упростим заданное выражение:

= .

Задание 2

Заданы множества кортежей:

.

Показать, что эти множества представляют собой соответствия между множествами N

1 и N₂ , если N₁ = N₂ =

. Дать полную характеристику этих соответствий

Решение:

Найдем декартово произведение:

Видно, что заданные множества являются подмножествами этого пря-мого произведения. Следовательно, данные множества есть соответствия.

а)

.

Область определения:

. Следовательно, соответствие является частично определенным.

Область значений:

. Следовательно, соответствие является сюръективным.

Образом элемента

являются два элемента . Значит соответствие не является функциональным. Из этого следует, что соответствие не является функцией, отображением.

б)

.

Область определения:

. Следовательно, соответствие является частично определенным.

Область значений:

. Следовательно, соответствие не является сюръективным.

Образом любого элемента из

является единственный элемент из . Следовательно, соответствие является функциональным, функци-ей. Соответствие является частично определенным. Это означает, что функция является частично определенной и не является отображением.

в)

.

Область определения:

.Следовательно, соответствие всюду определено.

Область значений:

. Следовательно, соответствие не является сюръективным.

Образом любого элемента из

является единственный элемент из . Следовательно, соответствие является функциональным, функцией. Так как соответствие всюду определено, то имеем полностью определенную функцию, т.е. имеем отображение N₁ в N₂ .

г)

.

Область определения:

. Значит, соответствие полностью определено.

Область значений:

. Значит, соответствие сюръективно.

Образом любого элемента из N₁ является единственный элемент из N₂ . Следовательно, соответствие является функциональным, функцией.

Так как соответствие всюду определено, сюръективно, функционально и прообразом любого элемента из

является единственный элемент из , то соответствие является взаимно однозначным.

mirznanii.com

Вариант 8.

Задание №1.

Исходя из определения равенства множеств и операций над множествами, доказать тождество и проверить его с помощью диаграмм Эйлера-Венна.

Решение:

Что и требовалось доказать.

Проверим с помощью диаграмм Эйлера-Венна:

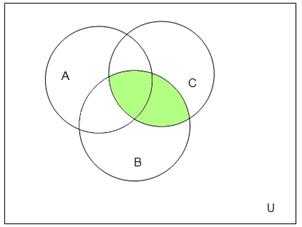
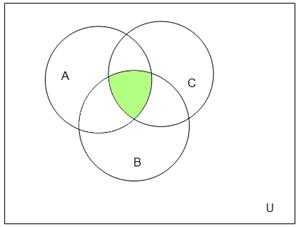
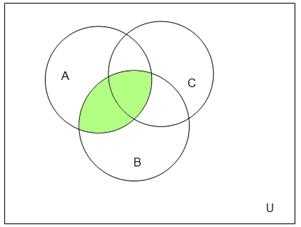
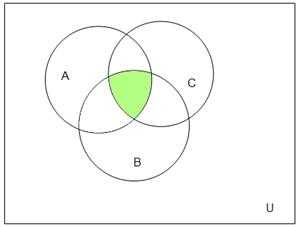
Результаты совпали.

Задание №2.

С помощью таблицы истинности установите эквивалентны ли данные формулы:

Решение:

0	0	1	1	0	0	1	1
0	1	1	0	0	0	1	1
1	0	0	1	0	1	1	1
1	1	0	0	1	1	0	1

Итак, данные формулы неэквивалентны, поскольку в выделенных столбцах значения не совпали.

Задание № 3.

Проверьте, является ли данное отношение отношением эквивалентности.

Отношение «число x больше или равно числа y».

Решение:

Отношение является отношением эквивалентности, если оно рефлексивно, симметрично и транзитивно.

Проверим выполнимость рефлексивности (отношение рефлексивно на множестве М, если ).

.

Тогда рефлексивность выполняется.

Проверим выполнимость симметричности (отношение симметрично на множестве М, если ).

Если , то не для всех пар будет выполняться условие , следовательно, рефлексивность не выполняется.

Таким образом, отношение «число x больше или равно числа y» не является отношением эквивалентности.

Задание № 4 .

Нарисовать на плоскости граф G=[V, E] (единственный с точностью до изоморфизма), имеющий заданную матрицу úçdijúçсвоей матрицей смежности. Найти матрицу инцидентности úçrijúçграфа G.

Решение:

Матрица симметрична, тогда граф не является ориентированным. Искомый граф имеет 4 вершины и 4 ребра. Построим его:

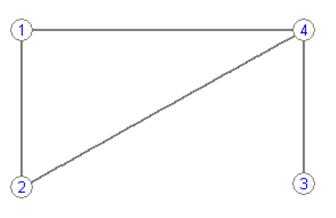
Перенумеруем ребра:

Составим матрицу инцидентности:

Задание № 5.

Нарисовать на плоскости орграф G=[N, A] (единственный с точностью до изоморфизма), имеющий заданную матрицу úçdijúçсвоей матрицей смежности. Найти матрицу инцидентности úçcijúçграфа G.

Решение:

Матрица симметрична. Искомый граф имеет 4 вершины, 4 пары обычных ребер, каждая из которых направлена в противоположном направлении, а также 4 петли. Построим его:

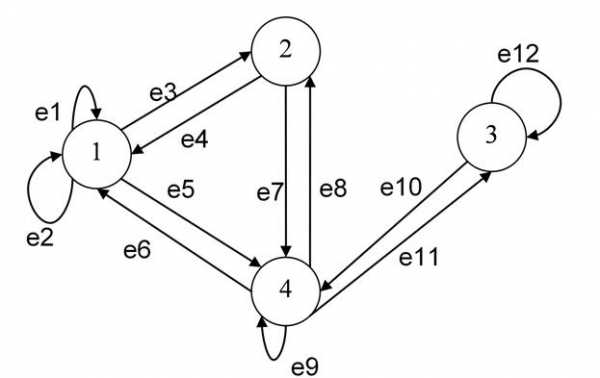
Матрица инцидентности:

< Предыдущая		Следующая >

matica.org.ua

Сборник заданий и упражнений по дискретной математике

Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

«Омский государственный технический университет»

В.В. Аристов, В.Н. Гудинов

Практикум

Омск 2006

УДК 519(075)

ББК 22.176я73

А 81

Р е ц е н з е н т ы :

Палий И.А., доцент каф. «Прикладная информатика в экономике» СибАДИ,

Галдин Н.С., д.т.н., профессор каф. «ПТТМ и Г» СибАДИ

Аристов В.В., Гудинов В.Н.

А81 Сборник заданий и упражнений по дискретной математике. – Омск: Изд-во ОмГТУ, 2006. 51 с.

Сборник содержит в краткой форме теоретические сведения, необходимые для решения задач и упражнений. Даны задания на практическую и самостоятельную работу, а также по выводу доказательств логических выражений по таким разделам дискретной математики, как множества, логика Буля, логика высказываний, логика предикатов.

Предназначен для студентов дневного, вечернего и заочного обучения по специальностям: 220301 – «Автоматизация технологических процессов и производств» и 220401 – «Мехатроника».

УДК 519(075)

ББК 22.176я73

Печатается по решению редакционно-издательского совета Омского государственного технического университета.

© В.В. Аристов, В.Н. Гудинов, 2006

© Омский государственный

технический университет, 2006

Введение

Дискретная математика является одним из основных разделов теоретической кибернетики – науки, являющейся основой анализа и синтеза современных вычислительных систем. Широкое и повсеместное использование ЭВМ и микропроцессорных систем управления требует фундаментальных знаний прикладных специализированных дисциплин, читаемых в технических вузах, таких как «Теоретическая информатика», «ЭВМ и вычислительные системы», «Теория конечных автоматов» и др. Среди всех этих дисциплин «Дискретная математика» составляет базу для создания математического обеспечения современных компьютерных и информационных технологий. Формальные языки дискретной математики позволяют создавать математические модели вычислительных процессов и цифровых логических устройств, используемых в современных автоматизированных системах. Вот почему основная цель настоящего сборника – привить навыки решения логических задач, описанных с помощью формального языка дискретной математики, что позволит развить в дальнейшем способности к логическому мышлению в любой прикладной области.

В сборнике уделено основное внимание таким разделам дискретной математики, как «множества» и «логика». В свою очередь логика делится на три подраздела: «логику Буля», «логику высказываний» и «логику предикатов».

Для наглядного восприятия основных положений теории множеств использованы диаграммы Венна и круги Эйлера. На этих диаграммах рассмотрены основные логические операции над множествами.

Логика Буля имеет особое прикладное значение для проектировщика систем автоматизации, так как формализм ее языка позволяет описывать логические процессы, характеризующие работу дискретных автоматов. Впервые в мире возможность использования методов логики Буля для описания и преобразования релейно-контактных схем электроавтоматики была доказана в 1938 году В.И.Шестаковым. А спустя 10 лет М.А. Гавриловым были решены проблемы формального анализа и синтеза дискретных устройств управления на основе основных положений логики Буля. В нашем сборнике основная часть заданий по логике Буля посвящена преобразованию и минимизации булевых функций, а также представлению булевых функций в различных формах.

Логика Буля основывается на отношении эквивалентности, при котором левая и правая части логического выражения содержат равное количество «истины». Логика высказываний и логика предикатов базируются уже на отношении порядка, при котором правая часть выражения (заключение) содержит больше «истины», чем левая часть (посылка), т.е. «истинность» заключения оказывается выше «истинности» посылки. Логика высказываний исходит корнями из философии древности, от Платона и Аристотеля. На первый взгляд некоторые высказывания лишены здравого смысла, однако формализм логики высказываний позволяет моделировать многие субъектные ситуации на ЭВМ.

В каждой теме перед заданиями для практической и самостоятельной работы приводятся основные необходимые теоретические положения и рассматриваются примеры решений и доказательств.

studfiles.net

Задачи по дискретной математике [RTF]

Методическое пособие — Сборник задач и упражнений по курсу Дискретная математика. В пособии приведена теория, примеры решения задач и задачи для самостоятельного решения по разделу «Элементы теории множеств и теории графов». Элементы теории множеств: Теоретико-множественные операции, Соответствия, Отображения, Отношения. Элементы теории графов.

• 641,09 КБ
• дата добавления неизвестна
• изменен 24.05.2012 20:08

Учебное пособие. — Уфа: Уфимский государственный авиационный технический университет, 2000. — 126 с. Элементы комбинаторики. Перестановки. Размещения. Сочетания. Задачи по комбинаторике. Функции алгебры логики. Элементарные функции алгебры логики. Формульное задание функций алгебры логики. Принцип двойственности. Разложение булевой функции по переменным. Полнота, примеры полных…

• 878,80 КБ
• дата добавления неизвестна
• изменен 06.08.2018 07:26

Решебник содержит решения задач дискретной математики: диаграммы Эйлера-Венна; высказывание в виде формулы логики высказываний и формулы логики предикатов; СДНФ и СКНФ булевой функции. При помощи алгоритма Вонга и метода резолюции определяется является ли клауза теоремой и др.

• 147,61 КБ
• дата добавления неизвестна
• изменен 27.04.2011 18:49

Математика. Дискретная математика: методические указания для самостоятельной работы студентов очной формы обучения (I семестр). — Брянск: БГТУ, 2008. – 35 с. БГТУ, 1 семестр Предисловие Разбор типичных задач Элементы теории множеств Множества. Операции над множествами Отображения. Инъективные и сюръективные отображения Отношение эквивалентности Элементы теории…

• 558,04 КБ
• дата добавления неизвестна
• изменен 12.12.2009 13:38

Архив содержит 10 вариантов.

• 389,16 КБ
• дата добавления неизвестна
• изменен 26.05.2008 10:39

СПб.: БХВ-Петербург, 2008. — 352 с: ил. — (Учебная литература для вузов) — ISBN 978-5-9775-0232-0 Учебное пособие составлено на основании материалов лекционного курса, содержит краткую теорию, варианты заданий и примеры решения по следующим разделам дискретной математики: множества, декартовы произведения, соответствия, отношения, булевы функции, теория алгоритмов, предикаты,…

• 9,64 МБ
• дата добавления неизвестна
• изменен 24.09.2010 22:09

www.twirpx.com

Задачи по дискретной математике и их быстрое решение на заказ

Каждый может получить ту или иную специальность. Однако будущие студенты должны знать, что в процессе обучения их ждет знакомство не только с предметами, необходимыми по специальности или же с общими дисциплинами, но еще и с рядом других наук, изучение которых не дает особых профессиональных навыков, но входит в учебную программу. К таким предметам стоит отнести и дискретную математику.

Этот предмет отличается повышенной сложностью, поэтому и решение задач по этому предмету является самой большой проблемой современного ученика или студента.

Какие есть варианты избежать необходимости самостоятельной работы?

Для того чтобы самостоятельно не выполнять задачи по такому предмету как дискретная математика, существует несколько иных вариантов. К примеру, это может быть:

• помощь сокурсников, также изучающих дискретную математику;
• обращение к человеку, который предлагает выполнение таких заданий за деньги;
• или же можно обратиться в специализированную компанию, которая сможет оказать подобные услуги.

В первом случае, если написание работы будет осуществляться вашими сокурсниками, то существует риск, что студенты, разбирающиеся в таком предмете как дискретная математика, ничуть не лучше вас, сделают работу такой, что претендовать с ней на высокую оценку будет весьма проблематично.

В то же время многие обращаются к знакомым знакомых и так далее, которые могут предложить выполнение подобной задачи недорого.

К сожалению, такие люди вряд ли одинаково хорошо разбираются во всех предметах, тем более в таких же сложных как дискретная математика.

Чтобы написать по ней качественную работу, нужно знать на отлично, что такое дискретные математические структуры, какие манипуляции можно совершить с конечными группами, автоматами и графами.

Поэтому и такое исполнение может быть мало качественным.

Обращение в специализированные компании

Еще один вариант, который будет наиболее приемлемым, это обращение в специализированную компанию, которая помимо скромной стоимости может предложить еще и высокое качество выполненного заказа.

Цена за подобную услугу будет весьма скромной. Тем более, качество работ будет на высоте. Любой, кто решит обратиться в компанию за помощью, может предварительно убедиться в способности штата сотрудников такой организации качественно выполнить любой заказ, даже по дискретной математике.

Так, можно обратить внимание на отзывы, которые оставили другие заказчики. В большинстве случаев, именно так и можно понять, может ли компания и ее сотрудники качественно выполнить задание – написать его в полном объеме, в нужной тематике, правильно и точно в срок.

А далее, можно уже обратить внимание и на репутацию. Исполнитель, обладающий хорошей репутацией, вряд ли рискнет ею и сделает один из своих заказов плохо, тем самым обрушив свои многолетние старания, а наша компания находится на рынке уже более 8 лет, и нареканий на работу ее сотрудников не было.

Иные плюсы и преимущества

Еще один неоспоримый плюс, который может предложить специалист – это возможность написать работу в самые короткие сроки. В частности, есть возможность срочно заказать любую работу, включая и по дискретной математике. Так, сотрудники, принявшие у вас заказ, смогут написать и закончить задание точно в срок, пусть он даже будет сильно ограниченным. Конечно же, такая спешка потребует дополнительной оплаты. Однако если не затягивать с заказом, не пытаться самостоятельно разобраться со сложным заданием, вовремя отдать его специалистам, можно не только вовремя получить уже законченный труд, но еще и сэкономить – ведь за срочность платить не нужно.

Так, дискретная математика и задачи по ней, любые другие предметы могут быть с легкостью решены и написаны нашими специалистами, среди которых есть люди самых разных профессий.

matematiku5.ru

Решение задач по дискретной математике на заказ

Дискретная математика – это нелюбимая студентами часть математики, которая изучает дискретные структуры в математике. Среди них есть графы и утверждения в логике. Конечно же, название предмета «дискретная математика» вгоняет студента в дрожь, ибо считается одной из самых сложных отраслей математики

Дискретная математика на заказ

Существует множество причин, по которым студенты заказывают разнообразные работы. Одной из самых популярных причин является наличие работы, которая отбирает основную часть времени. Более того, работающий человек мыслит совсем по-другому, и ему крайне важно сохранить хотя бы часть личного времени.

Иногда, недопонимание предмета приводит к тому, что приходится заказывать решение задач по дискретной математике, а не решать самому. Кстати, заказ — это отличный способ разобраться, ибо по развернутому решению можно идти, как по ступенькам к знаниям. Нелишним будет также перерешать самостоятельно примеры, которые вы заказывали. Это стоит делать лишь после того, как вы уверены, что усвоили материал полностью.

Еще одной причиной является неуверенность в своих силах, что часто бывает, когда материал слишком сложный. Студенты считают, что лучше всего подстраховаться и заказать.

Плохие отношения с преподавателем тоже веская причина для обращения за помощью. Когда преподаватель относится к вам не лучшим образом, то проверяя работы, он относится к вашей предвзято, и потому она должна быть идеальна, из чего следует, что лучше доверить это профессионалам.

И последняя из основных причин, — это просто нехватка времени и желание нормально провести свой досуг вместо того, чтобы тратить свои силы на решение задач по дискретной математике.

Как можно сэкономить на решении задач?

Разумное распределение финансов – это ключ к успеху. А что у нас является разумным распределением финансов? Правильно, экономия. Так как же можно сэкономить на решении задач по дискретной математике?

Сделать это можно проще, чем вы думаете. Для начала, когда вам выдают задание, попробуйте сделать то, что вы можете, и только потом заказывайте решение всего остального. Ибо, именно так, вы сможете сэкономить неплохую сумму денег.

Где можно заказать решение задач по дискретной математике?

Решение задач можно заказать самыми разнообразными способами и основные из них мы с вами разберем, дабы сэкономить вам время раздумий.

Первым способом, который приходит на ум, это попросить помощи у однокурсников или знакомых. Это прекрасное решение в плане финансовой выгоды, так как знакомые не будут брать с вас слишком много. Но ведь и опыта у них в этом деле меньше, да и образование еще не законченное. Тем более, как может помочь человек, который не знает всех тонкостей решения задач по дискретной математике. Как вы видите, этот вариант отметается за непригодностью.

Часто спасителем в таких ситуациях называют Интернет, в котором вы можете найти решебники. Чем плохие решебники? Да тем, что они дают сразу же ответ и не дают развернутого решения, что важно для преподавателя, да и для вас, если вы заказать хотите в целях обучения.

Заказывать решения у непроверенных людей в Интернете также чревато последствиями, так как вам могут решить неправильно, а деньги вам не вернут, либо просто заберут деньги. И тот, и тот вариант не считается приятными.

Наконец, мы добрались к лучшему решению вопроса. Ваш выбор — это специализированный коллектив, который работает в компании, которая уже длительное время находится в устойчивом положении на рынке в сфере услуг. Это наша компания, которая на плаву уже 8 лет и является лучшей в своем роде, что доказывают приятные отзывы о нашей деятельности. Вам всегда рады в нашем реальном офисе. Вас встретят радушно и с уважением. Если желаете ускорить процесс заказа, то воспользуйтесь сайтом, где вы можете оформить заявку в мгновение ока, и примут ее сию же минуту. С вами гарантированно будут работать лучшие из лучших, и все это для вашего удовлетворения.

fiziku5.ru