Экспонента в степени натурального логарифма: Mathway | Популярные задачи

2

Экспонента и число е: просто и понятно

Перевод большой статьи «An Intuitive Guide To Exponential Functions & e»

Число e всегда волновало меня — не как буква, а как математическая константа. Что число е означает на самом деле?

Разные математические книги и даже моя горячо любимая Википедия описывает эту величественную константу совершенно бестолковым научным жаргоном:

Математическая константа е является основанием натурального логарифма.

Если заинтересуетесь, что такое натуральный логарифм, найдете такое определение:

Натуральный логарифм, ранее известный как гиперболический логарифм, является логарифмом с основанием е, где е – иррациональная константа, приблизительно равная 2.718281828459.

Определения, конечно, правильные. Но понять их крайне сложно. Конечно, Википедия в этом не виновата: обычно математические пояснения сухи и формальны, составляются по всей строгости науки. Из-за этого новичкам сложно осваивать предмет (а когда-то каждый был новичком).

С меня хватит! Сегодня я делюсь своими высокоинтеллектуальными соображениями о том, что такое число е, и чем оно так круто! Отложите свои толстые, наводящие страх математические книжки в сторону!

Число е – это не просто число

Описывать е как «константу, приблизительно равную 2,71828…» — это все равно, что называть число пи «иррациональным числом, приблизительно равным 3,1415…». Несомненно, так и есть, но суть по-прежнему ускользает от нас.

Число пи — это соотношение длины окружности к диаметру, одинаковое для всех окружностей. Это фундаментальная пропорция, свойственная всем окружностям, а следовательно, она участвует в вычислении длины окружности, площади, объема и площади поверхности для кругов, сфер, цилиндров и т.д. Пи показывает, что все окружности связаны, не говоря уже о тригонометрических функциях, выводимых из окружностей (синус, косинус, тангенс).

Число е является базовым соотношением роста для всех непрерывно растущих процессов. Число е позволяет взять простой темп прироста (где разница видна только в конце года) и вычислить составляющие этого показателя, нормальный рост, при котором с каждой наносекундой (или даже быстрее) всё вырастает еще на немного.

Число е участвует как в системах с экспоненциальным, так и постоянным ростом: население, радиоактивный распад, подсчет процентов, и много-много других. Даже ступенчатые системы, которые не растут равномерно, можно аппроксимировать с помощью числа е.

Также, как любое число можно рассматривать в виде «масштабированной» версии 1 (базовой единицы), любую окружность можно рассматривать в виде «масштабированной» версии единичной окружности (с радиусом 1). И любой коэффициент роста может быть рассмотрен в виде «масштабированной» версии е («единичного» коэффициента роста).

Так что число е – это не случайное, взятое наугад число. Число е воплощает в себе идею, что все непрерывно растущие системы являются масштабированными версиями одного и того же показателя. 4=16 частей. Общая формула выглядит так:

рост = 2^x

Другими словами, удвоение – это 100% рост. Мы можем переписать эту формулу так:

рост = (1+100%)^x

Это то же равенство, мы только разделили «2» на составные части, которыми в сущности и является это число: начальное значение (1) плюс 100%. Умно, да?

Конечно, мы можем подставить и любое другое число (50%, 25%, 200%) вместо 100% и получить формулу роста для этого нового коэффициента. Общая формула для х периодов временного ряда будет иметь вид:

рост = (1+прирост)^x

Это просто означает, что мы используем норму возврата, (1 + прирост), «х» раз подряд.

Приглядимся поближе

Наша формула предполагает, что прирост происходит дискретными шагами. Наши бактерии ждут, ждут, а потом бац!, и в последнюю минуту они удваиваются в количестве. Наша прибыль по процентам от депозита магическим образом появляется ровно через 1 год. На основе формулы, написанной выше, прибыль растет ступенчато. Зеленые точки появляются внезапно.

Но мир не всегда таков. Если мы увеличим картинку, мы увидим, что наши друзья-бактерии делятся постоянно:

Зеленый малый не возникает из ничего: он медленно вырастает из синего родителя. После 1 периода времени (24 часа в нашем случае), зеленый друг уже полностью созрел. Повзрослев, он стает полноценным синим членом стада и может создавать новые зеленые клеточки сам.

Эта информация как-то изменит наше уравнение?

Не-а. В случае с бактериями, полусформированные зеленые клетки все же не могут ничего делать, пока не вырастут и совсем не отделятся от своих синих родителей. Так что уравнение справедливо.

В следующий статье мы посмотрим на пример экспоненциального роста ваших денег.

Продолжение

Логарифмы обыкновенные и натуральные – объяснение и примеры

Логарифм числа – это степень или показатель степени, на которую нужно возвести другое значение, чтобы получить эквивалентное значение данного числа.

Понятие логарифмов было введено в начале 17 века шотландским математиком Джоном Нейпиром. Позже ученые, мореплаватели и инженеры переняли концепцию выполнения вычислений с использованием логарифмических таблиц.

Логарифм числа выражается в виде;

log _b N = x, где b — основание и может быть любым числом, кроме 1 и нуля; x и N — показатель степени и аргумент соответственно.

Например, , логарифм 32 по основанию 2 равен 5 и может быть представлен как;

log ₂ 32 = 5

Узнав о логарифмах, мы можем отметить, что основанием логарифмической функции может быть любое число, кроме 1 и нуля. Однако два других специальных типа логарифмов часто используются в математике. Это десятичный логарифм и натуральный логарифм.

Что такое десятичный логарифм?

Десятичный логарифм имеет фиксированное основание 10. Логарифм числа N выражается как;

log ₁₀ N или log N. Десятичные логарифмы также известны как десятичный логарифм и десятичный логарифм.

Если log N = x, то мы можем представить эту логарифмическую форму в экспоненциальной форме, т. е. 10 ^x = N.

Двойные логарифмы имеют широкое применение в науке и технике. Эти логарифмы также называются логарифмами Бриггса, потому что в 18 9В 0035-м -м веке их ввел английский математик Генри Бриггс. Например, кислотность и щелочность вещества выражаются экспоненциально.

Шкала Рихтера для измерения землетрясений и децибел для звука обычно выражается в логарифмической форме. Это настолько распространено, что вы можете предположить, что это журнал x или общий журнал, если вы не найдете записанной базы.

основных свойства десятичных логарифмов такие же, как свойства всех логарифмов.

К ним относятся правило произведения, правило частного, правило степени и правило нулевого порядка.

• Правило произведения

Произведение двух десятичных логарифмов равно сумме отдельных десятичных логарифмов.

⟹ log (m n) = log m + log n.

• Правило отношения

Правило деления десятичных логарифмов гласит, что частное двух значений десятичного логарифма равно разности каждого десятичного логарифма.

⟹ log(m/n) = log m – log n

• Степенное правило

Десятичный логарифм числа с показателем степени равен произведению показателя степени на его десятичный логарифм.

⟹ log (m ⁿ ) = n log m

• Правило нулевой степени

⟹ log 1 = 0

Что такое натуральный логарифм?

Натуральный логарифм числа N – это степень или показатель степени, в которую нужно возвести «e», чтобы оно равнялось N. Константа «e» – это константа Нейпира, которая приблизительно равна 2,718281828.

ln N = x, что совпадает с N = e ^x .

Натуральный логарифм в основном используется в чистой математике, например, в вычислениях.

Основные свойства натуральных логарифмов такие же, как и у всех логарифмов.

• Правило продукта

⟹ ln (ab) = ln (a) + ln (b)

• Частное правило

⟹ ln (a/b) – = ln (a/b) – = ln (a/b)

• Правило взаимности

⟹ ln (1/a) = −ln (a)

• Power Rule

⟹ ln (a ^b ) = b ln (a)

• E ^{LN (x)} = x
• LN (E ^x ) = x
• LN (E) = 1
• LN (∞) = ∞
• LN (1) = 0

777777777777777777777777777777777 гг.

Научные и графические калькуляторы имеют ключи как для десятичных, так и для натуральных логарифмов. Ключ для натурального бревна помечен «9».0141 e» или «ln», а десятичный логарифм помечен как «log».

Теперь давайте проверим наше понимание урока, попробовав решить несколько задач на натуральные и десятичные логарифмы.

Пример 1

Решение для x if, 6 ^{x + 2} = 21

Раствор

Экспресс.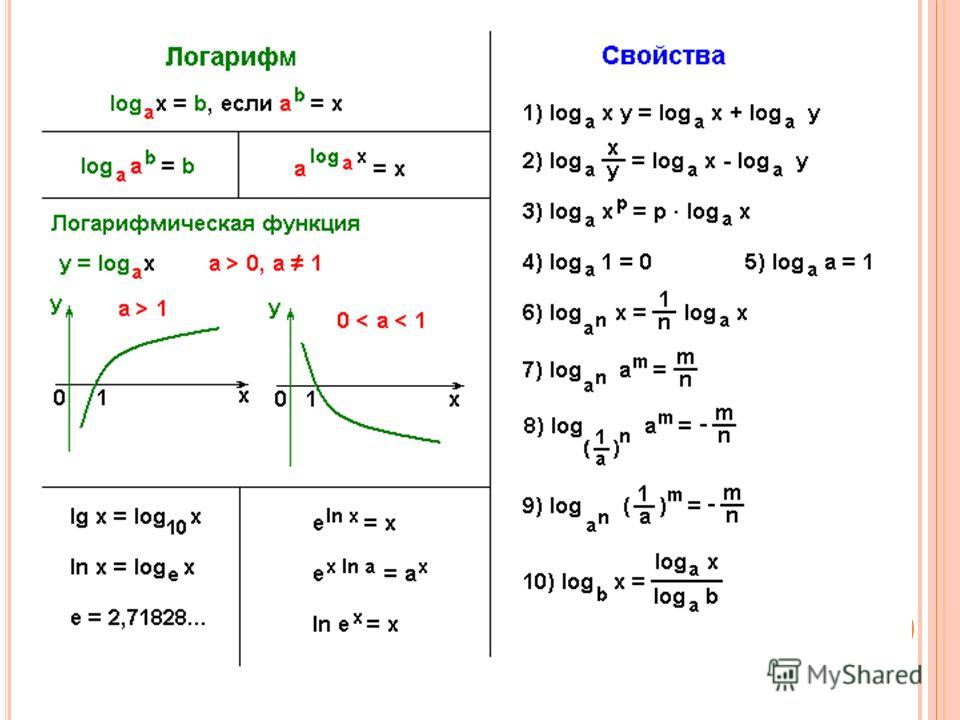 + 2  = логарифм 21

Применяя правило степенных логарифмов, получаем;
( x  + 2) log 6 = log 21

Разделить обе стороны на log 6.

x + 2 = log 21/log 6

x = -1.4559

Example 2

Solve for x in e ^{2 x}  = 9

Solution

ln e ^{3 x}  = ln 9
3 x  ln e = ln 9
3 x = LN 9

Изолат x, деляя обе стороны на 3.

x = 1/3LN 9

x = 0,732

Пример 3

Solve для x в log 0,0001. = x

Решение

Переписать общий журнал. в экспоненциальной форме.

10 ^x = 0,0001

Но 0,0001 = 1/10000 = 10 ^-4

Следовательно,

x = -4

Примеры Натуральный логарифм

Определение Натуральный логарифм0001

Натуральные логарифмы — это логарифмы по основанию e (число Эйлера = 2,71828 . ..). Они выражаются как и могут быть сокращенно записаны как ln (x).

Преобразование натуральных логарифмов в экспоненциальные функции

Начните с обычного натурального логарифма: Вы можете легко переписать это как.

Как всегда, вам нужно пометить каждую часть функции: основание e (как и с натуральными логарифмами), показатель степени y , а ответ экспоненты х.

Поэтому вы можете переписать логарифмы как .

Решите 3 sf

1. Обозначьте каждую часть функции следующим образом: основание равно e, показатель степени равен x, а ответ экспоненты равен 5. то же самое, что сказать Ln, вы можете записать это как натуральный логарифм

Каковы правила для натуральных логарифмов?

Наряду со специальными правилами для натуральных логарифмов вы можете использовать общие законы журналов, а также экспоненциальные правила.

Правила для натуральных логарифмов

• IF, затем

Доказывают, что натуральные правила, которые вам нужно, чтобы понять, что вам нужно, чтобы понять, что вам нужно, чтобы понять, что вам нужно для понимания.

правило натурального логарифма — вам не нужно чувствовать, что вы могли бы добраться до этой точки без посторонней помощи.

Доказательство Ln (1) = 0

можно записать как

. Вы перепишете это как экспоненциальную функцию, где основание равно e, ответ экспоненты равен 1, а показатель степени равен m. Эта экспонента будет выглядеть так:

Используя наш экспоненциальный закон степени = 0, вы знаете, что показатель степени (в данном случае m) должен быть равен 0, чтобы ответ на показатель был равен 1.

Таким образом,

можно переписать так, где основание равно e, ответ на экспоненту равен e, а показатель степени равен n.

В результате вы переписываете как .

В соответствии с нашими экспоненциальными правилами, когда ответ экспоненты совпадает с основанием, тогда степень должна быть равна 1.

Таким образом,

Доказательство Ln(e

^x )=x

Поскольку экспонента и логарифм являются обратными функциями, они компенсируют друг друга, когда их помещают в одну и ту же функцию.

Эта концепция аналогична умножению числа на 2 и последующему делению на 2 — вы получите то же число, что и в начале.

Таким образом, Ln и e сократятся, и у вас останется только x.

Доказательство того, что Ln (y) = Ln (x), означает, что y = x

Если вы установите Ln (y) = a и Ln (x) = b, вы можете переписать каждую функцию как показательную.

Где основание равно e, показатель степени равен a, а ответ на показатель степени равен y. Следовательно, экспонента есть.

Где основание равно e, показатель степени равен b, а ответ на показатель степени равен x. Следовательно, экспонента есть.

Поскольку вам сказали, что Ln (y) = Ln (x), должно быть равно, поэтому y = x.

Доказательство e

^Ln(x) =x

e и Ln компенсируют друг друга, потому что экспоненты и логарифмы являются обратными функциями друг друга. Таким образом, вы остаетесь с x.

Следовательно,

Этот закон использует тот же принцип, что и

Применение правил натурального логарифма

Пример 1: Решить

Выражение можно записать в виде натурального логарифма, так как основание равно e, показатель степени равно 2x, а ответ на экспоненту равен 6.

Таким образом, натуральный логарифм можно записать как Ln (6) = 2x.

Следовательно,

Пример 2: Решите

Выражение можно записать в виде логарифма, при этом основание равно е ; показатель степени равен x + 3, а ответ на экспоненту равен 10.

Следовательно,

Пример 3: Решить

Другой.

Таким образом,

Пример 4: Решите

Чтобы получить x самостоятельно, нам нужно преобразовать логарифм в экспоненту, где основание равно e, показатель степени равен 1,4, а ответ на экспоненту равен x + 1.

Следовательно, и

Пример 5: Решить

1. По правилу степенного логарифма можно записать как

Следовательно,

2. Используя правило произведения и частного, мы можем сделать это дальше:

Натуральный логарифм – основные выводы

• Натуральный логарифм – это логарифм с основанием e.

  No related posts.