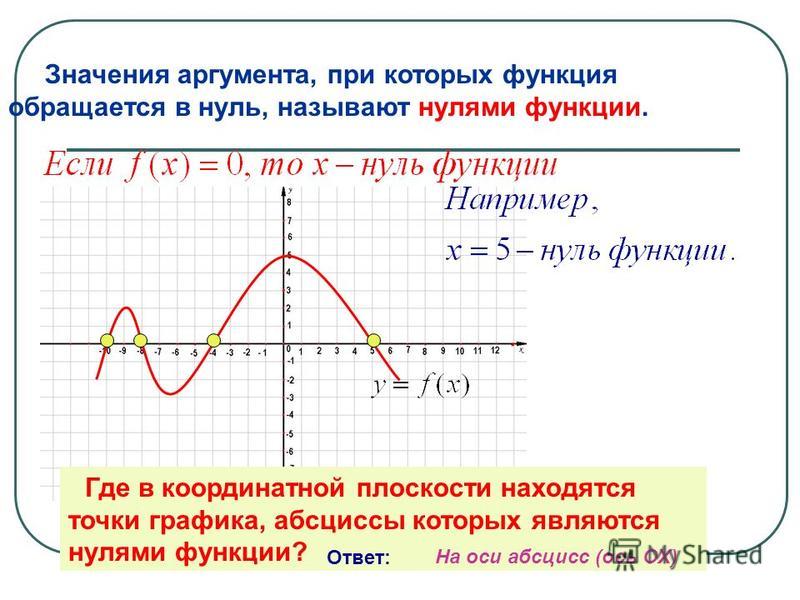
Экстремумы функции – что это такое: как найти критическую точку максимума и минимума
Из данной статьи читатель узнает о том, что такое экстремум функционального значения, а также об особенностях его использования в практической деятельности. Изучение такого концепта крайне важно для понимания основ высшей математики. Эта тема является основополагающей для более глубокого изучения курса.
…
Содержание
Что такое экстремум?
В школьном курсе дается множество определений понятия «экстремум». Данная статья призвана дать самое глубокое и четкое представление о термине для несведущих в вопросе лиц. Итак, под термином понимают, насколько функциональный промежуток приобретает минимальное либо максимальное значение на том или ином множестве.
Экстремум – это и минимальное значение функции, и максимальное одновременно. Различают точку минимума и точку максимума, то есть крайние значения аргумента на графике. Основные науки, в которых используют данный концепт:
- экономика,
- статистика,
- биология,
- машинное управление,
- эконометрика.

Точки экстремума играют важную роль в определении последовательности заданной функции. Система координат на графике в лучшем виде показывает изменение экстремального положения в зависимости от изменения функциональности.
Это интересно! Свойства натуральных логарифмов: график, основание, функции, предел, формулы и область определения
Экстремумы производной функции
Имеет также место такое явление, как «производная». Она необходима для определения точки экстремума. Важно не путать точки минимума либо максимума с наибольшим и наименьшим значением. Это разные понятия, хотя могут показаться похожими.
Производная функция
Значение функции является основным фактором для определения того, как найти точку максимума. Производная не образуется от значений, а исключительно от крайнего ее положения в том или ином его порядке.
Сама же по себе производная определяется на основе данных точек экстремума, а не наибольшего или наименьшего значения. В российских школах недостаточно четко проводят грань между этими двумя концептами, что влияет на понимание данной темы вообще.
В российских школах недостаточно четко проводят грань между этими двумя концептами, что влияет на понимание данной темы вообще.
Это интересно! Как определить определенные интегралы от нуля, константы и с доказательством
Острый экстремум
Давайте теперь рассмотрим такое понятие как «острый экстремум». На сегодняшний день выделяют острый минимум значения и острый максимум значения. Определение дано в соответствии с российской классификацией критических точек функции. Концепт точки экстремума лежит в основе нахождения критических точек на графике.
Острый экстремум Важно! Процесс нахождения точек острого экстремума функции называется дифференцированием и используется как в школьном курсе изучения алгебры и начала анализа, так и в ходе освоения высшей математики в университете.
Экстремальное значение функции
Для определения такого понятия прибегают к использованию теоремы Ферма. Она является важнейшей в ходе изучения крайних точек и дает четкое представление об их существовании в том или ином их виде. Для обеспечения экстремальности важно создать определенные условия для убывания либо возрастания на графике.
Для обеспечения экстремальности важно создать определенные условия для убывания либо возрастания на графике.
Для точного ответить на вопрос «как найти точку максимума», необходимо следовать таким положениям:
- Нахождение точной области определения на графике.
- Поиск производной функции и точки экстремума.
- Решать стандартные неравенства на область нахождения аргумента.
- Уметь доказывать, в каких функциях точка на графике определена и непрерывна.
Экстремальное значение функции Внимание! Поиск критической точки функции возможен только в случае существования производной не менее второго порядка, что обеспечивается высокой долей наличия точки экстремума.
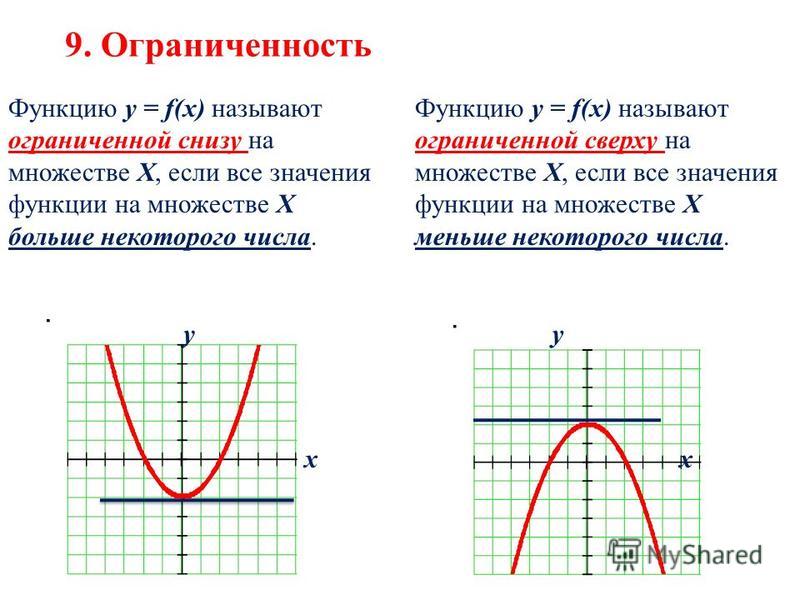
Необходимое условие экстремума функции
Для того чтобы существовал экстремум, важно, чтобы были как точки минимума, так и точки максимума. В случае если это правило соблюдено лишь частично, то условие существование экстремума нарушается.
Точки минимума и максимума
Каждая функция в любом положении должна быть продифференцирована с целью выявления ее новых значений.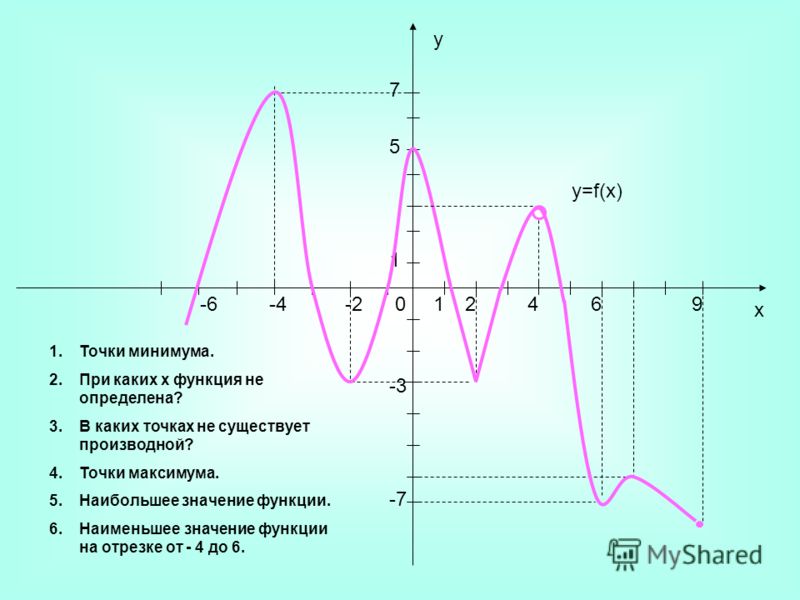 Важно понимать, что случай обращения точки в ноль не является основным принципом нахождения дифференцируемой точки.
Важно понимать, что случай обращения точки в ноль не является основным принципом нахождения дифференцируемой точки.
Острый экстремум, также как и минимум функции – это крайне важный аспект решения математической задачи с использованием экстремальных значений. Для того чтобы лучше понимать данную составляющую, важно обратиться к табличным значениям по заданию функционала.
| Полное исследование значения | Построение графика значения |
| 1. Определение точек возрастания и убывания значений. 2. Нахождение точек разрыва, экстремума и пересечение с координатными осями. 3. Процесс определения изменений положения на графике. 4. Определение показателя и направления выпуклости и выгнутости с учетом наличия асимптот. 5. Создание сводной таблицы исследования с точки зрения определения ее координат. 6. Нахождение промежутков возрастания и убывания крайних и острых точек. 7. Определение выпуклости и вогнутости кривой. 8. Построение графика с учетом исследования позволяет найти минимум либо максимум. | Основным элементом при необходимости работы с экстремумами является точное построение его графика. Школьные учителя не часто уделяют столь важному аспекту максимум внимания, что является грубейшим нарушением учебного процесса. Построение графика происходит только по итогам исследования функциональных данных, определения острых экстремумов, а также точек на графике. Острые экстремумы производной функции отображаются на графике точных значений, с использованием стандартной процедуры определения асимптот. Точки максимума и минимума функции сопровождаются более сложными построениями графика. Это обусловлено более глубокой необходимостью прорабатывать проблему острого экстремума. Необходимо также находить производную сложной и простой функции, так как это одно из самых главных понятий проблематики экстремума. |
Экстремум функционала
Для того чтобы отыскать вышеозначенное значение, необходимо придерживаться следующих правил:
- определить необходимое условие экстремального отношения,
- учитывать достаточное условие крайних точек на графике,
- осуществлять расчет острого экстремума.

Используются также такие понятия, как слабый минимум и сильный минимум. Это необходимо учитывать при определении экстремума и точного его расчета. При этом острый функционал – это поиск и создание всех необходимых условий для работы с графиком функции.
Это интересно! Легкие правила округления чисел после запятой
Экстремумы функции. 10 класс.
Исследование функции. Экстремумы функции bezbotvy
Вывод
После прочтения и осознания данной статьи любой новичок в математике имеет возможность понять возможности острых экстремумов в том виде, в каком они используются в образовательном процессе. Вышеперечисленные моменты позволяют разобраться в крайних точках без помощи репетиторов.
5.10.09 Экстремум функции.
 Наибольшее и наименьшее значения
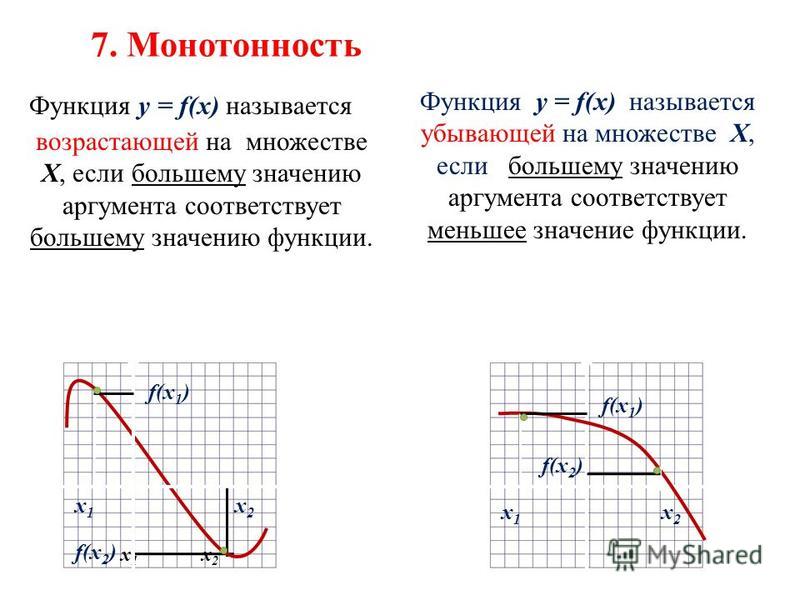
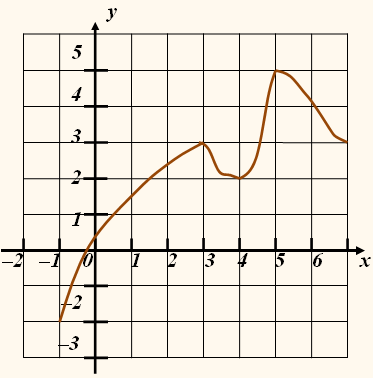
Наибольшее и наименьшее значенияОпределение. Говорят, что функция , заданная на некотором промежутке, имеет максимум (минимум) в точке из этого промежутка, если существует такая окрестность точки , что для всех из этой окрестности .
Максимум или минимум называют экстремумом функции.
По определению максимума и минимума функции они могут достигаться только во внутренней точке области ее определения, так как требуется чтобы имела смысл во всех точках окрестности .
Понятие экстремума нельзя смешивать с понятием наибольшего и наименьшего значений функции на всем промежутке ее задания. Экстремальные значения функции являются наибольшими или наименьшими только по отношению к близлежащим точкам, а по отношению к другим точкам значение может оказаться и не наибольшим или не наименьшим. Когда же говорят о наибольшем значении на , то под этим понимают такое ее значение, больше которого нет ни в одной точке этого отрезка, включая и концы. Следовательно, наибольшим и наименьшим значениями функции на отрезке могут быть либо экстремальные значения, либо значения на концах .
Практические способы нахождения точек, в которых функция имеет экстремум, базируются на следующих теоремах.
Теорема 1. (Необходимое условие экстремума).
Если функция имеет экстремум в точке и существует , то .
Условие не является достаточным для существования экстремума, то есть производная может обращаться в нуль и в точках, где нет экстремума. Например, для производная , если , однако экстремума в этой точке нет, поскольку в любой окрестности нуля есть точки, значения функции в которых будут и больше, и меньше, чем .
Точки, в которых производная обращается в нуль, называют стационарными. Функция может иметь экстремум также в точках, где обращается в бесконечность или не существует. Все такие точки называют подозрительными на экстремум или критическими.
Для того чтобы решить вопрос о наличии экстремума в подозрительной точке, надо каждую точку подвергнуть дополнительному исследованию.
Первый способ исследования. (Первый достаточный признак экстремума).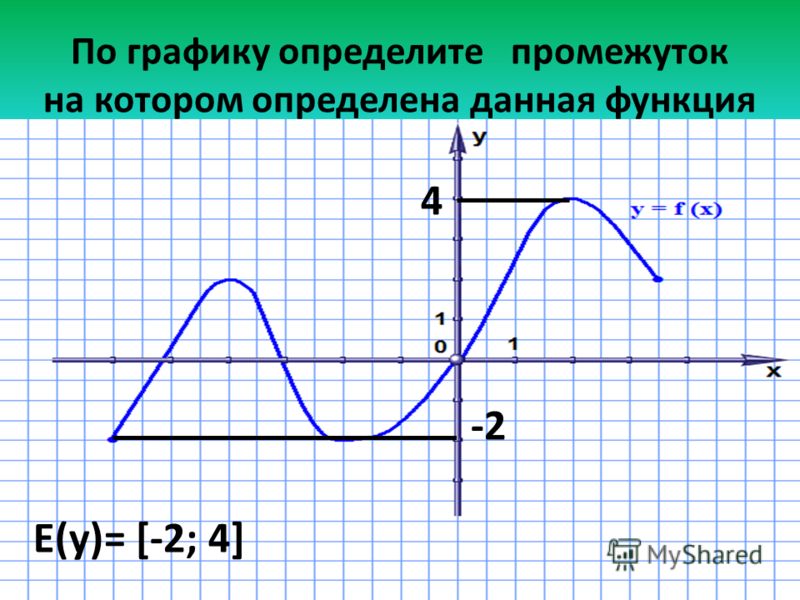
Если при переходе через подозрительную точку в направлении возрастания меняет знак, то в этой точке имеет экстремум, причем: 1) если знак меняется с на , то в точке – максимум,
2) если с на , то в точке – минимум.
Если же при переходе через точку не меняет знака, то в этой точке нет экстремума.
Пример 1. Исследовать на экстремум функцию .
Решение. Функция определена на всей числовой оси. Ее производная всюду конечна, следовательно, подозрительными на экстремум будут только стационарные точки. Решая уравнение , получим . Исследуем знак производной в непосредственной близости от точек и : и , то есть при переходе через точку слева направо изменила знак с на , следовательно, в этой точке максимум, ; и , следовательно, в точке – минимум, .
Пример 2. Исследовать на экстремум функцию .
Решение. Производная не обращается в нуль ни при каком конечном значении .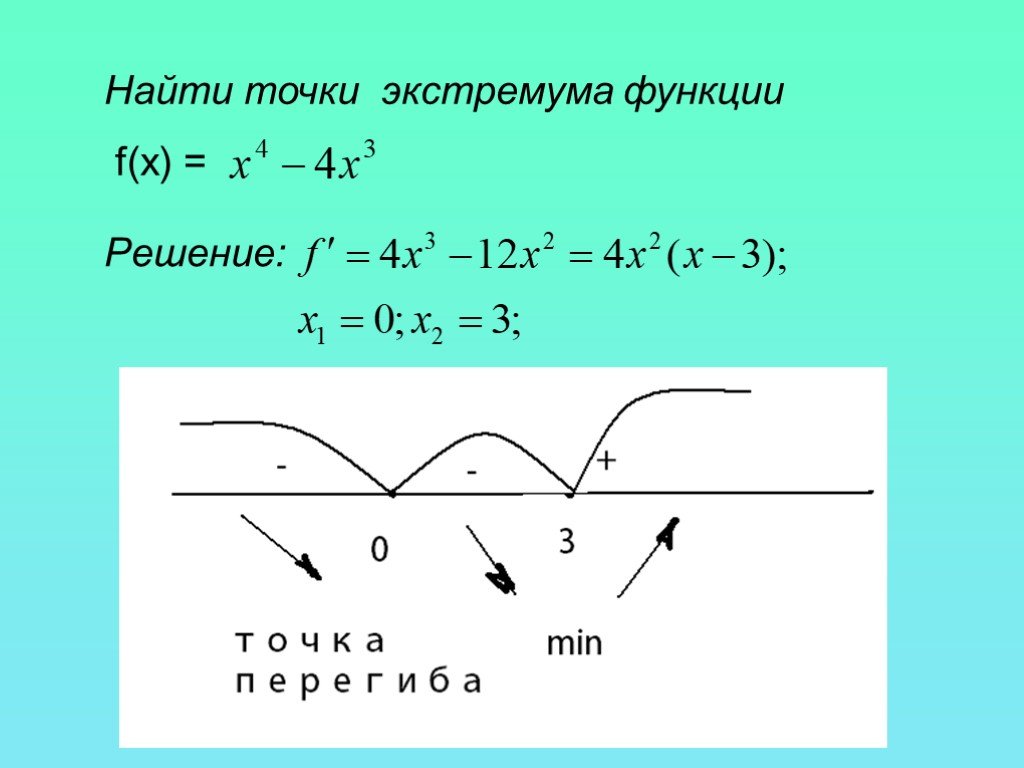 В точке она обращается в бесконечность. Так как при и при , то в точке функция имеет минимум, .
В точке она обращается в бесконечность. Так как при и при , то в точке функция имеет минимум, .
Если имеет несколько критических точек, то поступают следующим образом. Расположим эти точки в порядке возрастания:
. (1)
В каждом из интервалов существует конечная , имеющая постоянный знак в каждом интервале (если бы меняла знак, то в силу непрерывности внутри интервала нашлась бы точка, в которой , что невозможно, так как все такие точки перечислены в (1)). Взяв по одной точке из каждого интервала, получим некоторую последовательность знаков , что позволит сразу решить вопрос о наличии экстремума в каждой подозрительной точке.
Пример 3. Исследовать на экстремум функцию
.
Решение. Функция определена на промежутке .
Производная всюду конечна, следовательно, подозрительными на экстремум будут только стационарные точки. Решая уравнение , найдем . (Точки уже записаны в порядке возрастания.)
Промежуток этими точками разобьется на интервалы .
Учитывая, что на знак влияют только два ее сомножителя и , определение ее знаков в каждом из интервалов проведем по следующей схеме:
— | — | — | + | |
— | — | + | + | |
Знак | + | + | — | + |
Отсюда делаем вывод, что в точке экстремума нет, в точке – максимум, , а в точке – минимум, .
Второй способ исследования. (второй достаточный признак экстремума).
Пусть имеет в точке и в ее окрестности непрерывные первую и вторую производные, причем . Тогда имеет в точке минимум (максимум), если .
Пример 4. Исследовать на экстремум функцию .
Решение. Находим , стационарные точки . В точке имеем максимум, так как , а в точке – минимум, так как , причем .
Второй способ исследования практически более удобен, так как он быстрее приводит к цели, но он не всегда применим. Этим способом не охватываются случаи, когда в исследуемой точке не существует первой производной, а также когда вторая производная равна нулю. Иногда и вычисление второй производной настолько громоздко, что проще воспользоваться первым способом.
Пример 5. Исследовать на экстремум функцию .
Решение. По определению модуля заданную функцию перепишем в виде
Очевидно, что для и для , то есть имеются разные односторонние производные, следовательно, в точке не существует. Так как стационарных точек нет, то единственной точкой, подозрительной на экстремум, является . Второй достаточный признак экстремума неприменим, так как . Воспользуемся первым достаточным признаком. Поскольку при переходе через точку слева направо сменила знак с на , то в этой точке имеет минимум и .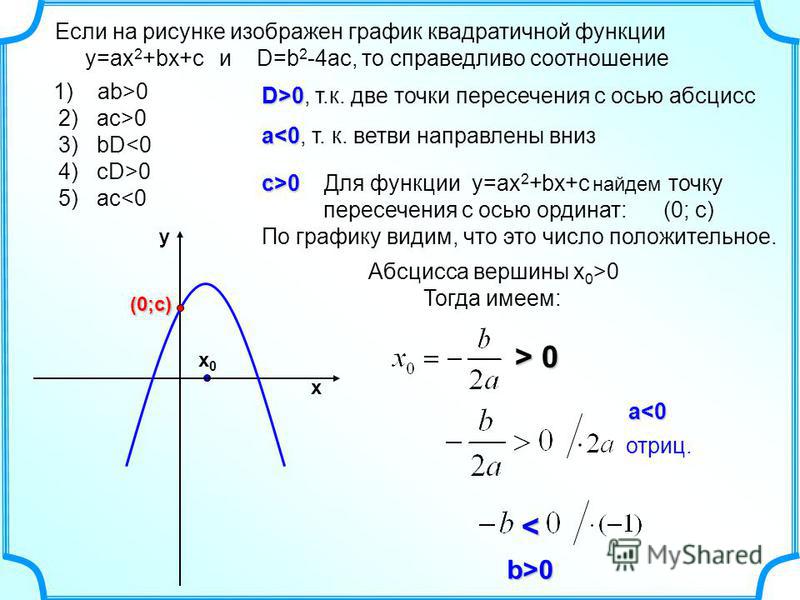
Пример 6. Найти наибольшее и наименьшее значения функции на отрезке .
Решение. Для решения задачи достаточно вычислить значения функции в критических точках и на концах отрезка, а затем, не проводя исследования на экстремум, сравнить полученные значения и выбрать из них наименьшее и наибольшее значения. Найдем . Из уравнения находим стационарные точки . Других подозрительных точек нет. Сравнивая значения , , , заключаем, что является наименьшим, а – наибольшим значениями функции на .
Вопросы для самопроверки и упражнения.
1. Может ли значение максимума функции оказаться меньше минимума этой же функции?
Ответ: Да.
2. Известно, что если слева от возрастает, а справа убывает, то в точке функция имеет максимум. Верно ли обратное утверждение?
Ответ: Нет.
3. Может ли монотонная функция иметь экстремум?
Ответ: Нет.
4. Может ли функция, имеющая максимум, не иметь наибольшего значения? Может ли функция, имеющая наибольшее значение, не иметь максимума?
Ответ: Да (в обоих случаях).
5. Найти точки экстремума функций:
A) . Ответ: при , при .
Б) . Ответ: экстремума нет.
6. Найти наибольшее и наименьшее значения функций:
А) на . Ответ: и .
Б) на . Ответ: 0 и 8.
7. Существуют ли наименьшее и наибольшее значения функции на ?
Ответ: наименьшее не существует, а наибольшее равно 1.
| < Предыдущая | Следующая > |
|---|
Первую производную можно использовать для нахождения относительного минимума и относительного максимума значений функции на открытом интервале. Эти значения часто называют экстремальными значениями или экстремумами
Точка считается минимальной точкой , если значение функции в этой точке меньше, чем значения функции для всех значений x в интервале.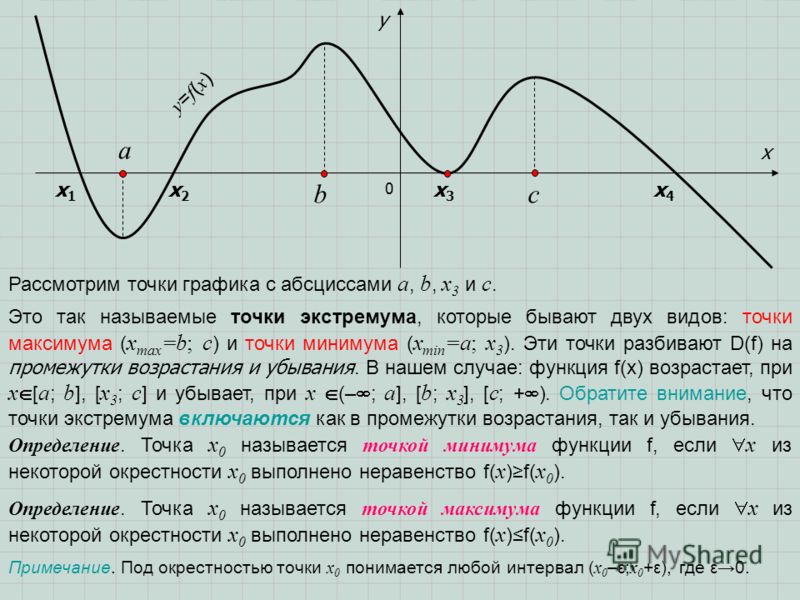
И наоборот, точка считается максимальной точкой , если значение функции в этой точке больше, чем значения функции для всех значений x в интервале.
Посмотрите на график f(x) = x 3 + 4x 2 — 12x на интервале [0, 3], рис. 1а. Из графика видно, что он имеет максимум при (3, 27) и минимум при (1,07, -7,04). На замкнутом интервале эти точки называются абсолютным или глобальным минимумом/максимумом баллов.
ТЕОРЕМА ЭКСТРЕМАЛЬНОГО ЗНАЧЕНИЯ:
Если функция непрерывна на отрезке, то функция имеет минимум и максимум.
Если вы посмотрите на этот же график по всему домену, вы заметите, что нет абсолютного минимального или максимального значения.
Однако существуют минимальные и максимальные точки, в которых холмы на графике достигают своей наивысшей (-3,7, 48,52) или самой низкой точки (1,07, -7,04). Эти точки называются относительный или локальный минимум/максимум точек.
Поскольку относительные минимумы/максимумы встречаются на вершине или в долине холма, уклон в этих точках либо равен нулю, либо не определен. Значения x в этих точках называются критическими числами . Критические числа f(x) = x 3 + 4x 2 — 12x составляют -3,7, 1,07.
Таким образом, экстремумы на замкнутом интервале могут быть определены с помощью первой производной и этих ориентиров.
РЕКОМЕНДАЦИИ ПО ПОИСКУ ЭКСТРЕМАМ ДЛЯ ЗАКРЫТОГО ИНТЕРВАЛА:
1. Найдите критические числа f в (a, b) .
2. Оцените f при каждом критическом числе, найденном на шаге 1, по (a, b).
3. Вычислить f в каждой конечной точке интервала [a, b].
4. Наименьшее из этих значений является минимальным, а наибольшее — максимальным.
Давайте посмотрим на пару примеров.
Пример 1. Найдите экстремумы f(x) = 2x 3 — 3x 2 на интервале [0, 3]
Шаг 1: Найдите критические числа f(x) на открытом интервале (a, b). Найдите первую производную и оцените ее для f ′(x)=0 или f ′(x) не существует. | f(x) = 2x 3 — 3x 2 Оригинальная функция f′(x)=6×2−6xf ′(x) 0 = 6х 2 — 6х Установлен f′(x)=0 0 = 6х(х — 1) Фактор из 6x 6х = 0; х = 0 Установите коэффициенты на 0 х — 1 = 0; х = 1 Решите для х ф ‘(х)
всегда будет существовать, значит, все критические числа найдены. Критические числа: {0, 1} | ||||||||
Шаг 2: Оцените f(x) при каждом критическом числе. | f(0)=2(0)3−3(0)2=0 е (0) = 0 f(1)=2(1)3−3(1)2=−1 f(1) = -1 | ||||||||
Шаг 3: Оцените f(x) в каждой конечной точке на закрытом интервале [a, b]. | е (0) = 0 е (0) = 0 f(3)=2(3)3−3(3)2=27 f(3) = 27 | ||||||||
Шаг 4.
| |||||||||
Пример 2.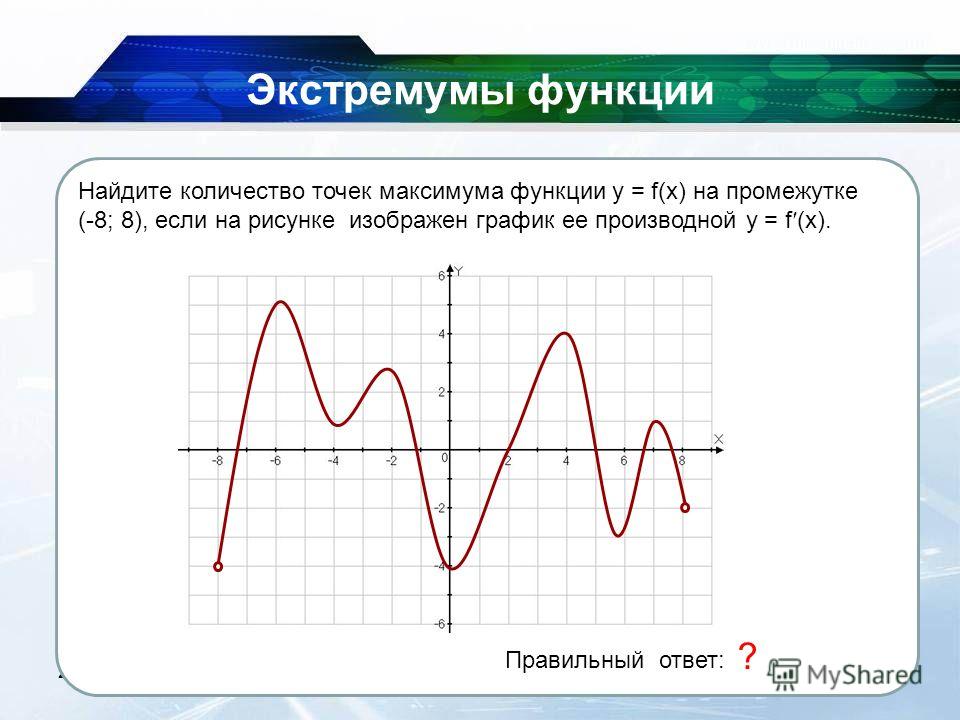 Найдите экстремумы f(x) = 3x — 4x 3 на интервале [0, 2]
Найдите экстремумы f(x) = 3x — 4x 3 на интервале [0, 2]
Шаг 1: Найдите критическую точку на открытом интервале (a, b). Найдите первую производную и оцените ее для f′(x)=0 или f′(x) не существует. | f(x) = 3x — 4x 3 Оригинальная функция f′(x)=3−12x2f′(x) 0 = 3 — 12x 2 Установить f′(x)=0 0 = 3 (1 — 4 х 2 ) Фактор из 3 0 = 3 (1 — 2х) (1 + 2х) Квадратичный фактор 1−2x=0;x=12 Установите коэффициенты на 0 1+2х=0;х=-12 Решите для х f′(x) всегда будет существовать, поэтому все критические числа найдены. Критические числа: {1,2, -12} | ||||||||
Шаг 2: Оцените f(x) при каждом критическом числе. | f(12)=3(12)−4(12)3=1 f(12)=1 f(−12)=3(−12)−4(−12)3=−1f(−12)=−1 | ||||||||
Шаг 3: Оцените f(x) в каждой конечной точке на закрытом интервале [a, b]. | f(0)=3(0)−4(0)3=0 е (0) = 0 f(2)=3(2)−4(2)3=−26 f(2) = -26 | ||||||||
Шаг 4.
| |||||||||
Теорема об экстремальном значении – формула, примеры, доказательство, утверждение .
 Эта теорема используется для доказательства теоремы Ролля в исчислении. Теорема об экстремальном значении специфична по сравнению с теоремой об ограниченности, которая дает границы непрерывной функции на отрезке.
Эта теорема используется для доказательства теоремы Ролля в исчислении. Теорема об экстремальном значении специфична по сравнению с теоремой об ограниченности, которая дает границы непрерывной функции на отрезке.В этой статье мы обсудим концепцию теоремы об экстремальных значениях, ее формулировку и доказательство. Мы также узнаем, как использовать теорему с помощью нескольких решенных примеров для лучшего понимания концепции.
| 1. | Что такое экстремальное значение теоремы? |
| 2. | Утверждение теоремы об экстремальных значениях |
| 3. | Доказательство теоремы об экстремальных значениях |
| 4. | Как использовать теорему об экстремальных значениях? |
| 5. | Часто задаваемые вопросы по теореме об экстремальных значениях |
Что такое экстремальное значение теоремы?
Теорема об экстремальных значениях помогает доказать существование максимального и минимального значений непрерывной функции с действительным знаком на замкнутом интервале.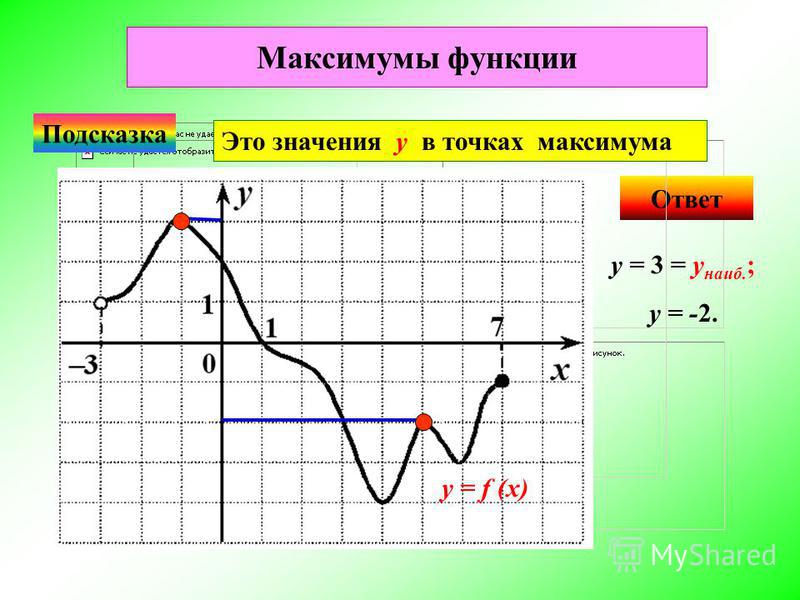 Как только существование максимального и минимального значений будет доказано, нас могут попросить определить эти значения, используя производную функции и найдя критические точки. Теорема Ролля и теорема о среднем значении являются следствием теоремы об экстремальном значении. Давайте поймем значение экстремального значения ниже, когда мы приступим к формулировке теоремы и ее доказательству.
Как только существование максимального и минимального значений будет доказано, нас могут попросить определить эти значения, используя производную функции и найдя критические точки. Теорема Ролля и теорема о среднем значении являются следствием теоремы об экстремальном значении. Давайте поймем значение экстремального значения ниже, когда мы приступим к формулировке теоремы и ее доказательству.
Экстремальное значение Значение
Экстремальные значения функции f(x) — это значения y = f(x), которых функция достигает для определенного входа x, такого, что никакое другое значение f(x) в диапазоне больше или меньше этих значений. У нас есть два типа экстремальных значений: максимальное и минимальное. Максимальное значение функции — это такое значение, при котором никакое другое значение функции не может быть больше этого, а минимальное значение функции — такое значение, при котором никакое другое значение функции не меньше этого значения.
Утверждение теоремы об экстремальных значениях
Теорема об экстремальном значении утверждает, что «если вещественнозначная функция f непрерывна на отрезке [a, b] (с a < b), то существуют два действительных числа c и d в [a, b], такие что f(c) является минимальным, а f(d) является максимальным значением f(x). Математически мы можем записать формулу для теоремы об экстремальных значениях как f(c) ≤ f(x) ≤ f(d), ∀ x ∈ [a, b] .
Математически мы можем записать формулу для теоремы об экстремальных значениях как f(c) ≤ f(x) ≤ f(d), ∀ x ∈ [a, b] .
Теорему об экстремальном значении можно также сформулировать так: «Если вещественнозначная функция f непрерывна на [a, b], то f достигает своего максимума и минимума на [a, b].
Доказательство теоремы об экстремальных значениях
Теперь, когда мы поняли теорему об экстремальном значении и ее формулировку, давайте теперь докажем ее, используя метод противоречия и теорему об ограниченности. Докажем, что f достигает своего максимума на отрезке [a, b]. Доказательство того, что f достигает своего минимума на [a, b], можно доказать аналогичным образом.
По условию f непрерывна на [a, b], поэтому f ограничена на [a, b] такие, что существуют m, M такие, что m ≤ f(x) ≤ M по теореме об ограниченности. Здесь предположим, что M — точная верхняя граница f. Теперь, если существует c в [a, b] такое, что f(c) = M, то это означает, что f достигает максимума на [a, b].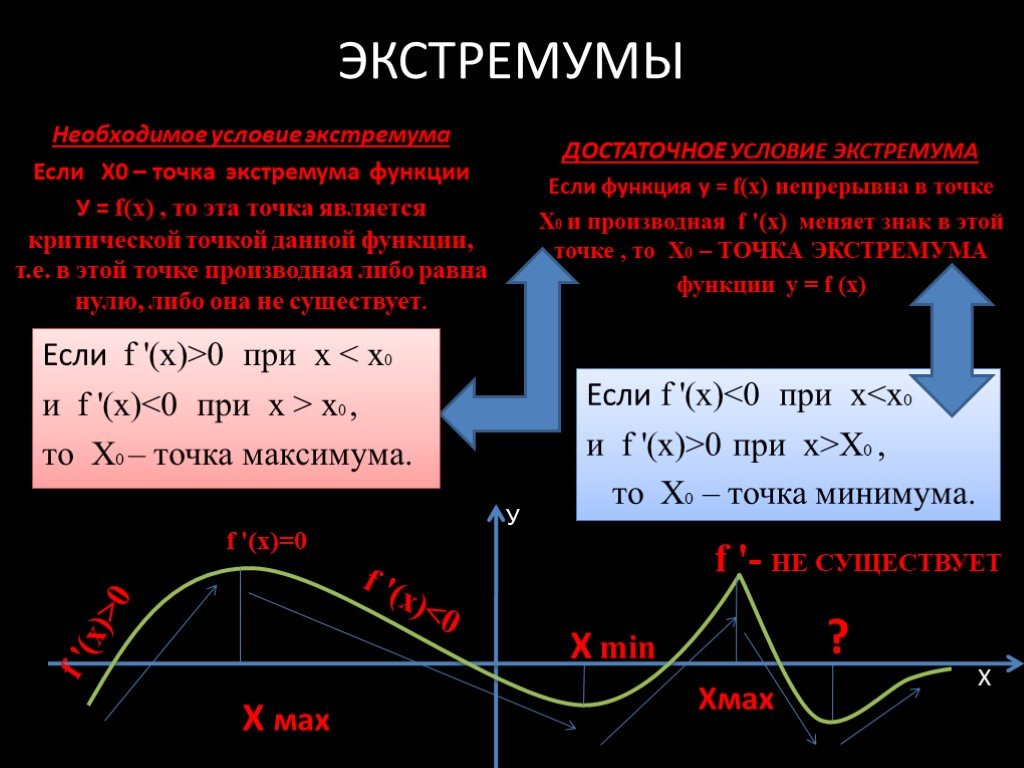 Мы доказали требуемый результат.
Мы доказали требуемый результат.
Теперь предположим, что такого c в [a, b] нет, тогда f(x) < M для всех x в [a, b]. Определим функцию h(x) = 1/[M - f(x)] на [a, b]. Теперь мы знаем, что h(x) > 0, потому что f(x) < M для всех x в [a, b] и h также непрерывен на [a, b]. Итак, по теореме об ограниченности имеем, что h(x) ограничено на [a, b]. Это означает, что существует K > 0 такое, что h(x) ≤ K для всех x в [a, b].
⇒ 1 / [M — f(x)] ≤ K
⇒ M — f(x) ≥ 1/K
Прибавив f(x) — 1/K с обеих сторон, получим
⇒ M — 1/K ≥ f(x)
⇒ f(x) ≤ M — 1/K
Это противоречит тому факту, что M является наименьшей верхней границей f(x). Следовательно, наше предположение о том, что в [a, b] не существует такого c, что f(c) = M, неверно. Следовательно, f достигает своего максимума на [a, b].
Можно доказать, что f достигает своего минимума на [a, b] на аналогичных прямых.
Как использовать теорему об экстремальных значениях?
Теперь, когда мы доказали теорему об экстремальных значениях, давайте научимся ее использовать на примере. Рассмотрим функцию f(x) = x 3 — 27x + 2. Найдите максимальное и минимальное значения f(x) на [0, 4], используя теорему об экстремальных значениях.
Рассмотрим функцию f(x) = x 3 — 27x + 2. Найдите максимальное и минимальное значения f(x) на [0, 4], используя теорему об экстремальных значениях.
Решение: Поскольку f(x) = x 3 — 27x + 2 дифференцируемо, значит, оно непрерывно. Поскольку [0, 4] замкнуто и ограничено, мы можем применить теорему об экстремальном значении. Дифференцируем f(x) = x 3 — 27x + 2.
f'(x) = 3x 2 — 27
Установив f'(x) = 0, мы имеем
3x 2 — 27 = 0
⇒ 3x 2 = 27
⇒ x 2 = 27/3 = 9
⇒ x = -3, 3
Итак, x = -3, 3 являются критическими точками. Теперь найдем значение f(x) в критических точках и на концах интервала.
f(-3) = (-3) 3 — 27(-3) + 2 = -27 + 81 + 2 = 56
f(3) = (3) 3 — 27(3) + 2 = 27 — 81 + 2 = -52
f(0) = (0) 3 — 27(0) + 2 = 2
f(4) = (4) 3 — 27(4 ) + 2 = -42
Таким образом, минимальное значение f(x) на [0, 4] равно -52, а максимальное значение на [0, 4] равно 56.
Важные замечания по теореме об экстремальном значении
- Теорему об экстремальном значении можно также сформулировать так: «Если вещественнозначная функция f непрерывна на [a, b], то f достигает своего максимума и минимума [a, б].
- Мы можем найти максимальное и минимальное значения функции, найдя критические точки функции, используя ее производную.
- Теорему об экстремальном значении можно доказать с помощью теоремы о противоречии и ограниченности.
☛ Статьи по теме:
- Формула дифференциальных уравнений
- Применение деривативов
- Домен и диапазон функции
Часто задаваемые вопросы по теореме об экстремальных значениях
Что такое теорема об экстремальных значениях в математике?
Теорема об экстремальных значениях — важная теорема в исчислении, которая используется для нахождения максимального и минимального значений непрерывной функции с действительным знаком на замкнутом интервале.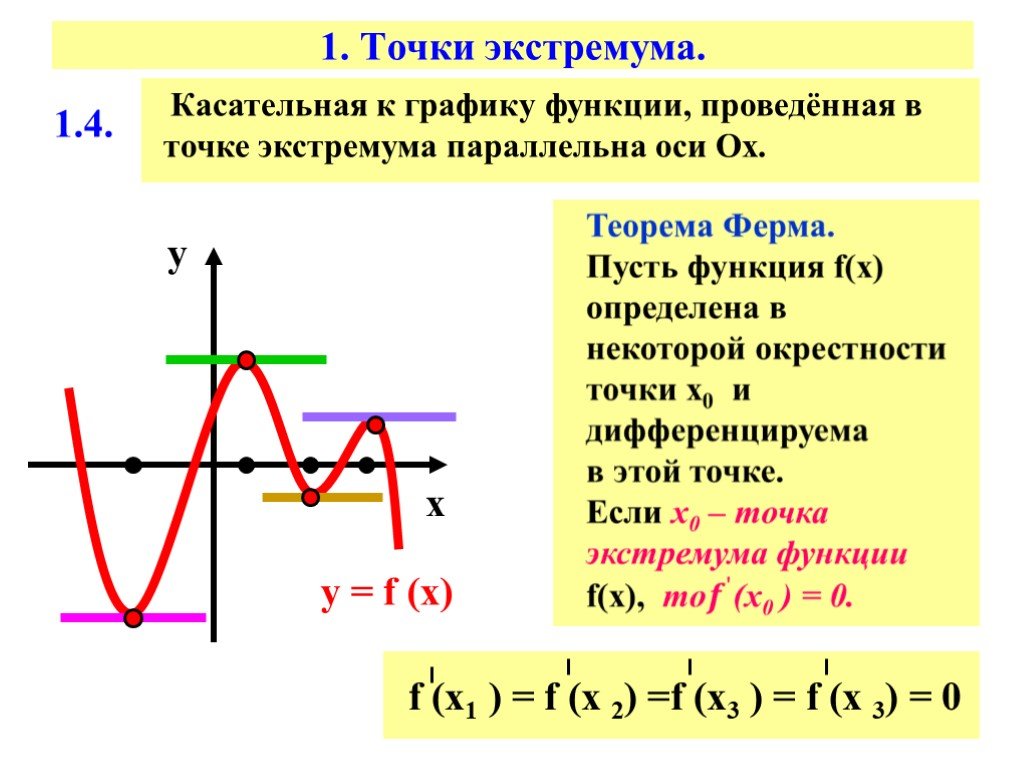
Что такое формула теоремы об экстремальных значениях?
Математически формулу теоремы об экстремальном значении можно записать в виде интервал [a, b] и c, d лежат в [a, b].
Что такое формулировка теоремы об экстремальных значениях?
Теорема об экстремальном значении утверждает, что «если вещественнозначная функция f непрерывна на отрезке [a, b] (с a < b), то существуют два действительных числа c и d в [a, b], такие что f(c) является минимальным, а f(d) является максимальным значением f(x).
Как использовать теорему об экстремальных значениях?
Теорема об экстремальном значении используется для доказательства существования максимального и минимального значений вещественной непрерывной функции на замкнутом интервале. Как только существование максимального и минимального значений будет доказано, нас могут попросить определить эти значения, используя производную функции и найдя критические точки. Находим значение функции в критических точках и концах интервала до максимального и минимального значений.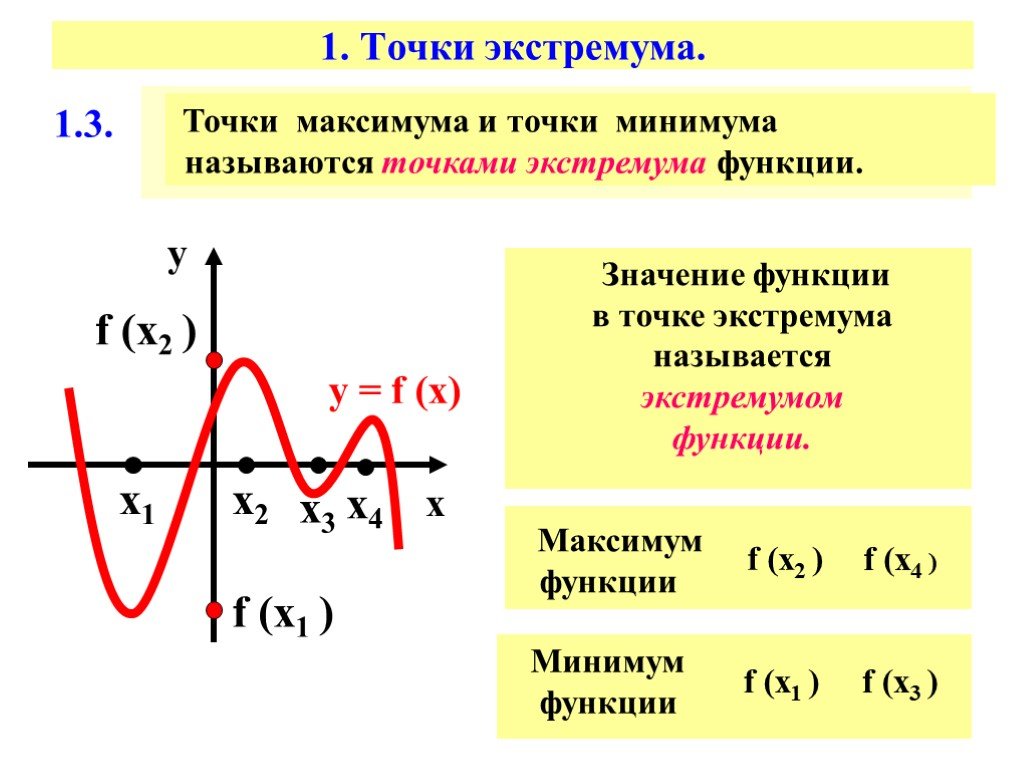




 Наименьшее из этих значений является минимальным, а наибольшее — максимальным.
Наименьшее из этих значений является минимальным, а наибольшее — максимальным. 
 Наименьшее из этих значений является минимальным, а наибольшее — максимальным.
Наименьшее из этих значений является минимальным, а наибольшее — максимальным.