НОУ ИНТУИТ | Лекция | Эквивалентность формул и нормальные формы
< Лекция 3 || Лекция 4: 1234 || Лекция 5 >
Аннотация: Эквивалентность булевых формул. Основные эквивалентности (законы логики). Эквивалентные преобразования формул. Принцип замены эквивалентных. Дизъюнктивные и конъюнктивные нормальные формы (ДНФ и КНФ). Совершенные ДНФ и КНФ. Сокращенные ДНФ и их построение методом Блейка. Многочлены Жегалкина и их построение с помощью эквивалентных преобразований формул и методом неопределенных коэффициентов по таблицам
Ключевые слова: булева формула, эквивалентные формулы, булева функция, тождество, законы логики, основные эквивалентности (законы логики), законы ассоциативности, законы коммутативности, Законы дистрибутивности, Закон двойного отрицания, Законы де Моргана, законы упрощения, Законы идемпотентности, Закон противоречия, Закон исключенного третьего, Законы 0 и 1, импликация, сложение, отрицание, значение формулы, операция конъюнкции, внешняя функция, подформула, основные тождества, законы поглощения, элементарная конъюнкция, элементарная дизъюнкция, дизъюнктивная нормальная форма (ДНФ), совершенная ДНФ, конъюнктивная нормальная форма (КНФ), совершенная КНФ, процедура проверки эквивалентности формул, сокращенная ДНФ, Элементарная конъюнкция допустимая для f, Элементарная конъюнкция максимальная для f, Сокращенные ДНФ, максимальная эк, метод Блейка, эквивалентная ДНФ, допустимая эк, многочлен Жегалкина, подкласс, Элементарная конъюнкция положительная (монотонная), множества, конъюнкция, функция, эквивалентность, коэффициенты, равенство, линейное уравнение, представление, метод неопределенных коэффициентов
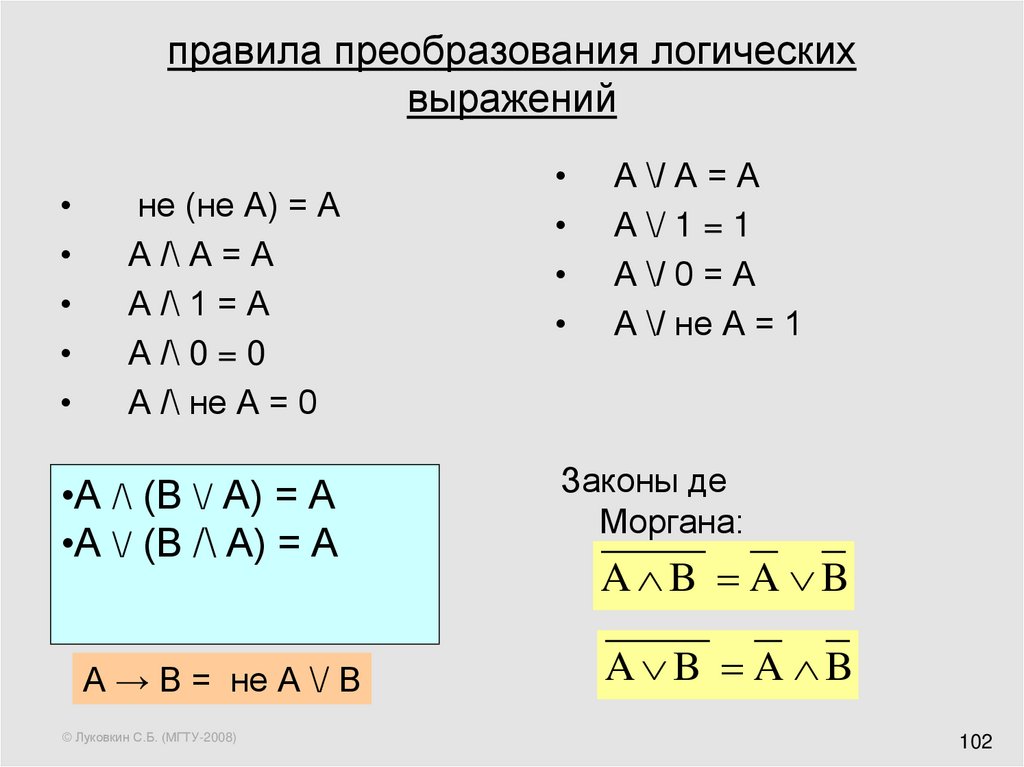
Эквивалентность булевых формул
intuit.ru/2010/edi»>Определение 4.1. Булевы формулы и называются эквивалентными, если соответствующие им функции и равны.Обозначение: . Эквивалентные формулы называют также тождественно равными, а выражения вида логическими тождествами .
Основные эквивалентности (тождества)
Таким образом, эквивалентные формулы являются различными заданиями одной и той же булевой функции. Ниже мы приводим ряд пар эквивалентных формул (тождеств), отражающих существенные свойства логических операций и важные соотношения между различными операциями. Они часто позволяют находить для булевых функций по одним задающим их формулам более простые формулы. Большинство из приводимых тождеств имеют собственные имена. Часто их называют законами логики.
Пусть — это одна из функций .
Для этих трех функций выполнены следующие две эквивалентности
( законы ассоциативности и коммутативности ).
- Ассоциативность:
- Коммутативность:
( 2) - Дистрибутивные законы:
( 3) intuit.ru/2010/edi»>
Двойное отрицание: - Законы де Моргана (внесение отрицания внутрь скобок):
( 5) - Законы упрощения:
( 6)
| ( 4) |
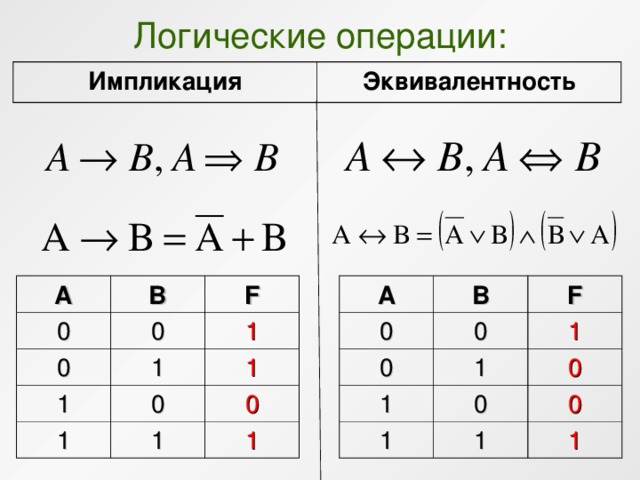
Следующие две эквивалентности позволяют выразить импликацию и сложение по модулю 2 через дизъюнкцию, конъюнкцию и отрицание.
| ( 7) |
| ( 8) |
Эквивалентные преобразования формул
Соглашения об упрощенной записи формул.
- Законы ассоциативности показывают, что значения формул, составленных из переменных и одних операций конъюнкции, не зависят от расстановки скобок. Поэтому вместо формул и мы будем для упрощения писать выражение , которое не является формулой, но может быть превращено в нее с помощью расстановки скобок. Аналогично, будем использовать выражения и (X1 + X2 + X3) для сокращения формул, состоящих из одних дизъюнкций или одних сложений по модулю 2, соответственно.
- Если внешней функцией в формуле является одна из функций , то внешние скобки в записи формулы можно опустить.
может быть записана как
Из определения эквивалентности формул непосредственно следует Принцип замены эквивалентных подформул:
пусть формула является подформулой формулы формула эквивалентна и формула получена из посредством замены некоторого вхождения на . Тогда эквивалентна т.е. .
Применяя этот принцип и используя основные тождества, можно находить для
заданной формулы другие эквивалентные ей формулы. Часто это может приводить к
существенному упрощению исходной формулы.
Например, если в формуле заменим на
основании тождеств (6) подформулу на 0, то получим эквивалентную формулу .
По закону коммутативности (2) эта формула эквивалентна
формуле , которая, в свою очередь, по одному из тождеств группы
(6) эквивалентна формуле Y.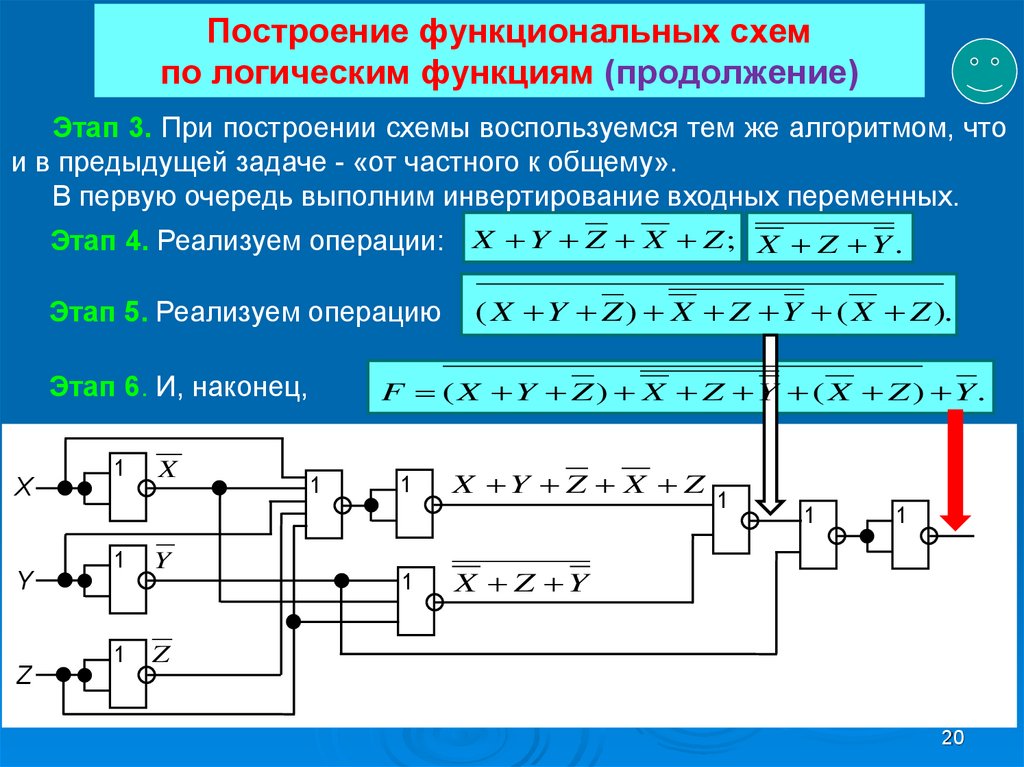
В этой цепочке вспомогательные номера под знаками эквивалентности указывают, с помощью какой группы основных тождеств эта эквивалентность получается.
Выведем еще несколько важных логических тождеств, позволяющих проводить упрощения сложных формул. Их называют законами поглощения.
( П1) Действительно,
Действительно,( П2) intuit.ru/2010/edi»>
| ( П3) |
Дальше >>
< Лекция 3 || Лекция 4: 1234 || Лекция 5 >
2.1.6. Основные эквивалентные соотношения в булевой алгебре
1. Ассоциативность конъюнкции и дизъюнкции:
,
.
2. Коммутативность конъюнкции и дизъюнкции:
3. Дистрибутивность конъюнкции относительно дизъюнкции:
.
4. Дистрибутивность дизъюнкции относительно конъюнкции:
.
5. Идемпотентность:
6. Закон двойного отрицания: .
7.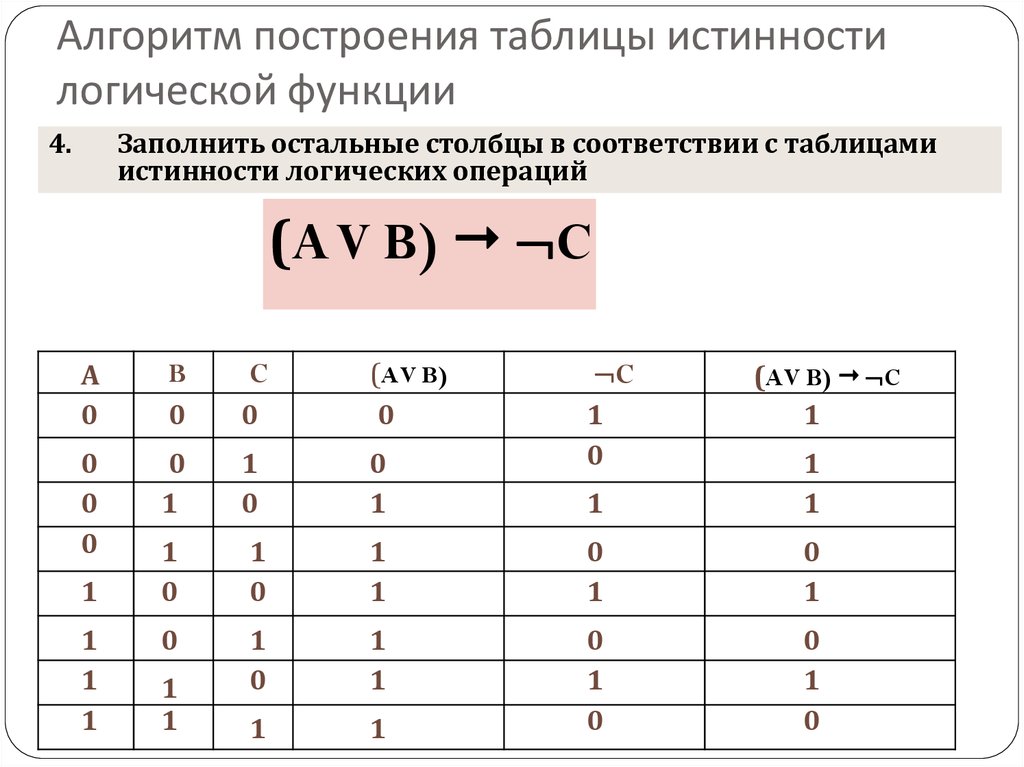 Свойства констант 0 и 1:
Свойства констант 0 и 1:
8. Правила де Моргана
, .
9. Закон противоречия: .
Особенность данных эквивалентных соотношений в том, что:
Кроме основных соотношений часто используются следующие соотношения, выводимые из основных:
(поглощение),
( склеивание),
.
На основе основных и дополнительных эквивалентных соотношений булевой алгебры возможно проведение преобразований логических формул с целью получения более простых выражений.
Примеры.
Упростить булеву формулу .
Решение : .
Упростить булеву формулу .
Решение : .
2.1.7. Переход от днф к сднф методом расщепления
Иногда
возникает задача восстановления для
логической функции, описываемой ДНФ
произвольного вида к совершенной
дизъюнктивной нормальной форме,
реализующей ту же логическую функцию. Этот переход возможен, конечно, через
таблицу истинности, однако более простым
является так называемый мотод расщепления.
Рассмотрим его на примере. Пусть
логическая функция трех переменных
представлена следующей логической
формулой
Этот переход возможен, конечно, через
таблицу истинности, однако более простым
является так называемый мотод расщепления.
Рассмотрим его на примере. Пусть
логическая функция трех переменных
представлена следующей логической
формулой
.
Переход к СДНФ проведем путем следующих очевидных преобразований
.
2.2. Формы представления булевых функций
Выше рассмотрены две формы представления булевых функций – таблицы истинности и логические формулы. Познакомимся с некоторыми другими формами.
2.2.1. Геометрическое представление булевых функций
В
геометрическом смысле каждый набор
значений переменных можно рассматривать как – мерный вектор, определяющий точку в
–мерном
пространстве. Все множество двоичных
наборов значений аргументов образует
геометрическое множество вершин
–мерного
единичного куба. Выделяя вершины, на
которых значение функции равно 1, можно
получить геометрический образ истинностной
функции.
Пример. Функция задана таблицей истинности 2.7. Геометрическим представлением ее области истинности являются вершины куба, отмеченные на рис. 2.2 черными точками.
Таблица 2.7.
f() | |
000 001 010 011 100 101 110 111 | 0 0 0 1 1 1 1 1 |
Расстоянием
между двумя вершинами называется число
переменных, значения которых следует
изменить, чтобы преобразовать вектор
координат одной вершины в вектор
координат другой.
2.2.2. Интервальное представление булевых функций
Интервальное представление устанавливает более тесную связь между геометрическим представлением логической функции и ее записью в виде логической формулы в булевом базисе. Обозначим – множество всех вершин единичного n –мерного куба. Пусть – множество всех таких вершин куба, на которых функция . Для вышеприведенного примера . Множество является, фактически, отношением на вида .
Сформулированное
в разделе 2.1.5 правило получения СДНФ
связывает с каждой вершиной n
–мерного куба конъюнкцию членов, а со всей областью истинности
функции – дизъюнкцию этих конъюнкций.
Пусть для некоторой функции
.
Тогда СДНФ имеет вид
.
Применив к полученной формуле операцию
склеивания по получим
.
Легко заметить, что исходные вершины
соединены ребром. Если связать с этим
ребром конъюнкцию
,
то можно построить цепочку: конъюнкция
трех составляющих – вершина куба,
конъюнкция двух составляющих – ребро
куба и т. д.
д.
Для формализации полученной связи между конъюнкциями и элементами гиперкуба введем несколько определений.
Элементарной конъюнкцией называется конъюнкция переменных или их отрицаний , где , в которой каждая переменная встречается не более одного раза. Часто, в литературе, переменную или ее отрицание вида называют первичным термом. Число называется рангом конъюнкции. В случае конъюнкция называется пустой и полагается равной 1.
Подмножество называется интервалом r–ого ранга, если оно соответствует элементарной конъюнкции –ого ранга.
Очевидно, каждой конъюнкции соответствует интервал , состоящий из всех вершин гиперкуба, у которых а значения остальных координат произвольны. Таким образом, каждая вершина куба является интервалом –ого ранга, множество всех вершин – интервалом нулевого ранга.
Пример.
В трехмерном кубе, конъюнкции соответствует ребро
,
являющееся интервалом 2–го ранга (такой
интервал часто обозначают (X11)),
а конъюнкции – грань
,
являющаяся интервалом 1–го ранга.
Для некоторой логической функции можно ввести понятие комплекса интервалов –ого ранга. Например, для функции, заданной выше таблицей истинности 2.7 и рисунком 2.2, можно выделить следующие комплексы:
Аффинная эквивалентность булевых функций, симметричных мономиальному вращению: подход на основе теорем Полиа
Ключевые слова: аффинная эквивалентность; симметрия вращения; булевы функции; Счетная теорема Полиа
1 Введение
Предмет булевых функций хорошо известен и составляет краеугольный камень криптографии и теории кодирования. Пусть 𝔽2 — бинарное конечное поле и
𝔽2n — n -мерное векторное пространство над 𝔽2. Булева функция для n переменных может рассматриваться как отображение из
𝔽2n→𝔽2. В наборе все n -переменные булевы функции обозначаются ℬn. Функции, инвариантные относительно действия циклической группы, называются вращательно-симметричными функциями. Эти функции были впервые введены Пепшиком и Ку в 1999 году [19] и использовались в качестве компонентов в алгоритмах хэширования для ускорения реализации криптографической хеш-функции. С тех пор симметричные по вращению булевы функции оказались очень полезными в нескольких областях криптографии [3, 10, 9, 14, 19, 22]. Эти функции чрезвычайно богаты с точки зрения криптографически значимых функций. Булева функция называется мономиально-вращательной симметричной (MRS), если она порождена циклическими перестановками переменных в одном мономе.
С тех пор симметричные по вращению булевы функции оказались очень полезными в нескольких областях криптографии [3, 10, 9, 14, 19, 22]. Эти функции чрезвычайно богаты с точки зрения криптографически значимых функций. Булева функция называется мономиально-вращательной симметричной (MRS), если она порождена циклическими перестановками переменных в одном мономе.
Проблема перечисления типов булевых функций в группе переменных перестановок и дополнений была впервые поставлена Джевонсом в 1870-х годах, но не была решена удовлетворительным образом до работы Полиа [20] в 1937 году. Аффинное преобразование дает метод группировки подобных булевых функций в классы. Это имеет смысл по следующим двум причинам: во-первых, эквивалентные функции имеют такие же свойства, как распределение веса Хэмминга, и одинаковую нелинейность; во-вторых, число представителей намного меньше числа булевых функций. Две функции f,g∈ℬn называются аффинно эквивалентными, если существует невырожденная матрица размера n × n A на 𝔽2 и вектор
b∈𝔽2n такое, что g(x)=f(Ax⊕b). Мы говорим, что f(Ax⊕b) является неособым аффинным преобразованием функции f(x). Первая заметная попытка решить проблему аффинной эквивалентности была сделана в статье Харрисона 1964 года [12]. В 1972 г. Берлекамп и Уэлч [1] определили и описали полный набор классов эквивалентности для функций пяти входов, используя их алгебраическую нормальную форму. В 1991 году Майорана [17] вычислил 150 357 классов эквивалентности шести переменных булевых функций. Из-за своей сложности и размера аффинная эквивалентность по-прежнему остается сложной проблемой, особенно для общего решения, которое касается любого n∈ℕ. В 2009Ким, Парк и Хан [15] изучали аффинную эквивалентность квадратичных булевых функций MRS. Кьюсик [4] нашел классы аффинной эквивалентности в некоторых случаях для кубических функций MRS, введя новое понятие, называемое шаблонами. Была дана точная формула числа классов в случае, когда число переменных n — простое число. В 2014 г. Кьюсик и Чеон [6] расширили работу [4] на булевы функции MRS четвертой степени, включив точную формулу для n простых чисел.
Мы говорим, что f(Ax⊕b) является неособым аффинным преобразованием функции f(x). Первая заметная попытка решить проблему аффинной эквивалентности была сделана в статье Харрисона 1964 года [12]. В 1972 г. Берлекамп и Уэлч [1] определили и описали полный набор классов эквивалентности для функций пяти входов, используя их алгебраическую нормальную форму. В 1991 году Майорана [17] вычислил 150 357 классов эквивалентности шести переменных булевых функций. Из-за своей сложности и размера аффинная эквивалентность по-прежнему остается сложной проблемой, особенно для общего решения, которое касается любого n∈ℕ. В 2009Ким, Парк и Хан [15] изучали аффинную эквивалентность квадратичных булевых функций MRS. Кьюсик [4] нашел классы аффинной эквивалентности в некоторых случаях для кубических функций MRS, введя новое понятие, называемое шаблонами. Была дана точная формула числа классов в случае, когда число переменных n — простое число. В 2014 г. Кьюсик и Чеон [6] расширили работу [4] на булевы функции MRS четвертой степени, включив точную формулу для n простых чисел. В 2015 г. Станицэ [23] использовал идеи теории циркулянтных матриц для нового доказательства результатов работы [6], а также получил точную формулу для случая, когда n — первичная мощность. Недавно Кьюсик и Станика [8] вывели асимптотическую формулу для числа Ad,p классов аффинной эквивалентности при всех перестановок для степени d MRS булевых функций, где число переменных p простое, а именно
В 2015 г. Станицэ [23] использовал идеи теории циркулянтных матриц для нового доказательства результатов работы [6], а также получил точную формулу для случая, когда n — первичная мощность. Недавно Кьюсик и Станика [8] вывели асимптотическую формулу для числа Ad,p классов аффинной эквивалентности при всех перестановок для степени d MRS булевых функций, где число переменных p простое, а именно
Ad, p=1d!pd-2+1d!d2-d-22pd-3+𝒪(pd-4) если d≥5.
Они также дали точную формулу для функций MRS пятой степени, когда n — степень простого числа. Тем не менее перечисление аффинной эквивалентности булевых функций MRS степени d для произвольного количества переменных остались без ответа.
Мы решаем частный случай этой проблемы перечисления аффинной эквивалентности булевых функций MRS, используя теорию Полиа. Определим некоторую группу перестановок, действие которой на множестве мономов от n переменных дает аффинную эквивалентность булевых функций MRS относительно этой группы перестановок.
Остальная часть статьи организована следующим образом: В разделе 2 мы приводим основные определения и обозначения. В разделе 3 мы указываем Теорема о перечислении Полиа для полноты картины. В разделе 4 мы объясняем результаты, необходимые нам для изучения аффинной эквивалентности. В разделе 5 мы доказываем теоремы, которые дают подсчеты классов эквивалентности для мономиальных булевых функций, симметричных относительно вращения, относительно некоторых групп перестановок. Этот раздел содержит основные результаты настоящей статьи. В разделе 6 мы обсуждаем некоторые возможности для будущей работы и, наконец, в разделе 7 мы подводим итоги статьи.
2 Предварительные сведения
Булева функция для n переменных может рассматриваться как отображение из 𝔽2n→𝔽2 и может быть представлена как многочлен от множества переменных над 𝔽2, то есть
f(x1,x2,…,xn) =∑j=(j1,j2,…,jn)∈GF(2)najx1j1x2j2⋯xnjn,
, где aj∈𝔽2, а сложение и умножение больше 𝔽2. Это представление называется алгебраической нормальной формой (АНФ). Алгебраическая степень числа f определяется как максимальное количество переменных в терминах АНФ числа 9.0007 ф . Если все члены АНФ f имеют одинаковую степень, то функция называется однородной.
Это представление называется алгебраической нормальной формой (АНФ). Алгебраическая степень числа f определяется как максимальное количество переменных в терминах АНФ числа 9.0007 ф . Если все члены АНФ f имеют одинаковую степень, то функция называется однородной.
Пусть x=(x1,x2,…,xn)∈F2n. Тогда мы можем распространить определение ρnk на кортежи и мономы следующим образом:
ρnk(x)=(ρnk(x1),ρnk(x2),…,ρnk(xn)) и ρnk(xi1xi2⋯)=ρnk(xi1)ρnk(xi2 )….
Обратите внимание, что симметричная логическая функция вращения f имеет одно и то же значение для каждого из подмножеств, созданных из вращательной симметрии. Входы вращательно-симметричной булевой функции можно разделить на орбиты так, чтобы каждая орбита состояла из всех циклических сдвигов одного входа. Орбита, порожденная (x1,x2,…,xn), равна
On(x1,x2,…,xn)={ρnk(x1,x2,…,xn)∣0≤k и функция имеет одинаковое значение для всех входов на одной и той же орбите. On(xi1xi2⋯xid)={ρnk( xi1xi2⋯xid) для 0≤k из xi1xi2⋯xid. Результаты в [4] и [6] дают метод явного определения классов эквивалентности при перестановках, сохраняющих вращательную симметрию для любой кубической или четвертой МРС-функции от n переменных, а также дают
точная формула для числа классов, если n — простое число. В кубическом случае классы эквивалентности при перестановках, сохраняющих симметрию вращения, когда n — простое число, совпадают с классами эквивалентности при всех перестановках. Впервые это было доказано в
[5, теорема 3], а затем было обобщено на случай функций (любой степени), где n — любое простое число из [8]. Соответствующий результат заведомо неверен для составных n , так как уже для МКР-функций четвертой степени с n=8 имеется пример [6, замечание 1. Некоторые из наиболее сложных математических задач связаны со счетом. Есть несколько причин этой трудности, некоторые из которых технические, а другие более концептуальные. Часто встречающаяся техническая трудность заключается в том, что подлежащие подсчету объекты могут располагаться не последовательно. Чтобы вычислить количество шаблонов с помощью леммы Бернсайда, мы должны сначала вычислить размер Inv(σ) для всех σ∈G. Полиа заметил, что элементы G с одинаковой структурой цикла вносят одинаковый вклад в наборы неподвижных точек. Пусть G1, G2 — группы перестановок, действующие на множествах X1, X2 соответственно. Пусть G=G1×G2 — прямое произведение групп, а X=X1×X2 — декартово произведение соответствующих множеств. Для элемента x=(x1,x2) из X и элемент g=(g1,g2) из G , мы определяем действие g на x как ϕ(g,x)=(ϕ1(x1,g1), ϕ2(x2,g2)). Харари [11, с. 746] ввел комбинаторное умножение полиномов (мы используем обозначение ⊛), чтобы найти полином индекса цикла группы произведений G1×G2 через полином индекса цикла групп G1 и G2. Пусть ZG1(f1,f2,…,fl)=∑(j)c(j)∏p=1lfpjp,ZG2(f1,f2,…,fm)=∑(k)d(k) ∏q=1mfqkq. Тогда ZG1⊛ZG2=∑(j)c(j)∑(k)d(k)∏p=1lfpjp⊛∏q=1mfqkq, , где операция ⊛ над неопределенными определяется как ∏p=1lfpjp⊛∏q=1mfqkq=∏p=1l∏q=1mfpjp⊛fqkq и fpjp⊛fqkq=flcm(p,q)jpkqgcd(p,q). Отметим, что некоторые приложения этой леммы ранее были даны Харрисоном [13]. Теперь объясним версию теоремы Полиа, которую мы будем использовать.
Пусть X будет множеством. Раскраска X — это присвоение цвета каждому элементу х . То есть раскраске соответствует функция f:X→C, где C — набор цветов. Когда |X|=k и |C|=m, существует mk раскрасок X с использованием цветов из C .
Весовая функция w — это любая функция из набора цветов C в набор X . Учитывая набор цветов C , мы хотим назначить вес wc для всех c∈C; тогда мы определяем вес раскраски как произведение весов окрашенных элементов. В этой статье X будет набором всех мономов заданной степени d в n переменных, со взвешенными раскрасками, как объяснено в следующем абзаце, и действие группы G перестановок вызовет отношение эквивалентности на Х . Классами эквивалентности будут шаблоны в теореме Полиа (см. В нашем контексте логических функций MRS в n переменных набор цветов будет C={0,1}, а соответствующие два веса будут w0=1 и w1=y. Для любого монома из n переменных мы окрашиваем переменную xi, 1≤i≤n, в цвет 1, если xi не входит в моном, и в цвет y , если xi входит в моном. Таким образом, вес любого одночлена степени d всегда равен yd, и по симметрии вращения все одночлены в любой функции MRS в n переменных будут иметь одинаковый вес. Простейшие невырожденные аффинные преобразования функции MRS f получаются, если мы просто переставляем n переменных, и в этом случае A является матрицей перестановки и b=. Аффинная эквивалентность — полезное понятие в криптографии, поскольку многие криптографически важные свойства булевой функции f сохраняются при аффинной эквивалентности и поэтому называются аффинными инвариантами . Например, легко видеть, что вес Хэмминга (обозначение wt(f)) и нелинейность (обозначение nl(f)) (определения см. Чтобы начать наше исследование перестановочной эквивалентности булевых функций MRS степени d , мы определим группу Gn перестановок. Пусть gτj — перестановка на
ℤn определяется формулой (мы опускаем зависимость от n из обозначений, так как она будет понятна из контекста всякий раз, когда мы ее используем) (4.1)gτj(i)=(i+j-1) τ+1(modn), , где обозначение amodn означает уникальное целое число b в {1,2,…,n} такое, что b≡amodn. Ниже мы приведем несколько примеров групп Gn. Мы используем обозначение e для тождества и даем другие перестановки как произведение циклов с опущенными неподвижными точками. Группа G10 имеет 4 элемента gτ1 с τ∈{1,3,7,9}, а именно e и (1,4,3,10)(2,7)(5,6,9,8),(1,8,7,10)(2,5, 6,3)(4,9),(1,10)(2,9)(3,8)(4,7)(5,6). Остальные 36
элементы gτj с j>1 выводятся из них по (4.1). Группа G15 имеет 8 элементов gτ1 с τ∈{1,2,4,7,8,11,13,14}, а именно e и (1,3,7,15)( 2,5,11,8)(4,9)(6,13,12,10),(1,5,6,10,11,15)(2,9,7,14,12, 4)(3,13,8), (1,8,12,10,11,3,7,5,6,13,2,15)(4,14,9),(1, 9,13,15)(3,10,6,4)(5,11,14,8)(7,12), (1,12,13,9,10,6,7,3,4,15)(2,8,14,5,11),(1,14,3,10,11,9,13) ,5,6,4,8,15)(2,12,7), (1,15)(2,14)(3,13)(4,12)(5,11 )(6,10)(7,9). Остальные 112 элементов gτj с j>1 получаются из них по (4.1). Определим Md,n={все функции MRS степени d от n переменных}. Кажется, что мы также должны рассмотреть множество Fd,n={Md,n плюс функции, порожденные действием Gn на Md,n}, , но на самом деле в нашей следующей лемме мы показываем, что это множество совпадает с Md,n. Наши доказательства ниже требуют использования другой группы Hn, определенной следующим образом: Пусть n — натуральное число, и пусть σt,s — перестановка на ℤn, определяемая равенством σt,s(i)=it +s (модн.). Пусть Hn={σt,s:gcd(t,n)=1 и 0≤t,s≤n-1}. Тогда Hn образует группу порядка nϕ(n) с помощью операции композиции перестановок. Как и прежде, пусть X будет множеством всех мономов степени d от n переменных. Определить действие Hn на X следующим образом: σt,s(xi1xi2⋯xik)=xσt,s(i1)xσt,s(i2)⋯xσt,s(ik). Вей и Сюй [24, с. 180–181] нашли полином индекса цикла для этой группы Hn, используя следующую лемму (мы исправили несколько опечаток в [24]). Учитывая лемму 4.2, мы можем найти полином индекса цикла ZHn для любого n , используя умножение ⊛ из раздела 3 и леммы 3.2.
Это было сделано в [24], авторы которой, по-видимому, не знали о гораздо более ранней работе, упомянутой в разделе 3, с использованием операции ⊛. Нам нужна группа Hn, потому что оказывается, что полиномы индекса цикла ZGn и ZHn совпадают. Мы были не в состоянии
для прямого вычисления ZGn. Легко видеть, что группы Gn и Hn изоморфны, но этого недостаточно, чтобы показать, что они имеют одинаковые полиномы индекса цикла. Мы докажем это в нашей следующей лемме. Этот раздел содержит основные результаты этой статьи. Наша следующая теорема применяет механизм, развитый в разделе 4, к функциям MRS. Отметим, что теорема 5. Мы применим теорему Полиа 3.3 к действию Gn на Md,n, а затем докажем следующую теорему. Пусть Ed,n обозначает количество классов аффинной эквивалентности для Md,n в группе Gn. Тогда теорема 5.2 утверждает, что (5.1)Ed,n=коэффициент yd в ZGn(1+y,1+y2,…,1+yn). Приведем явную оценку формулы (5.1) при n — нечетное простое число в нашей следующей теореме. В качестве иллюстрации полезности теоремы 5.3 читатель может легко восстановить формулу E3,p=[p/6]+1 для кубических функций MRS
[4, теорема 4.2], оценивая E3,p с помощью (5.2). Вычисление Ed,n быстро усложняется по мере увеличения числа простых множителей n , но для этих вычислений легко написать компьютерную программу. У авторов есть такая программа, использующая программное обеспечение SAGE для быстрой оценки Ed,n для
д<10 и n с общим количеством до шести простых множителей, учитываемых с учетом кратности. Пусть cd,n обозначает количество булевых функций MRS степени d в n переменных; тогда из [16] имеем (5.3)cd,n=1n∑t|gcd(d,n)ϕ(t)(ntdt). Комбинируя это с теоремой 5.3, мы получаем следующую теорему. Было бы интересно найти доказательство теоремы 5.4, не использующее теорему 5.3. Если n=∏i=1rpiαi, то
по лемме 3.2 индекс цикла группы Gn равен (5.4)ZGn(x1,x2,…,xn)=⊛i=1sZGpiαi. Если EGn обозначает многочлен ZGn(1+y,1+y2,…,1+yn), , то по (5.1) коэффициент при yd равен
Эд, н. Таким образом, мы можем использовать (5.4) для вычисления полиномов индекса цикла, а также полиномов EGn. Приведем несколько примеров, рассчитанных с помощью
программа SAGE. и ZG15=(1/120)(x115+15x1x27+5x13x26+3x15x25+10x13x43+30x1x2x43 +20x3x12+10x3x62+2×35+12x5x10+4×53+8×15). Обратите внимание, что правильная формула ZGn=(1/(nϕ(n))p(x1,…,xn) должна иметь сумму целых коэффициентов, например ci,
многочлена p равным nϕ(n), и каждый моном cixi(1)a(1)⋯xi(k)a(k) должен удовлетворять a (1)i(1)+⋯+a(k)i(k)=n. Напомним, что коэффициент xd в EGn(x) равен Ed,n. У нас есть следующие результаты: EG10=1+x+3x2+4x3+9x4+9x5+9x6+4x7+3x8+x9+x10, EG15=1+x+3 x2+7x3+18x4+34x5+54x6+66x7+66x8+54x9 +34x10+18x11+7x12+3x13+x14+ x15, EG24=1+y+7y2+23y3+97y4+294y5+870y6+2051y7+4272y8+7352y9 +10,980y10+13,790 y11+15,008y12+13,790y13+10,980y14+7352y15 +4272y16+2051y17+870y18+294y19+97y20+23y22+23y22+ у24. Теоремы 5.2 и 5.3 дают полное описание перестановочной эквивалентности для функций MRS любой степени, когда число n переменных
— простое число, но для других значений n получаются только классы группы Gn. Хотелось бы получить более подробную информацию о классах, когда n составное, тем более что пример для n=8 в последнем абзаце раздела 2 показывает, что ответ не может быть таким же простым, как в простом случае. Было бы интересно узнать, для общего n , насколько большими можно было бы сделать группы Gn или Hn без уменьшения числа классов эквивалентности, указанных в теореме 5.3. Для этого может быть полезно более глубокое знание структуры этих групп. Мы даем некоторую информацию об этих группах в оставшейся части этого раздела. Группы Gp и Hp для простых чисел p изучаются давно (см., например, [18]). В этом случае мы можем дать очень явное описание структуры групп.
Пусть GA(p) обозначает известные общая аффинная группа Zp⋊Zp* (полупрямое произведение) для нечетных простых чисел p . Из их определений ясно, что и Gp, и Hp изоморфны GA(p). Поскольку (6.1)σ1,1(i)=i+1(modp) дает p -цикл, а σk,p-1(i) дает (p-1)-цикл для подходящего
выбрали k , мы можем доказать следующие леммы о группе Hp. Мы определили группу перестановок, действие которых на множестве мономов дает классы аффинной эквивалентности булевых функций MRS в n переменных при определенных больших группах перестановок. Эта статья распространяется в соответствии с условиями некоммерческой лицензии Creative Commons Attribution, которая разрешает неограниченное некоммерческое использование, распространение и воспроизведение на любом носителе при условии правильного цитирования оригинальной работы. Восточно-Европейский журнал корпоративных технологий 2021, 4(4( 112), 23–39. дои: 10. 17 страниц Опубликовано: 22 окт 2021 Посмотреть все статьи Михаила Соломко Национальный университет водного хозяйства и природопользования Национальный университет водного хозяйства и природопользования Киевский национальный университет имени Тараса Шевченко Ровенский государственный гуманитарный университет Университет таможенного и Финансы Ровенский государственный гуманитарный университет Дата написания: 30 августа 2021 г. В данной статье сообщается об исследовании, установившем возможность повышения эффективности метода фигуративных преобразований с целью минимизации симметричных булевых функций в главный и полиномиальный базисы. Выявлены перспективные резервы в аналитическом методе, такие как упрощение конъюнктур полиномиальной функции с помощью созданных эквивалентных преобразований на основе метода вставки одинаковых конъюнктур с последующей операцией суперсклейки переменных. Метод фигуративных преобразований распространен на процесс минимизации симметричных булевых функций с помощью алгебры в терминах правил упрощения функций основного и полиномиального базиса и разработаны эквивалентные преобразования конъюнктермов. Установлено, что упрощение симметричных булевых функций методом фигуративных преобразований основано на блок-схеме с повторением, которая является фактической таблицей истинности заданной функции. Это достаточный ресурс для минимизации симметричных булевых функций, что позволяет обойтись без вспомогательных объектов, таких как карты Карно, кубы и т. д. Совершенная нормальная форма симметричных функций может быть представлена бинарными матрицами, которые представляют члены симметричных булевых функций и операции ИЛИ или XOR для них. Экспериментальное исследование подтвердило, что метод фигуративных преобразований, использующий комбинаторные системы 2-(n, b)-плана и 2-(n, x/b)-плана, повышает эффективность минимизации симметричных булевых функций. Есть основания утверждать о возможности повышения эффективности минимизации симметричных булевых функций в главном и полиномиальном базисах методом фигуративных преобразований. Это обеспечивается, в частности, использованием разработанных эквивалентных преобразований конъюнктеров полиномиальной функции, основанных на методе вставки однотипных конъюнктур с последующей операцией суперсклейки переменных. Ключевые слова: минимизация симметричных булевых функций методом фигуративных преобразований, сингулярная функция, главный базис Рекомендуемое цитирование: Рекомендуемая ссылка Соломко, Михаил и Тадеев, Петр и Зубик, Людмила и Бабич, Степания и Мала, Юлия и Войтович, Оксана, Реализация метода фигуративных преобразований для минимизации симметричных булевых функций (30 августа 2021 г. Пусть gn — число таких орбит. Тогда число симметричных по вращению булевых функций равно 2gn.
Заметим, что если АНФ вращательно-симметричной функции содержит член xi1xi2⋯xid, то по определению вращательной симметрии в нем есть все члены из орбиты
Пусть gn — число таких орбит. Тогда число симметричных по вращению булевых функций равно 2gn.
Заметим, что если АНФ вращательно-симметричной функции содержит член xi1xi2⋯xid, то по определению вращательной симметрии в нем есть все члены из орбиты 10], где имеется пять классов эквивалентности при всех перестановках, но шесть, если только перестановки сохраняют учитываются вращательная симметрия. Известно
[8, теорема 2.3], что группа перестановок, сохраняющих симметрию вращения, когда число переменных простое p , имеет порядок p-1. В этой статье мы рассматриваем классы эквивалентности для МРС-функций в n переменных в группе (определенной ниже) перестановок порядка
nϕ(n), и оказывается, что для простого числа n классы эквивалентности в этой группе такие же, как классы для группы перестановок, сохраняющих симметрию вращения, и, следовательно, такие же, как классы при всех перестановки.
10], где имеется пять классов эквивалентности при всех перестановках, но шесть, если только перестановки сохраняют учитываются вращательная симметрия. Известно
[8, теорема 2.3], что группа перестановок, сохраняющих симметрию вращения, когда число переменных простое p , имеет порядок p-1. В этой статье мы рассматриваем классы эквивалентности для МРС-функций в n переменных в группе (определенной ниже) перестановок порядка
nϕ(n), и оказывается, что для простого числа n классы эквивалентности в этой группе такие же, как классы для группы перестановок, сохраняющих симметрию вращения, и, следовательно, такие же, как классы при всех перестановки. 3 Теорема Полиа о перечислении
 Общая концептуальная трудность возникает, когда для целей перечисления идентифицируются разные объекты. Тогда проблема состоит в том, чтобы перечислить классы эквивалентности. Двумя основными теоремами комбинаторики, касающимися подсчета математических объектов с точки зрения симметрии, являются лемма Бернсайда и теорема о перечислении Полиа [20]. Теорема Полиа о перечислении, также известная как теорема Редфилда-Пойа (из-за работы в [21]), является мощным обобщением леммы Бернсайда, которое учитывает симметрию при подсчете математических объектов. Лемма Бернсайда, хотя и мощная сама по себе, может потребовать значительного объема вычислений. Теорема Полиа о перечислении сводит к минимуму вычисления, необходимые за счет использования индекса цикла, и исследует идею весов, которая позволяет решать более сложные задачи.
Общая концептуальная трудность возникает, когда для целей перечисления идентифицируются разные объекты. Тогда проблема состоит в том, чтобы перечислить классы эквивалентности. Двумя основными теоремами комбинаторики, касающимися подсчета математических объектов с точки зрения симметрии, являются лемма Бернсайда и теорема о перечислении Полиа [20]. Теорема Полиа о перечислении, также известная как теорема Редфилда-Пойа (из-за работы в [21]), является мощным обобщением леммы Бернсайда, которое учитывает симметрию при подсчете математических объектов. Лемма Бернсайда, хотя и мощная сама по себе, может потребовать значительного объема вычислений. Теорема Полиа о перечислении сводит к минимуму вычисления, необходимые за счет использования индекса цикла, и исследует идею весов, которая позволяет решать более сложные задачи. Он определил понятие полинома индекса цикла (или, для краткости, индекса цикла), чтобы отслеживать циклическую структуру элементов G .
Он определил понятие полинома индекса цикла (или, для краткости, индекса цикла), чтобы отслеживать циклическую структуру элементов G .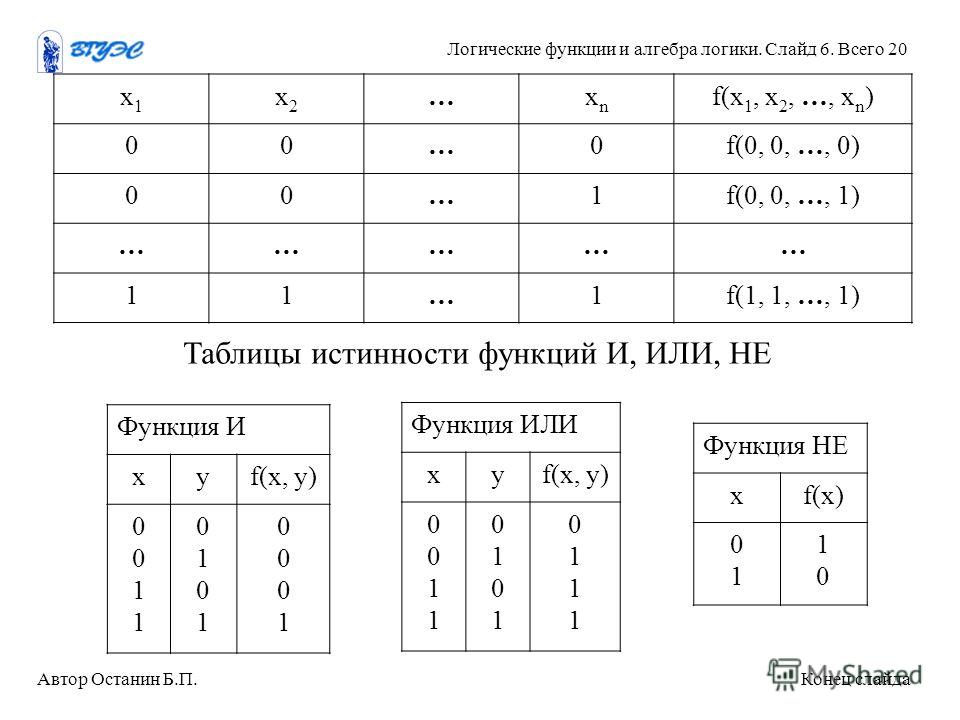
 лемму 3.1 и обсуждение подсчета шаблонов, следующее за леммой), а индекс цикла будет производящей функцией для числа классов эквивалентности, как объяснено в теореме 5.2 ниже. Подробное изложение нашей версии теоремы Полиа (с весами) дано в [2].
лемму 3.1 и обсуждение подсчета шаблонов, следующее за леммой), а индекс цикла будет производящей функцией для числа классов эквивалентности, как объяснено в теореме 5.2 ниже. Подробное изложение нашей версии теоремы Полиа (с весами) дано в [2]. 4 Аффинная эквивалентность булевых функций MRS
 В настоящее время кажется слишком сложным иметь дело с аффинной эквивалентностью вообще, поэтому
в этой статье мы будем рассматривать эквивалентность только относительно перестановок или относительно подгрупп группы всех перестановок. Если σ является перестановкой n переменных, имеем
σ(f)=f(Ax), где A — матрица перестановок, которая
переставляет индексы переменных в соответствии с σ. Обратите внимание, что такая перестановка переменных не обязательно сохраняет симметрию вращения. Если мы имеем
σ(f)=f(Ax)=g для некоторой функции MRS g , тогда мы говорим, что f и g эквивалентны перестановкам .
В настоящее время кажется слишком сложным иметь дело с аффинной эквивалентностью вообще, поэтому
в этой статье мы будем рассматривать эквивалентность только относительно перестановок или относительно подгрупп группы всех перестановок. Если σ является перестановкой n переменных, имеем
σ(f)=f(Ax), где A — матрица перестановок, которая
переставляет индексы переменных в соответствии с σ. Обратите внимание, что такая перестановка переменных не обязательно сохраняет симметрию вращения. Если мы имеем
σ(f)=f(Ax)=g для некоторой функции MRS g , тогда мы говорим, что f и g эквивалентны перестановкам . , например,
[7, с. 6–7]) булевой функции являются аффинными инвариантами. Для двух квадратичных функций f,g∈ℬn мы имеем хорошо известный более сильный результат, что f и g аффинно эквивалентны тогда и только тогда, когда wt(f)=wt(g) и nl(f)= nl(g), но это неверно для функций более высокой степени. Также известно [4, теорема 2.7], что если две квадратичные функции МРП в ℬn аффинно эквивалентны, то они перестановочно эквивалентны. Таким образом, в квадратичном случае без потери общности рассматривается эквивалентность только при перестановках, но опять же это неверно для более высоких степеней.
, например,
[7, с. 6–7]) булевой функции являются аффинными инвариантами. Для двух квадратичных функций f,g∈ℬn мы имеем хорошо известный более сильный результат, что f и g аффинно эквивалентны тогда и только тогда, когда wt(f)=wt(g) и nl(f)= nl(g), но это неверно для функций более высокой степени. Также известно [4, теорема 2.7], что если две квадратичные функции МРП в ℬn аффинно эквивалентны, то они перестановочно эквивалентны. Таким образом, в квадратичном случае без потери общности рассматривается эквивалентность только при перестановках, но опять же это неверно для более высоких степеней. Пусть Gn={gτj:gcd(τ,n)=1 и 1≤j≤n}. Тогда Gn образует группу порядка nϕ(n) с помощью операции композиции перестановок. Пусть X — множество всех мономов степени d от n переменных. Определим действие Gn на X следующим образом: j(идентификатор).
Пусть Gn={gτj:gcd(τ,n)=1 и 1≤j≤n}. Тогда Gn образует группу порядка nϕ(n) с помощью операции композиции перестановок. Пусть X — множество всех мономов степени d от n переменных. Определим действие Gn на X следующим образом: j(идентификатор). Примеры групп Gn


5 Перестановочная эквивалентность функций MRS
 1 для простых значений n была ранее доказана Кьюсиком и Станикэ [8].
1 для простых значений n была ранее доказана Кьюсиком и Станикэ [8].
Примеры полиномов индекса цикла 4x10)

Примеры полиномов EGn и количества классов эквивалентности Ed,n
6 Будущая работа
 Оказывается, эта же проблема возникает и в некоторых задачах теории графов [25, § 9].
Оказывается, эта же проблема возникает и в некоторых задачах теории графов [25, § 9]. 7 Заключение
 Если n простое, мы получаем классы при всех перестановках. Используя теорему Полиа, мы дали явное количество этих классов. Мы также дали рекуррентное соотношение, которое для простого числа n выражает число классов эквивалентности степени d булевых функций MRS через три значения считающей функции
который дает количество булевых функций MRS данной степени в заданном количестве переменных.
Если n простое, мы получаем классы при всех перестановках. Используя теорему Полиа, мы дали явное количество этих классов. Мы также дали рекуррентное соотношение, которое для простого числа n выражает число классов эквивалентности степени d булевых функций MRS через три значения считающей функции
который дает количество булевых функций MRS данной степени в заданном количестве переменных. Реализация метода фигуративных преобразований для минимизации симметричных булевых функций Михаил Соломко, Петр Тадеев, Людмила Зубик, Степания Бабич, Юлия Мала, Оксана Войтович :: SSRN
 15587/1729-4061.2021.239149
15587/1729-4061.2021.239149 Реферат

 По сравнению с аналогами это позволяет повысить производительность минимизации симметричных булевых функций на 100‒200 %.
По сравнению с аналогами это позволяет повысить производительность минимизации симметричных булевых функций на 100‒200 %.