Элементарный исход — Энциклопедия по экономике
Более строго случайная величина X определяется как функция, заданная на множестве элементарных исходов (или в пространстве элементарных событий), т.е. [c.24]Допустим, мы ставим задачу угадать, какой вариант произойдет из следующих элементарных исходов дождь, мокрый снег, снег, облачно, ясно или что-то иное. При равной вероятности событий для каждого из них Р = 1 6. Это значит, что мы «угадаем» именно с этой вероятностью. [c.192]
Пространство элементарных исходов Q = со,- . у со- [c.105]
Поскольку множество элементарных исходов И дискретно (и конечно ), любое его подмножество измеримо и, следовательно, может быть интерпретировано как случайное событие. [c.105]
Для упрощения обозначений здесь рассматривается лишь случай строгих упорядочений, т. е ситуации, когда принципиально невозможна неразличимость рангов (объединение рангов). Общий случай имеет лишь технические отличия, связанные с увеличением общего числа М элементарных исходов.
Статистический анализ взаимосвязей порядковых переменных строится на базе различных вариантов моделей вероятностного пространства, в котором роль пространства элементарных исходов играет множество всех возможных перестановок из п элементов (п — число статистически обследованных объектов). [c.124]
С точки зрения самого обучающегося, привлекательность образования тоже возрастает. Не только общество осознает важность финансирования образования, но и сам желающий получить образование. При этом он элементарно исходит из данных конкретных затрат на образование и отдачи от него (рис. 29). [c.228]
Нули траекторий броуновского движения. Пусть (Bt(u))f o -некоторая траектория броуновского движения, соответствующая элементарному исходу ш 2, и пусть [c.300]
Прежде всего отметим, что для удовлетворительного решения вопроса о представимости локальных мартингалов по локальному мартингалу Нс и мартингальной мере ц — v на структуру пространства fJ элементарных исходов ш приходится накладывать некоторые дополнительные предположения.
Общее вероятностное пространство. Пространство элементарных исходов, о — алгебра событий. Вероятностная мера. Дискретное вероятностное пространство. [c.30]
Вероятность события определяется как мера, число, показывающее отношение числа благоприятствующих этому событию исходов к общему числу всех единственно возможных и равновозможных элементарных исходов в системе намечаемых мероприятий. [c.87]
БЮДЖЕТ ПОТРЕБИТЕЛЬСКИЙ — среднестатистический баланс доходов и расходов семьи за определенный срок (месяц, год), характеризующий сложившийся уровень жизни населения, его различных групп. Выделяют нормативный и фактический бюджеты. Нормативный бюджет, в свою очередь, разделяется на рациональный и минимальный бюджеты. Рациональный Б.
 п.), не предусматривает расходы на приобретение автомобиля, квартиры и дачи, поездку всей семьей на курорт. В России до 1992 г. минимальный Б.п. использовался в качестве основы определения размеров оплаты труда, пенсий, стипендий и некоторых др. соц. выплат. Затем был выбран новый ориентир — прожиточный минимум, который обеспечивает более низкий жизненный стандарт. Считается, что соответствие рациональному Б.п. свидетель-
[c.24]
п.), не предусматривает расходы на приобретение автомобиля, квартиры и дачи, поездку всей семьей на курорт. В России до 1992 г. минимальный Б.п. использовался в качестве основы определения размеров оплаты труда, пенсий, стипендий и некоторых др. соц. выплат. Затем был выбран новый ориентир — прожиточный минимум, который обеспечивает более низкий жизненный стандарт. Считается, что соответствие рациональному Б.п. свидетель-
[c.24] Для определения массы перевозимого груза в зависимости от его назначения (технологические и эксплуатационные нужды, ремонт оборудования и коммуникаций, строительство и т.д.) используют данные, содержащиеся в соответствующих документах (годовые нормы расхода на технологические или ремонтно-эксплуатационные нужды, выделенные фонды материально-технических ресурсов, графики планового ремонта, технические паспорта перевозимого оборудования, проектно-сметная документация на строительство скважин и других объектов и т.д.). В некоторых из этих документов указана масса грузов, подлежащих перевозке (например, в технических паспортах на комплектующее оборудование, в фондовых извещениях на выделенные материально-технические ресурсы и т.

Кроме того, сравнение проводится исходя из элементарной предпосылки, что каждая цифра имеет значение только в сопоставлении с другой, используемой для оценки и контроля. Это дает возможность аналитику делать выводы по отклонениям. Сравнение используется и для выбора альтернативных вариантов, например вложения свободных средств и т. п. [c.24]
Существуют два основных подхода к определению элементарной единицы статистического наблюдения в экономике. В первом случае наблюдение ведется исходя из технологии конкретного производства (например, наблюдение за производством телевизоров или оказанием какого-то определенного вида услуг). На этом принципе строится отраслевой подход к экономическому анализу. Он получил довольно широкое распространение в нашей стране, однако необходимо иметь в виду важную особенность, на которой он основан. Дело в том, что в современной экономике редкие предприятия занимаются производством какого-либо одного вида продуктов или услуг. Чаще всего предприятие объединяет несколько достаточно обособленных производств, например производство автомобилей, холодильников и инструмента. При этом одни производства, которые в настоящий момент могут приносить больше прибыли, используются для субсидирования других. В СНС такие однородные с технологической точки зрения производства, организационно объединенные в одно предприятие, принято обозначать как заведения. При реализации отраслевого подхода полученную от предприятий первичную экономическую информацию приходится условно разбивать по заведениям, что может привести к значительным искажениям.
В первом случае наблюдение ведется исходя из технологии конкретного производства (например, наблюдение за производством телевизоров или оказанием какого-то определенного вида услуг). На этом принципе строится отраслевой подход к экономическому анализу. Он получил довольно широкое распространение в нашей стране, однако необходимо иметь в виду важную особенность, на которой он основан. Дело в том, что в современной экономике редкие предприятия занимаются производством какого-либо одного вида продуктов или услуг. Чаще всего предприятие объединяет несколько достаточно обособленных производств, например производство автомобилей, холодильников и инструмента. При этом одни производства, которые в настоящий момент могут приносить больше прибыли, используются для субсидирования других. В СНС такие однородные с технологической точки зрения производства, организационно объединенные в одно предприятие, принято обозначать как заведения. При реализации отраслевого подхода полученную от предприятий первичную экономическую информацию приходится условно разбивать по заведениям, что может привести к значительным искажениям.
Экономист тут же отверг и это предложение. Кому нужны бобы, пропитанные кислотой — сказал он. Физику и биохимику этот всемирно известный экономист уже надоел. Они спросили А что вы предлагаете, чтобы открыть банку Это элементарно, — ответил экономист. — Давайте начнем с предположения, что у нас имеется консервный нож, и исходя из этого разработаем план действий . [c.70]
При выработке финансовой политики следует исходить из конкретных исторических условий. Они должны учитывать специфику каждого этапа развития общества, особенности как внутренней, так и международной обстановки, реальные экономические и финансовые возможности государства. Прямая зависимость намеченных и осуществленных расходов от объема финансовых ресурсов является свидетельством элементарного финансового благоразумия и должна поддерживаться на всех уровнях хозяйствования.
Итак, школьная выучка имеет громадные преимущества перед заводской. Развивая ум ребенка еще в том возрасте, в котором он не способен К производительной работе, она дает ему потом возможность гораздо быстрее усваивать все технические навыки и достигать значительно лучших результатов, чем тем работникам, которые попадают на завод мимо школы. Исходя из данных табл. 28, нетрудно сделать примерный расчет громадного хозяйственного значения даже весьма элементарной школы и общей экономике страны. [c.84]
Заметим, что «исход» — не единственный термин для обозначения факта свершения случайного события. В разных дисциплинах, связанных с теорией В., то же означают случай, выборочная точка, элементарное событие, состояние и др. Вероятность обычно обозначается буквой Р. Напр., выражение Р А) = 0,5 означает, что В. наступления события А равна 0,5. [c.46]
[c.46]
Отметим, то важное обстоятельство, что для многих задач знание функции благосостояния 5(TV, M) не обязательно, достаточно лишь знания ее дифференциала (6.8), в котором зависимость r(7V, M) может быть получена на основе обработки статистического материала или исходя из модельных представлений о поведении элементарных участников экономического взаимодействия. В этом отношении ситуация та же, что с уравнением состояния термодинамических систем, связывающим друг с другом энтропию, объем, внутреннюю энергию и количества веществ, содержащихся в системе. Для идеального газа уравнение состояния найдено из модельных представлений, для других систем — экспериментально. [c.222]
Технологические процессы обработки деталей и сборки машин разрабатываются укрупненно. Это объясняется тем, что выполняемые заказы обычно не повторяются, поэтому затраты на детальную разработку технологических процессов экономически не оправданы. Исходя из этих же соображений обычно стремятся сократить количество специальной оснастки, используя универсальные приспособления и универсальный режущий инструмент. В единичном производстве широко применяются универсально-сборные приспособления (УСП), которые собирают из нормализованных элементов, а после использования расчленяют на элементарные детали. Многократное использование элементов УСП экономически эффективно., [c.76]
В единичном производстве широко применяются универсально-сборные приспособления (УСП), которые собирают из нормализованных элементов, а после использования расчленяют на элементарные детали. Многократное использование элементов УСП экономически эффективно., [c.76]
Следует отметить, что многомиллионное крестьянство, освобожденное Октябрьской революцией от кабалы помещиков, кулаков, торговцев и чиновничества, получившее благодаря этому огромные экономические выгоды, почти совсем не привлекалось к уплате налогов, способы его обложения только разрабатывались. Советская власть исходила из того, что усилить участие крестьян ства в общегосударственных расходах возможно лишь на основе подъема его производительных сил, для чего ему необходимо оказать крупную помощь со стороны государства. Только при этом условии производительность труда сельскохозяйственных работников достигнет той необходимой высоты, лри которой, в отличие от прежнего времени, платежи на общегосударственные нужды будут производиться крестьянами не путем недоедания и ограничения самых элементарных потребностей, а из избытков правильно организованного производительного хозяйства «. [c.41]
[c.41]
Блок определения приоритетности БОП оценивает или рассчитывает приоритеты (приоритетные характеристики) элементарных блоков модели, если в этом возникает необходимость. Приоритетность трактуется как оценка отношений порядка между блоками, когда возникает проблема приоритетной передачи управления от одного блока к другому или задачи распределения управляющих воздействий между блоками и выбора интенсивности этих сигналов для различных блоков. Аналогичную природу имеют проблемы распределения ресурсов исходя из приоритетной оценки или оценок объектов распределения ресурсов. [c.293]
Наряду с розовыми мечтами свой черный вклад вносит и математическая неграмотность. Большинство участников рынка, как это ни странно, не только не знакомы с такими понятиями, как математическая вероятность, дисперсия, статистика, et ., но и считают, что знакомство с этими понятиями избыточно. Упоминая теорию вероятностей, невольно на ум приходит анекдот из студенческой жизни. Идет экзамен по теории вероятностей и математической статистике. Профессор задает вопрос студентке Скажите, какова вероятность того, что, выйдя из дома, вы встретите динозавра . Экзаменуемая, не долго думая, отвечает, что вероятность составляет 50%. Профессор в изумлении Позвольте, но на чем основано ваше утверждение . Это элементарно, профессор, ведь существует только два исхода либо встречу, либо нет… — не моргнув глазом, восклицает студентка.
[c.186]
Профессор задает вопрос студентке Скажите, какова вероятность того, что, выйдя из дома, вы встретите динозавра . Экзаменуемая, не долго думая, отвечает, что вероятность составляет 50%. Профессор в изумлении Позвольте, но на чем основано ваше утверждение . Это элементарно, профессор, ведь существует только два исхода либо встречу, либо нет… — не моргнув глазом, восклицает студентка.
[c.186]
Применительно к какому-то определенному опыту (эксперименту) говорят о совокупности элементарных событий, представляющих собой все мыслимые и неразложимые исходы испытаний. Эти исходы называют пространством, или полем элементарных событий для данного опыта. [c.172]
Сформулируем задачу трейдера так, как она представляется с точки зрения теории вероятности. Как отмечалось выше, поле элементарных событий содержит два равноценных элемента, что, следовательно, дает соотношение вероятностей исходов 50 50. [c.215]
Событие (исход) — это результат мысленных или реальных испытаний. События различают по степени сложности элементарные и составные.
[c.45]
События различают по степени сложности элементарные и составные.
[c.45]
Пространство (поле) элементарных событий (ПЭС) — совокупность (множество) элементарных событий, которые представляют собой все мыслимые исходы испытаний. Это позволяет характеризовать каждый отдельный опыт (эксперимент) с точки зрения объемности того места, которое он занимает в ПЭС. [c.45]
Случайная величина (переменная) — некоторая функция, определенная на пространстве элементарных событий через исходы некоторого опыта или эксперимента. [c.46]
Так, приведенное пространство элементарных событий содержит только 2 элемента (и, и. .. и, и) и (и, и. .. и, у), где в каждом ряду по г исходов. Из этих двух элементарных и равновероятных событий есть одно, которое нас интересует (и, и. … и, у), что и дает неизменность шансов 50 50 при любом г. [c.57]
Число успехов как случайная величина. Под случайной величиной понимается переменная, которая определена на пространстве элементарных событий через исходы некоторого опыта или эксперимента. [c.62]
[c.62]
Поскольку эти исходы представляют собой пространство элементарных событий, сумма их вероятностей должна быть равной 1, что и имеет место [c.203]
При решении проблем исчерпаемых ресурсов нельзя избежать расчетов вариаций, включая даже новейшие исследования в этой области математики. Однако с помощью элементарных методов и различных упрощающих предпосылок можно выявить на следующих нескольких страницах некоторые принципы добывающей экономики. Позднее они будут обобщены при рассмотрении ряда случаев путем постепенного ввода некоторых усложнений, связанных с настоящим положением. Мы везде будем исходить из предположения, что владелец ис-черпаемого ресурса добивается, чтобы приведенная ценность [c.265]
Эти методы исходят прежде всего из общей количественной характеристики информации. Представляется что каждый из них имеет свою область применения одни удобны для описания информационных связей между подразделениями, другие — между группами задач, отдельными задачами и группами элементарных процедур. [c.108]
[c.108]
Считается, что в литературе впервые четко разделил счета на элементарные и коллективные Жан Са-вари (1675 г.). Писавшие после него исходили из непременного деления счетов на эти две группы (аналитический и синтетический учет). Однако медленно росло сознание того, что система счетов является не двухступенчатой, а более сложной иерархической структурой. [c.54]
Supp(8(x) = x . Определим функцию и ( ) на множестве элементарных исходов X по формуле [c.240]
Естественно, что невозможно внедрять новые формы менеджмента, если не освоены хотя бы азы давно наработанных управленческих методик. Предприятию было рекомендовано организовать службу маркетинга, произвести инвентаризацию, организовать учет перемещения то-варо-материальных ценностей, зафиксировать нормы затрат сырья и комплектующих для калькуляции стоимости и, лишь наведя хоть какой-то элементарный порядок, ориентировать производственный процесс на потребителя, исходя прежде всего из всего того нового, что накопил в последнее время менеджмент. [c.268]
[c.268]
ПРИНЦИП ОПТИМАЛЬНОСТИ [optimally prin iple] — 1. Общеэкономический принцип, согласно которому любое хозяйственное решение, начиная от элементарного, на уровне индивидуума, семьи, фирмы и вплоть до принятия плана социального и экономического развития страны, должно исходить из задачи получения оптимального результата — оптимального с точки зрения общенародных интересов (см. Социально-экономический критерий оптимальности). 2. См. Беллмана принцип оптимальности. [c.281]
Для того чтобы заложить опыт с заданной приближенной точностью, нужно определить среднюю квадратическую ошибку б для элементарной делянки и для комбинированных делянок различных величин. Исходя из того что средняя ошибка опыта м обратно пропорциональна квад- [c.166]
1.4.1. Понятие случайного события | Электронная библиотека
Информатика и вычислительная техника / Информатика и математика / 1.4.1. Понятие случайного события
В повседневной жизни мы имеем дело с явлениями или событиями, которые происходят всякий раз при реализации некоторого комплекса условий.
Если в результате эксперимента всякий раз происходит некоторое событие, то это событие называется достоверным (обозначается ).
Если в результате эксперимента некоторое событие не происходит никогда, то оно называется невозможным (обозначается ).
Если в результате эксперимента событие может произойти, либо не произойти, то оно называется случайным (обозначается А, В, С, …).
Теория вероятностей изучает случайные события, которые можно наблюдать неограниченное число раз при одних и тех же условиях, и не рассматривает случайных уникальных событий.
С каждым случайным событием связан некоторый опыт или эксперимент.
Множество всевозможных, взаимоисключающих исходов (результатов) эксперимента называется пространством элементарных исходов или элементарных событий (обозначается ).
Пример 1
Эксперимент – подбрасывание монеты.
Возможны два исхода: – монета выпала гербом, – монета выпала надписью. Пространство элементарных исходов:
.
Пример 2
Эксперимент – подбрасывание игральной кости.
Элементарные исходы: – на выпавшей грани игральной кости – i очков, . Пространство элементарных исходов:
.
Пример 3
Эксперимент – извлечение карты из тщательно перемешанной колоды.
Элементарные исходы: – карта определенной масти и определенного достоинства . Пространство элементарных исходов – .
Пример 4
Эксперимент – регистрация вызовов в течение часа на АТС.
Элементарные исходы: – в течение часа на АТС поступило i вызовов. Пространство элементарных исходов:
.
Пример 5
Эксперимент – стрельба по плоской мишени.
Элементарные исходы: – точки некоторой области на плоскости. Пространство элементарных исходов:
Пространство элементарных исходов:
.
В первых трех примерах пространство элементарных исходов – конечное, в четвертом – бесконечное, но счетное, в пятом – бесконечное и несчетное.
Назовем некоторый элементарный исход эксперимента благоприятствующим событию А, если в результате эксперимента, в котором имел место данный элементарный исход, происходит событие А.
Тогда любое случайное событие можно представить как совокупность (множество) случайных исходов, благоприятствующих этому событию, т.е. как некоторое подмножество из пространства элементарных событий .
Например, в примере 2 можно рассмотреть событие А – на грани игральной кости выпало число очков, кратное 3. Тогда это событие представляется как совокупность двух элементарных исходов .
В примере 3 – событие А – из колоды карт извлечен туз (каждая девятая карта в масти), тогда
.
В примере 4 – событие А – в течение часа поступило не более 10 вызовов, тогда
.
В примере 5 – событие А – произошло попадание в круг радиуса R = 1, здесь
.
Суммой А + В (АВ) случайных событий А и В называется случайное событие, состоящее из элементарных исходов, благоприятствующих хотя бы одному из событий, т.е. в результате эксперимента происходит хотя бы одно событие (рис. 1.8, а).
Произведением А•В (АВ) случайных событий А и В называется случайное событие, состоящее из элементарных исходов, благоприятствующих и событию А, и событию В, т.е.
в результате эксперимента события А и В происходят одновременно (рис. 1.8, б).
Разностью А – В (АВ) случайных событий А и В называется случайное событие, состоящее из элементарных исходов, которые благоприятствуют событию А и не благоприятствуют событию В, т. е. в результате эксперимента происходит событие А и не происходит событие В (рис. 1.8, в).
е. в результате эксперимента происходит событие А и не происходит событие В (рис. 1.8, в).
События А и В называются несовместными, если нет элементарных исходов, благоприятствующих и событию А, и событию В, т.е. в результате эксперимента эти события не могут произойти одновременно или .
Событие называется противоположным событию А, если выполняются два условия: 1) , 2) (рис. 1.8, г).
Рис. 1.8. Свойства случайных событий
Если каждому элементарному исходу поставить в соответствие некоторую точку на плоскости, то пространство элементарных исходов и любое случайное событие изобразятся некоторыми множествами точек на плоскости, что дает наглядное представление о введенных арифметических операциях (диаграммы Эйлера-Венна).
Введенные операции обладают следующими свойствами:
1) перестановочным (коммутативный закон):
, ;
2) сочетательным (ассоциативный закон)
, ;
3) распределительным (дистрибутивный закон)
;
4) правилом де Моргана
, ;
5) ; ; ; ; ; .
Все свойства доказываются непосредственно из определений операций. Необходимо рассмотреть произвольный элементарный исход, благоприятствующий левой части равенства, и показать, что он благоприятствует и правой части тоже, и наоборот. Кроме того, при доказательстве можно использовать диаграммы Эйлера-Венна. Для этого необходимо изобразить множества элементарных исходов, благоприятствующих левой и правой частям на разных картинках, и визуально убедиться, что они совпадают.
Покажем, например, что справедливо равенство:
.
Фигуры, заштрихованные на диаграммах (рис. 1.9), совпадают, значит:
.
Система (совокупность) случайных событий Â называется алгеброй случайных событий, если выполняются свойства:
1) ;
2) ;
3) ;
4) .
Таким образом, алгебра случайных событий – это множество случайных событий, содержащее достоверное событие и замкнутое относительно операций сложения и умножения.
Рис. 1.9. Доказательство тождества при помощи диаграмм Эйлера-Венна
Наиболее простой алгеброй случайных событий является множество, состоящее из двух событий: .
В дальнейшем везде будет использоваться алгебра случайных событий, которая является множеством всевозможных подмножеств из пространства элементарных событий (легко проверить, что все свойства в определении алгебры случайных событий выполняются для этого множества).
Утверждение. В алгебре с конечным числом элементов в пространстве элементарных исходов случайных событий.
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Комплексной системы оценки состояния охраны труда на производственном объекте (КСОТ-П): Цели и задачи Комплексной системы оценки состояния охраны труда и определению факторов рисков по охране труда. Оценка эффективности инструментов коммуникационной политики: Внешние коммуникации — обмен информацией между организацией и её внешней средой… История развития методов оптимизации: теорема Куна-Таккера, метод Лагранжа, роль выпуклости в оптимизации… Интересное: Мероприятия для защиты от морозного пучения грунтов: Инженерная защита от морозного (криогенного) пучения грунтов необходима для легких малоэтажных зданий и других сооружений… Уполаживание и террасирование склонов: Если глубина оврага более 5 м необходимо устройство берм. Варианты использования оврагов для градостроительных целей… Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 3 из 24Следующая ⇒
Советы по построению пространства элементарных исходов. Имейте в виду задачу, которую вы хотите решить — то случайное событие, вероятность которого вам необходимо найти, должно описываться с помощью указания элементарных исходов, приводящих к этому событию. На первых порах старайтесь вводить наиболее детальное описание опыта, – потом начнете понимать, в каких случаях можно, без ущерба для конечного результата, упростить модель. Между разными подходящими моделями предпочтительнее выглядит модель, в которой элементарные исходы симметричны и равновероятны. Очень удобно выбирать элементарные исходы в виде векторов (в смысле точек в пространстве), размерность которых равна количеству различных случайных факторов (источников) в случайном явлении, а координаты которых соответствуют различным вариантам значений этих факторов. Определения Подмножества Если пространство элементарных исходов определено, то появляется возможность описать любое событие, происшедшее в опыте, просто указав, какие элементарные исходы ему соответствуют. · Пример.3.5 Элементарные исходы, 5 вариант: числа очков на костях с различением игральных костей [(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),(2,2),…] –36 исходов. · Элементарный исход можно представить в виде · , · где i – число очков на первой кости, j – второй кости. · Тогда событие «на двух костях выпало в сумме 7 очков» можно представить в виде следующего подмножества элементарных исходов: ·
Заметим, что порядок перечисления элементарных исходов может быть произвольным. A = Пустое подмножество обозначим Так как пустое подмножество не содержит никаких элементарных исходов, в теории вероятностей оно обозначает невозможное событие. Множество всех элементарных событий W называется, естественно, достоверное событие. Элементарный исход как случайное событие представляет собой одноточечное подмножество. Операции над подмножествами Стандартные операции над подмножествами применяются в теории вероятностей и имеют вероятностную интерпретацию. Дополнение Дополнение до подмножества A — это подмножество т. е. дополнением к A является подмножество, включающее в себя все элементарные исходы, не содержащиеся в A. С точки зрения теории вероятностей подмножество A представляет событие, которое естественно назвать отрицание A или не-A. Объединение Объединением двух подмножеств A и B является подмножество Соответственно и интерпретация : произошло или A или B. Пересечение Пересечением двух подмножеств : A и B является подмножество Соответственно и интерпретация : и A и B произошли одновременно. Разность Разностью двух подмножеств A и B является подмножество Соответственно и интерпретация : A произошло, B — нет. Симметричная разность Симметричной разностью двух подмножеств A и B является подмножество Соответственно и интерпретация : произошло только одно из этих двух событий. ⇐ Предыдущая12345678910Следующая ⇒ Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни. Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого… Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой… Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства… |
НОУ ИНТУИТ | Лекция | Предварительные сведения
Аннотация: Необходимые сведения об основных принципах и формулах комбинаторики. Основные понятия элементарной теории вероятностей: пространство элементарных исходов, события и операции над ними
Ключевые слова: множества, перестановка, сочетания, Исход, конечные, пространство, место, лист, операции, Пустое множество, объединение множеств, пересечение, объединение
Элементы комбинаторики
Научимся подсчитывать число «шансов».
О числе шансов говорят, когда возможно несколько результатов
какого-либо действия (выбор карты из колоды, подбрасывание кубика или
монетки). Формулы комбинаторики позволяют посчитать число
способов проделать действие или число его возможных результатов.
Формулы комбинаторики позволяют посчитать число
способов проделать действие или число его возможных результатов.
Теорема о перемножении шансов. Основной принцип комбинаторики заключается в следующем: если первый элемент можно выбрать способами, а второй элемент — способами, то упорядоченную пару элементов можно составить способами.
Теорема 1. Пусть множество состоит из элементов, а множество — из элементов. Тогда можно образовать ровно пар взяв первый элемент из множества а второй — из множества .
Доказательство.
С элементом мы можем образовать пар: .
Столько же пар можно составить с элементом или с любым другим из элементов множества .
Таким образом, всего возможно пар, в которых первый элемент выбран из множества
а второй — из множества .
Урновые схемы. Есть урна (ящик), содержащая пронумерованных шаров. Мы выбираем из урны шаров; результат этого выбора — набор из шаров. Нас интересует, сколькими способами можно выбрать шаров из т. е. сколько различных результатов возможно.
На этот вопрос нельзя дать однозначный ответ, пока мы не знаем:
- как организован выбор;
- что понимать под различными результатами выбора.
Рассмотрим следующие возможные способы выбора.
- Выбор с возвращением: каждый вынутый шар возвращается в урну, каждый следующий шар выбирается из полной урны. В полученном наборе из номеров шаров могут встречаться одни и те же номера. intuit.ru/2010/edi»>Выбор без возвращения: вынутые шары в урну не возвращаются, и в полученном наборе не могут встречаться одни и те же номера.
Условимся, какие результаты выбора (какие наборы номеров шаров) мы будем считать различными. Есть ровно две возможности.
- Выбор с учетом порядка: два набора номеров шаров считаются различными, если они отличаются составом или порядком номеров. Так, наборы и считаются различными наборами.
- Выбор без учета порядка: два набора номеров шаров считаются различными, если они отличаются составом. Так, наборы и различны, а наборы и не различаются.
Количество результатов в урновых схемах. Подсчитаем, сколько возможно различных результатов
для каждой из четырех схем выбора: с возвращением или без возвращения,
и в каждом из этих случаев — с учетом порядка или без учета.
Выбор без возвращения и с учетом порядка
Теорема 2. Общее количество различных наборов при выборе элементов из без возвращения и с учетом порядка равняется
Число называется числом размещений из элементов по элементов, а сами результаты выбора — размещениями.
Доказательство. Первый шар можно выбрать способами. При любом выборе первого шара есть способ выбрать второй шар, при любом выборе первых двух шаров есть способа выбрать третий шар и т. д. Применяя последовательно теорему 1, получаем, что общее число возможных наборов из шаров равно произведению сомножителей . Здесь последний сомножитель есть число способов выбрать -й шар из оставшихся в урне шаров.
Следствие 1. В множестве из элементов возможно ровно ! перестановок
этих элементов.
Доказательство. Перестановка — результат выбора без возвращения и с учетом порядка элементов из . Их число равно !
Выбор без возвращения и без учета порядка
Теорема 3. Общее количество различных наборов при выборе элементов из без возвращения и без учета порядка равняется
Число называется числом сочетаний из элементов по элементов, а сами результаты выбора — сочетаниями.
Доказательство. Упорядочить различных номеров шаров можно ! способами. Поэтому из каждого сочетания можно перестановками образовать ! размещений. Следовательно, число наборов, порядок в которых не учитывается (сочетаний), в ! раз меньше числа наборов, отличающихся еще и порядком (размещений).
Выбор с возвращением и с учетом порядка
intuit.ru/2010/edi»>Теорема 4. Общее количество различных наборов при выборе элементов из с возвращением и с учетом порядка равняется .Доказательство. Первый шар можно выбрать способами. При каждом из этих способов второй шар можно выбрать также способами, и так раз. Общее число наборов равно .
Выбор с возвращением и без учета порядка. Рассмотрим урну с двумя пронумерованными шарами и перечислим результаты выбора двух шариков из этой урны при выборе с возвращением. Если учитывать порядок, то исходов получится четыре:
Если порядок не учитывать, то следует объявить два последних исхода одним и тем же результатом эксперимента. Исходов окажется три:
Видим, что в схеме выбора без учета порядка получилось три различных
результата, тогда как при выборе с учетом порядка различных результатов было
четыре. Ни каким делением на «число каких-нибудь перестановок»,
которое помогло избавиться от учета порядка при выборе без возвращения,
число 3 из числа 4 получить не удастся.
Ни каким делением на «число каких-нибудь перестановок»,
которое помогло избавиться от учета порядка при выборе без возвращения,
число 3 из числа 4 получить не удастся.
Теорема 5. Общее количество различных наборов при выборе элементов из с возвращением и без учета порядка равняется
Доказательство. Рассмотрим, чем отличаются друг от друга два разных результата такой схемы выбора. Нам не важен порядок следования номеров, т. е. мы учитываем только, сколько раз в нашем наборе из номеров шаров появился каждый номер. Поэтому результат выбора можно представить набором чисел , в котором — число появлений шара номер в наборе, . Два результата выбора с возвращением и без учета порядка различаются, если соответствующие им упорядоченные наборы не совпадают.
Представим себе другой эксперимент, имеющий точно такие же результаты,
и посчитаем их количество. Есть ящиков, в которых размещаются шаров.
Нас интересует только число шаров в каждом ящике.
Результатом эксперимента снова является набор
чисел ,
где равно числу шаров в ящике с номером .
Есть ящиков, в которых размещаются шаров.
Нас интересует только число шаров в каждом ящике.
Результатом эксперимента снова является набор
чисел ,
где равно числу шаров в ящике с номером .
А теперь изобразим результат такого размещения в виде схемы, в которой вертикальные линии обозначают перегородки между ящиками, а точки — находящиеся в ящиках шары:
Мы видим результат размещения девяти шаров по семи ящикам. Первый ящик содержит три шара, второй и шестой ящики пусты, третий ящик содержит один шар, в четвертом и пятом ящиках лежит по два шара. Переложим один шар из первого ящика во второй и изобразим таким же образом еще два результата размещения:
Видим, что все размещения можно получить, меняя между собой шары и перегородки или расставляя шаров на местах.
Число получается так: у ящиков есть ровно перегородка,
считая крайние, но из них перемещать можно лишь внутреннюю перегородку. Таким образом, имеется мест, которые
можно занять шарами либо внутренними перегородками. Перебрав все возможные
способы расставить шаров на этих местах,
переберем и все нужные размещения.
Осталось заметить, что по теореме 3 существует способов выбрать
места для шаров на местах.
Таким образом, имеется мест, которые
можно занять шарами либо внутренними перегородками. Перебрав все возможные
способы расставить шаров на этих местах,
переберем и все нужные размещения.
Осталось заметить, что по теореме 3 существует способов выбрать
места для шаров на местах.
События и операции над ними. Относительные частоты и их свойства
п. 1.2. События и операции над ними.
Относительные частоты и их свойства
Первичным понятием теории вероятностей, неопределяемым через другие понятия, является пространство элементарных исходов Ω. Обычно в качестве пространства элементарных исходов берутся единственно возможные неразложимые результаты эксперимента.
Пример
1. Предположим, что бросается симметричная монета. Тогда (герб и решка).
2. Игральная кость .
3. Бросаются две монеты .
4. Бросаются две игральных кости . Число элементарных исходов 36.
5. На [AB] числовой оси
w бросается наудачу точка.
На [AB] числовой оси
w бросается наудачу точка.
6. На [AB] бросаются две точки .
B
y
x
Определение. Событием называется произвольное подмножество А пространства элементарных исходов Ω. Те элементарные исходы, из которых состоит событие А, называются благоприятствующими событию А.
Говорят, что событие А произошло, если в результате эксперимента происходит элементарный исход wA, т.е. благоприятствующий событию А.
Рассмотрим пример 2. , –событие, состоящее в выпадении нечетного числа очков; –событие, состоящее в выпадении четного числа очков.
o Все пространство элементарных исходов Ω, если взять в качестве события, называют достоверным событием, поскольку оно происходит в любом эксперименте (всегда).
o
Пустое множество (т.е. множество, которое не содержит ни
одного элементарного исхода) называется невозможным событием, поскольку
оно никогда не происходит.
Все остальные события, кроме Ω и , называются случайными.
Операции над событиями.
0.1 Суммой событий А и В называется объединение этих множеств АB.
или .
–событие, которое происходит тогда и только тогда, когда происходит хотя бы одно из событий А или В.
0.2 Произведением событий А и В называется пересечение множеств А и В, т.е. АВ. Обозначается как АВ.
АВ–событие, когда А и В происходят одновременно.
и .
0.3 Разностью событий А и В называется разность множеств А\В.
А\В–событие, которое происходит <=>, когда происходит А и не происходит В.
и .
o События А и В называются несовместимыми, если . Если А и В несовместимы, то будем обозначать .
o Говорят, что событие А влечет событие В, если А является подмножеством В, т.е. (когда происходит А, происходит В).
.
o
Событие называется противоположным к событию А.
Пример 2. . происходит тогда, когда А не происходит.
o Говорят, что события Н1,Н2,…,Нnобразуют полную группу, если Н1+Н2+…+Нn=Ω (т.е. Н1, Н2, Нn–несовместимы, т.е. Нi Нj=, если i≠j).
Например, А и образуют полную группу: .
Предположим, что производится некоторый случайный эксперимент, результат которого описывается пространством Ω. Произведем N экспериментов. Пусть А—некоторое событие (), N(A)—число тех экспериментов, в которых произошло событие А.
Тогда число называется относительной частотой события А.
Свойства относительных частот.
Свойство 1. Относительная частота произвольного события А. .
Свойство 2. Относительная частота достоверного события равна 1. .
Свойство 3. (Аддитивность) Относительная частота суммы несовместимых событий
§2. Аксиомы теории вероятностей.
Аксиомы теории вероятностей.
Пусть Ω—пространство элементарных исходов. Предположим, что F—некоторый класс подмножеств Ω.
o Событие—это подмножество Ω, принадлежащее классу F. Любому ставится в соответствие действительное число P(A), называемое вероятностью А, так что при этом выполняется аксиомы:
Аксиома 1.
Аксиома 2. ,т.е. вероятность достоверного события равна 1.
Аксиома 3. (счетной аддитивности) Если и , то (для несовместимых событий).
§ 3 Дискретные пространства элементарных исходов.
Классическое определение вероятности.
o Бесконечное множество называется счетным, если элементы этого множества можно занумеровать числами натурального ряда (натуральными числами).
Все другие бесконечные множества называются несчетными. Примером несчетного множества может служить [а,b], счетного N.
o
Пространство элементарных исходов
называется дискретным, если оно конечно или счетно, т. е. или .
е. или .
Любому элементарному исходу ставится в соответствие число , так что при этом . Т.е.
o Вероятностью события А называется число .
Теория вероятности — Математика — Тесты
При решении этих задач сначала нужно определить, в чем состоит случайный эксперимент, какие у него элементарные исходы и убедиться, что они равновозможны.
Далее следует найти общее число элементарных событий .
Теперь нужно определить, какие элементарные события благоприятствуют интересующему нас событию , и найти их число .
Вероятность события найдём по формуле .
Задача 1.
Вася, Петя, Коля и Лёша бросили жребий — кому начинать игру. Найдитевероятность того, что начинать игру должен будет Петя.
Решение.
Случайный эксперимент — бросание жребия.
В этом эксперименте элементарным событием является участник, который выиграл жребий.
Перечислим возможные элементарные события:
(Вася), (Петя), (Коля), (Лёша).
Их будет будет , т.е. .
Жребий подразумевает, что все элементарные события равновозможны.
Событию = {жребий выиграл Петя} благоприятствует только одно элементарное событие (Петя). Поэтому .
Тогда .
Ответ: 0,25.
Задача 2.
Игральный кубик (кость) бросили один раз. Какова вероятность того, что выпало число очков, большее чем ?
Решение.
В этой задаче случайным экспериментом является бросание кубика. Элементарным исходом является число на выпавшей грани. Граней всего шесть.
Можно перечислить все элементарные исходы:
, , , , и .
Следовательно, .
Событию = {выпало больше чем 4} благоприятствуют два элементарных исхода: и . Поэтому .
Подразумевается, что кубик честный, следовательно, все элементарные события равновозможны. Поэтому
Ответ: .
Задача 3.
В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз.
Найдите вероятность того, что орел выпадет ровно один раз.
Решение.
Обозначим буквой О выпадение орла, а выпадение решки буквой Р. В приведённом эксперименте могут быть следующие элементарные исходы:
ОО, ОР, РО и РР.
Всего исходов , поэтому .
Событию = {выпал ровно один орел} благоприятствуют элементарных события ОР и РО, следовательно, .
Теперь можно найти вероятность того, что орёл выпадет ровно один раз .
Ответ: .
Задача 4.
В случайном эксперименте бросают два игральных кубика. Найдите вероятность того, что в сумме выпадет очков.
Решение.
Элементарным исходом в этом опыте является упорядоченная пара чисел. Первое число выпадает на первом кубике, а второе — на втором. В таких задачах множество элементарных исходов удобно представить в виде таблицы. В первой строке этой таблицы записываем возможный результат первого броска, а в первом столбце — возможный результат второго броска. Количество элементарных исходов .
Количество элементарных исходов .
1 | 2 | 3 | 4 | 5 | 6 | |
1 | (1;1) | (2;1) | (3;1) | (4;1) | (5;1) | (6;1) |
2 | (1;2) | (2;2) | (3;2) | (4;2) | (5;2) | (6;2) |
3 | (1;3) | (2;3) | (3;3) | (4;3) | (5;3) | (6;3) |
4 | (1;4) | (2;4) | (3;4) | (4;4) | (5;4) | (6;4) |
5 | (1;5) | (2;5) | (3;5) | (4;5) | (5;5) | (6;5) |
6 | (1;6) | (2;6) | (3;6) | (4;6) | (5;6) | (6;6) |
Напишем в каждой клетке таблицы элементарные исходы и закрасим клетки, где сумма равна (см. рис.). Таких клеток будет пять. Значит, событию = {сумма равна } благоприятствуют элементарных исходов, а, следовательно, . Поэтому вероятность того, что в сумме выпадет очков, можно найти по формуле .
рис.). Таких клеток будет пять. Значит, событию = {сумма равна } благоприятствуют элементарных исходов, а, следовательно, . Поэтому вероятность того, что в сумме выпадет очков, можно найти по формуле .
Ответ: .
Задача 5.
В случайном эксперименте монету бросили три раза. Какова вероятность того, что орел выпал ровно два раза?
Решение.
Обозначим буквой О выпадение орла, а буквой Р – выпадение решки. Элементарными исходами в данной задаче являются всевозможные тройки, составленные из букв О и Р. Запишем их все в таблицу:
Элементарный исход | Число орлов |
ООО | |
ООР | |
ОРО | |
ОРР | |
РОО | |
РОР | |
РРО | |
РРР |
Всего разных исходов получилось 8. Значит, .
Значит, .
Событию = {орел выпал ровно два раза} благоприятствуют элементарные события ООР, ОРО и РОО (они выделены в таблице зелёным цветом),поэтому .
Тогда
Ответ: .
Задача 6.
В соревнованиях по толканию ядра участвуют 4 спортсмена из Финляндии, 7 спортсменов из Дании, 9 спортсменов из Швеции и 5 — из Норвегии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Швеции.
Решение.
В этой задаче элементарным исходом является спортсмен, который выступает последним. Последним может оказаться любой. Всего спортсменов .
Событию = {последний из Швеции} благоприятствуют только исходов (это число спортсменов из Швеции). Следовательно, .
Вероятность того, что спортсмен, выступающий последним, будет из Швеции, найдём по формуле .
Ответ:
Задача 7.
В среднем из аккумуляторов, поступивших в продажу, неисправны. Найдите вероятность того, что один купленный аккумулятор окажется исправным.
Найдите вероятность того, что один купленный аккумулятор окажется исправным.
Решение.
1 способ.
Элементарным исходом в этой задаче является случайно выбранный аккумулятор. Всего аккумуляторов , поэтому .
Событию = {аккумулятор исправен} благоприятствуют 994 исхода, поскольку исправных аккумуляторов . Следовательно, .
Тогда .
2 способ.
Эту задачу можно решить с помощью формулы вероятности противоположного события = {аккумулятор неисправен}. Имеем .
Значит, .
Ответ: .
Задача 8
В чемпионате по гимнастике участвуют спортсменок: из России, из США, остальные — из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Китая.
Решение.
Элементарное событие — спортсменка, выступающая первой. По условию задачи все элементарные события равновозможны, поэтому .
Чтобы найти число элементарных событий, благоприятствующих событию = {первой выступает спортсменка из Китая}, подсчитаем число спортсменок из Китая:
.
Вероятность того, что спортсменка, выступающая первой, окажется из Китая найдём по формуле .
Ответ: .
Задача 9
В чемпионате мира участвуют команд. С помощью жребия их нужно разделить на четыре группы по четыре команды в каждой. В ящике вперемешку лежат карточки с номерами групп:
, , , , , , , , , , , , , , , .
Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется во второй группе?
Решение.
Пусть элементарный исход — это карточка, выбранная капитаном российской команды. Поскольку карточек , то . Событию = {команда России во второй группе} благоприятствуют четыре карточки с номером , то есть .
Тогда .
Ответ: .
Элементарные события (элементарные исходы) опыта — простейшие события, которыми может окончиться случайный опыт.
Сумма вероятностей всех элементарных событий опыта равна .
Вероятность события равна сумме вероятностей элементарных событий, благоприятствующих этому событию.
Объединение событий — событие, состоящее из элементарных исходов, благоприятствующих хотя бы одному из событий , .
Пересечение событий — событие, состоящие из элементарных исходов, благоприятствующих обоим событиям и .
Противоположное событие.
Событие , состоящее из тех и только тех элементарных исходов опыта, которые не входят в , называется противоположным событию .
Несовместные события — события, которые не наступают в одном опыте. Например, противоположные события несовместны.
Вероятности противоположных событий:
; .
Формула сложения вероятностей:
и = .
Формула сложения вероятностей для несовместных событий:
.
Задача 1.
Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна . Покупатель в магазине выбирает одну такую ручку. Найдите вероятность того, что эта ручка пишет хорошо.
Покупатель в магазине выбирает одну такую ручку. Найдите вероятность того, что эта ручка пишет хорошо.
Решение.
Определим событие = {выбранная ручка пишет хорошо}.
Тогда противоположное событие = {выбранная ручка пишет плохо}.
Из условия нам известна вероятность противоположного события: .
Используем формулу вероятности противоположного события:
.
Ответ: .
Задача 2.
На экзамене по геометрии школьнику достается один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Вписанная окружность», равна . Вероятность того, что это вопрос на тему «Параллелограмм», равна . Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Решение.
Определим события:
= {вопрос на тему «Вписанная окружность»},
= {вопрос на тему «Параллелограмм»}.
События и несовместны, так как по условию в списке нет вопросов, относящихся к этим двум темам одновременно.
Событие = {вопрос по одной из этих двух тем} является их объединением: .
Применим формулу сложения вероятностей несовместных событий:
.Ответ: .
Задача 3.
В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна . Вероятность того, что кофе закончится в обоих автоматах, равна . Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
Решение.
Определим события
= {кофе закончится в первом автомате},
= {кофе закончится во втором автомате}.
По условию задачи и .
По формуле сложения вероятностей найдем вероятность события
и = {кофе закончится хотя бы в одном из автоматов}:
.
Следовательно, вероятность противоположного события {кофе останется в обоих автоматах} равна
.
Ответ: .
Задача 4.
Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна . Найдите вероятность того, что биатлонист первые три раза попал в мишени, а последние два раза промахнулся. Результат округлите до сотых.
Вероятность попадания в мишень при одном выстреле равна . Найдите вероятность того, что биатлонист первые три раза попал в мишени, а последние два раза промахнулся. Результат округлите до сотых.
Решение.
В этой задаче предполагается, что результат каждого следующего выстрела не зависит от предыдущих. Поэтому события «попал при первом выстреле», «попал при втором выстреле» и т.д. независимы.
Вероятность каждого попадания равна . Значит, вероятность каждого промаха равна . Воспользуемся формулой умножения вероятностей независимых событий. Получаем, что последовательность
= {попал, попал, попал, промахнулся, промахнулся} имеет вероятность
=
= .
Ответ: .
Задача 5.
В магазине стоят два платежных автомата. Каждый из них может быть неисправен с вероятностью независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.
Решение.
В этой задаче также предполагается независимость работы автоматов.
Найдем вероятность противоположного события
= {оба автомата неисправны}.
Для этого используем формулу умножения вероятностей независимых событий:
.
Значит, вероятность события = {хотя бы один автомат исправен} равна .
Ответ: .
В следующих задачах для решения удобно использовать дерево вероятностей. В части задач дерево построено прямо в условии. В других задачах это дерево следует построить. Попробуйте решить с помощью дерева вероятностей также некоторые из предыдущих задач, например, задачи и .
Задача 1.
Павел Иванович совершает прогулку из точки по дорожкам парка. На каждой развилке он наудачу выбирает следующую дорожку, не возвращаясь обратно.
Схема дорожек показана на рисунке. Найдите вероятность того, что Павел Иванович попадет в точку .
Решение.
Схема дорожек представляет собой граф, а именно — дерево. Рёбра (ветви) дерева соответствуют дорожкам. Около каждого ребра напишем вероятность того, что Павел Иванович пройдет по соответствующей дорожке. Выбор пути на каждой развилке происходит наудачу, поэтому вероятность поровну делится между всеми возможностями. Предположим, что Павел Иванович пришел в вершину . Из неё выходит три ребра , и .Следовательно, вероятность того, что Павел Иванович выберет ребро , равна . Аналогично можно расставить все вероятности.
Выбор пути на каждой развилке происходит наудачу, поэтому вероятность поровну делится между всеми возможностями. Предположим, что Павел Иванович пришел в вершину . Из неё выходит три ребра , и .Следовательно, вероятность того, что Павел Иванович выберет ребро , равна . Аналогично можно расставить все вероятности.
Каждый маршрут из начальной точки в любую из конечных точек является элементарным событием в этом эксперименте. События здесь не равновозможные. Вероятность каждого элементарного события можно найти по правилу умножения.
Нам нужно найти вероятность элементарного события
= {Павел Иванович пришел в точку }.
Это событие состоит в том, что Павел Иванович прошел маршрутом . Вероятность находится умножением вероятностей вдоль ребер и : .
Ответ: .
Задача 2.
Павел Иванович совершает прогулку из точки А по дорожкам парка. На каждой развилке он наудачу выбирает следующую дорожку, не возвращаясь обратно. Схема дорожек показана на рисунке. Часть маршрутов приводит к поселку , другие — в поле или в болото . Найдите вероятность того, что Павел Иванович забредет в болото.
Схема дорожек показана на рисунке. Часть маршрутов приводит к поселку , другие — в поле или в болото . Найдите вероятность того, что Павел Иванович забредет в болото.
Решение.
В болото ведут три маршрута. Обозначим вершины на этих маршрутах и напишем на ребрах вдоль этих маршрутов соответствующие вероятности. Остальные маршруты не будем рассматривать.
Вероятность события {Павел Иванович попадет в болото}, равна =
= .
Ответ:
Задача 3.
В некотором эксперименте вероятность события равна . Если событие наступает, то вероятность события равна , а в противоположном случае вероятность события равна . Найдите вероятность события .
Решение.
В таких задачах удобно изобразить эксперимент графически деревом вероятностей. Отличие от предыдущих задач состоит в том, что вероятности на ребрах получаются не из равновозможности, а иначе.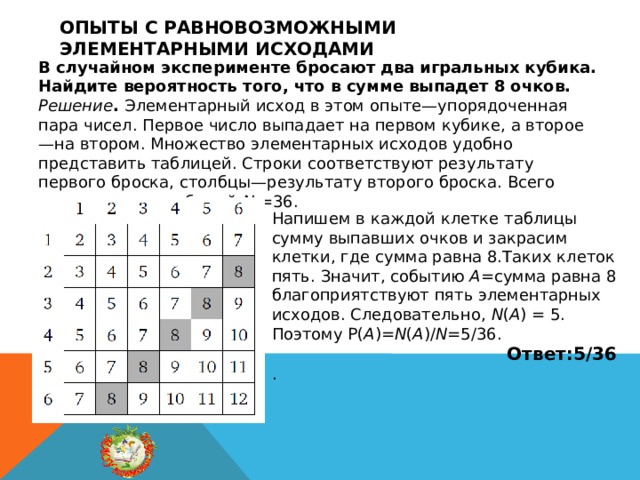
Весь эксперимент обозначим буквой (большая омега) и поставим точку около этой буквы — корень дерева, из которого ветви-ребра растут вниз. Из точки проведем ребро вниз-влево в точку . Событие имеет вероятность , поэтому подпишем у этого ребра вероятность . Противоположное событие А имеет вероятность . Проведем второе ребро в точку .
Если осуществилось событие , то событие по условию имеет вероятность . Поэтому из точки проведем ребро вниз-влево в точку и подпишем вероятность. Действуя так же и дальше, достроим все дерево (см. рис.).
Чтобы найти вероятность события , нужно выделить только те пути, которые ведут из корневой точки к событию . На рисунке эти пути яркие, а пути, не приводящие к изображены бледно. Выделенные пути и являются элементарными событиями, благоприятствующими событию .
Теперь нужно вычислить вероятности выделенных путей и сложить их. Пользуясь правилами умножения и сложения вероятностей, получаем:
=
= .
Ответ:
Задача 4.
Две фабрики одной фирмы выпускают одинаковые мобильные телефоны. Первая фабрика выпускает % всех телефонов этой марки, а вторая — остальные телефоны. Известно, что из всех телефонов, выпускаемых первой фабрикой, % имеют скрытые дефекты, а у выпускаемых второй фабрикой — %. Найдите вероятность того, что купленный в магазине телефон этой марки имеет скрытый дефект.
Решение.
Введем обозначения для событий:
= {телефон выпущен на первой фабрике},
= {телефон выпущен на второй фабрике},
= {телефон имеет скрытый дефект}.
По условию задачи составим дерево и найдём необходимые вероятности.
.
Ответ:
Задача 4.
Две фабрики одной фирмы выпускают одинаковые мобильные телефоны. Первая фабрика выпускает % всех телефонов этой марки, а вторая — остальные телефоны. Известно, что из всех телефонов, выпускаемых первой фабрикой, % имеют скрытые дефекты, а у выпускаемых второй фабрикой — %. Найдите вероятность того, что купленный в магазине телефон этой марки имеет скрытый дефект.
Найдите вероятность того, что купленный в магазине телефон этой марки имеет скрытый дефект.
Решение.
Введем обозначения для событий:
= {телефон выпущен на первой фабрике},
= {телефон выпущен на второй фабрике},
= {телефон имеет скрытый дефект}.
По условию задачи составим дерево и найдём необходимые вероятности.
.Ответ:
Элементарная Вероятность — СДЕЛАЙТЕ МЕНЯ АНАЛИТИКОМ
Вероятность сама по себе большая тема и здесь невозможно обсудить все и вся. В этом учебном пособии затронуты все соответствующие основы, которые дадут вам концептуальную основу, необходимую для анализа данных и логической статистики.
Случайность:В случайном процессе мы знаем, какие результаты могут произойти, но мы не знаем, какой конкретный результат произойдет.
Пример:
Подбрасывание монеты, бросание игральных костей, режим воспроизведения в случайном порядке на музыкальном проигрывателе, фондовая биржа и т. д.
д.
Если вы подбрасываете монету, вы знаете, что может быть только два исхода, но мы не знаем, какой именно. С другой стороны, в режиме воспроизведения в случайном порядке на музыкальном проигрывателе вы знаете, какие песни вы сохранили в своем музыкальном проигрывателе. Итак, вы знаете, каков возможный результат, и ваша следующая песня будет чем-то из всей вашей музыкальной библиотеки, но вы не знаете, какая песня будет играть следующей. Иногда может быть полезно смоделировать процесс как случайный, хотя на самом деле он не является случайным. Пример — фондовый рынок.
Для описания вероятности события используется следующая запись: P(A) = Вероятность события A . Есть несколько возможных интерпретаций вероятности, но они (почти) полностью согласуются с математическими правилами, которым должна следовать вероятность 0 <= P(A) <=1. Это означает, что вероятность и событие всегда находятся между 0 и 1.
Традиционная интерпретация вероятности — это относительная частота. Это называется частотной интерпретацией.
Это называется частотной интерпретацией.
Вероятность исхода — это доля случаев, когда исход возник бы, если бы мы наблюдали случайный процесс бесконечное число раз. Альтернативной интерпретацией является байесовская интерпретация.
Байесовская интерпретация вероятности:Байесовская интерпретация вероятности как субъективная степень уверенности. На одно и то же событие два разных человека могут иметь разные точки зрения и поэтому присваивать ему разные вероятности. Эта интерпретация позволяет интегрировать предшествующую информацию в структуру логического вывода. В значительной степени популяризирован революционным прогрессом в вычислительных технологиях и методах за последние двадцать лет.
Закон больших чисел: Закон больших чисел гласит, что по мере сбора большего количества наблюдений доля событий с определенным результатом сходится к вероятности этого результата. Например, если вы бросите кубик 6 раз, нет гарантии, что выпадет хотя бы одна пятерка. Но если вы бросите кости 600 раз или 6000 раз. Тогда вы должны увидеть как минимум 1/6 раз, чтобы получить пять.
Например, если вы бросите кубик 6 раз, нет гарантии, что выпадет хотя бы одна пятерка. Но если вы бросите кости 600 раз или 6000 раз. Тогда вы должны увидеть как минимум 1/6 раз, чтобы получить пять.
Непересекающиеся события не могут происходить одновременно. Синоним для этого является взаимоисключающим.
- Результат одного подбрасывания монеты не может быть орлом и решкой одновременно.
- Учащийся не может одновременно провалить и сдать класс.
- Одна карта, взятая из колоды, не может быть тузом и дамой.
- Событие не объединяется, поэтому используется термин «непересекающийся».
- Для непересекающихся событий P(A и B) = 0
Одновременно может произойти непересекающееся событие. Например, студент может получить пятерку по статистике и экономике в одном семестре. P(A и B) не равно 0,
Объединение непересекающихся событий: Какова вероятность вытянуть валета или тройку из хорошо перетасованной полной колоды карт.
P( J или 3) = P(J) + P(3) = 4/52 + 4/52 = 0,154
Для непересекающихся событий A и B, P(A или B) = P(A) + P(B)
Объединение непересекающихся событий:Какова вероятность вытянуть валета или красную карту из хорошо перетасованной полной колоды карт. Чем это отличается от предыдущего вопроса. Вот ситуация ниже.
Здесь у нас есть 4 валета и 26 красных карт в колоде, и обратите внимание, что есть перекрытие. Два красных валета соответствуют обоим критериям. Итак, нам нужно учитывать это перекрытие, поскольку мы хотим дважды подсчитать его при расчете вероятности.
P(J или красный) = P(A) + P(красный) -P(J и красный) = 4/52 + 26/52 -2/52 = 0,538
Для непересекающихся событий A и B, P(A или B) = P(A) + P(B) -P(A и B)
Общее правило сложения:P(A или B) = P(A) + P(B) -P(A и B)
Обратите внимание, что когда A и B не пересекаются, P(A и B) = 0, поэтому формула упрощается до P(A или B)= P(A) + P(B)
Пространство выборки: Пространство выборки представляет собой совокупность всех возможных результатов следа. Например, у пары двое детей, какова выборка пола этих малышей. Предположим, что пол может быть только мужским или женским.
Например, у пары двое детей, какова выборка пола этих малышей. Предположим, что пол может быть только мужским или женским.
{MM, FF, FM, MF } — Пример места для секса двоих детей на пару.
Вторым примером может быть: вы подбрасываете монету два раза, какова будет площадь выборки? Это будет
{HH, TT, HT, TH } . Так, как результат может случиться равновероятным. у нас есть 25% шанс, что каждый результат может произойти. Распределение вероятностей перечисляет все возможные результаты в выборочном пространстве и вероятности, с которыми они происходят.
Обратите внимание, что это распределение вероятностей для дискретных событий. В следующем разделе вы получите представление о распределении вероятностей непрерывной переменной. Распределение вероятностей следует трем основным правилам.
Правила распределения вероятностей:- Перечисленные события должны быть непересекающимися.
- Каждая вероятность должна быть между 0 и 1
- Сумма вероятностей должна быть равна 1.

Дополнительные события — это два взаимоисключающих события, вероятность которых в сумме равна 1.
Обратите внимание, что дополнительные и непересекающиеся события — это не одно и то же. Потому что сумма вероятностей двух непересекающихся исходов не обязательно равна единице. Но сумма вероятностей двух дополнительных исходов всегда составляет в сумме 1,9.0003
Независимое событие:Событие является независимым, если его исход не зависит от предыдущих исходов. Два процесса независимы, если знание результата одного не дает полезной информации о результате другого. Допустим, вы подбрасываете монету 10 раз, и каждый раз она падает решкой. Как вы думаете, какова вероятность того, что при следующем броске выпадет еще одна голова? Вероятность по-прежнему 50%.
P( H на 11 м броске) = (PH на 10 th toss) =0.5
С другой стороны, вы можете думать, что независимое событие занимает меньше памяти. Он не помнит, что было в прошлом.
Он не помнит, что было в прошлом.
С другой стороны, если вы берете карту из колоды и в 1 st розыгрыше вы получаете J . Теперь в 2 -м -м тираже вероятность J, т.е. P(J) = 3/51. Поскольку вы уже вытащили карту, теперь у нас 52-1=51 карта, и теперь число J будет 4-1=3. До розыгрыша 1 st вероятность выпадения J была 4/52, но в конце розыгрыша она составляет 3/51. Итак, это пример зависимого события.
Проверка на независимость:Если вероятность A при данном B равна вероятности A, то A и B являются независимыми событиями. Что в основном говорит нам, что знание B ничего не говорит об A.
P (A|B) =P(A), тогда A и B независимы.
Правило умножения для независимых событий:Правила произведения для независимых событий гласят: если A и B независимы, то вероятность того, что A и B произойдут, является просто произведением их вероятности.
Если A и B независимы, то P( A и B) = P(A) * P(B)
Если вы подбросите монету дважды, какова вероятность того, что выпадет две решки подряд?
P (Две решки подряд) = P( T на 1-м -м -м броске) * P( T на 2-м -м -м броске) = P(0,5) * P(0,5) =0,25
Если A1 , A2, A3,………AK независимы, P(A1 и A2 и A3…. .Ak)= P(A1)*P(A2)*P(A3)*…..*P(AK)
.Ak)= P(A1)*P(A2)*P(A3)*…..*P(AK)
Название исследования «ПОНИМАНИЕ ПОДРОСТКОВ СОЦИАЛЬНОГО КЛАССА» посвящено изучению представлений подростков об их социальном классе. Выборка состоит из 48 представителей рабочего класса, 50 представителей высшего среднего класса в возрасте 16 лет.
Исследование было разработано следующим образом:
- «Объективное» отнесение к социальному классу на основе самооценки занятий и образования обоих родителей и дохода домохозяйства.
- «субъективная» ассоциация на основе вопросов опроса
Вот краткое изложение исследования в виде таблицы непредвиденных обстоятельств.
Какова вероятность того, что объективное положение учащегося в социальном классе выше среднего? Если вы видите в таблице объективный столбец высшего среднего класса, он показывает всего 50 учеников, принадлежащих к этой категории. Таким образом, вероятность будет P (объективный верхний средний класс) 50/9. 8 -0,51 . Термин «маргинальная вероятность» происходит от того факта, что подсчет, который мы используем, исходит из поля таблицы непредвиденных обстоятельств. Здесь 50 и 98 взяты из итогового столбца, который является границей этой таблицы непредвиденных обстоятельств.
8 -0,51 . Термин «маргинальная вероятность» происходит от того факта, что подсчет, который мы используем, исходит из поля таблицы непредвиденных обстоятельств. Здесь 50 и 98 взяты из итогового столбца, который является границей этой таблицы непредвиденных обстоятельств.
Какова вероятность того, что и объективная позиция учащегося, и его субъективная идентичность принадлежат к верхнему среднему классу?
P (объективный верхний средний класс и субъективный верхний средний класс) = 37/98 = 0,38. См. рисунок выше, отмеченный кружком. Важным термином в совместной вероятности является И. Здесь рассматриваются студенты, которые находятся на пересечении двух интересующих событий.
Условная вероятность:Какова вероятность того, что студент, который объективно принадлежит к рабочему классу, относится к верхушке среднего класса?
P(субъективная высшая буржуазия | объективный рабочий класс) = 8/48 =0,17
Здесь важно отметить вертикальную черту, которая называется данностью, которая разделяет то, что мы ищем, и то, что мы знаем как истинное. студенты. Это называется условным, потому что 1 st мы обусловили только рабочий класс, а затем вероятность рассчитывается на основе подсчета только в этом столбце.
студенты. Это называется условным, потому что 1 st мы обусловили только рабочий класс, а затем вероятность рассчитывается на основе подсчета только в этом столбце.
Формально мы вычисляем условную вероятность на основе теоремы Байеса.
P(A|B) = P(A и B) / P(B)
Здесь объединенная вероятность в числителе и то, что мы определили в знаменателе. Рассмотрим тот же вопрос, упомянутый в разделе условной вероятности, и рассчитайте вероятность, используя теорему Байеса.
P (субъективный верхний средний класс | объективный рабочий класс) = P (субъективный верхний средний класс и объективный рабочий класс) / P (объективный рабочий класс) = (8/98) / (48/98) = 8/48 = 0,17 ( мы получаем тот же ответ, что и ранее. Мы уже пришли к тому же ответу, просто рассмотрев таблицу непредвиденных обстоятельств. Но если у нас нет подсчетов, аккуратно организованных в таблице, тогда с помощью теоремы Байеса вычисление условной вероятности будет быть намного более интуитивным
Предположим, что в карточной игре игроку нужно взять две карты одной масти, чтобы выиграть. Из 52 карт по 13 карт каждой масти. Предположим, что сначала игрок рисует сердце. Теперь игрок хочет нарисовать второе сердце. Поскольку одна черва уже выбрана, в колоде из 51 карты осталось 12 червей. Таким образом, условная вероятность P(вытянуть второе сердце|первая карта сердце) = 12/51.
Из 52 карт по 13 карт каждой масти. Предположим, что сначала игрок рисует сердце. Теперь игрок хочет нарисовать второе сердце. Поскольку одна черва уже выбрана, в колоде из 51 карты осталось 12 червей. Таким образом, условная вероятность P(вытянуть второе сердце|первая карта сердце) = 12/51.
Предположим, человек, поступающий в колледж, определяет, что у него есть 80% шансов быть принятым, и он знает, что общежитие будет предоставлено только 60% всех принятых студентов. Шанс поступления студента в общежитие определяется коэффициентом 9.0003
P(Принято и общежитие) = P(Общежитие|Принято)P(Принято) = (0,60)*(0,80) = 0,48.
Общее Правило произведения:Выше было показано, что правило произведения для независимых событий будет P(A и B) = P(A) * P(B), если A и B независимы. Если они не преднамеренны, то совместная вероятность должна быть рассчитана несколько иначе. Поскольку в теореме Байеса нет условия независимости, мы можем просто переформулировать теорему Байеса, чтобы получить совместную вероятность P(A и B) как произведение условной вероятности P(A|B) на вероятность P(b)
Общее правило произведения: P(A и B) = P(A|B) * P(B)
Здесь мы перемешиваем теорему Байеса, чтобы получить новое правило для совместной вероятности. Рассмотрим приведенный ниже пример.
Рассмотрим приведенный ниже пример.
Предположим, человек, поступающий в колледж, определяет, что у него есть 80% шансов быть принятым, и он знает, что общежитие будет предоставлено только 60% всех принятых студентов. Вероятность того, что студент будет принят и получит общежитие, определяется как
P(Принято и общежитие) = P(Общежитие|Принято)P(Принято) = (0,60)*(0,80) = 0,48.
Независимость и условная вероятность:В общем случае, если P(A|B) = P(A), то события A и B называются независимыми.
Концептуально предоставление B ничего не говорит нам об A
Математически, если события A и B независимы, P(A и B) = P(A) * P(B). Тогда
P(A|B) = P( A и B) / P(B) = P(A)*P(B) / P(B) = P(A)
Ранее мы предложили правила, что P (A | B) = P(A) Теперь, используя теорему Байеса, мы можем математически доказать, почему это так.
Деревья вероятностей: Деревья вероятностей очень важны, когда P (A | B) уже задано для вопроса, а затем они запрашивают P (B | A).
В вашем почтовом ящике 100 писем. 60 спам, 40 нет. Из 60 спам-писем 35 содержат слово «бесплатно». Из остальных 3 содержат слово «бесплатно». Если и письмо содержит слово «бесплатно», какова вероятность того, что это спам?
Пытаемся узнать P (Спам | «бесплатно»). Сначала посмотрите на картинку ниже, чтобы понять, как организовать их в дерево вероятностей.
Поскольку нас интересует только слово «бесплатно», то 35 из папки со спамом и 3 из папки без спама. Всего слов, содержащих слово «бесплатно», 35+3=38.
P ( Спам | «бесплатно») = 35 / (35+3) = 35/38 = 0,92
Здесь мы неявно использовали теорему Байеса. Числитель имеет совместную вероятность, а знаменатель имеет предельную вероятность того, что мы обуславливаем словом «бесплатно».
Рассмотрим другой пример:
По состоянию на 2009 год в Свазиленде была самая высокая распространенность ВИЧ в мире. 25,9 % населения этой страны инфицированы ВИЧ. ИФА – один из первых и наиболее точных тестов на ВИЧ. Для тех, кто является носителем ВИЧ, точность теста ELISA составляет 99,7%. Для тех, кто не является носителем ВИЧ, точность теста составляет 92,6%. Если человек из Свазиленда дал положительный результат, какова вероятность того, что он является носителем ВИЧ?
Для тех, кто является носителем ВИЧ, точность теста ELISA составляет 99,7%. Для тех, кто не является носителем ВИЧ, точность теста составляет 92,6%. Если человек из Свазиленда дал положительный результат, какова вероятность того, что он является носителем ВИЧ?
P (ВИЧ) = 0,259
P (+ | ВИЧ) = 0,997 и P (– | ВИЧ) = 0,926
Теперь найдите P (ВИЧ | +) = ?
Итак, здесь условная вероятность была задана обратным образом относительно данной вероятности, т. е. P (+ | ВИЧ) = 0,997. Мы должны следовать древовидной схеме.
Использование процесса опроса в начальной школе для улучшения результатов обучения
Образовательный фонд Джорджа Лукаса
EdutopiaEdutopia
Поиск
Совместная работа учителей для оценки учителей на ранних этапах
03 для лучшего удовлетворения потребностей всех учащихся.
Аннетт Перес
25 июля 2022 г.
SolStock / iStock
Учителя начальных классов находятся на переднем крае, когда дело доходит до учета потребностей каждого учащегося, чтобы не только гарантировать, что они соответствуют ежегодным контрольным показателям, чтобы перейти к в следующий класс, но также убедитесь, что они станут учениками на всю жизнь. Процесс исследования — это инструмент, который развивает мастерство учителя и фокусирует внимание на достижимой цели — положительных результатах учащихся.
Процесс исследования — это инструмент, который развивает мастерство учителя и фокусирует внимание на достижимой цели — положительных результатах учащихся.
По мере того, как база знаний учителя расширяется для достижения положительных результатов учащихся, учитель берет на себя руководящую роль в школе, чтобы «двигать систему» для удовлетворения потребностей учащихся, пересматривая планы уроков и разделы или выступая за услуги и ресурсы.
Шаг 1. Постановка целей и теория действий
Разработка целей и теории действий: В начале учебного года учителя оценивают учащихся по английскому языку (ELA) и математике. Основываясь на этих оценках, учителя решают, на чем (английском языке или математике) сосредоточить внимание. После того, как они выбрали фокус, учителя разрабатывают цели SMART и теорию действий, которые объясняют изменения, которые они внесут для улучшения преподавания и обучения.
Определить учащихся: Учителя затем выбирают учащихся, которые будут участвовать в процессе запроса, как правило, тех, кто набрал в нижней трети оценки. Отслеживание студентов жизненно важно для расследования, поскольку выбранные студенты будут в центре внимания стратегий.
Отслеживание студентов жизненно важно для расследования, поскольку выбранные студенты будут в центре внимания стратегий.
Шаг 2. Внедрение протоколов
«Уведомление и удивление»: Протокол «Уведомление и удивление», который мы используем в моей школе, основан на книге Дэниела Р. Венейблса «Практика аутентичных ПЛК» . Протокол «Уведомление и удивление» позволяет учителям объективно оценивать работу учащихся. Учителя встречаются еженедельно в течение циклов продолжительностью от шести до восьми недель, каждый из которых приносит на собрание работу своей целевой группы учеников. Учителя прикрепляют рабочий лист «Уведомление и чудо» к работам каждого учащегося, а затем ходят по классу и пишут в рабочих листах учащихся (по 5 минут на каждого учащегося):
- Я заметил, что…
- Интересно, почему, если, как, если…
- Какие дополнительные данные необходимы, например данные о посещаемости учащегося, поскольку это может повлиять на успеваемость учащегося?
- Следующие шаги должны быть?
После того, как каждый учитель написал в рабочем листе каждого учащегося, учитель собирает работу и просматривает комментарии, что занимает около 15 минут. Затем учителя по очереди задают уточняющие вопросы, например, работал ли учащийся самостоятельно или в группе при выполнении задания, или учащемуся требовалась помощь в выполнении задания со стороны учителя или сокурсника? Затем учителя переходят к следующему протоколу.
Затем учителя по очереди задают уточняющие вопросы, например, работал ли учащийся самостоятельно или в группе при выполнении задания, или учащемуся требовалась помощь в выполнении задания со стороны учителя или сокурсника? Затем учителя переходят к следующему протоколу.
Стратегии преподавания: Рабочий лист стратегий преподавания — это рабочий лист, который я разработал для своей школы и который документирует методы, которые мы используем для исследования. Он состоит из двух частей:
- После того, как учителя завершили протокол «Уведомление и удивление», они собирают комментарии и обсуждают стратегию, которую они будут применять в своем классе, например, уроки в малых группах, конференции, дифференцированные рабочие листы. Учителя получают предложения от других учителей в команде и могут использовать эти предложения.
- После того, как учителя внедрили стратегию, они анализируют результаты. Это сработало? Почему или почему нет?
Затем учителя возвращают свои размышления команде и делятся результатами.
Настройка плана урока: Мы адаптировали протокол настройки, разработанный Джозефом Макдональдом и Дэвидом Алленом, для включения межклассных посещений группой учителей. Учителя обеспечивают обратную связь по реализации стратегии и дают друг другу обратную связь, что приводит к «настройке» плана урока.
В моей школе учителя делятся планами уроков, поэтому полезно увидеть стратегию в действии, а не слушать об уроке. Учителя в классе работают в команде и делятся уроками для согласованности между классами. Конечно, мы включаем дифференциацию в уроки для наших учеников с ограниченными возможностями.
Шаг 3. Перемещение системы
Выполнение шагов один и два приводит к тому, что учителя делают то, что я называю «перемещением системы», подстраивая и обновляя планы уроков, чтобы они лучше соответствовали потребностям учащихся. Учителя пересматривают цель после того, как они проводят следующий набор оценок, и отслеживают часть запроса учащихся, чтобы увидеть, продемонстрировали ли они положительное улучшение.
Если процесс опроса оказывает положительное влияние на обучение учащихся на основе цикла опроса, команда учителей разрабатывает новый фокус исследования, создавая новую цель и цикл опроса. Если процесс опроса не влияет на обучение учащихся на основе данных, команда пересматривает цель опроса и определяет, нужно ли им скорректировать цель и продолжить другой цикл опроса.
Я твердо верю в то, что все мы руководим с той позиции, которую занимаем, и в результате процесса запроса учителя могут взять на себя роль лидера. Процесс запроса дает учителям право голоса в удовлетворении потребностей учащихся на основе данных. И когда учителя перемещают систему для удовлетворения потребностей учащихся, это оказывает большое влияние на их образовательный опыт.
Поделиться этой историей
, поданные в соответствии с
- Учительский Collaboration
- Оценка
- K-201 Первичный
- 3-5.
 период в первый раз (En español)
период в первый раз (En español)Кристина Нгуен
Впервые в Austin ISD мы даем учителям начальных классов больше времени на совместное планирование и подготовку в так называемых сообществах профессионального обучения на уровне класса.
Почему это важно : Успеваемость учащихся не только резко упала во время пандемии после многих лет застоя, но и увеличился разрыв в успеваемости.
Цифрами : Данные по элементарному чтению до пандемии показывают, что успеваемость учащихся оставалась на прежнем уровне и колебалась в пределах 51–53%, что соответствует стандартам чтения на уровне класса в 2017–2019 годах.
По данным начала года оценка роста MAP, 40% учащихся находятся на уровне класса в чтении.
В настоящее время существует разрыв в 37% между экономически неблагополучными учащимися (19%) и не экономически неблагополучными (56%).
Что они говорят : «Если мы хотим получить другие результаты, мы должны делать что-то по-другому», — сказала главный академический директор Элизабет Касас.

Как мы туда доберемся : У классных учителей будет дополнительное время для планирования и сотрудничества с коллегами, пока учащиеся будут заниматься по основным предметам.
Мы предлагаем выделить 15-20 минут занятий для здоровья, W.O.W., время вне расписания классных учителей и объединить их в 45-минутный блок физкультуры каждый день.
Углубление : В соответствии с этим предложением будет выделено 6 миллионов долларов США для найма дополнительных основных учителей, в том числе помощников учителей для классов физкультуры, в которых теперь будет соотношение учеников и учителей 1:45, что соответствует требованиям штата. закон и общий в других школьных округах области.
Да, но: Это все еще предложение на ранней стадии. Шеф Касас представил информацию учителям музыки, искусства и физкультуры, а также библиотекарям и консультантам в среду днем и пригласил сотрудников помочь сгенерировать идеи, возможные потребности и предложить обучение.

Итог: Руководители кампуса могут гибко подходить к расписанию и работать с руководителями центрального офиса над разработкой творческих решений, включая поиск способов добавления дополнительных произведений искусства и музыки в неделю.
Погрузитесь глубже: Ознакомьтесь с часто задаваемыми вопросами об изменениях периода планирования.
Por primera vez en el Austin ISD, les estamos dando a los maestros de primaria más tiempo de planificación y preparación colaborativa en las que se denominan comunidades de aprendizaje profesional por grado.
Por qué es Importante: Los resultsados académicos de los estudiantes no solo empeoraron marcadamente durante la pandemia después de años de estancamiento, sino que las brechas en el rendimiento se han ensanchado.
- Este tiempo para planificar y colaborar con colegas ayudará a los maestros a abordar estas brechas al Individualizar el aprendizaje para cada estudiante.

Según las cifras : Los datos de la lectura en primaria antes de la pandemia muestran que el rendimiento estudiantil estaba estancado y rondando entre un 51-53% de estudiantes que cumplían con los del 7 de 19 estándares de lectura
- Los estudiantes con desventaja económica estaban retrasados en aproximadamente 17%: entre 33% y 36% cumplían con los estándares de lectura del grado antes de la pandemia.
- Según la Evaluación MAP Growth de principios de año, el 40% de los estudiantes están al nivel de su grado en lectura.
- Ahora hay una brecha de 37% entre los estudiantes con desventaja económica (19%) y aquellos sin desventaja económica (56%).
Lo que están diciendo : «Si queremos obtener diferentes resultsados, tenemos que hacer las cosas de manera diferente», директор генерального академического директора Элизабет Касас.

Cómo llegaremos ahí: Лос-маэстрос с салонами де clases tendrían tiempo adicional para planificar y colaborar con colegas mientras los estudiantes están en clases de áreas esenciales.
- Estamos proponiendo eliminar los 15–20 minutos de Ejercitando para el Bienestar (W.O.W., por sus siglas en inglés) de los horarios de los maestros con Salons de clases y agregarlos tosica un bloque de Educa 45 minutos диас.
- Las clases Arte y Música serían un bloque semanal de una hora para Allowirles a lo estudiantes profundizar más en sus proyectos.
- Esto también eliminaría la necesidad de maestros de Educación Física itinerantes.
Profundizando : Según esta propuesta, habría una contratar de $6millones para contratar más maestros de áreas esenciales, incluyendo asistentes de maestro para las clases de Educación Física, que ahora tentrán de una proporcióntesn cual cumple con la ley estatal y es común en otros distritos escolares del área.

Sí, пер.. . esto todavía es una propuesta en su etapa inicial. La Directora Casas les Presentó la información los maestros de Música, Arte y Educación Física, así como a los bibliotecarios y consejeros, el miércoles en la tarde e invitó al personal ayudar a generar идеи, posibles necesidades y sugerencias de capacitaciones.
В заключении : Лос-директора escolares pueden ser flexibles con los horarios y trabajar con los lideres de las oficinas Centrales para crear soluciones creativas, incluyendo encontrar maneras de agregar más Arte y Música a la semana.
Lea nuestras preguntas frecuentes sobre los cambios en lo periodos de planificación.
Как найти вероятность исхода
Все математические ресурсы начального уровня SSAT
12 диагностических тестов 526 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 4 Следующая →
SSAT Elementary Level Math Help » Анализ данных и вероятность » Вероятность » Результаты » Как найти вероятность исхода
На каждой из десяти карт напечатан номер.
 На пяти напечатана 1, на трех — 2, а на двух — 3. Карты перемешиваются и сдается карта. Какова вероятность того, что карта не будет 3?
На пяти напечатана 1, на трех — 2, а на двух — 3. Карты перемешиваются и сдается карта. Какова вероятность того, что карта не будет 3?Возможные ответы:
Правильный ответ:
Объяснение:
Всего десять карт, и восемь карт не являются тройками. Таким образом, вероятность вытянуть тройку
Сообщить об ошибке
Если в банке 2 синих и 18 красных шариков, какова вероятность того, что Джефф выберет красный шарик?
Возможные ответы:
Правильный ответ:
Объяснение:
Сначала добавьте общее количество шариков, которое равно . Есть 18 красных шариков, поэтому вы устанавливаете дробь .
Если упростить, разделив числитель и знаменатель на 2, получится .

Сообщить об ошибке
Фокусник держит в сумке 3 зеленых, 4 красных и 7 синих шаров. Какова вероятность того, что из мешка вынут красный шар?
Возможные ответы:
Правильный ответ:
Объяснение:
Вероятность = общее количество возможных результатов/выборочное пространство.
=
=Сообщить об ошибке
Найти вероятность исхода. Выразите результат в виде дроби, приведенной к наименьшему значению.
Мистер Томас отправился на автомобильную стоянку, чтобы купить новую машину. Из 68 автомобилей на лоте 22 были черными, 16 серебристыми, 8 белыми, 12 синими и 10 красными. Какова вероятность того, что мистер Томас купит синюю машину?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти вероятность исхода, составим дробь:
Так как всего 12 синих машин (часть) из 68 (всего возможных), то дробь выглядит так:
Если уменьшить дробь на 4 (поскольку числитель и знаменатель делятся на 4, что дает 4 GCF (наибольший общий множитель), то получится:
Сообщить об ошибке
Мешок шариков содержит зеленые шарики, синие шарики и красные шарики.

Если шарики вынимаются из мешка при каждом извлечении, какое максимальное количество выниманий может произойти без извлечения красного шарика?
Возможные ответы:
Правильный ответ: 6
0 3 Объяснение:
В мешке есть зеленые и красные шарики. Если сложить эти суммы, в мешке появятся шарики не красного цвета. Если бы все они были вытащены до любого красного шарика, это потребовало бы розыгрыша по шарикам за розыгрыш (). Следовательно, можно рисовать сколь угодно раз, не рисуя красный шарик.
Сообщить об ошибке
У Майки есть коробка с печеньками. У него есть 6 шоколадных печений, 4 сахарных печенья и 2 овсяных печенья с изюмом. Каков шанс, что Майки достанет из коробки сахарное печенье?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти вероятность того, что из мешка с печеньем вынут сахарное печенье, нам нужно составить такую дробь:
Задача говорит нам, что у Майки есть 4 сахарных печенья, поэтому мы можем поставить их на первое место в дроби.
 Общее количество печенья равно 6 шоколадным печеньям + 4 сахарным печеньям + 2 овсяным печеньям с изюмом, что дает нам сумму 12 (которое идет в нижней части дроби). Это дает Майки шанс выбрать сахарное печенье!
Общее количество печенья равно 6 шоколадным печеньям + 4 сахарным печеньям + 2 овсяным печеньям с изюмом, что дает нам сумму 12 (которое идет в нижней части дроби). Это дает Майки шанс выбрать сахарное печенье!Сообщить об ошибке
У Софии есть пицца с 8 кусочками. 4 ломтика пепперони, 3 ломтика грибов и 1 ломтик оливок. Если София случайным образом выберет кусок пиццы, чтобы съесть его, какова вероятность того, что на кусочке пиццы есть грибы?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти вероятность того, что кусок гриба будет взят из пиццы, мы должны составить такую дробь:
Задача говорит нам, что у нас есть 3 кусочка гриба, поэтому мы можем положить его сверху. фракции. Задача также говорит нам, что всего у нас 8 кусочков пиццы, так что это может оказаться в нижней части дроби.
 Это дает Софии шанс сорвать кусочек гриба!
Это дает Софии шанс сорвать кусочек гриба!Сообщить об ошибке
Сара, Митч и Бен идут на концерт. Если они сидят в ряд, какая доля представляет вероятность того, что Сара будет сидеть в середине ряда?
Возможные ответы:
Правильный ответ:
Объяснение:
Общее количество возможных расположений трех элементов подряд равно или .
Мы можем выписать все возможные расстановки и сосчитать число, в котором Сара сидит посередине.
1)
2)
3)
4)
5)
6)
Сара сидит посередине. Выраженное в виде дроби, это , что эквивалентно .
Сообщить об ошибке
У Шеннон есть коробка с 9 рубашками внутри. 4 рубашки розовые, 3 рубашки желтые, 1 рубашка красная и 1 рубашка зеленая. Какова вероятность того, что Шеннон наугад выберет из коробки розовую рубашку?
Возможных ответов:
Правильный ответ:
Объяснение:
Чтобы найти вероятность того, что из коробки будет вынута розовая рубашка, нам нужно составить дробь: .
 Задача говорит нам, что у Шеннона 4 розовых рубашки, поэтому мы можем поставить их на вершину дроби. Общее количество рубашек равно 9, что идет на дно дроби. Это дает Шеннон шанс выбрать розовую рубашку из коробки!
Задача говорит нам, что у Шеннона 4 розовых рубашки, поэтому мы можем поставить их на вершину дроби. Общее количество рубашек равно 9, что идет на дно дроби. Это дает Шеннон шанс выбрать розовую рубашку из коробки!Сообщить об ошибке
Такер собирается порыбачить в местном пруду с 15 рыбами. 5 рыб — тунец, 4 — лосось, 3 — желтохвост и 3 — форель. Какова вероятность того, что первой пойманной Такером рыбой будет тунец или форель?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти вероятность того, что Такер поймает тунца или форель, нам нужно составить такую дробь: . Задача говорит нам, что в пруду 5 тунцов и 3 форели, поэтому мы можем положить 8 на вершину дроби. Общее количество рыб в пруду равно 15, так что фракция идет на дно. Это дает Такеру 8/15 шанс поймать тунца или форель!
Сообщить об ошибке
← Назад 1 2 3 4 Далее →
Уведомление об авторских правах
Все математические ресурсы начального уровня SSAT
12 диагностических тестов 526 практических тестов Вопрос дня Карточки Learn by Concept
Управление институциональной эффективности Результаты обучения учащихся — начальное образование
Управление институциональной эффективности Тринити-колледжа Флориды (TCF) поддерживает миссию, ценности и основные обязательства, проводя институциональные исследования и лидерство в области аккредитации и оценки .
 Тринити-колледж Флориды измеряет и сообщает о результатах академического, профессионального и духовного опыта студентов. Ниже перечислены результаты обучения учащихся, процент удержания, процент выпускников, размер когорты (данные о зачислении) и трудоустройство выпускников по профессиям, связанным с программой (включая академические результаты).
Тринити-колледж Флориды измеряет и сообщает о результатах академического, профессионального и духовного опыта студентов. Ниже перечислены результаты обучения учащихся, процент удержания, процент выпускников, размер когорты (данные о зачислении) и трудоустройство выпускников по профессиям, связанным с программой (включая академические результаты).Цели Департамента начального образования:
Базовые академические знания по истории и философии образования как в христианских, так и в государственных школах, включая способность сравнивать и противопоставлять эти соответствующие философии.
Владение различными техниками, методами и стратегиями, необходимыми для того, чтобы быть эффективным учителем.
Понимание и владение профессиональной терминологией, педагогикой и этикой, необходимые для эффективного преподавания как в христианских, так и в государственных школах.
Пять заданий из пяти классов начального образования, которые соответствуют этим целям.
Стажировка на местах – ELED 3091 – Учащиеся должны посмотреть серию видео ACSI и выбрать, какие книги ACSI они будут читать, и разработать свою собственную 4-6-страничную личную философию образования для сертификации ACSI. Учащиеся этого класса готовятся к своей последней стажировке, но у них было достаточно времени, чтобы подумать о своей философии образования с момента их первого урока «Введение в образование» и на протяжении всех других учебных занятий. Сейчас их путь в колледж подходит к концу, и этот полевой опыт проходит в местной христианской школе. Студентам дается базовый план статьи, и они могут свободно говорить то, во что они действительно верят. Это одно из кульминационных заданий для основного образования. У нас 100% участие со средней оценкой 93%. Студенты в этот момент обычно имеют некоторые сильные чувства по поводу того, во что они верят, и способны хорошо сформулировать свою личную философию. (Цели отдела 1,2,3)
Методы преподавания словесности-EDE1228 – Учащиеся должны создать учебный центр, чтобы их учащиеся могли самостоятельно работать над навыками по разделу, который учащиеся изучают в классе.
 Это способствует более практическим навыкам, открытиям и навыкам независимого мышления для своих учеников. Это также помогает нашим учащимся понять, что они могут создавать и персонализировать материалы для работы в своих классах, чтобы удовлетворить уникальные потребности своих учеников. (Цели отдела 2, 3) Показатель завершения обучения составил 100 %, в среднем 93%. Студенты создали отличные учебные центры, которые можно было сразу же использовать в профессиональной среде.
Это способствует более практическим навыкам, открытиям и навыкам независимого мышления для своих учеников. Это также помогает нашим учащимся понять, что они могут создавать и персонализировать материалы для работы в своих классах, чтобы удовлетворить уникальные потребности своих учеников. (Цели отдела 2, 3) Показатель завершения обучения составил 100 %, в среднем 93%. Студенты создали отличные учебные центры, которые можно было сразу же использовать в профессиональной среде.Философия Образование – ELED1302 – Учащиеся должны подумать о своей собственной философии дисциплины в классе и создать свой собственный проект Плана управления классом. Это требует, чтобы они приняли решение о своих правилах в классе для своих учеников и разработали план, чтобы отслеживать поведение своих учеников и мотивировать своих учеников соблюдать правила в классе. Они объяснят причины введения правил и покажут, как их план управления классом для отдельных учащихся будет работать в их классе.
 Они будут поощрять и дисциплинировать поведение учеников, а также создавать мотивационное вознаграждение для всего класса, если все будут выполнять задание. Наши студенты представляют свой план управления классом нашему классу колледжа и другим студентам, а профессору разрешается задавать вопросы, критиковать и обсуждать, как их планы управления классом будут эффективно работать, чтобы поддерживать порядок и дисциплину в классе, чтобы максимизировать обучение студентов. Это также очень философски, потому что учащиеся должны понимать, что разные философии образования имеют разные философии дисциплины. Мы исследуем библейское мировоззрение о причине обучения детей дисциплине и о том, как это должно быть достигнуто в христианской и светской образовательной среде. (Цели отдела 1, 2, 3) 100 % выполнения со средним баллом 9.5%, с отличными и профессиональными планами управления классом, демонстрируемыми и обсуждаемыми.
Они будут поощрять и дисциплинировать поведение учеников, а также создавать мотивационное вознаграждение для всего класса, если все будут выполнять задание. Наши студенты представляют свой план управления классом нашему классу колледжа и другим студентам, а профессору разрешается задавать вопросы, критиковать и обсуждать, как их планы управления классом будут эффективно работать, чтобы поддерживать порядок и дисциплину в классе, чтобы максимизировать обучение студентов. Это также очень философски, потому что учащиеся должны понимать, что разные философии образования имеют разные философии дисциплины. Мы исследуем библейское мировоззрение о причине обучения детей дисциплине и о том, как это должно быть достигнуто в христианской и светской образовательной среде. (Цели отдела 1, 2, 3) 100 % выполнения со средним баллом 9.5%, с отличными и профессиональными планами управления классом, демонстрируемыми и обсуждаемыми.Методы преподавания естественных наук, здоровья и безопасности — EDE4317 — промежуточные классы 3–6, план урока и презентация в классе.
 Учащиеся должны разработать план урока естественных наук, который является практическим и включает в себя различные методы и стратегии, обсуждаемые в классе и в их учебнике, и преподать свой урок нашему классу, как мы притворяемся учениками 3-6 классов. После того, как они закончат преподавать в нашем классе, мы обсудим и проанализируем урок, где ученики нашего класса обсуждают, что им понравилось в уроке и как, по их мнению, он мог бы быть еще лучше. Учащиеся высказывают свои критические замечания обучающему студенту, чтобы этот студент мог их просмотреть позже. Наша цель состоит в том, чтобы совершенствоваться и учиться друг у друга, участвуя в различных уроках и критических анализах, которые помогают учащимся научиться принимать конструктивную критику от других учащихся и с которой они должны чувствовать себя комфортно, когда им приходится работать с контролирующими учителями и администрации в будущем. (Цели отдела 2,3) У нас было 100 % учащихся со средним баллом 9.6%. Они добились больших успехов в планировании и проведении уроков.
Учащиеся должны разработать план урока естественных наук, который является практическим и включает в себя различные методы и стратегии, обсуждаемые в классе и в их учебнике, и преподать свой урок нашему классу, как мы притворяемся учениками 3-6 классов. После того, как они закончат преподавать в нашем классе, мы обсудим и проанализируем урок, где ученики нашего класса обсуждают, что им понравилось в уроке и как, по их мнению, он мог бы быть еще лучше. Учащиеся высказывают свои критические замечания обучающему студенту, чтобы этот студент мог их просмотреть позже. Наша цель состоит в том, чтобы совершенствоваться и учиться друг у друга, участвуя в различных уроках и критических анализах, которые помогают учащимся научиться принимать конструктивную критику от других учащихся и с которой они должны чувствовать себя комфортно, когда им приходится работать с контролирующими учителями и администрации в будущем. (Цели отдела 2,3) У нас было 100 % учащихся со средним баллом 9.6%. Они добились больших успехов в планировании и проведении уроков.
Методы обучения Чтение – EDE3318 Чтение под руководством Промежуточный план урока Задание – Каждый учащийся должен был преподавать группе чтения под руководством Луи Лоури. Каждому учащемуся дается глава для преподавания, и они должны разработать все вопросы, используя четыре уровня вопросов, и направлять чтение главы и все обсуждение главы с профессионализмом. Это делается для того, чтобы подготовить их к обучению в группах чтения среднего уровня и вести все обсуждения, чтобы убедиться, что учащиеся понимают то, что они прочитали, развить навыки понимания и увлечь учащихся книгой, которую они читают. Это также учит наших специальностей начального образования диагностировать потребности учащихся и тех, кому может потребоваться дополнительная помощь или исправление. Это подготавливает студентов к обучению групп чтения под руководством в своих будущих классах и к стажировке. (Цели отдела 2, 3) У нас было 100 % учащихся, завершивших обучение, со средним баллом 9.
 5%. Это был большой успех наших студентов в обучении управляемому чтению.
5%. Это был большой успех наших студентов в обучении управляемому чтению.Отношения между учителем и детьми в раннем возрасте и траектория школьных достижений детей до восьмого класса на JSTOR
журнальная статья
Ранние отношения учитель-ребенок и траектория школьных достижений детей до восьмого классаБриджит К. Хамре и Роберт К. Пьянта
Развитие ребенка
Том. 72, № 2 (март — апрель 2001 г.), стр. 625-638 (14 страниц)
Опубликовано: Wiley
https://www.jstor.org/stable/1132418
Читать и скачивать
Войти через школу или библиотеку
Альтернативные варианты доступа
Для независимых исследователей
Читать онлайн
Читать 100 статей в месяц бесплатно
Подписка на JPASS
Неограниченное чтение + 10 загрузок
Товар для покупки
34,00 $ — Скачать сейчас и позже
Чтение онлайн (бесплатно) основано на сканировании страниц, которое в настоящее время недоступно для программ чтения с экрана. Чтобы получить доступ к этой статье, обратитесь в службу поддержки пользователей JSTOR. Мы предоставим копию в формате PDF для программы чтения с экрана.
Чтобы получить доступ к этой статье, обратитесь в службу поддержки пользователей JSTOR. Мы предоставим копию в формате PDF для программы чтения с экрана.С помощью личного кабинета вы можете читать до 100 статей каждый месяц за бесплатно .
НачатьУже есть учетная запись? Войти
Ежемесячный план- Доступ ко всему в коллекции JPASS
- Читать полный текст каждой статьи
- Загрузите до 10 статей в формате PDF, чтобы сохранить их
- Доступ ко всему в коллекции JPASS
- Читать полный текст каждой статьи
- Загрузите до 120 статей в формате PDF, чтобы сохранить и сохранить
Купить PDF-файл
Купите эту статью за 34,00 долларов США.
Как это работает?
- Выберите покупку
вариант.

- Оплатить с помощью кредитной карты или банковского счета с PayPal.
- Прочитайте свою статью в Интернете и загрузите PDF-файл из своей электронной почты или своей учетной записи.
Предварительный просмотр
Предварительный просмотр
AbstractВ этом исследовании приняли участие 179 детей от детского сада до восьмого класса, чтобы изучить степень, в которой восприятие воспитателями детских садов своих отношений с учениками предсказывает диапазон школьных результатов. Воспитатели детских садов оценивали поведение детей и качество взаимоотношений педагог-ребенок. Последующие данные с первого по восьмой классы были организованы по эпохам и включали академические оценки, результаты стандартизированных тестов, рейтинги рабочих привычек и записи о дисциплине. Реляционная негативность в детском саду, отмеченная конфликтами и зависимостью, была связана с академическими и поведенческими результатами вплоть до восьмого класса, особенно у детей с высоким уровнем поведенческих проблем в детском саду и у мальчиков в целом.
Информация о журнале Эти ассоциации оставались значимыми после учета пола, этнической принадлежности, когнитивных способностей и оценок поведения. Результаты имеют значение для теорий детерминант успеха в школе, роли отношений между взрослыми и детьми в развитии, а также ряда мер раннего вмешательства и профилактики.
Эти ассоциации оставались значимыми после учета пола, этнической принадлежности, когнитивных способностей и оценок поведения. Результаты имеют значение для теорий детерминант успеха в школе, роли отношений между взрослыми и детьми в развитии, а также ряда мер раннего вмешательства и профилактики.Как флагманский журнал Общества исследований в области развития ребенка, развитие ребенка публикует статьи, эссе, обзоры и учебные пособия по различным темам в области детского развития с 1930 года. Охватывая многие дисциплины, журнал предоставляет последние исследований не только для исследователей и теоретиков, но и для детских психиатров, клинических психологов, психиатрических социальных работников, специалистов по дошкольному воспитанию, педагогов-психологов, педагогов специального образования и других исследователей.
Информация об издателеWiley — глобальный поставщик контента и решений для рабочих процессов на основе контента в областях научных, технических, медицинских и научных исследований; профессиональное развитие; и образование.
 Наши основные виды деятельности выпускают научные, технические, медицинские и научные журналы, справочники, книги, услуги баз данных и рекламу; профессиональные книги, продукты по подписке, услуги по сертификации и обучению, а также онлайн-приложения; а также образовательный контент и услуги, включая интегрированные онлайн-ресурсы для преподавания и обучения для студентов, аспирантов и учащихся на протяжении всей жизни. Компания John Wiley & Sons, Inc., основанная в 1807 году, уже более 200 лет является ценным источником информации и понимания, помогая людям во всем мире удовлетворять свои потребности и воплощать в жизнь свои стремления. Wiley опубликовал работы более 450 нобелевских лауреатов во всех категориях: литература, экономика, физиология и медицина, физика, химия и мир.
Wiley сотрудничает со многими ведущими мировыми обществами и ежегодно публикует более 1500 рецензируемых журналов и более 1500 новых книг в печатном и онлайн-формате, а также базы данных, основные справочные работы и лабораторные протоколы по предметам STMS.
Наши основные виды деятельности выпускают научные, технические, медицинские и научные журналы, справочники, книги, услуги баз данных и рекламу; профессиональные книги, продукты по подписке, услуги по сертификации и обучению, а также онлайн-приложения; а также образовательный контент и услуги, включая интегрированные онлайн-ресурсы для преподавания и обучения для студентов, аспирантов и учащихся на протяжении всей жизни. Компания John Wiley & Sons, Inc., основанная в 1807 году, уже более 200 лет является ценным источником информации и понимания, помогая людям во всем мире удовлетворять свои потребности и воплощать в жизнь свои стремления. Wiley опубликовал работы более 450 нобелевских лауреатов во всех категориях: литература, экономика, физиология и медицина, физика, химия и мир.
Wiley сотрудничает со многими ведущими мировыми обществами и ежегодно публикует более 1500 рецензируемых журналов и более 1500 новых книг в печатном и онлайн-формате, а также базы данных, основные справочные работы и лабораторные протоколы по предметам STMS.

 Обозначается пространство элементарных исходов обычно так:
а сам элементарный исход так
Можно записать отношение между пространством элементарных исходов и элементарными исходами так
Обозначается пространство элементарных исходов обычно так:
а сам элементарный исход так
Можно записать отношение между пространством элементарных исходов и элементарными исходами так
 Например, при бросании двух костей элементарный исход имеет размерность 2 и каждая координата 6 значений. При одновременном бросании монеты и кости вектор имеет размерность 2, первая координата 2 значения, вторая – 6 (или наоборот). Если бросаем 10 монет, то в качестве пространства элементарных исходов можно взять множество различных двоичных векторов размерности 10 из нулей и единиц.
Например, при бросании двух костей элементарный исход имеет размерность 2 и каждая координата 6 значений. При одновременном бросании монеты и кости вектор имеет размерность 2, первая координата 2 значения, вторая – 6 (или наоборот). Если бросаем 10 монет, то в качестве пространства элементарных исходов можно взять множество различных двоичных векторов размерности 10 из нулей и единиц. В дальнейшем подмножества пространства элементарных исходов будем обозначать большими латинскими буквами A, B, C…
В дальнейшем подмножества пространства элементарных исходов будем обозначать большими латинскими буквами A, B, C… Т.е. A в опыте не произошло («не наступило»).
Т.е. A в опыте не произошло («не наступило»). ..
..